Using Fuzzy Modeling, to Study Flood Routing in Natural Rivers.
Patrícia Chagas1- and Raimundo Souza1
1
Department of Hydraulics and Environmental Engineering Center of Technology – Federal University of Ceara
Campus do Pici, P. O. Box 6018 60451 - 970, Fortaleza Ceará-Brazil Emails: pfchagas@yahoo.com; rsouza@ufc.br
Abstract
The Saint Venant’s equations have been applied to study flood routing in natural rivers. However, considering that such models are deterministic, there are difficulties in finding ways to work with the inherent uncertainties in flood routing. To resolve that inconvenience, this research applies fuzzy set theory, on the hydrodynamics modeling, to figure out uncertainties, present in the flood routing. To do so, a set of membership functions was defined representing hydraulics and hydrologic parameters. In this way, the hydrodynamics model can be solved, yielding a membership function that represents the flow field in a river. The results show that fuzzy theory could be a very useful methodology to evaluate uncertainties, and predict engineering risk analysis concerning with flood routing processes in rivers.
Introduction
The Saint-Venant’s equations are used to describe problems of waves propagation of floods in open channels. This is a physical process of high complexity, caused by an intense rain or a dam breaking, which represents an interesting problem to be studied.
The solution of this class of problem passes, invariably, for the development of methods that allow a solution of these equations. These, non-linear, equations contain, in its mathematical representation, all of the elements that, direct or indirectly, play an important relationship in the flow processes of the channel. These equations can be used to determine all the hydrodynamics of a river. It is enough that, the function must be modeled appropriately. Evidently, the modeling of such functions implies in more efforts in the process of solution of the equations.
This work develops a hydrodynamic fuzzy model to simulate the propagation of a flood wave, and trying to find out the capacity of the fuzzy number theory to measure uncertainty. The model solves the Saint-Venant’s fuzzy equations using the explicit outline of the method of the finite differences, with discretization proposed by Chow (1988). In the numeric solution of the differential equations of the dynamic wave, it will be considered the rectangular channel, with constant width.
Hydrodynamic Model
The dynamic modeling of the flow in river is obtained through the numeric solution of the acquaintances equations of Saint-Venant. Those two equations, the continuity and the momentum, are described in this way (Keskin and Agiralioglu, 1997):
Continuity Equation, 0 = + t A x Q (1) Momentum Equation
(
)
0 ) ( / 0 2 = + ++ S gASf
x y gA x A Q t Q (2) Where,
x is the longitudinal distance along the channel (m), t is the time (s),
A is the area of the traverse section of the channel (m2),
y is the level of the surface of the water of the channel (m), S0 is the slope of the bed channel,
Sf is the slope of energy grade line;
B is the width of the channel (m); and
g is the acceleration of the gravity (m/s2).
Fuzzy Set Theory
Fuzzy set theory is a mathematical method used to characterized and quantify uncertainty and imprecision in functional relationships. This theory is very important in situation that the number of data is not sufficient to characterize uncertainty, by means and statistical measures, involving estimation of frequency (Ganoulis, 1994).
The central concepts of fuzzy set theory are the membership function, which represents, numerically, the degree by which an element belongs to a set.
A pair of equation defined into some interval can represent a membership function. For example a membership function of a fuzzy number may be described mathematically by means of two strict functions L and R defined by
) ( ) ( 1 x x x L x m x =
µ x<xm; x1>0 (3)
) ( ) ( 2 x x x R x m x =
µ x>xm; x2>0 (4)
Where,
xm is the value of x that makes µx(x) =1;
x1 is the lower limit to the interval of confidence;
x2 is the upper limit to the interval o f confidence;
µx(x) is the membership function.
The principal characteristic of the membership function is that its values range in the interval [0,1]. Another important fact is that the membership function represents, within this interval, the degree of confidence that one should have for a particular value of a fuzzy number (Kaufmann and Gupta, 1991). Thus, in general, it can be concluded that fuzzy numbers are equivalent to random variables, with membership function corresponding to probability density functions. A complete review of the fuzzy set theory was presented by Dou at al. (1997).
Application to the Hydrodynamic System
To develop a fuzzy model for the transport equation, it is necessary to define several parameters in the hydrodynamic equations as fuzzy functions. The boundary conditions and the initial conditions were defined as fuzzy numbers, such that
Q(0,t)=[qL; qM; qU], where qL and qu represent the 0 levels of confidence, and qm
represents the 1 level of confidence, while Q(x,0)=[qiL; qiM; qiU], qi represents a triangular membership function. Thus, the hydrodynamic model can be written, in its fuzzy form as
Continuity Equation
0 ~ ~
= +
x Q t A
(5)
Momentum Equation
(
~ ~)
0 ~~ ~
~ 1 ~
~ 1
0 2
= +
+ g S Sf
x y g A Q x A t Q
A (6)
Where,
A~ is the membership function for the cross sectional area;
Q~ is the membership function for the flow;
y
~ is the membership function for the depth;
0 ~
S is the membership function for the bed slope;
f
S~ is the membership function for the friction slope.
The solution of this pair of equations allows determining the dependent variables, as membership functions. These functions are calculated along the river, for different
time. Like this, the hydrodynamic fuzzy equation will produce a fuzzy flow field with its membership function calculated by the solution of the fuzzy model.
Results
With the objective of getting a better analysis of the application of the fuzzy theory on the hydrodynamic model, a simulation was done. In this simulation, the boundary and initial conditions were defined as fuzzy numbers. Therefore, the boundary
conditions was defined as Q(0,t)=[qL;qM;qU], where qL=0.25*qM; qU=1.25*qM. The
initial conditions was defined as Q(x,0)=[qL;qM;qU], where qL=0.5*qM; qU=1.5*qM. With respect to the hydraulics parameters, it was considered the bed slope equal to 0.0004 and for Manning’s resistance coefficient, it was considered equal to 0.01. The channel was considered rectangular with width equal to 50 m. The flow was
considered 50 m3/s.
0 0,25 0,5 0,75 1
0 100 200 300
Q (m 3/s)
M
e
m
be
rs
hi
p
x=10km
Figure 1. Membership function of the flow at 10 km from the origin.
Figure 1 shows the results obtained for the solution of the fuzzy model considering the channel was 50 m wide, for a section 10 km from the origin. The figure indicates
that the fuzzy flow ranges from 80 m3/s to 240 m3/s with the value of the highest
confidence at 160 m3/s.
0 0,25 0,5 0,75 1
0 50 100 150 200 250
Q (m 3/s)
M
e
m
be
rs
hi
p
x=20km
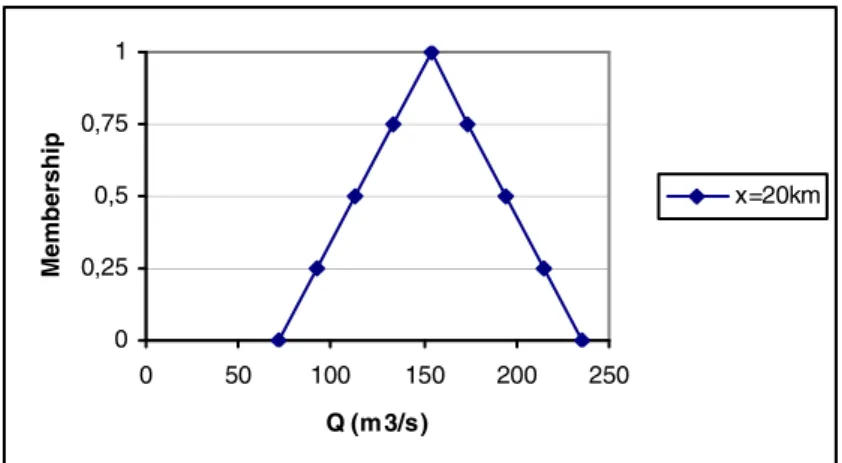
Figure 2. Membership function of the flow at 20 km from the origin.
Figure 2 shows the membership function for the fuzzy flow number, considering a section 20 km from the origin. At this section, the lower and upper flow values were
72 m3/s and 235 m3/s, respectively, while the high level of confidence was 150
m3/s. Both memberships were considered at a time of 6 h after the beginning of
observation. Through the figures one can see that, for each section, and each time, there is a dynamic membership function defining the condition of flow rate, with a different distribution level of confidence. This implies that the membership function for the flow is a function that depends on the all conditions, hydrological and hydraulics, of the river.
0 50 100 150 200 250
0 3 6 9 12
Tim e (h)
Q
(
m
3
/s
) Qu
Qm QL
Figure 3. Flood wave propagation for different levels of confidence.
Figure 3 shows the evolution of the membership function of the flow, at a section 20
km from the origin. In this case, QL, and Qu represent the 0 level of confidence while
Qm represents the 1 level of confidence. Through the figure, one can see that only after 10 hours the flood wave is reaching the section. In other words, the fuzzy model is able to give a solution to fuzzy flow function for all sections of the channel at all times. This permits to say that the transformation of a deterministic differential
equation, to a fuzzy differential equation can be done, without any loss of generality. These results permit one to conclude that the fuzzy theory could be a very good way to measure uncertainty and could be a useful way to work with engineering risk analysis.
Conclusion
After the analysis of the results, obtained by the simulation of model, through a computational program, developed for this research, one can conclude that the fuzzy theory is a new, but important, way to study hydraulic and hydrology model, considering uncertainties. In this study, the fuzzy number has been applied to solve the hydrodynamic equations, and it has shown to be a very good way to solve the flow field, along of the channel, in fuzzy number form. Therefore, this methodology appears as an alternative, considering the stochastic differential equations, to analyze engineering risk analysis in Water Resources field.
References
Chow, V. T. (1988). “ Applied Hydrology.” New York: McGraw-Hill, 572p.
Dou, C.; Woldt, W.; Bogardi, I.; Dahab, M. (1997). “Numerical solute transport
simulation using fuzzy sets approach.” Journal of Contaminant Hydrology, n.
27, p. 107-126.
Ganoulis, J. G. (1994). “Engineering Risk Analysis of Water Pollution: Probabilities and Fuzzy sets.” VCH – Weinheim; New York; Basel; Cambridge; Tokyo. Kaufmann, A., Gupta, M. M., (1991). “Introduction to Fuzzy Arithmetic.” Van
Nostrand Reinhold, New York.
Keskin, M. E. and Agiralioglu, N. (1997). “A Simplified Dynamic Model for Flood
Routing in Rectangular Channels.” Journal of Hydrology, 202, p. 302-314.