Vórtices em ModelosSigma O acoplados NãoMinimamente num Background Gravitacional

Vórties em Modelos

σ

O

(3)

Aoplados

não-Minimamente e num Bakground Gravitaional.

Pablo Rodrigo Alvesde Souza

UNIVERSIDADE FEDERAL DO CEARÁ

Vórties em Modelos

σ

O

(3)

Aoplados não-Minimamente e num Bakground Gravitaional.

Pablo Rodrigo Alvesde Souza

Dissertaçãosubmetida ao Departamento de Físia

omo requisito para obtenção do grau

de mestre emFísia.

Orientador

e Luila, e a minha

linda lhinha

Agatha, que dedio

todo o esforço desta

Gostaria de agradeer ao Professor Carlos Alberto Santos de Almeida, pois

alémdeguardaremsiaguradeumorientadornageneralidadedessapalavra,

demonstrou-se uma pessoa de aráter privilegiado, inomum indulgênia e extremamente paiente

para om nossas faltase equívoos.

Aosmeuspais,poissemseusesforçosnadadissoteriasidosequerpossívelogitar-se

tempoalgum.

AmeusamigosdeMatoGrossoqueaquimereeberamprontamente, eespeialmente

aminhasuperamigaEuzenil,pois,não fossesuaguarida,minhaaomodaçãonaidade

de Fortaleza teria sido muito mais difíil.

A minha amiga Luiana, do grupode teoria de ampo, que meofereeu sua

presti-mosa ajuda no momento de minha defesa e posterior à ela na organização do material

digitado. Obrigado Luiana.

Ao professor Marony S. C., pelas suas valiosíssimasonversas e insightssobre o

tema.

A todos osamigos do sem dúvidanobilíssimo grupo de Teoria Quântia de

Camposda UFC. Avoês, meusamigos,exorodesulpassemansarpornãoitaraqui

nenhum nome para que assim deixe de ser injusto om algum que seja. Desulpem-me,

mas obrigado!

Ao professor Soares, oordenador dourso de pósgraduação.

Aos prestimosos e eduados funionários do departamento de físia.

A CAPES, por onsignar-metodo oapoio naneiro.

Para abreviar gostariamos de dizer que, talvez ainda mais que nosso trabalho emsi,

queporelemesmojádeixa-nosbastantefelizeseanimados,hajasidoagrandeexperiênia

Então, sem onseguir segurar as lágrimas, não posso deixar de expressar a imensa

dívidade gratidãoque arregarei para om todos. Tantosaos queem mimdepositaram

sua valiosíssimaonança, quantoaos quenenhuma quiseramdar rédito.

Senhoras eSenhores

Consideramos neste trabalho o modelo Maxwell-Chern-Simons-HiggsAbeliano

σ

O(3)

não-linear om momento de dipolo magnétio anmalo e imerso num bakground

grav-itaional de métria onforme. Usamos o método de Bogomol'nyi para obtenção das

equações auto-duais do sistema. Com a esolha adequada para se ompletar

quadra-dos no funional de energia veriamos ser possível obter-se equações auto-duais sem

a neessidade de se levar em onta um ampo auxiliar. Por outro lado, a erta

gener-aliedade do método possibilita que isso seja feito, ofereendo equações om tal ampo

auxiliar,mostrandouma grandesimilaridadeom asequaçõesparaoaso deum modelo

de dinâmiadupla (Maxwelle Chern-Simons) num bakground minkowskiano, disutido

We onsider in this work the

σ

O

(3)

Maxwell-Chern-Simons-Higgs Abelian Model with magnet dipole moment immersed in a gravitational bakground. We used

Bogo-mol'nyimethod for the get autoduals equations of the system. Withappropriate hoie

for the whether omplete square inenergy funtionalwe verify to bepossibleobtain

au-todual equations withoutneessity totake in onsiderationan aideld. The other side,

the rightgeneralityofthe methodpossibilitatethat itbemade,oeringautoduals

equa-tions with aideld,showing agrate similaritywith aequations forthe ase of the doble

dinamimodel(MaxwellandChern-Simons) anagravitationalbakground,disussedin

Agradeimentos . . . i

Resumo . . . iii

Abstrat . . . iv

Índie . . . iv

Introdução 1 1 Quebra Espontânea de Simetria 6 1.1 SimetriaseAssimetrias . . . 7

1.2 QuebraEspontânea deSimetrianaMateriaCondensada: OsF erromagne-tosde Ising . . . 13

1.3 OModelo de Ising esua versão Clássia de Campo . . . 18

1.4 Grupos de Simetriae os Multipletosde Partíulas . . . 21

1.5 Quebras de Simetria emTeorias de Campo . . . 24

1.5.1 Quebra Espontânea de Simetriae oSurgimento de Partíulas V e-toriais sem Massa: OsBósons de Goldstone . . . 24

1.6 OMeanismode Higgse a geraçãode Massa para Campos de Calibre . . 30

2 Sólitons 36 2.1 Coneitos eDenições . . . 37

dade . . . 44

2.4 Vorties num Modelo Relativístio. . . 48

2.5 Obtenção das Equaçõesde Movimento eo Métodode Bogamol'nyi. . . . 50

3 Soluções de Vórties om Aoplamento Mínimo 57 3.1 SimetriaAbeliana Loal ea EDQ . . . 58

3.2 Divergênia daLinha de Vórtie ea Emergêna daDerivada Covariante. 68 3.3 Soluções de Vórties naEletrodinâmiaMaxwelliana . . . 69

3.4 A lagrangeanade Chern-Simons e Sua Soluçãode Vórtie . . . 78

3.5 Soluções de Vortiesno Modelo Maxwell-Chern-Simons . . . 85

4 Soluções de Vórties em Aoplamento não-Mínimo 91 4.1 OTermo de Pauliou Momento de DipoloMagnétioAnmalo MDMA . 92 4.2 SistemaMaxwell-Higgs om MDMA. . . 95

4.3 Modelo Maxwell-Chern-Simons-Higgsom MDMA. . . 99

5 Vórties Abelianos num Bakground Gravitaional 102 5.1 PanoramaRelativístio . . . 103

5.2 A ConexãoGravitaional . . . 107

5.3 Métrias . . . 108

5.4 Teoria Quântia de Campo emum Espaço-Tempo Geral . . . 114

5.5 Modelo Maxwell-Higgs-AbelianoGravitaional . . . 117

5.6 ModeloMaxwell-HiggsAbelianonumBakgroundGravitaionalMétria Isotrópia . . . 118

ional: Métria estaionária . . . 126

6 Soluções Solitnia Abelianas via Modelo

σ

-O

(N

)

não-Linear 133 6.1 OModelo Abeliano

σ

-O(

N

)não Linear om AoplamentoMínimo . . . . 134

6.2 SimetriaLoalU

(1)

noModelo

σ

-O

(3)

. . . 137 6.3 SistemaMaxwell-Higgs Abeliano

σ

-O

(3)

om Aoplamento Mínimo . . . 141 6.4 SistemaChern-Simons-Higgs Abeliano

σ

-O

(3)

om AoplamentoMínimo 144 6.5 SistemaMaxwell-Chern-Simons-HiggsAbeliano

σ

-O

(3)

omAoplamento

não-Mínimo . . . 147

7 Modelo Maxwell-Chern-Simons-Higgs

σ

O

(3)

não-Linear om MDMA

num Bakground Gravitaional 151

7.1 ModelodeMaxwell-Chern-Simons-HiggsAbeliano

σ

-O

(3)

não-Linearnum Bakground Gravitaionalom Métria Conforme de simetriaCilíndria. 152

A Cálulo do Tensor Momentum-Energia 161

1-1 Sequêniade ongurações domodelode Isingpara quatro temperaturas

difer-entes. Osspinsnoestado+1estãorepresentadosabranoeosspinsnoestado-1

apreto. A baixastemperaturas, é visivela ordem. Notea desordemprovoada

por onta da ompetição entrea energia magnétia ea energia térmia. . . . 14

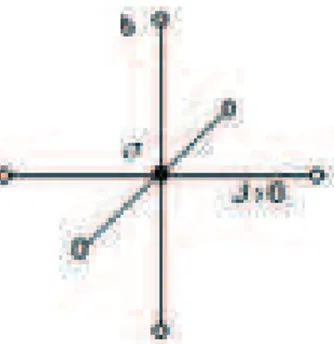
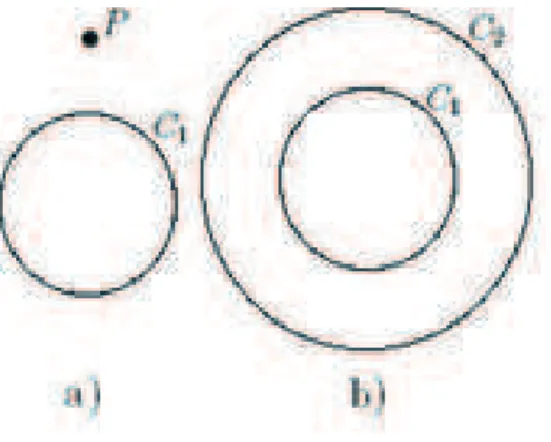
1-2 Aglomerado ferromagnétio ontendo um spin entral e quatro vizinhos mais

próximos.

J >

0

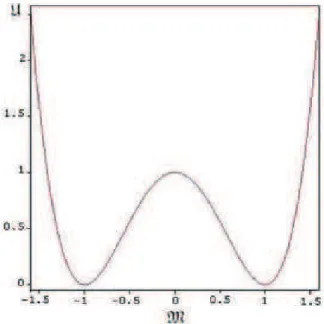
garante o ordenamento ferromagnétio. . . 15

1-3 Potenial

U

e seusmínimosrelativos

M

0

=

±

1

(admensional). . . 20

1-4 Aima temos

I

= +1

/

2

,

−

1

/

2

gerandoosdois estadospossíveis parao nuleon,

osestadosdeprótone denêutron,nahamadasimetria

SU

(2)

. Embaixo temos

I

= +1

,

0

,

₋

1

,forneendo o tripletode mésons

π

+

,

π

0

e

π

−

. . . 22

1-5 Na primeira oluna de diagramas: poteniais tipo

λ

2

_φ

4

_/

_2!

e

λ

2

₍

_φ

2

₋

_n

2

₎

2

_/

_2!

,

respetivamente. Segunda oluna de diagramas: urvas de níveis no plano

(

φ

1

, φ

2

)

de suas versões tridimensionais. Tereira oluna de diagramas:

fun-ionais

U

(

φ

1

, φ

2

)

paraada umdesses poteniais. É mostradotambém os

mín-imosrelativosparao asodopotenial deHiggs. . . 27

2-1 Kinke anti-kingom energia nitaebem loalizadaentre os extremos

(

±

η

=

±

1)

do potenial. . . 38

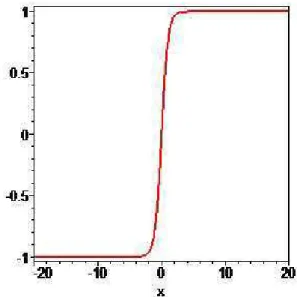
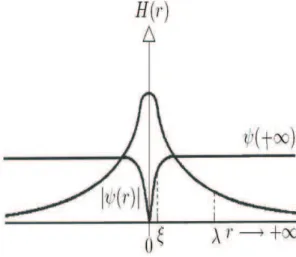
ritmiamente amedidaqueeleseaproximadopontoondeoampofoiapliado.

Dentrodomaterialtemosuma

ψ

que depende daposiçãoeforadaentidadeela

tende para seu valor mínimo, o valor esperado da função no estado do váuo,

quando

r

−→ ∞

. . . 48

3-1 Mapeamentodo vetor

φ

numírulode raio unitário. . . 60

3-2 Potenial

U

om doismínimosem

η

=

±

1

e ummáximo relativo em

φ

(

o

)

.. . . 77

3-3 Potenial topológio

U

de sexta ordem do modelo de Chern-Simons. A gura

mostraseus mínimosem

±

1

e

0

,e doismáximo relativo em

±

0

.

65

. . . 85

3-4 Potenial

U

do modelo Maxwell-Chern-Simons-Higgs. A gura mostra valores

para os quais

|

η

|

= 1

. O aráter topológio é reuperado apenas no aso de

vórtiedesarregado (

Φ = 0

), ouquando elimina-se aontribuiçaõ do termo de

Chern-Simons fazendo

k

→

0

. . . 90

4-1 Efeitodo MDMAnopotenial

U

. Asurvas1,2e3 foram plotadasomosvalores

de 0.0,0.1 e0.3para otermo

γ

2

_/

₂

respetivamente.. . . 99

5-1 Agrandes deistâniasda fonteamétriasimplia-separa sua forma isotrópia. . 119

6-1 Potenial de Higgsdo modeloMaxwell

σ

-O(

3

) om aoplamento mínimo. Aqui

zemos

e

2

_/

_{2 = 1}

e

|

n

b

|

= 1

. . . 143

6-2 Potenial U om suas duas ondições de mínimo: quando

φ

tende

assintótia-mente para

±

n

b

em

x

→ ±∞

. Observe omo o primeiro fator em olhetes de

(6.51) "puxa"o máximo paramaispróximoda região onde

φ

é negativo, dando

V órties são entidades que foram primeiramente observados na matéria ondensada,

nodomíniodosmateriaissuperondutoresenoonheidoefeitoHallquântiofraionário.

Aindaemmeânia, oenárioéotunelamentooorrendo ompoteniaisonstantes

uni-dimensionais. Em duas dimensões, uma importante aquisição foi a resolução exata do

modelo de Ising. Na versão para a teoria de ampos o mesmo modelo em

(2 + 1)D

foi tratado mediante o uso de um ampo esalar real na presença de um potenial que

ofereia esolha para mínimos da energia. Ou seja, um sistema om simetriaquebrada.

Foineste ontexto de transição de fases queos sólitonsonsolidadaram-seomo defeitos

topológios.

Os trabalhos pioneiros em teoria de ampo foram aqueles que tratavam de modelos

om dinâmia dada pelo termo eletromagnétio, o termo de Maxwell. Em seguida foi

a vez do modelo governado om dinâmia vinda dum termo de Chern-Simons. Todos

eles,emgeral,ompotenialquepermitiamquebra desimetria. Oshamadospoteniais

de Higgs. Naturalmente o passo seguinte foi o de se trabalhar om uma lagrangeana

ontendo ambos os termos. A araterístia de todos eles era o de se ter energia e

uxo magnétioquantizadosa nívellássio. Abrindo aminhopara modelosainda mais

generalizados, Torres e olaboradores [40℄ prinipiaram om a introdução do momento

modeloeadeMDMA. Posteriormenteobservou-seque,noâmbitode quebraespontânea

de simetria,podia-seeliminarum ououtro termo dessesdalagrangeana omnomeações

adequadas de onstantes.

Contudo, foram Cavalante, Marony e Almeida [51℄, no afã de trabalhar-se num

modelodedinâmiaduplaeomsimetriasoorrendoapenasnumplanointernoemtorno

de um tereiro eixo,que se onsolidou o modelo

σ

O

(3)

não-linearom aoplamentode MDMA numa lagrangeanado tipoMaxwell-Chern-Simons-Higgs.

Naturalmenteostrabalhosposteriores seguiram-senun ontextode ovariâniageral.

Atualmenteestuda-se todos osmodelosanterioresmasom umamétriaquenão apenas

a minkowiskiana [46℄.

Amiúde,asequaçõesdemovimentonão-linearesdesses sistemasforamatéagorabem

tratadasmedianteum engenhoso métodode redução de suas ordens;métodoesse riado

por Bogomol'nyi na déada de 60[31℄, que onseguia baixar de segunda para primeira

ordem asequaçõesdifereniais.

Para failitar a ompreensão deste trabalho, julgamos a seguinte distribuição mais

adequada, prinipalmenteàqueles de primeira viagem: No apítulo 1, preferimos

intro-duzir o tema quebra espontânea de simetria,mostrando mui qualitativamenteexemplos

vários e ulminando noimportantemeanismo de Higgs de geração de massa para

am-posde alibre. Noapítuloseguintezemosentão asneessárias onlusõesquedenem

um sóliton,e issotantono ontexto de matériaondensada quantoemteoria de ampo,

apresentando os vórties omo defeitos topológios em

(2 + 1)D

. No apítulo 3 estu-damos os prinipaissistemas solitniosplanares no aso de aoplamento mínimo para,

noapítulo seguinte, seguir-seom o aso não-mínimo. A essa altura,já sendo bastante

gravitaional diferente do minkowskiano, tanto no aso de aoplamentomínimo quanto

não-mínimo. No apítulo6 mostramos omose proedersegundo aabordagemdo

mod-elo

σ

O

(3)

não-linear. Ao nal guardamos um pequeno apêndie a respeito de omo se obter otensor de energia-momentopara um sistemaMaxwell-Chern-Simons-Higgs.

O apítulo

7

é aquele ao qual trouxemos nossa tão esperada ontribuição ao estudo dos vórties, quando alios estudamos numa versão não-mínima do modelo

σ

O

(3)

om dinâmiadupla e imersonum bakground gravitaional de métriaonforme.

Cumpre-nosapenasmaisum adendo,umasdeniçõesúteisutilizadasextensivamente

aqui: para

x

ν

_{= (x}

0

_{, x}

1

_{, x}

2

_{, x}

3

₎

_≡

_{(t, x, y, z)}

, om

c

=

~

= 1

em unidades gaussianas, seguem-se os operadores

∂

µ

=

∂/∂x

µ

, ∂

µ

=

∂/∂x

µ

;

∂

0

_≡

∂/∂t;

∂

i

_{≡ ∇}

i

.

Tém-se tambémas derivadas ovariantes mínimase não-mínimas,respetivamente

D

µ

≡

∂

µ

+

ieA

µ

;

D

µ

≡

∂

µ

+

ieA

µ

+

ieγǫ

µνβ

F

νβ

,

om

γ

a orreção de momento de dipolo magnétio anmalo (MDMA). No aso das

esalar omplexo

φ

,elas, é laro, mudam de sinal:

∇

µ

φ

= (∂

µ

−

ieA

µ

)φ;

D

µ

φ

= (∂

µ

−

ieA

µ

−

ieγǫ

µνβ

F

νβ

)φ,

om

e

a onstantede aoplamento mínimo.

No ontexto domodelo

σ

O

(3)

,todos osampossão esalaresreais. Dessaforma,as derivadasovariantes perdem sua unidade imaginária,passando paraum espaçovetorial

interno.

O tensor ompletamente anti-simétrio reebe tal denição por este troar de sinal

tantoporâmbiode índies quanto porlevantamentoe abaixamentodos mesmos:

ǫ

µν

=

₋

ǫ

νµ

,

ǫ

µν

=

₋

ǫ

µν

,

ǫ

µν

=

ǫ

νµ

.

om sua versão ovariante geraldada por

E

µν

₌

ǫ

µν

√

_g

.

O tensor intensidade de ampoé grafado omo

g

µν

=













1 0

0

0 1

0

0 0

₋

1













.

Para nalizar, os objetos sio-matemátios enontrados neste trabalho são de

na-tureza mui espeía, habitando região bém delimitada. Fazem parte desta oleção,

em espeial, lagrangeanase suas densidades. Por vezes trataremos tais objetos ora por

"lagrangeana"ora por "densidade"apenas, sem que este pequeno abuso linguístio

on-são alguma traga nos oneitos em jogo. Será o aso também dos termos "modelo"e

"teoria"que, omo sabemos da losoa do onheimento, é neessário que se faça lara

distinção, mesmo que,porvezes, issoseja impossível.

Como nosso trabalho versa sobre modelos om observáveis omutativos, estará

Quebra Espontânea de Simetria

Iniiamosnossotrabalhomedianteumabrevíssimaexposiçãoemujaqualassenta-seo

fundamentode suas idéias. E apropósitodos sólitons,veremosquetaisentidadessó

po-demexistirnoontexto dahamadaquébraespontâneadesimetria,fenmeno

matemáti-amente notado quando da inlusão na lagrangeana de poteniais a onterem mais de

um mínimo[27℄. Noque sesegue,em 1.1expusemos osprinipaisfatosqueoloarama

quebradesimetrianumlugardedestaquenafísia. Naparte1.2demosprossegimentoao

temaomumexemplobastentesimplesadvindodamatériaondensadaomoshamados

materiasferromagnétios,prosseguindoem1.3omsua naturalversãolássiade ampo

servindo omo motivação iniial aos aspétos matemátios que adiante serão relevantes

naonstruçãodateoriadossólitos,tendo omoorruptelalássia-relativístiaomodelo

kinkinio. Dando ontinuidade aos importântes desdobramentos do oneito, em 1.4

abordamosmuiqualitativamenteaquestão da"produção"de partíulasemfísiateória

ao mode de Weegner de busa das respreseentações algébrias irredutíveis. Fizemos

re-lagar somente à seção 1.5 a demosntração de que a québra espontânea de simetria está

diretamente ligada à produção de partíulas sem massa quando a simetria do modelo

é quebrada ao nível de suas soluções. A seção é nalizada em 1.6 onde tratamos do

Ab initio,qualquer que sejaomodeloproposto, deveele passarpelorivodas hamadas

transformações de simetria, omo requerimento mesmo de uma apoditiidade dos

on-eitos nele impliados. Noutros termos,já queas leis físiassão universais e neessárias

portantoapodítiassegue-se dauniversalidadeeneessidade domodeloapresentado.

A exigênia de simetria nas tranformações, sobretudo as que oorrem na estrutura do

espaço-tempo simetriasexternas são um meiopelaqualgarante-sea homogeneidade

das leis fenomênias. Numa palavra, as leis físias devem oorrer em todos os pontos do

universo (universalidade), bem omo sempre e da masma maneira (neessidade). Isso é

muito agradável, já que gostamos de existir em um universo que não ontém nenhum

tipo de anomalia emsuas leis: é óbvio quenão existem, dentro de seus limites, eessões

das leis de Newton neste universo. Nesse sentido são então as simetrias elevadas a um

status de prinípio fundamental da natureza. De maneira mais espeía, é fáil ver

isso na versão analítia da meânia lássia justamente no momento em que a ação

não muda frente a uma transformação dada. A essa invariânia de ação segue-se a tão

neessária onservação de grandezas físias, e a espeiação da grandeza onservada

momentum,momentaeenergiadependedaestruturadogrupode simetriaemquestão

translaçõesespaiais,rotaçõesdeeixosedesloamentosnotempoapliadaàação. A

própria transformação galileana é um grupo linear que deixa invariante as equações de

movimentode Newton.

Como exemplo trivial, levemos em onta a lei lássia da onservação da energia

meânia

E

f

=

E

i

, vinda da expressão

dada, por exemplo,por

x(t) =

A

sin(kx

₋

ωt),

(1.2)

permanee onstante:

E

m

=

C

(1.3)

Isso também será notado aso tenhamos um observador a olhar o mesmo pêndulo a

partirdeumsistemarotaionado,omaequaçãomultipliadaporumamatrizderotação;

ou mesmo no aso de um movimento defasado por um fator

e

iφ

, om

φ

um ângulo de

partida tipode transformaçãoque mais será usadaneste trabaho. Neste ultimoaso a

nova oordenada será esrita omo

x(t)

_→

x

′

(t) =

e

iφ

x(t).

(1.4)

É láro que aquela equação da energia permaneerá sempre a mesma, qualquer que

seja oângula

φ

E

m

→

E

m

′

=

E

m

=

C

.

(1.5)

Faxsimiliemeletromagnetísmolássio,quando opotenialémudadode umaesala

onstante

c

φ(r)

_−→

φ

′

(r) =

c

+

φ(r).

(1.6)

A não variâniadaregrade formaçãodas eqauçõesdoeletromagnetísmooorre

tam-bém noaso mais geral, quando adiiona-se àsequaçõesuma divergênia

∇

φ

(

r

)

:

φ

_−→

φ

′

(r) =

c

+

φ(r) +

_∇

φ(r).

(1.7)

E

′

(r) =

_−∇

φ

′

(r) =

_−∇

φ(r) = E(r).

(1.8)

À semelhança da meânia lássia aqui também oorrerá onservação de alguma

grandeza físia. Neste aso será a onvenional argaelétria.

Em relatividade restrita, o grupo de simetria que deixa invariante as equações de

Maxwellsãoastransformaçõesde Lorentz,uma vez queasdeGalileunãosão apazesde

o fazer, omo sabemos. Teremos oportunidade de as ver em um apítulo mais a frente.

Já em meânia quântia, o prinípio de simetria naqual subjazem leis de onservação

é expresso peloomutador dooperador

H

ˆ

que aqui deve ser independente dotempoe

representar a energia de um sistema fehado e um operador hermitiano

ˆ

O

, que fará o

papelde um observável de interesse:

[ ˆ

H,

O] = 0.

ˆ

(1.9)

E omo onsequênia mesmode se presindir dotempo,teremosque

h

ψ

_|

O

ˆ

_|

ψ

_i

=

_C

,

(1.10)

sendo talgrandeza então dita onservada[2℄. Indoum pouo mais além,emteoria

quân-tia de ampos,é neessário,amiúde,que alagrangianadomodelo sejainvariantefrente

as hamadas transformações de alibre (gauge), termo este entendido omo uma esala.

Uma vez que em tais teorias a lagrangeana é geralmente onstruida om polinmios

se alagrangiana for dada por

k

omponentes e suas derivadas

L

=

_L

[φ

k

(x

µ

), ∂φ

k

(x

µ

)] =

X

k,n

=1

{|

φ

k

(x

µ

)

|

2

n

+

|

∂φ

k

(x

µ

)

|

2

n

}

,

(1.11)

elanão variará sereesrita emtermos daseguinte mudançade fase nas omponentes

φ

′

k

φ

k

(x

µ

)

→

φ

′

k

(x

µ

) =

e

iα

k

φ

k

(x

µ

),

(1.12)

om

α

k

parâmetros onstantes no espaço-tempo. De fato, para esta mudança

L

per-maneeinvariável

L → L

′

=

_L

[φ

′

_k

(x

µ

)

2

n

,

(∂φ

′

k

(x

µ

))

2

n

] =

L

.

(1.13)

Essamesmatransfortmaçãopossuiumaversãoontínuaasosequeiraqueoparâmetro

do espaço-tempo varie ponto-a-ponto. Como onsequênia de invariâniasde fase omo

estas, em estágios mais eleborados da teoria, a grandeza a se onservar será a arga.

Mas um tipomais geral que a onvenional,tendo uma versão simétria, aso as

trans-formações impliquem uma simetria dita simples, e uma om simetria superior, aso as

tranformações sejam ditas supersimétrias[3, 4, 5℄, sendo estas últimas diretamente

re-sponsáveis pela orrelação entre bósons e férmions, gerando as superargas e

superor-rentes, nashamadas algebrasdeorrentedadéadade 60,noqueou onheidodesde

então omo modelo padrão das partíulas elementares[6 ℄. Posteriormente ao modelo

padrãoe sua superalgebra, tivemos o adveto dateoria das ordasemmeados dadéada

de 70. De iníio, aqui, a transformação de simetriaque essa teoria teve de obedeer foi

adaversão supersimétria, já queéra assoladaporinonsistêniasaso seusasse apenas

a versão simples da tranformação. Oorria que a gravidade só surgia naturalmente da

estrutura dateoria seatranformação usadafosse adasuper versão, sóassim uniando

as forças gravitaional (relatividade geral), eletrofraa (eletrodinâmiaquântia) e forte

netísmo. Isto é,nasua formatensorial. Usando alagrangiana de Maxwellsem termode

interação orrente-ampo

A

µ

J

µ

L

=

1

4

F

µν

F

µν

_,

(1.14)

om

F

µν

₌

_∂

ν

_A

µ

₋

_∂

µ

_A

ν

o hamada tensor intensidade de ampo eletromagnétio, que

aopla emuma únia estrutura matemátia tanto oampo elétrioquantoo magnétio.

Nesse formalísmolança-se mão do ampo de alíbre

A

µ

=

A

(

ρ,

J

)

, om

ρ

a densidade de

arga eJ aorrente. Assim, astransformaçõesde alíbre serão levadas aabomediante

mudanças de esala nesse ampo

A

µ

. E realmente, usando-se uma transformação tal

omo aanterior

A

_→

A

′

=

e

iα

A,

(1.15)

a lagrangianade Máxwellnão muda de forma

L → L

′

=

1

4

F

(A

′

_)F

_(A

′

_{) =}

L

.

(1.16)

De maneirasurpreendentetodas essastransformaçõesde simetriapodem ser

onden-sadas num elegante e poderoso teorema, este reportado a Sra Noether, e ujo teor da

armaçãoéoseguinte[8℄: Atodatransformação desimetriaestáassoiadaumagrandeza

onservada. Sua presteza vai desde as teorias não relativístiasaté aquelas que dela

in-orporama estrutura formaldo espaço-tempo.

Poroutrolado,mesmoaonservaçãodasimetriatendoseuimportantelugaradquirido

doravante ea guisa de provasexperimentais, tão importantequanto elaveio aser a sua

ontraparte,aquebradesimetria. Atéondeolimitementaleporonseguinteolingüístio

enormediferençaentrepartíulaseanti-partíulas[10℄?. Emessênia,aprópriaperepção

das oisas omo uxo imanente de vivênias requer omo prinípio a difereniação das

formas e uja qual, omo é fáil de se notar, a própria possibilidade de existênia do

tempo aha-se tão e ompletamente ondiionada, pois basta que essa assimetria esse

para o tempo deixar de existir e, por onseguinte, a nossa própria perepção auto

perepçãoenquantoexistênia. Vejamosagoraoneitualmentealgunsimportântesfatos

quedemonstraramagrandeemergêniadosfenmenoqueenvolveramquebradesimetria

emfísia.

A paridade foium dos mais importantes fatosem físiasa demonstrara neessidade

deemergêniadeumnovooneitofísio 1

. Estanãoseonservanasinteraçõesfraas. Foi

aSra. Wu queodemonstrouexperimentalmente[13℄, resultadoesse obtidoteoriamente

um ano antes por Lee e Yang [47℄. Em suma, o fato era que a direção preferenial dos

elétronsemumdeaimento

β

doCo

60

deveriaseramesmafrenteumareexãoespelho 2

,e

nãoofez,jáqueosexperimentosmostravamqueoselétronseramemitidosontrariamente

aospin donúleo. Mas,diantedamesmaexperiêniafeitasegundoumareexãoespelho,

oselétronsseguiamamesmadireçãodospindonúleo,queagoraestavanadireçãooposta

à anterior. É ao nível dessas mesmas interações que uma outra simetria é quebrada. A

heliidade, denida por

Λ =

J

·

P/

|

P

|

, é diferente no deaimento do

π

+

_−→

_ν

µ

+

µ

+

em

relação ao deaimento do

π

−

_−→

_ν

µ

+

µ

−

. A onjugação de argas, operação envolvida

1

Só não devemos esqueer que tal oneito não surgil na físia. Basta folhear qualquer testo de

iênia avançadaantigapara se observarque aquebrade simetriaé oprinipal meanismo queentra

emenanosurgimentodouniverso. Eisssoestábemexplisito nosantigostestosindus,anteipadores

porexelêniadoquedizhojeasnossasmaisavançadasteoriasientías[11,12℄.

2

Reexãoqueoorrequandofaz-seasseguintesmudançasnasoordenadas:

x

−→

x,

y

−→

y,

z

−→ −

z,

momentos lineares P e angulares L preservam-se. Isso deveria apenas troar o sinal do

π

+

transformando-o na sua anti-partíula, deixando

Λ

invariante. Mas Duas e seus

olaboradores [15℄ mostraram, nas experiênia dos referidos deaimentos, justamente o

ontrário, umavez queambas aspartíulas apresentaram heliidades opostas.

Vejamos agora mais uma fértil região onde a quebra de simetria representa papel

fundamental,a matériaondensada.

1.2 Quebra Espontânea de Simetria na Materia

Con-densada: Os Ferromagnetos de Ising

Anaturalligaçãoàteoriadeamposqueamiúdeéfeitoomrespeitoaquebraespontânea

de simetria vem da matéria ondensada. Mais espeiamente em sistemas magnétios

onheidos omoferromagnetos. Estes podem ser estudados emsua versãolássia mais

elaborada, hamada de modelo de Ising, onde os spins são "pontos"xados nos vérties

de redes ristalinasvariando aleatriamente de

±

1

ou

±

1

/

2

. Pode-se também

implemen-tar uma versão quântia para esses ferromagnêtos por meio de sistemas modelados por

hamiltonianasdotipoHeisembergondeosspinssão tratadosomooperadoresquântios.

De forma bém geral, estudos em sistemas magnétios em torno da ritialidade o

ponto onde oorre uma das quebras de simetria,a da fasedo sistema 3

resumem-seem

enontrar os valores das grandezas físias de interesse para quando nesse ponto elas se

enontrarem[17, 18℄. Em geral, mede-se grandezas tais omo a magnetizaçãomédia por

spin

h

m

i

, energiamédia do sistema por spin

h

E

i

e a suseptibilidade magnétia

χ

. Esta

ultimaexpressa a failidade/diuldadequeo sistematem emorientaros spinssegundo

poiseleesta imersoemum grandereservatóriode alormenorserásua magnetização

média por spin

h

m

i

, existindo mesmo um valorrítio

T

c

naqual elavaipratiamentea

zero. A título de ilustração, mostramos na gura.1 uma típia urva da magnetização

versus temperatura para um ferromagneto simples(sem ampo externo apliado) om

suas duas soluções possíveis. Vinular então tal sistema à temperatura signia, nas

equações, multipliar a hamiltoniana

H

do sistema ao negativo do fator de Boltzmann

β

: -

βH

=

E

(

σ

i

, E

m

/k

B

t

)

. Isto é, agora a energia do sistema depende inversamente da

temperatura,onde

σ

i

sãoasvariáveisdespinqueenontram-se,porexemplo,nosvérties

deumarede quadrada. Aqui

E

m

éaenergiamagnétiadosistemae

E

T

=

k

B

T

atérmia.

Figura1-1: SequêniadeonguraçõesdomodelodeIsingparaquatrotemperaturasdiferentes.

Os spins no estado +1 estão representados a branoe osspins no estado -1 a preto. A baixas

temperaturas, é visivel aordem. Notea desordem provoada por onta da ompetição entre a

energia magnétia e aenergia térmia.

A quebra de simetria aontee quando a tranzição de fase, fenmeno relevanteaqui,

arateriza-se: a medida que a temperatura do sistema magnétio almenta, segue-se o

surgimentodoshamadossítiosmagnétios,ontendoporçõesdeátomosorientando-sena

mesma direção dos demais spins do mesmo sítio, mas diferente da dos ispins dos outros

domínios magnétios que também surgiram, até que a desordem ompleta é atingida

quando a temperatura dita rítiaé alançada emtodos ospontosdaamostra. Então a

velha simetria foi espontaneamente quebrada ou, melhor dizendo, substituida por uma

nova. Naterminologia quântia, adauma ontém seu próprioestado de menorenergia,

partíulas, propagando-se pela rede eristalina transportandoapenas energia. São omo

ondas advindas das vibrações térmias, movimentando-se ao longo dos lados dos ubos

darede.

É bastante simples, através do modeo de Ising, alular-se a função magnetização

que desreve ambas as urvas mostradas na gura 1. Pode-se fazê-lo em pouas linhas

levando-seemontaargumentos deaproximaçãobastanterazoáveisnumaredequadrada

ontendo apenas um spin entral rodeado pelos seus vizinhos mais próximos, omo

mostrado na guraseguinte

Figura1-2: Aglomerado ferromagnétioontendoumspinentral equatrovizinhosmais

próx-imos.

J >

0

garante oordenamento ferromagnétio.

O modelo omeça por esrever a hamiltoniana do sistema, a hamada hamiltoniana

de spin

H(σ) =

Jbzσ.

(1.17)

Aqui

J

representa a energia de interação entre o spin entral

σ

(que pode variar

aleatoreamente de

±

1

) e seus

z

vizinhos mais imediatos que ontribuem, ada um, om um valormédio

b

para doampototal

zb

, om

b

parte dautuação pruduzido por ada

um desses spins periférios. O próximo passo é vinular o sistema magnétio à

−

βH(σ) =

Kbzσ,

(1.18)

om

K

=

J/kT

o aoplamento spin-spin,

T

a temperatura absoluta e

k

a onstante de Boltzmann. A função magnetização é denida omo uma média da energia sobre as

possibilidades de orientação de

σ

h

m

_i

=

1

N

T r

P

_i

σ

i

exp[

−

βH]

T r

exp[

₋

βH]

,

(1.19)

on

N

aquantidade de spins entrais dentro de um aglomerado. O número de

miroes-tados aessíveis ao sistema é dado por

2

N

. Como no aso

N

= 1

, teremos as seguintes possibilidades: (+1) ou spin up, e (-1) ou spin down. Notemos também que a

magneti-zação a mais simpliada

h

m

_i

=

T rσ

1

exp[Kbzσ]

T r

exp[Kbzσ]

.

(1.20)

Levando-se em onta que o traço

T r

é feito sobre todas possibilidades, a fáil

alulara magnetizão desse sistema

h

m

_i

=

(+1)e

Kbz

(+1)

_{+ (}

₋

_1)e

Kbz

(

−

1)

e

Kbz

(+1)

₊

_e

Kbz

(

−

1)

=

tanh[Kbz].

(1.21)

Usamos aquias relações de Euler das hiperbólias

2 sinh(x) =

e

x

₋

_e

−

x

e

2 cosh(x) =

e

x

₊

_e

−

x

. Deste ponto ostuma-se lançar mão de uma ténia de aproximação bastante

simpleshamadade TéniadeCampoMédio

(T CM

)

,resumindo-seemargumentarque, próximoda temperaturarítia

T

c

, tanto

h

m

i

quantoseus

z

vizinhos mais próximos tem

h

m

_i

=

tanh[K

_h

m

_i

z],

(1.22)

forneendo-nos exatamente as urvas da gura 1. Como

h

m

i

=

b

→

0

quando

T

→

T

c

, justia-se espandir (1.22) emuma série de Taylorentorno dese ponto

h

m

_{i ≈}

K

_h

m

_i

z

+

_O

[

_h

m

_i

2

],

(1.23)

donde, desprezando-se os termos a partir de segunda ordem, valores numérios da

tem-peratura rítiade tranzição podem ser obtios de

kT

c

J

=

z

= 2d,

(1.24)

om

J

e

T

c

onstantesparaadatipodemateriale

d

adimensãodoaglomerado. Observe

que

T

c

depende apenas de

z

: para

z

= 4(d

= 2)

temos

kT

c

/J

= 4

, e para

z

= 6(d

= 3)

kT

c

/j

= 6

,valoresmuitosuperioresaoobtidoporOnsagernumáluloexato paraaqual

kT

c

/J

= 2,

246

. Estas são, portanto,as duas soluçoes possíveis para aurva mostrada.

Este foi, em síntese e qualitativamente, o modelo apresentado por Ernst Ising em

1925

, a menos da ténia de aproximação, para expliar o ferromagnetismo om

mo-mentosloalizadosvariandoaleatoriamentede

±

1

[16℄. Seu análogoquântio éo modelo

de Heisenberg, onde os spins são substituídos por operadores difereniais. No modelo

de Heisenberg usa-se uma argumentação semelhante à anterior a m de se desaoplar

as funções de orrelação entre pares de spins ao se fazer

hh

s

x

;

s

y

ii ≈ h

s

x

ih

s

y

i

=

h

m

i

2

,

hamadade aproximaçãodas fasesaleatóreas,simpliando-seonsideravelmenteos

os hamadosestados de mágnons eos de fónons. No modelo de Ising taisentidades não

são observadas explisitamente nas equações, mas são a resposta que justia ofato da

temperatura rítia diminuir a medida que o tamanho do aglomerado aumenta: om o

aumentodonúmerodespinsentraisnosistemaresetambémaquantidadedevibrações

aolongodarede(osmágnonsefónons),fazendodiminuirassimovalordaenergiatérmia

neessária para levar o bloo à desordem ompleta. Por outro lado, a versão quântia

permite obter-se explisitamentetais estados nomomento da imposição das relaçõesde

omutação,levando-nos aosestadosde bosons,equandodaimposiçãodeantiomutação,

nos hamadosestados de férmions.

1.3 O Modelo de Ising e sua versão Clássia de Campo

A físia da matéria ondensada foi terreno fértil para o surgimento de novas e furtivas

ideias. O próprio estudo dos hamados defeitos topológios, grupo mui geral na qual

enontram-se inseridos os sólitons, teve omo maro iniial esta vasta região de

onhe-imento. No plano da modelagem teória o estudo das tranzições de fase desempenhou

umpapeladavezmais relevantenaompreensãodamatériaemseustrês estados

odier-nos e, devido ao renamento das ténias e oneitos, noreonheimento de seu quarto

estado possível, oplasmátio, nahamada ondensaçãode BoseEinstein aodesrever a

dinâmiadeumgásde elétrons. EomodelodeIsingémaisumadessasontribuições

rel-evantes surgidasdoestudode sistemasmarosópiosmedianteargumentções

meânio-estatístias. Dois dados importantes julgamos aqui: primeiro, tal modelo insere-se no

ontexto das tranziçõesde fase,região omum aos vórties eoutros defeitos topológios;

e segundo porque talmodelo pode, omo veremos, ser tratado omo uma orruptela do

modelokinkiniodevidoaofatodeambospossuiremsuluçãonaformade umatangente

de uma maneira muito simples ao se reonheer que (1.21) é na verdade a solução da

equação de EulerLagrange

∂

∂

m

˜

∂

_L

∂(∂

M

_/∂

_m)

_˜

−

∂

L

∂

M

= 0,

(1.25)

quando esta opera sobre a seguinte lagrangiana

L

=

1

2

∂

2

_M

∂

m

˜

2

−

κ

2

4

M

2

−

M

2

0

2

,

(1.26)

om

κ

umfatoronstanteomdimensõesdeenergia,

M

umafunçãolássiade

m

˜

=

βJm

,

m

o termo de ampo magnétio e

β

aquele fator de Boltzmann neessário para oloar

o modelo no ontexto miroannio. O primeiro termo do lado direito desta última

equação representa a parte inátia do modelo enquanto que o segundo faz o papel do

potênial de interação. Fenomenológiamentetrata-se de um potenialefetivo uma vez

queéde grau quatro,enaesfera dateoriade ampodevetraxer algumaontribuiçãode

auto-interação. A relevânia de se modelar a teoria om esse potenial espeío e não

ouro qualquer basea-se nofato desta esolha ser a únia que fornee asolução na forma

de uma tangentehiperbólia. Retornando(1.26) em(1.25) teremos

∂

∂

m

˜

∂

_L

∂(∂

M

_/∂

_m)

_˜

−

∂

L

∂

M

=

d

2

_M

d

m

˜

2

+

d

U

d

M

=

d

2

_M

d

m

˜

2

+

κ

2

_M

₍

_M

2

−

M

0

2

₎

(1.27)

= 0,

om

oreferidopotenial. Aformaordináriade(1.27)refere-seaofatode

M

ser funçãoapenas

davariávelglobal

m

˜

= ˜

m(m, T

)

,om

m

oampomagnétipe

T

atemperaturaabsoluta. Veremos mais adiante pertenerem os kinks tambem à região linear (1+1)D. Notemos

agora a existênia do termo

±

M

0

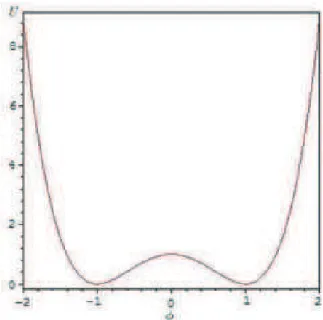
, este representa os valores dos mínimos relativos do

potenial, omo pede ser visto na gura 3. Observe que a primeira derivada de

U

é

Figura1-3: Potenial

U

eseus mínimosrelativos

M

0

=

±

1

(admensional).

suientepara forneer-nos opontode máximo

M

=

0

eosmínimosrelativos

M

0

=

±

1

,

d

U

d

m

˜

=

κ

2

_M

₍

_M

2

−

M

₀

2

_{) = 0.}

(1.29)

Aequaçãodiferenial(1.27)éagrantementenãolinear. Esta éumaoutra

araterís-tia apresentada por modelos que envolvem quebra de simetria. Sua solução pode ser

enontradafailmenteutilizando-se,porexemplo,soluçõeporsérie. Nãoédifíilmostrar

que talsolução terá justamentea formade uma tangentehiperbólia

omo já haviamos menionado. É interessante frizar que os valores

M

=

M

0

=

±

1

são aqueles para os quais

m

˜

→ ±∞

, ou seja, quando

T

→

0

, temperatura na qual o sistema apresenta magnetização espontânea. O valor de máximo será então aquele na

qual

M

=

0

, ouseja, quando

T

=

T

c

→ ∞

.

Pode-se ainda estudaro modelo de Ising atravéz dahamada fenomenologiade

Lan-dau, que onsistena minimização de funionais de energia quando se onhee a energia

interna e a entropia do sistema. Esta também levará ao potenial anterior mostrando

queasdiferentesabordágenslevamaomesmoresultado. Vejamosagoraasonsequênias

da quebra espontânea de simetria emum outro grande ampo dafísia, a de partíulas

elementares.

1.4 Grupos de Simetria e os Multipletos de Partíulas

Vimosnasseçõespreedentesomoentidadesfísiaspodemsurgirdomodelo

exeutando-sesobreeleuma tranziçãode fase. É interessantevermos entãoomo ohamadomodelo

padrão pde dar onta daquela miríade de partíulas elementares apareendo em meio

aos emaranhados daquelasequações todas.

Emteoriadeampo,abasedomodelopadrão,issofoilevadoaabodeduasmaneiras:

a primeirafoi quebrar a simetria domodelo ao nível de soluções das equações de

movi-mentodos ampos envolvidos. Este foi ohamado meanismo de Higgsna qual

tratare-mosomdetalhesnaseção1.5equeéumdosfundamentosdenossotrabalho. Asegunda,

e na qual daremos apenas uma ênfase qualitativa, utilizou o formalismo dos grupos de

simetria[19℄. Esta foi aformade Weegner, quetiravadasimetriamais geral(maior)suas

partesomponentesúltimas. Istoé,expliitavadasimetriatodasassuasformas menores

e irredutíveis[3, 4, 6, 7℄, identiando ada modalidade de interaçõae por onseguinte

omo mostrado na gura abaixo . Foi Heisenberg que postulou, em 1932, que o próton

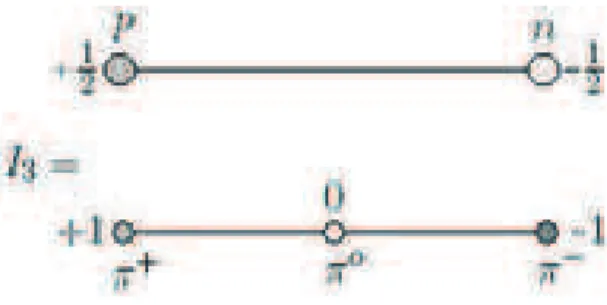
Figura1-4: Aima temos

I

= +1

/

2

,

−

1

/

2

gerandoosdois estadospossíveis parao nuleon,os estados de próton e de nêutron, na hamada simetria

SU

(2)

. Embaixo temos

I

= +1

,

0

,

−

1

, forneendo otripleto de mésons

π

+

,

π

0

e

π

−

.

e onêutron são dois estados de argas possíveis parao nuleon. Assim, agura 4

repre-senta um onguração hadrnia om dois estados possíveisde isospin: +1/2 dopróton

e -1/2do nêutron. De fato,sejam osdois estadospossíveispara o nuleon

|

p

_i

=







1

0







;

(1.30)

|

n

_i

=







0

1







.

(1.31)

Em meânia quântia usa-se o formalismo das matrizes de Pauli para se estudar

partíulas de spin 1/2. Vamos introduzirentão os seguintes operadores matriiais

I

1

=

1

2







0 1

1 0







;

(1.32)

4

Élaroqueaspartíulasdeummesmomultipletopodemter massasligeiramentediferentes,omo

defato oorre. Masessa pequena diferençaéexpliadapelaexistêniadaenergiamagnétiadevidoàs

I

2

=

1

2







0

1

−

1 0







;

(1.33)

I

3

=

1

2







1

0

0

₋

1







.

(1.34)

Observe que tais operadores apresentam a mesmo forma das matrizes de Pauli a

menosdeumfator2. Podemosentão pensaremumoperadorIonstruidoomessas três

omponentes possuindoas mesmasaraterístias dooperador de spin J. Este operador

I, onstruio num espaço interno tridimensional das omponentes

I

1

,

I

2

e

I

3

, é hamado

de spin isotópio ou isospin. É mais um número quântio que surge para lassiação

das partíulas e seus grupos. Dessa forma, o nuleon é pensado omo uma partíula

de isospin 1/2 tendo 2I+

1 = 2

possíveis estados de arga, o estado

|

p

i

e o estado

|

n

i

. Realmente, apliando aomponente

I

3

de Inesses estadosenontraremosexatamenteas

respetivas equações de autovaloresque os araterizam

I

3

|

p

i

=

1

2







1

0

0

₋

1













1

0







= +

1

₂

|

p

i

;

(1.35)

I

3

|

p

i

=

1

2







1

0

0

₋

1













0

1







=

₋

1

2

|

n

i

;

(1.36)

Um outro exemplo é o dos mésons, que possuem três possibilidades para

I

3

: +1, 0

e -1. Neste aso temos I

= 1

(gura 4). O grupo de simetria SU(2) também é usado paraagruparpartíulas emmultipletospoisdesrevemorientaçõesde spinom possíveis

estados de arga omo o exemplo aima. Foi através do grupo de simetria SU(3) que se

podeobservarqueem prinípiopoder-se-iaonstruir multipletosdemésonsebárionspor

Este pode ser esrito omo SU

c

(3)SU

l

(2)SU

y

(1), onde o subgrupo irredutível SU

c

(3)

de-sreve as partíulas da romodinâmia e o subgrupo SU

l

(2)SU

y

(1), também irredutível,

fornee-nos as partíulas querespondempelas interações fraas nos deaimentos

radioa-tivos.

Aabamos de apresentar muito qualitativamente o modo de Weegner de realização

das simetrias a m de se observar o surgimento de partíulas. Mostraremos agora o

modo enontrado por Goldstone, que utilizou justamente a quebra de simetria ao nível

das soluçõesdas equações difereniaisde sistemasmodeladosporpoteniais de Higgs.

1.5 Quebras de Simetria em Teorias de Campo

Naseçãoanterior tivemosuma idéiageralde omoaspartíulas sãogeradaspormeiode

gruposde simetria. Mostraremosagora,eomertodetalhe, aindaemteoriasde ampo,

uma outra maneirabastante simplesde omo issotambémpode aonteer.

1.5.1 Quebra Espontânea de Simetria eo Surgimento de

Partíu-las Vetoriais sem Massa: Os Bósons de Goldstone

Vimos que oque se busava à maneira de Weegner éram as simetrias do modelo para

delas seinferiras entidadesfísias, agoraoorreráo oposto, poisbusar-se-a justamente

quebra-las de alguma maneira para dai poder-se observar os entes. E isso será levado

a abo ao nível das soluções das equações de movimento. Ou seja, nos ampos. Um

pontoruial desse métodoé queeleonsegue preservaronúmerode graus de liberdade

da teoria. Noutras palavras, o número de ampos antes e depois da quebra de simetria

permanee o mesmo.

Issoéobservado tabémemteoriasdeampoquandoosistema dinâmiopossui simetria,

mas seu váuo não é invariante segundo essa mesma simetria. Tal quebra pode ser

exeutadanapresençade duasondições, asaber:

i)

quandoomodeloapresentasimetria

globaloparametronãodependedospontosdoespaço-tempo;

ii)

quandoseobservauma

simetriade alibreloal quandooparâmetro dependeponto-a-pontodoteido

espaço-temporal. Na primeira nota-se o surgimento de bósons(esalares ou arregados) sem

massa. Noúltimoaso taispartíulas são eliminadasdateoria medianteum proessode

geraçãodemassa paraamposde alibre. Noquesesegue vamosprinipiarom ampos

bosnios esalares e neutros, ndando om bosniosarregados.

Campo Esalar Real

Seja então o modelo desrito pela seguinte lagrangeana onstruida apenas om ampos

φ

′

s

esalares ereais

L

=

1

2

∂

µ

φ∂

µ

_φ

−

U(φ),

(1.37)

om o primeiro termo fazendo o papel da parte inétia. A espeiação do sistema

depende então da forma de

U

que mara a intensidade da interaçãoentre ampos que,

neste aso, paree ser uma autointeração de

φ

. Notem que se esolhermos um sistema

modelado por um potenial tipo

λ

2

_φ

4

, o sistema não terá degeneresênia, já que

ap-resentará apenas um mínimo trivial. Esta situação não permite quebra espontânea de

simetria, fato que só aontee quando se tem opções de váuos. Vejamos então o que

oorre quando se insere um potenialdo tipoHiggs seguinte

U(φ) =

λ

2

4

(φ

2

om

η

2

_{= 2(}

_µ/λ

₎

2

um valor do ampo num dado váuo diferente de zero,

µ

2

a massa do

ampo

φ

e

λ

omdimensão de

m

−

1

(veja gura5). Aqui

±

η

éobtidoatravésdaondição

assintótia

φ

(

±∞

) =

±

η

. Geralmente requer-se, omo no teorema da divergênia, que

o ampo no innito seja nulo. Mas este será diferente de zero 5

devido a quebrada da

simetria. Calulando a tangentesobre a urva dopotenialtemos

dU

dφ

=

λ

2

_(φ

2

−

η

2

)φ.

(1.39)

Para

µ

2

_>

₀

e

λ

6

= 0

(quando

λ

= 0

temos o aso de ampos livres), o estado de mínimo

do sistema oorre no váuo verdadeiro da teoria, ou seja, em

φ

(

x

=

∞

) = 0

. Por outro

lado, quando

µ

2

_<

₀

(

µ

um imagináriopuro) ateoria onterá táquions[20℄,entidades om

massas negativase veloidades superiores ao daluz, desestabilizando a teoria. Aparee

então um máximoem

φ

= 0

e dois mínimosem

φ

=

±

η

(gura5).

A presrição, omo dissemos, é que ovaloresperado doampo nováuo sejanúlo:

φ

0

=

h

0

|

φ(

±∞

)

|

0

i

= 0.

(1.40)

Mas issonão oorre pois,neste aso

φ

0

=

h

0

|

φ(

±∞

)

|

0

i

=

±

η.

(1.41)

Uma maneira de se obter o valor médio de

φ

no váuo verdadiro (1.40) é então

desloando-ode seu valor

η

. Ou seja,oloando

φ

′

=

φ

_∓

η,

(1.42)

5

Issoporque os amposno innito onvergempara osprópriosansatz domodelo assoluçõesdas

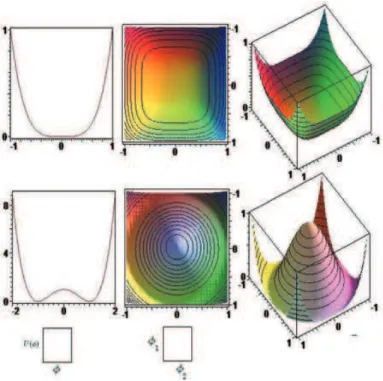
Figura 1-5: Na primeira oluna de diagramas: poteniais tipo

λ

2

_φ

4

_/

_2!

e

λ

2

₍

_φ

2

₋

_n

2

₎

2

_/

_2!

,

respetivamente. Segunda oluna de diagramas: urvas de níveis no plano

(

φ

1

, φ

2

)

de suas versões tridimensionais. Tereira oluna de diagramas: funionais

U

(

φ

1

, φ

2

)

para ada um dessespoteniais. Émostrado também osmínimosrelativos paraoasodo potenialde Higgs.

donde tem-se

φ

′

0

=

h

0

|

φ(

±∞

)

∓

η

|

0

i

= 0.

(1.43)

Mas este proedimento, omo se vê, lava o sistema a transiionar de uma fase om

váuos

±

η

parauma omváuo nulo(o váuoverdadeiro). Essa redeniçãodoampo

re-sultanaperdadasimetria

Z

2

disretaque,natroade

φ

por

−

φ

,fazmudaralagrangeana

(1.37). Veja, troando-se

φ

por

φ

′

₊

_η

(ou

φ

′

₋

_η

) teremos

L

′

=

1

2

∂

µ

(φ

′

−

η)∂

µ

(φ

′

₋

η)

₋

U

(φ

′

)

=

1

2

∂

µ

φ

′

_∂

µ

_φ

′

−

(

1

2

λ

2

_φ

′

4

_{+ 2λ}

2

_φ

′

3

_{+ 2λ}

2

_η

2

_φ

′

2

₎

6

Perebaque

L

′

ganhaagoraumsinalnegativonosegundotermodopotenial. Destarte

podemos notar também que o ampo

φ

′

adquire uma massa positiva

m

2

φ

= 2

λ

2

η

2

. Isso

nos faz onluir que a quebra espontânea de simetria apresenta omo onsequênia o

surgimentode partíulas massivas. Vejamos agora o aso om ampoarregado.

Campo Esalar Complexo

O modelo anterior desreve partíulas neutras, uma vez que

φ

é um esalar real 6

. Ao

tratarmos aquestão om amposesalares omplexos estamosquerendo dizeragora que

nosso modelo apresenta partíulas om arga. Bastará, pois, usar-se a mesma forma

anterior para a lagrangeana, mas levando-seem onta desta vez quantidades omplexas

φ

e

φ

. Esrevamos então

L

=

∂

µ

φ∂

µ

φ

−

1

2

λ

2

₍

|

φ

_|

2

₋

η

2

)

2

,

(1.45)

om as onstantes tendo os mesmos signiados anteriores. Calulando os extremos do

potenial

dU

dφ

=

λ

2

|

φ

_|

2

φ

+

µ

2

4

φ,

(1.46)

que,para

µ

2

_>

₀

,possuiráum úniomínimoem

φ

= 0

. Mas, se

µ

2

_<

₀

,o sistemaonterá

táquions,desestabilizandoopotenial. Agoraapareem,levando-seemontaesteultimo

aso, dois mínimos em

±

η

e um máximo relativo em

φ

= 0

. Note que o modelo (1.45)

é invariante frente transformações de simetria

U

(1)

global, quando troa-se

φ

por

e

i

Λ

_φ

′

,

om

Λ

umparâmetro onstanteem

x

µ

;eloal, quandomuda-se

φ

por

e

i

Λ(

x

)

_φ

′

,aqora om

Λ(

x

)

dependente pontualmente daquadridimensão. De fato, efetuando-se qualquer uma

dessas troas teremos

L

′

=

_L

.

(1.47)

6

Elatambémésimétriafrenteamudançade

φ

por

−

φ

. Oorreque,aoparametrizarmos

φ

pordois ampos esalares neutros

ϕ

e

χ

φ

=

η

+ (ϕ

+

iχ)/

√

2,

(1.48)

a lagrangeanamuda para

L

=

1

2

∂

µ

ϕ∂

µ

_ϕ

₊

1

2

∂

µ

χ∂

µ

_χ

−

2λ

2

ϕ

2

+

√

2λ

2

ηϕ(ϕ

2

+

χ

2

) +

λ

2

8

(ϕ

2

₊

_χ

2

₎

2

,

(1.49)

que não émais invariantefrentetransformações

U

(1)

loais de

ϕ

→

ϕ

=

e

i

Λ(

x

)

_ϕ

,

χ

→

χ

=

e

i

Ω(

x

)

χ

, globais de

ϕ

→

ϕ

=

e

i

Λ

_ϕ

,

χ

→

φ

=

e

i

Ω

_χ

, nem por transformações

Z

2

disretas

ϕ

_{→ −}

ϕ

e

χ

→ −

χ

. Entãoédito queasimetria

U

(1)

(globaleloal)foi espontaneamente

quebradapelaparametrização(1.48),eseagoraquisermosovaloresperadodoampono

váuo igual a zero, teremos de desloa-lo, assim omo zemos noaso doampoesalar

neutro,de seu valor de váuo

η

. Ou seja, pondo

φ

′

=

φ

₋

η

= (ϕ

+

iχ)/

√

2.

(1.50)

Portanto

φ

′

₀

=

_h

0

_|

φ

₋

η

_|

0

_i

= 0,

(1.51)

e o sistema transiiona de fase. De (1.49) nota-se que o ampo

ϕ

adquire massa de

m

2

_ϕ

= 2

λ

2

η

2

, sendo que o ampo

χ

nenhuma massa apresenta. Este é justamente o

teorema de Goldstone[21℄, a dizer que, quando uma simetria de alibre loal

U

(1)

for

Campos de Calibre

Vejamosomoamasoisasnoasode ummodelodeampoesalaromplexoaoplado

a um ampo de alibre

A

µ

via derivada ovariante

D

µ

=

∂

µ

+

ieA

µ

,

(1.52)

om

e

aonstantedeaoplamentomínimojáqueaderivadaapresentaapenasumtermo

linear em

A

µ

. Aqui

A

µ

≡

(

A

0

;

A

i

)

, om

A

0

≡

ψ

(

r

)

o potenial esalar eletromagnétio e

A

i

≡

−

→

A

o potenial vetor 7

. No apítulo três argumentos físios plausíveis serão usados

para essa introduçõa. Por enquanto sua apresentação sem maiores expliações servira

apenas para os ns propostos nesta seção. A lagrangeana éentão esrita omo

L

=

₋

1

4

F

µν

F

µν

₊

_D

µ

φD

µ

φ

−

λ

2

2

(

|

φ

|

2

−

η

2

)

2

,

(1.53)

om

U

=

λ

2

₍

_|

_φ

_|

2

₋

_η

2

₎

2

_/

₂

o potenial de Higgs. Agora temos um modelo governado

por duas dinâmias, um para o ampo

A

µ

dada pelo termo eletrodinâmio

−

1

4

F

µν

F

µν

,

om

F

µν

₌

_∂

µ

_A

ν

₋

_∂

ν

_A

µ

um tensor anti-simétrio onheido omo intensidade de ampo

eletromagnétio. Sua anti-simetriadeorre dofatode que,natroados índies

µ

e

ν

, seu

sinalétroado:

F

µν

₌

₋

_F

νµ

. Aoutradinâmiaaporontadotermobosnio

D

µ

φD

µ

_φ

.

É natural então omeçarmos a pensar a partir de (1.53) em possíveis modelos onde a

matériaarregada interage mediantetroa de fótons, om estes últimossendo os bosons

de Higgs da interação eletromagnétia, e os bosons esalares arregados omo sendo as

subpartíulasmensageirasdaforçafortenuleon-nuleon 8

. Para

Λ(

x

ν

₎

umparâmetroque

7

Paraordensmaioresnaderivadade

A

µ

,omomaisafrenteoorrerá,elaseráditanãomínima 8

De maneirageralos físios areditam queexistam apenas doistiposde partíulas nouniverso, os

transformaçõesde alibre

U

(1)

loais denidas por

φ

_−→

φ

=

e

i

Λ(

x

ν

)

φ

′

;

(1.54)

φ

_−→

φ

=

e

−

i

Λ(

x

ν

)

φ

′

_;

A

µ

−→

A

µ

=

A

′

µ

−

e

−

1

∂

µ

Λ(x

ν

)

(1.55)

Em verdade, para se ser orreto, o que deve ser levado em onta é a ivariânia da

orrespondente ação integral segundo alguma transformação, e não a invariânia de

la-grangiana. Se tal ação integral

S

não muda frente a uma transformação dada então é

dito o modelo ser invariante frente a referida transformação. E o modelo (1.53) o é, já

que, para atransformação

U

(1)

numa versão innitesimalpode-se demonstrarque 9

δ

_S

=

δ

Z

t

2

t

1

dt

_L

[φ,

φ;

˙

A,

A] =

˙

Z

t

2

t

1

dtδ(

_L

[φ,

φ;

˙

A,

A]) = 0.

˙

(1.56)

Esta última obreoquevema ser oprinípiode D'Alambert damínima ação adizer

que todo sistema físio prefere ar sempre em seu estado de menor energia. Noutros

termos, é sempre núlo o trabalho virtual exeutado(ou sofrido) por qualquer sisteme

físio:

δW

= 0

. Este prinípio,juntamente om as quatro leis de Newton,onstituem-se

nospilaresde todaameânialássia. Analisandonovamenteosextremosdopotenial,

temos

dU

dφ

= 2λ

2

₍

|

φ

_|

2

₋

η

2

)φ,

(1.57)

que, para

µ

2

_<

₀

apresenta um máximo relativo em

|

φ

|

= 0

e dois mínimos em

|

φ

|

=

η

. Este potenial é innitamente degenerado pois suas urvas de níveis são írulos

enquantoosprimeirossãotodasaspartíulasmensageirasdasquatrointeraçõesfundamentais.

9

Notemosaquiqueafatoração

δ

R