FABIO A.C.C. CHALUB∗
IMPA, Estrada Dona Castorina, 110 – 22460-320 Rio de Janeiro, RJ, Brazil Manuscript received on July 20, 2001; accepted for publication on August 22, 2001;
presented byManfredo do Carmo
ABSTRACT
We study the behavior of massless Dirac particles, i.e., solutions of the Dirac equation withm=0 in the presence of an electromagnetic field. Our main result (Theorem 1) is that for purely real or imaginary fields any Huygens type (in Hadamard’s sense) Dirac operators is equivalent to the free Dirac operator, equivalence given by changes of variables and multiplication (right and left) by nonzero functions.
Key words:Huygens’ principle, Dirac operators, electromagnetic fields, Hadamard’s problem.
1. INTRODUCTION
By 1690 two different theories were disputing the nature of light: for Newton (Newton, 1979), light was composed of particles propagating along straight lines; whereas Huygens believed that light was a mechanical wave propagating in the æther, the hypothetical medium that fulfilled all the space (Shapiro 1980).
Huygens’ theory was particularly useful to explain diffraction (‘‘the strange refraction of the Iceland crystal’’), but had some remarkable difficulties to explain the apparent propagation of the light along straight lines. To overcome this difficulty, he wrote his masterpiece ‘‘Treatise on Light’’ (Huygens 1920) where he formulated the principle that bears his name.
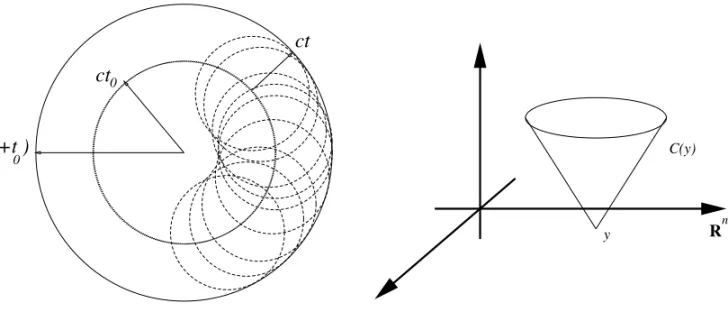
In more modern terms (in a formulation essentially due to Fresnel (Fresnel 1816) — for a historical overview, see (Born and Wolf 1980)) we say that each point in the wave front acts as a secondary source of wave and all these waves interfere to produce the new wave front. See Figure 1. Despite the large use of the term ‘‘Huygens’ principle’’ in the physical community, its precise mathematical formulation is seldom made clear. In 1923, the French mathematician J. Hadamard,
∗Present address:
c(t+t )
ct
ct0
0 C(y)
Rn
y
Fig. 1 – Huygens’ construction of a wave front from the previous one (left). Forward light cone with vertex iny(right).
in a series of lectures at Yale University, formulated in mathematical terms three different meanings of ‘‘Huygens’ principle’’ he found in the literature of his time (Hadamard 1953). This work is concerned with the second definition, called ‘‘Hadamard’s minor premise.’’
We define the forward light cone with vertex iny as
C+(y)=
x ∈Rn+1
(x
0−y0)2− n
i=1
(xi−yi)2=0, x0> y0
.
and the fundamental solution (also known as Green’s function)φ of an operatorL Lφ=δy,
whereδyis the Dirac-delta distribution supported iny.
We say thatL(and, by extension, its fundamental solutionφ) possesses Huygens’ property (or obeys Huygens’ principle) if, for everyy,φis supported in the forward light cone with vertex iny.
This definition is called ‘‘Hadamard’s minor premise.’’ See Figure 1.
As Huygens’ principle was originally formulated for light propagation, a physical phenomenon modeled by the wave equation, it is useful to discuss Huygens’ principle in Hadamard’s minor premise sense in this case first.
The wave equation is a partial differential equation inn+1 variables,(x0, x1,· · · , xn), where x0is taken astime, and the other variables are thespacevariables. Explicitly, it is an equation for a functionusuch that
udef= ∂
2u
(∂x0)2 − n
i=1 ∂2u (∂xi)2 =0.
It is a well known fact that the wave operator possesses Huygens’ principle for oddngreater than or equal to 3 and does not posses it otherwise. See (Folland 1997).
Hadamard’s problemconsists in classifying all second order hyperbolic operators which obey Huygens’ principle, up to trivial relations. The latter consist in successive combinations of changes of variables, and left or right multiplication of the operator by a never-singular smooth function. This problem has not been fully solved, but progress has been made recently. An extensive and up-to-date review can be found in Berest’s work (Berest 1998). Previous work on the subject of Huygens’ principle for Dirac operators are (Chalub and Zubelli 2000, Chalub and Zubelli 2001a). In this work we will study the validity of Huygens’ principle for Dirac operators in the presence of an electromagnetic field. In Section 2, we briefly introduce Clifford Algebras, that are instru-mental to the definition of Dirac Operators. In Section 3, we present the Hadamard expansion and re-define Huygens’ principle in terms of its truncation. In Section 4, we develop some comments about the physical nature of Huygens’ principle, in particular in the presence of electromagnetic field and prove the main theorem of this article, namely, that every Dirac operator in the presence of a real or purely imaginary field with Huygens’ property is trivially equivalent to the free Dirac operator (Theorem 1).
2. CLIFFORD ALGEBRAS AND DIRAC OPERATORS
Dirac operators appear in Mathematical Physics in the framework of the construction of a relativistic electron theory. In a celebrated paper, Dirac (Dirac 1928) defined a Lorentz-covariant Hamiltonian (and consequently first-order in space variables, as Schrödinger equation is first order in time) whose square furnishes the Klein-Gordon equation.
Letgµν = diag[1,−1,· · · ,−1] denote the Minkowski tensor. Associated to gµν we can
construct a Clifford Algebra. It is an associative algebra (with identityI) over the reals generated by all linear combinations of the form(γ0)m0(γ1)m1· · ·(γn)mn, m
µ∈ {0,1}, where the matrices
{γµ}, obey the relationγµγν+γνγµ=2gµνI. The matrices{γµ}, which are called Dirac matrices, are linearly independent (Gilbert and Murray 1991, Marchuk 1998).
Dirac operators are defined by:
D=γµ∂µ+v,
where the summation for repeated indices is implied. See (Thaller 1992) for an introduction on the subject. We shall adopt the notation∂ =γµ∂
µand restrict ourselves to the case wherevis of
electromagnetic (orvector) form,v=aµγµ.
3. HUYGENS’ PRINCIPLE AND HADAMARD EXPANSIONS
In this section we shall look for fundamental solutions of Dirac operators. Afundamental solution for∂ +vis a solution of(∂ +v)=δy,whereδydenotes Dirac-delta distribution supported at
Letλ(x, y) =
(xµ−yµ)(x
µ−yµ)denote the Minkowski distance between two points x
andy.
The first important concept to be recalled is the so-called Riesz kernel. It was introduced by M. Riesz in order to unify the treatment of elliptic and hyperbolic problems. They are given by distributions inD′(
Rn+1)defined first forRe(α)sufficiently large by
α =
N (α)λα , if(xµ−yµ)(xµ−yµ)≥0
0 , otherwise.
Here, the normalizations constantN (α)is given by
N (α)= [2α+nπ(n−1)/2Ŵ(α+n+1
2 )Ŵ(
α
2 +1)] −1
.
Then,α is extended analytically for all values of α in the complex plane by means ofα = α−2, which is satisfied for all α with sufficiently large real part. It is not hard to check that
−n−1=δy. See (Folland 1997).
We shall say that a fundamental solutionobeysHuygens’ principleifsupp ⊂C+(y)∀y ∈ Rn+1.
Adapting Hadamard’s seminal idea from the wave operator case to the one at hand, we look for series expansion for the fundamental solution
=
∞
m=0
∂−m"−α0s m=
∞
m=0
"α0+2ms
2m+α0+2ms2m+1
,
wheresmis a matrix coefficient,α0→ −n+1,"α = ∂ α, which we call Dirac kernels, andα
are Riesz kernels. It can be shown that"α satisfies Huygens’ property forα = 0,−2,−4,· · ·; whileα does it forα= −2,−4,· · ·.
Ifis a fundamental solution, using the properties of Riesz and Dirac kernels, we have the
Hadamard’s recursionfor the coefficientssm
s0+
2
α0+n−1
(xµ−yµ)(∂µ+aµ)s0 = 1, α0→ −n+1, (1)
s2m+1 = (∂+v)s2m, (2) s2m+
1
m(x
µ−yµ)(∂
µ+aµ)s2m = −(∂+v)s2m−1. (3)
In all these casessmshould be smooth (in particular whenyµ →xµ) and we impose normalization s0(y, y)=1.
We solve equation (1)
s0(x, y)=exp
−
1
0
(xµ−yµ)aµ(y+z(x−y))dz
An important property of this series is that it is unique, provided we requiresmto be smooth. The
uniqueness for (2) is trivial. In the case of (3) it should be proved. Lets1ands2be two different
solutions of (3). So, the differences1−s2=S
2mis smooth and satisfies
S2m+
1
m(x µ
−yµ)(∂µ+aµ)S2m=0.
We find that
S2m= ˜Sexp
−
1
0
(xµ−yµ)aµ(y+z(x−y))dz
,
withS˜ satisfying
˜
S+ 1
m(x
µ−yµ)∂
µS˜ =0.
The only smooth solution in the vicinity of the vertexyis given byS˜ =0, thenS2m=0.
Bearing in mind this fact it is easy to prove the equivalence between Huygens’ principle and the truncation of the Hadamard series:
Remark 1. A Dirac operator in the form ∂ +v possesses Huygens’ property in odd spatial dimensionn ⇐⇒ its Hadamard series truncates atn, i.e,sm=0 form≥n.
Proof. Proving this remark is quite simple. In the⇐ direction, it follows from the properties of Dirac and Riesz kernels. In the other direction, it is a consequence of the uniqueness of the
Hadamard expansion.
4. HUYGENS’ PRINCIPLE IN AN ELECTROMAGNETIC FIELD
In this section we shall consider potentials of the formv=aµγµ.
Potentials of the formaµγµ are calledelectromagnetic potentialsbecause they correspond
to including an electromagnetic field in the physical situation under consideration, except for a multiplication by the complex uniti. If the physical potential is given by the ‘‘four-vector’’Aµ
the new momentum is given byi∂µ−Aµ, so the ‘‘physical case’’, in the expression ofv, is given
by purely imaginary components.
If we write the potential as a 1-forma = aµdxµ, the electromagnetic field is given by its
exterior derivative
F=da.
The 2-formFis often described by its tensor components,
Fµν =∂µaν −∂νaµ.
Electromagnetic fields obey Maxwell’s equation, which in vacuum are written
In these equations jν is the density of electrical charge and current, and the notation [·] means
that we sum over all the permutation of the indexes in brackets, taking in consideration the parity of the permutation (For example: B[µν] = Bµν −Bνµ, B[µCν] = BµCν −BνCµandB[µCνρ] =
BµCνρ +BνCρµ+BρCµν −BµCρν−BνCµρ −BρCνµ.). The second equation is automatically
obeyed, as long asFµν is obtained from a potential. Inside matter the second Maxwell equation
remains valid (which implies, from Poincaré’s lemma that, locally, the electromagnetic field can be obtained from a potential).
In classical physics the field at each point is observable, while the potentials are considered just a technique for calculating such field, having no separate reality (This changes dramatically in Quantum Mechanics, as can be seen by the Aharonov-Bohm effect. See, for example (Sakurai 1967)). This means that adding an exact formdθto the potential should not change the field (which is obvious from the fact that d2=0). In terms of its components, this means to change from a
µ
toaµ′ = aµ+∂µθ. As the Huygens’ property is a physically sound problem, the validity or not
of the Huygens’ principle cannot depend on the particular choice of the electromagnetic gauge (to understand the idea that Huygens’ principle is physically observable we should understand the meaning of,, the solution of Dirac equation. Following Section 1.7.3 of (Thaller 1992), we say that for every Borel-measurable setB∈R3the probability of finding the particle inBis given by ,, E(B),, whereE(B)is a projection operator inBand the inner product should be interpreted as Hilbert space inner product where the Dirac operator is acting and the solution , lives. In simpler words, we have a non-zero probability of finding the particle only on the support of the wave-function.).
The change of the gauge is a particular kind of trivial transformation, as defined in the intro-duction. We see immediately
∂ +(aµ+∂µθ )γµ=e−θ(∂ +aµγµ)eθ ,
so the change of the gauge does not change the validity of the Huygens’ principle.
Thus, the invariance of Huygens’ principle by change of gauge can be concluded by two distinct reasonings, coming from two different points of view, historically unrelated. We point out that, as far as we know, the fact that the change of electromagnetic gauge is a particular case of trivial transformations as defined by Hadamard was never mentioned in the literature.
After these remarks we are ready to state:
Theorem1. If a Dirac operator∂+aµγµobeys Huygens’ property for real or purely imaginary potentialsaµin 3+1 dimensions, then it is equivalent to the free operator∂.
Proof. Let us define
fµ(x, y) def
= aµ(x)−∂µ 1
0
(xν −yν)aν(ξ(z))dz ,
whereξ(z)=y+z(x−y). The first remark is that
which shows thatf andaare gauge equivalent. Explicitly, the change of gauge is given by
∂ +fµγµ=e−θ(∂ +aµγµ)eθ ,
where
θ (x, y)def= −
1
0
(xµ−yµ)aµ(ξ(z))dz .
From now on, the calculations will be made in the new gauge. The functionsfµcan be re-written as
fµ(x, y)= 1
0
(xν −yν)Fνµ(ξ(z))z dz , (4)
and, so, by the anti-symmetry of the tensorFµν we have
(xµ−yµ)fµ(x, y)=0 ∀x, y ∈R4. (5)
Since Hadamard’s recursion stops at the second term, Hadamard’s recursion becomes
s0+
2
α0+n−1
(xµ−yµ)∂µs0 = 1, α0→ −n+1,
s1=(∂ +fµγµ)1 = γµfµ def
= f .
s2+(xµ−yµ)∂µs2 = −(∂+f )f , (∂+f )s2 = 0.
(6)
The first equation can be easily solved to gets0=1.
We shall study compatibility conditions between the last two equations. We start applying Dirac operator to the first:
2∂ u2+(xµ−yµ)∂µ∂ u2= −∂ (∂ +f )f .
With the second condition this can be written
2f u2+(xµ−yµ)(∂µf )u2+f (xµ−yµ)∂µu2= ∂ (∂+f )f .
Applying∂ν to equation (5) we find that(xµ−yµ)∂νfµ = −fν which allows one to write the
equation
(xµ−yµ)∂µf =γµ(xν−yν)Fνµ−f .
Finally we write
γµ(xν−yν)Fνµu2=(∂ +f )(∂ +f )f . (7)
The RHS of last equation is
Forx = y, it is immediate to see thatf (x, y) = 0. So, the only non-zero term inx = y in the RHS isf. Actually,
fµ=∂ρ∂ρ 1
0
(xν −yν)Fνµ(ξ )z dz=2 1
0
∂ρFρµ(ξ )z2dz+ 1
0
Fνµ(ξ )z3dz .
Lettingy →x
f (x, x)= 2 3γ
µ∂νF νµ(x) .
As the LHS of equation (7) is zero at(x, x), we conclude that
∂νFµν =0 µ=0,· · · , n (8)
is a necessary condition for the operator∂ +aµγµto be a Huygens one. This can be interpreted
as the absence of sources.
To get a second necessary condition, we apply
˜
∂η def
= ∂
∂yη
to the LHS of equation (7) and evaluate it at(x, x). We get
˜
∂ηf (x, x) =
1 6γ
µ∂
η∂ρFρµ−
1 4γ
µ Fηµ;
˜
∂η∂ f (x, x)2 = 2γµ(∂µfν)(x, x)(∂˜ηfν)(x, x);
˜
∂η(f∂ f )(x, x) = (∂˜ηf )(x, x)(∂ f )(x, x);
˜
∂ηf (x, x)3 = 0.
Taking into account equations (4) and (8) the above system can be re-written as
˜
∂η(∂ +f )2f (x, x)=
1 2γ
µ
(F2)µν −
1 4γ
µ
γνγρFηµFνρ,
where(F2)
µν indicates the(µ, ν)component of the tensor given by the square of the matrixF, (F2)
µν def
=FµρFρν.
The RHS of equation (7) gives
˜
∂η[γµ(xν−yν)Fνµu2](x, x)= −γµFηµu2(x, x) ,
andu2(x, x)can be easily obtained from equation (6):
u2(x, x)= −(∂+f )f (x, x)=
1 2γ
µγνF µν.
We gather all this information in a single equation, written in the Clifford base as
γµ(F2)µη+
3 4
µ<ν<ρ
where, as before[·]means that we sum over all the permutation ofµ,νandρtaking in consideration the parity of the permutation.
From the independence of the generators of the Clifford Algebra, we conclude that
(F2)µν =0 and Fη[µFνρ]=0 ∀µ, ν, ρ, η=0,· · · ,3.
Let us write(F2)componentwise:
(F2)µν =FµρFρν =
=
Ex2+Ey2+Ez2 EzBy−EyBz ExBz−EzBx EyBx−ExBy EzBy−EyBz By2+Bz2−Ex2 −ExEy−BxBy −ExEz−BxBz ExBz−EzBx −ExEy−BxBy Bx2+Bz2−Ey2 −EyEz−ByBz EyBx−ExBy −ExEz−BxBz −EyEz−ByBz Bx2+By−Ez2
,
whereEx,Ey,Ez,Bx,ByandBzare thex,yandzcomponents of the electric and magnetic fields,
respectively.
From the conditionF2=0 and the hypothesis that all the potentials are either real or purely imaginary (so are the fields), we conclude thatEx =Ey=Ez =Bx =By=Bz=0, soFµν =0
andais gauge equivalent to the zero field.
Remark2. If we relax the hypothesis that the potential is real or purely imaginary, then we can find a large class of Huygens potentials. One family of examples is given by
a0= −a3= R
ε(ω)eiω(x3−x0)(x1−ix2)dω a1=a2=0,
whereε(ω)is any function such thatε(ω)=ε∗(−ω)and∗denotes complex conjugation.
5. CONCLUSIONS
Huygens’ principle has been subject of extensive investigation in recent times. For reviews in two different directions, see (Berest 1998) and (Belger et al. 1997). One of its most striking characteristics is its relations to integrability (see (Berest and Veselov 1994)). In the wave operator case, potentials of Huygens’ type are, after a suitable change of variables, solutions of the Korteweg-de Vries equation
ut =uxxx−6uux.
For Dirac operators, the relation between Huygens’ principle and integrability involves the AKNS (after Ablowitz, Kaup, Newell and Segur) hierarchy, which in turn is an example of integrable matrix systems. This is proved in (Chalub and Zubelli 2001b).
ACKNOWLEDGMENTS
I thank Prof. Jorge P. Zubelli for introducing me on this subject and for many suggestions. This work was supported by the Brazilian Agencies CNPq and CAPES.
RESUMO
Neste artigo estudamos o comportamento das soluções da equação de Dirac sem massa (‘‘massless Dirac particles’’) na presença de um campo eletromagnético. Nosso resultado (Teorema 1) indica que para campos reais ou puramente imaginários todo operador de Dirac que obedece ao princípio de Huygens é equivalente ao operador trivial, equivalência dada por mudanças de variáveis e multiplicação, à direita ou esquerda, por funções não singulares.
Palavras-chave: princípio de Huygens, operadores de Dirac, campos eletromagnéticos, problema de Hadamard.
REFERENCES
Belger M, Schimming R and Wünsch V.1997. A survey on Huygens’ principle. Z Anal Anwendungen, 16(1): 9–36. Dedicated to the memory of Paul Günther.
Berest Y and Veselov AP.1994. The Huygens principle and integrability. Uspekhi Mat Nauk, 49(6(300)): 7–78.
Berest Y.1998. Hierarchies of Huygens’ operators and Hadamard’s conjecture. Acta Appl Math, 53(2): 125–185.
Born M and Wolf E.1980. Eletromagnetic Theory of Propagation, Interference and Diffraction of Light. Pergamon Press, sixth edition.
Chalub FACC and Zubelli JP.2000. Integrable systems, Huygens’ principle, and Dirac operators. In Proceedings of the Workshop on Nonlinearity, Integrability and All That: Twenty Years after NEEDS ’79 (Gallipoli, 1999), pages 89–96, River Edge, NJ. World Sci. Publishing.
Chalub FACC and Zubelli JP.2001a. On Huygens’ Principle for Dirac Operators and Nonlinear Evolution Equations. J Nonlin Math Phys, 8, Supplement: 62–68.
Chalub FACC and Zubelli JP.2001b. Huygens’ Principle, Dirac Operators and Rational Solutions of the AKNS Hierarchy. Submitted.
Dirac PAM.1928. The Quantum Theory of the Electron. Proc Roy Soc of London A, 117: 610–624.
Fresnel A.1816. Ann Chim et Phys, (2), 1, 239. in Oeuvres, Vol 1, 89, 129.
Folland GB.1997. Fundamental solutions for the wave operator. Exposition Math, 15(1): 25–52.
Gilbert JEand Murray MAM. 1991. Clifford algebras and Dirac operators in harmonic analysis. Cambridge University Press, Cambridge.
Publica-tions, New York.
Huygens C. 1920. Traité de La Lumiére, où sont expliquées les causes de ce qui luy-arrive dans la reflexion, et dans la refraction et particulièrement dans l’etrange refraction du Cristal D’Islande. Societé Hollandaise des Sciences, 1920. Reprint of the 1690 original, Librarie Marchand.
Marchuk NG.1998. Diracγ-equation, classical gauge fields and Clifford algebra. Adv Appl Clifford Algebras, 8(1): 181–225.
Newton I.1979. Opticks. A treatise of the Reflexion, Inflexion and Colours of Light. Dover Publications, New York.
Sakurai JJ.1967. Advanced Quantum Mechanics. Addison Wesley.
Shapiro A. 1980. Huygens’ kinematic theory of light. In Studies on Christiaan Huygens. Swets and Zeitlinger B.V., Lisse.