Arquivos - Teoria das Estruturas UnB

SUMÁRIO

1. Introdução... 3

2. Energia de Deformação... 6

2.1. Energia de Deformação Elástica para Tensões Normais ...6

2.2. Energia de Deformação Elástica para Tensões na Flexão...10

2.3. Energia de Deformação Elástica para Tensões de Cisalhamento ...13

2.4. Energia de Deformação Elástica para a Torção ...15

2.5. Energia de Deformação Elástica para Estados Múltiplos de Tensão ...18

2.6. Deformações pelo Método da Energia...21

3. Método Dos Trabalhos Virtuais ... 25

3.1. Corpos Rígidos ...25

3.1.a. Introdução... 25

3.1.b. A Idéia do Trabalho Virtual... 26

3.1.c. Princípio e Aplicação do Método dos Trabalhos Virtuais... 27

3.1.d. Conclusões e Vantagens do Método dos Trabalhos Virtuais ... 29

3.2. Corpos Deformáveis ...33

3.2.a. Equações dos Trabalhos Virtuais para Sistemas Elásticos... 35

3.2.b. Cálculo de Deformações devidas à Variação de Temperatura... 39

3.2.c. Cálculo de Deformações causadas por Recalques ... 40

3.2.d. Cálculo de Deformações devidas à Montagem... 41

4. Teoremas Complementares ... 56

4.1. Teorema de Betti-Maxwell ...56

4.2. Método da Energia Potencial Total...63

4.3. Teorema de Castigliano ...68

4.3.a. Conceitos Preliminares de Energia de Deformação e Energia Complementar de Deformação ... 68

4.3.b. Demonstração dos Teoremas (Trabalho Real de Deformação)... 68

4.3.c. Discussões ... 70

5. Referências Bibliográficas ... 80

1.

INTRODUÇÃO

Nos casos anteriores, as equações de equilíbrio foram sempre utilizadas na solução dos

problemas básicos de Mecânica das Estruturas. Um outro conceito fundamental para a solução destes

problemas é baseado no Princípio da Conservação de Energia. Métodos de análise dos problemas, que

apresentam aplicações genéricas, resultam do uso deste conceito, e serão os objetos de estudo desta parte

inicial da disciplina.

Em Mecânica, a energia é definida como a capacidade de produzir trabalho. O trabalho, por sua

vez, é definido como o produto de uma força pela distância na direção em que a força se move.

Nos corpos sólidos deformáveis, as tensões multiplicadas pelas áreas são forças, enquanto as

deformações (deslocamentos) são distâncias. O produto destas duas grandezas constitui o trabalho interno

efetuado em um corpo pelas forças externas aplicadas. Este trabalho interno é armazenado no corpo como

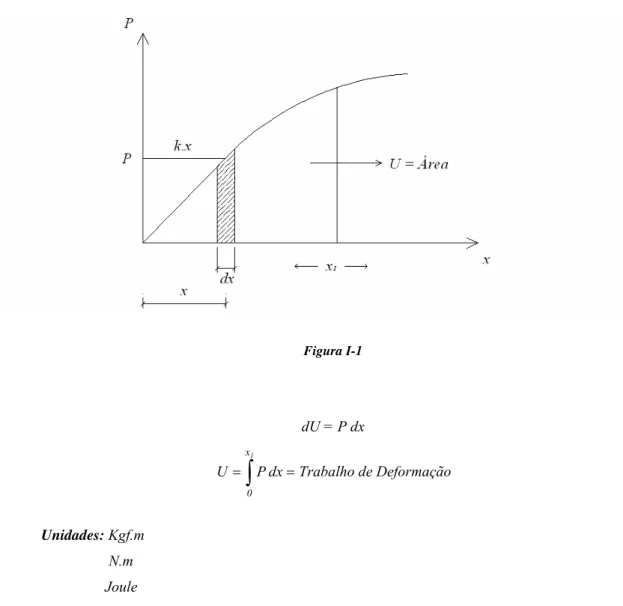
Energia Interna Elástica de Deformação ou Energia Elástica de Deformação ou Trabalho de Deformação.

Figura I-1

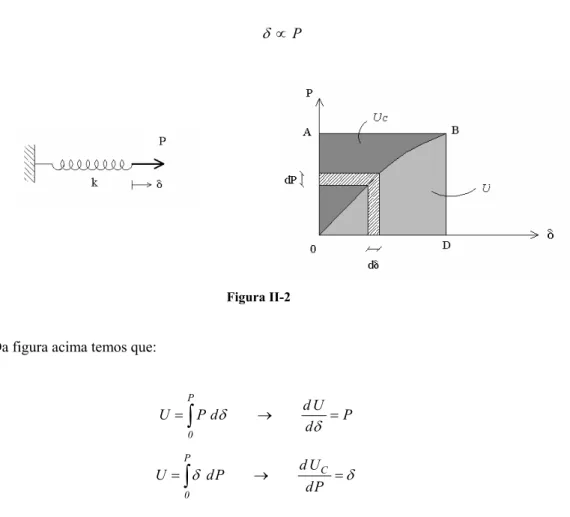
dU = P dx

∫

=

1 x

0 dx P

U Trabalho de Deformação

Para a zona linear do diagrama, tem-se:

P = K x

∫

U Æ Kx₁2

2 1 U =

Determinar o Trabalho de Deformação do sistema abaixo:

As barras c e d são do mesmo material.

A Energia de Deformação Elástica para Tensões Normais é dada pela equação

A E 2 L P U 2 = .

Para a situação dada, tem-se:

U = U1 + U2

2 2 2 2 1 1 2 1 A E 2 L P A E 2 L P

U = +

2 L L L₁= ₂ =

P1 = P2 = P

2 2

2

2 2

P L P L

U

2 .2 .E . A 2 .2 .E .η . A

= +

2

2 2

P L 1

U 1

4 E A η

⎡ ⎤

= ⎢ + ⎥

⎣ ⎦

ª Para η = 1,0 Æ A1 = A2

2 2 1 A E 2 L P U =

A1 = η2 . A2

A E 2 d . A 4 2 π = E

ª Para η = 2,0 Æ A1 = 4,0 A2

⎥⎦ ⎤ ⎢⎣ ⎡ ₊

= 1

2 1 A E 4

L P U

2 2 2

2

⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ =

2 2

2

A E 2

L P 8 5 U

Portanto, para η > 1,0, tem-se: U2 < U1.

A P máx =

σ Æ Com uma dada σadm o aumento da seção diminui a capacidade de absorção da

2.

ENERGIA DE DEFORMAÇÃO

2.1.

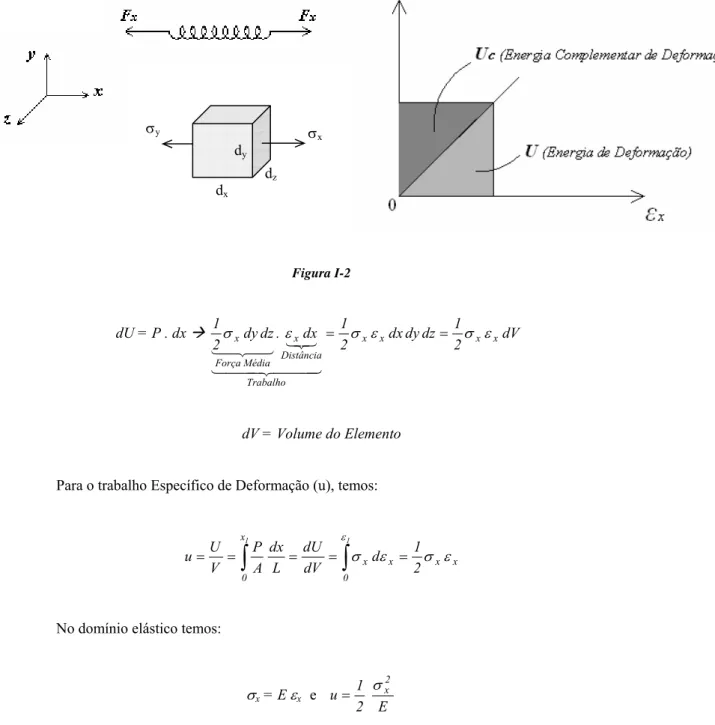
Energia de Deformação Elástica para Tensões Normais

Figura I-2

dU = P . dx Æ dV

2 1 dz dy dx 2 1 dx . dz dy 2 1 x x x x Trabalho Distância x Média Força

x ε σ ε σ ε

σ = =

4 4 4 3 4 4 4 2 1 3 2 1 43 42 1

dV = Volume do Elemento

Para o trabalho Específico de Deformação (u), temos:

x x x x 0 0 x 2 1 d dV dU L dx A P V U u 1 1 ε σ ε σ ε = = = = =

∫

∫

No domínio elástico temos:

σx = E εx e

E 2 1 u 2 x σ = ou 2 x vol

U d V

Figura I- 3

dV E 2

1 A N U

l

0 2 2

∫

l 2

0

N d x

U

2E A( x )

=

∫

Para A(x) = A = constante,

2 N L U

2 E A =

A seguir, apresentamos algumas aplicações:

Determinar o Trabalho de Deformação do sistema abaixo:

Energia de Deformação Elástica para Tensões Normais Æ

EA 2 PL U

2 =

E

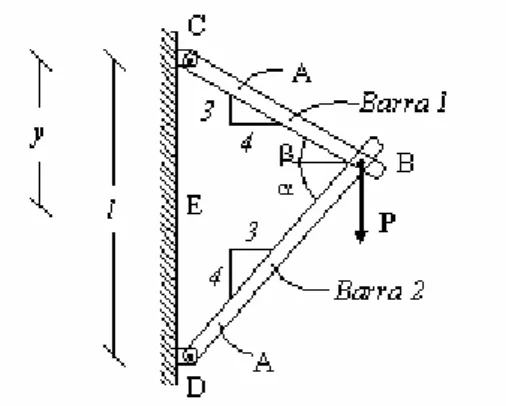
EXXEERRCCÍÍCCIIOO22

Equilíbrio no nó B: ° ≅ → = → = ° ≅ → = → = 13 , 53 3 4 tg arc 3 4 tg 87 , 36 4 3 tg arc 4 3 tg α α α β β β BD 6 , 0 EB BD EB cos BC 8 , 0 EB BC EB cos = → = = → = α β : 0 F_x

∑

( )

− β α

: 0 F_y

∑

( )

0,48 N 0,64 N 0,8 P

N 0,8 P

N 0,8 P

− − = ⎧⎪ ⎨ − = ⎪⎩ − = = − P 6 , 0 N 0 P ) P 8 , 0 ( 8 , 0 N 6 , 0 1 1 = = − − 0,8 0,8 0, 6 0, 6 EB

EB BC BC

EB

EB BD BD

= → =

= → =

0, 6 0,8

0, 6 0,8

0,8 0, 6

y l y

sen sen

BC BD

BC y BD l y

EB EB

y l y

β = α = −

= = −

= = −

0,8 0, 6

0, 6 0,8

0, 48 0, 48 0, 6 0,8 0, 48 0,8 0, 6 EB EB l EB l l BC l l BD l = − = = = = = 2 1 U U

U = +

2 2 2 2 2 1 1 1 2 1 A E 2 L P A E 2 L P

As duas barras são feitas do mesmo material, portanto, E1 = E2.

A1 = A2 = A

P1 = N1 = 0,6 P

P2 = N2 = 0,8 P

L1 = BC = 0,6 l

L2 = BD= 0,8 l

A E 2

l P 512 , 0 A E 2

l P 216 , 0 U

A E 2

l 8 , 0 ) P 8 , 0 ( A E 2

l 6 , 0 ) P 6 , 0 ( U

2 2

2 2

+ =

+ =

2 P l U 0,3 6 4

E A

=

Determinar o Trabalho de Deformação do sistema abaixo:

As duas barras (1 e 2) são feitas do mesmo material (E1=E2=E).

Equilíbrio no nó C: E

2 1

1 1 2

2

0 : cos 60 0

0 : 60 0

2 3

3

2 3 1

0 3 2 3 3 x y

F N N

F N sen P

P N P N P N = − − × ° = = × °− = = − − × = = −

∑

∑

U = +

2 2 2 2 2 1 1 1 2 1 A E 2 L P A E 2 L P

U= +

1 1 1

2 2 2

2 3 2 3 3 3 P

P N L B C l

P

P N L C D l

= = = =

= − = = =

2 2 2

4 3 P 2l 3 P l 27 P L

U

9 2 E A 9 2 E A 18 E A

⎛ × × ⎞

=⎜_⎜ × ⎟_⎟+ × =

⎝ ⎠

2 3 P L U

2 E A =

2.2.

Energia de Deformação Elástica para Tensões na Flexão

Sabe-se que:

2 x

vol

U d V

2 E σ

=

∫

I My x =−

σ (ii)

(

)

M y 1

U dV

2 E I

dV d A d x

M

U y d A dx

2 E I

y d A I

= = = =

∫

∫

∫

U d x

2 E I

=

∫

Para a área de seção transversal e M(x) constantes, temos:

2 M L U

2 E I

=

Determinar o Trabalho de Deformação da estrutura abaixo:

Energia de deformação devido à flexão:

I E 2 L M U 2 =

MS = – P x

∫

∫

S _{( Px) dx}

I E 2 1 U dx I E 2 M U l 2 2 0 x l 3 2 x 0 1

U P x d x

2E I

1 x

U P

2E I 3

= = = = × ×

∫

6 E I =

E

Determinar o Trabalho de Deformação da estrutura abaixo: Dado: E = 190 GPa

Energia de deformação devido à flexão:

2 M L U

2E I =

(DMF)

Trecho A,1Æ MS = 30x

Trecho 1,2Æ M = 9,0 KN.m Trecho 2,B Æ MS’ = 30x’

0 ,3 2 2 0 ,3 2

0 0

3 3

( 30 x ) ( 9,0 ) 0,6 ( 30 x )

U d x d x

2E I 2E I 2E I

900 0,3 81 0,6 900 0,3

U

2E I 3 2E I 2E I 3

32,4 U

E I

×

= + +

⎛ ⎞ ⎛ × ⎞ ⎛ ⎞

=⎜_⎜ × ⎟_⎟+_{⎜ ⎟}+⎜_⎜ × ⎟_⎟

⎝ ⎠

⎝ ⎠ ⎝ ⎠

=

∫

∫

6 2

3 3 3 3

4 x

E 190 10 K N /m

b h 40 10 ( 80 10 )

I I I m

12 12

− −

= ×

× × ×

= = → =

U=99,92 N .m E

2.3.

Energia de Deformação Elástica para Tensões de Cisalhamento

De maneira análoga ao que foi feito para o Trabalho Específico de Deformação (u) para as

Tensões Normais, podemos entender as Tensões Cisalhantes, isto é:

0

xy

xy xy

u d

γ

τ γ

=

∫

Figura I-4

Para materiais elásticos: τxy =Gγxy (ii) Substituindo (ii) em (i), obtemos:

0 2

2

2

2 x y

x y x y

x y

x y

u G d

G u

u G

γ

γ γ

γ

τ =

=

=

∫

Como dV dU

u= , obtemos:

2 xy

U dV

2 G τ

Determinar o Trabalho de Deformação da estrutura abaixo:

Energia de deformação para tensões cisalhantes:

2 x y U dV 2 G τ =

∫

3 Q y

1

2 A c

Q P

1 3 P y

U 1 dV

2G 2 b h c

dV b d x d y

1 3 P y

U 1 b d x d y

2G 2 b h c

τ = ⎛⎜_⎜ − ⎞⎟_⎟

⎝ ⎠ = ⎛ ⎞ ⎡ ⎤ = _{⎢ ⎥} × ⎜_⎜ − ⎟_⎟ ⎣ ⎦ _{⎝ ⎠} = ⎛ ⎞ ⎡ ⎤ = _{⎢ ⎥} × ⎜_⎜ − ⎟_⎟ ⎣ ⎦ _{⎝ ⎠}

∫

∫∫

2 2 2

c 0

c

2 2 4

2 2 4

c

y c

2 3 5

2 2 4

y c 2 2 2 2 9P y

U b 1 d y 1d x

2 4 G b h c

9P l 2 y y

U 1 d y

8 G b h c c

9P l 2 y y

U y

8 G b h 3c 5c

9P l 2c 2c c c

U 2c

3 3 5 5

8 G b h

9P l 30c 10c 10c 3c 3c

U

15 8 G b h

− − = =− ⎛ ⎞ = × × ⎜_⎜ − ⎟_⎟ × × _{⎝ ⎠} ⎛ ⎞ = × ⎜_⎜ − + ⎟_⎟ ⎝ ⎠ ⎛ ⎞ = ⎜_⎜ − + ⎟_⎟ ⎝ ⎠ ⎛ ⎞ = _⎜ − − + + _⎟ ⎝ ⎠ ⎛ − − + + ⎞ = _{⎜ ⎟} ⎝ ⎠

∫

∫

∫

2

2

2 2

2

2

2

9P l 16c

U

15 8 G b h

h 9P l 16 h 3P l

c U U

2 8 G b h 15 2 5 G b h

E 3P l

G U

E

3 _{5 b h}

3

9 P l U

5 E A

= ×

= → = × × → =

≥ → =

=

2.4.

Energia de Deformação Elástica para a Torção

Como _xy P T

J ρ

τ = , temos:

2 xy

2 2

T ₂

P

2 2

T ₂

P

2 P

2

T

P

U dV

2 G

T

U dV

2 G J

dV d A d x

T

U ( d A )d x

2 G J

d A J

T

U d x

2 G J τ

ρ

ρ

ρ =

=

=

=

=

=

∫

∫

∫

∫

∫

Para A = constante, temos:

L 2

P 0

2

P T

U d x

2 G J

T L U

2 G J

=

=

∫

Seção circular (diâmetro d) Æ

4

P d J

32 π

=

Determinar o Trabalho de Deformação do eixo maciço ABC abaixo: Dado: G = 41,4 GPa (o eixo é todo feito do mesmo material)

Energia de deformação para torção:

2

P T L U

2 G J

=

4

P d J

32 π

=

1 2

1 2

2 2

1 1 2 2

P P

U U U

T L T L

U

2 G J 2 G J

= +

= +

1 1

2 2

4

7 4 1

1 1 P P

4

7 4 2

2 2 P P

d

T 1,01 K N .m L 0,76 m J J 3,68 10 m

3 2 d

T 0,39 K N .m L 0,61 m J J 1,03 10 m

3 2 π

π

−

−

= − = = → = ×

= = = → = ×

E

EXXEERRCCÍÍCCIIOO77

d1 = 44 mm

d2 = 32 mm

TB = 1,4 kN.m

TC = 0,39 kN.m

A

C B

0,61 m 0,76 m

3 2 3 2

9 7 9 7

( 1,01 10 ) 0,76 ( 0,39 10 ) 0,61

U

2 41,4 10 3,68 10 2 41,4 10 1,03 10

U 36 ,32 N .m

− −

− −

− × × × ×

= +

× × × × × × × ×

=

Determinar o Trabalho de Deformação (U) e o deslocamento (δ_vc) em C para a estrutura abaixo:

a) U

F C N

l l

2 2 2 2 2 2 2

S S S"

0 0

l l

2 2 2 2 2 2

2 2

0 0

U U U U

M M 9 P l 9 P l N l

U dx d x

2 E I 2 E I 5 4 2 E A 5 4 2 E A 2 E A

1 P 1 P 9 P l P l

U x d x x d x

2 E I 4 2 E I 4 20 E A 8 E A

′

= + +

= + + + +

= + + +

∫

∫

∫

∫

E

EXXEERRCCÍÍCCIIOO88

2 3 2 2

2 3 2

2 2

2P l 18P l 5P l

U

8 E I 24 40 E A

P l 23P l

U

96 E I 40 E A

P l l 23

U

8E 12 I 5 A

+

= +

= +

⎛ ⎞

= ⎜_⎜ + ⎟_⎟

⎝ ⎠

b) δ_vc

c v

2 2 c

v

2 c

v 1

P U

2

1 P l l 23

P

2 8E 12 I 5 A

P l l 23

4E 12 I 5 A

δ

δ

δ

=

⎛ ⎞

= ⎜_⎜ + ⎟_⎟

⎝ ⎠

⎛ ⎞

= ⎜_⎜ + ⎟_⎟

⎝ ⎠

2.5.

Energia de Deformação Elástica para Estados Múltiplos de Tensão

Para um corpo elástico, isotrópico, submetido a um caso geral de tensões caracterizado pelas

suas componentes de tensão, o trabalho específico de deformação pode ser expresso por:

x x y y z z xy xy xz xz yz yz

xy xy xz xz yz yz

dU 1

u ( E E E )

dV 2

G G G

σ σ σ τ γ τ γ τ γ

τ γ τ γ τ γ

= = + + + + +

= = =

Utilizando as expressões acima e levando-se em conta a Lei de Hooke Generalizada, temos:

2 2 2 2 2 2

x y z x y y z x z xy yz xz

1 1

u 2v ( ) ( )

2 E σ σ σ σ σ σ σ σ σ 2 G τ τ τ

⎡ ⎤

= _⎣ + + − + + _⎦+ + +

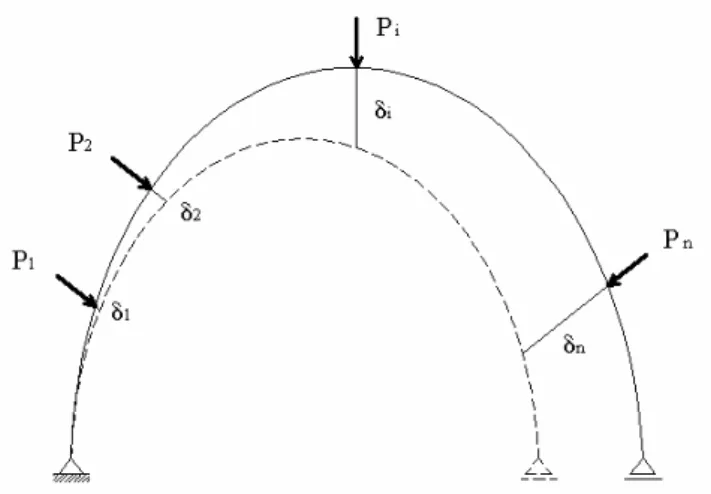
Para o caso geral de solicitação podem surgir simultaneamente todos os esforços externos (Nx,

Vy, Vz, Mx, My, Mz) em cada uma das seções transversais. O ponto de aplicação dos esforços sofre, ao

corpo deformar-se, certos deslocamentos devido aos quais unicamente realizam-se trabalhos na direção de

cada um dos esforços individualmente, isto é, numa dada direção de um esforço, só este realiza trabalho,

Logo, a energia de deformação de uma barra pode ser interpretada como o somatório das

energias independentes de cada um dos seis esforços.

U=U ( N )_x +U (V )_y +U (V )_z +U ( M )_x +U ( M )_y +U ( M )_z (i)

Considerando uma estrutura reticulada com n barras e levando-se em conta as equações

anteriores, (i) pode ser escrita da seguinte forma:

i i i i i i

i i i i i i

l 2 l 2 l 2 l 2 l 2 l 2

n

x y z x x y

i i i i i i i i

i i i i i i i i i i i i

i 1 0 0 0 0 0 0

M M M N V V

1

U d x d x dx d x y d x z d x

2 ₌ E I E I E I E A Χ G A Χ G A

⎡ ⎤

⎢ ⎥

= + + + + +

⎢ ⎥

⎣ ⎦

∑ ∫

∫

∫

∫

∫

∫

Nem sempre todos os termos da equação (ii) têm a mesma importância. Na maioria dos sistemas

que trabalham à flexão ou à torção os três últimos termos da referida equação são muito menores e podem

ser desprezados.

A seguir, faremos uma aplicação para tornar mais claro o assunto aqui tratado.

Obter UTOTAL para a viga da figura abaixo:

UT = U (Mz) + U (Vy)

Estes dois termos já foram determinados nas partes anteriores de nosso estudo.

2

l ₂ l

xy T

0 0

M ( x )

U d x dV

2 E I 2 G

τ

=

∫

∫

ou seja,

2 3 2

T

P l 9 P l

U

6 E I 5 E A

= +

E

EXXEERRCCÍÍCCIIOO99

Mz (x) Vy (x)

2 3 3

T 2

2 3 2

T ₂

P l 9 b h 6

U 1

6 E I 5 l b h 12

P l 18 h

U 1

6 E I 20 l

⎛ ⎞ = ⎜_⎜ + ⎟_⎟ ⎝ ⎠ ⎛ ⎞ = ⎜_⎜ + ⎟_⎟ ⎝ ⎠

2 3 2

T ₂

P l h

U 1 0,9

6 E I l

⎛ ⎞

= ⎜_⎜ + ⎟_⎟

⎝ ⎠

Para h 1 ( 1 0,09 ) 0,9 %

l ≤10 → + ≠

Na prática, costuma-se desprezar o efeito de cisalhamento para relações h 1

l ≤10 .

ª Existe uma outra forma de evidenciar a Energia de Deformação devido ao cisalhamento:

2 xy V 2 y z z V 2 l 2 y z 2 2 z 0 2 l y y 0 1 U dV 2 G

V ( x ) Q ( y ) d A

U d x

I b( y ) 2 G

V ( x ) A Q ( y )

U d A

2 G A I b ( y )

V ( x )

U d x

2 G A

τ τ τ τ τ Χ = ⎡ ⎤ = _{⎢ ⎥} ⎣ ⎦ = =

∫

∫

∫

∫

I b y

Χ =

∫

y

Χ é função da configuração geométrica da seção.

Para A = constante = bh, temos:

2 h h 2 2 y 2 3 _h y 2 y

b h 1 6

y b d y d y

b 5 b h 12 6 5 Χ Χ − ⎛ ⎞ ⎜ ⎟ = _{⎜ ⎟} = ⎡ ⎤ ⎜_⎝ ⎟_⎠ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ =

∫

∫

Seção retangular Æ

Determinar U para uma barra circular com um momento torçor (T) constante, em termos de

τ

2 xy

V

2 2 máx

2 V

2 R

máx 3

2 0

U dV

2 G

U 2 d L

2 G R

2 L

U d

2 G R τ

τ ρ

π ρ ρ

τ _π

ρ ρ

=

=

=

∫

∫

∫

2 ₄

máx 2

2 máx

2 L R U

2 G R 4

1

U V

2 G 2

τ π

τ

=

⎛ ⎞

= _{⎜ ⎟}

⎝ ⎠

2.6.

Deformações pelo Método da Energia

Com a determinação da Energia de Deformação conforme as expressões desenvolvidas nos

parágrafos anteriores, podemos calcular as deformações (deslocamentos) num dado ponto da estrutura,

provocado unicamente por uma força aplicada na direção e no ponto em que se deseja conhecer o

deslocamento, ou seja: E

EXXEERRCCÍÍCCIIOO1100

xy 0

xy máx T

J

R

d A 2 d

ρ τ

ρ

τ τ

π ρ ρ

=

=

U =W_ext (trabalho externo provocado pela força aplicada)

ext 1

U W P

2 Δ

= = ×

A força externa é aplicada gradualmente, isto é, o efeito final sobre o material é atingido

gradualmente a partir do valor inicial igual a zero.

As aplicações seguintes esclarecerão o assunto aqui tratado.

Calcular o deslocamento δ na estrutura da barra submetida ao esforço apresentado na figura abaixo:

2 xy

l 2 xy 0

l 2

2 0

2

U dV

2 E

b h

U d x

2 E

b h P

U d x

2 E A

P l U

2 E A τ

τ

=

=

=

=

∫

∫

∫

Como U W_e 1P _b

2 δ

= = ,

2

b

b

P l 1

P 2 E A 2

P l E A

δ

δ

=

=

E

Calcular a rotação φ indicada da barra submetida ao esforço apresentado na figura abaixo:

Sabemos que: _máx P T R

J

τ = V =πR l2

4

P R J

2 π

=

2 xy

V

2 máx

2 2

2 2 P

2

P

U dV

2 G

V U

2 G 2

T R 1

U R l

2 2 G J

T l U

2 G J τ

τ

π

=

=

=

=

∫

e

2

P

P 1

U W T

2

T l 1

T 2 2 G J

T l G J

φ

φ

φ

= =

=

=

E

EXXEERRCCÍÍCCIIOO1122

T

a

Para a estrutura abaixo, calcular o δ_B levando-se em conta a flexão e o cisalhamento.

z y

2 3 2 U U( M ) U(V )

P l 9 P l

U U U

6 E I 5 E A

= +

= _σ + _τ = +

e B

2 3 2

B

3

B

1

U W P

2

1 P l 9 P l

P

2 6 E I 5 E A

P l 18 P l

3 E I 5 E A

δ

δ

δ

= =

= +

= +

3 3

B 2

3 2

B ₂

P l 54 b h

1

3 E I 5 l 12 A

P l h

1 0,9

3 E I l

δ

δ

⎛ ⎞

= ⎜_⎜ + ⎟_⎟

⎝ ⎠

⎛ ⎞

= ⎜_⎜ + ⎟_⎟

⎝ ⎠

Para

3

B

h 1 P l

l ≤10 → δ ≅ 3 E I

E

EXXEERRCCÍÍCCIIOO1133

3.

MÉTODO DOS TRABALHOS VIRTUAIS

3.1.

Corpos Rígidos

3.1.a.Introdução

Seja, por exemplo, o conceito do trabalho realizado por uma força sobre uma partícula (P).

Figura I-5

Para um deslocamento diferencial dr, temos que:

dU= ×F d rr r (1) ou,

dU=F ( ds cos ) ( F cos )dsθ = θ (2) ds= drr

Forças perpendiculares ao deslocamento não produzem trabalho. (θ = ° →90 U=0)

Sinal:

9 U > 0 quando F cos θ e ds têm o mesmo sentido; 9 U < 0 quando F cos θ e ds têm sentidos opostos.

Podemos interpretar ainda F cos θ como a componente de F (Ft) tangente à trajetória.

ds=arco=ρ θd onde: ρ = raio instantâneo de curvatura

De (2) vem:

t

M=F ρ= momento de F em relação ao centro de curvatura

O conjunto de forças que atuam sobre um corpo pode ser reduzido a um sistema força-binário,

em relação a qualquer ponto de referência (0).

R

ur

é independente de (0), mas não M .uur

O trabalho de todas as forças externas sobre o corpo rígido pode ser dado como:

dU=ur ur uuurR dr₀+M dθ₀ (4)

A equação (4) apresenta uma dualidade:

“Rur, que independe do ponto de referência (0) x escalarmente drur₀ (do ponto de referência), ao

passo que M0

uuur

, que depende de (0) é x escalarmente pelo deslocamento angular (dθ) que independe do

referencial.”

Para um corpo rígido só as forças externas realizam trabalho.

Figura I-6

Devido à rigidez do corpo rígido, os deslocamentos δA e δB têm componentes iguais ao longo da

linha de ação do par de forças urF .

3.1.b.A Idéia do Trabalho Virtual

O Método dos Trabalhos Virtuais está baseado nas relações entre as forças aplicadas e os

movimentos dessas forças que correspondem a um pequeno movimento do sistema.

Este possível movimento (que na realidade não ocorre) é qualquer movimento infinitesimal que

seja compatível com os vínculos do sistema.

ª “Deslocamento Virtual” (δr)

De (1) temos:

Seja, por exemplo, determinar Furem CD quando atua urPem AB, para manter-se o equilíbrio do

sistema. Esta tarefa se torna simples utilizando-se o Método dos Trabalhos Virtuais (MTV). Para sua aplicação, basta utilizarmos a seguinte expressão:

n

ext virtual i 1

F δ 0

=

× =

∑

A partir de um deslocamento compatível com as vinculações do sistema, por exemplo, o da

Figura I-7(b), onde a estrutura é deslocada ligeiramente da posição de equilíbrio, obtemos de (6):

P F

s s

P (δ )=F (δ )

onde o valor de F é encontrado, uma vez que são conhecidos os valores de P s δ e

F s

δ . Logo, o problema

de equilíbrio é transformado num problema geométrico. Como em muitos casos é fácil analisar a

geometria do movimento, as soluções são simples.

Vantagens:

9 Eliminam-se as reações de apoio (não existe movimento Æ os mesmos não realizam trabalho); 9 Trabalha-se com quantidades escalares.

3.1.c.Princípio e Aplicação do Método dos Trabalhos Virtuais

Seja utilizar o Método dos Trabalhos Virtuais (MTV) para dois problemas de equilíbrio:

1º) Determinar os esforços para manter o equilíbrio;

2º) Achar a posição de equilíbrio, quando todas as forças são conhecidas.

Nota: Nenhum trabalho real é realizado e nenhum movimento ocorre (as quantidades são vinculares, potenciais, hipotéticas).

Para tal traçam-se alguns vínculos especificados ou algumas condições de uma dada situação.

Podemos supor que ocorre um dado movimento, que é pequeno (diferencial) para não mudar a geometria

da configuração original. Troca-se o símbolo diferencial d por δ. De (4) temos:

0

r 0

dU =Rδ +M δ_θ

0

x y z

0 x y z

r x y z

x y z

R ( F )i ( F ) j ( F )k

M ( M )i ( M ) j ( M )k

i j k

i j k

θ θ θ θ

Σ Σ Σ

Σ Σ Σ

δ δ δ δ

δ δ δ δ

= + +

= + +

= + +

= + +

r r r

r r r

r r r

r r r

Efetuando os produtos escalares:

U ( F )x x ( F )y y ( F )z z ( M )x θx ( M )y θy ( M )z θz

δ = Σ δ + Σ δ + Σ δ + Σ δ + Σ δ + Σ δ

ou seja,

0 0 r

U R M _θ

δ =urδur+uuurδur

Como pra um sistema em equilíbrio ΣurF= =Rur 0 e ΣuuurM₀ =Muuur₀ =0 (em relação a um ponto arbitrário (0)), vem:

U 0

δ =

isto é:

“O Trabalho Virtual realizado sobre um corpo rígido ou um sistema de corpos rígidos em equilíbrio é nulo para qualquer deslocamento virtual compatível com os vínculos do sistema.”

Princípio dos Trabalhos Virtuais

Com relação aos vínculos de um sistema, estão associados aos graus de liberdade do sistema

(igual ao número de coordenadas independentes para dar uma configuração única ao sistema). Por

exemplo, vínculos de um ponto de referência fixo e de movimento no plano, nos dão somente um grau de

liberdade (ver Figura I-8(a)).

Logo, o número de incógnitas (forças ativas ou posições de equilíbrio que podem ser

determinadas pelo Método dos Trabalhos Virtuais) é igual ao número de graus de liberdade do sistema, já

que para cada coordenada independente pode mos escrever uma equação de trabalhos virtuais. Ou seja,

para vários graus de liberdade o trabalho virtual total é dado pela seguinte equação:

U U

U x y

x y

δ =∂ δ +∂ δ

∂ ∂

onde várias equações independentes podem ser obtidas variando-se um deslocamento independente por

vez.

3.1.d.Conclusões e Vantagens do Método dos Trabalhos Virtuais

1. Somente as forças externas realizam trabalho Æ não há necessidade de desmembrar o sistema; 2. As reações nas articulações fixas ou forças que são perpendiculares a um deslocamento virtual

não realizam trabalho. Ao invés de representarmos todas as forças externas como no D.C.L.,

usamos um diagrama de forças ativas (DFA) que mostra apenas as forças que realizam trabalho

durante um deslocamento virtual;

3. Tem-se pouca vantagem para aplicá-lo a um único corpo, e apresenta dificuldades para ser

aplicado a sistemas que envolvem forças de atrito.

Para a estrutura abaixo, calcular o V_B e o M_C.

Cálculo de VB :

ª E

EXXEERRCCÍÍCCIIOO1144

A B C

B C

y 0 y 4 y 2

y 4 _θ y 2 _θ

θ θ

δ δ δ δ

= = =

= =

PTV (corpos rígidos) Æ δU_E =0 4,0 2δ_θ

− × +V_B×4δ_θ

B

0

V 2,0 t

=

Cálculo de MC :

Calcular, no sistema abaixo, θ para a nova posição de equilíbrio.

PTV (corpos rígidos) ÆδU_E =0 Æ P yδ _B−Fδy_C =0 F =K s

(

)

C C

y h s s y h s 2l sen h

F k 2l sen h

θ θ

= + → = − → = −

= −

E

EXXEERRCCÍÍCCIIOO1155

A D C E B

D C E

y 0 y y 2 y y 0

y _θ y 2 _θ y _θ

θ θ θ

δ δ δ δ δ δ

= = = = =

= = =

PTV (corpos rígidos) ÆδU_E =0 2,0δ_θ −M_C×δ_θ −M_C×δ_θ +2,0δ_θ

C

C

0

2,0 M 4,0 . ( 1 )

M 2,0 t.m

=

− = − −

=

B

C B

B y

C

C y

y

sen y l sen l cos

l

y

sen y 2l sen 2l cos

2l

θ

θ

θ θ δ θ δ

θ θ δ θ δ

= → = → =

P l cosθ δ_θ − k 2l sen

(

)

(

)

2

2

2

0

P l cos 4 k l sen cos 2 k l h cos 0 cos

P l 4 k l sen 2 k l h 0

4 k l

θ θ θ θ θ

θ

⎡ ⎤ =

⎣ ⎦

− + = ÷

− + =

− senθ = −P l −2 k lh . ( 1 )

P 2 k h

sen

4 k l θ

− +

=

P 2 k h

arc sen

4 k l θ= ⎛_⎜ + ⎞_⎟

⎝ ⎠

Determinar o θ para a nova posição de equilíbrio, sendo dada a estrutura abaixo: Dado: k = 60 N/m

B D

B D

x 0,4 sen x 0,2 sen

x 0,4 cos _θ x 0,2 cos _θ

θ θ

δ θ δ δ θ δ

= =

= =

1 B s D

s D

U M 2 x F x

F k x

θ

δ = δ + δ − δ =

E

PTV (corpos rígidos) Æ Uδ =0

(

)

0,5 2 0,4 cos 60 0,2 sen 0,2 cos 0

0,5 0,8 cos 2,4 sen cos 0

sen 2 2sen cos

0,5 0,8 cos 1,2 sen2 0 . ( 2 )

1,0 1,6 cos 2,4 sen2 0 . ( 1 )

2,4 sen2 1,6 cos 1,0 0

36 ,3

θ θ θ

θ

δ θ δ θ θ δ

θ θ θ δ

θ θ θ

θ θ

θ θ

θ θ

θ

+ × − × × =

+ − =

=

+ − =

+ − = −

− − =

≅ °

Para o sistema abaixo determinar Q em função de P e F.

SF SB SC

SP SB

SQ SB

1 2 1 2

δ δ δ

δ δ

δ δ

= =

=

=

Aplicando o conceito do trabalho e do princípio dos trabalhos virtuais, temos Æ Uδ =0:

( )

(

)

SB SB SB

1 1

P cos F cos Q sen 0

2 2

P cos 2F cos Q sen 0

Q P 2F co tg

δ θ δ θ δ θ

θ θ θ

θ

⎛ ⎞ _{+ −} ⎛ ⎞ ₌

⎜ ⎟ ⎜ ⎟

⎝ ⎠ ⎝ ⎠

+ − =

= +

E

3.2.

Corpos Deformáveis

As idéias vistas nas seções anteriores servem como fundamento para a compreensão do Método

dos Trabalhos Virtuais aplicado aos corpos deformáveis.

Não é fácil imaginar que um corpo (estrutura) ou sistema mecânico em equilíbrio, pode ser

arbitrariamente deslocado (deformado) de forma compatível com suas condições de contorno (vínculos).

Durante este processo, as forças reais que agem sobre o corpo movem-se ao longo de deslocamentos

imaginários (virtuais). Da mesma forma às forças imaginárias ou virtuais ou equilíbrio no sistema

considerado, podem ser dados deslocamentos reais e cinematicamente admissíveis. Nos dois casos

pode-se formular o trabalho virtual depode-senvolvido.

Em virtude da extensão do programa de Teoria das Estruturas 1, e a conseqüente necessidade de

tornar este curso mais aplicado, deixar-se-á de apresentar neste texto a formulação mais geral e elegante,

baseada na análise tensorial, e em seu lugar, mostramos o Método dos Trabalhos Virtuais por um

caminho mais físico e intuitivo. Para um maior aprofundamento, sugerimos ao leitor se reportar às

referências nos 23,24 e 26 do Programa do Curso.

Para as forças e deslocamentos que ocorrem no sistema, o princípio da conservação da energia

permanece válido, e a variação virtual no trabalho externo (δW_e,i), isto é:

δW_e =δW_e,i (7) Esta equação expressa matematicamente o Princípio dos Trabalhos Virtuais.

e,i

W 0

δ = Æ para sistemas rígidos

e,i

W U

δ =δ Æ para sistemas elásticos

U

δ =variação virtual na energia de deformação interna

A equação (7) é absolutamente geral para qualquer comportamento do material, carregamento ou

vinculações.

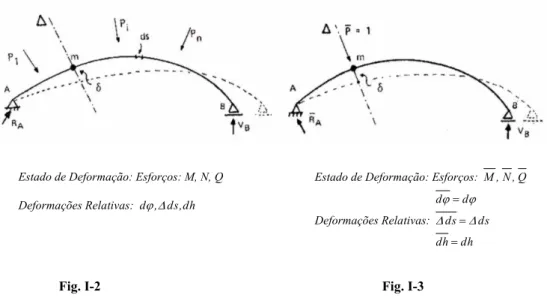
Seja o esquema da Figura I-9 para a demonstração do Princípio dos Trabalhos Virtuais (PTV).

(a) Estado A _{(b) Estado B}

1 2 n

P ,P ,...,P =forças externas (reais); F

δ =força virtual aplicada no corpo descarregado na direção AB;

f

δ =forças internas (que podem ser calculadas no sistema estaticamente determinado)

provocadas por Fδ

Com δF aplicado ao corpo (Estado A) introduz-se as forças reais (P ,P ,...,P_{1 2 n}) ou deformações específicas, como as provocadas pela temperatura, recalques, etc., que por sua vez, provocam

deslocamentos (deformações) internas reais (ΔL), que podem ser calculadas.

Em conseqüência destas deformações (ΔL), a força virtual desenvolveu um trabalho. Portanto, o trabalho interno desenvolvido pela força virtual δF movendo-se de um deslocamento real (Δ) na sua própria direção, é igual ao trabalho total desenvolvido nos elementos internos pelas forças virtuais δ f , movendo-se em suas respectivas direções de deslocamentos reais (ΔL), tem-se:

δF× =Δ Σ δf ×ΔL (8) F e f

δ δ Æ Termos Virtuais e L

Δ Δ Æ Termos Reais

Como todas as forças virtuais atingem seu valor final antes que as deformações reais sejam

impostas, não aparecem os fatores iguais a 1

2 nesta equação (fato observado para o trabalho ou energia potencial elástica interna de deformação, vista no início deste Curso).

F e f

δ δ não necessariamente precisam ser quantidades infinitesimais, pois apenas a sua relação tem significação. Em conseqüência, é altamente conveniente reescrever a equação anterior adotando

F 1

δ = , isto é:

1× =Δ Σ f×ΔL (9) 1 e f Æ Termos Virtuais

e L

Δ Δ Æ Termos Reais Onde:

Δ = deslocamento real de um ponto na direção da força virtual unitária aplicada;

f =forças internas provocadas pela força virtual unitária; ΔL = deslocamentos internos reais no corpo.

Um resultado positivo (+) indica que o deslocamento se deu no mesmo sentido da força virtual

aplicada, e vice-versa.

3.2.a.Equações dos Trabalhos Virtuais para Sistemas Elásticos

Seja a seguinte equação obtida e demonstrada na primeira parte deste curso:

i i i i i i

i i i i i i

l 2 l 2 l 2 l 2 l 2 l 2

n

x y z x x y

i i i i i i i i

i i i i i i i i i i i i

i 1 0 0 0 0 0 0

M M M N V V

1

U d x d x dx d x y d x z d x

2 ₌ E I E I E I E A Χ G A Χ G A

⎡ ⎤

⎢ ⎥

= + + + + +

⎢ ⎥

⎣ ⎦

∑ ∫

∫

∫

∫

∫

∫

A mesma permite generalizar o Princípio dos Trabalhos Virtuais para corpos elásticos

(estruturas), submetidos aos mais diferentes tipos de solicitações internas.

Para corpos linearmente elásticos a equação (9) pode ser particularizada e assimilada para cada

termo da equação anterior, a fim de facilitar a solução dos problemas.

Vejamos como podemos de uma maneira físico-intuitiva entender a aplicação do Princípio dos

Trabalhos Virtuais a partir de um caso simples (hastes carregadas axialmente), aos vários tipos e formas

de solicitações.

Seja a barra carregada axialmente (AB), onde se deseja calcular o deslocamento em (B) devido à

(P).

F F 1 N ( x ) f f p

δ = = → =δ = =

1º) Uma força virtual unitária (δ =F 1) deve ser aplicada no ponto e na direção em que se deseja determinar o deslocamento;

2º) Se as deformações reais são linearmente elásticas e devidas unicamente a cargas axiais,

tem-se, genericamente:

N( x ) L L

E A Δ

Estado A

Estado B

No Estado A:

provoca

Virtual Virtual

F F 1 f f N ( x )

δ = = ⎯⎯⎯⎯→ δ = =

฀ ฀฀฀฀฀฀฀ ฀ ฀฀฀฀฀฀฀฀฀฀ (esforço interno)

Forças Reais P

provocam

⎯⎯⎯⎯→ Deslocamentos Reais em ΔL e B (=Δ)

Aplicando o Princípio dos Trabalhos Virtuais, associam-se os esforços com os deslocamentos

nas respectivas direções:

f L e F

δ →Δ δ →Δ

ou seja:

F f L

1 p L

P L p

E A

δ Δ δ Δ

Δ Δ

Δ

× = ×

× = ×

=

Se o corpo possuir (n) barras submetidas unicamente a esforços axiais, como as treliças, vem

pelo Método dos Trabalhos Virtuais:

n

i i i

i i i 1

p P L 1

A E Δ

= × =

∑

F 0 N( x ) F

Σ = → =δ

x

F 0 N( x ) P

Σ = → =

L

0

N( x ) P L

L dx L

E A E A

i

p =força axial (interna) em uma barra devido à ação da força vertical unitária

i

P =força na mesma barra devido ao carregamento real

Como na aplicação do Método dos Trabalhos Virtuais, no segundo membro da equação temos o

produto (escalar) do esforço interno provocado pelo carregamento virtual unitário, pelo deslocamento

(deformação) real, provocado pelo carregamento real, torna-se importante rever as expressões que

permitem o cálculo dos deslocamentos devido aos esforços simples em estruturas.

Para isto, o leitor deve se reportar ao cálculo das deformações vistas em Mecânica dos Sólidos II

e III, ou então, rever o cálculo das deformações pelo Método da Energia visto na parte inicial deste curso.

Ou seja, os esforços reais atuando sobre as estruturas (reticuladas) provocam as seguintes

deformações:

P T dx d

G J φ =

N( x )

d d x

E A δ =

z M ( x )

d d x

E I θ =

y y

V ( x )

d d x

G A γ Χ=

y

Χ → Fator de Forma

dx

Determinar o deslocamento vertical em B para a situação abaixo:

E

EXXEERRCCÍÍCCIIOO1188

B v

y

l B v

0

l B

v ₀

N( y ) N( y )

1,0 d y

E A

1,0 P d y E A

1,0 P y E A δ

δ

δ

× =

=

=

∫

∫

B v

Retomando as anotações anteriores, tem-se:

x n

i i i 1

F M

F f L

θ

δ δ

δ Δ δ Δ

= + × =

∑

144243

n

i 1

F N d M d T d V d

δ Δ δ θ φ γ

=

⎡ ⎤

× =

∑ ∫

∫

∫

∫

Pelo método da carga unitária: δF=1

l l l l

z P

0 0 0 0

N N M M T T V V

F d x d x d x d x

E A E I G J G A

Δ Χ

× =

∫

∫

∫

∫

Pelo método da carga unitária: F=1

3.2.b.Cálculo de Deformações devidas à Variação de Temperatura

(i) Deslocamento axial relativo:

(

)

f i i e

x g

i i

L L L L t t

t

L L d x 2

α

Δ Δ

ε= − = ε = = + =α

(

)

L d x

2 α

Δ = +

“Carregamento”

P, W(x), M

“Deformação”

(ii) Rotação relativa:

(

)

(

)

d d x

h d x h d x h

α θ α θ α Δ

θ= + → = + → =

2

2

d t 1 d y M ( x )

d x h d x E I

θ α Δ ρ

= = = =

Pelo Método dos Trabalhos Virtuais ÆW_e=W_i

x x

t g

x x

1 N d M d

t

N t d x M d x

h

Δ δ θ

Δ

Δ α α

× = +

= +

∫

∫

∫

∫

3.2.c.Cálculo de Deformações causadas por Recalques

e i W =W

z

x x

zero

N N M M

1 d x d x

E A E I

Δ

× =

∫

∫

14444244443

r

r

1 R 0

R

Δ Σ ρ

Δ Σ ρ

× + =

= −

Para o caso em estudo, tem-se:

A A A B

A V A H A B H

V H M _θ H

Δ_{= − −}⎡ _×ρ _{− ×}ρ _{+ ×}ρ _{− ×}ρ ⎤

⎣ ⎦

Estado de Carregamento Estado de Deformação

B H

ρ

A V

ρ

A H

ρ

A θ

ρ

A

V

A

H MA

B

V

B

3.2.d.Cálculo de Deformações devidas à Montagem

e

W = ×P δ Æ Trabalho Virtual das forças externas tir

i

W =N ×Encurtamento Æ Trabalho Virtual das forças internas

Determinar a rotação da tangente à elástica no ponto C da estrutura abaixo:

E

(

)

C

C

C x

2 2

2 M ( x ) M ( x )

1 d x

E I

1 l P l 1 l P l

E I 0,5 2 0,5 1,0

3 2 4 6 2 4

P l P l E I

48 24

P l 16 E I

θ

θ

θ

θ

δ

δ

δ

δ

× =

× = + × +

× = +

=

∫

Para o pórtico abaixo, determinar o deslocamento horizontal no ponto C.

E

C H

x

2 C

H

4 C H

M ( x ) M ( x )

1 d x

E I

1 P l

E I l l

3 8

P l 24 E I δ

δ

δ

× =

× = × ×

=

∫

Seja a seguinte estrutura isostática:

Calcular:

a) O deslocamento horizontal do ponto B

E

( ) (

) ( )

( ) (

) ( )

B H

x

B H

B H

4 2

B 3

H

M ( x ) M ( x )

1 d x

E J

1 1

E J 3,0 15,0 3,0 5,0 15,0 3,0

3 2

157 ,5 m E J

E J 2,0 10 tm

7 ,875 10 m δ

δ

δ

δ −

× =

× = × × × + × × ×

=

= ×

= ×

∫

b) A rotação em C

( ) ( ) (

)

C x

C

C

4 2

3 C

M ( x ) M ( x )

1 d x

E J

1

E J 5,0 1,0 15,0

3

25 rad E J

E J 2,0 10 tm

1,25 10 rad 0,072 θ

θ

θ

θ −

× =

× = × × ×

=

= ×

= × ≅ °

Para a estrutura abaixo determinar a reação vertical em A (VA).

(

)

A V

x

l 2

A

A V

0

l 3

A 2

A V

0

M ( x ) M ( x )

1 d x

E I

q x

E I 1,0 x V x d x

2

q x

E I V x

2 δ

δ

δ

× =

⎛ ⎞

× = ⎜_⎜ − ⎟_⎟

⎝ ⎠

⎛ ⎞

× = ⎜_⎜ − ⎟_⎟

⎝ ⎠

∫

∫

∫

3 4

A A V

V l q l E I

3 8

δ

× = −

Mas,

3

A A

V

V l 0

δ = → q l4

3 = 8

A 3 q l V

8

=

E

EXXEERRCCÍÍCCIIOO2222

2 A

q l V l

2

−

2 A

q l V l

2

−

2

Para a treliça abaixo, determinar o deslocamento vertical do nó 3. Dados:

A = 10 cm2 E = 21.000 kN/cm2 sen α = 0,6 e cos α = 0,8

ª S1: Seção de Ritter (treliça simétrica)

3

24

24

M 0

20 2,4 F 1,8 0

80

F k N

3

Σ =

× + × =

⎛ ⎞

= −_{⎜ ⎟}

⎝ ⎠

4

23

23

M 0

20 2,4 F cos 1,8 0

100

F k N

3 Σ

α

=

× + × =

⎛ ⎞ = ⎜_⎝ ⎟_⎠

E

ª S2: Seção de Ritter (treliça simétrica)

3

24

24

M 0

0,5 2,4 F 1,8 0

2

F k N

3

Σ =

× + × =

⎛ ⎞ = −_{⎜ ⎟} ⎝ ⎠

4

23

23

M 0

0,5 2,4 F cos 1,8 0

5

F k N

6 Σ

α =

× + × =

⎛ ⎞ = ⎜ ⎟_{⎝ ⎠}

Barra Ni Ni li N N l_i i _i

1 – 2 - 20 - 0,5 180 1800

2 – 4 - 80/3 - 2/3 240 4267

1 – 3 0 0 240 0

2 – 3 100/3 5/6 300 8333

3 – 4 - 40 0 180 0

5 – 6 - 20 - 0,5 180 1800

4 – 6 - 80/3 - 2/3 240 4267

3 – 5 0 0 240 0

3 – 6 100/3 5/6 300 8333

Σ = 28.800

3 V

x

3 V

3 V

3 1

V

N( x ) N( x )

1 d x

E A

E A 28800

28800 21000 10

1,37 10 cm

δ

δ

δ

δ −

× =

× =

=

×

= ×

Seja a estrutura abaixo:

Calcular:

a) O deslocamento horizontal do ponto B

ª Estado B – Estado de Deformação:

s

s

M P x x R sen

M PR sen

ds R d

θ θ θ

= =

= =

ª Estado A – Estado de Carregamento:

B H

s

B H

M ( s ) M ( s )

1 ds

E I

E I M ( ) M ( ) R d

θ

δ

δ θ θ θ

× =

× =

∫

∫

(

)

2 B H

0

E I R 1 cos PR sen R d

π

δ θ θ θ

× =

∫

E

EXXEERRCCÍÍCCIIOO2244

(

)

R y

cos R y R cos

R

y R R cos y R 1 cos

θ θ

θ θ

−

= → − =

= − → = −

(

)

s

s

M 1,0 y

M R 1 cosθ

′

′ =