Tecnologia em Análise
e Desenvolvimento de Sistemas
(Sistema Presencial Mediado)
Lógica
para
Governador Eduardo Braga Vice-Governador
Omar Aziz Reitora
Marilene Corrêa da Silva Freitas Vice-Reitor Carlos Eduardo S. Gonçalves Pró-Reitor de Planejamento Osail Medeiros de Souza Pró-Reitor de Administração Fares Franc Abnader Rodrigues Pró-Reitor de Extensão e Assuntos Comunitários
Rogelio Casado Marinho Filho Pró-Reitora de Ensino de Graduação
Ednéa Mascarenhas Dias Pró-Reitor de Pós-Graduação e Pesquisa
José Luiz de Souza Pio
Coordenador Geral do Curso de Tecnologia em Análise e Desenvolvimento de Sistemas
(Sistema Presencial Mediado) Odwald Schreder Coordenadora Pedagógica Ângela Timótia Pereira Lima Coordenador Técnico Administrativo
Ednaldo Coelho Pereira Diagramação, Formatação e Capa
Salvador Ramos Bernardino da Silva (Coordenador)
Professor da Escola Superior de Tecnologia (EST/UEA) Especialista em Desenvolvimento de Sistemas –UFAM
Manoel S. S. Azevedo
Professor da Escola Superior de Tecnologia (EST/UEA) Mestre em Engenharia Elétrica-UFCG
Cláudio de Oliveira Santos
Nós últimos anos, o avanço da tecnologia da informática mudou os conceitos de ensino e de trabalho. A preocupação com o que se denominou de “inclusão digital” passou a ser um problema urgente a ser enfrentado pelos dirigentes do País, já que todos os processos de novas tecnologias deságuam no conhecimento de informática. No Amazonas, a dificuldade de locomoção na região, por falta de rodovias, por sua grande extensão territorial, pela baixa densidade demográfica e pelo subdesenvolvimento secular imposto à população ribeirinha, torna-se árduo o esforço do Governo para tornar realidade à inclusão digital.
A UEA, que já nasceu moderna, incorporando tecnologias educacionais de ponta, utilizando-se particularmente da informática pela massificação do uso de microcomputadores combinados com uma rede complexa de acesso à Internet, não poderia ficar alheia a essa necessidade premente. Por isso, propôs e realizou o primeiro vestibular para levar a 12 municípios um curso que formasse a mão-de-obra inicial que tornasse a inclusão digital uma realidade em nosso Estado.
A proposta do curso de Tecnologia em Análise e Desenvolvimento de Sistemas oferecido pela UEA vislumbra criar mão-de-obra qualificada em um número significativo de localidades do Estado, cabendo às pessoas beneficiadas com essa iniciativa a tarefa de irradiar o uso de tecnologias de informática, abrindo caminhos novos e suscitando novos empregos para a população local, consolidando, assim, o exercício da cidadania.
09
1. INTRODUÇÃO . . . 11
1.1 O que é lógica? . . . 11
1.2 Origem da lógica . . . 12
1.3 Classificação da lógica: . . . 13
2. A LÓGICA PROPOSICIONAL . . . 15
2.1 Elementos fundamentais da sintaxe da linguagem da Lógica Proposicional: . . . 15
2.1.1 Formalização de uma proposição: . . . 19
2.2 Semântica da lógica proposicional . . . 22
2.2.1 Interpretação dos conectivos lógicos . . . 23
2.2.1.1 Negação de uma proposição . . . 23
2.2.1.2 Conjunção de duas proposições . . . 26
2.2.1.3 Disjunção . . . 27
2.2.1.4 Condicional . . . 28
2.2.1.5 Bicondicional . . . 29
2.2.1.6 Disjunção exclusiva . . . 30
2.2.2 Interpretação de uma fbf . . . 31
3. O CÁLCULO PROPOSICIONAL . . . 34
3.1 Ordem de precedência entre os operadores . . . 34
3.2 Tabela verdade. . . 35
3.3 Propriedades semânticas da lógica proporcional . . . 43
3.3.1 Tautologia . . . 43
3.3.2 Contradição . . . 43
3.3.3 Fórmula satisfatível . . . 44
3.3.4 Equivalência lógica . . . 45
3.3.5 Implicação lógica . . . 45
4. VALIDADE DE UM ARGUMENTO. . . 49
4.1 Argumento . . . 49
4.2 Métodos para avaliar a validade de um argumento . . . 53
4.2.1 Método da tabela verdade . . . 54
4.2.2 Método da Árvore Semântica . . . 55
4.2.3 Método da negação (ou absurdo) . . . 61
4.2.4 Dedução lógica . . . 65
4.2.4.1 Regras de dedução . . . 65
6. RECORRÊNCIA . . . 88
6.1 Seqüência definida por recorrência . . . 88
6.2 Algoritmo definido por recorrência . . . 91
6.2.1 Construindo uma algoritmo recorrente . . . 91
6.2.2 Como um algoritmo recorrente executa . . . 95
Bibliografia . . . 97
Respostas dos Exercícios . . . 98
Exercícios . . . 114
A atividade de desenvolver sistemas leva, com freqüência, o desenvolvedor a lidar com raciocínios e estruturas lógicas.
Um programa de computador é um problema estruturado dentro de um formato lógico específico. A programação de computadores é uma atividade que requer o desenvolvimento da lógica de programação, que, por sua vez, tem seus fundamentos na lógica matemática.
A lógica é uma ciência de índole matemática e fortemente ligada à Filosofia. Já que o pensamento é a manifestação do conhecimento, e que o conhecimento busca a verdade, é preciso estabelecer algumas regras para que essa meta possa ser atingida. Assim, a lógica é o ramo da filosofia que cuida das regras do bem pensar, ou do pensar correto, sendo, portanto, um instrumento do pensar.
A lógica estuda os princípios e métodos usados para distinguir o raciocínio correto do incorreto. (COPI, 1978, p. 19).
1.1 O que é lógica?
11
Introdução
“Lógica é a ciência do raciocínio.”
(Malba Tahan)
“Lógica é a ciência das leis do pensamento e a arte de aplica-las corretamente na pesquisa e na demonstração da
verdade.”
(R. Solivete)
“A Lógica é a ciência que dirige, por meio de leis, as operações de nossa razão, para que ordenada, facilmente
alcance a verdade.”
(Sinibaldi)
Não se pretende afirmar, com essas definições, que só se pode argumentar corretamente com uma pessoa que tenha estudado lógica. Assim como um bom nadador não necessita estudar física e a fisiologia do seu corpo para nadar bem, uma pessoa pode argumentar corretamente sem ter estudado lógica. No entanto, quando a pessoa estuda lógica e pratica os exercícios correspondentes, tem maior possibilidade de raciocinar corretamente. (COPI, 1978, p. 19).
O estudo da lógica foi iniciado pelo filósofo grego Aristóteles (384 – 322 a.C.), nascido em Estagira, na Macedônia. Criou a Ciência da lógica, cuja essência era a teoria do silogismo.
Reuniu essa teoria nos escritos denominados Órganon, ou
Instrumento da Ciência.
Ainda na Grécia, distinguiram-se duas escolas, a PERIPATÉTICA, derivada de Aristóteles e a ESTÓICA, fundada por Zenão (326 – 264 a.C.) e desenvolvida por Crisipo (280 – 250 a.C.).
1.2 Origem da lógica.
No período que vai de Aristóteles até o século XIX, não foram registrados estudos significativos sobre lógica, exceto os trabalhos desenvolvidos por Gottfried Wilhem Leibiniz (1646 – 1716), que só foram apreciados e conhecidos no século XIX.
O Período Booleano (1840 – 1920) iniciou-se com as obras de George Boole e Augustus de Morgan, que publicaram os fundamentos da chamada Álgebra da lógica, respectivamente
com MATHEMATICAL ANALYSIS OF LOGIC e FORMAL LOGIC.
A partir do século XIX, diversos estudiosos dedicaram-se ao estudo da lógica. Surgiram outros ramos da lógica.
Não há unanimidade quanto à classificação da lógica. Alguns autores classificam a lógica como:
a) Lógica Indutiva – ocupa-se dos argumentos indutivos e dos testes para medir a probabilidade indutiva.
b) Lógica dedutiva – é a lógica na qual, dada uma causa, é possível determinar suas conseqüências.
A lógica dedutiva é, freqüentemente, dividida em:
a) Lógica clássica – Considerada como o núcleo da lógica dedutiva. É o que chamamos hoje de CÁLCULO DE PREDICADOS.
Três princípios regem a Lógica Clássica:
1. da IDENTIDADE: “A é A”, ou seja, uma coisa é ela própria sem possibilidade de contestação.
1.3 Classificação da lógica:
2. da CONTRADIÇÃO: A não pode ser, ao mesmo tempo A e não-A, ou seja, ou é A ou não é A.
3. do TERCEIRO EXCLUÍDO: A ou é Y ou é Z, não admitindo uma terceira possibilidade. Exemplo: A ou tem valor verdadeiro ou tem valor falso e não admite um terceiro valor.
b) LÓGICAS COMPLEMENTARES DA CLÁSSICA: São lógicas que têm alguns princípios além dos princípios da lógica clássica e, de alguma forma complementam a lógica clássica.
Exemplos: lógicas modal, que adiciona à lógica clássica o princípio das possibilidades; lógica deôntica, que agrega os princípios dos direitos, obrigações e proibições; lógica epistêmica, agrega o princípio da certeza, etc.
c) LÓGICAS NÃO-CLÁSSICAS: Assim caracterizadas por derrogarem algum ou alguns dos princípios da lógica clássica.
Exemplos: paracompletas e intuicionistas (derrogam o princípio do terceiro excluído); paraconsistentes (derrogam o princípio da contradição); não-aléticas (derrogam o terceiro excluído e o da contradição); não-reflexivas (derrogam o princípio da identidade); a lógica difusa (fuzzy logic), que trabalha com estados intermediários ou gradações, como é o caso, ao se estudar a variável temperatura, que pode assumir estados intermediários entre o estado “quente” e “frio”, entre outras.
15
2.1 Elementos fundamentais da sintaxe
da linguagem da Lógica Proposicional:
Uma linguagem é um conjunto de símbolos destinados a transmitir idéias. Toda linguagem tem sua sintaxe: as regras que dizem quais formações simbólicas são válidas para aquela linguagem.
Na língua portuguesa os símbolos “caza”, “cekql”, não têm significado porque não estão de acordo com a sintaxe da língua.
De acordo com Souza (2002, p. 4), o conjunto de símbolos que constitui a sintaxe da linguagem da Lógica Proposicional é composto dos seguintes elementos:
a) Alfabeto – constituído por: a) símbolos de pontuação: () , . b) símbolos de verdade: true, false.
c) símbolos proposicionais: P, Q, R, S, P1, Q1, S1, A, B, ... d) conectivos proposicionais: Ø, Ù, Ú, ®, «.
A lógica proposicional (simbólica ou matemática) não difere da lógica clássica em essência, mas distingue-se dela pelo uso de uma linguagem técnica específica, que lhe dá mais rigor, tornando-se um instrumento mais eficaz para a análise e dedução formal.
Capítulo II
b) Proposição
É uma sentença declarativa afirmativa, a respeito da qual se pode afirmar que é falsa ou verdadeira.
Vejamos as seguintes sentenças: Manaus é uma capital.
— Proposição
Ela é muito inteligente.
— Não é proposição pois “ela” não está especificada. Que horas são?
— É uma pergunta e não pode ser uma proposição. Paris é uma cidade brasileira.
16
Os símbolos de pontuação são diferentes dos utilizados na sintaxe da língua portuguesa.
Os símbolos de verdade são originários da língua inglesa. Há autores que utilizam T e F para representá-los. Nesse contexto, serão utilizados os símbolos V e F, significando os valores “verdadeiro” e “falso”, respectivamente.
Quantos símbolos proposicionais existem? Pelo exemplo acima, percebe-se que são infinitos, o que torna o alfabeto da linguagem da Lógica Proposicional infinito, ao contrário do alfabeto de muitas outras linguagens, como o da língua portuguesa.
Os conectivos proposicionais são utilizados com freqüência na Matemática. ¬ é denominado “não”. Alguns autores utilizam ’ (apóstrofo) como símbolo de negação. Será adotado ~ (til) para representar negação. Os outros conectivos são , que se lê “e”,
, denominado “ou”, , para representar implicação e
denominado “se e somente se”, “bi-implicação” ou “bicondicional”.
Os conectivos lógicos serão vistos em detalhe na seção 2.2
Ù
— Proposição
Cinco é menor que oito. — Proposição.
Proposições podem ser representadas por letras. Na forma acima, uma proposição está em linguagem corrente. Quando se representa uma proposição por uma letra, usa-se a linguagem simbólica.
Exemplos:
A casa número 5 é amarela. Pode ser representada pela letra maiúscula P.
A lua é feita de queijo. Pode ser representada pela letra Q. P e Q, acima, são proposições, pois são sentenças às quais se pode atribuir um valor verdade (ou valor lógico) falso ou verdadeiro.
Proposições podem ser:
Simples (ou atômicas): quando expressam uma única idéia. “A lua é quadrada” é um exemplo de proposição simples.
Compostas (ou moleculares): quando são formadas por
duas ou mais proposições simples, como: “A casa é grande e o carro é bonito”,
Proposições compostas podem não serem unidas por conectivos. Exemplo: João gosta de correr. José gosta de andar.
O valor de uma proposição é chamado de valor lógico ou valor verdade da proposição e pode ser VERDADEIRO ou FALSO.
c) Fórmulas
Construídas a partir dos símbolos do alfabeto, conforme as seguintes regras:
a) Todo símbolo de verdade é uma fórmula; b) Todo símbolo proposicional é uma fórmula;
c) Se H é uma fórmula então ~H é uma fórmula (negação) d) Se H e G são fórmulas então:
H G é uma fórmula (disjunção) H G é uma fórmula (conjunção) H G é uma fórmula (condicional) H G é uma fórmula (bicondicional)
Ú Ù ® «
18
1. Marque as sentenças abaixo que são proposições, simples ou compostas. Para as sentenças que não são proposições, explique porque não o são.
a) ( ) Os gatos têm três patas. b) ( ) João é alto.
c) ( ) Ela é bonita. d) ( ) A casa é pequena.
e) ( ) Quem está batendo à porta?
f) ( ) Muitos foram chamados, mas poucos foram selecionados.
g) ( ) Talvez eu vá ao teatro. h) ( ) 2 + 2 = 4
i) ( ) x + y = 8
j) ( ) O planeta Marte é habitado. k) ( ) Possivelmente choverá hoje. l) ( ) Falar é fácil. Difícil é fazer. m) ( ) Quem falou?
19
O item a) define as fórmulas mais simples: os símbolos de verdade, que são VERDADEIRO e FALSO.
O item b) define os símbolos proposicionais. Se Q representa uma proposição, Q é uma fórmula da lógica proposicional.
A negação de uma proposição também é considerada uma fórmula, conforme a regra c).
A quarta regra define que duas fórmulas (lembre que um símbolo proposicional é uma fórmula) combinadas por um conectivo lógico formam uma nova fórmula.
Fórmulas do tipo
))A B C, A não são fórmulas
válidas na lógica proporcional, pois não estão de acordo com as regras de formação acima. Pode-se dizer que são fórmulas mal formuladas.
As cadeias (A C) B e (A B C) (B B1), são cadeias válidas na Lógica Proposicional.
Uma cadeia válida é chamada de fórmula bem formulada,
ou, de forma abreviada, fbf.
Obs.: Alguns autores adotam wff (em vez de fbf) que á a abreviação da expressão well formed formula, no idioma inglês.
«Ù ÚÚ B Ú ®, PÙ«
«Ù ÚÚ®Ù
As informações da Tabela 1 ajudam a escrever fórmulas da lógica proposicional, a partir de sentenças na linguagem corrente.
Seja a sentença:
Se João Gosta de Maria, então Maria é feliz. João gosta de Maria. Logo, Maria é feliz.
Nessa afirmação, algumas proposições simples poderão ser identificadas:
Proposição simples - João gosta de Maria - Maria é feliz
Representação na lógica proporcional: (P Q) P Q.®Ù®
Representação P
Q
Outro exemplo:
Se Maria gosta de José e José é feliz, então Maria é feliz. Mas, se Maria não gosta de José, e José não é feliz, então Maria não é feliz.
Identificamos:
Proposição simples Maria gosta de José José é feliz
Maria é feliz
Representação P
Q R
20
Expressão em Português
E, mas, também, além disso, ponto final entre duas proposições
Ou
Se A então B A implica B A logo B
A só se B, A somente se B
A é uma condição suficiente para B Basta A para B
B é uma condição necessária para A
A se e somente se B
A é condição necessária e suficiente para B
Conectivo
lógico Expressão Lógica conjunção A BÙ
disjunção A BÚ
Condicional A ® B
Bicondiconal
(equivalência) A « B
Não há uma única maneira de escrever cada uma das fórmulas acima como uma sentença do nosso idioma. Apresentamos, abaixo, alguns exemplos de como cada uma pode ser escrita:
a) Se José é atleta, então gosta de correr. José é atleta, logo gosta de correr.
José ser atleta implica em gostar de correr. b) José é atleta, gosta de correr mas não é magro.
José é atleta, gosta de correr e não é magro.
José é atleta. José gosta de correr. José não é magro. c) José será atleta se, e somente se, gostar de correr. d) Se José é atleta ou gosta de correr, então José é magro.
José é atleta ou gosta de correr. Portanto, José é magro. e) José será atleta se, e somente se, gostar de correr e for
magro.
21
Representação da sentença, como uma fbf: (P Q) R ((~P ~Q) ~R)Ù®ÙÙ®
Tendo-se uma fórmula da lógica proposicional e conhecendo-se o significado de cada proposição simples que a compõe, é possível escrever uma sentença na linguagem corrente que represente essa fórmula.
Considerando A “José é atleta”, B “José gosta de correr” e C “José é magro” é possível escrever as fórmulas da lógica proposicional dadas abaixo, como uma sentença na linguagem corrente:
a) A B b) A B ~C c) A B d) (A B) C e) A (B C)
®
ÙÙ
«
Ú®
EXERCÍCIOS
1. Considere as proposições simples A “Está frio”, B “Está chovendo” e C “Está quente”. Observando a Tabela 1 e usando o alfabeto da lógica proposicional, representar as proposições:
a) Está frio e está chovendo.
b) Está frio mas não está chovendo. c) Está chovendo ou está quente. d) Se está frio então não está quente.
e) Estará frio se, e somente se, estiver chovendo. f) Está quente ou está chovendo.
g) Se está frio e está chovendo, então não está quente. h) Se está quente, então não está chovendo nem está frio. i) Estar frio é condição suficiente para chover.
j) Está chovendo, logo não está quente. k) Estar chovendo implica em estar frio.
2. Considere P “A casa é bonita”, Q “A porta é pequena” e R “A janela é grande”. Escreva uma sentença em linguagem corrente correspondente às seguintes fórmulas da lógica proposicional:
a) P Q f) P Q
b) P Q g) P Q
c) ~P h) ~(P Q)
d) (P Q) R i) (P Q) (P R)
e) ((P Q) R) Q j) Q (P R)
Ù Ú
« ®
Ù
Ù® ®Ú®
ÚÙ®®Ù
2.2 Semântica da lógica proposicional
A semântica de uma linguagem se ocupa dos significados dos símbolos sintáticos dessa linguagem.
Não basta escrever corretamente uma fbf. Faz-se necessário atribuir valores a essas fórmulas.
Uma proposição P
V F
Duas proposições P
V V F F
Q V F V F
2.2.1.1 Negação de uma proposição
A negação de uma proposição P é obtida acrescentando-se “É falso que” ou “Não é verdade que” antes de P ou inserindo-se a palavra “não” em P. Representa-se a negação por ~P (alguns
autores usam ¬ P, outros preferem P').
23
2.2.1 Interpretação dos conectivos lógicos
A semântica dos elementos sintáticos da Lógica Proposicional é uma função cujo domínio são as fbf da lógica proposicional e cujo contradomínio é o conjunto {V, F}, ou seja, a interpretação de uma proposição simples resultará em V ou F. Por esse motivo, ela é chamada lógica bivalente.
Antes de passar à semântica de cada conectivo lógico, vejamos algumas considerações sobre a construção de tabela verdade.
Uma forma de avaliar o valor lógico de uma proposição é construir a tabela verdade para essa proposição.
Inicia-se a construção de uma tabela verdade fazendo todas as combinações possíveis dos valores verdade de cada proposição simples.
É importante observar que, ao negar uma proposição composta, quando se nega cada proposição simples deve-se negar também o conectivo.
24
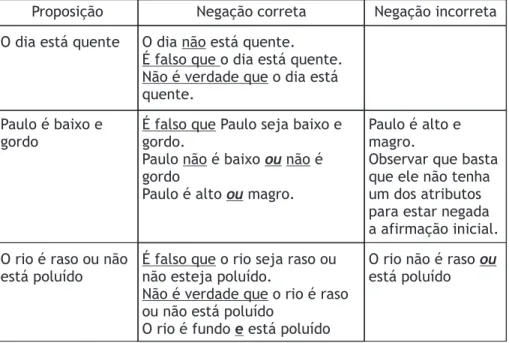
Observe exemplos de negação de uma proposição na Tabela 2.
Proposição Negação correta Negação incorreta
O dia está quente O dia não está quente. É falso que o dia está quente. Não é verdade que o dia está quente.
Paulo é baixo e
gordo É falso que Paulo seja baixo e gordo. Paulo não é baixo ou não é
gordo
Paulo é alto ou magro.
Paulo é alto e magro.
Observar que basta que ele não tenha um dos atributos para estar negada a afirmação inicial.
O rio é raso ou não está poluído
É falso que o rio seja raso ou não esteja poluído.
Não é verdade que o rio é raso ou não está poluído
O rio é fundo e está poluído
O rio não é raso ou
está poluído
Tabela 3 – Negação de uma proposição.
Proposição Valor verdade(valor lógico) Representaçãosimbólica
Manaus está no Brasil. Manaus não está no Brasil. É falso que Manaus está no Brasil.
Não é verdade que Manaus não está no Brasil 3 + 4 = 5
É falso que 3 + 4 = 5 3 + 4 5
V F F V F V V P ~P ~P ~(~P) Q ~Q ~Q Tabela 2 – Valor verdade de uma proposição.
1. Dê a negação das seguintes proposições:
a) O processador é rápido, mas a impressora é lenta. b) O processador é rápido ou a impressora é lenta. c) Pepinos são verdes e não têm sementes.
d) A comida é boa ou o serviço é excelente.
e) Nem a comida é boa nem o serviço é excelente.
2. Dê o valor lógico das proposições: a) 16 não é um número ímpar.
b) Não é verdade que 14 é um número ímpar. c) Não é verdade que 11 não é um número par. d) 3 + 5 8
e) O Solimões é o menor rio do mundo.
3. Qual das seguintes proposições representa ~A se A é a proposição “Júlia gosta de sorvete mas detesta creme”.
a) Júlia detesta sorvete e creme.
b) Júlia não gosta de sorvete nem de creme. c) Júlia não gosta de sorvete mas adora creme. d) Júlia odeia sorvete ou gosta de creme.
¹
EXERCÍCIOS
25
Tabela verdade da negação:
P
V F
~P
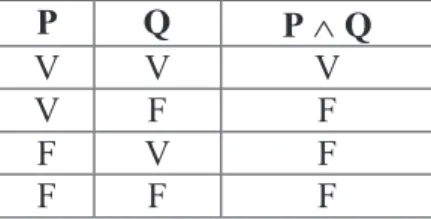
2.2.1.2 Conjunção de duas proposições
Quando duas proposições são combinadas pelo conectivo “e” formam uma proposição composta, chamada conjunção.
A conjunção e entre duas proposições – P, Q – é representada por P Q e se lê “P e Q”.Ù
P Q P Ù Q
V V V
V F F
F V F
F F F
Exemplos:
(1) Paris está na França e 2 + 2 = 4.
(2) Paris está na França e 2 + 2 = 5.
(3) Paris está na Inglaterra e 2 + 2 = 4.
(4) Paris está na Inglaterra e 2 + 2 = 5.
As quatro proposições acima podem ser representadas por P e Q ou, na linguagem simbólica, por P Q.
No exemplo (1), P e Q são ambas verdadeiras. Nesse caso, a conjunção é verdadeira.
Nos exemplos (2) e (3) uma é verdadeira e outra é falsa. A conjunção resulta em valor verdade (ou valor lógico) falso.
No último exemplo, ambas as proposições, P e Q, são falsas e a conjunção também resulta em falso.
Conclusão:
A conjunção entre duas proposições só é verdadeira se ambas o forem.
Tabela verdade da conjunção:
Ù
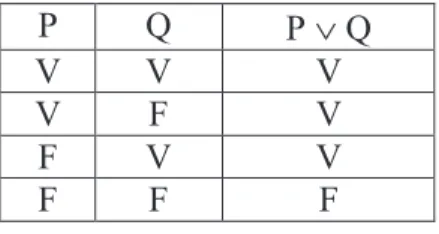
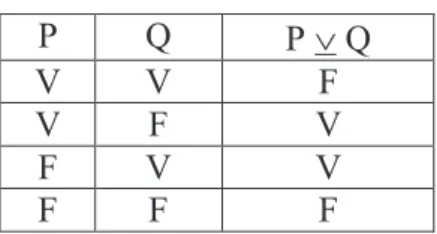
2.2.1.3 Disjunção
A proposição “João é alto ou Maria é bonita” é uma proposição composta, onde “João é alto” é uma proposição simples e “Maria é bonita” é outra proposição simples. Quando se unem essas duas proposições simples pelo conectivo “ou”, tem-se uma proposição composta. A proposição composta obtida pela combinação de duas proposições simples e a palavra “ou” (com sentido “e/ou”), é chamada de disjunção.
A disjunção das proposições P e Q é representada por “P Q”.
O valor verdade da proposição composta acima será determinado pelo valor verdade de cada uma das proposições simples que a formam. Se for verdade apenas a proposição “João é alto” ou apenas a proposição “Maria é bonita” ou, ainda, se ambas as proposições forem verdadeiras, a conjunção resultará em valor lógico verdadeiro.
A disjunção de duas proposições será falsa somente quando ambas as proposições forem falsas.
Tabela verdade da disjunção:
Ú
P Q P Ú Q
V V V
V F V
F V V
F F F
27
EXERCÍCIOS
1. Dê o valor lógico das proposições abaixo: a) 4 é par e 6 é ímpar
b) 4 = 2 + 2 e 5 + 5 = 10
c) A lua é um satélite e a Terra é um planeta.
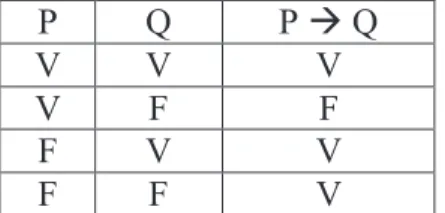
2.2.1.4 Condicional
Uma proposição do tipo “se P então Q” é chamada condicional e é designada por P Q.
Em P Q, P é a proposição antecedente, e Q é a conseqüente.
® ®
Considere a frase “Se eu me sair bem na prova, então irei ao cinema”.
Se essa pessoa sair-se bem na prova, dizer que ela não irá ao cinema, é atribuir o valor lógico falso à proposição condicional, pois a mesma afirmou que, saindo-se bem na prova, irá ao cinema. Ou seja, quando o antecedente é verdadeiro e o conseqüente é falso, o condicional é falso.
Caso a pessoa saia-se mal na prova, nada se pode afirmar sobre se irá ou não ao cinema. A frase não dá nenhuma informação nesse sentido. Por isso, convencionou-se que P Q será verdadeira quando P for falsa.
®
A declaração “o fogo é condição necessária para a fumaça” pode ser dito “se houver fumaça então haverá fogo”. Antecedente: “há fumaça”, conseqüente “há fogo”. Por outro lado, o fato de haver fogo não leva à conclusão de há fumaça. Dizendo de outra forma: em P Q, se o fato de P ser verdadeira levar a Q ser verdadeira, não quer dizer que quando Q é verdadeira P também será.
®
28
1. Dê o valor verdade das proposições: a) O homem é um animal ou 5 + 4 = 15
b) Fleming descobriu a penicilina ou Newton foi um físico. c) Ou Brasília é a capital do Ceará ou Fortaleza é a capital do Ceará.
d) Ou o Sol é um satélite de Marte ou a Terra é uma estrela. e) Ou o Sol é uma estrela ou Plutão é um planeta.
EXERCÍCIOS
1. Dê o antecedente e o conseqüente das seguintes proposições:
a) Se a chuva continuar, então o rio vai transbordar.
b) Uma condição suficiente para faltar energia, é que a chave central desligue.
c) Uma boa dieta é uma condição necessária para um gato ser saudável.
d) A definição ficará errada apenas se for alterada.
2. Dê o valor verdade das proposições abaixo: a) Se a Lua é um satélite então a terra é um planeta.
b) Um corpo celeste não é um satélite se gira em torno de um planeta.
c) Se Mimi é um gato, então tem quatro patas. (Supor que existe um gato chamado Mimi)
d) Se a Terra é uma estrela então a Lua é um planeta.
2.2.1.5 Bicondicional
Uma proposição da forma “P se, e somente se, Q” é dita bicondicional. É representada por P Q.
Uma proposição bicondicional será verdadeira quando ambas as proposições componentes são de mesmo valor verdade. E será falsa quando as duas proposições têm valores opostos.
«
29
Tabela verdade do condicional:
P Q P à Q
V V V
V F F
F V V
EXERCÍCIOS
1. Dê o valor verdade das seguintes proposições:
a) Amarelo será preto se, e somente se, vermelho for branco.
b) 3 + 4 = 7 se e somente se 8 x 5 = 50. c) 1 + 1 = 4 se, e somente se, 7 + 3 = 10.
d) Azul não é verde se, e somente se, preto for lilás. e) Não é verdade que 1 + 1 = 3 se, e somente se, 2 + 2 = 5.
2.2.1.6 Disjunção exclusiva
Dadas duas proposições P e Q, a disjunção exclusiva é definida como sendo verdadeira se apenas uma delas é verdadeira. Pode-se ler “P ou Q mas não ambas”. Representaremos por .
A disjunção exclusiva é representada em programação pelo operador XOR, que é um acrônimo da expressão inglesa “exclusive or”.
Ú
30
P Q P « Q
V V V
V F F
F V F
F F V
31
EXERCÍCIOS
1. Dê o valor verdade das proposições:
a) Quando você ligou eu estava dormindo ou estava passeando.
b) Quando você ligou eu estava em casa ou estava dormindo.
c) Quando você ligou eu não estava em casa ou estava dormindo.
d) Para sobremesa, ou escolho goiabada ou bananada. Tabela verdade do ou exclusivo:
P Q P Ú Q
V V F
V F V
F V V
F F F
Observe que a disjunção exclusiva não foi apresentada como um conectivo do alfabeto da lógica proposicional. Não só esse como outros conectivos podem ser definidos a partir daqueles.
O significado de “P ou Q mas não ambos” como um conectivo é uma simplificação da fórmula (P Q) ~(P Q).ÚÙÙ
2.2.2 Interpretação de uma fbf
A interpretação de uma fbf composta depende da interpretação de cada proposição simples da fórmula.
Exemplo 1:
Seja H = (P Q). Existem quatro interpretações possíveis para H. Basta observar a tabela verdade da disjunção.
Qual a interpretação de H, se H = (P Q) P, sabendo que I[P] = V e I[Q] = F?
Ú
Com I[P] = V e I[Q] = F, P Q resulta em verdadeiro.
Verdadeiro P (verdadeiro verdadeiro) resulta em
verdadeiro. Logo, I[H] = V
Ú
® ®
P ÚQ ®P H
V F V
P ÚQ ®P H
V V F V V V
Exemplo 2:
Qual a interpretação da fórmula E = (( ~P Q) (R P), sabendo que I[P] = V e I[Q] = F?
Solução:
Como na análise da fórmula anterior, inicialmente lança-se na tabela os valores das interpretações conhecidas:
Ù®Ù
(~ P ÙQ) ®(R ÙP) E
V F V
Sendo I[P] = V, I[~P] tem valor F. Conseqüentemente, I[~P Q] = F. Não se conhecendo a interpretação de R, não é possível concluir pela interpretação de R P. Por outro lado, ~P Q é o antecedente do condicional. Quando o antecedente de um condicional é falso, este resulta em verdadeiro, independente do valor lógico do conseqüente. Dessa forma, pode-se concluir que I[E] = V, mesmo não se conhecendo I[Q]. O quadro final dessa análise será:
Ù
Ù Ù
(~ P ÙQ) ®(R ÙP) E
F V F F V V V
32
1. Seja I uma interpretação tal que I[P Q] = F. O que se pode deduzir a respeito dos resultados das interpretações:
a) I[~P Q] b) I[P ~Q] c) I[Q P]
®
Ù
Ú ®
EXERCÍCIOS
Solução
Só há uma situação em que I[P Q] = F: quando I[P] = V e I[Q] = F. Com esses valores lógicos de P e Q, analisa-se cada uma das fórmulas dadas para concluir, ou não, pelo seu valor verdade.
®
2. Qual a interpretação da fórmula G, abaixo, sabendo que I[P] = V e I[Q] = V?
G = (P (~Q R)) ~(Q (P ~R))®ÚÙÚ«
33
Exemplo 3:Sendo G = P Q e sabendo-se que I[G] = V, o que se pode concluir a respeito de I[P] e I[Q]?
Solução:
A disjunção é verdade quanto pelo menos um de seus componentes é verdadeiro, existindo três situações possíveis. Dessa forma, nada se pode concluir sobre o valor verdade de P e de Q.
Ú
Capítulo 3
O Cálculo Proposicional
34
Tem por objetivo avaliar o valor verdade de uma fórmula.
3.1 Ordem de precedência entre os operadores
Para avaliar o valor verdade de uma fórmula da lógica proposicional, a precedência dos operadores deve ser observada. Abaixo são apresentados os operadores lógicos, da maior para a menor precedência:
1. expressões entre parênteses, resolve-se a partir dos parênteses mais internos para os mais externos.
2. ~ (negação)
3. , (conjunção e disjunção têm a mesma precedência, operando-se o que ocorrer primeiro, da esquerda para a direita).
4. 5.
Isto significa que, para avaliar a fórmula A B C, como não há parênteses, avalia-se primeiro a conjunção ( ), depois o condicional ( ).
ÙÚ
® «
®Ù
35
A B C
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
Quando os conectivos lógicos foram apresentados, tínhamos tabelas verdade com duas proposições simples, cada uma com quatro linhas. No exemplo acima, temos uma fórmula com três proposições simples e a respectiva tabela verdade tem oito linhas. Podemos concluir que o número de linhas de uma
n
tabela verdade é obtido por 2 linhas, sendo n o número de proposições simples que a fórmula contém.
O passo seguinte é analisar a fórmula, de acordo com a precedência dos operadores, um operador por coluna da tabela.
Exemplos:
Construir a tabela verdade para as fórmulas G e H abaixo: a) G = A B A B
Como a fórmula acima não contém parênteses, deve-se, então, seguir a ordem de precedência dos operadores na análise
Ù®Ú
3.2 Tabela verdade.
Para construir a tabela verdade de uma fórmula, inicia-se pela composição, em conjunto, de todos os valores lógicos das proposições simples que compõem uma fórmula.
Considerando a fórmula (A B) C, vemos que a mesma possui três proposições simples. Fazendo todas as combinações possíveis dos valores verdade dessas proposições simples temos:
36
Conclui-se que o valor da fórmula G é VVVV.
Outra maneira de fazer uma tabela verdade é criar uma coluna para cada símbolo da fórmula e realizar as operações seguindo a ordem de precedência dos operadores.
Dessa segunda maneira, a tabela verdade da fórmula acima A seguir, acrescenta-se outra coluna e faz-se a operação do
conectivo Ú
A B A Ù B A Ú B
V V V V
V F F V
F V F V
F F F F
Por fim, acrescenta-se mais uma coluna e avalia-se o conectivo , considerando como antecedentes os valores da 3a coluna e como conseqüentes os valores da 4a coluna, completando a tabela verdade.
®
A B A Ù B A Ú B A Ù B ® A Ú B
V V V V V
V F F V V
F V F V V
F F F F V
A B A Ù B
V V V
V F F
F V F
F F F
da mesma. Após fazer as combinações possíveis dos valores
1 2 3 4 5 6 7 8 9 A B A Ù B ®A Ú B V V
V F F V F F Etapa
inicia escrevendo toda a fórmula, cada símbolo em uma coluna, e fazendo a composição de todas as possibilidades dos valores lógicos de A e B.
37
1 2 3 4 5 6 7 8 9 A B A Ù B ®A Ú B
V V V V V V V V
V F V F F V V F
F V F F V F V V
F F F F F F F F
Etapa 1 2 1 3 4 3
O primeiro conectivo a ser avaliado é o , o que é feito em duas etapas: na etapa 1, repete-se os valores verdade de A e B das colunas 1 e 2 nas colunas 3 e 5, respectivamente e na etapa 2 opera-se o :
Ù
Ù
1 2 3 4 5 6 7 8 9 A B A Ù B ®A Ú B
V V V V V
V F V F F F V F F V F F F F F Etapa 1 2 1
A seguir opera-se o . De forma semelhante ao que foi feito nas etapas 1 e 2, a etapa 3 consiste em copiar os valores de A e B para as colunas 7 e 9, respectivamente, e na etapa 4 anota-se o resultado da disjunção entre A e B, gerando a tabela:
38
A B C A Ú B
V V V V V V F V V F V V V F F V F V V V F V F V F F V F
F F F F
Obs.: A diferença básica entre uma e outra maneira de construir a tabela verdade é que na primeira forma a última coluna sempre corresponde ao conectivo principal, enquanto na segunda, o conectivo principal continua sendo o último a ser avaliado mas não está situado na última coluna.
b) H = ((A B) C) (B ~C)
Após fazer as combinações de valores verdade das proposições simples, procede-se à avaliação da expressão do parêntese mais interno (A B):
Ú®«®
Ú
Finalmente, passa-se à etapa 5, que é avaliar o condicional, sendo o antecedente os valores da coluna 4 (etapa 2) e os conseqüentes os valores constantes da coluna 8 (etapa 4), gerando a tabela verdade final:
1 2 3 4 5 6 7 8 9 A B A Ù B ®A Ú B
39
O valor da fórmula H é: FFVFFFVV.
Obs.: Caso as combinações de valores verdade iniciais (três primeiras colunas da tabela) estejam em uma ordem diversa da apresentada acima a ordem dos valores verdade (V, F) do resultado poderá ser diferente da apresentada. No caso do exemplo acima, se a combinação da 1a e da 2a linhas, estiverem Depois, faz-se a avaliação de ~C, seguindo-se a avaliação do condicional (B ~C) e, por fim, do bicondicional, entre os valores das colunas 5 e 7.
®
1 2 3 4 5 6 7 8
A B C A Ú B ((A Ú B) ® C) ~C (B ® ~C) «
V V V V V F F F V V F V F V V F V F V V V F V V V F F V F V V F F V V V V F F F F V F V F V V F F F V F V F V V F F F F V V V V
A seguir, considera-se a quarta coluna como o antecedente e a terceira coluna como conseqüente, e avalia-se o condicional
( ) do parêntese mais externo ((A B) C).® Ú®
A B C A Ú B ((A Ú B) ® C)
V V V V V
V V F V F
V F V V V
V F F V F
F V V V V
F V F V F
F F V F V
40
1 2 3 4 5 6 7 8 9 10 11 12 13 A B C ((A Ú B) ® C) « (B ® ~ C)
V V V V V V V V F V V V V F V V V F V F F V V F F V V F V V F V F F V V F F V F F F F F F F F F Etapa 1 2 1
1 2 3 4 5 6 7 8 9 10 11 12 13 A B C ((A Ú B) ® C) « (B ® ~ C)
V V V V V F V F V V F F F V V F V F F F V F F F
O parêntese mais interno é o primeiro a ser avaliado. A etapa 1 é repetir os valores verdade de A e B e a etapa 2 é fazer a conjunção de A e B. Após a etapa 2 a tabela verdade assume o aspecto abaixo:
em outra posição, os dois valores F iniciais do resultado não serão os primeiros. Seja qual for a ordem das combinações iniciais, o resultado sempre terá 5 valores F e três V.
A fórmula H = ((A B) C) (B ~C), do exemplo anterior, avaliada pelo segundo método, onde se escreve cada símbolo em uma coluna, é feita como da forma abaixo. Notar que é importante representar os parênteses da fórmula, já que esses influem na ordem das operações. Também vale destacar que o símbolo de negação deve figurar em uma coluna, separado da proposição que está negando.
41
Coluna 1 2 3 4 5 6 7 8 9 10 11 12 13 A B C ((A Ú B) ® C) « (B ® ~ C)
V V V V V V V V V F F V V V F V V V F F V V V F V F V V V F V V F V F V V F F V V F F F F V V F F V V F V V V V V F F V F V F F V V F F V V V F F F V F F F V V F V F V F F F F F F V F F V V F Etapa 1 2 1 4 3 5 7 6 5 Coluna 1 2 3 4 5 6 7 8 9 10 11 12 13
A B C ((A Ú B) ® C) « (B ® ~ C)
V V V V V V V V
V V F V V V F F
V F V V V F V V
V F F V V F F F
F V V F V V V V
F V F F V V F F
F F V F F F V V
F F F F F F V F
Etapa 1 2 1 4 3
A etapa 5 é transcrever os valores verdade de B e C para as colunas 10 e 13, respectivamente.
É importante observar que a negação precede todos os outros operadores. Por isso, antes de operar o condicional da coluna 11 é necessário fazer a negação de C (coluna 12), que constitui a etapa 6. O passo 7 é avaliar o condicional da coluna 11, gerando a posição abaixo da tabela verdade:
A etapa 3 é transcrever os valores verdade de C para a coluna 8. A etapa 4 será fazer o condicional entre a coluna 5 ( ), como antecedente e a coluna 8 (C), como conseqüente.
EXERCÍCIOS
1. Faça a tabela verdade para as fbf abaixo: a) (A B) C
b) A B ~A c) (A B) ~A B
d) (P (~Q R)) ~(Q (P ~R))
Ú®
Ú®
®«Ú
®ÚÙÚ«
42
1 2 3 4 5 6 7 8
9
10 11 12 13 A B C ((A Ú B) ® C)«
(B ® ~ C)V V V V V V V V
F
V F F V V V F V V V F FF
V V V F V F V V V F V VV
F V F V V F F V V F F FF
F V V F F V V F V V V VF
V F F V F V F F V V F FF
V V V F F F V F F F V VV
F V F V F F F F F F V FV
F V V F Etapa 1 2 1 4 3 8 5 7 6 5A coluna da etapa 8 contém o resultado. Como já se esperava, esse resultado coincide com o encontrado na tabela verdade feita anteriormente. E não poderia ser diferente, pois a mesma fórmula só pode gerar um único resultado, seja qual for o método empregado para fazer sua avaliação.
3.3.2 Contradição
Uma fórmula é contraditória (ou uma contradição) se, e somente se, para toda interpretação I, I[H] = F.
Exemplo: (P Q) ~(P Q)ÙÙÚ
P Q P Ù Q ( P Ú Q) ~(P Ú Q) Ù
V V V V F F
V F F V F F
F V F V F F
F F F F V F
43
3.3 Propriedades semânticas da lógica proporcional
3.3.1 Tautologia
Uma fórmula H é uma tautologia ou é válida se, e somente se, para toda interpretação I, I[H] = V
Fazendo-se a tabela verdade para a fbf H = P ~( P Q), tem-se
ÚÙ
P Q P Ù Q ~( P Ù Q) P Ú ~( P Ù Q)
V V V F V
V F F V V
F V F V V
F F F V V
Observa-se que o valor lógico de H é V, ou seja, para toda interpretação I, I[H] = V. Nesse caso, H é uma tautologia.
EXERCÍCIOS
1. Fazer a tabela verdade para a fórmula H = (P Q) (P Q) e verificar se a mesma é uma tautologia.
2. Mostre que a fórmula abaixo é uma tautologia: (P Q) (~P Q)
Ù®Ú
EXERCÍCIOS
1) Mostre que as fórmulas abaixo são contradições: a) ~(P Q) Q
b) ~(P (P Q))
®Ù
®Ú
3.3.3 Fórmula satisfatível.
Uma formula é satisfatível (uma indeterminação ou uma
contingência), se existe pelo menos uma interpretação I, tal que
I[H] = V
Por essa definição, basta que apenas uma interpretação I, de H, seja verdadeira, ou seja, basta que apenas uma linha da tabela verdade de H resulte em V, para que a fórmula seja classificada como satisfatível.
Exemplo: construir a tabela verdade para a fórmula
G = ~((A B) A)®®
A B (A ® B) (A ® B) ® A ~
V V V V F
V F F V F
F V V F V
F F V V F
EXERCÍCIOS
1) Construa a tabela verdade para as fórmulas abaixo e prove que são satisfatíveis:
a) H = (P Q) Q b) G = (P Q) (P Q)
«Ú
®®Ù
3.3.4 Equivalência lógica (rtepresentada por )Û
Dadas duas fórmulas H e G, G equivale a H (G H), se e somente se, para toda interpretação I, I[G] = I[H]
Fazendo a tabela verdade para a fbf H = (A B) (B A), temos:
®Ù®
Û
A B A ® B B ® A (A ® B) Ù(B ® A)
V V V V V
V F F V F
F V V F F
F F V V V
Comparando a tabela verdade da fórmula H, acima, com a tabela verdade fórmula P Q (bicondicional, vista no item 2.2.5), verifica-se que são idênticas. Diz-se, então, que a fórmula H e o bicondicional são equivalentes.
«
Fazer as tabelas verdade para as fórmulas G e H abaixo e verificar se são equivalentes (verificar se G H):
a) G = A B e H = ~(A B) b) G = ~(A B) e H = ~A ~B
® Ú
Ú Ù
Û
EXERCÍCIOS
3.3.5 Implicação lógica (representada por Þ)
Sejam as fórmulas G e H. As três condições seguintes são equivalentes:
(1) ~G Ú H é uma tautologia.
(2) G Ù ~H é uma contradição.
(3) G ® H é uma tautologia.
K L (lê-se K implica logicamente em L) se satisfizer a uma das três condições acima especificadas. Escolhendo a condição (1), sua tabela verdade será:
Þ
K L ~K ~K Ú L
V V F V
F F V V
V F F F
F F V V
que não é uma tautologia. Logo, K não implica logicamente em L.
46
K L M
P Q P Ù Q Ú Q P Ù Q P Ú Q
V V V V V V
V F F F F V
F V F V F V
F F F F F F
Resumindo:
P Q K L M
V V V V V
V F F F V
F V V F V
F F F F F
Uma fórmula G implica logicamente uma fórmula H (G H) se uma das condições acima for satisfeita.
Exemplos: Considere as fórmulas a) K = (P Q) Q
b) L = P Q c) M = P Q
As tabelas verdade de K, L e M são:
Þ
ÙÚ
EXERCÍCIOS
1) Considerando as fórmulas K, L, e M do último exemplo, verificar se:
a) L Þ M
b) M Þ K
c) L Þ K
d) K Þ M
47
Usando a mesma condição (1) para testar se L Þ K, temos:
K L ~L ~L Ú K
V V F V
F F V V
V F V V
F F V V
resulta em uma tautologia. Logo, L implica logicamente em K.
Aplicando o critério (2), G ~H, para verificar se L Þ K,
faz-se a tabela verdade para L ~K, chega-se ao seguinte resultado:
Ù Ù
K L ~K L Ù ~K
V V F F
F F V F
V F F F
F F V F
que é uma contradição.
Aplicando o critério (3), que é fazer a tabela verdade para L K, verifica-se que é uma tautologia.
Chega-se à conclusão que, se duas fórmulas atendem a um dos critérios acima, pode-se afirmar que uma implica logicamente na outra, mesmo que não se teste os outros dois critérios.
48
Outra maneira de verificar a implicação lógica:
Dadas duas fórmulas G e H, G implica H (G H) se, e somente se, para toda interpretação I,
se I[G] = T, então I[H] = T
Pela definição de implicação acima, K implica M. Observe que para as duas interpretações I[K] = V , I[M] = V também. Quando I[K] = F, nada se pode afirmar sobre I[M]. Da mesma forma, L implica K e L implica M. Já não se pode dizer o mesmo a respeito de M em relação a L e K, uma vez que para todas as interrpretações I[M] = V, nem todas as interpretações de I[L] e I[K] são também verdadeiras.
Þ
EXERCÍCIOS
2) Construa as tabelas verdade para as fórmulas A = (~P Q) e B = (P Q) e verifique se A Þ B, usando este último critério
de implicação.
49
4.1 Argumento
Suponha que seja feita a pergunta: “A Terra tem luz própria?”. Uma forma de buscar a resposta é procurar um termo intermediário que se relacione com outros termos da pergunta. Esse termo pode ser “planeta”. A partir desse termo, pode-se formular as seguintes sentenças:
Um planeta não tem luz própria. A Terra é um planeta.
Logo, a Terra não tem luz própria.
A terceira sentença é uma conclusão, que foi tirada a partir das duas primeiras e, com isso, a pergunta foi respondida.
Outro exemplo: 3 + 2 = 5
5 = 4 + 1 3 + 2 = 4 + 1
Raciocínios como os apresentados acima, são da forma
silogística.
Capítulo 4
50
Aristóteles definiu o silogismo como:
“O silogismo é uma série de palavras em que, sendo admitidas certas coisas, delas resultará necessariamente alguma outra, pela simples razão de se terem admitido aquelas.”
Silogismo significa ligação, ou seja, a ligação de dois termos através de um terceiro.
As sentenças que servem para provar ou, pelo menos, para fornecer alguma evidência para a conclusão são chamadas de premissas. Um conjunto de sentenças, onde algumas são premissas e outra é a conclusão é chamado de argumento.
Um argumento pode ser escrito de diversas formas. Vejamos o seguinte exemplo:
Andar de bicicleta é um ótimo exercício. Josefina anda de bicicleta. Josefina pratica um ótimo exercício.
Alguns autores preferem representar o argumento da forma:
Andar de bicicleta é um ótimo exercício. Josefina anda de bicicleta.
Josefina pratica um ótimo exercício. (três pontos para identificar a conclusão.)
\
Outros autores preferem a forma:
Andar de bicicleta é um ótimo exercício. Josefina anda de bicicleta.
ÞJosefina pratica um ótimo exercício. (o símbolo condicional
51
Indicadores de conclusão logo
portanto assim
por conseguinte dessa maneira neste caso daí
de modo que então
assim sendo segue-se que
o(a) qual implica que resulta que
podemos deduzir que
Indicadores de premissa desde que
como porque
assumindo que visto que admitindo que
isto é verdade porque a razão é que
em vista de
como conseqüência de
como mostrado pelo fato que sabendo-se que
supondo que
Um argumento acontece quando se pretende provar ou demonstrar uma conclusão, a partir de uma ou mais premissas.
Uma maneira de representar, na lógica proposicional, um argumento é:
O importante é caracterizar a conclusão. Na álgebra proposicional as premissas e conclusão são representadas por símbolos proposicionais (letras maiúsculas).
Um argumento onde a conclusão decorre das premissas é um argumento válido. Argumentos dessa forma são conhecidos
pela expressão latina modus ponens (método de afirmação).
Proposição simples
- O criminoso é primário
- O criminoso cometeu um descuido - O criminoso terá sua pena diminuída.
Representação
P Q R
Representação na lógica proporcional: (P Q) (P R) ~P ~R.
Note que (P R) tem, obrigatoriamente, que vir entre parênteses. A fbf acima, se escrita da forma (P Q) P R ~P
~R, nos levaria a duas situações:
— primeiro, surgiria a dúvida: qual é a conclusão, o primeiro ou o segundo condicional?
— em segunda instância, a sua avaliação seguiria a precedência dos operadores e primeiro seria feito ((P Q) P), depois seria avaliado (R ~P) e, por fim, os dois condicionais restantes , o que levaria a um resultado diferente do esperado.
Úٮٮ
®
ÚÙ®Ù
®
ÚÙ
Ù ®
52
Na lógica proposicional, temos: A B C.
Como o operador conjunção ( ) tem precedência sobre o condicional ( ), não é necessário escrever (A B) C. Porém, há situações que os parênteses são obrigatórios.
Vejamos o argumento abaixo:
O criminoso é primário, ou cometeu um descuido. Se o criminoso for primário, então terá sua pena diminuída. O criminoso não é primário. Logo, sua pena não será diminuída.
Ù®
Ù
® Ù®
A viagem para Manacapuru dura uma hora. A
João irá a Manacapuru B
4.2 Métodos para avaliar a validade de um argumento
Verificar se um argumento é válido é verificar se o mesmo é uma tautologia, ou seja, se todas as interpretações (linhas) de sua tabela verdade resultam em valor lógico verdadeiro (V). Em última instância, é verificar se o valor verdade do conectivo principal (o último que será analisado) é verdadeiro, para todas as interpretações do argumento.
Argumentos podem ser escritos como fórmulas da linguagem da Lógica Proposicional. Entretanto, nem todas as fórmulas são escritas em formato de argumento, composto de premissas e uma conclusão.
Os métodos de avaliação de um argumento, que serão vistos a seguir, são métodos de avaliação geral e se prestam para avaliar fbf quaisquer. Assim, adotaremos o termo fórmula e não argumento, ao longo dos próximos itens.
Serão estudados quatro métodos para verificar a validade de fórmulas da lógica proposicional: método da tabela verdade, método da árvore semântica, método da negação ou absurdo e
dedução lógica.
53
EXERCÍCIOS
1. Represente na linguagem simbólica da Lógica Proposicional os argumentos:
a) Se Jonas andar e o trem sair no horário, ele perde o trem. Se ele perder o trem, então ele fica triste e volta para casa. Jonas andou. Portanto, Jonas voltou para casa.
P Q P ® Q ~Q ~P ~Q® ~P (P ® Q) « (~Q® ~P)
V V V F F V V
V F F V F F V
F V V F V V V
F F V V V V V
Para todas as interpretações I, I[H] = V. Então, H é uma fórmula válida (é uma tautologia).
Mas o número de linhas de uma tabela verdade é dado por
n
2 , onde n é o número de proposições simples. Quando o número dessas proposições simples aumenta, a tabela verdade torna-se não recomendável.
Existem outros métodos de prova que abreviam o processo e que serão vistos a seguir.
EXERCÍCIOS
1) Usando o método da tabela verdade, verificar se o argumento (S (~C ~Q)) (~C Q) ~S (letra b) do exercício da seção anterior) é válido.
®ÙÙÙ®
4.2.1 Método da tabela verdade
O método da tabela verdade é conhecido, também, como método da força bruta, por ser um método exaustivo de prova. Através dele, tem-se os resultados de todas as interpretações possíveis de uma fbf.
Exemplo
Verificar se a fbf H = (P Q) (~Q ~P) é válida.
A construção da tabela verdade deve ser feita conforme o item 3.2.
®«®
Na árvore do exemplo acima, o nó 1 é chamado de raiz e está no primeiro nível da árvore, os nós 2 e 3 estão no segundo nível, os nós 4 a 7 estão no terceiro nível, e assim, sucessivamente. Os nós que não estão ligados a nenhum nó em um nível abaixo, são chamados de nós folha. No exemplo acima, são nós folha: 4, 5, 7, 9, 10 e 11.
Uma árvore binária pode ser utilizada para verificar a validade de uma fórmula da lógica proposicional.
Exemplo 1:
Verificar se a fbf H = (P Q) (~Q ~P) é válida, utilizando o método da árvore semântica.
®«®
O primeiro passo é construir uma árvore binária com os nós 1, 2 e 3, como no exemplo acima. A seguir, escolher uma proposição simples para analisar, por exemplo, a proposição P. Cada aresta da árvore construída representará um dos valores
lógicos possíveis de P.
55
4.2.2 Método da Árvore Semântica
Uma árvore é uma estrutura de dados, composta por nós, unidos por arestas. Quando cada nó se liga a, no máximo, dois outros nós, essa árvore é chamada de árvore binária.
Exemplo de árvore binária:
1
2 3
4 5 6 7
8 9
56
A interpretação de um nó corresponde a todas as interpretações (arestas) encontradas no caminho percorrido da raiz até o nó em questão.
A análise de um nó consiste em partir da interpretação desse nó e tentar concluir pelo seu valor verdade.
Temos:
1
2 3
I[P] = V I[P] = F
Para analisar o nó número 2, começamos atribuindo o valor V a todas as ocorrências de P na fórmula H, dada. Esquematicamente:
(P Q) (~Q ~P) Nó 2 = V V
Como P é verdadeiro, podemos concluir que ~P é falso (segunda ocorrência de P na fórmula).
(P Q) (~Q ~P) Nó 2 = V FV
®«®
®«®
O lado esquerdo do bicondicional é um condicional, cujo antecedente é verdadeiro. Nesse caso, o valor verdade desse condicional depende do conseqüente. O lado direito do bicondicional é outro condicional, cujo conseqüente é falso (se P é verdadeiro, ~P é falso), e depende do antecedente para se poder concluir pelo seu valor lógico. Como não se tem o valor
1
2 3
I[P] = V I[P] = F
V
57
Quando o antecedente de um condicional é falso, esse condicional tem valor lógico V, independente do valor lógico do conseqüente. Quando o valor lógico do conseqüente de um condicional é falso, esse condicional tem valor lógico V, independente do valor lógico do antecedente. Dessa forma, é possível concluir pelo valor lógico do bicondicional, uma vez que se tem os valores lógicos das expressões à direita e à esquerda deste.
nem da expressão do lado direito (~Q ~P), nada se pode afirmar sobre o valor lógico desse bicondicional e, portanto, nada se pode afirmar sobre o valor do nó 2:
(P Q) (~Q ~P) Nó 2 = V ? ? ? FV
De forma semelhante, analisa-se o nó 3:
(P Q) (~Q ~P) Nó 3 = F VF
®
®«®
®«®
(P Q) (~Q ~P) Nó 3 = F V V V VF
®«®
Procede-se à análise do valor verdade dos nós 4 e 5. A interpretação do nó 4 é obtida percorrendo-se a árvore a partir da raiz até o nó em questão. O nó 4 significa que P e Q têm, ambas, valor lógico V. Lança-se esses valores na fórmula e busca-se concluir pelo valor verdade desta:
(P Q) (~Q ~P) Nó 4 = V V V V FV V FV
Procedimento semelhante deve ser adotado em ralação ao nó 5. Para esse nó tem-se I[P] = V e [Q] = F:
(P Q) (~Q ~P) Nó 5 = V F F V VF F FV
Como ambos os condicionais resultam em F, o bicondicional resulta em V.
Árvore semântica final de H:
®«®
®«®
58
Como nada se pode concluir a respeito do nó 2, acrescenta-se a esacrescenta-se nó a interpretação de outra proposição simples da fórmula sob análise:
I[P] = V I[P] = F
I[Q] = V I[Q] = F V
1
2 3
I[P] = V I[P] = F 1
2 3
Interpretação do nó 2: O conectivo principal é o segundo condicional. Como P é verdadeiro, nada se pode concluir a respeito do antecedente do conectivo principal, ou seja, não é possível concluir pelo valor da expressão (P Q). Mas o conseqüente do conectivo principal tem valor verdadeiro e, nesse caso, a implicação é verdadeira. Logo, o nó 2 tem valor verdadeiro.
(P Q) P Nó 2 = V ? V V
®
®®
59
I[P] = V I[P] = F
I[Q] = V I[Q] = F V
1
2 3
4 5
V V
Como todos os nós folha resultaram em V (verdadeiro), conclui-se que H é válida (é uma tautologia).
Exemplo 2:
Verificar se a fórmula G = (P Q) P é válida. Solução:
Iniciando com a interpretação de P, tem-se a árvore:
Para que uma fbf não seja válida, basta que 1 nó folha apresente valor lógico falso. Como para I[P] = F tem-se I[G] = F, está demonstrado que G não é uma fbf válida.
Observações:
1) Como foi possível concluir pelo valor verdade dos nós 2 e 3, conhecendo-se apenas o valor de P, a árvore não prossegue em nenhum dos dois nós. Está concluída.
2) Se todos os nós folha tiverem valor lógico falso, a fórmula será uma contradição. Caso nem todos tenham valor falso, diz-se que a mesma é satisfatível.
60
I[P] = V I[P] = F 1
2 3
V F
A interpretação do nó 3 é feita assumindo que P tem valor falso. Independente do valor de Q, o valor do antecedente do conectivo principal será verdadeiro e seu conseqüente falso. A fórmula resulta em falso.
(P Q) P Nó 3 = F V F F
A árvore semântica de G tem o seguinte aspecto:
Exemplo 1:
Verifique, através do método da negação (ou absurdo) se a fórmula G, abaixo, é válida:
G = ((A B) (B C)) (A C)®Ù®®®
61
EXERCÍCIOS
1) Construir uma árvore semântica para as fórmulas F, G e H, abaixo, e verificar se são válidas. Caso a fórmula não seja válida, diga para que interpretação I a fórmula tem valor lógico falso.
a) F = (P (P Q)) (P Q) b) G = ~(P Q) ~P
c) H = ((A B) (A C)) A
2) Mostre que o argumento (S (~C ~Q)) (~C Q) ~S é válido, usando o método da árvore semântica.
Ù®®«
Ù®
ÚÙ®®
®ÙÙÙ®
4.2.3 Método da negação (ou absurdo)
Esse é um método geral de demonstração. Será utilizado nesse contexto para provar se uma fbf é uma tautologia.
Suponha que se quer provar a validade de uma fórmula H. Procura-se demonstrar, a princípio, que H é falsa. Recorrendo a uma série de deduções, pode-se chegar à conclusão que, de fato, H é falsa, ou pode-se chegar a um absurdo.
Na hipótese de se concluir que H é falsa, está provado que a fórmula não é uma tautologia.
Para que o antecedente do conectivo principal, que é a conjunção – , seja verdadeiro, as expressões à esquerda e à direita deste devem ser, ambas, verdadeiras. Na situação acima, depende-se do valor de B para se tirar uma conclusão. Para que a expressão A B resulte em V, com A sendo V, B teria que ter valor V. Já a expressão B C só resulta em V se B tiver valor F. Todavia, é um absurdo atribuir valor verdadeiro e falso a B, ao mesmo tempo. Não há como provar que G tem valor lógico falso.
Conclusão:
Dizer que G é falso é um absurdo logo, G é válida. G é uma tautologia.
Ù
®
®
62
O primeiro passo para a solução é identificar o conectivo principal, aquele que será analisado por último e atribuir valor falso a esse conectivo:
G = ((A B) (B C)) (A C) F
Sendo o conectivo principal um condicional, o único caso em que será falso é quando o antecedente é verdadeiro e o conseqüente falso. Faz-se essa suposição:
G = ((A B) (B C)) (A C) V F F
Como o conseqüente é uma expressão mais simples que o antecedente, faz-se primeiro sua análise. Este será falso, somente quando seu antecedente for V e o conseqüente for F. Assim, atribui-se valor V à proposição A e F à proposição C. Depois, atribui-se esses mesmos valores às demais ocorrências das proposições A e C, na fórmula, obtendo-se a situação:
G = ((A B) (B C)) (A C) V V F F V F F
®Ù®®®
®Ù®®®
O bicondicional resulta em falso em duas situações: quando o termo à esquerda é falso e o da direita é verdadeiro ou quando a situação é inversa, o termo da esquerda é verdadeiro e o da direita é falso. Faz-se necessário testar as duas situações.
Poissibilidade 1: H = (P Q) (~P ~Q) V F F
As expressões à direita e à esquerda são ambas condicionais. Há três possibilidades de um condicional ser verdadeiro e uma de ser falso. Por esse motivo, inicia-se pelo lado direito, onde, para o antecedente ser verdadeiro e o consequente falso, P deve ter valor F e Q ter valor V. Aplicando
®«®
63
Ausência de absurdoAo se tentar negar uma fórmula que se supõe, inicialmente, verdadeira pode-se não chegar a nenhum absurdo. Em outras palavras, pode-se chegar à conclusão de que, para uma determinada interpretação I, a fórmula é falsa. Nesse caso, pode-se afirmar que a mesma não é válida, que não é uma tautologia. Entretanto, não se pode dizer que é uma contradição ou que é apenas satisfatível.
Exemplo 2:
Verificar se a fórmula H = (P Q) (~P ~Q)
Solução
Tenta-se provar que H é falsa. Para tal, atribui-se o valor lógico falso ao conectivo principal, aquele que será avaliado por último. Vê-se que é .
H = (P Q) (~P ~Q) F
®«®
«