APLICAÇÕES DA ANÁLISE LIMITE NUMÉRICA A PROBLEMAS DE ESTABILIDADE AXISSIMÉTRICOS EM GEOTECNIA

MINISTÉRIO DA EDUCAÇÃO E DO DESPORTO Universidade Federal de Ouro Preto

Escola de Minas – Departamento de Engenharia Civil

APLICAÇÕES DA ANÁLISE LIMITE NUMÉRICA A

PROBLEMAS DE ESTABILIDADE AXISSIMÉTRICOS

EM GEOTECNIA

AUTOR: WAGNER NAHAS RIBEIRO

ORIENTADORES: PROF. DR. LUIZ GONZAGA DE ARAÚJO

PROFª. DRª. CHRISTIANNE DE LYRA NOGUEIRA

UNIVERSIDADE FEDERAL DE OURO PRETO – ESCOLA DE MINAS DEPARTAMENTO DE ENGENHARIA CIVIL

PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA CIVIL

APLICAÇÕES DA ANÁLISE LIMITE NUMÉRICA A

PROBLEMAS DE ESTABILIDADE AXISSIMÉTRICOS

EM GEOTECNIA

AUTOR: WAGNER NAHAS RIBEIRO

ORIENTADORES: PROF. DR. LUIZ GONZAGA DE ARAÚJO

PROFª. DRª. CHRISTIANNE DE LYRA NOGUEIRA

Dissertação apresentada ao Programa de Pós-Graduação do Departamento de Engenharia Civil da Escola de Minas da Universidade Federal de Ouro Preto, como parte integrante dos requisitos para obtenção do título de Mestre em Engenharia Civil, área de concentração: Geotecnia.

Catalogação: sisbin@sisbin.ufop.br R484a Ribeiro, Wagner Nahas.

Aplicações da análise limite numérica a problemas de estabilidade

axissimétricos em geotecnia [manuscrito]. / Wagner Nahas Ribeiro. - 2005. x, 51f. : il., color. graf., tabs.

Orientador: Prof. Dr. Luiz Gonzaga de Araújo. Orientador: Profª. Dr.ª Christianne de Lyra Nogueira. Área de concentração: Geotecnia.

Dissertação (Mestrado) – Universidade Federal de Ouro Preto. Escola de Minas. Departamento de Engenharia Civil. Programa de Pós Graduação em Engenharia Civil, área de concentração: Geotecnia.

1. Geotecnia - Teses. 2. Análise numérica - Teses. 3. Programação não-linear. 4. Estabilidade - teses. 4. Fundações (Engenharia) - Teses. I. Universidade Federal de Ouro Preto. Escola de Minas. Departamento de Engenharia Civil. Programa de Pós-graduação em Engenharia Civil. II. Título.

iii

AGRADECIMENTOS

Ao professor Luiz Gonzaga de Araújo pela orientação neste trabalho e pelos ensinamentos passados ao longo destes anos de convivência.

À professora Christianne de Lyra Nogueira pelo auxílio e pelos esclarecimentos.

À minha família e amigos, pelo apoio e incentivo na realização deste trabalho.

Aos amigos de mestrado: Deilton, Eleonardo, Fernanda, Germano, Júnio, Rodrigo e Tadeu que passaram comigo um bom pedaço nestes dois anos.

Aos colegas do curso de pós-graduação e do LAMEC.

Aos funcionários do DECIV.

iv

RESUMO

A análise limite, via método dos elementos finitos (MEF), tem sido bastante empregada para solução de problemas de estabilidade em geotecnia. Nas formulações existentes, o problema de estabilidade é colocado como um problema de programação matemática, que pode ser linear ou não linear.

Este trabalho apresenta uma formulação mista de análise limite, via MEF, para solucionar problemas de estabilidade em geotecnia sob condição axissimétrica, onde o problema de programação matemática resultante é tratado por métodos não lineares.

O solo pode ser modelado como contínuo ou reforçado. Para discretização do contínuo são empregados elementos quadrilaterais de 4 nós. As interfaces (solo-estrutura e solo-reforço) podem ser modeladas através de elementos de interface sem espessura de 4 nós. O reforço pode ser discretizado através de elementos especiais, sem espessura, de 2 nós.

O solo e as interfaces são idealizados como rígido-plásticos perfeitos com lei de fluxo associado. Para o solo é empregado o critério de escoamento de Mohr-Coulomb e para as interfaces, o critério de Coulomb.

v

ABSTRACT

Limit analysis using the finite element method (FEM) has been used for the solution of stability problems in geotechnical engineering. In existing formulations, the stability problem is treated as a mathematical programming problem, that can be linear or non linear.

This work presents a limit analysis formulation using FEM to solve stability problems in geotechnical engineering under axisymmetrical conditions, where the obtained mathematical programming problem is treated by non linear methods.

The soil can be modeled as continuous or reinforced medium. The continuum is discretized using 4-node quadrilateral elements. The interfaces (structure and soil-reinforcement) can be modeled using 4-node zero-thickness elements. The reinforcement can be discretized through special 2-node elements, without thickness.

The soil and the interfaces are idealized as perfect rigid-plastic materials and the associated rule of plasticity is obeyed. For the soil description, the Mohr-Coulomb yield criterion is used. The yield condition for the interfaces is described by the Coulomb criterion.

vi

SUMÁRIO

LISTA DE FIGURAS ...ix

LISTA DE TABELAS... x

CAPÍTULO 1

INTRODUÇÃO ... 1

1.1 - GENERALIDADES ... 1

1.2 - FORMULAÇÕES NUMÉRICAS DE ANÁLISE LIMITE... 2

1.2.1 – Formulação de Limite Inferior... 2

1.2.2 – Formulação de Limite Superior ... 3

1.2.3 – Formulação Mista ... 3

1.2.4 – Problema de Programação Matemática ... 4

1.3 - OBJETIVOS E ORGANIZAÇÃO DO TRABALHO... 5

CAPÍTULO 2

FORMULAÇÃO MISTA DE ANÁLISE LIMITE PARA

PROBLEMAS DE DEFORMAÇÃO PLANA E AXISSIMÉTRICOS . 7

2.2 – FORMULAÇÃO MISTA PARA MEIOS CONTÍNUOS EM PROBLEMAS DE DEFORMAÇÃO PLANA... 8

2.2.1 - Equilíbrio do elemento finito... 9

2.2.2 - Condição de escoamento do material ... 10

2.2.3 – Montagem do problema de PL para meios contínuos na condição de deformação plana... 11

2.2.4 – Montagem do problema de PNL para meios contínuos na condição de deformação plana... 12

vii

2.3.1 - Equilíbrio do elemento finito... 13

2.3.2 - Condição de escoamento do material ... 14

2.3.3 - Montagem do problema de PNL para meios contínuos em problemas axissimétricos... 16

2.4 - FORMULAÇÃO PARA ELEMENTO DE REFORÇO E ELEMENTO DE INTERFACE EM PROBLEMAS AXISSIMÉTRICOS... 17

2.4.1 - Formulação do elemento de reforço ... 17

2.4.2 - Formulação do elemento de interface... 20

2.4.3 - Montagem do problema de PNL para meio reforçado ou com elemento de interface ... 24

CAPÍTULO 3

IMPLEMENTAÇÃO NUMÉRICA ... 25

3.1 - INTRODUÇÃO ... 25

3.2 – MODELOS DE ELEMENTOS IMPLEMENTADOS... 26

3.3 – FLUXOGRAMA E PROCEDIMENTO DE ANÁLISE ... 27

3.4 – EXEMPLO ILUSTRATIVO ... 28

3.4.1 - Arquivos de saída gerados pelo ANALIM ... 30

3.4.2 - Arquivos de saída gerados pelo LINDO e LINGO ... 33

CAPÍTULO 4

PROBLEMAS ESTUDADOS... 35

4.1 – INTRODUÇÃO... 35

4.2 – FUNDAÇÃO SUPERFICIAL E EMBUTIDA... 35

4.2.1 – Fundação superficial ... 36

4.2.2 – Fundação embutida ... 39

4.3 – ESCAVAÇÃO CIRCULAR... 41

4.4 – FUNDAÇÃO SUPERFICIAL EM SOLO REFORÇADO ... 42

viii

4.4.2 – Fundação superficial circular... 43

4.5 – CAPACIDADE DE CARGA DE UMA ESTACA SUJEITA À TRAÇÃO.... 44

4.6 – CONSIDERAÇÕES GERAIS SOBRE O OTMIZADOR EMPREGADO.... 46

4.6.1 – Características gerais ... 46

4.6.2 – Comentários sobre o desempenho ... 46

CAPÍTULO 5

CONCLUSÕES E SUGESTÕES... 48

5.1 - CONCLUSÕES... 48

5.2 - SUGESTÕES ... 48

ix

LISTA DE FIGURAS

CAPÍTULO 2

Figura 2.1 – Representação esquemática do elemento c 4

Q ... 8

Figura 2.2 – Elemento de solo na condição axissimétrica... 13

Figura 2.3 – Elemento de reforço ... 17

Figura 2.4 – Representação esquemática do elemento de reforço... 18

Figura 2.5 – Modelo de interface e seu sistema de coordenadas ... 21

CAPÍTULO 3

Figura 3.2 – Compressão simples de um elemento de solo ... 28

CAPÍTULO 4

Figura 4.2 – Capacidade de carga de uma fundação embutida... 39

Figura 4.3 – Escavação circular... 41

Figura 4.4 – Capacidade de carga de uma fundação em solo reforçado... 42

x

LISTA DE TABELAS

CAPÍTULO 4

Tabela 4.1 – Capacidade de carga de uma fundação corrida superficial para γ = 0 ... 37

Tabela 4.2 – Capacidade de carga de uma fundação corrida superficial para γ = 1 ... 37

Tabela 4.3 – Capacidade de carga de uma fundação circular superficial para γ = 0 ... 38

Tabela 4.4 – Capacidade de carga de uma fundação circular superficial para γ = 1 ... 38

Tabela 4.5 – Capacidade de carga de uma fundação corrida embutida para γ = 1 ... 40

Tabela 4.6 – Capacidade de carga de uma fundação circular embutida para γ = 1 ... 40

Tabela 4.7 – Capacidade de carga de uma fundação (kPa) em solo reforçado... 43

CAPÍTULO 1

INTRODUÇÃO

1.1 - GENERALIDADES

Os problemas mecânicos em geotecnia podem ser classificados em dois tipos distintos: problemas de estabilidade e de análise de tensão e deformação. Os problemas de estabilidade se referem a problemas que envolvem as condições de colapso do material, como capacidade de carga, empuxo de terra e estabilidade de taludes.

Para solução dos problemas de estabilidade, tem sido tradicionalmente empregado o método de equilíbrio limite (ver, p. ex., Terzaghi, 1943 e Taylor, 1948). Um outro tipo de abordagem para estes tipos de problemas vem sendo empregada nas últimas décadas: a Análise Limite.

A Análise Limite se baseia em dois teoremas clássicos da plasticidade, conhecidos como teoremas dos limites inferior e superior, demonstrados por Drucker et al. (1952).

A partir destes teoremas, a carga de colapso pode ser colocada entre os limites inferior e superior, possibilitando a aplicação da análise limite a problemas de estabilidade.

A Análise Limite considera a relação tensão-deformação do material como rígido plástico ideal com lei de fluxo associado.

São várias as aplicações da Análise Limite em geotecnia: cargas de colapso de fundações, empuxos de terra, estabilidade de taludes em solos e estudo de problemas de estabilidade em meio fraturado e reforçado.

2

Aplicações da Análise Limite, via MEF, vêm sendo desenvolvidas geralmente utilizando técnicas de programação matemática linear (PL) ou não linear (PNL) e condição de deformação plana em diversos problemas em geotecnia.

Uma importante aplicação proposta neste trabalho é o caso de problemas geotécnicos onde se têm condições axissimétricas de carregamento e geometria, como o caso de estacas, tubulões e sapatas circulares, sendo utilizadas técnicas de programação não linear (PNL) para solução do problema resultante da formulação.

1.2 - FORMULAÇÕES NUMÉRICAS DE ANÁLISE LIMITE

A aplicação da Análise Limite a problemas de estabilidade em geotecnia permite formulações numéricas do problema, via MEF, que podem ser colocadas sob a forma de um problema de programação matemática. Estas formulações podem ser classificadas em três grupos:

• Formulação de limite inferior; • Formulação de limite superior; • Formulação mista.

Nestas formulações, o solo ou a rocha pode ser modelado como contínuo, fraturado ou reforçado.

A maioria das formulações são propostas para problemas de deformação plana com o critério de escoamento do material na forma linearizada.

1.2.1 - Formulação de Limite Inferior

Para a aplicação da formulação de limite inferior em problemas de estabilidade, deve-se satisfazer exatamente as condições de contorno em tensão, a condição de equilíbrio e o critério de escoamento do material.

3

Os autores anteriores adotam uma aproximação do critério de escoamento para obtenção de um problema de PL para condição de deformação plana.

As formulações de Botero et al. (1978) e Sloan (1987) adotam uma sistemática que coloca as tensões como variáveis primárias e diferem-se no algoritimo para solução do problema de matemática linearizado (Lemos, 2002).

Araújo et al. (2000) empregam uma formulação em que o meio pode ser modelado como contínuo ou descontínuo, tratando de problemas de capacidade de carga e estabilidade de taludes em maciços fraturados.

Sousa (2001) utiliza uma formulação para a análise de problemas de solos reforçados onde o meio pode ser modelado como contínuo ou reforçado.

1.2.2 - Formulação de Limite Superior

As formulações de limite superior para aplicação em problemas de estabilidade devem satisfazer exatamente as condições de contorno em deslocamentos, as condições de compatibilidade e as condições de escoamento do material.

Exemplos destas formulações são os trabalhos de Tamura et al. (1984, 1987), Sloan (1989) e Turgeman e Pastor (1982). Neste último trabalho é apresentada uma formulação de limite superior em problemas axissimétricos com a aplicação dos critérios de escoamento de von Mises e de Tresca na forma linearizada.

1.2.3 - Formulação Mista

Na formulação mista procura-se atender de forma aproximada as condições necessárias para as aplicações dos teoremas de limite inferior e limite superior conjuntamente, sendo que as condições de escoamento são satisfeitas exatamente e as condições de equilíbrio e de contorno em tensão são satisfeitas aproximadamente pela interpolação dos campos de tensão e velocidade no interior do elemento (Lemos, 2002).

4

Destacam-se os trabalhos de Casciaro e Cascini (1982), Faria (1992), Araújo (1997) e Lemos (2002), como aplicações da formulação mista em condições de deformação plana.

Farfán (2000) apresenta uma formulação mista para aplicação em meios contínuos convencionais e meios de Cosserat em problemas 3D.

1.2.4 - Problema de Programação Matemática

A aplicação da Análise Limite via elementos finitos em problemas de geotecnia pode conduzir à solução de problemas de programação matemática lineares ou não lineares. Estes problemas podem ser colocados na forma padrão abaixo (Arora, 1989):

Encontre x que maximize ou minimize f(x) = f(x1,x2,...,xn)

sujeito a p restrições de igualdade:

hj(x) = hj(x1,x2,...,xn) = 0; j = 1,...,p

e sujeito a m restrições de desigualdade:

gj(x) = gj(x1,x2,...,xn) 0; j = 1,...,m

em que x é o vetor das variáveis do problema.

Os problemas podem ainda se apresentar sem qualquer função de restrição, são os problemas sem restrição.

Nos casos em que todas as funções f(x), g(x) e h(x) são funções lineares, tem-se os chamados problemas de programação linear (PL) e quando uma destas funções apresentar-se não linear, trata-se de um problema de programação não linear (PNL).

As soluções analíticas de problemas de otimização em engenharia tornam-se, geralmente, impraticáveis, devido principalmente ao grande número de variáveis e restrições envolvidas. Assim, foram desenvolvidos métodos numéricos para aplicação a estes problemas.

5

Para solução de problemas de PNL podem ser empregados diversos métodos: método do máximo declive, método do gradiente conjugado, método de Newton e métodos Quase-Newton.

O emprego de técnicas numéricas em problemas de programação matemática, associadas com programas computacionais, permite tratar problemas complexos que apresentem grande quantidade de variáveis e restrições.

Neste trabalho, para solução do problema de programação matemática resultante das formulações, são utilizados os softwares comerciais LINDO (Schrage, 1991), para solução de problemas lineares, e LINGO (Lindo Systems, 2001), para solução de problemas não lineares.

1.3 - OBJETIVOS E ORGANIZAÇÃO DO TRABALHO

Este trabalho tem como objetivos a apresentação e a validação de formulações mistas de análise limite, via MEF, para problemas planos de deformação ou axissimétricos.

Os meios podem ser modelados como contínuos ou reforçados. Podem ser utilizados, também, elementos de interface para modelagem da interação solo-estrutura e solo-reforço.

O presente trabalho está dividido em cinco capítulos, organizados de maneira que reproduza a sequência dos procedimentos realizados durante a implementação computacional das formulações.

O capítulo 1 apresenta uma breve introdução ao trabalho.

No capítulo 2 apresentam-se as formulações para meios contínuos em problemas de deformação plana e axissimétricos, as formulações para elemento de reforço e elemento de interface para problemas axissimétricos.

Apresenta-se um esboço da formulação para problemas planos de deformação descrita em Lemos (2002) e uma formulação para problemas axissimétricos.

6

(solo-estrutura e solo-reforço) são utilizados elementos sem espessura de 4 nós e para o reforço, elementos especiais de 2 nós.

No capítulo 3 está descrita sucintamente a implementação realizada e os procedimentos para a análise de um problema de estabilidade.

CAPÍTULO 2

FORMULAÇÃO MISTA DE ANÁLISE LIMITE PARA

PROBLEMAS DE DEFORMAÇÃO PLANA E

AXISSIMÉTRICOS

2.1 - INTRODUÇÃO

A formulação mista busca fornecer um valor aproximado para a verdadeira carga de colapso, atendendo de forma aproximada as condições necessárias para as aplicações dos teoremas de limite inferior e limite superior, como visto no capitulo 1.

Várias formulações numéricas mistas de análise limite, para problemas de deformação plana em meios contínuos, têm sido apresentadas nas últimas décadas.

Os trabalhos de Casciaro e Cascini (1982), Faria (1992), Araújo (1997) e Lemos (2002) são exemplos de aplicação da formulação mista.

Lemos (2002) apresenta em seu trabalho formulações para o emprego de elementos de reforço e interface em meios contínuos, fraturados ou reforçados, em problemas de deformação plana.

Neste trabalho apresentam-se formulações para meios contínuos e reforçados para problemas em deformação plana e axissimétrico. São apresentadas, também, formulações de elementos de interface e reforço para problemas axissimétricos.

Para problemas de deformação plana são consideradas as seguintes condições:

; 0 yz xz

z ==== ==== ====

e o estado de tensão é definido por:

[[[[

]]]]

= == = σ σ σ

σT .

Para problemas axissimétricos são consideradas as seguintes condições:

;

0

z rθ ====γ θ ====

γ

8

[[[[

]]]]

T

= = = = σ σ σ

σ .

Para a discretização do meio contínuo são utilizados elementos quadrilaterais bidimensionais de 4 nós com a interpolação do campo de velocidades bilinear e do campo de tensões constante no interior do elemento, elemento c

4

Q . A Figura 2.1 mostra um arranjo de elementos quadrilaterais de 4 nós para o caso de tensão constante.

Figura 2.1 – Representação esquemática do elemento c 4

Q

A formulação para elementos de reforço e de interface é apresentada, ao final deste capítulo, para o caso de interpolação linear da velocidade e de tensão constante, ao longo do elemento.

2.2 - FORMULAÇÃO MISTA PARA MEIOS CONTÍNUOS EM PROBLEMAS DE DEFORMAÇÃO PLANA

Várias formulações mistas de análise limite, em deformação plana e em meios contínuos, têm sido apresentadas nestas últimas décadas. Os trabalhos de Christiansen (1981), Casciaro e Cascini (1982), Faria (1992), Araújo (1997) e Lemos (2002) são exemplos de emprego destas formulações.

Nesta seção, é apresentado um esboço da formulação para meio contínuos, descrita por Lemos (2002), para a condição de deformação plana.

9

2.2.1 - Equilíbrio do elemento finito

Para a obtenção da condição de equilíbrio de um elemento finito é aplicado o princípio dos trabalhos virtuais que conduz à uma equação da forma (Araújo, 1997; Vargas et al. 2004):

e

T _f

B σσσσ ====

V dV ;

em que:

u

H B====∇∇∇∇

é a matriz que relaciona deslocamento e deformação (Cook, 1989);

∇ ∇∇ ∇ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ = x y y 0 0 x

é o operador diferencial para condição de deformação plana;

[[[[

]]]]

Hu ==== N1 N2 N3 N4

é a matriz que contém as funções de interpolação do deslocamento;

I é a matriz identidade (2x2);

k

N são as funções de interpolação (Cook, 1989), k = 1, ..., 4; σ

σ σ

σ é o vetor das componentes de tensão no domínio do elemento;

e

f é o vetor de carregamento nodal equivalente do elemento.

A interpolação das tensões, σσσσ, no domínio do elemento pode ser definida pela seguinte expressão: σ σ σ σ σ σ σ

σ====Hσσσσˆ ;

em que para elemento de tensão constante:

I Hσσσσ ==== ,

Ié a matriz identidade (3x3), e

[[[[

]]]]

= == = σ σ σ σˆT

é o vetor das componentes de tensão no domínio do elemento;

(2.1)

10

A substituição de σσσσ, equação (2.2), na equação (2.1), fornece a equação de equilíbrio do elemento:

e T

e ˆ f

C σσσσ==== ; em que: = = = = V dV T T e B C

é a matriz de equilíbrio do elemento.

A obtenção da matriz de equilíbrio do elemento, T e

C , pode ser feita pelo método de integração numérica de Gauss (Bathe, 1982).

2.2.2 - Condição de escoamento do material

Como visto no Capítulo 1, o problema de programação matemática pode ser classificado em linear (PL) e não linear (PNL). Nas aplicações deste trabalho estes tipos de problemas aparecem da aplicação do critério de escoamento de Mohr-Coulomb, como descrito a seguir.

A relação que representa o critério de escoamento, na sua forma não linear, é definida abaixo, para problemas de deformação plana (Sloan, 1987):

0 ] sen ) ( ccos 2 [ ) (2 ) ( ) F( 2 y x 2 xy 2 y

x −−−− ++++ −−−− −−−− ++++ ≤≤≤≤

= = = =

σ ,

que pode ser colocada na forma simbólica abaixo:

0 ) F(σ ≤≤≤≤ .

Nesta relação estão envolvidas as três componentes de tensão para o caso de deformação plana, em que c é a coesão do material e é o ângulo de atrito do material.

Para formular o problema de estabilidade como problema de programação linear, é necessário aproximar a relação (2.5) sob forma linear das tensões incógnitas. Isto pode ser feito pela aproximação da superfície de escoamento por um poliedro interno ou externo constituído de NH hiperplanos (Sloan, 1987).

A utilização deste procedimento fornece a seguinte relação para a condição de escoamento do material (Sloan, 1987):

e T

e R

Q σσσσ ≤≤≤≤

em que:

(2.3)

(2.4)

(2.5)

11 = = = = NH NH NH 2 2 2 1 1 1 C B A C B A C B A T e Q

é a matriz das restrições de escoamento do material no elemento e, onde a tensão é

definida; NH) cos( sen NH) k 2 cos(

A_k ==== ++++ ; k = 1, 2, ..., NH NH) cos( sen NH) k 2 cos(

B_k ====−−−− ++++ ; k = 1, 2, ..., NH NH)

k 2 sen( 2

C_k ==== ; k = 1, 2, ..., NH

T e

R =

[

(

)

(

)

(

)

]

é o vetor dos termos independentes das restrições de escoamento do material no elemento e, com NH componentes.

Neste trabalho as técnicas não linear e linear são utilizadas.

2.2.3 - Montagem do problema de PL para meios contínuos na condição de deformação plana

Para o caso de linearização do critério de escoamento e condição de deformação plana, o problema final de programação matemática é da forma (Lemos, 2002):

Max λ sujeito a

0 p

T_{X f f}

C ==== ++++ (restrições de equilíbrio)

R X QT ≤ ≤ ≤

≤ (conjunto de todas restrições de escoamento) em que:

T

C é obtida pela montagem das matrizes de equilíbrio para cada um dos elementos da malha;

[[[[

]]]]

xy ne y ne x 1 xy 1 y 1 x = = = = T X

é o vetor das variáveis do problema com 3⋅⋅⋅⋅ne componentes, onde ne é o número de

elementos da malha;

(2.7)

12 = = = = T ne T 1 Q 0 0 0 0 0 0 Q QT

é a matriz global das restrições de escoamento do material obtida para o caso de critério de escoamento linearizado aplicado a cada elemento da malha;

[[[[

]]]]

ne T

2 T 1

T _{R R R}

R ====

é o vetor global dos termos independentes das restrições de escoamento do material;

f é o vetor de carregamento global equivalente que pode ser desmembrado em duas parcelas (Faria, 1992):

p 0 p

v f f f

f

f ==== ++++ ==== ++++ ; em que:

0

v f

f ====

é o vetor do carregamento nodal equivalente devido às cargas variáveis;

0

f é o vetor do carregamento equivalente devido às cargas iniciais que são ampliadas pelo fator escalar de proporcionalidadeλ;

p

f é o vetor do carregamento nodal equivalente devido às cargas permanentes que são aquelas que não são ampliadas pelo fator .

A montagem dos vetores f_p e f₀ segue a sistemática convencional do MEF e o valor de λ que resolve o problema anterior é chamado fator de colapso.

2.2.4 - Montagem do problema de PNL para meios contínuos na condição de deformação plana

Para o caso de aplicação do critério de escoamento na sua forma não linearizada, o problema final de programação matemática é da forma:

Max λ sujeito a

0 p

T_{X f f}

C ==== ++++λ (restrições de equilíbrio)

0 )

13

No problema anterior as restrições de equilíbrio são as mesmas apresentadas no caso de problema linear. O símbolo F(X)≤≤≤≤0 representa um sistema de desigualdades

referentes à aplicação do critério de escoamento, relação (2.5), a todos elementos da malha.

Os problemas de programação matemática resultantes, PL e PNL, podem ser resolvidos por programas comerciais. Neste trabalho foram utilizados o software LINDO (Schrage, 1991) para solução dos problemas de PL e o software LINGO (Lindo Systems, 2001) para solução dos problemas de PNL.

2.3 - FORMULAÇÃO MISTA PARA MEIOS CONTÍNUOS EM PROBLEMAS AXISSIMÉTRICOS

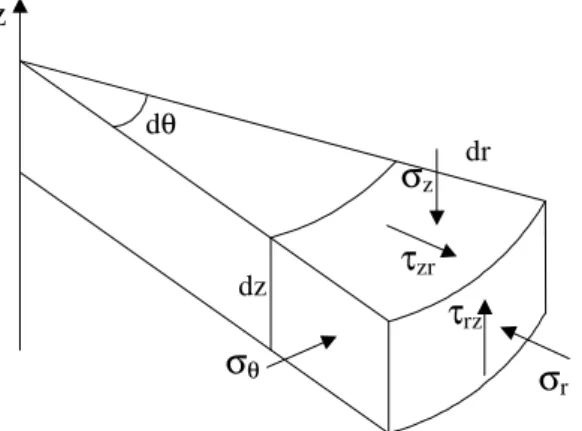
A Figura 2.2 apresenta um elemento de solo na condição axissimétrica e as componentes de tensão σr, σz, σθ e τrz atuantes no elemento.

Figura 2.2 –Elemento de solo na condição axissimétrica

2.3.1 - Equilíbrio do elemento finito

Como dito anteriormente, o equilíbrio de um elemento finito pode ser representado pela relação (2.1).

Para problemas axissimétricos a matriz B que relaciona as deformações com deslocamentos é dada por:

u

H

B====∇∇∇∇ (2.9)

σr

σz

σθ

τzr

τrz

dr

dz dθ

14 em que: ∇ ∇∇ ∇ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ∂ = 0 r

1z r

z 0

0 r

é o operador diferencial para o caso axissimétrico.

A interpolação das tensões no domínio do elemento, σσσσ, é definida por expressão análoga à apresentada para o caso de deformação plana:

σ σ σ σ = = = = σ σ σ

σ Hˆ ;

em que, para elemento de tensão constante:

I

Hσ = , e Ié a matriz identidade (4x4) e

[[[[

]]]]

= == = σ σ σ

σˆT .

A substituição de B, equação (2.9) e σσσσ, equação (2.10), na equação (2.1), fornece a equação de equilíbrio do elemento:

e T

e ˆ f

C σσσσ==== ; em que:

=

VB HdV

CT T

e

é a matriz de equilíbrio do elemento.

A obtenção da matriz de equilíbrio do elemento, T e

C , pode ser feita de maneira análoga ao caso de deformação plana, em que dV=2πrdrdz.

2.3.2 - Condição de escoamento do material

O critério de escoamento de Mohr-Coulomb pode ser colocado, em termos das tensões principais, sob a forma:

) cos( c 2 + ) sen( ) + ( = )

-(σ₁ σ₃ σ₁ σ₃ ϕ ϕ .

O critério de Mohr-Coulomb envolve somente as tensões principais extremas σ1 e

σ3, não considerando a tensão intermediária σ2.

(2.10)

(2.11)

(2.12)

15

σ1, σ2 e σ3 são as tensões principais organizadas em ordem decrescente.

A relação (2.13) pode ser colocada sob a forma: cn

m

3 1=σ +

σ ; em que: ) sen( -1 ) sen( 1 m ϕ ϕ + ++ + = = =

= e

) sen( -1 ) cos( 2 n ϕ ϕ = == = .

Em problemas axissimétricos, a tensão circunferencial σθ é uma tensão principal.

As outras duas tensões principais podem ser definidas pelas expressões a seguir:

2 rz 2 z r z r a 2 2 τ σ σ σ σ

σ ====( ++++ )−−−− −−−− ++++ ,

2 rz 2 z r z r b 2 2 τ σ σ σ σ

σ ====( ++++ )++++ −−−− ++++ .

Portanto, as tensões principais são σa, σb e σ =c ===σθ.

Assim, as tensões principais devem satisfazer às seguintes hipóteses: 1) Hipótese 1

b c

a σ σ

σ ≤≤≤≤ ≤≤≤≤

= == = = = = = = == = b 1 c 2 a 3 σ σ σ σ σ σ

2) Hipótese 2

c b

a σ σ

σ ≤≤≤≤ ≤≤≤≤

= == = = = = = = = = = c 1 b 2 a 3 σ σ σ σ σ σ

3) Hipótese 3

b a

c σ σ

σ ≤≤≤≤ ≤≤≤≤

= = = = = = = = = = = = b 1 a 2 c 3 σ σ σ σ σ σ

Empregando-se as tensões principais σ1 e σ3 definidas nas hipóteses 1, 2 e 3 e a

relação (2.14), obtêm-se a condição de escoamento definida pelas relações:

(

)

(

)

2 m 1 2 ) ( 2 rz 2 z r z

r +σ _{− +} σ −σ _{+τ + − ≤}

σ

;

(2.14)

(2.15)

16 0 cn m 2 2 ) ( 2 rz 2 z r z

r +σ ₋ σ −σ _{+τ − ≤}

σ −

σθ ;

(

)

Para o caso particular de material de Tresca, ϕ = 0º, a relação (2.15) fornece m = 1 e n = 2. Aplicando-se estes valores nas relações (2.16), (2.17) e (2.18), estas relações se tornam as mesmas apresentadas por Turgeman e Pastor (1982).

2.3.3 - Montagem do problema de PNL para meios contínuos em problemas axissimétricos

Para o caso de aplicação do critério de escoamento de Mohr-Coulomb em problemas axissimétricos, dado pelas relações (2.16), (2.17) e (2.18), o problema final de programação matemática é da forma:

Max λ sujeito a

0 p

T_{X f f}

C ==== ++++λ (restrições de equilíbrio)

0 X

F( )≤≤≤≤ (conjunto de todas restrições de escoamento) Neste problema, o símbolo F(X)≤≤≤≤0 representa o conjunto das relações (2.16),

(2.17) e (2.18) aplicadas a cada elemento da malha.

A montagem dos vetores f_pe f₀segue a sistemática apresentada para o caso de problemas planos de deformação, sendo que para o caso de problemas axissimétricos o volume elementar é dado por dV = 2πrdrdz.

O problema de programação matemática resultante, que constitui um problema de PNL, como já destacado, pode ser resolvido por programas comerciais. Neste trabalho foi utilizado o software LINGO (Lindo Systems, 2001) para solução dos problemas de PNL.

(2.17)

17

2.4 - FORMULAÇÃO PARA ELEMENTO DE REFORÇO E ELEMENTO DE INTERFACE EM PROBLEMAS AXISSIMÉTRICOS

Neste item são apresentadas formulações para elemento de reforço e elemento de interface para condições axissimétricas. Uma formulação desses elementos para problemas de deformação plana pode ser encontrada em Lemos (2002).

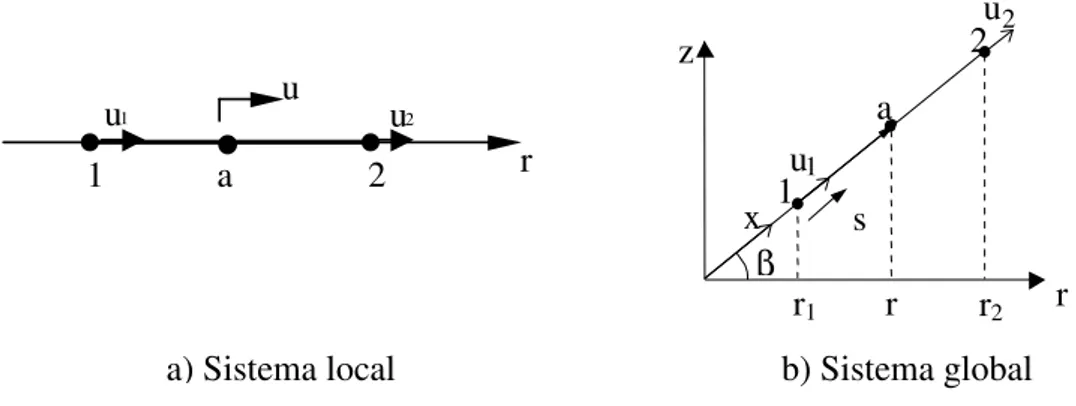
2.4.1 - Formulação do elemento de reforço

A Figura 2.3 apresenta um elemento de reforço, visto em perspectiva e projetado no plano horizontal, e as tensões atuantes.

Figura 2.3 – Elemento de reforço

2.4.1. a) - Equilíbrio do elemento de reforço

A seguir, apresenta-se a formulação do elemento de reforço, interpolado de forma linear em velocidade e constante em tensão, para problemas axissimétricos. A Figura 2.4 ilustra um elemento de reforço de comprimento Lr, e o ângulo (β) formado entre o

elemento de reforço e o eixo or no sistema global de coordenadas. b) Projeção

r σx

σx

σθ

σθ

β1

2

espessura e x

θ z

18

Figura 2.4 – Representação esquemática do elemento de reforço

O campo de velocidade u(x) no sistema local de coordenadas do elemento, tem-se a equação abaixo:

u H u(x)==== uˆ;

em que:

[[[[

]]]]

== =

T

uˆ

é o vetor das velocidades nodais e

[[[[

]]]]

= = = = u H

é matriz das funções de interpolação dos deslocamentos do elemento de reforço definidas no sistema de coordenada natural s ∈ [0,1] onde h₁ ====1−−−−s e h₂ ====s.

O vetor de deformações para o reforço axissimétrico pode ser definido como:

u H H u u r ˆ x dx d x = = = = = = = =

em que εx é a deformação radial e εθ é a deformação circunferencial do reforço.

O vetor das forças internas, fin, do elemento de reforço é definido pela expressão

abaixo: = = = =

vB tdV

f T in ; em que: − = = x h x h L 1 L 1 x dx d 2 1 r r u u H H B (2.19) (2.20) (2.21) a) Sistema local b) Sistema global

r u 1

1 a 2

u

u 2

1

2 u 2

u 1 a r z s x β

19

é a matriz que relaciona velocidade e taxa de deformação e

[[[[

]]]]

= = = = T t

é o vetor das componentes de tensão no elemento de reforço.

Na expressão (2.20), dV representa o volume elementar gerado pela revolução de um elemento de arco do reforço de espessura er em torno do eixo oz, cuja expressão

pode ser dada pela fórmula abaixo: dV = er dS;

em que dS é o elemento de área dado por:

dS = 2πr

((((

))))

((((

))))

Para elemento de tensão constante, tˆ====t, a equação (2.20) permite escrever a relação abaixo:

T C

f T

R

in ==== ˆ ;

em que: = == = = = = = 1

0 2 eLrrds

dV T π

V T T

R B B

C

é a matriz de equilíbrio do elemento de reforço no sistema local de coordenadas, e empregando-se a relação (2.21) na relação (2.23), obtém-se a expressão:

. ds L e 2 x r h L r x r h L r 1

0 r r

2 r 1 r − −− − = = = = T R C

A Figura 2.4 permite escrever a relação r = x cos(β), que incluída na relação anterior, conduz à seguinte matriz integrada analiticamente:

= = = = ) cos( L ) r + (r ) cos( L ) r + (r -e r 2 1 r 2 1 r β β T R C = = = = 2 1 T T ˆ

T = x

r

e

(2.22)

(2.23)

20

é o vetor das forças internas atuantes no elemento de reforço, onde T1 representa a

tensão radial σ_x e T2 representa a tensão circunferencialσθ, multiplicadas pela

espessura do reforço er.

Para exprimir a matriz T R

C do elemento de reforço no sistema global de coordenadas, basta multiplicar a matriz T

R

C da relação (2.24) pela matriz R apresentada abaixo (Cook, 1989):

= = = =

β β β

β

sen 0

cos 0

0 sen

0 cos

T

R .

Assim, a matriz T gl

C , em coordenadas globais, pode ser expressa por:

T R T T

gl R C

C ==== .

2.4.1. b) - Condição de escoamento do reforço

Neste trabalho considerou-se que não há escoamento do reforço. Assim, não são aplicadas restrições às tensões no reforço no problema final de programação matemática.

A aplicação do critério de escoamento do reforço, entretanto, pode ser perfeitamente incorporada nesta formulação, bastando acrescentar as restrições referentes ao critério de escoamento aplicadas a cada elemento de reforço.

2.4.2 - Formulação do elemento de interface

Uma formulação para elemento de interface é apresentada a seguir para o caso de problemas axissimétricos. É utilizado o elemento constante em tensão e linear em velocidades.

2.4.2. a) - Equilíbrio do elemento de interface

A Figura 2.5 ilustra um elemento de interface de comprimento Li, com 4 pontos

21

Figura 2.5 – Modelo de interface e seu sistema de coordenadas

A deformação do elemento de interface no sistema de referência local da interface pode ser definida por:

b a

j ====u −−−−u

εεεε .

Interpolando-se as velocidades nos pontos a e b, de mesmas coordenadas, obtêm-se as obtêm-seguintes equações:

4 3

a u u

u ====h2 ++++h1 ;

2 2

1 h

h u u ub ==== 1 ++++ ;

em que:

[[[[

]]]]

= = = = T a u

é a velocidade no ponto a;

[[[[

]]]]

= = = = T b u

é a velocidade no ponto b; s

1

h₁==== −−−− e h₂ ====s

são as funções lineares de interpolação das velocidades; s ∈ [0,1];

[[[[

]]]]

= = = = T k u

é a velocidade no ponto nodal k (k = 1, ..., 4).

A substituição das velocidades nos pontos a e b, equações (2.26) e (2.27), na equação (2.25), fornece a deformação da interface εεεεj, na forma abaixo:

j j

j ====B uˆ

εεεε ;

(2.25)

(2.26) (2.27)

(2.28) a) Modelo com interface

u 1

1 4

3

2 u 3

u 4

u 2

v 4

v 3

v 1

v 2

u a

u b

n _t a

r, u z, v

b) Elemento de interface solo

solo

interface

L i

22 em que:

[[[[

]]]]

j H H H H

B ==== −−−− −−−− ;

I

Hk ====hk ; k = 1,2; Ié a matriz identidade (2x2);

[[[[

]]]]

4 T 3 T 2 T 1

ˆ u u u u

uT

j ====

é o vetor das velocidades nos pontos nodais do elemento da interface.

O vetor das forças internas, f_in, do elemento de interface pode ser expresso pela equação abaixo: σ σ σ σ = = = =

S jdS

T j in B f ; em que:

[[[[

]]]]

σTj

é o vetor das tensões de cisalhamento e normal atuantes na interface.

Na expressão (2.29), dS representa a área elementar gerada pela revolução de um elemento de arco da interface em torno do eixo oz, cuja expressão pode ser dada por:

dS=2πLirds.

Para o elemento de interface de tensão constante, vale a seguinte expressão:

j j ====Iσσσσ

σ σ σ

σ ˆ .

Aplicando-se a equação (2.30) à equação (2.29), a equação de equilíbrio do elemento de interface pode ser colocada sob a forma:

j T j

in C

f ==== σσσσˆ .

Integrando-se T j

B , obtém-se a matriz de equilíbrio no sistema local de coordenadas da interface, sob a seguinte forma:

+ ++ + + + + + + ++ + − −− − + + + + − −− − = == = = == = I ) ( I ) ( I ) ( I ) ( I B C T j T j 2 1 2 1 2 1 2 1 i s r r 2 r 2 r r 2 r r r 2 3 L

dS π .

A integral na relação (2.32) é calculada no sistema local de coordenadas com dS=2πLirds e s ∈ [0,1].

(2.29)

(2.30)

(2.31)

23 A transformação da matriz T

j

C para o sistema global de coordenadas é realizada pelo produto de I pela matriz M de rotação de vetores, dada abaixo:

− −− − = = = = β β β β cos sen sen cos T M .

Desta forma, a matriz T glj

C no sistema global pode ser colocada na forma:

+ ++ + + ++ + + + + + − −− − + + + + − −− − = = = = T T T T T glj M ) ( M ) ( M ) ( M ) ( C 2 1 2 1 2 1 2 1 i r r 2 r 2 r r 2 r r r 2 3 L π .

2.4.2. b) - Condição de escoamento da interface

O critério de escoamento de Coulomb é usado para modelar a condição de escoamento da interface e pode ser escrito sob a forma:

in N

in tg

c σ φ

τ≤≤≤≤ −−−− ;

in N

in tg

c σ φ

τ≤≤≤≤ −−−− −

−−

− ;

em que c é a coesão da interface solo-reforço e _in φ_iné o ângulo de atrito da interface solo-reforço.

As relações (2.34) e (2.35) definem uma região viável para as tensões no elemento de interface (Lemos, 2002), que podem ser colocadas na forma matricial abaixo:

j i j i T j i R

Q ) σσσσ ≤≤≤≤

( ; em que: − −− − = = = = in in tg 1 tg 1 ) ( φ φ T j i Q

é a matriz das restrições de escoamento num elemento de interface;

[[[[

]]]]

= = = = σ σ σ σij)T (

é o vetor das tensões atuantes no interior do elemento de interface;

[[[[

]]]]

)

(Rj_i T ====

é o vetor dos termos independentes das restrições de escoamento num elemento de interface.

(2.33)

(2.34) (2.35)

24

2.4.3 - Montagem do problema de PNL para meio reforçado ou com elemento de interface

A montagem na forma matricial das condições equilíbrio do solo, equação (2.4), do reforço, equação (2.23), e da interface, equação (2.33), para todos os elementos de solo, reforço e interface, conduz à equação de equilíbrio global, na forma abaixo:

p 0

T_{X f f}

C ==== λ ++++ ; em que:

[[[[

]]]]

r T j T s

T _{C C C}

C ==== ( ) ( ) ( )

é a matriz global de equilíbrio resultante da contribuição dos elementos de solo, interface e reforço;

[[[[

]]]]

T j T j T T T T

X ==== σ σ σ σ σ

é o vetor das componentes de tensão em todos os elementos de solo, interface e reforço,

nt é o número de elementos onde as tensões são definidas, nj é o número de elementos

de interface e nr é o número de elementos de reforço.

Da imposição da condição de escoamento do solo, relações (2.16), (2.17) e (2.18) aplicadas a cada elemento da malha, obtêm-se o conjunto de restrições abaixo:

0 ) X F( ≤≤≤≤ .

Da imposição da condição de escoamento da interface, relação (2.36), obtêm-se um conjunto de restrições lineares da forma:

R X QT ≤ ≤ ≤ ≤ .

Assim, a formulação conduz a um problema de PNL, que pode ser colocado sob a forma:

Max λ sujeito a

0

f f X

CT = p+ (restrições de equilíbrio) 0

) X

F( ≤≤≤≤ (conjunto de todas restrições de escoamento do solo, não linear)

R X QT

≤ ≤≤

CAPÍTULO 3

IMPLEMENTAÇÃO NUMÉRICA

3.1 - INTRODUÇÃO

Neste trabalho foram utilizadas as implementações inicialmente elaboradas por Araújo (1997) e modificadas por Lemos (2002). Estas implementações são baseadas na formulação mista da Análise Limite e foram realizadas utilizando-se a linguagem de programação Fortran no ambiente Microsoft Fortran Power Station 4.0 para Windows (Microsoft, 1995) e recursos de alocação dinâmica de memória.

A versão elaborada por Lemos (2002), programa ANALIM, permite a modelagem do meio como contínuo, fraturado ou reforçado, na condição de deformação plana, com a solução do problema pela programação linear (PL).

A implementação realizada neste trabalho consistiu na extensão da implementação realizada por Lemos (2002) e na aplicação de programação não linear e análise de problemas em condições axissimétricas.

O procedimento para implementação da formulação proposta neste trabalho foi realizado de acordo com as seguintes etapas:

• aplicação de critério de escoamento na forma não linear e adaptação da saída do programa ao formato de entrada do software de solução;

• obtenção e impressão das restrições de equilíbrio do elemento para problemas axissimétricos;

• implementação da formulação de elementos de reforço em condições axissimétricas e

• implementação da formulação de elementos de interface em condições axissimétricas.

26

A seguir são apresentados os aspectos da implementação realizada, como os modelos implementados, o fluxograma e um exemplo ilustrativo de uso da implementação.

3.2 - MODELOS DE ELEMENTOS IMPLEMENTADOS

Para modelagem de problemas em meios contínuos em condições de deformação plana e axissimétricos foram utilizados elementos quadrilaterias de 4 nós com interpolação do campo de velocidades de forma bi-linear e de tensões constante (elemento c

4

Q ).

Para o critério de escoamento do solo é utilizado o critério de Mohr-Coulomb ou de Tresca, como caso particular do de Mohr-Coulomb (ϕ = 0º). Foram implementadas, para problemas planos de deformação, as formas não linear e linearizada destes critérios. Para análise de problemas axissimétricos foi implementado o critério de Mohr-Coulomb na forma não linear.

27

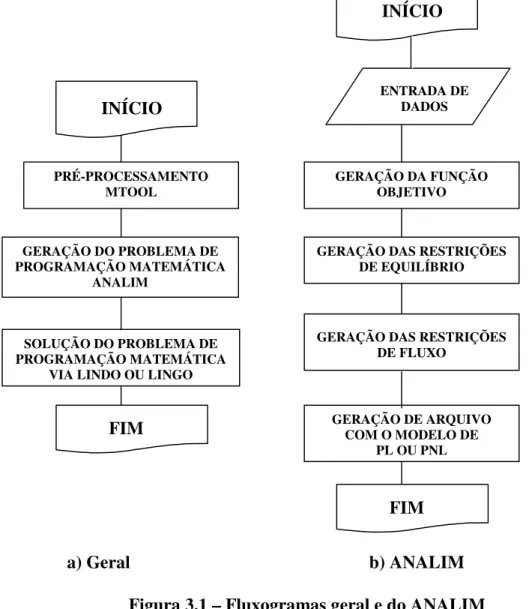
3.3 - FLUXOGRAMA E PROCEDIMENTO DE ANÁLISE

O procedimento geral utilizado nesta implementação para se obter a carga de colapso está mostrado na Figura 3.1a e pode ser dividido em três etapas: pré-processamento através do programa Mtool, geração do problema de PL ou PNL via ANALIM (Lemos, 2002) e solução deste problema através de software comercial, LINDO ou LINGO.

Figura 3.1 – Fluxogramas geral e do ANALIM

O pré-processamento é realizado através do software Mtool que permite a modelagem da geometria, do carregamento e das propriedades dos materiais. Nesta etapa, o domínio do problema é discretizado em elementos quadrilaterais e elementos de interface, se for o caso. Um arquivo de extensão .nf é gerado pelo Mtool para entrada de

INÍCIO

ENTRADA DE DADOS

GERAÇÃO DA FUNÇÃO OBJETIVO

GERAÇÃO DE ARQUIVO COM O MODELO DE

PL OU PNL

FIM

GERAÇÃO DAS RESTRIÇÕES DE EQUILÍBRIO

GERAÇÃO DAS RESTRIÇÕES DE FLUXO

INÍCIO

PRÉ-PROCESSAMENTO MTOOL

SOLUÇÃO DO PROBLEMA DE PROGRAMAÇÃO MATEMÁTICA

VIA LINDO OU LINGO

FIM

GERAÇÃO DO PROBLEMA DE PROGRAMAÇÃO MATEMÁTICA

ANALIM

28

dados no programa ANALIM. Este arquivo pode ser também utilizado por editores de texto para introdução de elementos de reforço e suas características.

Com o arquivo de entrada gerado pelo Mtool e palavras chaves criadas por um editor de texto, o programa ANALIM é executado e o problema de programação matemática é gerado em arquivo.

A modelagem de problemas planos de deformação ou axissimétricos é realizada em uma mesma implementação, a seleção entre estes tipos de análise é realizada pela introdução de uma palavra chave no arquivo gerado pelo Mtool.

De acordo com o problema de programação matemática, o ANALIM pode gerar dois tipos de arquivos: arquivo com extensão .lin para problemas de PL e arquivo com extensão .lng para problemas de PNL.

Como etapa final é realizada a solução do modelo de programação matemática gerado pelo ANALIM. Para problemas de PL é utilizado o software LINDO e para problemas de PNL, o software LINGO.

3.4 - EXEMPLO ILUSTRATIVO

Para ilustrar a utilização da implementação realizada, é apresentada neste item a análise de um exemplo de compressão simples tratado pela técnica não linear nas condições de deformação plana e axissimétrica.

O problema está esquematicamente mostrado na Figura 3.2. Para solução numérica, o meio é discretizado em um único elemento retangular com o solo tendo as seguintes propriedades: c = 1, ϕ = 0º e γ = 0.

Figura 3.2 – Compressão simples de um elemento de solo

λq0

AB = BC = CD =DA = 1.0

A B C

D

Ponto Nodal (A-B-C-D) Elemento 1

29

De acordo com a teoria de Terzaghi (1943), a carga de colapso (resistência à compressão simples), para este caso, pode ser dada por:

σc = 2 c tg (45o + ϕ/2) = 2,

em que:

σc = carga de colapso = resistência à compressão simples;

c é a coesão do material;

ϕ é o ângulo de atrito do material;

A solução numérica do problema (qu) é dada pela expressão:

qu = λq0.

Como q0 é unitária, resulta que:

qu = λ,

em que λ é o fator de colapso.

A análise numérica via ANALIM forneceu um resultado para a carga de colapso igual a 2 (dois), tanto para o caso de deformação plana quanto para o caso axissimétrico, coincidindo com o resultado de Terzaghi.

Este problema foi escolhido por se tratar de um dos exemplos mais simples encontrados na literatura, que pode ser resolvido com um só elemento finito, e que servirá de exemplo para os arquivos mostrados a seguir para os casos de deformação plana e axissimétrico.

30

Quadro 1 - Modelo de PNL gerado pelo ANALIM

3.4.1 - Arquivos de saída gerados pelo ANALIM

A geração dos modelos de programação matemática em arquivo segue o fluxograma mostrado na Figura 3.1b. Além disso, no arquivo de saída, todas as variáveis são declaradas como “FREE”, para que possam ter sinal positivo ou negativo.

3.4.1. a) - Análise de deformação plana

As componentes de tensão para problemas de deformação plana e elemento

c 4

Q são associadas às variáveis matemáticas na seguinte forma para o primeiro elemento: X3 → Componente de tensão cisalhante no elemento 1 (τxy);

%HEADER

File created by mtool program %ANALYSIS.TYPE 2

%PL.PNL.PROGRAMMING 2

%NODE 4

%NODE.COORD 4

1 0.000000 0.000000 0.000000 2 1.000000 0.000000 0.000000 3 0.000000 1.000000 0.000000 4 1.000000 1.000000 0.000000 %NODE.SUPPORT

3

1 0 1 0 0 0 0

2 0 1 0 0 0 0

3 1 0 0 0 0 0

%MATERIAL 1

%MATERIAL.LABEL 1

1 'comp 1'

%MATERIAL.MOHR_COULOMB 1

1 0 24 1 0

%ELEMENT 1

%ELEMENT.Q4 1

1 1 0 1 4 3 1 2

%LOAD.CASE.EDGE.FORCES 1

1 3 4 0 0 -1 -1

31

X2 → Componente de tensão vertical no elemento 1 (σy);

X1 → Componente de tensão horizontal no elemento 1 (σx).

Para o caso de uma malha mais refinada, a associação de variáveis para os elementos da malha é da forma: componente de tensão cisalhante no elemento i → X(3*i), componente de tensão vertical no elemento i → X((3*i)-1) e componente de tensão horizontal no elemento i → X((3*i)-2).

A variável matemática imediatamente posterior às variáveis associadas às componentes de tensão representa o fator de proporcionalidade λ (ver seção 2.2.3), no caso X4, como pode ser visto no Quadro 2.

Quadro 2 - Modelo de PNL gerado pelo ANALIM

No modelo de PNL do Quadro 2, a linha 1 representa a condição de escoamento imposta às componentes de tensão do elemento e as linhas 2-6 representam as equações de equilíbrio para o elemento.

3.4.1. b) - Análise axissimétrica

As componentes de tensão para problemas axissimétricos e elemento c 4

Q são associadas às variáveis matemáticas na seguinte forma:

X4 → Componente de tensão circunferencial no elemento 1 (σθ);

MAX =X4; !SUBJECT TO;

!restrições de fluxo da rocha intacta; ! 1);

(X1-X2)^2+(2*X3)^2-(2*1.00*(1.00)-(X1+X2)*(0.00))^2 < 0.00; ! restrições de equilíbrio;

! 2);

+2.00000*X1 +2.00000*X3 = .000000; ! 3);

-2.00000*X1 +2.00000*X3 = .000000; ! 4);

-2.00000*X2 +2.00000*X3 -2.00000*X4 = .000000; ! 5);

-2.00000*X1 -2.00000*X3 = .000000; ! 6);

-2.00000*X2 -2.00000*X3 -2.00000*X4 = .000000; @FREE(X1);

32

X3 → Componente de tensão cisalhante no elemento 1 (τrz);

X2 → Componente de tensão vertical no elemento 1 (σz);

X1 → Componente de tensão horizontal no elemento 1 (σr).

Para os demais elementos, no caso de uma malha mais refinada, a associação é da forma: componente de tensão circunferencial no elemento i → X(4*i); componente de tensão cisalhante no elemento i → X((4*i)-1); componente de tensão vertical no elemento i → X((4*i)-2); e a componente de tensão horizontal no elemento i → X((4*i)-3).

A variável matemática imediatamente posterior às variáveis associadas às componentes de tensão representa o fator de proporcionalidade λ (ver seção 2.2.3),, no caso X5. O Quadro 3 apresenta o modelo de PNL para análise axissimétrica.

Quadro 3 - Modelo de PNL gerado pelo ANALIM

No modelo de PNL do Quadro 3, a linha 1 representa a condição de escoamento, expressa por três inequações, imposta às componentes de tensão do elemento e as linhas 2-6 representam as equações de equilíbrio para o elemento.

MAX =X5; !SUBJECT TO;

!restricoes de fluxo da rocha intacta; ! 1);

0.5*(X1+X2)*(1-1.00)+(((0.5*(X1-X2))^2+(X3)^2)^0.5)*(1+1.00)-(1.00)*2.00 < 0.00; 0.5*(X1+X2+(((X1-X2))^2+4*(X3)^2)^0.5)-X4*1.00-(1.00)*2.00< 0.00;

X4-(0.5*(X1+X2)-(((0.5*(X1-X2))^2+(X3)^2)^0.5))*1.00-(1.00)*2.00< 0.00; ! restricoes de equilibrio;

! 2);

+25.13200*X1 +16.75467*X3 -25.13200*X4 = .000000; ! 3);

-25.13200*X1 +33.50933*X3 -25.13200*X4 = .000000; ! 4);

-16.75467*X2 +25.13200*X3 -16.75467*X5 = .000000; ! 5);

-25.13200*X1 -33.50933*X3 -25.13200*X4 = .000000; ! 6);

-33.50933*X2 -25.13200*X3 -33.50933*X5 = .000000; @FREE(X1);

33

3.4.2 - Arquivos de saída gerados pelo LINDO e LINGO

A partir dos arquivos gerados pelo ANALIM, mostrados no item anterior, são executados os programas de solução de problemas de programação matemática.

Para problemas de PL gera-se em arquivo, de extensão .prn, os valores das variáveis para a condição de ótimo, via software LINDO.

Para problemas de PNL, as saídas são exibidas no monitor de vídeo do computador podendo ser armazenadas em arquivos textos. Para o exemplo em estudo, são apresentadas, a seguir, as saídas geradas pelo LINGO para o caso de deformação plana, Quadro 4, e axissimétrico, Quadro 5.

Quadro 4 – Resultado apresentado pelo LINGO para análise de deformação plana

Local optimal solution found at step: 4 Objective value: 2.000000

Variable Value Reduced Cost X4 2.000000 0.0000000 X1 0.0000000 0.0000000 X2 -2.000000 0.0000000 X3 0.0000000 0.0000000

34

Quadro 5 - Resultado apresentado pelo LINGO para análise axissimétrica

_{Local optimal solution found at step: 4}

Objective value: 2.000000

Variable Value Reduced Cost X5 2.000000 0.0000000 X1 0.0000000 0.0000000 X2 -2.000000 0.0000000 X3 0.0000000 0.0000000 X4 0.0000000 0.0000000

CAPÍTULO 4

PROBLEMAS ESTUDADOS

4.1 - INTRODUÇÃO

Neste capítulo são estudados alguns problemas comuns encontrados em geotecnia para validação das formulações apresentadas anteriormente. São analisados problemas de deformação plana e axissimétricos.

Em todos os exemplos os materiais são modelados como materiais rígido-plásticos perfeitos, adotando-se o critério de escoamento de Mohr-Coulomb.

Para problemas de deformação plana, são feitas comparações entre os resultados das técnicas de PNL e PL. A linearização do critério de escoamento é feita pela aproximação da superfície de escoamento por uma superfície piramidal de 24 lados (NH=24).

Os resultados numéricos obtidos para problemas de deformação plana e axissimétricos são comparados com soluções teóricas ou numéricas encontradas na literatura.

4.2 - FUNDAÇÕES SUPERFICIAL E EMBUTIDA

Neste item são estudados exemplos de fundações superficial e embutida, em condições de deformação plana e condições axissimétricas. Estes problemas foram estudados por Terzaghi (1943), através do método de equilíbrio limite, e Chen (1975), através do método da análise limite, entre outros.

Para uma fundação corrida, a capacidade de carga pode ser calculada pela fórmula geral de Terzaghi (1943):

q c

u BN DN

2 1 cN

36

em que qu é a carga de colapso ou capacidade de carga; c é a coesão do solo; γ é o peso

específico do solo; D é o embutimento da fundação (para fundação superficial D = 0); B é a largura da sapata e Nc, Nγ e Nq são os fatores de capacidade de carga de Terzaghi,

função apenas do ângulo de atrito do solo (ϕ).

Para o caso em que γ = 0 e fundação superficial, a relação (4.1) pode ser posta sob a formaq_u ====cN_c.

Aplicando-se então uma carga de referência unitária (q0 = 1), tem-se que:

qu = λq0, em que λ é o fator de colapso.

Para uma fundação circular superficial ou embutida, a capacidade de carga pode ser calculada pela fórmula geral de Terzaghi (1943), descrita na equação (4.1), corrigida pelos fatores de forma para sapata circular, conforme equação abaixo:

q q c

c

u BN s DN

2 1 s cN s

q ==== ++++ _γγ _γ ++++ γ

em que sc, sγ e sq são fatores de forma de Terzaghi para sapata circular e valem,

respectivamente, 1.3, 0.6 e 1.0.

4.2.1 - Fundação superficial

A Figura 4.1 apresenta o esquema do problema da determinação da capacidade de carga e a malha utilizada, levando em consideração a simetria do problema, para o caso de uma fundação superficial de largura B, apoiada em solo homogêneo. Esta malha é utilizada tanto para o caso de deformação plana quanto para o caso axissimétrico.

(4.2)

B/2

b) Malha de elementos finitos a) Esquema da Fundação

corrida finitos B

λq0

37

4.2.1. a) Fundação Corrida

Este exemplo trata da determinação da capacidade de carga de uma fundação superficial corrida de largura B sobre uma camada de solo homogêneo, sendo que o problema de programação matemática resultante da formulação proposta pode ser tratado como um problema de PL ou problema de PNL. A Figura 4.1 mostra o esquema do problema e a malha utilizada.

As propriedades do solo são as seguintes: c = 1, ϕ variável e γ variável.

A Tabela 4.1 apresenta valores para a capacidade de carga obtidos, em função de ϕ e solo sem peso (γ = 0), pela técnica linear (PL), pela técnica não-linear (PNL) e os valores de Terzaghi (1943) e os obtidos via análise limite por Chen (1975).

Tabela 4.1 – Capacidade de carga de uma fundação corrida superficial para γγγγ = 0

φ (°) PL PNL Terzaghi

(1943) (1975) Chen

0 5,23 5,22 5,14 5,14

10 8,57 8,53 8,35 8,35

20 15,40 15,26 14,84 14,8

30 31,18 30,89 30,14 30,1

A Tabela 4.2 apresenta os valores obtidos pelas técnicas de PL e PNL e pelas teorias de Terzaghi (1943) e Chen (1975) para o caso de solo com γ = 1.

Tabela 4.2 – Capacidade de carga de uma fundação corrida superficial para γγγγ = 1

φ (°) PL PNL Terzaghi (1943)

Chen (1975)

0 5,24 5,22 5,14 5,14

10 9,63 9,55 9,55 9,05

20 19,93 19,72 19,84 18,1

30 44,86 44,33 49,84 44,3

38

Os valores obtidos pelas técnicas PL, PNL e por Terzaghi (1943) e Chen (1975) são bastante concordantes, indicando a eficácia das técnicas para o caso de uma fundação corrida.

4.2.1. b) Fundação circular

O problema anterior, Figura 4.1, quando analisado na condição axissimétrica, trata de uma fundação superficial circular de diâmetro B sobre uma camada de solo homogêneo, e a malha deste exemplo, Figura 4.1b, pode ser utilizada para modelagem do problema.

As propriedades do solo são as seguintes: c = 1, ϕ variável e γ variável.

A Tabela 4.3 e a Tabela 4.4 apresentam valores da capacidade de carga obtidos em função de ϕ, para solo sem peso (γ = 0) e para o caso de γ = 1, respectivamente. São apresentados também os valores de Terzaghi (1943), equação (4.2), e os valores apresentados por Chen (1975).

Tabela 4.3 – Capacidade de carga de uma fundação circular superficial para γγγγ = 0

φ (°) PNL Terzaghi

(1943) (1975) Chen

0 6,47 6,68 5,69

10 11,91 10,86 9,98

20 24,87 19,29 20,1

30 52,76 39,18 49,3

Tabela 4.4 – Capacidade de carga de uma fundação circular superficial para γγγγ = 1

φ (°) PNL Terzaghi (1943)

Chen (1975)

0 6,41 6,68 5,69

10 13,03 11,56 10,4

20 27,72 22,29 22,4

30 61,64 51,00 60,6

39

Ainda destas tabelas pode-se observar, para ângulos de atrito mais elevados, uma boa concordância entre os valores obtidos por PNL e os apresentados por Chen.

4.2.2 - Fundação embutida

O problema da determinação da capacidade de carga é estudado neste item para o caso de uma fundação embutida num solo homogêneo, tanto para uma fundação corrida de largura B (condição de deformação plana) e como para uma fundação circular de diâmetro B (condição axissimétrica).

Este problema é analisado utilizando-se a malha da Figura 4.2, sendo empregadas as seguintes propriedades do solo: c = 1 e ϕ variável; γ variável.

Figura 4.2 – Capacidade carga de uma fundação embutida

b) Malha de elementos finitos B

D

B/2

D

a) Esquema da fundação embutida finitos