Clique aqui para acessar o arquivo da 1a., 2a. e 3a. Partes das Notas para o Acompanhamento das Aulas

(1)

Notas para o acompanhamento da

1a., 2a. e 3a. partes

das aulas de

C´

alculo Diferencial e Integral 3

Estat´ıstica

(2)

(3)

Sum´

ario

1 Fun¸cões Reais de Várias Variáveis Reais 5

1.1 Uma Rápida Apresenta¸cão dos Diversos Tipos de Fun¸cões. . . 5

1.2 Fun¸cões Reais de Várias Variáveis Reais: dom´ınio, contra-dom´ınio, imagem e gráfico . . . 7

1.3 Uma Brev´ıssima Revisão das Equa¸cões Reduzidas das principais Superf´ıcies Quádricas . . . 9

1.4 Curvas de Contorno, Curvas de N´ıvel e Superf´ıcies de N´ıvel . . . 12

Se¸c˜ao de Exerc´ıcios Propostos: Fun¸c˜oes f:X⊂Rm →R _{. . . .} ₁₇

2 Limites e Continuidade de Fun¸cões Reais de Várias Variáveis Reais 19 2.1 Limites de Fun¸cões Reais de Várias Variáveis Reais . . . 19

2.2 Continuidade em Fun¸cões Reais de Várias Variáveis Reais . . . 22

Se¸c˜ao de Exerc´ıcios Propostos: Limites de Fun¸c˜oes f:X_⊂Rm →R _{. . . .} ₂₄

3 Deriva¸cão de Fun¸cões Reais de Várias Variáveis Reais 25 3.1 Derivadas Parciais . . . 25

3.2 Plano Tangente a Gráfico de Fun¸cões de Duas Variáveis . . . 27

3.3 Derivadas Parciais de Ordem Superior . . . 29

3.4 Regra da Cadeia . . . 30

3.5 Deriva¸c˜ao Parcial Impl´ıcita . . . 32

3.6 Incrementos e Diferenciais . . . 33

Se¸cão de Exerc´ıcios Propostos: Deriva¸cão de Fun¸cões f:X⊂Rm →R _{. . . .} ₃₇

4 Aplica¸cões de Derivadas de Fun¸cões Reais de Várias Variáveis Reais 39 4.1 Derivada Direcional e Vetor Gradiente . . . 39

4.2 Interpreta¸c˜ao Geom´etrica do Vetor Gradiente . . . 42

4.3 O Vetor Gradiente como Vetor Normal a Curva ou Superf´ıcie . . . 43

4.4 Máximos e M´ınimos de Fun¸cões de Duas Variáveis . . . 45

4.5 O Teste da Derivada Segunda para Fun¸c˜oes de Duas Vari´aveis . . . 48

4.6 Problemas de Otimiza¸c˜ao . . . 49

4.7 Multiplicadores de Lagrange . . . 54

Se¸cão de Exerc´ıcios Propostos: Aplica¸cões de Derivadas de Fun¸cões f:X⊂Rm_→R _{. . . .} ₅₇

5 Integrais M´ultiplas 59 5.1 Integrais Duplas . . . 59

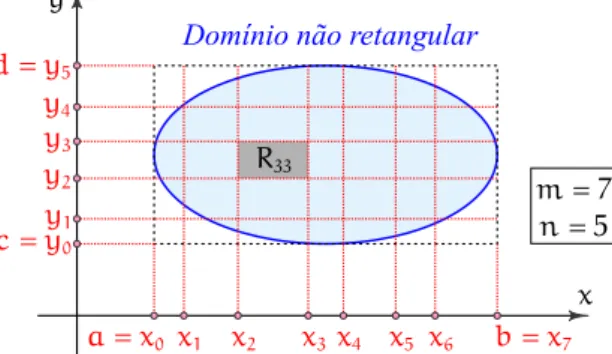
5.2 Integrais Duplas Sobre Regi˜oes mais Gerais . . . 61

5.3 Area por Integra¸c˜´ ao Dupla . . . 64

5.4 Integrais Duplas em Coordenadas Polares . . . 65

5.5 Integrais Triplas . . . 70

5.6 Integrais Triplas em Coordenadas Cil´ındricas . . . 71

5.7 Integrais Triplas em Coordenadas Esf´ericas . . . 74

Se¸c˜ao de Exerc´ıcios Propostos: Integrais M´ultiplas . . . 79

6 Fun¸cões f :X_⊂R_→Rn _comn_≥2: Fun¸cões Vetoriais ou Caminhos no Rn ₈₃ 6.1 Definindo Fun¸cões Vetoriais . . . 83

6.2 Limites e Continuidade de Fun¸c˜oes Vetoriais . . . 85

6.3 Derivadas de Fun¸c˜oes Vetoriais . . . 88

6.4 Integrais de Fun¸c˜oes Vetoriais . . . 91

7 Equa¸cões Diferenciais Ordinárias (EDO’s) de 1a . Ordem 93 7.1 Nomenclatura Relativa às Equa¸cões Diferenciais . . . 93

(4)

7.3 Técnica da “Separa¸cão de Variáveis” para Resolu¸cão de EDO’s de 1a_{. Ordem . . . .} ₉₇

7.4 Uma Palavra e Dois Significados: EDO’s de 1a_{. Ordem Homogˆeneas . . . .} ₉₉

7.5 Transformando EDO’s de 1a_{. Ordem em EDO’s de Vari´}_{aveis Separ´}_{aveis por meio de Mudan¸ca de Vari´}_aveis102 7.6 T´ecnica do “Fator Integrante” para Resolu¸c˜ao de EDO’s de 1a_{. Ordem Lineares} _{. . . 103}

7.7 Problemas Envolvendo a “Lei de Varia¸c˜ao Exponencial” . . . 106

7.8 Problemas Envolvendo a “Lei de Decaimento Radioativo” . . . 107

7.8.1 Curiosidade Histórica: Um Modelo Matemático para Detectar Falsifica¸cões em Obras de Arte de Van Meegeren . . . 108

7.9 Problemas Envolvendo a “Lei de Resfriamento de Newton” . . . 115

7.10 EDO’s de 1a. Ordem Exatas . . . 115

7.11 Extens˜ao da T´ecnica do “Fator Integrante”: transformando EDO de 1a_{. Ordem n˜}_{ao exata em EDO exata117} 7.12 EDO’s de 1a_{. Ordem de Bernoulli} _{. . . 125}

Se¸c˜ao de Exerc´ıcios Propostos: EDO de 1a_{. Ordem} _{. . . 126}

8 Equa¸c˜oes Diferenciais Ordin´arias (EDO’s) de 2a . Ordem 135 8.1 EDO’s de 2a_{. Ordem: defini¸c˜}_{ao e preliminares . . . 135}

8.2 Alguns Problemas Pr´aticos envolvendo EDO’s de 2a_{. Ordem . . . 136}

8.3 EDO’s de 2a_{. Ordem Lineares: preliminares . . . 137}

8.4 EDO’s de 2a_{. Ordem Lineares Homogˆeneas com Coeficientes Constantes . . . 138}

Se¸c˜ao de Exerc´ıcios Propostos: EDO de 2a_{. Ordem} _{. . . 143}

(5)

Cap´ıtulo 1

Fun¸c˜

oes Reais de V´

arias Vari´

aveis Reais

Neste cap´ıtulo apresentamos as chamadas fun¸cões reais de várias variáveis reais, que são fun¸cões cujo dom´ınio está em Rm_{, com} m_≥ 2, e o contradom´ınio é R_{. Tais fun¸c˜}_{oes são, costumeiramente, indicadas por} f : X_⊂Rm _→ R_e

ditas, de forma simplificada,fun¸cões de várias variáveis.

Embora a teoria envolvendo tais fun¸c˜oes possa ser feita sempre comm∈N_, _m_≥₂_{, vamos trabalhar}

predominante-mente com m=2 e, em algumas situa¸cões, comm=3. Essas restri¸cões se devem ao grande número de aplica¸cões práticas que esses casos apresentam. Entretanto, o leitor não terá dificuldade alguma para generalizar os diversos conceitos que serão estudados para uma dimensãommaior.

Além da apresenta¸cão das fun¸cões de várias variáveis, vamos introduzir neste cap´ıtulo oslimitesde tais fun¸cões, que é o conceito essencial para a introdu¸cão dasderivadas parciais e dasderivadas direcionais (veremos isso no Cap´ıtulo 3). Além disso, associado ao conceito de limite de fun¸cões de várias variáveis temos, também, o importante conceito de continuidade de tais fun¸cões. Diversos resultados matemáticos envolvendo otimiza¸cão estão associados à continuidade, da´ı a importância prática de tal conceito.

Antes de apresentarmos a defini¸c˜ao formal de fun¸c˜aof:X⊂Rm _→R_{, vejamos na se¸c˜}_{ao abaixo, sem muito}

compro-misso com o rigor matemático, os diversos tipos de fun¸cões que costumam surgir nos textos deCálculo Diferencial e Integral.

1.1 Uma R´

apida Apresenta¸c˜

ao dos Diversos Tipos de Fun¸c˜

oes.

(1)NoC´alculo Diferencial e Integral 1geralmente estudamos fun¸c˜oes do tipo

f:X_⊂R_→R_, _y₌_f₍_x₎_,

que são fun¸cões reais de uma variável real. Geralmente, os gr´aficos de fun¸cões dessa natureza são curvas no plano cartesiano. Por exemplo,f(x) =x2comx∈R_{, cujo gr´}_{afico é uma par´}_abola.

R

x

R

y= ( )f x f

X

x y

gráfico def x( ) =x2

(2)Fun¸c˜oes do tipo

f :X_⊂R_→R2_,_f₍_t_{) = (}_x₍_t₎_{, y}₍_t₎₎_,

(6)

R

t

R2

f t( ) = ( ( ), ( ))x t y t f

X

x y

imagem de

f t( ) = (cos t sen t( ), ( )) x

y

1

x t( )

y t( )

f :X⊂R_→R3_,_f(t) = (x(t), y(t), z(t)),

são fun¸cões vetoriais reais no espa¸co, de uma variável real. Também não é costume analisar os gráficos de fun¸cões desse tipo, mas sim, seus conjuntos imagens, que geralmente são curvas no espa¸co cartesiano. Por exemplo, f(t) = (cos(t),sen(t), t)comt∈R_{, cuja imagem é uma hélice circular de raio}₁_{com eixo no eixo cartesiano}_z_.

R

t

R3

f t( ) = ( ( ), ( ), ( ))x t y t z t f

X

x t( )

y t( )

y z

x

z t( )

y z

x

imagem de f t( ) = (cos t sen t t( ), ( ), )

(4)Fun¸cões vetoriais reais de uma variável podem ser generalizadas para espa¸cos de dimensões arbitrárias, ou seja, f :X_⊂R_→Rn_,_f₍_t_{) = (}_x

1(t), . . . , xn(t)).

Essas fun¸cões são chamadas de fun¸cões vetoriais reais no espa¸co cartesiano Rn_{, de uma vari´}_{avel real}_.

Frequentemente, tais fun¸cões são também chamadas decaminhos (ou curvas) no espa¸co Rn_.

f:X_⊂R2_→R_,z=f(x, y),

são fun¸cões reais de duas variáveis reais. Geralmente, os gráficos de tais fun¸cões são superf´ıcies no espa¸co cartesiano. Por exemplo, f(x, y) =p25−x2₋_y2_{, com} ₍_{x, y}₎_{em um disco com centro na origem e raio} ₅ _{no plano}

cartesiano, possui por gr´afico uma semiesfera de raio5 e centro na origem do espa¸co cartesiano.

R

f

gráfico de

f x y( , ) = 25 -x2-y2 x

y

R2

X

( , )x y

z= ( , )f x y y

z

x R3

5

(7)

f:X⊂R3_→R_,_w=f(x, y, z),

são fun¸cões reais de três variáveis reais. N˜ao é costume analisar os gráficos de fun¸cões desse tipo, mas sim, determinados subconjuntos de seu dom´ınio, chamados de pré-imagem ouimagem inversa. Por exemplo,f(x, y, z) =

x2₊_y2₊_z2_com₍_{x, y, z}₎_∈_R3_{, possui como pr´e-imagem de}₂₅_{uma esfera de raio} ₅_{com centro na origem do espa¸co}

cartesiano. Essa an´alise ´e feita considerando os pontos(x, y, z)_∈R3_{tais que}f(x, y, z) =25.

R

f

pré-imagem de pela função

dada por

25

f x y( , ,z)= x2+y2+z2

X

w= ( , , )f x y z y

z

x

R3

5

5 5

y z

x

R3

( , , )x y z

(7)Fun¸cões reais de duas ou três variáveis reais podem ser generalizadas para espa¸cos de dimensões arbitrárias, ou seja,

f:X_⊂Rm_→R_,y=f(x1, . . . , xm).

São asfun¸cões reais de várias variáveis reais, ditas, de forma simplificada,fun¸cões de várias variáveis.

(8)Por fim, podemos considerar asfun¸cões vetoriais reais de várias variáveis reais, ou seja, fun¸cões

f:X_⊂Rm

→Rn_,_f₍_t

1, . . . , tm) = (x1(t1, . . . , tm), . . . , xn(t1, . . . , tm)).

O caso mais comum de fun¸c˜oes dessa natureza ocorre quando m = 2 e n = 3. Neste caso, ´e comum escrevemos

f(u, v) = (x(u, v), y(u, v), z(u, v)) e o conjunto imagem de tais fun¸c˜oes ´e geralmente uma superf´ıcie, chamada de superf´ıcie parametrizada.

Como já dito, nosso objetivo é estudarmos as fun¸cões do Item(7). Notadamente nos casos particulares dos Itens(5)

e(6).

1.2 Fun¸c˜

oes Reais de V´

arias Vari´

aveis Reais: dom´ınio, contra-dom´ınio,

imagem e gr´

afico

Abaixo seja a defini¸cão formal de fun¸cões de várias variáveis.

Uma fun¸cão real f de várias variáveis reais é uma regra, geralmente dada por uma expressão anal´ıtica, que associa cada elemento de um conjunto não vazioX_⊂Rm_,m_∈N_,m_≥2, a um único número real. O conjuntoX é chamado de dom´ıniodef, enquanto que R_é_{contradom´ınio}_def.

Indicamos a fun¸c˜aof porf:X⊂Rm_→R_{ou , de forma mais rigorosa:}

f: X_⊂Rm ₋_→ R

(x1, . . . , xm) 7−→ f(x1, . . . , xm)

O número real z= f(x1, . . . , xm)é chamado de imagem do elemento (x1, . . . , xm) ∈X pela fun¸cão f. Todos os

números reais que são imagens de algum elemento do dom´ınio def formam o chamadoconjunto imagem def. O conjuntoG(f) =(x1, . . . , xm, z)∈Rm+1: (x1, . . . , xm)∈Xe z=f(x1, . . . , xm) é chamado degráficodef.

R

f

gráfico de

superfície em

f z f x y

:

= ( , ) R3 x

y

R2

X

( , )x y z= ( , )f x y

y z

x

R3

XÌR2:domínio def m=2

z

x y f

Î

: ( , )

imagem

de por

R R:contradomínio def

x y

z

(8)

Observa¸c˜oes.

(1)O casom=2 é de especial interesse, pois o gráfico G(f) =(x, y, z)_∈R3: (x, y)_∈Xez=f(x, y) de fé uma superf´ıcie no espa¸co cartesiano (veremos vários exemplos adiante). Tal superf´ıcie é obtida da equa¸cão cartesiana nas variáveisx,yez dada porz=f(x, y). Além disso, no espa¸co cartesiano onde representamos o gráfico de ftambém representamos o seu dom´ınio X, no planoxy, e o seu contradom´ınio R_{, como sendo o eixo} z.

y z

x

G f( ) ( , , ( , ))x y f x y

( , )x y X

z= ( , )f x y

domínio

contradomínio

gráfico

(2) Quando m = 3 temos G(f) = (x, y, z, w)∈R4_{: (}_{x, y, z}₎_∈_X_e_w₌_f₍_{x, y, z}₎ _{como subconjunto de} _R4 _{e n˜}_ao

temos como visualiz´a-lo no espa¸co tridimensional.

(3)Quando o dom´ınio a ser considerado para uma fun¸cãoffor o maior poss´ıvel, indicamos a fun¸cão apenas pela sua expressão anal´ıtica. Por exemplo, f(x, y) = x2₊_y2 _{significa que o dom´ınio de} _f _{é todo o} _R2_{. Tais dom´ınios são}

chamados dedom´ınios máximos oudom´ınios maximais def. Geralmente, quando nada é dito a respeito do dom´ınio de uma fun¸cão, consideramos como sendo máximo.

Exemplo 1.1 Qual ´e o maior dom´ınio poss´ıvel para f:X⊂R2_→R_{, dada por} _f(x, y) =p

25−x2₋_y2_?

Para que z= f(x, y) seja um n´umero real devemos ter 25−x2₋_y2_≥₀_{, ou seja,} _x2₊_y2_≤₅2 _{que representa um}

disco de raio 5 com centro na origem do plano cartesiano.

x

domínio ( , )x y y

x y

5 5

-5

Logo, o maior dom´ınio X_⊂R2_{poss´ıvel para} _f_{´e um disco de raio} ₅ _{com centro na origem do plano cartesiano.}

Exemplo 1.2 Encontremos o maior dom´ınio poss´ıvel da fun¸c˜ao f:X_⊂R3

→R_{, dada por} _f₍_{x, y, z}_{) =} _√x+y+z x2₊_y2₊_z2.

Devemos ter x2₊_y2₊_z2_{> 0}_{para que} _f₍_{x, y, z}₎_{seja n´}_{umero real. Logo, devemos excluir de} _X_⊂_R3 _pontos ₍_{x, y, z}₎

tais que x2₊_y2₊_z2_≤₀_{. Mas o ´}_{unico ponto de} _R3 _{que satisfaz} _x2₊_y2₊_z2_≤₀ _´e₍_{x, y, z}_{) = (}_{0, 0, 0}₎_{. Logo,} X=(x, y, z)_∈R3_{: (}_{x, , y, z}₎₆_{= (}_{0, 0, 0}₎ ₌R3₋_{₍_{0, 0, 0}₎_}

´e constitu´ıdo pelo espa¸co cartesiano menos a origem.

Exemplo 1.3 Encontremos o maior dom´ınio poss´ıvel da fun¸c˜ao f:X_⊂R2

→R_{, dada por} _f₍_{x, y}_{) =} _√ y y−x2.

Devemos ter y−x2_{> 0}_{, ou seja,}_{y > x}2_{. Logo,}

X=(x, y)_∈R2_:_{y > x}2

é constitu´ıdo pelos pontos “interiores” à parábola de equa¸cão y=x2 _{no plano cartesiano.}

x ( , )x y y

(9)

Exemplo 1.4 Esbocemos o gr´afico de f:X⊂R2_→R_{, dada por} _f(x, y) =p

25−x2₋_y2_.

Vimos, no Exemplo 1.1 acima, que o maior dom´ınio poss´ıvel para f´e o disco de raio 5com centro na origem do plano cartesiano.

De z=f(x, y) =p25−x2₋_y2 _temos _z2₌₂₅₋_x2₋_y2_{, ou seja,}_x2₊_y2₊_z2₌₅2_{, que ´e a equa¸c˜}_{ao cartesiana de}

uma esfera com centro na origem e raio 5.

Mas z=f(x, y)_≥0. Logo, o gr´afico de f´e uma semiesfera de raio 5com centro na origem localizada acima do plano

xy no espa¸co cartesiano.

gráfico (semiesfera)

y z

x R3

5

5 5

domínio (disco)

Outra observa¸cão importante: Nem sempre utilizamos as tradicionais letrasf, xeypara representar uma fun¸cão de duas variáveis. Por exemplo, o volume de um cone pode ser expresso em fun¸cão de sua altura e do raio de sua base, ou seja, V= 1

3πr

2_h _{pode ser escrito como fun¸c˜}_ao: _V₍_{r, h}_{) =} 1 3πr

2_h_{no lugar de}_f₍_{x, y}_{) =} 1 3πx

2_y_.

h

r

1.3 Uma Brev´ıssima Revis˜

ao das Equa¸c˜

oes Reduzidas das principais

Superf´ıcies Qu´

adricas

Para trabalharmos mais facilmente com alguns exemplos de gráficos de fun¸cões de duas variáveis, fa¸camos uma pequena revisão das principais equa¸cões reduzidas das superf´ıcies quádricas vistas na disciplinaGeometria Analitica.

(1)Elips´oidecom centro na origem e eixos paralelos aos eixos coordenados. Equa¸c˜ao reduzida:

x2

a2 +

y2

b2 +z 2

c2 =1 , sendoa,b, ecconstantes positivas.

Observa¸c˜oes:

(i)quandoa=b,a=coub=c o elipsóide é circular, ou seja, uma superf´ıcie de rota¸cão.

(10)

(2)Hiperbol´oide de uma folhacom eixoze centro na origem. Equa¸c˜ao reduzida:

x2

a2 +

y2

b2 −z 2

Observa¸c˜oes:

(i)quandoa=bo hiperbolóide de uma folha é circular, ou seja, uma superf´ıcie de rota¸cão.

(ii)o hiperbol´oide de uma folha com eixoye centro na origem possui equa¸c˜ao x_a22 −

y2 b2 +

z2

c2 =1, enquanto que o de eixo xpossui equa¸c˜ao−x2

a2+

y2

b2 + z 2

c2 =1.

(3)Hiperbol´oide de duas folhascom eixoze centro na origem. Equa¸c˜ao reduzida:

−x2

a2−

y2

b2 +

z2

Observa¸c˜oes:

(i)quandoa=bo hiperbolóide de duas folhas é circular, ou seja, uma superf´ıcie de rota¸cão.

(ii)o hiperbol´oide de duas folhas com eixo ye centro na origem possui equa¸c˜ao−_ax22 +

y2 b2 −

z2

c2 =1, enquanto que o de eixo xpossui equa¸c˜ao _ax22 −

y2 b2 −

z2

c2 =1.

(4)Parabolóide el´ıpticocom eixoze vértice na origem. Equa¸cão reduzida:

z c =

x2

a2+

y2

(11)

Observa¸c˜oes:

(i)quandoc > 0temos a convavidade do parabol´oide el´ıptico para cima e, quandoc < 0, para baixo.

(ii)quandoa=bo parabolóide el´ıptico é circular, ou seja, uma superf´ıcie de rota¸cão.

(iii) o parabol´oide el´ıptico com eixoy e centro na origem possui equa¸c˜ao y_b = x2 a2 + z

2

c2, enquanto que o de eixo x possui equa¸c˜ao x

a= y2

b2 + z 2

c2.

(5)Parabolóide hiperbólico com eixoze centro na origem. Equa¸cão reduzida:

z c =

x2

a2 −

y2

b2 ou z_c = −x 2

a2 +

y2

b2 , sendoaebconstantes positivas ec₆=0.

Observa¸cão: o parabolóide hiperbólico com eixoye centro na origem possui equa¸cão y_b= x_a22 −

z2

c2 ou

y b= −

x2

a2+

z2

c2, enquanto que o de eixo xpossui equa¸c˜ao x

a = y2

b2 −z 2

c2 ou x_a = −

y2

b2 +z 2

c2.

(6)Cone el´ıpticode eixo ze v´ertice na origem. Equa¸c˜ao reduzida:

z2₌ x2

a2+

y2

(12)

Observa¸c˜oes:

(i)quandoa=bo cone el´ıptico ´e circular, ou seja, uma superf´ıcie de rota¸c˜ao.

(ii) o cone el´ıptico com eixo y e v´ertice na origem possui equa¸c˜ao y2 ₌ x2 a2 + z

2

c2, enquanto que o de eixo xpossui equa¸c˜aox2= y_b22+ z

2

c2.

(7)Cilindro el´ıpticode eixoz. Equa¸c˜ao reduzida:

x2

a2 +

y2

b2 =1 , sendoaebconstantes positivas.

Observa¸c˜oes:

(i)quandoa=bo cilindro el´ıptico ´e circular, ou seja, uma superf´ıcie de rota¸c˜ao.

(ii)o cilindro el´ıptico com eixoypossui equa¸c˜ao x2

a2 +

z2

c2 =1, enquanto que o de eixoxpossui equa¸c˜ao

y2

b2 +

z2

c2 =1.

1.4 Curvas de Contorno, Curvas de N´ıvel e Superf´ıcies de N´ıvel

Nesta seçcão trabalhamos exclusivamente com fun¸cões de duas e de três variáveis.

As curvas de contorno do gráfico de uma fun¸cão de duas variáveis são ferramentas muito importantes para descrevermos o gráfico de uma tal fun¸cão. Essas curvas podem ser vistas, grosso modo, como resultado de “fatiamentos” que fazemos no gráfico da fun¸cão. É como se estivéssemos submetendo o gráfico a uma “tomografia”. Abaixo seguem as defini¸cões formais.

Seja f:X⊂R2_→R_fun¸c˜_{ao de duas vari´}_aveis.

Chamamos a interseçcão do plano z= k, k ∈ R_{, com o gr´}_{afico da fun¸c˜}_ao _f _de _{curva de contorno} _{de altura} _(ou cota)k do gráfico defrelativa ao eixoz.

A proje¸cão ortogonal da curva de contorno de altura k no plano xy (plano z = 0) é chamada de curva de n´ıvel f(x, y) =kda fun¸cão frelativa ao eixo z.

y z

x

G f( )

X

plano z=k k

curva de contorno de alturak

curva de nívelf x y k xy ( , ) = (projeção no plano )

Observa¸c˜oes.

(1)A equa¸cão cartesiana de uma curva de n´ıvel de uma fun¸cãof relativa ao eixozé dada porf(x, y) =k.

(13)

Exemplo 1.5 Consideremos a fun¸c˜ao f:R2_→R_{dada por} _f(x, y) =x2+y2. Esbocemos algumas curvas de contorno no espa¸co cartesiano e algumas curvas de n´ıvel no plano cartesiano da fun¸c˜ao f.

Curvas de n´ıvel:

• (i)Fa¸camos z=k,k constante, para encontrarmos as curvas de n´ıvel f(x, y) =k de frelativas ao eixo z. Temos x2₊_y2₌_k _{como equa¸c˜}_{ao de curvas de n´ıvel.}

Para k < 0 não há solu¸cão para a equa¸cão acima.

Para k =0 temos apenas o ponto O= (0, 0)como solu¸cão da equa¸cão acima, que é uma curva de n´ıvel degenerada (em um ponto).

Para k > 0 temos x2+y2=Ä√kä2 que é equa¸cão de um c´ırculo de centro na origem e raio √k no planoxy. Na figura abaixo à esquerda temos o mapa das curvas de n´ıvel f(x, y) =kde f, no plano xy, relativas ao eixo z.

x

x y

y

z z

• (ii) Fa¸camos y=k,k constante, para encontrarmos as curvas de n´ıvel f(x, k) =z de frelativas ao eixo y. Temos x2₊_k2₌_z_{como equa¸c˜}_{ao de curvas de n´ıvel, ou seja,}_z₌_x2₊_k2 _s˜_{ao par´}_{abolas com concavidades para cima}

no plano xz.

Na figura acima ao centro temos o mapa das curvas de n´ıvel f(x, k) =zde f, no plano xz, relativas ao eixo y. • (iii) Fa¸camos x=k,kconstante, para encontrarmos as curvas de n´ıvel f(k, y) =zde f relativas ao eixo x. Temos k2₊_y2₌_z _{como equa¸c˜}_{ao de curvas de n´ıvel, ou seja,} _z₌_y2₊_k2_s˜_{ao par´}_{abolas com concavidades para cima}

no plano yz.

Na figura acima `a direita temos o mapa das curvas de n´ıvel f(k, y) =zde f, no plano yz, relativas ao eixo x. Curvas de contorno:

• (i) A interseçcão do plano z = k com o gráfico de f é c´ırculo de raio √k, quando k > 0, e centro no ponto

(0, 0, k), contida no plano z=k. A figura abaixo `a esquerda ´e o esbo¸co de algumas dessas curvas de contorno.

x x x

y y

y z

z z

•(ii)A interseçcão do plano y=k com o gráfico de fé uma parábola com vértice em 0, k, k2

, concavidade para cima, contida no plano y=k. A figura acima ao centro ´e o esbo¸co de algumas dessas curvas de contorno.

• (iii) A interseçcão do plano x = k com o gráfico de f é uma parábola com vértice em k, 0, k2

(14)

z=f(x, y)é a equa¸cão z=x2+y2. Entretanto, o método de determina¸cão de curvas de n´ıvel ou curvas de contorno pode ser aplicado para qualquer fun¸cão.

Na figura abaixo à esquerda temos os três tipos de curvas de contorno de f esbo¸cadas em um mesmo sistema de coordenadas. No centro temos as curvas de contorno esbo¸cadas junto com o gráfico def e na direita apenas o gráfico de f.

Na figura abaixo à esquerda temos as curvas de contorno de frelativas ao eixo ze respectivas curvas de n´ıvel esbo¸cadas junto com o gráfico de f. Ao centro e à direita temos cada um dos outros dois tipos de curvas de contorno esbo¸cadas, separadamente, junto com o gráfico de f.

Na figura abaixo temos uma visão dos fatiamentos do gráfico de f por planos paralelos aos planos coordenados, cujas interseçcões dão origem às curvas de contorno.

Observa¸c˜oes.

(1)Conforme observado no exemplo acima, por meio das curvas de contorno ou das curvas de n´ıvel de uma fun¸c˜ao

f:X_⊂R2

→R_{´e poss´ıvel ter uma ideia do esbo¸co do gr´}_{afico da fun¸c˜}_ao.

(2)Quando f:X_⊂R3

→R_n˜_{ao temos como visualizar as “superf´ıcies de contorno” (que s˜ao as an´}_{alogas `}_{as curvas de}

contorno), entretanto, assuperf´ıcies de n´ıvel (que são as análogas às curvas de n´ıvel) relativas ao eixow(o eixow

é o quarto eixo do sistema de coordenadas cartesianas noR4_{) estão contidas no dom´ınio de}_f_{e são superf´ıcies dadas}

pelas equa¸cões cartesianas da formaf(x, y, z) =k. As superf´ıcies de n´ıvel também são chamadas de pré-imagens da fun¸cão de três variáveis. Assim, a superf´ıcie de n´ıvel de equa¸cão f(x, y, z) =k no dom´ınio de fé a pré-imagem de

(15)

Exemplo 1.6 Esbocemos o gr´afico de f:R2_→R_{dada por} _f(x, y) =y−x2. Curvas de n´ıvel:

• (i)Fa¸camos z=k,kconstante, para encontrarmos as curvas de n´ıvel f(x, y) =k de f relativas ao eixo z. Temos y−x2₌ _k _{como equa¸c˜}_{ao de curvas de n´ıvel, ou seja,} _y₌_x2₊_k _s˜_{ao par´}_{abolas com concavidades para cima}

no plano xy.

Na figura abaixo `a esquerda temos o mapa das curvas de n´ıvel f(x, y) =kde f, no plano xy, relativas ao eixo z.

x y

x

z z

y

• (ii)Fa¸camos y=k,k constante, para encontrarmos as curvas de n´ıvel f(x, k) =z de frelativas ao eixo y. Temos z=k−x2_{como equa¸c˜}_{ao de curvas de n´ıvel, ou seja,} _z_{= −}_x2₊_k _s˜_{ao par´}_{abolas com concavidades para baixo}

no plano xz.

Na figura acima ao centro temos o mapa das curvas de n´ıvel f(x, k) =zde f, no plano xz, relativas ao eixo y.

• (iii)Fa¸camos x=k,k constante, para encontrarmos as curvas de n´ıvel f(k, y) =z de frelativas ao eixo x. Temos z=y−k2 _{como equa¸c˜}_{ao de curvas de n´ıvel, ou seja,}_z₌_y₋_k2 _s˜_{ao retas no plano} _yz_.

Na figura acima `a direita temos o mapa das curvas de n´ıvel f(k, y) =zde f, no plano yz, relativas ao eixo x. Curvas de contorno:

•(i)A interseçcão do plano z=kcom o gráfico de fé uma parábola com vértice em(0, k, k), concavidade voltada para a parte positiva do eixo y, contida no plano z = k. A figura abaixo à esquerda é o esbo¸co de algumas dessas curvas de contorno.

y z

x y

z

x y

z

x

• (ii)A interseçcão do plano y=kcom o gráfico de fé uma parábola com vértice em (0, k, k), concavidade para baixo, contida no plano y=k. A figura acima ao centro é o esbo¸co de algumas dessas curvas de contorno.

• (iii) A interseçcão do plano x= k com o gráfico de f é uma reta, contida no plano x= k. A figura acima à direita é o esbo¸co de algumas dessas curvas de contorno.

Baseados nas curvas de n´ıvel, ou curvas de contorno, podemos esbo¸car o gráfico de f (que é uma quádrica de equa¸cão

z=y−x2_).

(16)

Na figura abaixo à esquerda temos as curvas de contorno de frelativas ao eixo ze respectivas curvas de n´ıvel esbo¸cadas junto com o gráfico de f. Ao centro e à direita temos cada um dos outros dois tipos de curvas de contorno esbo¸cadas, separadamente, junto com o gráfico de f.

Na figura abaixo temos uma visão dos fatiamentos do gráfico de f por planos paralelos aos eixos coordenados, cujas interseçcões dão origem às curvas de contorno.

O gráfico de fé uma quádrica cil´ındrica em “formato de párabola”.

Exemplo 1.7 Esbocemos algumas superf´ıcies de n´ıvel contidas no dom´ınio de f : R3

→ R_{,dada por} _f₍_{x, y, z}_{) =} x2₊_y2₊_z2_.

As superf´ıcies de n´ıvel s˜ao dadas pelas equa¸c˜oes f(x, y, z) =k, sendo k constante real. No nosso caso,

x2+y2+z2=k.

• Para k < 0não temos superf´ıcies de n´ıvel, pois a equa¸cão acima não possui solu¸cões.

• Para k=0 temos uma única solu¸cão: (x, y, z) = (0, 0, 0), ou seja, nesse caso, a superf´ıcie de n´ıvel f(x, y, z) =0 é degenerada e constitu´ıda de apenas um único ponto: a origem do sistema de coordenadas cartesianas no espa¸co. • Para k > 0 temos que a superf´ıcie de n´ıvel f(x, y, z) =k corresponde à esfera de raio r=√k e centro na origem, dada pela equa¸cão x2+y2+z2=Ä√kä2.

(17)

Se¸c˜

ao de Exerc´ıcios Propostos:

Fun¸

c˜

oes

f

:

X

_⊂

R

m

_→

R

Exerc´ıcio 1.1 Identifique e esboce o maior dom´ınio Xposs´ıvel da fun¸c˜ao:

(i)f:X⊂R2_→R_{dada por}_f(x, y) =ln x2−y2−1 .

(ii)f:X⊂R3

→R_{dada por}_f(x, y, z) = _√ 1 z−x2₋_y2. Respostas:

(i)Dom´ınio m´aximo: X=(x, y)_∈R2:x2₋_y2_{> 1} _{. Esboce o dom´ınio (delimitado por dois ramos de hip´erbole).}

(ii)Dom´ınio m´aximo: X=(x, y, z)_∈R3:z > x2₊_y2 _{. Esboce o dom´ınio (delimitado por um parabol´}_{oide circular).}

Exerc´ıcio 1.2 Esboce algumas curvas (ou superf´ıcies) de n´ıvel t´ıpicas contidas no dom´ınio da fun¸c˜ao:

(i)f:R2

→R_{, dada por}_f₍_{x, y}_{) =} 1 1+x2₊_y2.

(ii) f:R3

→R_{, dada por}_f₍_{x, y, z}_{) =}_z₊p_x2₊_y2_.

(iii)f:R3_→R_{, dada por}f(x, y, z) =x2₊_y2₋_z2_.

Respostas:

(i)(análise feita apenas para a variável z). Para z=k=1, a curva de contorno se reduz a um ponto: (0, 0, 1). Para z = k tal que 0 < k < 1, as curvas de contorno são circunferências (contidas nos planos z = k) de centros

(0, 0, k)e raios »1 k−1.

No plano xy, as curvas de n´ıvel são circunferências concêntricas com centro na origem sendo que, à medida que os raios das circunferências aumentam, os valores de zdiminuem tendendo a 0.

(ii)As superf´ıcies de n´ıvel w=f(x, y, z) =k formam o conjunto dos cones de revolu¸c˜ao com concavidade para baixo e v´ertice no eixo z.

(iii). Divida em 3 casos: f(x, y, z)> 0,f(x, y, z) =0 e f(x, y, z)< 0. Tratam-se de hiperbolóides de uma folha, um cone duplo e hiperbolóides de duas folhas, respectivamente, todos com eixo z, centros ou vértice na origem.

Exerc´ıcio 1.3 Esboce o gr´afico de:

(i)f:R2

→R_{dada por}_f₍_{x, y}_{) =}p_x2₊_y2_.

(ii)f:R2

→R_{dada por}_f₍_{x, y}_{) =}₁₀₋p_x2₊_y2_.

(iii)f:R2_→R_{dada por}_f(x, y) =y3−x2. Respostas:

(i)Trata-se de um cone com v´ertice na origem e concavidade para cima.

(ii)O gráfico de fé um cone de revolu¸cão com concavidade para baixo e vértice no ponto (0, 0, 10).

(iii)No plano yz(que ´e o plano x=0) considere a curva z=y3_{. Para cada ponto} _{P 0, k, k}3

dessa curva, no plano

y=k, considere a parábola z=k3−x2, com concavidade para baixo e vértice no ponto P. A reunião de todas essas parábolas formam o gráfico.

Exerc´ıcio 1.4 Associe gr´aficos e curvas de n´ıvel.

Obs.: este exerc´ıcio é apenas visual, ou seja, não é necessário encontrar equa¸cões de curvas de n´ıvel.

(i)

f(x, y) = ₁₊_x21₊_y2

(ii)

f(x, y) =

(x2_+y2_)cos2 Å

3arctg x y

2 ã

exp(x2_+y2₎

(1₎

(iii)

f(x, y) =cosÄp

x2₊_y2ä

1_{Esta superf´ıcie tamb´}_{em pode ser parametrizada como}_X_{(ρ, θ) =}_ρ_cos_(θ)_{, ρ}_sen_(θ)_,ρ2cos2(3θ2) eρ2

(18)

(iv)

f(x, y) = 3x2+9y2

ex2+y2

(v)

f(x, y) = x

ex2+y2

(vi)

f(x, y) = √ xy

ex2+y2

Curvas de n´ıvel:

(a) (b) (c)

(d) (e) (f)

(19)

Cap´ıtulo 2

Limites e Continuidade de Fun¸c˜

oes Reais

de V´

arias Vari´

aveis Reais

2.1 Limites de Fun¸c˜

oes Reais de V´

arias Vari´

aveis Reais

Podemos estender o conceito de limite estudado noCálculo1para fun¸cões de várias variáveis. Para tanto, recordemos que se P(a1, a2, . . . , am)eQ(x1, x2, . . . , xm)são pontos emRm_{, então a distância entre}_P_e_Q_{é dada por}

d(P, Q) =_kQ−P_k=_kPQ−→_k=»(x1−a1)2+ (x2−a2)2+· · ·+ (xm−am)2.

Quando m= 2 ou3 costumamos adotar a nota¸cão P(a, b)eQ(x, y), ou então P(a, b, c)eQ(x, y, z) e a expressão da distância fica _

 

 

d(P, Q) =»(x−a)2+ (y−b)2quandom=2

ou

d(P, Q) =»(x−a)2+ (y−b)2+ (z−c)2quandom=3

.

0 a

x y

x b

y

| -x a|

| -y b|

P

Q

d( ,P Q )

x

y y z

z

x

Q

O c

P

b a

A defini¸cão formal de limite de fun¸cão real de várias variáveis é dada abaixo. Antes, porém, é preciso introduzir a no¸cão deponto de acumula¸cão.

Um ponto P_∈Rm _{´e dito}_{ponto de acumula¸}_c˜_ao_{de um conjunto} X_⊂Rm _{quando existem pontos de} X, distintos de

P, arbitrariamente pr´oximos deP.

Notemos que um ponto de acumula¸c˜ao de um conjunto n˜ao precisa pertencer, necessariamente, ao conjunto.

Um exemplo simples: P(0, 0)_∈R2_{´e ponto de acumula¸c˜}_{ao de}_X₌₍_{x, y}₎_∈_R2_{: (}_{x, y}₎₆_{= (}_{0, 0}₎ _{, pois h´}_{a pontos de}_X

(distintos de P) arbitrariamente pr´oximos de P.

Agora sim, a defini¸cão formal de limite de uma fun¸cão de várias variáveis: Sejam f:X_⊂Rm

→R _e_P₍_a₁_{, a}₂_{, . . . , a}_m₎_∈Rm _{um ponto de acumula¸c˜}_{ao de} _X_{. Indiquemos um ponto gen´erico do}

dom´ınio XporQ(x1, x2, . . . , xm). Dizemos quef(Q) temlimiteL∈Rquando Qtende aP, e escrevemos

lim

Q→Pf(Q) =L ,

sempre que: para∀ε > 0,∃δ > 0tal que (1₎

0 < d(P, Q)< δ_⇒|f(Q) −L|< ε.

(20)

Desta forma, dizer que lim

Q→Pf(Q) =L significa que podemos fazer f(Q)arbitrariamente pr´oximo de L, tomando Q

suficientemente próximo deP, porém, diferente deP. Observa¸cões.

(1)Quandom=2 ou3costumamos escrever a nota¸c˜ao de limite do seguinte modo: 

  

  

lim

(x,y)→(a,b)f(x, y) =L, quandom=2 ou

lim

(x,y,z)→(a,b,c)f(x, y, z) =L, quandom=3 .

(2) Como X possui dimens˜ao m´ınima igual a 2, lim

Q→Pf(Q) = L tem a seguinte implica¸c˜ao: n˜ao importa por qual

“caminho” fa¸camosQ tender aPno dom´ınioXdef quef(Q)sempre se aproximar´a do n´umero realL.

R

f

x y

R2 X

( , )a b

f x y( , )1 1

( , )x y1 1

( , )x y2 2 f x y( , )2 2

L

Por outro lado, se existirem pelo menos dois “caminhos” distintos em X tal que o limite acima assuma dois valores distintos, dependendo do caminho adotado para fazer Qtender aP, ent˜ao o limiten˜ao existe.

(3) Todas as propriedades operatórias relativas aos limites de fun¸cões reais de uma variável real são válidas para fun¸cões de várias variáveis.

Exemplo 2.1 Calculemos lim (x,y)→(0,0)

x2₋_y2

x+y .

O dom´ınio de f(x, y) = x2_x₊−_yy2 ´eX=(x, y)_∈R2_:_y_{= −}₆ _x _{. Entretanto, arbitrariamente pr´}_{oximo de} ₍_{0, 0}₎_h´_{a pontos}

(x, y)∈X. Logo, podemos considerar o limite. Assim,

lim (x,y)→(0,0)

x2₋_y2

x+y =₍_x,ylim_)→(_0,0₎

(x−y)(x+y)

x+y =₍_x,ylim_)→(_0,0₎(x−y) =0.

Exemplo 2.2 Existe lim (x,y)→(0,0)

x2₋_y2

x2₊_y2 ?

O dom´ınio de f(x, y) = x_x22−₊_yy22 ´eX=

(x, y)_∈R2: (x, y)= (₆ 0, 0) . Entretanto, arbitrariamente pr´oximo de (0, 0)h´a pontos (x, y)_∈X. Logo, podemos considerar o limite.

Se o limite existir, seu valor independer´a do caminho escolhido para fazer (x, y)tender a (0, 0). Tomemos os seguintes caminhos.

(i)A reta C1 de equa¸c˜ao y=xpassa por (0, 0), Fa¸camos (x, y) tender a (0, 0) por ela.

Assim,

lim (x,y)→(0,0)

(x,y)∈C1

x2−y2 x2₊_y2 = lim

x→0 x2₋_x2

x2₊_x2 = lim

x→0 0

2x2 = lim

x→00=0.

(ii)A reta C2de equa¸c˜ao y=2x passa por (0, 0), Fa¸camos (x, y)tender a (0, 0)por ela.

Assim,

lim (x,y)→(0,0)

(x,y)∈C2

x2−y2 x2₊_y2 = lim

x→0

x2₋₍_2x₎2

x2₊₍_2x₎2 = lim

x→0

−3x2

5x2 = lim

x→0

−3 5 = −

3 5.

R

f

x y

R2

f x x( , ) =0

( , )x y

y=x

( , )0 0 ( , )x y

y=2x

(21)

Conclus˜ao: o limite depende do “caminho” escolhido para fazer(x, y)tender a(0, 0). Logo,n˜ao existe lim (x,y)→(0,0)

x2−y2 x2₊_y2.

Abaixo seguem algumas figuras do gr´afico def.

Exemplo 2.3 Estudemos o comportamento do limite lim (x,y)→(0,0)

xy x2₊_y2.

O dom´ınio de f(x, y) = _x2xy₊_y2 ´eX=

(x, y)_∈R2_{: (}_{x, y}₎_{= (}₆ _{0, 0}₎ _{. Entretanto, arbitrariamente pr´}_{oximo de} ₍_{0, 0}₎_h´_a

pontos (x, y)_∈X. Logo, podemos considerar o limite.

Se o limite existir, seu valor independer´a do caminho escolhido para fazer (x, y)tender a (0, 0). Tomemos os seguintes caminhos.

(i)A reta C1 de equa¸c˜ao y=xpassa por (0, 0), Fa¸camos (x, y) tender a (0, 0) por ela.

Assim,

lim (x,y)→(0,0)

(x,y)∈C1

xy

x2₊_y2 = lim

x→0 xx

x2₊_x2 = lim

x→0 x2

2x2 = lim

x→0 1 2=

1 2.

(ii)A reta C2de equa¸c˜ao y= −xpassa por (0, 0), Fa¸camos (x, y) tender a (0, 0)por ela.

Assim,

lim (x,y)→(0,0)

(x,y)∈C2

xy

x2₊_y2 = lim

x→0 x(−x)

x2₊₍₋_x₎2 = lim

x→0

−x2 2x2 = lim

x→0

−1 2 = −

1 2.

Conclus˜ao: o limite depende do “caminho” escolhido para fazer(x, y)tender a(0, 0). Logo, n˜ao existe lim (x,y)→(0,0)

xy x2₊_y2.

Exemplo 2.4 Estudemos o comportamento do limite lim (x,y)→(0,0)

x3₋_y3

x2₊_y2.

O dom´ınio de f(x, y) = x_x32−₊_yy32 ´eX=

(x, y)_∈R2: (x, y)= (₆ 0, 0) . Entretanto, arbitrariamente pr´oximo de (0, 0)h´a pontos (x, y)_∈X. Logo, podemos considerar o limite.

Inspirados pelos exemplos anteriores, se considerarmos alguns caminhos particulares em X passando por (0, 0) e fizermos (x, y) _→ (0, 0) por esses caminhos, constataremos que f(x, y) _→ 0. Isso ´e um sinal de que o limite pode existir.

Utilizemos o sistema de coordenadas polares, fazendo a seguinte mudan¸ca de vari´aveis:

x=rcos(θ)

y=rsen(θ) ,

(22)

q x

y R2

( , ) º ( ;q)x y r

0 _x₌_rcos_(q)

y=rsen(q) r

Assim, (x, y)_→(0, 0)significa r_→0 com θ livre. Logo,

lim (x,y)→(0,0)

x3₋_y3

x2₊_y2 = lim

r→0

(θlivre)

r3_cos3₍_θ₎₋_r3_sen3₍_θ₎

r2_cos2₍_θ₎₊_r2_sen2₍_θ₎ = lim

r→0r cos

3₍_θ_{) −}_sen3₍_θ₎

=0,

pois h(θ) =cos3₍_θ_{) −}_sen3₍_θ₎_{´e uma fun¸c˜}_{ao limitada, enquanto que} _g₍_r_{) =}_r

→0 `a medida que r_→0. Exemplo 2.5 Estudemos o comportamento do limite lim

(x,y)→(0,0)

xy

√

x2₊_y2.

O dom´ınio de f(x, y) = √xy

x2₊_y2 ´e X=

(x, y)_∈R2: (x, y)₆= (0, 0) . Entretanto, arbitrariamente pr´oximo de (0, 0)

h´a pontos (x, y)∈X. Logo, podemos considerar o limite.

Se considerarmos alguns caminhos particulares em Xpassando por (0, 0)e fizermos(x, y)_→(0, 0)por esses caminhos, constataremos que f(x, y)_→0. Isso ´e um sinal de que o limite pode existir.

Utilizemos o sistema de coordenadas polares, fazendo a seguinte mudan¸ca de vari´aveis:

x=rcos(θ)

y=rsen(θ)

sendo r_≥0 e θ_∈[0, 2π).

Assim, (x, y)_→(0, 0)significa r_→0 com θ livre. Logo,

lim (x,y)→(0,0)

xy

√

x2₊_y2 = _rlim_→₀ (θlivre)

(rcos(θ))(rsen(θ)) √

r2_cos2₍_θ₎₊_r2_sen2₍_θ₎ =_rlim_→₀

r2_cos₍_θ₎_sen₍_θ₎ |r| . Mas

   

  

lim

r→0+

r2_cos₍_θ₎_sen₍_θ₎ |r| = lim

r→0+

r2_cos₍_θ₎_sen₍_θ₎

r =_rlim_→₀+rcos(θ)sen(θ) =0

lim

r→0−

r2_cos₍_θ₎_sen₍_θ₎ |r| = lim

r→0−

r2_cos₍_θ₎_sen₍_θ₎

−r =_rlim_→₀−(−rcos(θ)sen(θ)) =0 ⇒

lim (x,y)→(0,0)

xy

√

x2₊_y2 =_rlim_→₀

r2_cos₍_θ₎_sen₍_θ₎ |r| =0,

pois h(θ) =cos(θ)sen(θ)é uma fun¸cão limitada, enquanto que g(r) =r→0 à medida que r→0.

2.2 Continuidade em Fun¸c˜

oes Reais de V´

arias Vari´

aveis Reais

Conforme o leitor perceberá na defini¸cão abaixo, a no¸cão de continuidade para fun¸cões de várias variáveis é oriunda, com as devidas adapta¸cões, da mesma no¸cão para fun¸cões reais de uma variável real.

Sejam f : X _⊂ Rm _→ R _e P(a1, . . . , am) ∈ X. Denotemos de modo gen´erico um ponto de X por Q(x1, . . . , xm).

Dizemos que f´econt´ınua emPquando existe lim

Q→Pf(Q)(como n´umero real) e

lim

Q→Pf(Q) =f(P).

Quando f for cont´ınua em todos os pontos de seu dom´ınio, dizemos quef ´econt´ınua emX, ou simplesmente que f

´econt´ınua.

Quandofnão for cont´ınua em algum pontoPde seu dom´ınio dizemos quefédescont´ınua emP. Neste caso também dizemos simplesmente que fédescont´ınua.

(23)

Exemplo 2.6 A fun¸c˜ao f:R2_→R_{dada por} _f(x, y) =x2+y2 ´e cont´ınua em P(1, 1), pois

lim

(x,y)→(1,1)f(x, y) =1

2₊₁2₌₂₌_f₍_{1, 1}₎_.

Generalizando,

lim

(x,y)→(a,b)f(x, y) =a

2₊_b2₌_f₍_{a, b}₎_,

ou seja, f´e cont´ınua em R2_.

Exemplo 2.7 A fun¸c˜ao f:R2

→R_{dada por} _f₍_{x, y}_{) =}

1, se (x, y)₆= (0, 0)

0, se (x, y) = (0, 0) ´e descont´ınua em P(0, 0), pois

lim

(x,y)→(0,0)f(x, y) =↓ (x,y)6=(0,0)

lim

(x,y)→(0,0)16=0=f(0, 0).

(24)

Se¸c˜

ao de Exerc´ıcios Propostos:

Limites de Fun¸

c˜

oes

f

:

X

_⊂

R

m

_→

R

Exerc´ıcio 2.1 Calcule:

(i) lim

(x,y)→(0,0) 7−x

2₊_5xy .

(ii) lim (x,y)→(0,0)

x+y 1+xy.

Respostas:

(i) lim

(x,y)→(0,0) 7−x

2₊_5xy

=7 e (ii) lim (x,y)→(0,0)

x+y 1+xy =0.

Exerc´ıcio 2.2 Calcule os limites lim

h→0

f(x+h,y)−f(x,y)

h e lim_k_→₀

f(x,y+k)−f(x,y)

k , sendo:

(i)f(x, y) =x+y.

(ii)f(x, y) =xy.

(iii)f(x, y) =xy2₋₂_.

Respostas:

(i) lim

h→0

f(x+h,y)−f(x,y)

h =1e _klim_→₀

f(x,y+k)−f(x,y)

k =1.

(ii) lim

h→0

f(x+h,y)−f(x,y)

h =y e _klim_→₀

f(x,y+k)−f(x,y)

k =x.

(iii) lim

h→0

f(x+h,y)−f(x,y)

h =y2 e _klim_→₀

f(x,y+k)−f(x,y)

k =2xy.

Exerc´ıcio 2.3 Use coordenadas polares para calcular:

(i) lim (x,y)→(0,0)

2x3₋_5y3

3x2₊_3y2.

(ii) lim (x,y)→(0,0)

8xy

√

2x2₊_2y2.

Exerc´ıcio 2.4 Utilize coordenadas esf´ericas para mostrar que lim (x,y,z)→(0,0,0)

xyz

x2₊_y2₊_z2 =0. Obs.: Deve-se utilizar a seguinte mudan¸ca de coordenadas:

 



x=ρsen(φ)cos(θ)

y=ρsen(φ)sen(θ)

z=ρcos(φ)

,

sendoρ≥0,φ∈[0, π]eθ∈[0, 2π). Exerc´ıcio 2.5 Mostre que lim

(x,y)→(0,0)

2xy

7x2₊_5y2 n˜ao existe.

Exerc´ıcio 2.6 Sejaf:R2₋_{₍_{0, 0}₎_}₋

→R_{dada por}_f₍_{x, y}_{) =} 2x2y x4₊_y2.

(i)Mostre quef(x, y)_→0 quando(x, y)_→(0, 0)ao longo de qualquer reta que passe pela origem.

(ii)Mostre quef(x, y)_→1 quando(x, y)_→(0, 0)ao longo da par´abolay=x2_.

Conclua que o limite def(x, y)quando(x, y)_→(0, 0)n˜ao existe. Exerc´ıcio 2.7 Mostre que f:R2_→R_{dada por}

f(x, y) =

x2+y2+2, se (x, y)₆= (0, 0)

0, se (x, y) = (0, 0)

(25)

Cap´ıtulo 3

Deriva¸c˜

ao de Fun¸c˜

oes Reais de V´

arias

Vari´

aveis Reais

3.1 Derivadas Parciais

Podemos derivar fun¸cões reais de várias variáveis reais. A diferen¸ca em rela¸cão às derivadas de fun¸cões de uma variável é que temos mais do que uma derivada. São as chamadas derivadas parciais e, de forma mais geral, as chamadas derivadas direcionais, que serão vistas mais adiante.

Comecemos definindo derivadas parciais para fun¸c˜oes de duas vari´aveis.

Sejam f:X⊂R2

→R_e(a, b)_∈X um ponto de acumula¸c˜ao de X.

Definimos a derivada parcial def, em rela¸c˜ao a x, no ponto(a, b), denotada por ∂f

∂x(a, b), como sendo ∂f

∂x(a, b) =_hlim_→₀

f(a+h,b)−f(a,b)

h

caso esse limite exista como n´umero real.

Analogamente, definimos a derivada parcial de f, em rela¸c˜ao a y, no ponto (a, b), denotada por ∂f

∂y(a, b), como

sendo

∂f

∂y(a, b) =_hlim_→₀

f(a,b+h)−f(a,b)

h

caso esse limite exista como n´umero real.

Observa¸c˜oes.

(i)Outras nota¸c˜oes para as derivadas parciais:  



∂f

∂x(a, b) =fx(a, b) ∂f

∂y(a, b) =fy(a, b)

(ii)Podemos considerar as derivadas parciais defem todos os pontos do dom´ınio def(onde elas existem) e considerar

novas fun¸c˜oes: _

         

         

∂f

∂x : X⊂R2 −→ R

(x, y) ₇₋_→ ∂f ∂x(x, y)

e

∂f

∂y : X⊂R

2 ₋

→ R

(x, y) 7−→ ∂y∂f(x, y)

(26)

(iii)A defini¸c˜ao de ∂f

∂x(a, b)permite que interpretemos ∂f

∂x(a, b)como sendo a “derivada de frestrita ao planoy=b,

no ponto de abscissa x=a”, o que significa que o n´umero ∂f

∂x(a, b)pode ser interpretado como o coeficiente angular

da reta tangente à curva de contorno, que é interseçcão do gráfico de f com o plano y= b, no ponto(a, b, f(a, b))

(veja figura abaixo). Observa¸c˜ao an´aloga vale para ∂f ∂y(a, b).

Interpreta¸c˜ao geom´etrica da derivada parcial:

y z

x

gráfico def planoy= b

f a b( , )

curva de contorno

reta tangente à curva de contorno

no ponto P

a b q P t x z P q t c c

Na figura acima, o plano em azul é o plano de equa¸cãoy=b, paralelo ao planoxz. A curva de contornoc, também em azul, é a interseçcão do plano y=bcom o gráfico de f. A retat, em vermelho, é tangente à curva de contorno

c no ponto P(a, b, f(a, b)). O coeficiente angular da reta t(no plano xz) no ponto P´e tg(θ). DoC´alculo 1 temos tg(θ) = ∂f

∂x(a, b).

(iv) A defini¸cão de derivada parcial, refor¸cada pelaObserva¸cão (iii)acima, indica um método para derivar parcial-mente: ∂f

∂x(x, y)´e calculada mantendo y como “constante” e derivando em rela¸c˜ao a x. Analogamente, ∂f

∂y(x, y) ´e

calculada mantendoxcomo “constante” e derivando em rela¸c˜ao ay(veja os exemplos abaixo).

(v) Podemos generalizar as defini¸cões de derivadas parciais de fun¸cões de 2 variáveis para fun¸cões com 3 ou mais variáveis. A quantidade de derivadas parciais é a quantidade de variáveis.

Exemplo 3.1 Calculemos as derivadas parciais de f:R2_→R_{, dada por} _f(x, y) =x2+2xy2−y3.

Temos: _





∂f

∂x(x, y) =2x+2y 2

∂f

∂y(x, y) =4xy−3y2

Exemplo 3.2 Calculemos as derivadas parciais de f:R2_→R_{, dada por} _f(x, y) = x2+y2

e−xy.

Temos, pela Regra do Produto:  



∂f

∂x(x, y) =2xe

−xy₊ _x2₊_y2

e−xy(−y) = 2x−yx2−y3

e−xy

∂f

∂y(x, y) =2ye−xy+ x2+y2

e−xy₍₋_x_{) =} _2y₋_xy2₋_x3

e−xy

Exemplo 3.3 Calculemos as derivadas parciais de f : X ⊂ R2 _→ R_{, dada por} _f(x, y) = ln(

√

x)y2

x2₊₁ , sendo X =

(x, y)_∈R2_:_{x > 0} _.

Temos:                      ∂f

∂x(x, y) =

Ä ₁ √

x. 1 2√xy

2ä

x2+1

−ln √x

y2(2x)

(x2₊₁₎2 =

y2₍_x2₊₁₎

2x −2xy

2_ln √_x

(x2₊₁₎2 =

y2_x2₊_y2₋_4x2_y2_ln₍√_x₎

2x(x2₊₁₎2

= x

2₊₁₋_x2_ln₍_x2₎

2x(x2₊₁₎2 y2 (pela Regra do Quociente)

∂f

∂y(x, y) =2

ln(√x)

x2₊₁ y= ln(x)

(27)

Exemplo 3.4 Calculemos as derivadas parciais de f:X⊂R2_→R_{, dada por} _f(x, y) =tg x2+y2

+cos x2 , sendo

X=(x, y)_∈R2:x2+y26= π

2+kπ,k∈Z .

Temos: _





∂f

∂x(x, y) =sec2 x2+y2

2x−sen x2

2x=2x sec2 _x2₊_y2

−sen x2

∂f

∂y(x, y) =2ysec

2 _x2₊_y2

3.2 Plano Tangente a Gr´

afico de Fun¸c˜

oes de Duas Vari´

aveis

Sejam f : X ⊂R2

→R _e ₍_{a, b}₎ _∈_X_{. Suponhamos que} ∂f ∂x e

∂f

∂y existam e sejam cont´ınuas em uma vizinhan¸ca em

torno de(a, b)_∈X. Vimos que ∂f

∂x(a, b)é coeficiente angular da reta tangentet1à curva de contornoc1, interseçcão

do gr´afico def com o planoy=b, no pontoT(a, b, f(a, b)). Analogamente, vimos que ∂f

∂y(a, b)é coeficiente angular da reta tangentet2 à curva de contornoc2, interseçcão do

gr´afico defcom o planox=a, no pontoT(a, b, f(a, b)).

y z

x f a b( , )

a b

T t1 t2

c1

c2

a

c1:z = ( , )f x b

c2:z = ( , )f a y t1,t2Ìa

O plano αque contém t1e t2é definido como sendo oplano tangente ao gráfico defno ponto T(a, b, f(a, b)).

Proposi¸c˜ao 3.1 Sejam f:X_⊂R2_→R_e(a, b)_∈Xtais que ∂f ∂x e

∂f

∂y existam e sejam cont´ınuas em uma vizinhan¸ca em

torno de (a, b). Então, a equa¸cão do plano tangente ao gráfico defno pontoT(a, b, f(a, b))é dada por

z−f(a, b) = ∂f

∂x(a, b) (x−a) + ∂f

∂y(a, b) (y−b).

Demonstra¸c˜ao.

Para deduzir a equa¸cão do planoα, tangente ao gráfico def no ponto T(a, b, f(a, b)), precisamos das coordenadas dos vetores diretores ~ue~vdas retas t1et2, tangentes às curvas de contornoc1 ec2, interseçcão do gráfico defcom

os planosy=bex=a, no pontoT(a, b, f(a, b)).

Sejam ~i,~j,~kbase ortonormal canônica do espa¸co cartesiano,~uvetor diretor det1que forma ângulo não reto (1_{) de} medida θcom~ie tal que~u=~i+w~, sendow~ paralelo a~k (figura abaixo).

f a b_{( , )}

a

x z

T

q q

w i

u t1

c₁

i k

f a b_{( , )}

a

x z

T

q

w

i

u t₁

c1

i k

q

Logo,w~ = (0, 0, z0). Temos tg(π−θ) = k~wk

k~ik =kw~k= −z0quandoz0< 0(figura acima `a esquerda) ou tg(θ) = k~wk

k~ik =kw~k=z0quando

z0≥0(figura acima `a direita). Como tg(π−θ) = −tg(θ), e ∂f

∂x(a, b) = tg(θ), podemos escrever ∂f

∂x(a, b) = z0 em qualquer situa¸c˜ao e, portanto,

~

w= _∂x∂f(a, b)~k.

(28)

Assim,~u=~i+ ∂f_∂x(a, b)~k, ou seja, ~u= 1, 0,∂f_∂x(a, b) .

Analogamente, ~v=Ä0, 1,∂f ∂y(a, b)

ä .

Sejan~ =~u_×~vvetor normal ao plano tangenteα(figura abaixo).

T

n _v

u a

Sabemos que

~

n=det 

    

~i ~j ~k

1 0 _∂x∂f(a, b)

0 1 _∂y∂f(a, b)



    

= −_∂x∂f(a, b)~i−_∂y∂f(a, b)~j+~k_⇒~n=Ä−_∂x∂f(a, b),−_∂y∂f(a, b), 1ä

SejaP= (x, y, z)_∈αe tomemos o vetorm~ =P−T = (x−a, y−b, z−f(a, b))que ´e vetor paralelo ao planoα(figura abaixo).

T n

m

a

P

Logo,~n´e ortogonal am~ e, portanto, n~ ·m~ =0(produto escalar usual).Assim, Ä

−_∂x∂f(a, b),−_∂y∂f(a, b), 1ä·(x−a, y−b, z−f(a, b)) =0_⇒

−∂f

∂x(a, b) (x−a) − ∂f

∂y(a, b) (y−b) +z−f(a, b) =0⇒ z−f(a, b) = ∂f_∂x(a, b) (x−a) + _∂y∂f(a, b) (y−b)

que é a equa¸cão geral do plano tangenteαao gráfico defno pontoT(a, b, f(a, b)). Exemplo 3.5 Determinemos a equa¸cão do plano tangente ao paraboloide circular de equa¸cão z=x2₊_y2 _{no ponto} T(1, 2, 5).

Esse paraboloide circular pode ser visto como gr´afico de f:R2_→R_{, dada por} _f(x, y) =x2+y2.

Sendo T(1, 2, 5)um ponto desse paraboloide temosT(a, b, f(a, b)) = (1, 2, 5)e, portanto,(a, b) = (1, 2)ef(a, b) =5.

O plano tangente ao paraboloide no ponto T possui equa¸c˜ao

z−f(1, 2) = ∂f

∂x(1, 2) (x−1) + ∂f

∂y(1, 2) (y−2).

Logo, precisamos das derivadas parciais:  



∂f

∂x(x, y) =2x⇒ ∂f

∂x(1, 2) =2.1=2 ∂f

∂y(x, y) =2y⇒ ∂f

∂y(1, 2) =2.2=4

.

Assim,

z−5=2(x−1) +4(y−2)_⇒ 2x+4y−z−5=0

(29)

Exemplo 3.6 Encontre os pontos do gr´afico dez=f(x, y) =xe−x2−y2 _{nos quais os planos tangentes s˜}_{ao horizontais.}

Sendo

z−f(a, b) = ∂f_∂x(a, b) (x−a) + _∂y∂f(a, b) (y−b)

a equa¸cão do plano tangente ao gráfico de f no ponto T(a, b, f(a, b)), para que ele seja horizontal, é necessário que

∂f

∂x(a, b) = ∂f

∂y(a, b) =0, ou seja, é necessário que a equa¸cão seja da forma z=k (neste caso,k=f(a, b)).

Assim, precisamos das derivadas parciais: 

 

 

∂f

∂x(x, y) =e−x

2₋_y2

+xe−x2₋_y2

(−2x) =e−x2₋_y2

1−2x2

∂f

∂y(x, y) =xe

−x2₋_y2

(−2y) = −2xye−x2−y2

.

Assim, _

 

 

∂f

∂x(a, b) =0⇒e

−a2₋_b2

1−2a2

=0

∂f

∂y(a, b) =0⇒−2abe

−a2₋_b2

=0

⇒

1−2a2₌₀

−2ab=0 ⇒a=±

√

2

2 eb=0.

Portanto, temos dois pontos do gr´afico de f onde o plano tangente ´e horizontal:

T1√₂2, 0,»_2e1 eT2−√2 2 , 0,−

»

1 2e

.

Abaixo seguem figuras com o paraboloide e o plano tangente encontrado.

3.3 Derivadas Parciais de Ordem Superior

´

E poss´ıvel derivar v´arias vezes uma fun¸c˜aof:X_⊂R2

→R_{em rela¸c˜}_{ao a}_x_ou_y_.

As derivadas parciais ∂f_∂x e _∂y∂f de f s˜ao as derivadas parciais de primeira ordem, ou derivadas parciais de ordem 1, de f.

Caso seja poss´ıvel derivar as derivadas parciais de f, temos as chamadas derivadas parciais de segunda ordem def.

∂2f

∂x2(x, y) = _∂x∂ _∂x∂f

(x, y) ∂2f

∂x∂y(x, y) = ∂ ∂x

Ä_∂f

∂y

ä (x, y)

∂2_f

∂y∂x(x, y) = ∂ ∂y

∂f ∂x

(x, y) ∂2_f

∂y2(x, y) = _∂y∂ Ä_∂f

∂y

ä (x, y)

As derivadas parciais de segunda ordem ∂2_f

∂x∂y e ∂2_f

∂yx s˜ao chamadas dederivadas parciais mistas def.

De modo an´alogo podemos obter derivadas parciais den-´esima ordem def, sendon∈N_.

(30)

(1)Na nota¸c˜aofx efyas derivadas parciais de segunda ordem def:X⊂R2_→R_{s˜ao escritas como} fxx(x, y) = (fx)x(x, y) fxy(x, y) = (fx)y(x, y)

fyx(x, y) = (fy)x(x, y) fyy(x, y) = (fy)y(x, y)

Percebemos que ∂2_f

∂x∂y(x, y) = fyx(x, y) e ∂2_f

∂y∂x(x, y) = fxy(x, y), ou seja, a posi¸c˜ao de x e y nas duas nota¸c˜oes

estabelecidas s˜ao trocadas.

(2)De modo an´alogo ao que apresentamos acima, podemos definir derivadas parciais de ordem superior para fun¸c˜oes

f:X_⊂Rm

→R_com_m_∈N_qualquer.

Proposi¸c˜ao 3.2 Sejam f:X⊂R2

→R_e₍_{a, b}₎_∈_X_{. Se} ∂2f

∂x∂y e ∂2_f

∂y∂x forem cont´ınuas em uma vizinhan¸ca em torno de

(a, b)_∈X, ent˜ao

∂2_f

∂x∂y(a, b) = ∂2_f

∂y∂x(a, b).

Exemplo 3.7 Calculemos as derivadas parciais de segunda ordem def:R2_→R_{, dada por}_f(x, y) =x2+2xy2−y3.

Temos ∂f

∂x(x, y) =2x+2y2e ∂f

∂y(x, y) =4xy−3y2.

Logo, ∂2_f

∂x2(x, y) =2, ∂ 2_f

∂y2(x, y) =4x−6y, ∂ 2_f

∂y∂x(x, y) =4ye ∂2_f

∂x∂y(x, y) =4y.

Observemos que do fato das derivadas mistas serem cont´ınuas em R2_{temos a igualdade entre elas, devido `}_{a Proposi¸c˜}_ao

3.2 acima.

3.4 Regra da Cadeia

Assim como no caso das fun¸cões reais de uma variável real, a chamadaRegra da Cadeiapara fun¸cões de várias variáveis serve para derivarmos fun¸cões compostas.

Vamos enunciar aRegra da Cadeia em quatro casos apenas, mas o leitor não terá a menor dificuldade em generalizar a regra para compostas envolvendo fun¸cões com quaisquer quantidades de variáveis.

No primeiro caso, por exemplo, temos z=f(x, y), x=x(t) ey=y(t)e a Regra da Cadeia fornece uma express˜ao que permite calcular z′₍_t₎_{sem precisar substituir}_x₌_x₍_t₎ _e_y₌_y₍_t₎_em_z₌_f₍_{x, y}₎_{e colocar}_z _{explicitamente em} fun¸c˜ao detapenas. E assim ocorre para os demais casos.

Proposi¸c˜ao 3.3 (Regra de Cadeia para fun¸c˜oes f:X⊂R2

→R_e_f_:_X_⊂R3

→R _{composta com fun¸c˜}_{oes de uma} ou duas vari´aveis)

(1)Sejamz=f(x, y),x=x(t) ey=y(t)fun¸cões com derivadas cont´ınuas definidas em dom´ınios onde fa¸ca sentido a composi¸cão. Então,z=z(t)é derivável e

dz dt =

∂f ∂x

dx dt +

∂f ∂y

dy dt

z

x y

t

(2)Sejamz=f(x, y),x=x(u, v)ey=y(u, v)fun¸cões com derivadas cont´ınuas definidas em dom´ınios onde fa¸ca sentido a composi¸cão. Então,z=z(u, v)possui derivadas parciais cont´ınuas e

  

 

∂z ∂u =

∂f ∂x

∂x ∂u +

∂f ∂y

∂y ∂u ∂z

∂v = ∂f ∂x

∂x ∂v+

∂f ∂y

∂y ∂v

z

x y

u v

z

x y

u v

(3)Sejam w= f(x, y, z), x =x(t), y =y(t)ez =z(t)fun¸cões com derivadas cont´ınuas definidas em dom´ınios onde fa¸ca sentido a composi¸cão. Então,w=w(t)é derivável e

dw dt =

∂f ∂x

dx dt +

∂f ∂y

dy dt +

∂f ∂z

dz dt

w

x z