Normal Modes Propagation in a Helial
Free-Eletron Laser with an Axial Guide Field
Riadh El-Bahi,MohamedNazih Rhimi, and AbdelWahab Cheikhrouhou
Department ofPhysis,Faulty ofSienes,
UniversityofSfax,
B.P802,Sfax 3018,Tunisia
Reeivedon5January,2001
Followingupthedetailedthree-dimensionalanalysisofthepartiledynamisinafreeeletronlaser
witha helialwiggler and auniform axialguide magnetield,ahievedby Rhimiet al. [1℄, we
studythe motionofthe eletronsinthe neighborhoodoftheideal trajetory. Thenormalmodes
^
h
of thequadrati Hamiltonianare analyzed numeriallyinboth thenormal and reversed-eld
ongurationsfordierentvaluesoftheratio ^
w= ^
0. Theeletrontrajetories arethusdisussed.
Itisfoundthatpseudo-irularandelliptitrajetoriesareharaterizingbothgroup-Iand
reversed-eldgroup-IImodeswhilethemotioninthenormalgroup-IImodeismuhmoreompliated.
I Introdution
TheeletrondynamisinaFreeEletron Laser(FEL)
with a helialwiggler eld and a uniform axial guide
eld hasbeenthesubjetofmanyresearhes[1-10℄,in
partiular when the spatial dependene ofthe wiggler
eld isinluded. Itwas establishedinearlyworksthat
apartiularase ofsteadymotionexists,in whih the
eletrons follow an axially entered helial path with
onstant axial veloity in suh a way that the
trans-verseveloityvetorof theeletronisparallel or
anti-parallel to thetransversemagnetield ateahpoint.
Of ourse, now eletron is likely to follow this ideal
trajetory,andthequestionofwhatthenon-ideal
tra-jetorieslook likearises. Freundand Ganguly[3℄have
studied the equations of motion in the neighborhood
of theidealtrajetory,andhaveobtainedtwosquared
frequenies, whih haraterize the osillations of the
eletronsaboutit. Rhimietal. [1℄haveextendedthis
workbyusingguidingentersoordinatestoshowthat
thekeyquantity(alledp^
z 0
)isaombinationoflinear
and orbital momentum whih is onserved along any
trajetoryasaonsequeneof thesrew-displaement
symmetry of the magnetield. For agiven eletron,
one determines thevalueof p^
z 0
from theinitial
ondi-tions,and provided ertainonditionsaremet, axed
point of the Hamiltonian exists. The Hamiltonian is
thenexpandedaboutthexedpoint,anditsquadrati
term may be redued by the use of the properties of
the\rotational"variable ^
htotwounoupledharmoni
osillators ofharateristifrequenies ^
, and
ampli-tudesj ^
h
(
^
t=0)j 2
thatareonstantsofmotion.
Inthispaper,weontinuetheworkofref. [1℄with
moni osillators. The general behavior of the
rota-tional variable ^
h
as afuntion of the normalized
ra-diushas been investigated for the values0.05 and 0.3
of theratio ^
w =
^
0
. Provided that the magnitudes of
theosillatoramplitudesarenottoolarge,theeletron
dynamisin theneighborhood ofthesteady-state
tra-jetoriesanbedesribedauratelyusingourmethod.
Itisthebehaviorofthoseamplitudeswithrighttothe
beam radius that is one of the most important tasks
ofourwork. As amatteroffat, itisthroughthe
ex-tensionofoftheanonialtransformationofChenand
Davidson[5℄andthedenitionoftherotationalvariable
^
hthatourformalismshowedtobeeÆienttodealwith
thephysial insightoftheproblem.
The organization of the paper is as follows: The
problem formulationis given in setion II.Setion III
isdevotedtothequadratiapproximationtothe
Hamil-tonianandtheinvestigationofnormalmodes. Weend
bytheonlusions.
II Problem formulation
Thephysialongurationweemployisthatofa
rela-tivistieletronbeampropagatingthroughanambient
magneti eld omposed of ahelially symmetri and
periodihelialwigglereld,and auniformguideeld
B=B
0 ^ e
z +B
w
(1)
whereB
0
denotesthemagnitudeoftheguideeld,and
thewigglereldB
w
B w =2B w L 0 1 (k w
r)sin ( k
w z)^e r +2B w [I 1 (k w r)=k w
r℄os( k
w z)^e 2B w I 1 (k w
r)os( k
w z)^e
z
(2)
represents the wiggler eld in ylindrial oordinates.
InEq. (2),B
w
desribesthe wiggleramplitude,k
w =
2=
w
isthewigglerwavenumber,
w
isthewiggler
pe-riod, and I
n (k
w
r) and I 0
n (k
w
r)represent themodied
Bessel funtion of order n and its derivative,
respe-tively.
The self-eletri and self-magneti elds are
ne-gleted within the neutral eletron beam. Then it
follows from the steady-state Maxwell equation that
B = rA and the vetor potential an be written
as
A= 2(B
w =k w )[I 1 (k w r)=k w r℄sin( k w z)^e r +[B 0 r=2 2(B w =k w )I 0 1 (k w
r)os( k
w z)℄^e
(3)
TheHamiltonianthatgovernsthemotionofaneletron
withinthebeamis:
H(x;P)=fm 2
2
+[P+(e=)A℄ 2 g 1=2 m 2 (4)
where P is the anonial momentum, is the
velo-ityof light, eand mare thehargeand themassof
theeletron,respetively;and istherelativistimass
fator
=[1+(p=m) 2
℄ 1=2
(5)
and the mehanial momentum p is related to the
anonialmomentumPby
p=P+eA= (6)
III Hamiltonian quadrati
ap-proximation and normal
modes
Inadditiontotheenergy,theseondonstantofmotion
^ p
z 0
isgivenby[1℄
^ p
z 0
=p^
z +( ^ h ^ h ^ h ^ h
)=p^
z + ^ L z (7) where ^ L z
is the z-omponent of the angular
momen-tum, ^ h = q ^ P exp(i) and ^ h = q ^
P exp(i ) are
the rotational variables orresponding to the angles
and , respetivelyr^
=(2 ^ P = ^ 0 ) 1=2
isthegyroradius
andr^
=(2 ^ P = ^ 0 ) 1=2
istheguidingradius[8℄.
Introduingdimensionlessparametersandvariables
dened by ^ 0;w = 0;w k w ; ^ P ; = k w P ; m ; ^ H = H m 2 ; ^ z 0 =k w z 0
; ^r=k
w r; ^ R= r k w m R ; ^
t=k
w t;
the Hamiltonian given by Eq.(4) is then expressed in
thedimensionlessformas
^ H( ^ h ; ^ h ; ^ h ; ^ h ; ^ P z )=[2
^ 0 ^ h ^ h ^ w (2 ^ 0 ) 1=2 (K ^ h +K ^ h ) ( ^ P z 0 ^ h ^ h + ^ h ^ h ) 2 + ^ 2 w KK +1℄ 1=2 (8) d where ^ 0w =eB 0;w =m 2 k w
arethedimensionless
non-relativistifrequeniesandtheomplexquantityK is
K=I
0 (k
w r)+I
2 (k w r) ^ R ^ R
The omplexquantity ^
R in the last equation is given
by ^ R= ^ h +i ^ h
=r^ q
^
0 =2e
i( z^ 0
)
Theone-dimensional aseorrespondingto K =1
has been studied extensivelyin the litterature[2,5-9℄.
Thethree-dimensionalasewasundertakenbyFreund
et al. [3℄ and Rhimi et al. [1℄ in dierent manners.
Provided axed point exists and after expanding the
Hamiltonian in aTaylorseriesabout it,and retaining
onlythelowest orderterms,weobtain[1℄
^
H(; ; ^
P
;
^
P ;p^
z 0 )= ^ H 0 0 =0; 0 = 2 ; ^ P 0 ; ^ P 0 ;p^
where ^
H
0
isthesteadystateHamiltonianevaluatedat
the xed points (exatly helial trajetories)and ^
H
Q
isthequadratipartoftheHamiltonian. Treating ^
H
Q
yieldedtwounoupledharmoniosillatorswhose
har-ateristi frequenies and amplitude are ^ + and ^ , and ^ h + and ^
h respetively. Thequadratipieeofthe
Hamiltonianisthuswritten as:
^ H Q = ^ + ^ h + ^ h + + ^ ^ h ^ h = ^ + ^ P + + ^ ^ P (10)
andthesolutiontoHamiltonsequationsaresimply
^ h ( ^ t)= ^ h ( ^
t=0)e i ^ ^ t = q ^ P ( ^
t=0)e i ^ ^ t (11)
givingtwoobviousonstantsofmotion ^
h
(t=0). The
ompletesolutionto theproblem, inthequadrati
ap-proximations,hasthusbeenfound.
Expressingtheosillatorrotationalvariables ^
h
as
alinearombinationofthedierentations ^ P and ^ P ,
andorrespondinganglesand
^ h = ( ^ P +i ^ P 0 )+ ( ^ P i ^ P 0 ) [ ^
P +i ( ^
P
0
+i=2)℄ [ ^
P i (
^
P
0
i=2)℄ (12)
d
The normalization of the rotational variable ^
h
is
obtained by requiring that the Poisson braket of ^
h
withitsomplexonjugate ^ h be [ ^ h ; ^ h
℄=i (13)
whihisequivalenttoimposing
2 2 + 2 2
=1=2 (14)
TheinvestigationoftheseoeÆientsthatdependonly
ontheratio ^ w = ^ 0
andthenormalizedradiusr^
0 ,will
allowthestudythedierentmodesofpropagationand
to identify, and then avoid the problemati operating
onditionsoftheonernedFEL.
The general behavior of these oeÆients as
fun-tions of ^r
0 and ^ w = ^ 0
is shown in Figs. 1-4. The
range of ^r
0
in eah gure has been limited to values
suhthatthelowerharateristifrequeny ^
isreal.
Both groupI (^r
0
<0) andgroupII(^r
0
>0)are
repre-sentedinFigs. 1and 3for ^ w = ^ 0
=0.05and inFigs.
2and 4for ^ w = ^ 0
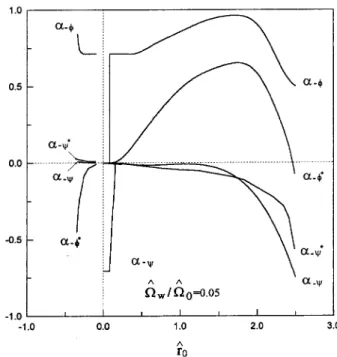
=0.3. First,wesee in bothFigs. 1
and 2, that for groupI, the oeÆient
+ 1= p 2; while + ; + and +
are muh smallerin
magni-tude. This implies that the rotational variable ^
h
+ is
quasi-idential with ( ( ^
P ^
P
0
) i( =2)). We
anexpet thatthe rotationalvariable ^
h should
pre-dominantlyentail( ^ P ^ P 0
+i)and( ^ P ^ P 0 i).
LookingatFigs3and4forgroupI showsthat the
o-eÆients and
areindeed small,whileat the
viinityofthestabilitylimits(wherethefrequeny ^
beomes imaginary), both oeÆients
and
diverge. This divergene is aompanied by a
vanish-remainsnite. Forsmallervaluesofj^r
0 j, 1= p 2 with
0andonsequently ^
h should mainly
in-volve ( ^ P ^ P 0
+i). This advantageous situation
(quazi-onstantgyroradius)requireseitherhighenergy
orsmall axial elds [1℄. The ontribution of the
on-jugate ( ^ P ^ P 0
i) inreases with inreasing j^r
0 j,
making the gyroradius trajetory ellipti rather than
irular. Quasi-irulartransversemotionispreferable,
sinethe trajetory is lose to thesteady-state orbits
and the axial veloity has less ripple. Hene, on the
basisof theabovestated explanation, we deduethat
group-Imotionisluidprovidedonestaysfarawayfrom
thestabilitylimits.
Thebehaviorofthegroup-IImotionis muhmore
ompliated, as is apparent in Figs. 1-4. First, in
group-II reversed-eldharaterized by small positive
valuesof ^r
0 (^r 0 < ^ w = ^ 0
) andwhere the beam and
the axial elds are anti-parallel, the urves are
self-explanatory. The oeÆients
+
and are very
loseto 1= p
2and 1= p
2, respetivelyand all others
are muh smaller in magnitude. The rotational
vari-able ^
h
+
may thus be identied with ( ^ P ^ P 0 i)
(onstantgyroradiustrajetory)while ^
h is desribed
by ( ^ P ^ P 0
i( =2)) (onstant guiding enter
radius trajetory). The trajetories of the gyroradius
andtheguidingenterradiusintheomplexplaneare
thusirlesenteredat(2 ^ P 0 = ^ 0 ) 1=2 and(2 ^ P 0 = ^ 0 ) 1=2
swept out with frequenies ^ + and ^ , respetively.
For group-II reversed eld where r^
0
is very lose to
zero,thesituationisompletelyomparabletothe
Figure1. TheoeÆientsofthenormalmode ^
h+ asa
funtionof^r0 with ^
w= ^
0=0:05:
Figure2. SameasinFig. 1,for ^
w= ^
0=0:30:
Figure3. TheoeÆientsofthenormalmode ^
h asa
funtionof^r
0 with
^
w =
^
0 =0:05:
Figure4.SameasinFig. 3,for ^
w =
^
For the normal group-II motion, the situation
re-mains the same up to the region of losest approah
where thefrequenies repel eah other (^r
0
0:1). In
Figs. 1and3,itislearthatthisfrequenyrossingis
behindtheabruptriseoftheoeÆients
and
+
tothevalueof1= p
2andtheaompanyingfallof
+
and tozero( ^
h
+
isonvertedto ^
h andvie-versa).
Inthis asefor ^r
0
0:01; ^
h
+
desribesairleof
on-stantgyroradiusatfrequeny ^
+
, whileforr^
0
0:05;
^
h
+
, it traes out a irle of onstant guiding enter
radius at the samefrequeny. On the otherhand, ^
h
movesfrom airularmotionof onstantguiding
en-ter radius to airular motion of onstant gyroradius
but withafrequeny ^
:Beyondr^
0
0:015,asis
ap-parentin Fig. 3,
beomesnon-negligibleleading
to ompliatedtrajetories. Forlargervaluesofr^
0 , all
oeÆientsbeomesigniant,andthesimplebehavior
oftheosillatoramplitudes ^
h
+ and
^
h isnolongereasy
to touh (seeFigs. 1and3).
Asseenin Figs. 2and4andforthelargervalueof
^
w =
^
0
=0:3,thetransitionregionbeingmuhlargerin
thevariablehatr
0
reahesthestabilitylimitsbefore
be-ing omplete. All theoeÆientsare almostdivergent
and doontributetotheosillatorrotational variables
^
h
on the same feet, the thing that ompliates the
trajetoriesbeyond thevalueof r^
0
0:25. Obviously,
suhasituation worsenswithinreasing ^
w =
^
0 .
IV Conlusions
In this work, we are following up the detailed
three-dimensionalanalysisofthepartiledynamisin aFree
eletronlaser withahelialwigglerandauniform
ax-ial guide magneti eld,ahievedby Rhimi et al. [1℄.
Using Eq. (12), thegeneralbehaviorofthe rotational
variable ^
h
asafuntion ofthenormalizedradiushas
beeninvestigatedforthevalues0.05and0.3oftheratio
^
w =
^
0
. Providedthatthemagnitudesoftheosillator
amplitudes arenottoolarge,theeletrondynamisin
theneighborhoodofthesteady-statetrajetoriesanbe
desribedauratelyusingourmethod. Itisthe
behav-ior of those amplitudes with right to the beam radius
thatisoneofthemostimportanttasksofourwork.A
uniformlyreversedguideeldanpresentabetter
qual-ityoftrajetoriesforaneletronbeamdriftingthrough
thewigglereld. Infat,weobservethatinthelimitof
intense axialguideeldstheelliptimotionreduesto
a irular onein whih theradial displaement of the
guiding-enter from the axis of symmetryis onstant.
This simple and favorable situation persists into the
normalgroup-IIregion,butforsmalleldfortheradius
^ r
0
. Asthelimitsofstability(whereoneofour
osilla-torfrequeniesvanish) areapproahed,ertainnormal
mode oeÆients beome large, and the
orrespond-ing movement unpreditable. Pseudo-irular and
el-lipti trajetories are haraterizing both group-I and
reversed-eldgroup-II whilethe motionin thenormal
group-IIisfoundtobemuhmoreompliated. Under
ertainonditions,thesimplepitureofthetransverse
motion as a superposition of the ideal helial motion
andtheparasitiylotronmotionisidentied.
Theexpliit alulationofthe orbitsfollowedbya
partileforwhihthepresentformalismisadequate,is
under way and the results are postponed to a
subse-quentpubliation.
Referenes
[1℄ M.N. Rhimi, R. El-Bahi, and A. W. Cheikhrouhou,
\Classial Harmoni Osillator Approah of a
Helial-Wiggler Free-Eletron Laser with Axial Guide Field,"
Can.J.Phys.,toappear.
[2℄ R.E.Aamodt,Phys.Rev.A28,2895 (1983).
[3℄ H.P.FreundandA.K.Ganguly,IEEEJ.Quant.Eletr.
7,1073(1985).
[4℄ J.Fajans,D.A.Kirkpatrik,and G.Beke,Phys.Rev.
A32,3448(1985).
[5℄ C. Chen and R.C. Davidson, Phys. Fluids B 2, 171
(1990).
[6℄ C. Chen and R.C. Davidson, Phys. Rev. A 43, 5541
(1991).
[7℄ L.Wang.D.L.Bosley andJ.Kevorkian,PhysiaD88,
87(1995).
[8℄ L. Wang and J. Kevorkian, Phys. Plasmas 3, 1162
(1996).
[9℄ V.L.B. de Jesus, A.P. Guimar~aes, and I. S. Oliveira,
Braz.J.Phys.29,541(1999).
[10℄ P.W. Milloni and J.H. Eberly, Lasers (Wiley, New
York,1998).
[11℄ J.P.BlewettandR.Chasman,J.Appl.Phys.48,2692
(1977).
[12℄ W. Dittrih and M. Reuter, Classial and
Quan-tum Dynamis: from Classial Paths to Path Integrals