Strethed Exponential Relaxation and
Independent Relaxation Modes
R.M.C. de Almeida 1
, N.Lemke 2
,and I.A. Campbell 3;4
1
InstitutodeFsia,UniversidadeFederaldoRioGrandedoSul,
CaixaPostal 15051{91501-970,PortoAlegre,RS,Brazil
2
CentrodeCi^eniasExatasedaTerra {Unisinos
Av. Unisinos,95093022-000{S~aoLeopoldo{RS{Brazil
3
LaboratoiredesVerres,Universite deMontpellierII
++34095MontpellierCedex5,Frane
4
Laboratoire de PhysiquedesSolides,Universite ParisSud,91405 Orsay,Frane
Reeivedon15Otober,2000
WedisusstheoriginofstrethedexponentialrelaxationindisorderedIsingspinsystemsbywriting
themasterequationonthephasespae,andtheevolutionofloalandglobalspinautoorrelation
funtions,intermsofindependentrelaxationmodes, whihareeigenvetors ofthetimeevolution
operator. Inthissenseitisshownthatwhentherelaxationmodesarespatially deloalized, both
loalandglobalautoorrelationfuntionsmaypresentnon-exponentialrelaxation. Wealsoanalyze
resultsforrandomwalksonthedilutehyperube,whihmaybeassoiatedwiththephasespaeofa
disorderedIsingspinsystem. Asexpeted,theresultsshowastrethedexponentialrelaxationnear
theperolationtransition,sineitdealswithrandomwalksonafratalperolatinglusterdened
onalosedsurfae. Wearguethatthesametypeof topologyispresent intheavailableregionof
ongurationspaeinIsingspin-glasssystemsneartheglasstransition,sinethesesystemspresent
verysimilarrelaxationpatternsinthistemperaturerange.
I Introdution
Slowrelaxationnearaphasetransition presentsmany
interestingfeatures thatreetthenature ofthe
tran-sition. This phenomenon may be observed in many
dierent kindsof materials, ranging from the original
observations by Kohlraush for the deay of residual
harge ona Leiden jar [1℄, to suh theoretial models
as the trapmodel [2, 3℄, or random walkers ondilute
hyperubes of high dimensions [4-8℄, and spin glasses
above,orferromagnetsbelowtheirtransition
tempera-tures, struturalglasses, et. [Forareent review,see
Ref. [9℄℄.
Thereisaontroversythatbeginswiththeform of
therelaxation,andintensieswhenthedisussionturns
to thepossibleoriginsforthisbehavior. Twodierent
forms ofnon-exponentialrelaxationofamemory
fun-tion q(t) are often found in the literature, originating
either in theoretial models or invoked in analysis of
experimental data. Therstis
q(t)exp[ (lnt) d
(d 1)
℄; (1)
asproposedbyRanderiaetal. [10℄forshort-rangeIsing
spin-glasses with loal spin dynamis above the
spin-hasneverbeenobserved[11℄. Thepointisthatsystems
shouldrelaxforverylongtimestoreahtheasymptoti
regime,renderingdiÆultaonlusivestatementbased
onnumerialsimulations.
The seond form of non-exponential relaxation of
memoryfuntions istypiallygiven byastrethed
ex-ponentialoftheform
q(t)Cexp[ (t=)
℄ (2)
where isarelaxationtimethat divergesasthe
tran-sitionisapproahedand <1( =1is theaseofa
pureexponentialrelaxation). Thisexpressionhasbeen
foundonsistentwithmanyexperimentsondisordered
systems[9℄andnumerialsimulationsofdierentmodel
systems[2-8,12℄.
In this paper we address this ontroversy by
on-sideringthemasterequationrepresentingtheevolution
ofaspinglassin phasespae. Inthismanner, wean
writetheevolvingdensityfuntionintermsofthe
relax-ationmodesrelatedto thetransition matrix
eigenve-tors. Thetransitionmatrixontainsinformationabout
thedynamisofthesystem,givingtherateforthe
se-spinsystem anddisuss someof the previous
theoret-ialand numerial resultsfrom this pointof view. In
setion III, we write the master equation for random
walkersonadeimatedhyperube,andusethismodel
asananalogyforthe phasespaeaspinglass. Inthis
waytheglasstransitionisassoiatedwithaperolation
transitionandtheslowrelaxationisexplainedasthe
ex-petedslowingdownofdispersionofrandomwalkerson
perolationlustersembeddedonlosed surfaes. The
results are presented and disussed in setion IV and
nallyonsetionVweonlude.
II The master equation and
re-laxation modes
Two models have been proposed that may yield
strethedexponentialrelaxationintheappropriate
lim-its. The trap model [2℄ onsiders random walkers in
a d-dimensional spae where traps are randomly
dis-tributed. The memory funtion here is given by the
number of living walkers after agiven time. The
ex-petedlifetimeofthewalkers,thatis,theaveragetime
it takesfor awalkerto meetatrap, isdetermined by
the initial distane to the nearesttrap. Consequently
thedistributionofrelaxationtimesontributingtothe
memoryfuntion depends onthedistributionof linear
sizes of trap-free regions. Also, eah walker is
relax-ing in a given region, with adened relaxation time,
thatis,eahwalkerisinanindependentrelaxingmode
of the dynamis of the system. The result of
averag-ing over these independent relaxation modes gives a
strethedexponentialduetothepartiularformofthe
relaxation-timedistributionoriginatingin therandom
loalizationoftraps.
Anothertheoretial modelyielding strethed
expo-nentialrelaxationis thehierarhialmodel [3℄. Inthis
model the spinsare organizedin dierent hierarhial
levels, eah level ontaining a given number of spins.
Thespinsinagivenlevelareallowedtohange states
onlyaftersomeonditionhasbeensatisedbythespins
at the level immediately below. As a onsequene,
the relaxationtimesare alwaysinreasing for
inreas-inglevels,sinesuperior levelsspinsmustwaitforthe
spinsatlowerlevelstorelaxbeforetheyanstart
relax-ing. Eahspinlevelthenanbeviewedasan
indepen-dentmodewithadenedrelaxationtime. Thememory
funtion is the spinautoorrelationfuntion and eah
spinrelaxationisessentiallyruledbyonlyone
indepen-dentmode. Theauthors of this model propose a
spe-i onstraint on the evolutionof upperlevelsyields
strethedexponentialrelaxationfortheglobalmemory
funtion.
Thekeyissueinbothmodelspresentedaboveisthe
fat that the (global) memory funtion is an average
over loal memory funtions that relax exponentially
al memory funtions are measuring the evolution of
independent relaxationmodesof thesystem. We an
verify this statementby onsidering a system with N
Isingspins,inwhihthemonitoredglobalmemory
fun-tionisgivenas
q(t)= 1 N N X i=1 S i (t)S i (0) (3)
and then writing a master equation, dened over the
phasespaeofthesystemas
( ~ S;t) t = X f ~ S 0 g h Q( ~ S; ~ S 0 )( ~ S 0
;t) Q( ~ S 0 ; ~ S)( ~ S;t) i (4) where Q( ~ S 0 ; ~
S) is the transition rate from
ongura-tion ~
S toonguration ~
S 0
and( ~
S;t)istheprobability
of nding the system in the onguration ~
S at time
t. The transition matrix ontains information about
the dynamis of the systemand is dierent for
dier-entmodels. Itisonvenienttoexpressthedynamisin
a Dira-like notation. Writing the aboveequation for
disrete time, the stateof the systemanbeformally
obtainedas
j(t)i=e t
j(t=0)i (5)
where j(t)i represents the probability of nding the
systemin eahpossibleongurationat time t,and
isgivenby
( ~ S; ~ S 0
)=Q( ~ S; ~ S 0 ) Æ( ~ S ~ S 0 ) X f ~ S g Q( ~ S ; ~ S) (6)
Theeigenvalueequationofthetransitionmatrixis
j k i= k j k i (7)
wherek=1;2;:::;2 N
andtheeigenvetorsfj
k igform
a basis for the spae of the solutions of the evolution
equation. Oneanalsobuildanotherbasis,onsidering
thestatesj ~
Sithatrepresentastatewherewehave
prob-abilityoneofndingthesystemin ~
S=(S
1 ;S
2 ;:::;S
N )
andzeroinanyotheronguration. Inthisase,
h ~ Sj ~ S 0 i=Æ(
~ S ~ S 0 ) (8) and ( ~
S;t) = h ~
Sj ~
(t) i. The stationary solution(s) of
Eq.(4) are the eigenstate(s) of Eq.(7) with eigenvalue
zero,normalizedsuhthat
X f ~ Sg h ~
Sj=0i=1 (9)
while for all other eigenstates, with Re() < 0, the
abovesumgiveszero. Itmeansthat someofthe
om-ponentsh ~
Sj6=0iarelessthanzero. Thishastwomain
rep-the evolution operator provided it ontains a
station-ary omponent suh that all omponents h ~
Sj ~
(t)i of
the physial state are non-negative and (ii) the role
playedbythesenonstationaryomponents,inrelation
to the stationarystates, is to addprobabilityto some
ongurationswhilesubtratingprobabilityfromother
ongurations,onservingtotalprobability. Thesetwo
features are valid due to the probability onservation
guaranteedbytheevolutionequation. Thestateofthe
systemattimet maythenbewrittenas
j(t)i= 2 N X k =1 e k t j k ih k
j(t=0)i (10)
whereitbeomeslearthattheeigenvaluesofthe
tran-sition matrixgivetherelaxationmodesof thesystem.
Letting
k
= 1=
k
, theaboveequationbeomes
j(t)i= 2 N X k =1 e t=k j k ih k
j(t=0)i: (11)
Now, Eq.(11) gives the relaxation of the system as a
wholeintermsofitsindependentmodes. Thequestion
now is to translate this relaxation of the probability
densityof thesystemdened overitsphasespaeinto
therelaxationofthespinautoorrelationfuntionthat
is the ommonly used memory funtion for Ising spin
systems. Forthat wersttake
j(t=0)i=j ~ S 0 i (12) where ~ S 0
istheinitialongurationofthesystem. We
thentaketheprodutofEq.(11)withh ~
Sj,multiplyby
S
i and S
0
i
,that are thevaluesof thei-th spinin
on-gurations ~ S and ~ S 0
,respetively,andaverageoverall
ongurations,toobtaintheloal spinautoorrelation
funtion: q i (t)= 2 N X k =1 e t= k f i ( k ; ~ S 0 ) (13) with f i ( k ; ~ S 0 )= X f ~ Sg S i S 0 i h ~ Sj k ih k j ~ S 0 i (14)
Finally, the global spin autoorrelation funtion
maybewritten as
q(t)= 2 N X k =1 e t= k g( k ; ~ S 0 ) (15) with g( k ; ~ S 0 ) = X f ~ Sg 1 N N X i=1 S i S 0 i ! h ~ Sj k ih k j ~ S 0 i = 1 N N X f i ( k ; ~ S 0 ) (16)
Both equationspresentastationary part,
orrespond-ingto
i
=1(
i
=0)andarelaxationpartrelatedto
smallerrelaxationtimes(
i <0).
Now,onsideringtherelaxingomponentforthe
hi-erarhial model, whih is a spin system so that the
abovememoryfuntion applies,weobservethat
essen-tiallyeah spinrelaxes aordingto its level
indepen-dent mode, that is, the sum over dierent relaxation
modes k splits into sums for dierent levels.
Conse-quently, eah spin is expeted to relax exponentially,
but the sum overindividual spin relaxationfuntions
mayyieldastrethedexponentialformforsuitable
on-straints.
In more general spin systems, it has been argued
that some unfrustrated spin lusters may form, suh
thattherelaxationwithinagivenlusterisexponential,
withrelaxationtimes dened by theluster size. The
sumofthese dierentmodesofexponentialrelaxation
withanappropriatelustersizedistributionouldyield
a global strethed exponential behavior. These
lus-ters would berelated to theGriÆths singularities[13℄,
and hene spatial inhomogeneities would be
responsi-ble for the observed slow relaxation. However, this
modelimpliesthateahspinshouldrelaxexponentially
(eah luster orresponding to an independent
relax-ationmode),andspatialorrelationbetweenloalspin
relaxation modes would signal the appearane of
un-frustratedlusters. Glotzeretal.[12℄monitoredthe
re-laxationoftwoandthreedimensionalIsingspinglasses
andfoundstrethedexponentialrelaxationfor
individ-ualspins,thatis,thesumintheexpressionfortheloal
autoorrelation funtion q
i
(t) in Eq.(13) also yields a
strethedexponential,implyingthatvariousrelaxation
modesontributetotherelaxationofindividualspins.
Infat,itisthestrutureofg(
k ;
~
S 0
)andf
i ( k ; ~ S 0 )that
governs the ontribution of eah relaxation mode for
theglobalandloalspinorrelationfuntions,dening
theiroverallrelaxationbehavior. Forexample,ifthe
re-laxationmodesarenotspatiallyloalized,q(t)ouldin
priniplepresentstrethedexponentialrelaxationwith
agiven and,andsoouldtheloalrelaxation
fun-tionswithdierentvaluesfortheseparameters.
Dier-ent valuesof and haveindeed beenfoundGlotzer
etal. [12℄.
III Ising spin systems and the
hyperube
From Eq.(4) and the evolution equations for the spin
autoorrelationfuntion,itbeomeslearthatitis
in-terestingto investigate the originsof non-exponential
relaxationbyfousingonthephasespaeofthesystem.
Infat,thephasespaeofasystemwithN Isingspins
is the set of the verties of a hyperube of N
onperolationlustersembeddedonatspaesyielda
sublinear diusion equation hr 2
i t
[14℄, while
ran-dom walkersonlosed surfaes suh as a hypersphere
giveapureexponentialdeayoftheaverage
autoorre-lation funtion, hos((t))i exp( t=), one is led to
theonjetureproposedbyCampbell[4℄thatdispersion
ofrandomwalkersonperolationlustersembeddedin
a losed surfae suh as the hyperube should follow
hr 2
iexp[ (t=)
℄, with !1=3and !1 asthe
perolationthresholdisapproahed.
Inreentsimulationsofaperolationluster
embed-ded inthe surfaeofahypersphere,Jund,Jullien and
Campbell [15℄ show that strethed exponential
relax-ationisdiretlyonnetedtothefratalnatureofthese
lusters. Campbell'sonjeturegoesfurther,by
onsid-eringtheimpliationsoftheseresultstotherelaxation
of suh disorderedsystemsas, for example,Ising spin
glasses. TheideaistoregardtherelaxationofanIsing
spin glass oupled to a heat bath as a random walk
throughtheavailablestatesinphasespae. This
high-dimensional,losedspaehasitslandsapehangedas
thetemperatureapproahesthetransitionfromabove,
sine the number of available states dereases in this
proess.
Nearthetransitionitisonjeturedthat thesetof
available states forms a perolating luster, and that
right at the transition point the giant luster breaks
intomanynitelusters, representingthemany
dier-entfreeenergyvalleystypialofspinglassesbelowthe
glass transition temperature. As temperature is
low-ered towards the transition, the topology of the
lus-ter beomes more labyrinthine, slowing down the
re-laxation towards equilibrium. Observe that this
pi-ture onsiders the relaxation of a density funtion on
the hyperube where eah siteis apossible
ongura-tion of the system. As the dierent verties hange
theiroupation density, theloal and globalspin
au-toorrelationfuntionshangeaordingly,and itmay
bepossiblethat theyaresimultaneouslyinuenedby
manydierentrelaxationmodes.
The simplest ase of the above senario has been
onsideredbyCampbellandollaborators[4-7℄through
MonteCarlosimulationsofarandomwalkeronan
N-dimensional hyperube in whih some of the verties
have been deleted or prohibited to the walker. There
is aritial fration p
of allowedor oupied verties
belowwhihnoperolationlusterisformed. The
sim-ulations,whihwereperformedforoupationfrations
pp
, monitoredtheaverageHammingdistane q(t)
betweentheurrentandinitial positions ofthewalker
asafuntionoftime,whihanbeassoiatedwiththe
global spin autoorrelation funtion. The results are
ompatible with Campbell's onjeture, but the noise
at small values of q(t) for longtimes did not allow a
deisiveonlusion. Analternativeproedureisto
on-sidertheevolutionoftheprobabilitydensityofnding
ter equation of the system[8℄, whih has yielded very
preiseresults.
Startbyimaginingahyperubein(high)dimension
N withafrationpofits2 N
vertiesoupiedat
ran-dom. Theritialperolationonentrationisgivenby
p
=+
3
2
2
+ 15
14
3
+::: (17)
where = 1=(N 1). For p > p
there exists a
gi-ant spanning luster made up of oupied sites
hav-ing one ormore oupied sites as neighbors [16℄. For
p<p
there are onlysmalllusters (withlessthan N
elements).
Consideringeahonguration ~
Sasthebinary
rep-resentationofaninteger,thedensityfuntion( ~
S;t)
beomesthenafuntionoftwointegervariables,(;t),
andthediretiterationofthemasterequationmay
eas-ilybeimplementedonaomputer. Consideringvalues
ofpabovep
,thesystemstartsatagivenvertex
0
be-longingtotheinniteluster. Theprobabilitythatthe
randomwalkerjumpstoaneighboringsiteis1=Nifitis
`oupied'andzerootherwise,inwhihasethewalker
stays where it is. The disrete-time master equation
thenreads
(;t+1)=(;t)+
X
f 0
g
[W(; 0
)( 0
;t) W( 0
;)(;t)℄ (18)
withtransitionmatrixW( 0
;)onvenientlyredened
to desribe the jumping probabilities during disrete
timeintervals.
As theiteration proedure evolveswemonitor the
memory funtion ofthesystem,the spinauto
orrela-tionfuntion,alulatedas
q(t)= 1
N N
X
i=1 X
fg
(;t)S 0
i S
i
; (19)
whereS 0
i andS
i
arethei-thspinsoftheongurations
assoiated,respetively,with
0
and,that is
S 0
i =
(2 i 1
AND
0 )
2 i 2
1
S
i =
(2 i 1
AND )
2 i 2
1: (20)
The advantage of this proedure is that for eah
transition matrix,representingonerealizationofa
hy-perubewithoupationprobabilityp,suessive
iter-ationsof themasterequation providetheaverageover
all possiblerandom walksstarting from the same
ini-tialondition. Averagesoverdierentsamplesarestill
required, butthe aurayissigniantlyenhanedin
omparisonto MonteCarloalulations.
Verynearp
equa-applied. Inthisase,wetakeadvantageoftheredued
numberofsitesintheperolatinglusterand
diagonal-ize theevolutionoperator,obtain theeigenvaluesand
eigenvetorsandusethemdiretlyinEq.(15).
Astheoupation probabilitypdereasesfrom1.0
down to the perolation threshold, the oupied
ver-ties develop a fratal perolation luster: the vetor
state ~
(t)diuseson afratalaggregate. Inthis ase,
wemayexpetanomalousdiusion. Wethereforestudy
therelaxationoftheautoorrelationfordierentvalues
of p,abovetheperolationthreshold.
IV Results
For eah p studied, we onsidered 100 realizations of
the hyperube. Sine we expliitly solve the master
equation for this system we obtain exat results (to
within numerialroundingerrors)fortheaverageover
allpossiblerandomwalksforeahombinationofa
re-alizationofthehyperubeandonegivenstartingpoint.
Thereforebystudyingevenarelativelysmallnumberof
samplesweanobtainverygood estimatesforthe
av-eragerelaxationfuntion q(t). Themain problemwith
this approahis thatevenwiththeoptimizationused,
putimeandmemoryrestritedusto\low"dimensions
N, sinethenumberofvertiesin thephasespae
in-reases exponentiallywithN (2 N
). Foronveniene
wehosetoarryoutexpliitalulationsindimension
N = 16. 100 samples were studied for eah value of
p : p=0.073, 0.10, 0.24, 0.36 and 0.5, while 500
sam-ples werestudied forp=0:12. Forp=0.073,verynear
the perolation thresholdforN =16, wediagonalized
the evolution operator,while for the other values the
dynamialequationwasdiretlyiterated.
Before disussing the results, it is interesting to
point outthat we expet three relaxation regimes: i)
At short times q(t) will behave as 1 t where is
the average probability per unit time that a stepwill
betaken,i.e.,itisproportionaltothefrationof
ou-piedneighborsofasiteonthegiantluster. Thisisthe
leadingtermintheexponentialfuntionexp( (t)),so
at veryshorttimestherelaxationwillalwaysbe
expo-nential. ii). Atlongertimes,asthesystemexploresthe
labyrinthinegeometryofthegiantluster,aslow
relax-ationregimeappears. iii)Finally,atevenlongertimes,
nite-size eets beome measurable and a rossover
baktoanexponentialrelaxationisexpetedtosetin.
This last rossovertimehasbeenshownto depend on
sample size for systems where relaxation arises from
twoompetingexponentialproesses[17℄.
The results for q(t) are presented in two dierent
ways to verify whether the relaxation is following a
strethedexponentialformand thenobtainthetting
parameters. Fig. 1showsthedata obtainedforq(t)in
alog-logplotfordierentvaluesofp,togetherwiththe
in Fig. 2. The normalization parameter C is always
loseto 1. Itanbeseenimmediatelythatthetsare
ofexellentquality.
Figure1. Deay of the autoorrelation funtionq(t) ona
log-logplotfor dierent valuesof p,as listed intheinset.
Thesolidlinesorrespondtostrethedexponentialts,with
(p)and(p)asindiatedinFig. (2). Theerrorbars
or-respondtoanestimateoftheunertaintyofthepointsdue
tolimitedsampling.
Inamorestringenttestforthestrethed
exponen-tialt,Fig. 3showsthesamedata asbefore but now
in a log(-log(q(t))) versuslog(t) plot. Inthis kind of
plots pure or strethed exponential funtions appears
as straight lines, with the slope giving the exponent
. As expeted, allurvesshowdeviations towardsa
pureexponentialbehaviorforveryshortandverylong
times. At intermediate times, however, the strethed
exponentialbehaviorislearlymarkedbytheextended
straightlineregions. Also,bothFigs. (2)and(3)show
thatasp!p
!1=3and !1.
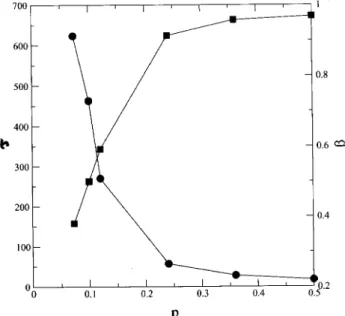
Figure2. Relaxationtime(p)(irles) andstrethed
Figure3.Amorestringenttestofthestrethedexponential
behaviorofq(t)isthelog[-log(q(t))℄againstlogtplot.The
dierentvaluesofp arelisted inthe inset. Thesolidlines
orrespond to astrethedexponentialt,with and as
indiatedinFig.(2).
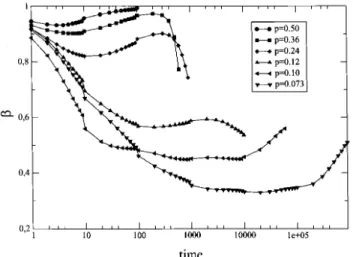
Finally,Fig. 4showsthevalueoftheloalslopeof
q(t)inthelog(-log(q(t)))versuslog(t)plot,thatis,this
gurepresentstheinstantaneousvalueoftheexponent
. The three regimes (exponential - strethed
expo-nential-exponential)maylearlybespotted, withthe
minimumvaluefor theinstantvalueof approahing
1/3asthetransitionisapproahed.
Figure4. Theinstantaneous(t)versuslog(t).Foraperfet
strethedexponentialbehavior the urvesshould be
hori-zontal lines. Theurvesshowthat as weapproahp
the
plateausgetlarger.
In summary, solutions of the master equation
strongly onrm earlier numerial work on random
walkers on the hyperube, but to muh higher
prei-sion[4-7℄.
V Conlusions
Thequestionmayberaisedastowhetherthestrethed
exponential is the true limiting long time relaxation
timerelaxationshouldbedominatedbylarge,ompat,
non-frustrated, isolated lusters of spins for
tempera-turesbelowthe GriÆths transition[10, 18,19℄, but no
numerialevidenehaseverbeenfoundfortheonsetof
thisregime[18,20,21℄. Theprobabilityofenountering
largeunfrustratedlustersinsamplesofthesizes
stud-iednumeriallyanbeestimatedandismirosopially
small;thusanyluster-dominatedregimewould
orre-spondto tinyvaluesofq(t) inhuge samples,and sois
unattainable inpratiefor numerialorexperimental
studies.
Insystems with quenhed-in disordersuh as spin
glasses,simulationsshowthatthereissomespatial
het-erogeneityof relaxationtimes, but that therelaxation
ofindividualspinsisgenerallystronglynon-exponential
[11, 12℄, in agreementwiththe fat that foreah spin
manydierentmodesmaybeontributingtoits
relax-ation, and dierent linear ombinations of relaxation
modesareestablishedfordierentspins,dependingon
initial onditions and on the spatial deloalization of
modes, as shown by the expression for the struture
funtions f
i (
i ;
~
S 0
) in Eq.(14). Inthis sense, loal
re-laxationratesareexpeted tobeheterogeneousandit
may well happen that dierent sites exhibit the most
rapid relaxation at dierent times. In spin-glass
sys-tems, where the probability of large unfrustrated
re-gions is very small, the independent relaxing modes
should notbeexpeted to be loalized, in ontrast to
systems where there are either independent relaxing
lusters or independent hierarhial levels. Hene, in
thepreseneofsomequenhed-instatiinhomogeneity,
heterogeneity an be expeted to be mainly dynami
and the argument for an overall fratal phase spae
topologyleadingtothestrethedexponentialglobal
re-laxationisnotaeted.
In onlusion, using a master equation approah
for random walks on the dilute hyperube, high
pre-ision resultshavebeenobtained ompatible with the
strethed exponentialbeingthe exat funtional form
for thedeayin the limitofinnitely high dimension.
Heterogeneitiesin loal relaxationforms naturally
ap-pear when the autoorrelation funtions are written
in terms of the independent modes of relaxation of
the density funtion dened on the hyperube. The
strethedexponentialappearsasaonsequeneof
fra-tality in a losed spae, both for global and loal
re-laxation funtions: the sum over simple exponentials
yielding astrethed exponential is then also valid for
the loal autoorrelation funtions when the
indepen-dentrelaxationmodesarenotspatially loalized. The
resemblane between the dilute hyperube relaxation
patternandtherelaxationatuallyobservedin
numer-ial studies of spin glasses or experiments on glasses
abovethe freezing temperature strongly suggeststhat
in physial systemsthe independent relaxationmodes
a fratal struture in this temperature range. For
sums suh as those in Eqs.(13) and (15) to give rise
to strethed exponentials,the weightof eah dierent
relaxationtimeomponentmust havesome
harater-istissuh that,forexample,asteepest-desent
alu-lation ofthesesumsyieldsastrethedexponential. As
astrethedexponentialappearsforthehyperubenear
the perolation threshold, as indeed it isexpeted for
randomwalkersoverperolationlustersembeddedon
losedsurfaes,wearguethatthesametypeoftopology
should bepresent in the available regionof Ising
sys-tems phasespaeneartheglass transition,sinethese
systemsalsopresentverysimilarpatternsofrelaxation
in thistemperaturerange.
Aknowledgements
Thisworkhasbeenpartiallysupported byF
renh-Brazilian Cooperation Program CAPES-COFECUB,
and by Brazilian agenies FAPERGS and CNPq. We
thankD. Stauerforvaluablesuggestions.
Referenes
[1℄ R. Kohlraush, Pogg. Ann. Phys. Chem. 91, 179a
(1854).
[2℄ M.D. Donsker and S.R.S. Varadhan, Commun. Pure
Appl.Math.32,721(1979),P.GrassbergerandI.
Pro-aia,J.Chem.Phys.77,6281(1982),J.C. Rasaiah,
J.Zhu,J.B.Hubbard,andR.J.Rubin,J.Chem.Phys.
93,5768(1990).
[3℄ R.G.Palmer,D.L.Stein, E. Abrahams,and P.W.
An-derson,Phys.Rev.Lett.53,958(1984).
[4℄ I.A. Campbell, J. Phys. (Frane) Lett. 46, L1159
(1985).
[5℄ I. A. Campbell, J.M. Flesselles, R. Jullien, and R.
Botet,J.Phys.C:SolidStatePhys.20,L47(1987).
[6℄ I.A.Campbell,Europhys.Lett.21,959(1993).
[7℄ N. Lemke and I. A. Campbell, Physia A 230, 554
(1996).
[8℄ R. M.C. de Almeida, N. Lemke and I. A. Campbell,
EuropeanPhysialJournalB,inpress.
[9℄ J.C.Phillips,Rep.Prog. Phys.59,1133(1996).
[10℄ M.Randeria,J.P.SethnaandR.G.Palmer,Phys.Rev.
Lett.54,1321(1985).
[11℄ T.Komori,K.HukushimaandH.Takayama,J.Phys.
So.Japan64,4418 (1995).
[12℄ S.C.Glotzer,N.Jan,T.Lookman,A.B.MaIssa and
P.H.Poole,Phys.Rev.E57,7350 (1998).
[13℄ R.B.GriÆths,Phys.Rev.Lett.23,17(1969).
[14℄ S.Alexanderand R.Orbah,J.Phys.Lett.43,L625,
(1982),Y.Gefen,A.AharonyandS.Alexander,Phys.
Rev.Lett.,50,77(1983).
[15℄ P.Jund,R.JullienandI.A.Campbell,tobepublished.
[16℄ P.EordosandJ.Spener,Comput.Math.Appl. 5,33
(1979); K.Weber, Elek. Inf.Verarb. Kybern. 22, 601
(1986).
[17℄ A.Bunde,S.Havlin,J.Klafter,G.Gra,andA.
She-hter,Phys.Rev.Lett.78,3338(1998).
[18℄ A.J.Bray,J.Phys.A22,LL81(1989).
[19℄ F.Cesi,C.MaesandF.Martinelli,Comm.Math.Phys.
188,135(1997)and189,323(1997).
[20℄ A.T.Ogielski,Phys.Rev.B32,7384(1985).