and cement pastes

L'objectif principal de cette étude est d'évaluer si l'homogénéisation de supports aléatoires est importante pour comprendre de manière prédictive le comportement mécanique du plâtre pris et de la pâte de ciment. Le chapitre 1 rappelle très brièvement, dans un cadre élastique linéaire, le principe de la méthode de mise à l'échelle que nous avons adoptée : une homogénéisation aléatoire des milieux basée sur le résultat d'inhomogénéité d'Eshelby.

Fig. 1.1 – Différentes échelles caractérisant une structure et son matériau constitutif Dans l’ensemble de ce document, on se place dans le cadre de l’hypothèse des petites pertur-bations [104].

Schéma auto-cohérent avec inhomogénéité sphérique

Mise en œuvre du schéma auto-cohérent
Estimations issues du schéma auto-cohérent
Mise en œuvre d’une méthode d’homogénéisation périodique
Comparaison des résultats d’homogénéisation périodique aux estimations

2.2 – Module d'Young et coefficient de Poisson effectif estimés avec un schéma auto-cohérent (pour différentes valeurs du coefficient de Poissonνs du solide) en fonction de la porosité ϕ. 2.5 – Module de compression effectif versus module de compression solide estimé par diagramme auto-cohérent (courbes) et calculé numériquement (points).

Fig. 2.1 – Problèmes auxiliaires d’élasticité à résoudre pour mettre en œuvre le schéma auto- auto-cohérent envisagé (forme sphérique pour représenter l’espace poreux p et le solide s)

Schéma ac avec inhomogénéité ellipsoïdale de révolution

Mise en œuvre du schéma auto-cohérent
Confrontation numérique (ellipsoïdes allongés)
Porosité critique
Remarque : influence de la forme représentant l’espace poreux

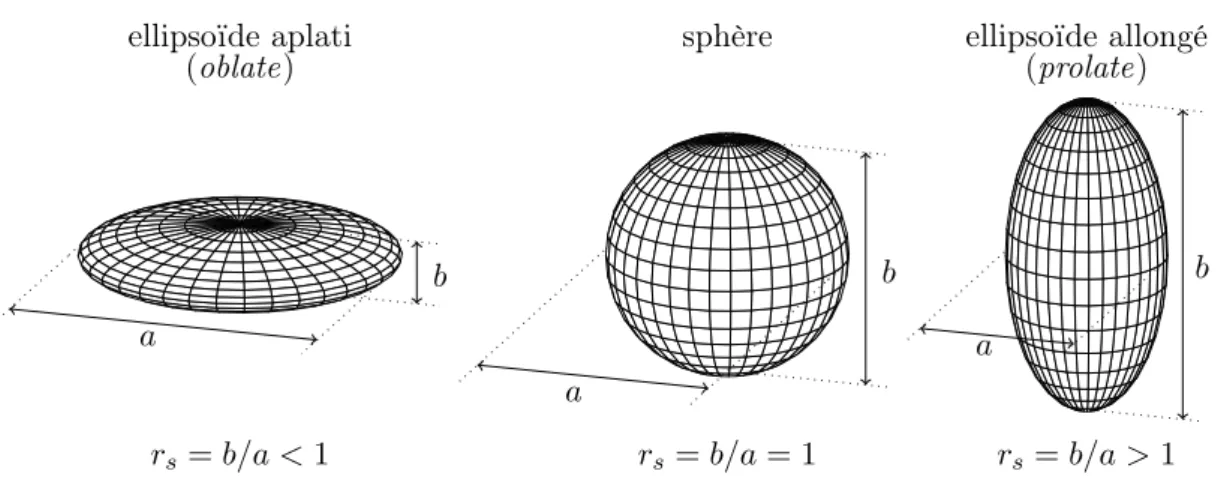
Sur la figure 2.13 nous représentons en traits pleins la variation de la fraction solide critique fsc = 1−ϕc résultant du diagramme auto-cohérent en fonction du rapport d'aspect rs. 2.3 – Porosité critique et coefficient de Poisson associé pour quelques valeurs limites du rapport d'aspect des ellipsoïdes de révolution.

Fig. 2.7 – Définition du rapport d’aspect r s d’un ellipsoïde de révolution et appellation selon la valeur de ce rapport d’aspect

Conclusion

Il suffit de mélanger (mélanger) de la poudre de plâtre et de l'eau pour obtenir, au bout de quelques instants, un matériau solide. Une fois la réaction (3.1) terminée, on a, si la quantité d'eau est suffisante (c'est toujours le cas), du gypse et de l'eau.

Tab. 3.1 – Masse molaire et masse volumique des réactifs et produits de l’équation (3.1) d’hy- d’hy-dratation du plâtre

Description morphologique

Observations

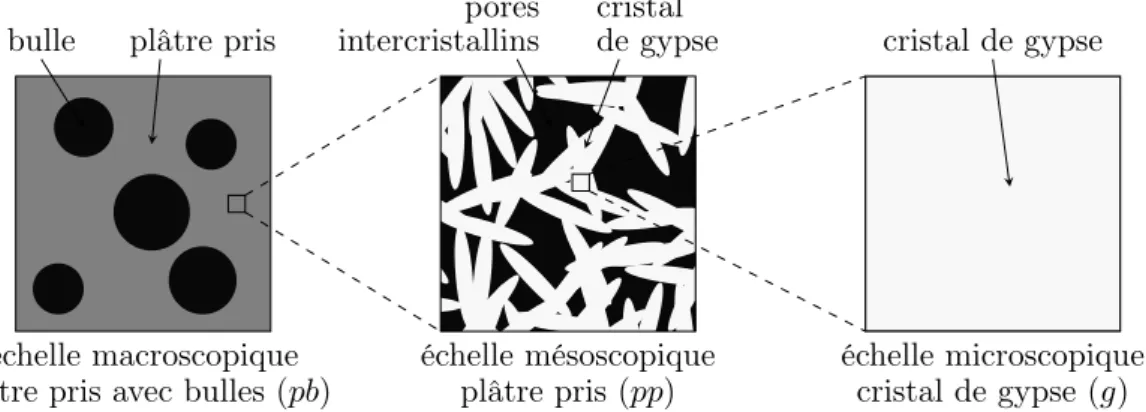
Description morphologique multiéchelle

RÉSUMÉ DES DONNÉES EXPÉRIMENTALES UTILISÉES - La mesure macroscopique est celle du gypse prise avec des bulles (notepéb).

Fig. 3.5 – Photo meb d’un échantillon de plâtre pris issu d’un gâchage avec de l’acide citrique [80]

Synthèse des données expérimentales utilisées

Rigidité du cristal de gypse

Dans le gypse considéré comme un polycristal poreux, chaque grain est en réalité un cristal de gypse. Les composantes non nulles de ce dernier sont incluses dans le tableau 4.1, qui doit être rempli de symétrie (cijkl=cjikl=cijlk=cklij).

Axe du cristal dans la maille élémentaire

RIGIDITÉ DE LA PHASE SOLIDE le maillage de De Jong et Bouman dans le cristal allongé. Meille indique [80] que le cristal de gypse croît préférentiellement dans la direction du réseau de De Jong et Bouman (voir Figure 4.3).

Fig. 4.2 – Représentation schématique des cristaux observés durant leur croissance par Klima [67]

Estimation de la rigidité du plâtre pris

Modèle morphologique

Schéma auto-cohérent

ESTIMATION DE LA RIGIDITÉ DU PLÂTRE IMPRIMÉ estimée par la déformation uniforme d'une cavité sphérique immergée dans le milieu de référence infini, dont l'élasticité est caractérisée par la rigidité recherchée Cpp, et soumise à la déformation homogène auxiliaire E0 à l'infini (figure 4.5 GAUCHE) . La déformation moyenne dans l'ensemble du domaine solide est alors obtenue par moyennage angulaire, la distribution orientationnelle étant isotrope.

Validation expérimentale

Applications

Effet du rapport d’aspect des particules solides

Il a été observé expérimentalement que le rapport d'aspect des cristaux affecte le module d'Young effectif. Tab.4.2 - Influence expérimentale du rapport d'aspect moyen des cristaux sur le module d'Young du plâtre obtenu [80].

Fig. 4.7 – Module de Young estimé par schéma auto-cohérent, selon l’orientation de l’axe des prolates dans la maille de De Jong et Bouman (r g = 15)

Effet des bulles

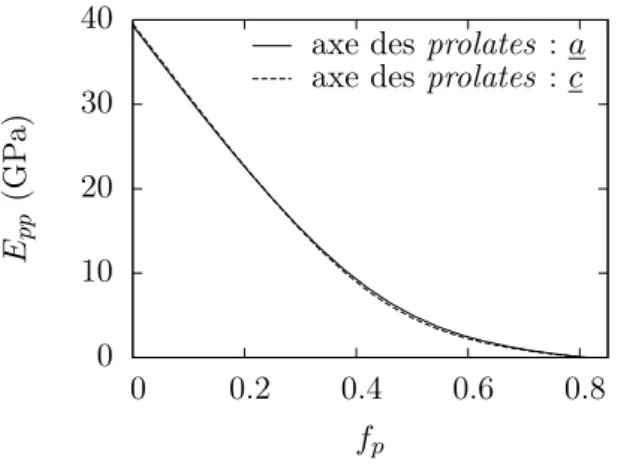
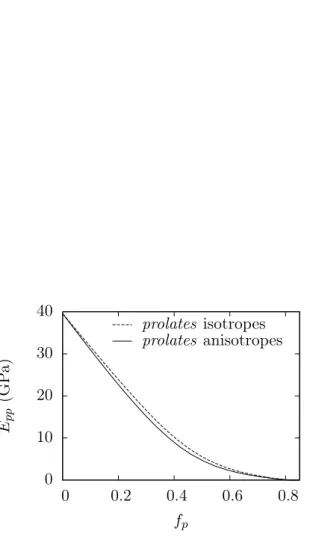
Il convient de noter qu'il n'est pas théoriquement certain que le rapport d'aspect des inhomogénéités du schéma auto-cohérent soit comparable au rapport d'aspect des particules formant la microstructure. Les résultats de la Figure 4.9 à gauche confirment le fait qu'il est préférable de privilégier les bulles (χb élevé) pour optimiser la rigidité effective, à porosité totale ϕ (et donc densité) constante.

Détermination d’une rigidité isotrope équivalente pour le solide

La limite élastique macroscopique est atteinte lorsqu'un des cristaux répond à son critère de fracture. Il s'agirait donc de considérer chaque cristal comme entouré d'une interface imparfaite, c'est-à-dire de supposer l'existence d'une discontinuité de déplacement.

Fig. 4.10 – Module de Young du plâtre pris, obtenu soit à partir d’ellipsoïdes de révolution anisotropes, soit à partir d’ellipsoïdes de révolution isotropes (r g = 15)

Forme du critère macroscopique de limite élastique

Localisation des contraintes en moyenne dans les cristaux

Le tenseur de localisation B dépend de l'orientation des cristaux et, selon l'analyse dimensionnelle, du coefficient de Poisson des cristaux de gypse νg, du rapport d'aspect des cristaux et de la porosité fp. Cg−1 (5.4) Rappelons que le tenseur de rigidité du gypse Cg est désormais considéré comme isotrope (section 4.4).

Cas d’une contrainte macroscopique isotrope

Pour cela, nous proposons de réutiliser l'approche détaillée dans la section 2.2.1, et en particulier (2.12), qui fournit une estimation de la déformation moyenne dans une famille de cristaux d'orientation donnée. Figure 5.3 – La pointe du cône, qui forme un critère macroscopique dépendant de la porosité (νg = 0,34), dans le cas limite des cristaux aciculaires (rg→.

Cas d’une contrainte macroscopique quelconque

Les modules kpp et µpp peuvent être calculés numériquement à partir de kg, µg et fp en résolvant le système d'équations composé de (2.17) et (2.18).

Cas d’un critère local portant seulement sur la traction

Localisation : détermination de σ N
Recherche de l’orientation critique
Détermination du critère macroscopique de limite élastique
Cas de la traction / compression simple

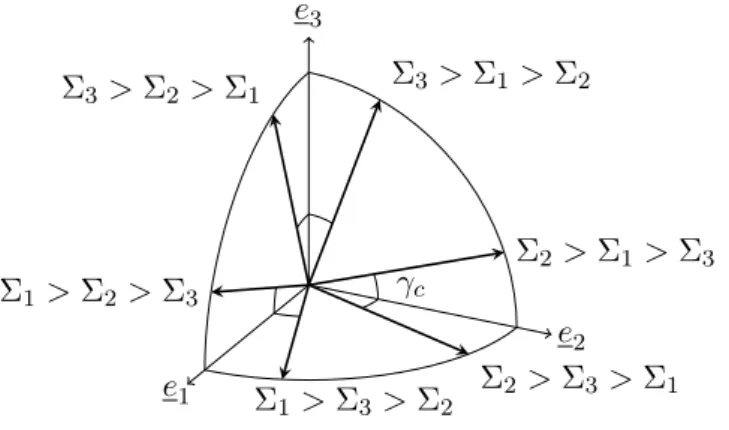
A noter qu'à partir du critère local unidirectionnel σN < σcr (le long de l'axe du cristal) on obtient un critère macroscopique en forme de cône, c'est-à-dire le frottement : le critère dépend de la contrainte moyenne Σm= trΣ/3. Nous avons déjà vu dans la section 5.3.2 que l'orientation de la famille des cristaux critiques (c'est-à-dire les premiers cristaux à atteindre le critère local) dépend de l'état de contrainte macroscopique.

Fig. 5.4 – Axe de la famille des cristaux critiques (représenté par une flèche en trait gras) selon la façon dont s’ordonnent les contraintes principales

Cas du critère local complet

Localisation : détermination de σ T
Recherche de l’orientation critique

La partie droite de la figure 5.14 représente la déformation macroscopique obtenue lorsque la limite élastique est juste atteinte (E33lim = Σlimt /Epp par exemple en traction simple). À forte porosité (fp > 0,6), le cristal critique subit presque uniquement une traction pure : σTcr ≈0.

Fig. 5.10 – Axe du cristal critique (représenté par une flèche en trait gras) selon la façon dont s’ordonnent les contraintes principales

Conclusion

Schéma auto-cohérent utilisé

Contrairement au schéma auto-cohérent décrit dans la section 2.2.1, l'orientation des cristaux n'est plus uniformément distribuée de manière isotrope, mais suit une distribution invariante avec rotation autour de l'axe e3.

Résultats

A partir des résultats tracés dans la partie droite des figures 6.2 et 6.3, nous représentons sur la figure 6.4 l'évolution du module d'Young apparent en fonction de la fraction solide. Lorsque fs = 0,3, on retrouve dans les deux cas une distribution isotrope des cristaux et le module d'Young est de 1,9 GPa.

Fig. 6.2 – Composantes du tenseur de rigidité homogénéisé et module de Young apparent selon e 3 en fonction de θ 0 (E g = 40 GPa, ν g = 0.34, f p 0 = 0.7)

Modélisation d’un essai de traction simple

Définition du chargement imposé

Conformément à l'intuition, c'est lorsque les cristaux sont placés autour de l'axe de contrainte (soit e3) que le module d'Young est le plus élevé (courbe en trait plein sur la figure 6.4). Il faut cependant veiller au fait que le paramètre ρ déterminé par (6.5) n’est pas constant pendant l’essai, car il dépend de l’état d’endommagement de la microstructure.

Repérage du cristal critique

Ainsi, ρ s'apparente davantage à un paramètre subi, à tel point qu'on ne peut en réalité parler que d'un "essai de déformation contrôlé par E33" avec un abus de langage. Cela peut s'expliquer en se référant à un effet Poisson sur l'échelle de l'échantillon, qui conduit à une diminution (puisque νpp>0) de la section efficace de l'échantillon à mesure que E33 augmente.

Détermination du comportement au delà de la limite élastique

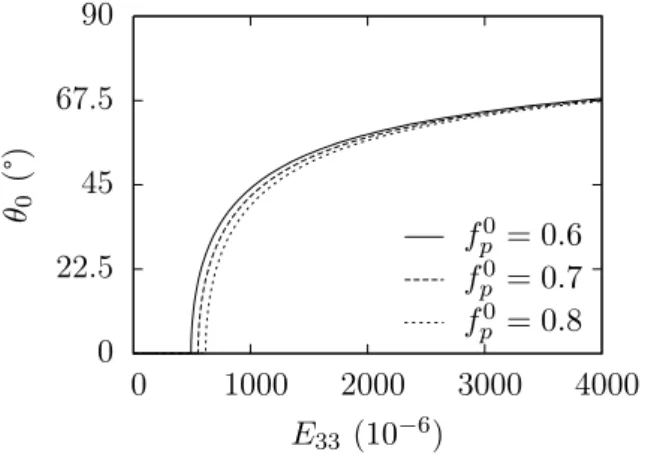
MODÉLISATION D'ESSAI DE TRACTION SIMPLE E33 n'a pas dépassé le seuil de la limite élastique macroscopique, tous les cristaux subsistent et θ0 = 0. La figure 6.8 présente l'évolution de E33, Σ33 et E11 au cours de l'essai de traction. simple traînée modélisée pour une certaine valeur de porosité fp0.

Fig. 6.7 – Loi d’évolution de la variable d’endommagement θ 0 en fonction de la déformation macroscopique (E g = 40 GPa, ν g = 0.34, σ cr = 15 MPa)

Modélisation d’un essai de compression simple

Définition du chargement imposé

Nous n'avons ainsi trouvé dans la littérature que des essais (avec parfois des propositions de modèle comportemental purement macroscopique) sur plâtre fibreux, en traction simple ou en flexion [16, 37]. Ainsi, pour valider l’approche développée ici, il faudrait envisager soit de modéliser un essai de flexion, soit d’incorporer les fibres via une étape d’homogénéisation supplémentaire.

Repérage du cristal critique

Fig.6.10 – Contrainte de traction dans l'axe du cristal d'orientation θ pour certaines valeurs de θ1, et en pointillés la contrainte de traction dans l'axe du cristal d'orientation θ1 pour tout θ1.

Détermination du comportement au delà de la limite élastique

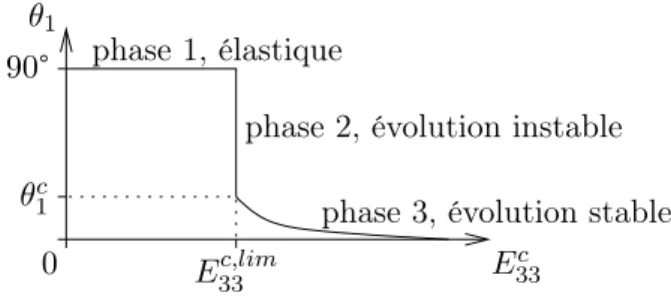
Fig.6.11 – Schématisation de la loi d'évolution de la variable d'endommagement θ1, en fonction de la déformation macroscopique en pression.

Fig. 6.11 – Schématisation de la loi d’évolution de la variable d’endommagement θ 1 , en fonction de la déformation de compression macroscopique

Remarques de conclusion

Description de la réaction

Ainsi, le rapport/c indique le mélange initial de ciment et d'eau, tandis que le degré d'hydratation α indique l'état du matériau. Il est possible de relier le volume des différentes phases au degré d'hydratation : c'est l'objet de la section suivante.

Évolution des fractions volumiques

En dessous (par exemple à e/c = 0,3), l'hydratation s'arrête pour α < 1 en raison de l'épuisement de l'eau : le résidu anhydre. Nous essayons maintenant de prédire l'influence des changements de volume relatif des différentes phases au cours de l'hydratation sur les propriétés mécaniques de la pâte de ciment.

Fig. 7.1 – Répartition volumique de l’anhydre, des hydrates et des pores capillaires estimée par le modèle de Powers, comme fonctions du degré d’hydratation

Morphologie des pâtes de ciment

À l’échelle de la pâte

La fraction solide (anhydre + hydrates) augmente, ce qui signifie que l'on s'attend intuitivement à ce que les propriétés mécaniques de la pâte augmentent avec le temps. Il est donc essentiel de clarifier cela à l'aide d'un modèle qui, à partir des fractions volumiques déterminées ici, évalue les propriétés mécaniques effectives de la pâte.

À l’échelle des c-s-h

Synthèse des données expérimentales utilisées

Élasticité
Résistance
Prise
Fluage

En particulier, du fait de la régression linéaire, il existe des points expérimentaux sur la figure 7.9 qui attestent d'une résistance à la compression non nulle, bien que le degré approximatif d'hydratation de la cure n'ait pas encore été atteint (σc > 0 pour α < αexp0. Les résultats obtenus sont représentés sur la figure 7.10, où la déformation élastique (déformation instantanée ε0 observée au moment du chargement) a été soustraite de la déformation mesurée.

Fig. 7.6 – Module de Young de pâtes de c 3 s mesuré par ultrasons [15]

Première tentative de modèle de pâte de ciment

Modélisation

Cependant, le schéma auto-cohérent avec des formes sphériques fournit une estimation relativement satisfaisante de l'élasticité effective d'un assemblage monodispersé de sphères perméables (au moins en termes de module de compression : voir section 2.1). PREMIÈRE TENTATIVE DE MODÈLE PÂTE DE CIMENT La déformation obtenue dans les phases a et h n'est pas homogène.

Fig. 8.1 – Problèmes auxiliaires d’élasticité à résoudre pour mettre en œuvre le schéma auto- auto-cohérent proposé pour modéliser le mélange anhydre+eau avant hydratation

Résultats

Introduction de deux familles de particules de taille initiale contrastée

Le module d'Young auto-cohérent ainsi obtenu est représenté en fonction de la porosité sur la figure 8.2. Il convient de construire un diagramme d'homogénéisation qui reflète la morphologie ciblée (schématisée sur la figure 8.3).

Modélisation

Observations morphologiques
Modèle morphologique
Modèle micromécanique
Données d’entrée

A l'échelle mésoscopique, on distingue la phase solide des pores des hydrates de haute et basse densité. Cependant, la fraction volumique d'hydrates de haute densité dans la pâte augmente en remplaçant les anhydres.

Fig. 8.10 – Section polie et grille de nano-indentation [22], pour une pâte à e/c = 0.5

Mise en œuvre et confrontation expérimentale

Calibration de la forme des ellipsoïdes des hydrates basse densité

De plus, la porosité critique des hydrates de faible densité est fonction uniquement du rapport d’aspect des plaquettes : ϕc(rsbd) (voir Figure 2.13). Ainsi, le taux d’établissement de l’hydratation dépend très peu du choix de la porosité ϕhd des hydrates de haute densité (partie droite de la figure 8.17).

Évolution du module de Young de la pâte en cours d’hydratation

Comme on pouvait s’y attendre intuitivement, la rigidité de la pâte augmente à mesure que la porosité diminue. 8.19 – Module d'Young estimé des pâtes de ciment sous hydratation, représenté en fonction de la porosité capillaire (à gauche) ou totale (à droite), pour différents /cm compris entre 0,25 et 0,6.

Module de Young de la pâte en fin d’hydratation

Cependant, la seule porosité variable ne permet pas de décrire les propriétés mécaniques d'une pâte de ciment. En particulier, la phase solide (complémentaire des pores) de la pâte n'est généralement pas homogène.

Quelques remarques sur le modèle

Module de Young des hydrates basse densité
Schéma d’homogénéisation alternatif à l’échelle de la pâte
Influence de la forme des particules d’hydrates basse densité
Retour sur la rigidité des briquettes élémentaires
Module de Young de la pâte au très jeune âge

On peut alors se demander quelle influence la forme des particules solides qui composent les hydrates de faible densité a sur le module d'Young de la pâte. La condition (i) (respectivement (ii)) correspond à la partie droite (respectivement gauche) de la courbe présentée sur chaque graphique de la figure 8.30.

Fig. 8.22 – Problème auxiliaire d’élasticité à résoudre pour mettre en œuvre le schéma de Mori Tanaka généralisé proposé comme modèle alternatif de la pâte

Conclusion

Introduction
Homogénéisation linéaire et niveau de déformation moyen des hydrates
Estimation du critère de rupture de la pâte
Application : résistance à la compression simple

132 9.1.2 Homogénéisation linéaire et niveau moyen de déformation des hydrates 1329.1.3 Évaluation du critère de rupture de la pâte. Finalement nous obtenons une relation entre la dérivée de l'énergie élastique et la valeur efficace de la déformation déviatorique dans les hydrates.

Fig. 9.1 – Taille du critère en fonction de la porosité pour des valeurs de χ proches de 1

Limite élastique d’un amas de plaquettes

Critère à l’échelle de la plaquette
Localisation : détermination de σ n ′
Recherche de la famille de plaquettes critiques

Dans le prolongement de ce travail, il faudra passer à une échelle macroscopique pour obtenir une estimation de la limite élastique de la pâte de ciment. Sur le côté droit de la figure 9.13, nous montrons la déformation macroscopique E33, atteinte juste à la limite élastique.

Fig. 9.5 – Plaquette d’axe N , vecteur contrainte sur une facette de normale n ′ et ses composantes normale et tangentielle

Glissement visqueux et raideur normale

Fluage à court terme
Fluage à long terme
Simulation numérique de la déformation de fluage
Effet du rapport d’aspect des particules solides

La pente initiale de l'évolution macroscopique de la déformation par fluage est représentée sur la figure 10.4. La figure 10.10 montre l'évolution de la déformation en fluage sphérique et déviatorique ainsi obtenue pour toute la gamme de porosités.

Fig. 10.4 – Pente initiale de l’évolution de la déformation de fluage Lorsque 2/5 < ϕ < 1/2, on reprend les expressions (B.25) et (B.26) :

Glissement visqueux et raideur isotrope

Fluage à court terme
Fluage à long terme
Simulation numérique de la déformation de fluage
Effet du rapport d’aspect des particules solides

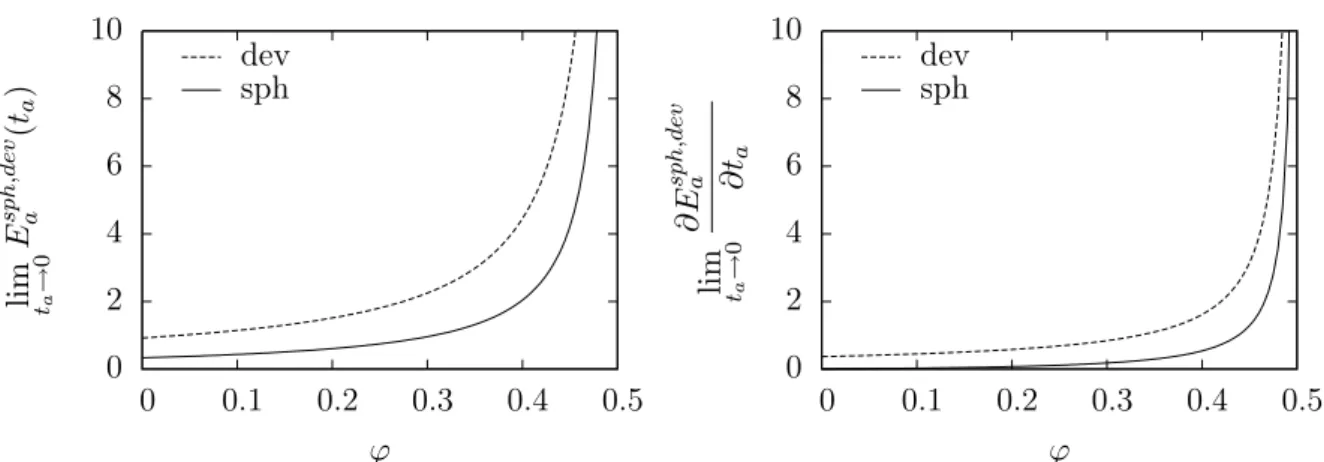
Cependant, l'évolution limitée établie dans la section B.3.2 permettra d'évaluer l'évolution de la déformation en fluage à court (ta → 0) et à long terme (ta → ∞). 10.32) ainsi la déformation de fluage sphérique s'écrit asymptotiquement. La figure 10.13 montre la déformation élastique instantanée et la pente initiale des contraintes de fluage sphérique et déviatorique.

Fig. 10.13 – Déformation élastique et pente initiales de l’évolution de la déformation de fluage (ν s = 0.27)

Estimation du fluage de la pâte

Modèle

Il est montré que les deux seuils évoluent avec le rapport hauteur/largeur des particules solides de la même manière que défini à la section 10.2.4. Pour les rapports d'aspect des particules solides d'hydrates de faible densité, leur porosité à pleine hydratation est toujours inférieure aux deux seuils.

Confrontation expérimentale

10.19 – Fluage compactage simple de la pâte estimé par modèle (sans séparation petits/grands pores capillaires : voir Figure 8.12) pour différentes mesures (d'après [72]). 10.20 – Fluage en compactage simple de la pâte estimé par modèle (avec séparation petits/grands pores capillaires : voir Figure 8.29) pour différents /c et mesuré (d'après [72]).

Fig. 10.18 – Influence du temps caractéristique τ à l’échelle microscopique sur le fluage de la pâte en compression simple (e/c = 0.5, α = α ult )

Questions et perspectives d’amélioration

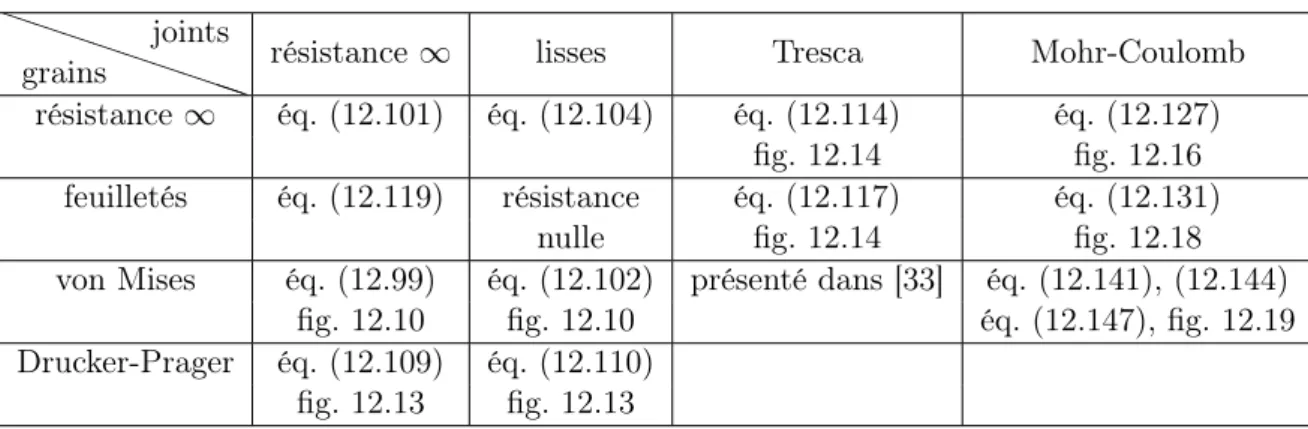
Enfin, dans la troisième étape (Section 12.3), nous déterminons le critère macroscopique de rupture du polycristal poreux. Tab.12.1 - Types de joints solides et intergranulaires abordés dans la section 12.3 de ce chapitre : références à l'équation donnant le critère de rupture macroscopique et une figure illustrant ce dernier.

Préliminaires indépendants de la morphologie

Déformations moyennes en élasticité linéaire

En nous inspirant encore de [68], nous obtenons l'expression microscopique (12.6) de la densité d'énergie élastique par rapport au module d'interface Kt. Comme précédemment, nous déduisons l'expression macroscopique (12.10) de la densité d'énergie élastique, puis nous exploitons le comportement macroscopique (12.5) pour finalement déterminer la moyenne souhaitée.

Critère de rupture macroscopique

Nous décomposons le saut de déplacement à l'interface (normal) en une partie normale et une partie tangentielle (figure 12.2) : JξK=JξnKn+JξtKme JξnK=JξK·n. Le saut effectif du déplacement tangentiel étant asymptotiquement grand, (12.30) et en choisissant (12.31) la déformation déviatorique effective donne

Morphologies envisagées

Lien entre les raideurs d’interface
Estimation de la surface spécifique de contacts
Estimation de moyennes
Grains isotropes et interface non parfaite
Grains isotropes transverses et interface non parfaite

La figure 12.4 montre l'interface réelle, séparant les grains, et l'interface fictive, entourant chaque grain. T ·JξKdS (12.44) Cependant, seule une partie de la périphérie de chaque grain est en contact avec les autres grains.