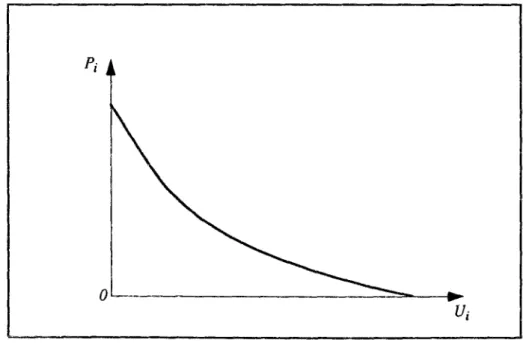
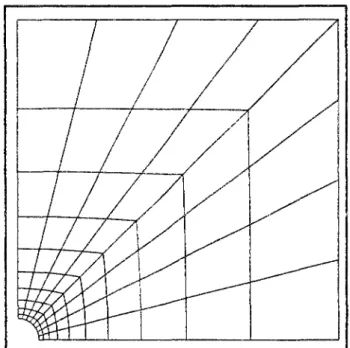
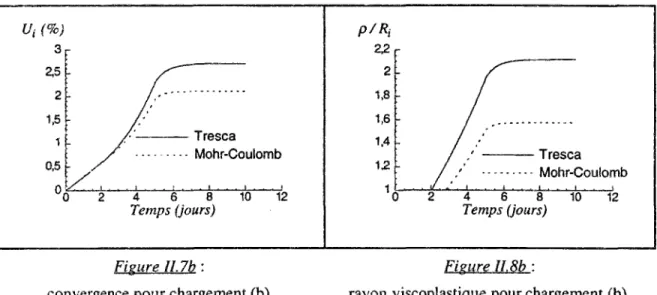
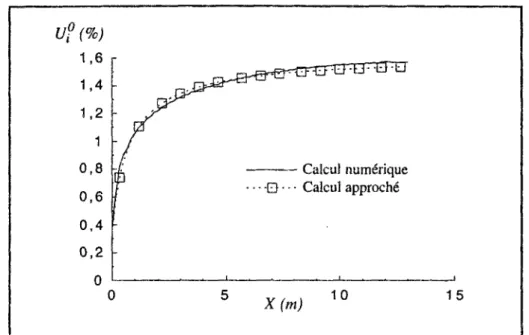
A one-dimensional analytical study reveals the influence of mechanical loading history and hydraulic boundary conditions on the tunnel wall. With the generalization of the fictitious stress, the analytical study allows the localization of the equilibrium point in the plane (convergence of the wall - the stress applied to the wall).
TUNNELS PROFONDS CREUSÉS EN MILIEUX ÉLASTO-VISCOPLASTIQUES
2.2 Justification du choix du modèle 39
3 ÉTUDE ANALYTIQUE 39 3.1 Hypothèses 40
4 ETUDE NUMÉRIQUE 51 5 MÉTHODE SIMPLIFIÉE DE DIMENSIONNEMENT DES TUNNELS EN
MILIEU ÉLASTO-VISCOPLASTIQUE 54
5.1 Tunnel non soutenu 55 5.2 Tunnel soutenu 61
11-6 APPLICATION A L'ÉTUDE D'UN PROBLÈME EN DÉFORMATION
II-6.1 Détermination de la pression fictive en fonction de l'avancement du
TUNNELS PROFONDS CREUSÉS EN MILIEUX POREUX SATURÉS
POREUX SATURES 78 III-2.1 Définition et historique 78
- 2.2 Formulation des équations de la poro-mécanique 79
- 2.3 Cas particuliers 84 3 ÉTUDE NUMÉRIQUE. 86
- 3.1 Méthode des éléments finis pour les problèmes couplés 86
- 3.2 Exemples de calculs numériques ID. 89
- 4.1 Hypothèses 99 4.2 Réponse instantanée 100
- 4.4 Remarques sur les solutions particulières 105 I1I-5 RÉPONSE TRANSITOIRE AU CREUSEMENT D'UN TUNNEL ID EN
106 III-5.1 Résolution des champs de contraintes et déplacement dans poro- III-5.1 Résolution des champs de contraintes et déplacement dans poro-. 111 III-6 RÉPONSE TRANSITOIRE AU CREUSEMENT D'UN TUNNEL ID III-6 RÉPONSE TRANSITOIRE AU CREUSEMENT D'UN TUNNEL ID.
DANS UN MASSIF PORO-PLASTIQUE PARFAIT 115
6.3 Cas où il existe des décharges élastiques 124 6.4 Cas particulier du chargement constant 134
6.7 Validation de l'hypothèse du chargement monotone 142
6.8 Conclusion partielle 143 7 ÉTUDE EN 2D AXISYMÉTRIQUE 145
7.1 Hypothèses 145 7.2 Exemples de calculs numériques 145
7.3 Temps caractéristiques 148 7.4 Détermination de la contrainte fictive de soutènement 149
7.5 Cas du tunnel soutenu 153 8 APPLICATION AU CALCUL 2D EN DÉFORMATION PLANE
8.1 Caractéristiques des sols 159
8.4 Conclusions de l'étude 163
- CONCLUSION 164
CONCLUSION GÉNÉRALE 166
BIBLIOGRAPHIE 168
Annexe A5 : Etude de la configuration ZP-ZD-ZP-ZE 192 Annexe A6 : Tunnel ID creusé en milieu poroplastique Mohr-Coulomb. Résistance simple à la compression du matériau ; Rc = 2Ccosç/(l-sin Certaines hypothèses de ce problème sont assez éloignées de celles envisagées dans la suite de la thèse, mais les études précédentes nous aident dans le choix du taux de déconfinement lors de la pose du soutènement, qui est un paramètre essentiel qui détermine l'équilibre final du tunnel ainsi que ainsi que l'amplitude des tassements de surface. INTRODUCTION ET SYNTHÈSE BIBLIOGRAPHIQUE SUR LES Généralement, à la fin de chaque phase, il y a un renforcement du mur et du plan de travail. Leurs recherches ont abouti à la conception de la nouvelle méthode autrichienne de tunneling (NATM : New Austrian Tunneling Method). Pour une section de tunnel donnée, le paramètre X dépend de la distance x au plan de travail ainsi que de la loi de comportement de la masse. Pj, dans le cas du tunnel non supporté, désigne la pression fictive, et à partir de (i), nous établissons la courbe donnant P¡ en fonction de x. Ceux-ci montrent clairement que la convergence UQ lors de la mise en place du support est affectée par la raideur de ce dernier. La difficulté réside donc dans le choix et la précision de la détermination de la valeur optimale de convergence du réseau avant d'installer le support. La figure II.2b, relative à un essai de fluage sur des bourdons (site de Mol, en Belgique, à environ 250 m de profondeur) montre quelques résultats typiques (Rousset 1988). Cela correspond à une nouvelle phase appelée fluage secondaire, qui conduit à des déformations relativement importantes. Ce modèle peut être généralisé à une échelle tridimensionnelle et l'augmentation du tenseur de déformation totale d'un matériau élasto-viscoplastique est décomposée en. D'après la figure II.3, on voit que les déformations viscoplastiques n'existent que lorsque le coussin est actionné, autrement dit lorsque le critère de plasticité F(o) (plasticité supposée parfaite, i.e. seuil constant du coussin) associé au modèle est atteint. ou dépassé. 2.2 Justification du choix du modèle Tunnels profonds creusés en milieu élasto-viscoplastique. . Modèle Madej) avec une loi de plasticité de type Mohr-Coulomb non couplée, mais ses solutions de contrainte et de déplacement dépendent explicitement du temps pour faciliter l'étalonnage dans les mesures in situ. Nguyen Minh (1986) qui présente des solutions semi-explicites au modèle élasto-viscoplastique de Bingham en relation avec Tresca puis au critère de Mohr-Coulomb avec écrouissage. 3.1 Hypothèses A tout instant, en tout point de la zone élastique, evp ~ 0 et donc èvp = 0 ; notamment à la limite entre les zones viscoplastiques et élastiques au point r-p. Le pic est la pression critique de confinement en dessous de laquelle la zone viscoplastique apparaît sur la paroi. Tandis que la zone viscoplastique apparaîtra instantanément à t~0+ avec un rayon p(t = 0+) calculé à partir de la relation (2.24). Durant cette phase, la convergence sur la paroi est déterminée à partir de la relation (2.24) (figure II.7b). Convergence des parois Ueq à l'équilibre de l'extrémité Y (long terme) pour une section du tunnel éloignée du plan de travail. Ce résultat démontre en effet l'interaction entre la viscosité de la masse et la vitesse de déplacement du plan de travail. Du chapitre précédent nous savons que le point d'équilibre final du tunnel soutenu (Ueq, Peq) dépend également de la vitesse de creusement, mais est situé sur la courbe de terrain U¡ - P¡ du massif élastoplastique. Le point d'équilibre (Ueq, Peq) appartient donc à la partie plastique (non linéaire) de la courbe de terrain P¿ - U¿ (figure 11.18) et donc la valeur de Ueq. Le schéma ci-dessus montre les étapes de résolution du NMI pour le cas d'un tunnel supporté par un milieu élasto-viscoplastique satisfaisant le critère de Tresca. K's<36 : cet intervalle correspond à une très large gamme de supports utilisables dans les tunnels profonds. Les étapes de résolution dans la nouvelle méthode implicite pour le cas d'un matériau de Mohr-Coulomb restent identiques à celles pour le cas d'un matériau de Tresca. Pour un tunnel non étayé, on sait que la convergence des parois (C/,-) dépend entre autres de la distance x au plan de travail. Pour obtenir Pf (x) à partir des courbes de la figure 11.22, il suffit de multiplier l'axe des abscisses par la vitesse de déplacement du plan de travail. Nous avons remarqué qu'à des taux d'excavation élevés (par exemple V > 5R¿ /jours pour l'ensemble de données ci-dessus) lors de la résolution de P¡ (t), des instabilités numériques se produisent à l'approche de la valeur zéro. L'extension de la nouvelle méthode implicite au cas des mesures viscopiastiques permet dans un premier temps d'identifier différents paramètres adimensionnels puis de réaliser facilement une étude de sensibilité à ces paramètres pour un calcul de taille préliminaire. Enfin, l'extension de la nouvelle méthode implicite aux massifs viscopiastiques permet la détermination la plus correcte du degré de déconfinement lors de la pose du support. Les principales variables du problème sont le champ de déplacement u et le champ de pression interstitielle p. Compte tenu des remarques sur les déformations plastiques effectives (voir III-2.2b), nous choisissons de prendre ß = b = 1. Ce résultat montre que la valeur finale de la convergence du mur dépend de l'historique de la charge appliquée. L'influence de la zone plastique sur le champ de pression interstitielle est mieux représentée sur la figure III. En revanche, une fois la vitesse de chargement nulle, l’expansion de la zone plastique s’arrête, indépendamment des conditions aux limites hydrauliques imposées au mur. Tunnels profonds creusés dans des milieux poreux saturés, Une baisse de pression interstitielle est observée dans toute la zone plastique (figure III. 14c). En considérant ici encore les mêmes données que celles utilisées pour l'étude de l'ID numérique (voir III-3.2), nous présentons les graphiques liés à la réponse mécanique en régime hydraulique permanent (figure III. Essayons d'abord de comparer avec les graphiques numériques résultats présentés au paragraphe III-3.2 (tableau III. En tenant compte de la relation (3.45d) dans l'équation de diffusion (3.36), on obtient l'équation de diffusion classique en poroélasticité linéaire. Pour ces deux cas on considère que très loin de la paroi la pression n'est pas perturbée : p(r-*™,t) = pm. L'algorithme de Stehfest nous fournit donc, de manière simple, la solution Ôp(r,t) qui sera insérée dans les relations (3.39) et (3.45a) avec (3.45d) pour établir la solution semi-analytique du problème. de tunneling ID en milieu poroélastique linéaire. Les figures iïï.17 à 01.23 sont obtenues en programmant la solution semi-analytique par rapport au cas où la paroi est drainée par p¡~0,. Jusqu'à présent, dans ce paragraphe III-6, toutes les solutions ont été exprimées en fonction de la pression interstitielle. Ensuite, dans chacun de ces intervalles, nous résolvons le problème semi-analytique en appliquant la transformée de Laplace. Cependant, si a¡(t) est constant (mais supérieur à Dans les zones ZP et ZD, X(r,t) sera ainsi entièrement déterminé de manière semi-analytique (en fonction de la pression interstitielle) à partir de la relation (3.96). Donc là aussi la solution du problème est obtenue dans la configuration ZD-ZE en fonction de la pression interstitielle. Ce cas peut provoquer deux types d'évolution (figure III.25c ou III.25d), principalement en fonction des valeurs des paramètres poro-plastiques et de la vitesse de chargement mécanique. Deux types d'évolutions peuvent être induits (figure III.25e ou III.25f) pour les mêmes raisons que celles évoquées dans le 3ème cas. Nous considérons le cas d'un tunnel profond (voir 1-2) de section circulaire, creusé dans un milieu poro-élastoplastique supposé homogène et dont le comportement est isotrope. Le front de taille du tunnel se déplace à une vitesse constante V et les éventuels points d'appui sont placés à une distance constante d0 de celui-ci. Les figures 111.33 et II.34 représentent respectivement les variations de la convergence et de l'ei de la pression interstitielle sur la paroi du tunnel non étayé, creusé dans un milieu poroélastique linéaire pour différentes vitesses de creusement, en fonction de la distance au plan de travail. Il est important de noter que toutes les courbes ci-dessus (figures 111.33 à 111.36) sont tracées à l'instant correspondant à la fin de la dernière étape de creusement. 7.2b Commentaires Celles-ci, comme leur nom l'indique, ne sont pas réelles, mais reflètent la proximité du visage de l'œuvre dans une représentation 2D en déformation plane ou ID. Par exemple, de la connaissance, même approximative, de U¡(x) on peut déduire l'expression de (x) à partir de la relation reliant U¡ et o¡ dérivée de l'ID analytique de l'étude (cf. II- 6.1 pour une cas de phase viscoplastique par exemple). Pour une section donnée du tunnel non étayé, dans une étude 2D en contrainte plane, si t = 0 définit l'instant de passage du front de taille, à l'instant donné î > 0, la contrainte fictive appliquée au mur est : de ( t) = de (x/V) où V est la vitesse d'avancement du front de taille (figure III.40b). Les expressions pour (x) et (t) (pour une vitesse de creusement donnée) ne sont valables que pour x > 0 et t > 0, c'est-à-dire derrière le front de taille, dans la zone excavée. Nous avons vu que la convergence d'équilibre sur la paroi du tunnel non soutenu, en condition drainée, est indépendante du taux d'excavation de la masse poroélastique linéaire. Ce résultat important peut être généralisé au cas du tunnel soutenu et également aux conditions non drainées. Cela dépend entre autres de la vitesse d’excavation et de la rigidité du support. En effet, quelle que soit la vitesse de creusement, le point d'équilibre appartient à une courbe de terrain fixe. HI-8.2b Calcul du taux de décomposition lors de la mise en place du support (XQ) La figure III.50 montre un schéma du tunnelier à air comprimé. Une partie de la contrainte totale supportée par le support est due à la pression interstitielle existant au voisinage de la structure. Dans la partie excavée, la convergence sur la paroi est indépendante de la vitesse de creusement si la masse reste linéairement poroélastique. En revanche, cette vitesse a une influence significative sur la convergence sur la paroi si la masse est poroplastique. La « nouvelle méthode implicite » de calcul des tunnels dans les environnements élastoplastiques et viscoplastiques. Development and application of a fully coupled two-dimensional finite element approach to borehole deformation and pressure diffusion. An approximate static elastoplastic interface solution for the Galina problem with a cohesive-frictional material. Analyse des contraintes tridimensionnelles de l'interaction en fonction du temps de la roche du tunnel avec son support dans le cadre d'un projet d'excavation rapide. Calcul du soutènement de tunnels circulaires par la méthode convergence-contrainte avec un champ de contraintes initiales anisotrope.INTRODUCTION GÉNÉRALE
OUVRAGES SOUTERRAINS
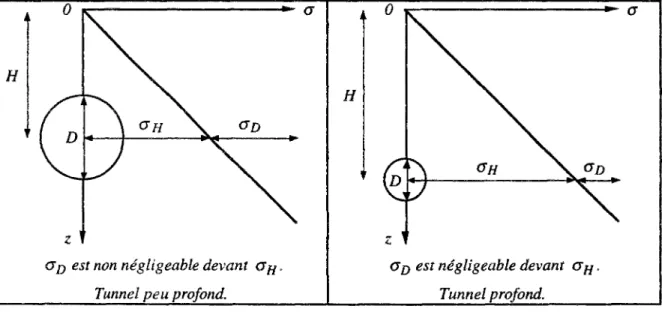
7.1b Taux de déconfinement
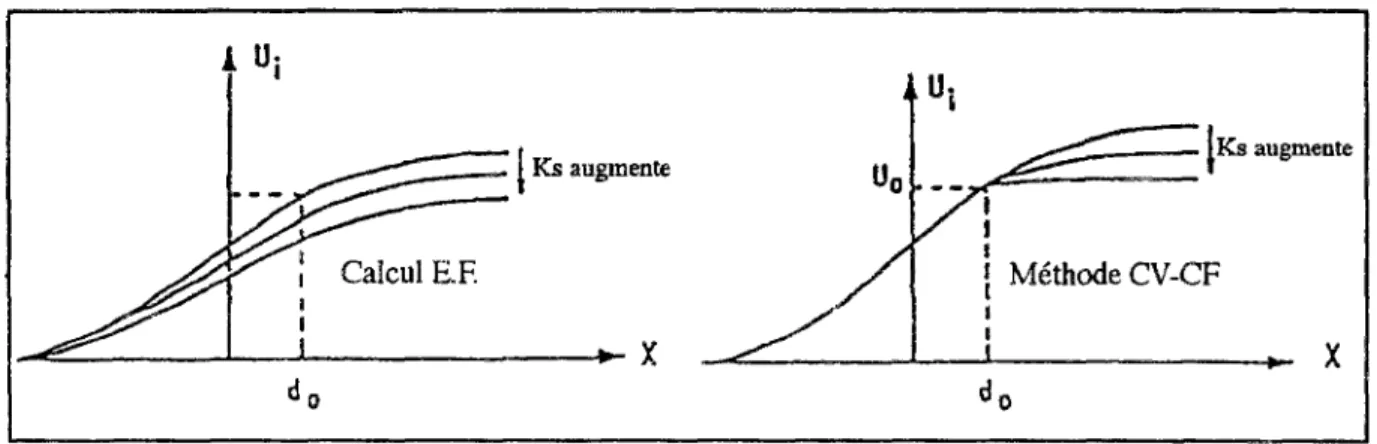
7.1c Courbes caractéristiques du terrain et du soutènement
TUNNELS PROFONDS CREUSES EN MILIEUX ÉLASTO-VISCOPLASTIQUES
1 INTRODUCTION
2.1 Modèle élasto-viscoplastique de Bingham
3.2 Calcul ID
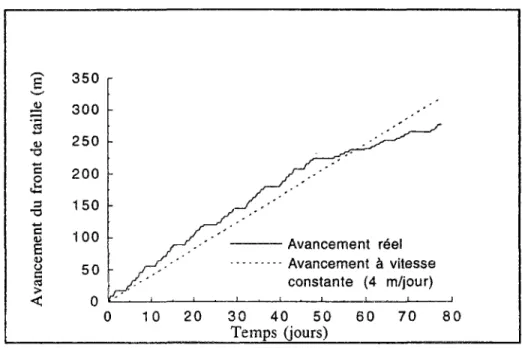
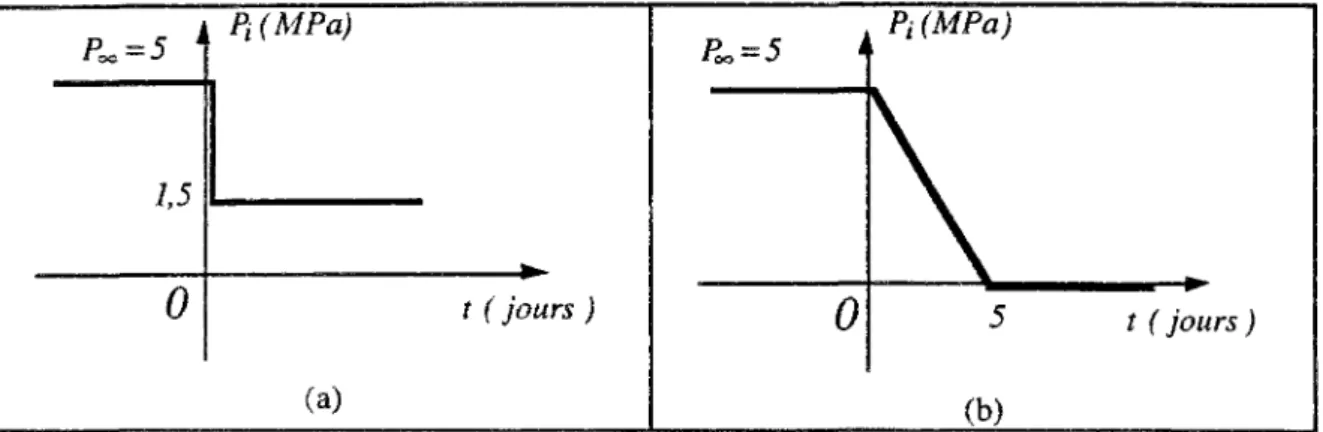
3.3 Exemple d'application

5 MÉTHODE SIMPLIFIÉE DE DIMENSIONNEMENT DES TUNNELS EN MILIEU ÉLASTO-VISCOPLASTIOUE

5.4 Résultats et validation
5.5 Cas d'un critère de Mohr-Coulomb

6.1b Cas d'un matériau de Mohr-Coulomb

6.2 Exemple d'application
TUNNELS PROFONDS CREUSES EN MILIEUX POREUX SATURÉS
3.1 Méthode des éléments finis pour les problèmes couplés
3.2c Conditions aux limites hydrauliques

4 SOLUTIONS ANALYTIQUES ID PARTICULIÈRES

4.3 Réponse sous régime hydraulique permanent (paroi drainante)

5.1 Résolution des champs de contraintes et déplacement en poro-élasticité
5.3 Résolution semi-analytique de l'équation de diffusion

6.2b Calcul du rayon plastique
6.3 Cas où il existe des décharges élastiques
6.3b Etude de l'évolution de 8a configuration ZP-ZD-ZE
6.5 Cas de la paroi imperméable

I I tor *
7 ÉTUDE EN 2D AXISYMÉTRIOUE
7.2 Exemples de calculs numériques

7.4a Cas du massif poro-élastique linéaire
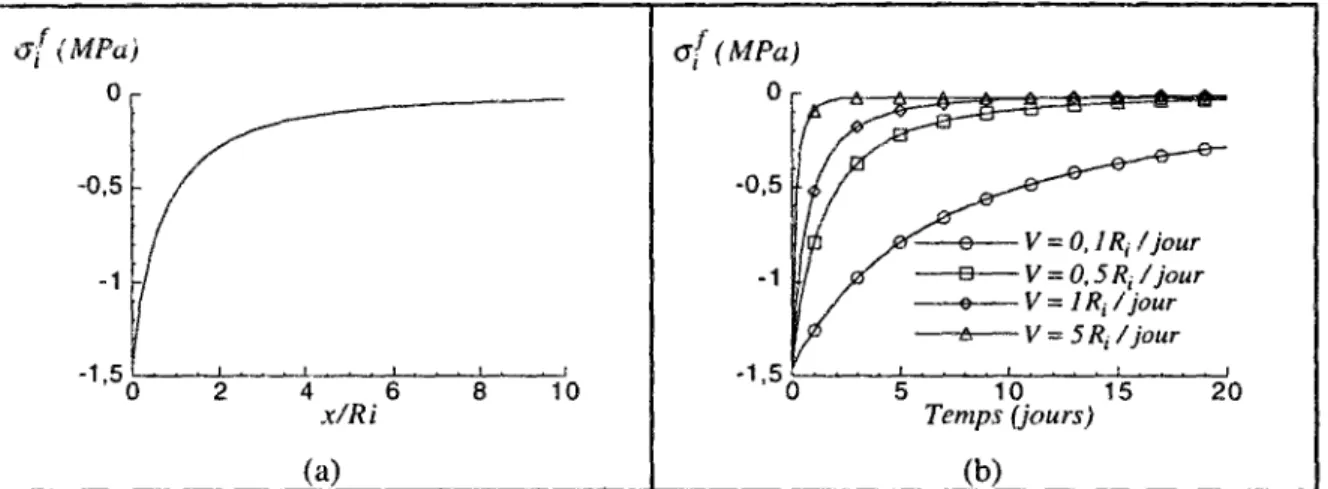
7.5 Cas du tunnel soutenu
7.5b Cas du massif poro-élasto-plastique de Tresca Cas drainé

8 APPLICATION AU CALCUL 2D EN DÉFORMATION PLANE
CONCLUSION GÉNÉRALE
BIBLIOGRAPHIE
Cook J.M., 1994
Dimov I.V., 1994