ANTI-SYNCHRONIZATION OF PAN AND LIU CHAOTIC SYSTEMS BY ACTIVE NONLINEAR CONTROL

(1)

ANTI-SYNCHRONIZATION OF PAN

AND LIU CHAOTIC SYSTEMS BY

ACTIVE NONLINEAR CONTROL

Dr. V. SUNDARAPANDIAN

Professor, Research and Development Centre

Vel Tech Dr. RR & Dr. SR Technical University, Avadi, Chennai-600 062, Tamil Nadu, INDIA sundarvtu@gmail.com

R. KARTHIKEYAN

Research Scholar, School of Electronics and Electrical Engineering Singhania University, Pacheri Bari, Dist. Jhunjhunu, Rajasthan-333 515, INDIA

and

Assistant Professor, Department of Electronics and Instrumentation Engineering

Vel Tech Dr. RR & Dr. SR Technical University, Avadi, Chennai-600 062, Tamil Nadu, INDIA rkarthiekeyan@gmail.com

Abstract :

In this paper, we derive new results for the anti-synchronization of identical Pan chaotic systems (2010), identical Liu chaotic systems (2004) and non-identical Pan and Liu chaotic systems by active nonlinear control. The stability results for the anti-synchronization schemes derived in this paper are established using Lyapunov stability theory. Since the Lyapunov exponents are not required for these calculations, the active nonlinear control method is effective and convenient to achieve anti-synchronization of the chaotic systems addressed in this paper. Numerical simulations are shown to illustrate the effectiveness of the anti-synchronization results derived in this paper for identical and non-identical Pan and Liu chaotic systems.

Keywords: Anti-synchronization, Chaos, Active Nonlinear Control, Pan System, Liu System.

1. Introduction

Chaotic systems are dynamical systems that are highly sensitive to initial conditions. This sensitivity is popularly known as the butterfly effect [1]. Since the pioneering work by Pecora and Carroll ([2], 1990), chaos synchronization problem has been studied extensively and intensively in the literature [2-17]. Chaos theory has been applied to a variety of fields such as physical systems [3], chemical systems [4], ecological systems [5], secure communications [6-8] etc.

In the last two decades, various schemes have been successively applied for chaos synchronization such as PC method [2], OGY method [9], active control [10-12], adaptive control [13-14], time-delay feedback approach [15], backstepping design method [16], sampled-data feedback synchronization method [17], sliding mode control [18], etc. Recently, active control method has been applied to anti-synchronize identical chaotic systems [19-20] and different hyperchaotic systems [21].

In most of the chaos anti-synchronization approaches, the master-slave or drive-response formalism is used. If a particular chaotic system is called the master or drive system and another chaotic system is called the slave or response system, then the goal of anti-synchronization is to use the output of the master system to control the slave system so that the states of the slave system have the same amplitudes but the opposite signs as the states of the master system asymptotically. In other words, anti-synchronization is achieved when the sum of the states of the master and slave systems converge to zero asymptotically with time.

In this paper, we derive new results for the global chaos anti-synchronization of identical Pan chaotic systems (Pan, Xu and Zhou, 2010), identical Liu chaotic systems (Liu et al. 2004) and non-identical Pan and Liu chaotic systems.

(2)

([23], 2004). In Section 5, we discuss the global chaos anti-synchronization of non-identical Pan and Liu chaotic systems. In Section 6, we summarize the main results obtained in this paper.

2. Problem Statement and Our Methodology

In this section, we state the problem statement for global chaos anti-synchronization and our methodology using active nonlinear control and Lyapunov stability theory.

Consider the chaotic system described by

x



=

Ax

+

f x

( )

(1) where

x

∈

_R

nis the state of the system,

A

is the

n n

×

matrix of the system parameters and

f

:

_R

n

→

_R

nis the nonlinear part of the system. We consider the system (1) as the master or drive system.

As the slave or response system, we consider the following chaotic system described by the dynamics

y



=

By

+

g y

( )

+

u

(2) where

y

∈

_R

n is the state of the system,

B

is the

n n

×

matrix of the system parameters,

g

:

_R

n

→

_R

n is the nonlinear part of the system and

u

∈

R

nis the active controller of the slave system.

If

A

=

B

and

f

=

g

,

then

x

and

y

are the states of two identical chaotic systems. If

A

≠

B

and

,

f

≠

g

then

x

and

y

are the states of two different chaotic systems.

For the anti-synchronization of the chaotic systems (1) and (2) using active control, we design a feedback controller

u

,

which anti-synchronizes the states of the master system (1) and the slave system (2) for all initial conditions of the systems.

If we define the anti-synchronization error as

e

= +

y

x

,

(3) then the error dynamics is obtained as

e



=

By

+

Ax

+

g y

( )

+

f x

( )

+

u

(4) Thus, the global chaos anti-synchronization problem is to find a feedback controller

u

such that

lim ( )

0

t→∞

e t

=

for all

(0)

n

e

∈

_R

We assume that the parameters of the master and slave systems are known and that the states of both systems (1) and (2) are available for measurement.

We use Lyapunov stability theory as our methodology. We consider the candidate Lyapunov function defined by

V e

( )

=

e Pe

T

,

where

P

is an

n n

×

positive definite matrix. Note that

V

:

R

n

→

R

is a positive definite function.

If we find a feedback controller

u

such that

V e



( )

=

e Qe

T

,

where

Q

is an

n n

×

negative definite matrix, then

V



:

R

n

→

R

is a negative definite function.

Thus, by Lyapunov stability theory [24], the error dynamics (4) is globally exponentially stable. Hence, the states of the master system (1) and slave system (2) will be globally and exponentially anti-synchronized.

3. Anti-Synchronization of Identical Pan Chaotic Systems

3.1 Theoretical Results

In this section, we derive results for the anti-synchronization of identical Pan chaotic systems ([22], 2010). Thus, the master system is described by the Pan dynamics

1 2 1

2 1 1 3

3 1 2 3

(

)

x

a x

x

cx

x x

x

x x

bx

=

−

=

−

=

−



(5)

(3)

The slave system is also described by the Pan dynamics

1 2 1 1

2 1 1 3 2

3 1 2 3 3

(

)

y

a y

y

u

y

cy

y y

u

y

y y

by

u

=

−

+

=

−

+

=

−

+



(6)

where

y y y

1

,

2

,

3are the states of the system and

u u u

1

,

2

,

3 are the active nonlinear controllers to be designed.

The Pan systems (5) and (6) are chaotic when

a

=

10, 8 / 3

b

=

and

c

=

16.

The chaotic portrait of the Pan system is illustrated in Fig. 1.

Fig. 1 Chaotic Portrait of the Pan System

The anti-synchronization error

e

is defined by

e

_i

=

y

_i

+

x

_i

, (

i

=

1, 2, 3)

(7) The error dynamics is easily obtained as

1 2 1 1

2 1 1 3 1 3 2

3 3 1 2 1 2 3

(

)

e

a e

e

u

e

ce

y y

x x

u

e

be

y y

x x

u

=

−

+

=

−

+

= −

+



(8)

We choose the nonlinear controller

u

defined by

1 2

2 1 2 1 3 1 3

3 1 2 1 2

u

ae

u

ce

e

y y

x x

u

y y

x x

= −

−

+

= −

−

(9)

Substituting (9) into (8), we obtain the linear system

1 1

2 2

3 3

e

ae

e

be

= −



(10)

Next, we consider the candidate Lyapunov function defined by

( )

1

1 (

₁2 ₂2 ₃2

)

2

T

(4)

Clearly,

V

:

R

3

→

R

is a positive definite function. Differentiating

V

along the trajectories of (10), we obtain

V e



( )

= −

ae

12

−

e

22

−

be

32

,

(12)

which is a negative definite function on

_R

3

.

Thus, by Lyapunov Stability Theory [24], the error dynamics (10) is globally exponentially stable. Hence, we have proved the following result.

Theorem 3.1.The identical Pan systems (5) and (6) are globally and exponentially anti-synchronized for any initial conditions with the active nonlinear controller

u

defined by (9).

3.2 Numerical Results

For the numerical simulations, the fourth-order Runge-Kutta method with time-step

h

=

10

−6is used to solve the systems (5) and (6) with the active nonlinear controller

u

given by (9) using MATLAB.

For the Pan systems (5) and (6), the parameter values are taken as those which result in the chaotic behaviour of the systems, viz.

a

=

10, 8 / 3

b

=

and

c

=

16.

The initial values of the master system (5) are taken as

x

₁

(0) 15,

=

x

₂

(0) 12,

=

x

₃

(0)

=

32

The initial values of the slave system (6) are taken as

y

₁

(0)

=

24,

y

₂

(0)

=

20,

y

₃

(0) 16.

=

Fig. 2 depicts the anti-synchronization of the identical Pan chaotic systems (5) and (6).

(5)

4. Anti-Synchronization of Identical Liu Chaotic Systems

In this section, we derive results for the anti-synchronization of identical Liu chaotic systems ([23], 2004). Thus, the master system is described by the Liu dynamics

1 2 1

2 1 1 3

2

3 3 1

(

)

x

x x

x

α

β

γ

δ

=

−

=

−

= −

+



(13)

where

x x x

₁

,

₂

,

₃are the states of the system and

α

>

0, 0,

β

>

γ

>

0, 0

δ

>

are parameters of the system. The slave system is also described by the Liu dynamics

1 2 1 1

2 1 1 3 2

2

3 3 1 3

(

)

y

u

y

y y

u

y

u

α

β

γ

δ

=

−

+

=

−

+

= −

+



(14)

where

y y y

₁

,

₂

,

₃are the states of the system and

u u u

₁

,

₂

,

₃ are the active nonlinear controllers to be designed. The Liu systems (13) and (14) are chaotic when

α

=

10, 40, 2.5

β

=

γ

=

and

δ

=

4.

The chaotic portrait of the Liu system is illustrated in Fig. 3.

Fig. 3 Chaotic Portrait of the Liu System

The anti-synchronization error

e

is defined by

e

_i

=

y

_i

+

x

_i

, (

i

=

1, 2, 3)

(

)

1 2 1 1

2 1 1 3 1 3 2

2 2

3 3 1 1 3

(

)

e

u

e

y y

x x

u

e

y

x

u

α

β

γ

δ

=

−

+

=

−

+

= −

+



(6)

u

defined by

(

)

1 2

2 1 2 1 3 1 3

2 2

3 1 1

u

e

u

e

y y

x x

u

y

x

α

β

δ

= −

−

+

= −

+

(17)

e



₁

= −

α

e e

₁

, ,



₂

= −

e

₂

e



₃

= −

γ

e

₃ (18) Next, we consider the candidate Lyapunov function defined by

( )

1

1 (

₁2 ₂2 ₃2

)

2

T

V e

=

e e

=

e

+

e

+

e

(19)

Clearly,

V

:

R

3

→

R

V

V e



( )

= −

α

e

₁2

−

e

₂2

−

γ

e

₃2

,

(20) which is a negative definite function on

_R

3

.

Theorem 4.1.The identical Liu systems (13) and (14) are globally and exponentially anti-synchronized for any initial conditions with the active nonlinear controller

u

defined by (17).

For the numerical simulations, the fourth-order Runge-Kutta method with time-step

h

=

10

−6is used to solve the systems (13) and (14) with the active nonlinear controller

u

given by (17) using MATLAB.

For the Liu systems (13) and (14), the parameter values are taken as those which result in the chaotic behaviour of the systems, viz.

α

=

10, 40, 2.5

β

=

γ

=

and

δ

=

4. x

₁

(0)

=

8,

x

₂

(0)

=

26,

x

₃

(0) 10

=

and the initial values of the slave system (14) are taken as

y

1

(0) 19,

=

y

2

(0) 10,

=

y

3

(0)

=

30.

Fig. 4 depicts the anti-synchronization of the identical Liu systems (13) and (14).

(7)

5. Anti-Synchronization of Pan and Liu Chaotic Systems

In this section, we derive results for the anti-synchronization of the non-identical Pan chaotic system ([22], 2010) and the Liu chaotic system ([23], 2004). We consider the Pan system (2010) as the master system and the Liu system (2004) as the slave system.

Thus, the master system is described by the Pan dynamics

1 2 1

2 1 1 3

3 1 2 3

(

)

x

a x

x

cx

x x

x

x x

bx

=

−

=

−

=

−



(21)

where

x x x

1

,

2

,

3are the states of the system and

a

>

0,

b

>

0,

c

>

0

are parameters of the system.

The slave system is described by the Liu dynamics

1 2 1 1

2 1 1 3 2

2

3 3 1 3

(

)

y

u

y

y y

u

y

u

α

β

γ

δ

=

−

+

=

−

+

= −

+



(22)

where

y y y

₁

,

₂

,

₃are the states of the system,

α

>

0, 0,

β

>

γ

>

0, 0

δ

>

are parameters of the system and

1

,

2

,

3

u u u

are the active nonlinear controllers to be designed. The anti-synchronization error

e

is defined by

e

_i

=

y

_i

+

x

_i

, (

i

=

1, 2, 3)

1 2 1 2 1 1

2 1 1 1 3 1 3 2

2

3 3 3 1 1 2 3

(

) (

)(

)

(

)

(

)

e

a

x

u

e

c

x

y y

x x

u

e

b x

y

x x

u

α

β

γ

δ

=

−

+

−

+

=

+

−

+

= −

+

−

+



(24)

u

defined by

1 2 2 1

2 1 2 1 1 3 1 3

2

3 3 1 1 2

(

)(

)

(

)

(

)

u

e

a

x

u

e

c

x

y y

x x

u

b x

y

x x

α

β

γ

δ

= −

−

= −

−

+

= −

−

(25)

e



1

= −

α

e e

1

, ,



2

= −

e

2

e



3

= −

γ

e

3 (26)

Next, we consider the candidate Lyapunov function defined by

( )

1

1 (

₁2 ₂2 ₃2

)

2

T

V e

=

e e

=

e

+

e

+

e

(27)

Clearly,

V

:

_R

3

→

_R

V

V e



( )

= −

α

e

₁2

−

e

₂2

−

γ

e

₃2

,

(28) which is a negative definite function on

_R

3

.

Theorem 5.1.The Pan system (21) and the Liu system (22) are globally and exponentially anti-synchronized for any initial conditions with the active nonlinear controller

u

defined by (25).

(8)

For the Pan system (21) and the Liu system (22), the parameter values are taken as those which result in the chaotic behaviour of the systems, viz.

10, 8 / 3,

16, 10, 40, 2.5

a

=

b

=

c

=

α

=

β

=

γ

=

and

δ

=

4. x

₁

(0)

=

24,

x

₂

(0)

=

36,

x

₃

(0)

=

9

and the initial values of the slave system (22) are taken as

y

₁

(0)

=

6,

y

2

(0) 12,

=

y

3

(0)

=

20.

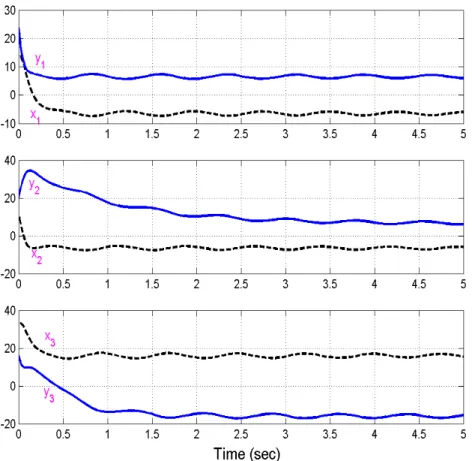
Fig. 5 depicts the anti-synchronization of the non-identical Pan system (21) and the Liu system (22).

Fig. 5 Anti-Synchronization of the Non-Identical Pan and Liu Chaotic Systems

6. Conclusions

In this paper, we have used active nonlinear control to achieve global chaos anti-synchronization for the following 3-dimensional chaotic systems.

(A) Identical Pan chaotic systems (2010) (B) Identical Liu chaotic systems (2004) (C) Non-Identical Pan and Liu chaotic systems.

(9)

References

[1] Alligood, K.T.; Sauer, T.; Yorke, J.A. (1997). Chaos: An Introduction to Dynamical Systems, Springer-Verlag, New York.

[2] Pecora, L.M.; Carroll, T.L. (1990): Synchronization in chaotic systems, Physical Review Letters, 64, pp. 821-824.

[3] Lakshmanan, M.; Murali, K. (1996). Chaos in Nonlinear Oscillators: Controlling and Synchronization, World Scientific, Singapore.

[4] Han, S.K.; Kerrer, C.; Kuramoto, Y. (1995) Dephasing and burstling in coupled neural oscillators, Physical Review Letters, 75, pp.

3190-3193.

[5] Blasius, B.; Huppert, A.; Stone, L. (1999): Complex dynamics and phase synchronization in spatially extended ecological system,

Nature, 399, pp. 354-359.

[6] Cuomo, K.M.; Oppenheim, A.V. (1993): Circuit implementation of synchronized chaos with applications to communications, Physical

Review Letters, 71, pp.65-68.

[7] Kocarev, L.; Parlitz, U. (1995): General approach for chaotic synchronization with applications to communication, Physical Review

Letters, 74, pp. 5028-5030.

[8] Murali, K.; Lakshmanan, M. (2003): Secure communication using a compound signal using sampled-data feedback, Applied

Mathematics and Mechanics, 11, pp. 1309-1315.

[9] Ott, E.; Grebogi, C.; Yorke, J.A. (1990): Controlling chaos, Physical Review Letters, 64, pp. 1196-1199.

[10] Ho, M.C.; Hung, Y.C. (2002): Synchronization of two different chaotic systems using generalized active network, Physics Letters A,

301, pp. 424-428.

[11] Huang, L.; Feng, R.; Wang, M. (2004): Synchronization of chaotic systems via nonlinear control, Physical Letters A, 320, pp.

271-275.

[12] Chen, H.K. (2005): Global chaos synchronization of new chaotic systems via nonlinear control, Chaos, Solitons and Fractals, 23, pp.

1245-1251.

[13] Lu, J.; Wu, X.; Han, X.; Lü, J. (2004): Adaptive feedback synchronization of a unified chaotic system, Physics Letters A, 329, pp.

327-333.

[14] Chen, S.H.; Lü, J. (2002): Synchronization of an uncertain unified system via adaptive control, Chaos, Solitons and Fractals, 14, pp.

643-647.

[15] Park, J.H.; Kwon, O.M. (2003): A novel criterion for delayed feedback control of time-delay chaotic systems, Chaos, Solitons and

Fractals, 17, pp. 709-716.

[16] Wu, X.; Lü, J. (2003): Parameter identification and backstepping control of uncertain Lü system, Chaos, Solitons and Fractals, 18, pp.

721-729.

[17] Zhao, J.; Lu, J. (2008): Using sampled-data feedback control and linear feedback synchronization in a new hyperchaotic system,

Chaos, Solitons and Fractals, 35, pp. 376-382.

[18] Yau, H.T. (2004): Design of adaptive sliding mode controller for chaos synchronization with uncertainties, Chaos, Solitons and

Fractals, 22, pp. 341-347.

[19] Li, G.H. (2005): Synchronization and anti-synchronization of Colpitts oscillators using active control, Chaos, Solitons and Fractals, 26,

87-93.

[20] Hu, J.; Chen, S.; Chen, L. (2005): Adaptive control for anti-synchronization of Chua’s chaotic system, Physical Letters A, 339, pp.

455-460.

[21] Zhang, X.; Zhu, H. (2008): Anti-synchronization of two different hyperchaotic systems via active and adaptive control, International

Journal of Nonlinear Science, 6, pp. 216-223.

[22] Pan, L.; Xu, D.; Zhou, W. (2010): Controlling a novel chaotic attractor using linear feedback, 5, pp. 117-124.

[23] Liu, C.; Liu, T.; Liu, L.; Liu, K (2004): A new chaotic attractor, Chaos, Solitons and Fractals, 22, pp. 1031-1038.