Notas de Aula de Mecˆ

(1)

Jos´e

Soares

Barbosa

Universidade do Estado do Rio de Janeiro

Instituto de F´ısica

Departamento de F´ısica Nuclaer e Altas Energia

(2)

Sum´

ario

1 Problemas sem solu¸c˜ao nos limites da f´ısica cl´assica 2

1.1 Breve hist´orico . . . 2

1.1.1 Radia¸c˜ao de corpo negro . . . 2

1.1.2 Efeito fotoel´etrico . . . 5

1.1.3 Modelos atˆomicos . . . 5

1.2 Novas id´eias de quantiza¸c˜ao . . . 6

2 Estado Quântico 8 2.1 Estrutura formal da mecânica quântica . . . 11

2.1.1 Espa¸co de Hilbert . . . 11

2.1.2 Amplitude transi¸c˜ao e densidade de probabilidade . . . 17

2.1.3 Produto Direto . . . 20

2.2 Comutador Q, P e Operador deslocamento espacial . . . 20

2.2.1 Aplica¸c˜oes . . . 22

2.2.2 Onda plana . . . 23

2.2.3 Fun¸c˜oes de operadores . . . 25

2.3 Princ´ıpio de incerteza e incerteza m´ınima . . . 26

2.3.1 Pacote de incerteza m´ınima . . . 29

3 Dinâmica Quântica: Equa¸cão de Schrödinger 32 3.1 Hipóteses e argumenta¸cão necessária para se chegar a equa¸cão de Schrödinger 32 3.2 Equa¸cão de continuidade e corrente de probabilidade . . . 34

3.3 Equa¸c˜ao de Schr¨odinger independente do tempo . . . 35

3.4 Analogia com os fenˆomenos ondulat´orios . . . 36

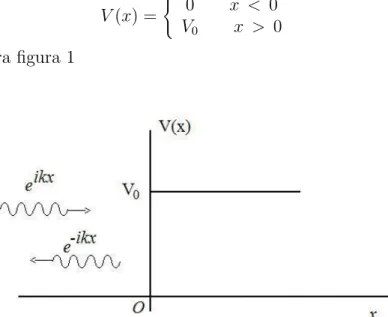
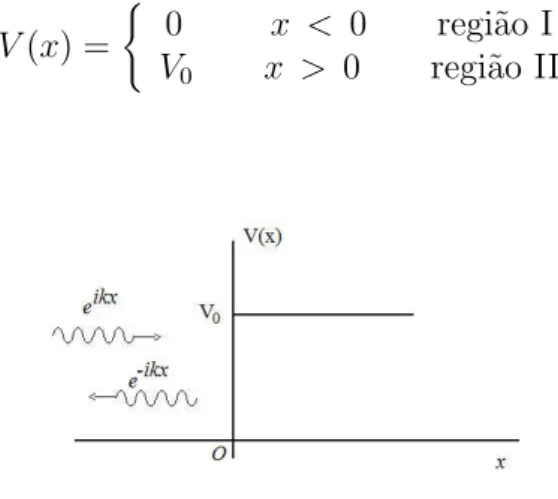
4 Equa¸cão de Schrödinger: aplica¸cões 38 4.1 Solu¸cão da equa¸cão de Schrödinger para um potencial V(x) =V0 . . . 38

4.1.1 Potencial degrau . . . 38

4.1.2 Coeficientes de reflexão e transmissão . . . 40

4.2 Problemas . . . 43

5 Oscilador harmˆonico Linear 48 5.1 operadores de levantamento e abaixamento A e A† _{. . . 48}

5.1.1 Espectro de energia e fun¸c˜ao de onda do oscilador harmˆonico . . . . 52

(3)

5.2.1 Fun¸c˜ao geratriz dos polinˆomios de Hermite . . . 57

5.2.2 Ortogonalidade dos polinˆomios de Hermite . . . 59

6 Operador momento angular 62 6.1 Momento angular em coordenadas esf´ericas . . . 62

6.2 Constru¸c˜ao dos autovetores comuns de r, L2 _e_Lz _{. . . 66}

6.3 Equa¸c˜ao diferencial de legendre . . . 68

6.3.1 Cálculo dos harmônicos esféricos . . . 71

6.3.2 Matrizes de Pauli . . . 78

7 Operadores e a ´algebra de matrizes 82 7.1 Matrizes do hamiltoniano H do oscilador e dos operadores A e A′ _{. . . 83}

7.2 Matrizes: propriedades gerais . . . 84

8 Equa¸cão de Schrödinger: Átomo de hidrogênio 87 9 Matriz de densidade 92 9.1 Equil´ıbrio térmico de um sistema quântico . . . 94

10 Teoria de perturba¸c˜ao 96 10.1 Perturba¸c˜ao independente do tempo . . . 96

10.2 Perturba¸c˜ao dependente do tempo . . . 99

11 Teoria Quˆantica de Espalhamento por um Potencial 103 11.1 Introdu¸c˜ao . . . 103

11.2 Espalhamento por um Potencial . . . 104

11.2.1 Se¸c˜ao de choque diferencial . . . 104

11.3 Espalhamento de Estados Estacionário, Cálculo da se¸cão eficaz . . . 105

11.3.1 Cálculo da se¸cão de choque eficaz a partir das correntes de proba-bilidade . . . 107

11.4 Equa¸c˜ao Integral do Espalhamento . . . 108

11.5 Fun¸c˜ao de Green . . . 110

11.5.1 Aproxima¸c˜ao de Born . . . 111

11.6 se¸c˜ao de choque diferencial de Rutherford . . . 112

11.6.1 Aproxima¸c˜ao de Born para o potencial de Yukawa . . . 112

11.6.2 Densidade estado . . . 114

12 Teoria de relatividade Especial 115 12.1 Introdu¸c˜ao . . . 115

12.2 Princ´ıpios de Relatividade Especial . . . 115

12.2.1 . . . 115

(4)

13 Mecˆanica Quˆantica Relativ´ıstica 116

13.1 Formula¸c˜ao da Teoria Quˆantica Relativ´ıstica . . . 116 13.1.1 Requisitos conceituais . . . 116

(5)

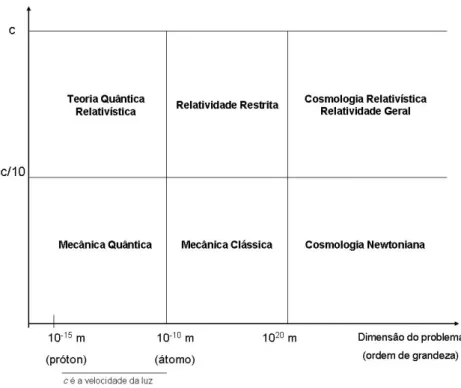
O quadro abaixo ilustra bem os limites de aplica¸cão das Teorias F´ısicas e sua correla¸cão com as dimensões e a velocidade dos objetos estudados.

Figura 1: Quadro geral dos diferentes ramos da f´ısica e seus limites de aplica¸c˜ao

(6)

Cap´ıtulo 1

Problemas sem solu¸c˜

ao nos limites

da f´ısica cl´

assica

1.1 Breve hist´

orico

No final do século XIX e inicio do século XX apesar de f´ısica clássica ter tido grande êxito na solu¸cão da maioria dos problemas –tais como máquinas térmicas e teoria cinética de gases; descri¸cão do movimento dos planetas com a mecânica celeste; unifica¸cão da eletricidade-magnetismo-ótica com as equa¸cões de Maxwell, dando origem a uma nova teoria a eletrodinâmica de Maxwell–, alguns problemas não puderam ser descritos pela f´ısica clássica. aqui neste curso estamos particularmente interessados em três proble-mas, são eles Radia¸cão de corpo negro, Efeito fotoelétrico e Modelos atômicos. A busca de solu¸cão destes problemas serviu de motiva¸cão para o desenvolvimento da Mecânica Quântica não relativ´ıstica. Na próxima se¸cão vamos descrever os três problemas apresen-tando as solu¸cões encontradas na época e apresentamos as novas idéias que surgiram em conseqüência das solu¸cões apresentas por Planck, Einstein e Bohr.

1.1.1 Radia¸c˜

ao de corpo negro

O problema da radia¸cão de corpo negro é um marco histórico das limita¸cões de f´ısica clássica para a descri¸cão microscópica da matéria. As tentativas de compreender o espec-tro da radia¸cão do corpo negro no contexto da f´ısica clássica falharam, então surgiu pela primeira vez a idéia de discretiza¸cão de grandezas tidas como cont´ınuas.

A discussão, pelo menos esquemáticamente desta tentativa, será o ponto de partida para uma breve revisão das origens da Mecânica Quântica.

Nosso trabalho consiste em explicar a distribui¸cão, em fun¸cão da frequência, da inten-sidade do campo de radia¸cão, em equil´ıbrio térmico com um ambiente de temperatura T. Um abordagem desse problema utilizando idéias clássicas foi levada a efeito por Rayleigh

em 1900 e porP. Jeansem 1905, a chave da quest˜ao era introduzir o aspecto estat´ıstico no

(7)

tratamento da dinâmica do campo de radia¸cão, descritos através das equa¸cões deMaxwell. ´

E importante ressaltar que utilizar tratamento estat´ıstico para sistemas de part´ıculas era algo consagrado, afinal de contas a mecânica estat´ıstica estava bem estabelecida. No en-tanto como estender este tratamento para a radia¸cão, se o campo de radia¸cão era uma entidade tão desvinculada do caráter corpuscular? O passo mais fundamental para que se tenha a compreensão do problema, é aquele que permite estabelecer a equivalência es-trutural entre as equa¸cões do campo de radia¸cão e de um sistema dinâmico de part´ıculas. Já que este tipo de racioc´ınio é extremamente fundamental e muito instrutivo, vamos a esta discussão.

O campo de radia¸cão, i. e. o campo eletromagnético, é expresso em termos de um campo vetorial a quatro componentes,

Aµ =_{A0(~r, t), ~A(~r, t)}, (1.1)

a partir do qual podemos expressar o campo el´etrico E~ e o campo magn´etico H~ dados por:

~

E(~r, t) = ₋1

c ∂ ~A

∂t −∇~A0

~

H(~r, t) = _{∇ ×}~ A.~

    

   

(1.2)

Das equa¸cõoes deMaxwell, em uma condi¸cão de gauge apropriada, nos leva a equa¸cão do campo vetorialAµ

1

c2

∂2

∂t2 − ∇ 2

!

Aµ = 0. (1.3)

De um modo geral, o campo de radia¸cão tem seus estados descritos por uma super-posi¸cão de ondas planas de diferentes frequências,

Aµ(~r, t) = 1 (2π)3

Z

aµ,k(t)ei~k·~rd3k, (1.4)

onde aµ,k(t) funcionam como novas variáveis dinâmicas em subistitui¸cão a Aµ. Tudo se passa como se os aµ,k(t) fossem as componentes dos Aµ’s numa base constitu´ıda pelo conjunto de todos as ondas planas, onde cada elemento da base está especificado pelo ´ındice (cont´ınuo) “k”. Tomando o campo expresso em termos destas componentesaµ,k(t),

a equa¸c˜ao de Maxwell (1.3) ﬁca:

1 (2π)3

Z ₁

c2 ¨aµ,k(t) +k

2_aµ,k₍_t₎_ei~k·~r_d3_k _{= 0} _(1.5)

a eq.(1.5) é identicamente nula. Isto será verdade se e somente se o termo entre parênteses for nulo, i. e.

¨

(8)

CAPÍTULO 1. PROBLEMAS SEM SOLUÇ ÃO NOS LIMITES DA FÍSICA CL ÁSSICA4

onde ω =_|k _|c.

A equa¸cão (1.6) mostra que qualquer componente aµ,k do campo de radia¸cão se com-porta como um oscilador harmônico simples. A equivalência entre a equa¸cãoMaxwell e a mecânica clássica agora fica mais n´ıtida, se considerarmos os aµ,k’s como variáveis gene-ralizadas, e que os graus de liberdade do sistema campo se traduzem nas oscila¸cões deste conjunto infinito de osciladores harmônicos clássicos. Assim sendo a dinâmica do campo fica expressa numa liguagem mecânica, permitindo a utiliza¸cão da mecânica estat´ıstica.

Neste sentido, o equil´ıbrio térmico do campo com o ambiente a temperaturaT pode ser tratado como o equil´ıbrio de um sistema de osciladores em contato com um reservatório térmico à temperatura T.

A equiparti¸cão da energia é o ingrediente adicional para o cálculo da distribui¸cão de intensidade do campo de radia¸cão, com base nesta equivalência, a expressão para a densidade de energia por intervalo de frequência assim obtida é conhecida por fórmula de

Rayleigh – Jeans;

du(ν)

dν =

8πKT c3 ν

2_. _(1.7)

Com tudo persiste ainda uma incompatibilidade com os dados experimentais, o fato é que a eq. (1.7) só consegue reproduzir as medidas na região de baixa frequência. Alêm disso, a energia total do campo, desse modo calculada será infinita, resultado inaceitável fisicamente. Portanto, existe algo de errado na expressão obtida porRayleigh – Jeans.

No final do ano 1900M. Planck apresentou uma proposta consideravelmente arrojada para resolver esse desacordo entre as predi¸cões Teóricas e os resultados Experimentais. No cálculo da fun¸cão de parti¸cão de “osciladores” harmônicos do campo com uma dada frequência, aparece uma integral sobre a configura¸cão inicial do oscilador, no espa¸co de fase. Ao realizar o cálculo desta integral Planck introduziu uma célula unitária para o espa¸co de fase do oscilador. Em outras palavras ao invés de realizar a integra¸cão sobre uma energia cont´ınua dos osciladores, a substituiu por um somatório sobre valores discretos de energia em intervalos ∆E

Z

dE _→ n

X

i=1

∆Ei

Planck mostrou que as diﬁculdades s˜ao eliminadas quando se escolhe

∆E =hν = ¯hω, sendo ¯h= h 2π

onde ω é a freqüencia do oscilador e ¯h é uma constante universal, chamada de constante

Planck

¯

h= 1,054_×10−27ergs˙

(9)

A f´ormula obtida porPlanckpara a densidadeu(ν) de energia por intervalo de freq¨ uen-cia ´e:

u(ν) = 16π

2_h_¯

c3

ν3

eKThν −1

. (1.8)

Se ν2 _≪ _ν_, _⇒ _eh ν

KT = 1 + h ν

KT +O

(h ν KT)

2 _≃ _{1 +} h ν

KT. E facil veriﬁcar que a eq.(1.8)´

tem a eq.(1.7) como limite

1.1.2 Efeito fotoel´

etrico

A manifesta¸cão de natureza corpuscular foi observada por Lenard, que observou que a energia cinética do elétron emitido por efeito fotoelétrico não depende da intensidade da luz incidente, mas sim apenas de sua freqüencia. Este fato foi explicado por Einstein em 1905, utilizando o conceito de quanta de radia¸cão de Planck. A conserva¸cão da energia estabelece que a energia cinética do elétron,Ee:

Ee =Eγ₋V (1.9)

sendoEγ a energia da radia¸cão incidente eV a energia necessária para arrancar o elétron do metal. Se há absor¸cão de “um”quantum de luz com energia ¯hω, a energia cinética do elétron será dada por:

Ee= ¯hω₋V. (1.10)

Desta maneira, a razão por que a energia do elétron não depende da intensidade da luz, mas sim depende apenas da freqüencia, ficava completamente esclarecida. Um aumento da intensidade da luz acarretaria apenas num aumento do número de elétrons que são ejetados do metal.

Comparando a eq.(1.10) com dados experimentais do efeito fotoel´etrico, veriﬁcou-se que o valor da constante ¯h coincidia com aquele que Planck havia estabelecido.

Posteriormente, em 1923, foi verificado que um quantum de luz comporta-se exata-mente como uma part´ıcula de energia ¯hω e de momento linear ¯hk, através da esperiência deCompton.

1.1.3 Modelos atˆ

omicos

O in´ıcio do nosso século também é marcado pela preocupa¸cão direta com a estrutura do átomo, tido como constituinte fundamental da matéria, dentre os vários trabalhos sobre o modelo atômico, destacamos os deRutherfordeBohr, o modelo deRutherfordapresentava uma falha com a experiência neste modelo o átomo era instável.

Em 1913N. Bohrlan¸cou uma proposta de quantiza¸cão do momento angular das órbitas dos elétrons, que combinado com a idéia do quantum de luz dePlanck, reproduzia a natu-reza discreta dos expectros atômicos. Da quantiza¸cão do momento angular, a conseqüência imediata era a quantiza¸cão da energia do sistema, permitindo-lhes apenas certos valores de energia,

En,ℓ =₋ mz

2_e4

(10)

CAPÍTULO 1. PROBLEMAS SEM SOLUÇ ÃO NOS LIMITES DA FÍSICA CL ÁSSICA6

O modelo atômico de Bohr, postulando a quantiza¸cão do momento angular, é confir-mado por Franck e Hertz em 1914 através do espalhamento de elétrons por átomos de mercúrio. O resultado experimental evidenciava a estrutura de n´ıveis discretos de energia. Apesar do sucesso fenomenológico e seu papel histórico, importante para indicar ca-minho da f´ısica, a velha mecânica quântica além de apresentar limita¸cões em sua aplica-bilidade, as regras de quantiza¸cão eram postas a “mão”numa estrutura clássica.

1.2 Novas id´

eias de quantiza¸c˜

ao

A década seguinte presencia o lan¸camento da idéia mais fundamental da atual formula¸cão da mecânica quântica. preocupado ainda com a dualidade onda-part´ıcula do campo eletro-magnético, de Broglie, em sua tese de doutorado, em 1924, lan¸cou uma proposta simples mas extremamente importante;

Se a radia¸c˜ao apresenta um carater dual estando associado a um “quantum”de momento e energia dados por

p= ¯hk E = ¯hω. (1.12)

Por que então uma part´ıcula, como por exemplo o elétron, não estaria associada a uma onda? Se for o caso, por simetria, esta onda deveria caracterizar-se por vetor de onda k e freqüência ω dados por

k = p ¯

h ω =

E

¯

h. (1.13)

Com esta associa¸cão de Brogliemostrou que a quantiza¸cão deBohrnada mais era que a condi¸cão de estacionariedade de uma onda num potencial esférico. Esta previsão de um comportamento ondulatório de part´ıcula só vai encontrar uma comprova¸cão experimental três anos depois, com a difra¸cão de elétrons num metal, através das experiências de

Davisson eGermer (1927).

Ainda em 1924, Heisemberg, analisando o mecanismo de emissão de radia¸cão dos átomos, no esquema da velha mecânica quântica, concluiu que uma formula¸cão autocon-sistente era obtida se as grandezas f´ısicas fossem representadas por matrizes. segundo ele, os valores medidos destas grandezas corresponderiam aos autovalores das matrizes que as representavam.

Seguindo outro caminho Schrödinger, em 1926, obtém a equa¸cão da onda, para a onda associada a uma part´ıcula, sugerida por de Broglie. As duas teorias apesar de tão diferenciadas em aparências, se mostraram igualmente capazes de calcular os espectros atômicos.

Na verdade, a posteriori, foi mostrada a completa equivalência das mesmas, através dos trabalhos do próprioSchrödinger, Dirac, Jordane outros, que estabeleceram a formula¸cão elegante da atual Mecânica Quântica.

(11)

(12)

Cap´ıtulo 2

Estado Quˆ

antico

Procuramos aqui, dentro de uma linguagem menos formal conceituar algumas carac-ter´ısticas de estado quântico de um sistema, que é o elemento fundamental para a estrutura da mecânica quântica. Consideremos para este fim, o sistema mais simples: Uma part´ıcula livre, sem grau de liberdade interno, descrevendo um movimento unidimensional.

No tratamento clássico, utiliza-se a variável de posi¸cãoq e o momento linear p para a descri¸cão da dinâmica da part´ıcula. Os valores assumidos por estas grandezas, i. e. dois

números reais, especificam completamente o estado de uma part´ıcula num dado instante de tempo. Um outro ponto que vale apena lembrar é que, na Mecânica Clássica supõe-se implicitamente que estas grandezas podem supõe-ser medidas, em principio, com precisão ilimitada, abstraindo-se a natureza do aparato de medida utilizado. O fato novo dos fenômenos quânticos é que, em contraste com a mecânica clássica, a medi¸cão é capaz de alterar profundamente o estado da part´ıcula. Não há, em principio, meios de observar o estado da part´ıcula sem perturba-lo. Sendo assim, um valor de q obtido após uma medida indica apenas um resultado da intera¸cão entre a part´ıcula e o sistema de medi¸cão, o material de um detector. Em outras palavras, este valor não necessáriamente carrega informa¸cões diretas sobre o estado da part´ıcula “antes” da medi¸cão. Se um valor, digamos

q1é obtido numa medi¸cão da posi¸cão, a única afirma¸cão que pode-se fazer é que a part´ıcula

foi ali observada “depois”da medida, a nada mais. Neste sentido, podemos notar que não há condi¸cão de determinar o momento linear p da part´ıcula através de medidas de suas posi¸cões sucessivas no tempo. Pois, para isto, precisaria-mos realizar medidas de posi¸c oes em pontos infinitesimalmente próximos, sem alterar a dinâmica da part´ıcula, isto é imposs´ıvel na mecânica quântica.

Por outro lado, suponha que numa medida de momento linear, encontramos o valor

p. Neste caso, segundo de Broglie, o estado da part´ıcula é caracterizado por uma onda planaexp_{ipq/¯h_}que se distribui no espa¸co inteiro, deixando em aberto a localiza¸cão da part´ıcula. Isto significa que a medi¸cão do momentum perturba o estado da part´ıcula e nada podemos saber sobre sua localiza¸cão prévia.

Sendo assim, se o processo de medi¸cão interfere e modifica da maneira imprevis´ıvel, as informa¸cões sobre o estado, como podemos descrever a dinâmica de uma part´ıcula? De

(13)

fato, no mundo microscópico, o processo de medida envolve uma intera¸c ao incontrolável entre o objeto e o instrumento de medida. Entretanto, as medi¸cões de um fenômeno quântico demonstram que é poss´ıvel tratar a dinâmica da part´ıcula dentro de um contexto probabil´ıstico. Para melhor situar a questão, consideremos a experiência de dupla fenda. Seja por exemplo, a montagem (ver fig. abaixo) onde A e B são duas fendas no anteparo

Figura 2.1: nesta figura há 3 configura¸cões: em (a) temos as fendas A aberta e B fechada, em (b) a situa¸cão é simétrica, na configura¸cão (c) ambas fendas estão abertas

se elétrons incidir, um a um, sobre o lado esquerdo do dispositivo, sendo detectados pela chapa de emulsão. Quando um só elétron é lan¸cado através das fendas, também ob-servamos uma única marca “ponteforme”na chapa. Nunca um fracionamento do elétron, nem mesmo um padrão de distibui¸cão sobre a chapa. Este fato representa nitidamente a natureza corpuscular do elétron. Entretanto, a marca deixada por um elétron, dificil-mente será reproduzida nos próximos lan¸camentos. Um outro elétron mesmo lan¸cado em condi¸cões idênticas será observado possivelmente em outra posi¸cão. Neste sentido é que a observa¸cão da posi¸cão q em cada lan¸camento é imprevis´ıvel. Em compensa¸cão, se levan-tarmos um histograma da freqüência das diferentes posi¸cões das marcas de milhares de lan¸camentos, encontramos uma distribui¸cão PA+B(q) como mostra figura (2.1). Esta

dis-tribui¸cão não depende da maneira de detectar a part´ıcula, ou seja independe do detector. Assim sendo esta distribui¸cão não deve ser associada ao processo de medida em si, mas sim, ao estado intr´ınseco da part´ıcula diante do arranjo experimental, antes mesmo da sua deteçcão. Apesar do carater imprevis´ıvel do resultado de cada medi¸cão, um conjunto de muitas medidas caracteriza a natureza do estado.

(14)

CAP´ITULO 2. ESTADO QU ˆANTICO 10

um carater probabil´ıstico ao próprio ao conceito de “estado”que é definido indepente da observa¸cão da part´ıcula. Tentaremos então, especificar o estado de uma part´ıcula por uma fun¸cão de distribui¸cão de probabilidadeP(q), que parece ser capaz de representar o “estado”da part´ıcula.

Mas especificar o estado de uma part´ıcula em termos de uma fun¸cão de distribui¸cão probabilidade não é satisfatório, em contraste ao que acontece na mecânica estat´ıstica. Veja a seqüência de experiências

Na primeira experiência fecha-se a fenda B com A aberta obtém-se a fun¸cão PA(q) depois, fecha-se A e abre B, obtém-se PB(q) a superposi¸cão destes dois resultados não coincide com aquele obtido quando as duas fendas estão abertas, PA+B(q) isto é,

PA(q) +PB(q)₆=PA+B(q)

Isto significa que quando ambas as fendas estão abertas, as duas ifluenciam no es-tado da part´ıcula simultaneamente! Além disto, a compara¸cão de PA(q) +PB(q) com PA+B(q) permite concluir que existe um processo t´ıpico de interferência ondulatória na

superposi¸cão de estados. Para resolver a questão desta interferência devemos introduzir fun¸cões complexas, Ψ(q) para representar o estado de uma part´ıcula de tal modo que

PA(q) =|ΨA(q)|2 PB(q) =|ΨB(q)|2

PA+B(q) =|ΨA+B(q)|2 .

Fa¸camos agora uma série de experiências medindo o momentopda part´ıcula na dire¸cão

q. Estas experiências forneceram as distribui¸cões de probabilidades, ou as amplitudes, em rela¸cão aos momentos.

Sejam ΦA(p), ΦB(p) e ΦA+B(p) as amplitudes correspondentes as experiˆencias com

somente a fenda A aberta, com somente a fenda B aberta e com ambas as fendas A

abertas respectivamente. Também neste caso, verificaremos que as amplitudes em p são complexas e satisfazem a superposi¸cão

ΦA+B(p) = ΦA(p) + ΦB(p).

Analisando as fun¸cões Ψ(q) e Φ(p) encontramos uma rela¸cão entre as elas Φ(p) nada mais é que a transformada de Fourier da correspondente Ψ(q) i. e.

Φ(p) = √1 2π¯h

Z

dqΨ(q)e−ipq/¯h

ou de modo inverso

Ψ(p) = √1 2π¯h

Z

dpΦ(p)eipq/¯h.

(15)

A universalidade da rela¸cão entre as amplitudes em rela¸cão a q e em rela¸cão a p, mostra que a medida depnão traz nenhuma informa¸cão f´ısica nova sobre o estado, todas as informa¸cões obtidas já estavam contidas em Ψ(q).E representar o estado da part´ıculas em termos da amplitude em rela¸cão a q oup seriam procedimentos equivalentes.

O fato de que Ψ(q) e Φ(p) são equivalentes para a descri¸cão de um estado quântico, sugere a idéia da que deve existir uma ûnica entidade capaz de especificar o estado, do qual Ψ(q) e Φ(p) são apenas duas diferentes reprenta¸cões desta entidade, de acordo com a o processo de observa¸cão. A existência de uma tal entidade constitui o pressuposto básico para a conceitua¸cão do “estado quântico”de um sistema. Assim é extremamente impor-tante encontrar um objeto matemático para que possamos associa-lo ao estado quântico e a partir deste desenvolver estrutura matemática da mecânica quântica.

2.1 Estrutura formal da mecˆ

anica quˆ

antica

Na se¸cão anterior, introduzimos a idéia de representar o estado quântico de um sistema por um vetor de um espa¸co vetorial linear abstrato, onde o princ´ıpio de Superposi¸cão fica automaticamente incorporado. As variáveis dinâmicas foram introduzidas como sendo operadores lineares que atuam sobre este espa¸co. Os autovalores destes operadores cor-respondem aos valores encontrados nas medidas destas variáveis.

2.1.1 Espa¸co de Hilbert

Antes de apresentar a estrutura formal da Mecânica Quântica é preciso definir, primeiro, o Espa¸co de Hilbert (_H), isto por que, todas as grandezas da mecânica quântica são definidas a partir de objetos do espa¸co _H. Espa¸co de Hilbert: O Espa¸co de Hilbert é um espa¸co vetorial linear de dimensão infinita e de quadrados integráveis, isto é, apesar de o espa¸co ser de dimensão infinita, as integrais quadráticas dos objetos deste espa¸co são finitas.

Agora vamos apresentar os conceitos básicos da mecânica quântica numa linguagem matemática mais rigorosa. Para isso, vamos enunciar alguns postulados:

Postulado I:

Os estados de um sistema quântico são representados por vetores do espa¸co Hilbert _H, de corpo complexo, _C. A correspondência é tal que dois vetores linearmente dependente represente o mesmo estado.

Denota-se por _| Ψ_i o vetor de _H correspondente a um dado estado quˆantico. Em H, deve ser deﬁnido o produto interno (produto escalar) entre dois vetores _| Ψ_i e _| φ_i, denotado por _hφ_|Ψ_i, que satisfaz as seguintes propriedades:

i) _hφ _|Ψ_i=_hΨ_|φ_i∗

ii) _hΨ_|Ψ_{i ≥}0

iii) Se _hΨ_|Ψ_i= 0 ent˜ao _|Ψ_i= 0

iv) _∀ x, y _{∈ C} vale propriedade _hφ_{| {}x_|Ψ_i+y_|ϕ_i}=x_hφ_|Ψ_i+y_hφ _|ϕ_i.

    

   

(16)

A propriedade iv) indica a linearidade da opera¸c˜ao de produto escalar.

A opera¸cão de produto escalar de_|Ψ_icom qualquer vetor_|φ_{i ∈ H}, com_|Ψ_ivarrendo todo o espa¸co_H, forma um novo espa¸co vetorial. Este por sua vez, é chamado de espa¸co dual de _H que aqui denotaremos por _H†. Por constru¸cão, para cada vetor de _H, _| Ψ_i, existe o seu dual, _|Ψ_i†_{, que denotaremos por} _h_Ψ_|_{, ou seja}

∀ |Ψ_{i ∈ H},

∃ hΨ_{| ≡ |}Ψ_i†_{∈ H}†_.

)

(2.2)

Desta maneira fica definida a opera¸cão de conjuga¸cão, “_†”, para os vetores _| Ψ_i. A opera¸cão de conjuga¸cão para os vetores_hΨ_|é tal que

hΨ_|† _{≡ |}Ψ_i.

Operadores no espa¸co _H

Um operador é definido como um mapeamento de_H sobre ele próprio. Isto é, trata-se de uma regra de associa¸cão que leva qualquer vetor _|Ψ_{i ∈ H} em outro vetor de_H,

|Ψ_{i → |}Φ_i=O _|Ψ_{i ∈ H}

Como exemplo de um operador linear, podemos usar o operador denotado por O =_| Ψ_ihΦ_|, constru´ıdos a partir de dois vetores _|Ψ_i e _|Φ_i, arbitrários, e do produto escalar. Consequências da aplica¸cão de O sobre _| ϕ_i: Seja O um operador que pertence a _H, definido por

O _≡|Ψ_ihΦ_| (2.3)

a aplica¸c˜ao de O em _|ϕ_item a seguinte consequˆencia:

O _|ϕ_{i ≡}(_|Ψ_ihΦ_|)_|ϕ_i=_hΦ_|ϕ_{i |}Ψ_i=_|Ψ′_i (2.4)

a expressão acima é válida para todo _|ϕ_{i ∈ H} e _|Ψ′_i _{também pertence ao espa¸co}_H_.

Ainda como conseqüência da defini¸cão do operador O, um teorema importante pode ser demonstrado a partir das equa¸cões acima, o chamado Teorema da Completeza.

Teorema da “Completeza”: Seja _{|i_i} uma base numerável ortogonal de _H, onde é válida a condi¸cão de normaliza¸cão _hi_|j_i=δij.

Ent˜ao vale a seguinte identidade:

n

X

i=1

|i_ihi_|≡ 11 . (2.5)

onde

δij =

(

1 _∀ i=j

(17)

A eq.(2.5) expressa a chamada de rela¸c˜ao de completeza, onde “1l ”representa o ope-rador identidade no espa¸co sobre _H.

Demonstra¸cão: O estado_|ψ_i, arbitrário, pode ser definido a partir de uma combina¸cão linear da base _{|i_i} do seguinte modo:

|ψ_i=

n

X

i=1

Ci _|i_i (2.6)

Ci pode ser calculado fazendo o produto escalar de _hi_|com _|ψ_i

hi_|ψ_i=_hi_| n

X

j=1

Cj _|j_i=

n

X

j=1

Cj_hi_|j_i=

n

X

j=1

Cjδij =Ci

Ci =_hi_|ψ_i (2.7)

substituindo a eq.(3.7) na eq.(3.6)

|ψ_i=

n

X

i=1

hi_|ψ_{i |}i_i=

n

X

i=1

|i_ihi_|

!

|ψ_i=_⇒ (2.8)

Sendo _|ψ_i arbitr´ario, conclui-se que

n

X

i=1

|i_ihi_|= 11 . (2.9)

No caso de uma base cont´ınua _{{ |}x_{i }}com normaliza¸c˜ao

hx′ _|x_i=δ(x₋x′) (2.10)

O estado _|ψ_ipode ser deﬁnido a partir da base _{{ |}x_{i }}do seguinte modo:

|ψ_i=

Z

dx C(x)_|x_i (2.11)

C(x) pode ser calculada usando a normaliza¸c˜ao da eq.(2.10). Tomando o produto escalar entre_hx′ _|_e _|_ψ_i _teremos:

hx′ _|ψ_i=_hx′ _|

Z

dx C(x)_|x_i

=

Z

dx C(x)_hx′ _|x_i=

Z

dx C(x)δ(x₋x′) =C(x′) (2.12) ent˜ao

C(x) =_hx_|ψ_i (2.13)

Substituindo a eq.(2.13) na eq.(2.11) teremos:

|ψ_i=

Z

dx_hx_|ψ_{i |}x_i=

Z

dx _|x_ihx_|

|ψ_i _⇒

Z

(18)

Nota-se que a opera¸cão de produto escalar definida no item i) induz naturalmente a atua¸cão, em _H†_{, de um operador} _A _{definido sobre} _H_{. Isto é, podemos definir o vetor}

ha_|A _{∈ H}†_. _{Admitindo-se a regra de associatividade,}

(_ha_|A)_|b_i=_ha_| (A_|b_i) (2.15)

ou seja do lado direito toma-se o produto escalar de _|a_icom o resultado da aplica¸c˜ao deA sobre _|b_{i ∈ H} e do lado esquerdo _ha_|A sobre _|b_i.

Com a defini¸cão de _ha _| A, e a opera¸cão de conjuga¸cão de vetores eq.(3.2) podemos definir a opera¸cão de conjuga¸cão hermitiana para operadores. Assim o operador conjugado hermitiano de de A,A′_{, é definido por:}

A†_|a_{i ≡}(_ha_| A)†. (2.16)

Da propriedade i) da eq.(2.1) do produto escalar, conclu´ımos que

ha _|A†_|b_i=_hb _|A_|a_i⋆. (2.17)

Exemplo 1: Sejam A e B dois operadores quaisquer do espa¸co _H. Prove que: a)A††₌_A

b) (AB)†₌_B†_A†

Solu¸c˜ao:

a)

Se _|Φ_i=A_|Ψ_i (2.18)

usando a propriedade _hΦ_|=_|Φ_i†_{, termos}

hΦ_|=_|Φ_i† = (A_|Ψ_i)†=_hΨ_|A†.

Tomando-se o conjugado hermitiano de_hΦ_| se conclui que

|Φ_i=_hΦ_|†=_hΨ_|A††= (A†)† _|Ψ_i (2.19)

Comparando as equa¸c˜oes (2.18) e (2.19) teremos, _| Φ_i = A _| Ψ_i = (A†₎† _| _Ψ_i _este

resultado permite concluir que:

A= (A†)†. (2.20)

b) sejam _| ψ_i e _| b_i dois vetores quaisquer de _H, que satisfazem a seguinte rela¸c˜ao: |ψ_i=AB_|b_i.

Se_|ψ_i=A_|a_i e _|a_i=B _|b_i tomando o conjugado hermitiano de_|ψ_i teremos |ψ_i†₌_h_ψ _|₌_h_b_|₍_AB₎†₌_h_a_|_A† ₌_h_b _|_B†_A†_, _{de onde se conclui que}

(19)

Operdores hermitianos

Quando um operador A† _{é idêntico a} _A_{, isto é,} _A† ₌_A_{, então} _A _{é chamado de operador}

hermitiano. Um teorema muito importante pode ser enunciado neste ponto, o teorema do operador hermitiano

Teorema do operador hermitiano: Sendo A, um operador hermitiano qulquer do espa¸co _H,

ent˜ao seus autovalores s˜ao reais.

Demonstra¸cão: Sejam A um operador hermitiano e _| a_i autoestado de A com autovalor “a”, a equa¸cão de autovalores deA será

A_|a_i=a_|a_i (2.22)

tomando o produto escalar da equa¸c˜ao acima com_ha_|

ha_|A_|a_i=a_ha_|a_i (2.23)

tomando o conjugado hermitiano da eq.(2.22) teremos

ha_|A†=a⋆_ha _| (2.24)

como A´e hermitiano A⋆ ₌_A _ent˜ao

ha_|A†=_ha_|A=a⋆_ha _| (2.25)

tomando o produto escalar da equa¸c˜ao acima com_|a_i tem-se

ha_|A _|a_i=a⋆_ha_|a_i (2.26)

subtraindo a eq.(2.23) da eq.(2.26)

a_ha_|a_{i −}a⋆_ha_|a_i= (a₋a⋆)_ha_|a_i= 0 (2.27) como _ha_|a_{i 6}= 0 a₋a⋆ _{= 0 ent˜ao}

a⋆ =a

logo o autovalor a´e real.

Postulado II: Qualquer variável dinâmica clássica será representada por operadores line-ares hermitianos cujos autovetores constuem uma base sobre o espa¸co _H.

Qualquer fun¸cão destas veriáveis dinâmicas, tambem fica representada por uma fun¸cão do operador. Estes operadores são ditos observáveis.

(20)

de observ´aveis do sistema se estas fossem realizadas. Para formalizar esse car´ater proba-bil´ıstico postula-se

Postulado III: A medida de um observ´avel A para um sistema no estado _|ψ_i, resulta numa transi¸c˜ao deste estado para um e somente um dos autoestados _|χi_ide A.

O valor da medida ´e dito autovalor χi do observ´avel.

Entretanto, para qualquer teoria fazer sentido, o estado após a realiza¸cão de uma medida de um observável deve poder ser reconfirmado por um medida subsequênte da mesma quantidade. O estado alcan¸cado pelo sistema após uma medida de um observável

A ´e dito autoestado deste observ´avel. Para caracterizar o processo de medida postula-se

Postulado IV: A probabilidade de transi¸cão _|ψ_{i →|}χi_i numa medi¸cão de Aé dada por _{| h}χi _|ψ_{i |}2_{, sendo}

ambos normalizados a um.

A mecânica quântica não se propõe a discutir o mecanismo de transi¸cão quântica do sistema f´ısico por ocasião de uma medi¸cão. É exigido, apenas, que a segunda medida de reconfirma¸cão, não mais altere o estado quântico do sistema. Do ponto vista matemático, podemos reformular o mecanismo do processo de medida acima, como sendo uma opera¸cão de proje¸cão do vetor_kψ_i na dire¸cão _|χi_i.

Podemos identificar um vetor estado após uma medida de um observável como sendo um autovetor do operador correspondente ao observável.

Teorema III: Os autoestados de um observável são autovetores do operador que representa o observável.

Prova:

Seja _| χi_i um autoestado de A. Pela deﬁni¸c˜ao de autoestado e usamos f(A) _≡ A no postulado III tem-se

hf(A)_i=_hA_i=_hχi _|A_|χi_i=χi. (2.28) Fazendo agora f(A) = (A_{− h}A_i)2 , o valor esperado de (A_{− h}A_i)2 representa a dis-pers˜ao estat´ıstica nas medidas deA.

h∆A2_i=_hχi _{| {}A_{− h}A_i}2 _|χi_i=_hχi _{| {}A₋χi_}2 _|χi_i= 0. (2.29)

(21)

Utilizando a propriedade hermitiana do operador A na eq(2.29), pode-se reescrever a eq.(2.28) do seguinte modo:

hχi _{| {}A₋χi_}2 _|χi_i=_hχi _{| {}A₋χi_}†

| {z }

hΦ|

{A₋χi_{} |}χi_i

| {z }

|Φi

= 0. (2.30)

Na equa¸cão acima o produto escalar entre dois vetores iguais é nulo, da defini¸cão do produto escalar, propriedade iii) da eq.(2.1) _hΦ _| Φ_i = 0 _{⇒ |} Φ_i = 0 então, da eq.(2.30)

{A₋χi_{} |}χi_i= 0. (2.31)

⇒ A_|χi_i=χi _|χi_i. (2.32)

ﬁcou provado.

2.1.2 Amplitude transi¸c˜

ao e densidade de probabilidade

O conjunto dos autovalores, _{χi_}, de um observável A é dito espectro de A. No caso de um observável de espectro cont´ınuo, os postulados IV e V devem compatibilizar a natureza cont´ınua do observável. A medida de um observável A do espectro cont´ınuo é caracterizada por um valor definido no intervalo (χ, χ+dχ). Os autovetores, neste caso, formam um conjunto cont´ınuo. A transi¸cão de um estado arbitrário _| ψ_i, causada pela medida do observável A, ocorre para um e só um dos autoestados,_| χ′_i_, _de_A_. _|_χ′_i _está

definido no subespa¸co _{|χ′_i_{; onde} _χ′ _∈ ₍_{χ, χ}₊_dχ₎_}_{, a rela¸cão entre} _| _ψ_i _e _| _χ_i _{é dada}

por:

|ψ_i=

Z

dχ C(χ)_|χ_i. (2.33)

Onde C(χ) ´e amplitude de probabilidade de transi¸c˜ao de_|ψ_i para _|χ_i.

Usando a normaliza¸cão definida na eq.(2.10) _hχ′ _| _χ_i ₌ _δ₍_χ₋_χ′_{), pode-se definir a}

densidade de probabilidade de transi¸c˜ao _| ψ_{i →|} χ_i, tomando o produto do estado _hχ′ _|

pela eq.(2.33)

hχ′ _|ψ_i=_hχ′ _|

Z

dχ C(χ)_|χ_i

=

Z

dχ C(χ)_hχ′ _|χ_i=

Z

dχ C(χ)δ(χ₋χ′) = C(χ′),

(2.34) logo

C(χ′) = _hχ′ _|ψ_i, (2.35)

hχ_|ψ_{i ≡}ψ(χ) é a proje¸cão do vetor _|ψ_i na base_|χ_i. Densidade de probabilidade ρé dada por;

(22)

Para δχ inﬁnitesimal, a probabilidade, dP, de encontrar o valorχ′ no intervalo (χ _≤ χ′ _≤_χ₊_δχ_{) ´e dada por:}

dP =ρ dχ =_{| h}χ′ _|ψ_{i |}2 dχ. (2.37)

Quando não há degenerescência no espectro de um observável, i.e., existe um único autoestado para cada autovalor de A, qualquer _|ψ_ido sistema deve ser especificado uni-vocamente por uma por uma fun¸cãoψ(χi), a fun¸cãoψ(χi) é a amplitude de probabilidade de obter o autovalor χi, onde χi cobre todos os autovalores de A. Neste caso, o conjunto dos autoestados de A, _{| χ_i}, contem todas as infor¸cões f´ısicas do sistema, sendo assim levando em conte o Princ´ıpio de Superposi¸cão, qualquer estado _| ψ_i pode ser definido como sendo uma combina¸cão linear dos _|χ_i′_s_{, seja}

|ψ_i=X

i

Ci _|χi_i (2.38)

levando-se em conta a rela¸c˜ao de ortogonalidade _hχj _|χi_i=δij

ψ(χi) = _hχi _|ψ_i=Ci (2.39)

δij =

(

1 _∀ i=j

0 _∀ i₆=j

As equa¸c˜oes (2.38) e (2.39) implicam que

n

X

i=1

|χi_ihχi _|=11 , (2.40)

Sendo assim, o conjunto dos autovetores_{|χi_i}de um observável, não degenerado, forma uma base de_H. A fun¸cão amplitudeψ(χi) é ditaproje¸cãodo estado|ψiina base{|χii}.

Quando existe degenerescência no espectro de A, a amplitude de probabilidade como fun¸cão dos autovalores de A não é suficiente para especificar um estado _| ψ_i, pois existe mais de um estado associado a um mesmo autovalor. Os vetores que estão associados a um mesmo autovalor formam um subespa¸co de _H. A dimensão deste subespa¸co é o grau da degenerescência do estoestado.

Neste caso necessita-se de um segundo observável por exemplo B, que levante a dege-nerescência do espectro deA –isto é, fa¸ca a distin¸cão dos estados que tenham autovalores deA iguais– em termos dos autovalores de B.

Por simplicidade, vamos considerar que os espectros de A eB sejam discretos. Ent˜ao seja_|χi, bi_ium autovetor comum deAeB cujos os autovalores s˜aoχi ebirespectivamente. Sendo assim

A_|χi, bji=χi |χi, bji, j = 1,2, . . . m (2.41)

(23)

ψ(χi, bj) = _hχi, bj _|ψ_i. (2.42)

Se persistir a alguma degenerescência, ou seja, ainda existe mais de um estado para um mesmo par de autovalores (χi, bi) é necessário um outro observável para a especi-fica¸cão completa do estados. Para resolver completamente a questão da degenerescência, a mecânica quântica postula:

Postulado V: Existe um conjunto finito de observáveis para os quais a amplitude de probabilidade, como fun¸cão de seus autovalores, especifica completamente qualquer estado _|ψ_i do sistema. Este conjunto é dito um conjunto completo de observáveis.

O postulado IV é equivalente a afirmar que, os autovetores comuns, dos observáveis completos, formam uma base no espa¸co _H.

Para fechar o quadro sobre a quest˜ao da degenerescˆencia vamos enunciar o seguinte teorema:

Teorema IV: Os operadores que correspondem as variáveis dinâmicas de um conjunto completo de observáveis, comutam entre si.

Demonstra¸c˜ao:

Seja V = _{A(1)_{, A}(2)_{, . . . A}(n)_} _{um conjunto completo de operadores cujos autovetores}

comuns, são dados pelo conjunto _{|a(1)_i₁ , a(2)_i₂ , . . . , a(_i_nn)_i}. Por defini¸cão

A(m) a

(1)

i1 , a (2)

i2 , . . . , a (m)

im , . . . , a

(n)

in

E

=a(_i_mm) a

(1)

i1 , a (2)

i2 , . . . , a (m)

im , . . . , a

(n)

in

E

.

para m = 1,2. . . , n (2.43)

onde _|a(1)_i₁ , a(2)_i₂ , . . . , a(_i_mm), . . . , a(_in_n)_i1 _{forma uma base em}_H_.

Podemos portanto, deﬁnir qualquer vetor _|ψ_i em termos de uma combina¸c˜ao linear destes vetores da base

|ψ_i=

n

X

i(m=1)

ai1,i2,...,im,...,in

a

(1)

i1 , a (2)

i2 , . . . , a (m)

im , . . . , a

(n)

in

E

. (2.44)

Aplicando agora os operadores A(α) _e_A(β) _∈_V _{no estado} _|_ψ_i _{deﬁnido na eq.(2.44)}

teremos

A(α)A(β)_|ψ_i=A(α)a(iββ)|ψi=a

(β)

iβ A

(α)

|ψ_i=a(iββ)a

(α)

iα |ψi. (2.45)

1_{O vetor} _|_a(1)

i

1 , a

(2)

i

2 , . . . , a

(m)

im , . . . , a

(n)

in i ´e dado pelo produto direto |a

(1)

i

1 , a

(2)

i

2 , . . . , a

(m)

im , . . . , a

(n)

in i =

|a(1)i₁ i ⊗ |a

(2)

i₂ i ⊗. . .⊗ |a

(m)

im i ⊗. . .⊗ |a

(n)

in idos autoestados dados no conjunto{|a

(m)

(24)

Onde usamos a identidade A(α)_a(β)

iβ = a

(β)

iβ A

(α) _porque _a(β)

iβ ´e um n´umero e portanto,

comuta com A(α)

De modo an´alogo

A(β)A(α)_|ψ_i=A(α)a(_iA_α(β))_|ψ_i=a_i(_αα)A(β)_|ψ_i=a(_i_ββ)a(_iα_α)_|ψ_i. (2.46) Subtraindo as eq.(2.45) e eq.(2.46)

A(α)A(β)₋A(β)A(α)_|ψ_i= 0 (2.47) como _|ψ_i´e arbitr´ario _⇒ A(α)_A(β)₋_A(β)_A(α) _{= 0 logo}

A(α)A(β) =A(β)A(α) ou hA(α), A(β)i= 0 (2.48)

2.1.3 Produto Direto

Espa¸co do produto direto de dois espa¸cos vetoriais. Sejam _{|ai_i} e _{|bj_i} duas bases de dois espa¸cos vetoriais _{V1} e {V2}, respectivamente. O conjunto de pares ordenados

{|aii, |bji} = {|aii ⊗ |bji} que constitui uma base para o produto direto ou produto

cartesiano das bases. O novo espa¸co vetorial ser´a dado por E1+2=E1⊗E2

O produto direto ´e tal que satisfaz as propriedades _|ai_{i ⊗}(_|bi_i+_|b′

ii) = |aii ⊗ |bii+

|aii ⊗ |b′ii

e

(_|aii+|a′ii)⊗ |bii=|aii ⊗ |bii+|a′ii ⊗ |bii onde {|aii,|a′ii} ∈V1 e {|bii,|b′ii} ∈V2

no espa¸co do produto direto, o produto interno ou produto escalar satisfaz propriedade

(_|a_{i ⊗ |}b_i,_|a′_{i ⊗ |}b′_i) = _ha_|a′_ihb_|b′_i

2.2 Comutador Q, P e Operador deslocamento

espa-cial

Neste cap´ıtulo, nota-se que até este ponto não se fez qualquer referência a ¯h, constante ca-racter´ıstica de Mecânica Quântica, isto é verdade por que até aqui o que se fez foi, apenas, estabelecer a estrutura matemática para a representa¸cão dos elementos básicos da teoria quântica. A constante ¯h aparece na formula¸cão quando estabelecemos a correspondência entre as variáveis dinâmicas clássica e os objetos da mecânica quântica, que pertencem ao espa¸co _H, dando a esses objetos uma interpreta¸cão f´ısica. Isto é natural porque os objetos do espa¸co de Hilbert são matemáticos abstratos desprovidos de qualquer inter-preta¸cão f´ısica. Já as variáveis dinâmicas clássicas tem significado f´ısico. A constante ¯h

(25)

Sendo portanto, fundamental para o estabelecimento da correspondˆencia entre assas quan-tidades.

Na Mecânica Clássica -para a descri¸cão da dinâmica de um sistema- define-se um con-junto de pares variáveis dinâmicas, ditas variáveis canônicas_{(qi, pi), comi= 1,2, . . . , n_}, onde qi epi satisfazem a seguinte rela¸cão

{qi, pj_}=δij (2.49)

onde a expressão da eq.(2.49) é dita parênteses de Poison das variáveis qi e pi e n é o número de graus de liberdade do sistema. qi epi são respectivamente coordenadas e mo-mentos linear generalizados do sistema f´ısico.

Em Mecânica Quântica para estabelecer a correspondência entre os objetos quânticos e as quantidades clássicas, postula-se

Postulado VI: Os operadores Qe P representativos de um par de varáveis canônicas, satisfazem a regra de comuta¸cão :

[Q, P]_≡ih¯11 (2.50)

ondeQ´e o operador coordenada generalizada eP ´e o operador momento linear. Para um sistema com n graus de liberdade

[Qi, Pj] =i¯hδij. (2.51)

O comutador de operadores representativos de variáveis canonicamente conjugadas, como no caso do postulado VII, é um número complexoi¯h, multiplicado pelo operador identi-dade 11 . Este por sua vez, comuta com qualquer outro operador.

Exercicios provar as identidades abixo: 1- [A, B] + [B, A] = 0

2- [A, A] = 0

3- [A, B +C] = [A, B] + [A, C] 4- [A+B, C] = [A, C] + [B, C] 5- [A, BC] = [A, B]C+B[A, C] 6- [AB, C] = [A, C]B+A[B, C]

7- [A,[B, C]] + [C,[A, B]] + [B,[C, A]] = 0 8- [x, px] = [y, py] = [z, pz] =i¯h

9- [Lx, Ly] =i¯hLz use [xi, pj] =i¯hδij

se f(P) =Pn_i₌₁Pn _ent˜ao

10- [Q, f(P)] =i¯h∂f_∂P(P) 11- seja L+ =Lx+iLy e L−=Lx−iLy prove que:

a) [L+, L−] = 2¯hLz

b)[L+, Lz] =−¯hL+

(26)

d)[L2, L±] = 0

2.2.1 Aplica¸c˜

oes

Aqui vamos utilizar esta formula¸cão para calcular quantidades f´ısicas de interesse par-tindo unicamente dos postulados estabelecidos. Operador deslocamento espacial ou de transla¸cão este operador é muito útil na demonstra¸cão de diversas identidades.

Sejam Q e P dois observáveis canonicamente conjugados podemos definir o operador unitárioU por:

U =eiaP¯h

Se _|q_i´e autoestado de Q com autovalor q.

Prove que:

U _|q_i=_|q₋a_i

isto ´e, U _|q_i ´e autoestado de Qcom autovalor (q₋a)

Demonstra¸c˜ao:

Do postulado VII, sabemos que [Q, P] = i¯h e por hip´otese Q_| q_i =q _| q_i. Usando a identidade

QU =QU₋U Q

| {z }

comutador

+U Q= [Q, U] +U Q, como [Q, U] =i¯h_∂P∂U =ih¯ia_¯_hU =₋aU ent˜ao

QU =i¯h∂U

∂P +U Q=−aU +U Q

QU =₋aU +U Q (2.52)

aplicando QU em _|q_iteremos:

⇒ Q U _|q_i= (q₋a)U _|q_i (2.53)

Portanto,U _|q_i´e autoestado deQcom autovaloresq₋a. Podemos ﬁnalmente escrever

U _|q_i=k _|q₋a_i

(27)

hq _|U†U _|q_i=_hq_|q_i= 1 =_hq₋a_|k†k _|q₋a_i=k2_hq₋a_|q₋a_i=k2

⇒k2 = 1 k=_±eiϕ

logo a menos de uma diferen¸ca de fase k= 1 ent˜ao ﬁca provado que:

U _|q_i=_|q₋a_i (2.54)

O operador U, é dito operador de deslocamento espacial ou operador de transla¸cão. neste sentido, o operador P é chamado de gerador das transla¸cões espaciais.

2.2.2 Onda plana

A amplitude de probabilidade de se encontrar um autoestado de um operador digamosA

num auto estado de um outro operadorB é dita fun¸cão de transforma¸cão da base B para a base A. Como exemplo vamos discutir a transforma¸cão da base _| p_i para a base _| q_i, esta transforma¸cão é dada por:

hp_|q_i= √1 2π¯he

ipq_¯_h_. _(2.55)

Exerc´ıcio use o operadorU =eiaP_¯_h _para:

a) Provar que o operador momento linear P, na base de coordenadas _|q_i, corresponde a um operador derivada dado por P _{→ −}i¯h_∂q∂;

b) prove que a fun¸c˜ao de onda plana ´e dada pela eq.(2.55).

Prova:

U _|q_i=eiaPh¯ |qi=|q−ai

multiplicando por_hp_| teremos:

D

p ei

aP

¯

h

q

E

=e−iap¯h hp|qi=hp|q−ai

por simplicidade vamos fazer ψp(q) = hp|qi, ent˜ao

(28)

expandindo ψp(q₋a) em s´erie de Taylor teremos

ψp(q−a) =ψp(q)− a

1!

∂ψp(q)

∂q + a2

2!

∂2_ψp₍_q₎

∂q2 +. . .+

an n!

∂n_ψp₍_q₎

∂qn (2.57)

e−iaP¯h = 1− i

1!

aP

¯

h +

1 2!(i

aP

¯

h )

2₊_{. . .}₊ 1

n!(−i

aP

¯

h )

n _(2.58)

substituindo as eq.(2.57 e 2.58) na eq.(2.56) teremos;

1₋ i 1!

ap

¯

h +

1 2!(i

ap

¯

h )

2₊_{. . .}₊ 1

n!(−i

ap

¯

h )

n_ψp₍_q_{) =} _ψp₍_q₎

−_1!a ∂ψp_∂q(q)+ a

2

2!

∂2_ψp₍_q₎

∂q2 +

+....+a

n n!

∂n_ψp₍_q₎

∂qn (2.59)

Comparando-se termo a termo as potˆencias deae simpliﬁcando o que for poss´ıvel, conclui-se que ₋_¯_hipψp(q) =₋∂ψp(q)

∂q logo

pψp(q) = ¯h

i

∂ψp(q)

∂q (2.60)

podemos concluir que o operador P _→ ¯h_i _∂q∂. Isto ´e, P corresponde a um operador derivada no espa¸co q.

b) podemos reescrever a eq.(2.60) do seguinte

d ψp(q) ψp(q) =

i

¯

hpdq

integrando equa¸c˜ao acima

Z ψp(q)

ψp(0)

d ψp(q)

ψp(q) =

i

¯

h

Z q

0 pdq ⇒ ln

ψp(q)

ψp(0)

!

=ipq

¯

h (2.61)

usando a identidade logar´ıtmica ln(a) = b _⇒ a=eb _ent˜ao

(29)

Ondeψp(0) é a constante de integra¸cão que pode ser calculada usando a normaliza¸cão

hq′ _|q_i=δ(q₋q′)

usando a completeza

1

=

Z _∞

−∞dp|pihp|

q′

Z _∞

−∞dp |pihp|

q

=

Z _∞

−∞ dphq

′ _|_p_ih_p_|_q_i₌Z ∞ −∞dp ψ

∗

p(q′)ψp(q) =δ(q−q′)

Z _∞

−∞dp ψ ∗

p(0)ψp(0)e

i

¯

hp(q′−q)=|ψp(0)|2

Z _∞

−∞dp e

i

¯

hp(q′−q) =δ(q−q′) (2.63)

como R_−∞∞ dk eik(q′₋_q₎

= 2πδ(q₋q′_{) e como} _k ₌ p

¯

h e dk = dp

¯

h substituindo na integral

teremos

R_∞

−∞ dp¯h ei

p

¯

h(q′−q)= 2πδ(q−q′)⇒ R∞

−∞2dpπ¯hei

p

¯

h(q′−q)=δ(q−q′)

1 2π¯h

Z _∞

−∞dp e

i_¯_hp(q′₋_q₎

=δ(q₋q′) (2.64)

Comparando as eq(2.63 e 2.64) pode-se concluir que _|ψp(0)_|2 = ₂_π1_h_¯ _{⇒ |}ψp(0)_| = q₂_π1_¯_h ﬁnalmente

ψp(q) = √1 2π¯he

ipq_¯_h _(2.65)

2.2.3 Fun¸c˜

oes de operadores

Seja A um operador linear arbitr´ario pode se deﬁnir o operador B = An_{. Onde} _B

corresponde a n aplica¸c˜oes do operador A sobre um estado f´ısico arbitr´ario qualquer

B =A_×A_×. . ._×A (2.66)

Se existir o operador A−1_{, tal que}

A−1A=AA−1 = 11 (2.67)

(30)

Como será poss´ıvel definir o operador mais geral, isto é, um operador fun¸cão de um operador arbitrário A qualquer? Para conceituar fun¸cão operador vamos considerar pri-meiro uma fun¸cão, F, de um observável variável x, cujo correspondente o operador é A. Assumindo um certo dom´ınio, F pode ser expandida em uma série de potências em x

dada por:

F(x) =

∞

X

n=0

fnxn (2.68)

O operador correspondente da fun¸cãoF(x), será um operadorF(A) definido por uma série que tem os mesmos coeficientes f′

ns

F(A) =

∞

X

n=0

fnAn=f0+f1A1+f2A2+. . .+fnAn (2.69)

Exemplos seja f(x) = ex _{= 1 +}_x₊ 1

2!x2 +. . .+ 1

n!xn uma fun¸c˜ao da vari´avel x. O

operador correspondente af(x) ser´a:

F(A) = eA= 1 +A+ 1 2!A

2₊_{. . .}₊ 1

n!A

n _(2.70)

Se _|χ_i´e autoestado de A com autovalor χ ent˜ao

A_|χ_i = χ_|χ_i e

An_|_χ_i ₌ _χn_|_χ_i (2.71)

Sendo assim

F(A)_|χ_i=

∞

X

n=0

fnAn_|χ_i=

∞

X

n=0

fnχn_|χ_i=F(χ)_|χ_i (2.72)

Quando _|χ_i é um autoestado de A com autovalor χ, _|χ_i é também autoestado de

F(A), com autovalorF(χ) exemplo

Provar que eA_eB ₆₌_eA+B ₆₌_eB_eA

Exerc´ıcos: a) Provar que

eA_Be−A₌_B_{+ [}_{A, B}_{] + [}_A,_[_{A, B}_{]] +}_{. . .}_{usando a fun¸c˜ao auxiliar} _F₍_λ_{) =} _eλA_Be−λA

2.3 Princ´ıpio de incerteza e incerteza m´ınima

(31)

simultaneamente. Se A e B são dois operadores hermitianos que não comutam entre si, é imposs´ıvel obter com precisão os valores esperados de A e B simultaneamente. Se [A, B] =AB₋BAdeAeBé diferente de zero, é inevitável a conclusão de que é imposs´ıvel medir com precisão os valores esperados desses observáveis. Definido

AB₋BA =iC (2.73)

onde a unidade imagin´aria “i”foi introduzida para assegurar que C ´e um operador hermitiano

A regra de comuta¸c˜ao entre dois observ´aveis canonicamente conjugados necessaria-mente contem o princ´ıpio de incerteza de Heisenberg.

Principio de incerteza: SejamAeB dois observáveis canonicamente conjugados, cujo comutador deles é diferentes de zero. Para qualquer estado _|ψ_i as dispersões estat´ısticas ∆A e ∆B destes observáveis, satisfazem a desigualdade:

h∆A2_ih∆B2_{i ≥}

₁

2|hCi|

2

(2.74)

ou

∆A∆B _≥ 1

2|hCi| (2.75)

onde ∆A=q_h∆A2_i₌q_h₍_A_{− h}_A_i₎2_i₌q_h_A2_{i − h}_A_i2_{e ∆}_B ₌q_h_∆_B2_i₌q_h_B2_{i − h}_B_i2

Demonstra¸c˜ao:

Sejam ∆A e ∆B dois operadores hermitianos deﬁnidos por:

∆A=A_{− h}A_i e ∆B =B_{− h}B_i, (2.76)

note que

[∆A,∆B] =iC (2.77)

Escolhendo os vetores _|φ′_i_{= ∆}_A_|_ψ_i_e _|_φ_i_{= ∆}_B_|_ψ_i

(

hφ′_|_φ′_i₌_h_ψ_|_∆_A2_|_ψ_i ₌ _h_∆_A2_i

hφ_|φ_i =_hψ_|∆B2_|_ψ_i ₌ _h_∆_B2_i (2.78)

Usando a desigualdade de Schwartz

hφ′_|φ′_ihφ_|φ_{i ≥ h}φ′_|φ_i2 (2.79)

hψ_|∆A2_|ψ_ihψ_|∆B2_|ψ_{i ≥ |h}ψ_|∆A∆B_|ψ_i|2

ou

(32)

∆A∆B = 1

2(∆A∆B+ ∆B∆A) + 1

2(∆A∆B−∆B∆A)

= 1₂[∆A,∆B]₊ +1₂[∆A,∆B]

= 1

2[∆A,∆B]+ + 1 2iC

(2.81)

onde “[,]+”denota anticomutador

é fácil concluir que o valor esperado de um anticomutador de operadores hermitianos é um número real. Assim sendo podemos escrever.

hψ_|∆A∆B_|ψ_i=

ψ

₁

2[∆A,∆B]+ +

1 2iC

ψ

= 1 2

D

[∆A,∆B]+

E

+ 1

2ihCi ⇒ (2.82)

hψ_|∆A∆B_|ψ_i=_ℜ+1

2ihCi (2.83)

onde _ℜ= 1 2

D

[∆A,∆B]+

E

.

Substituindo a eq(2.83) na eq(2.80) teremos

h∆A2_ih∆B2_{i ≥ |ℜ}+ 1 2ihCi|

2 ₌

|ℜ|2+1 2|hCi|

2 _(2.84)

Na desidualdade da equa¸cão (2.84) o termos da esquerda já é maior que soma _|ℜ|2 ₊

|1 2hCi|

2_{, do lado direito e, muito mais fortemente o ser´a que o termo} _|1 2hCi|

2_{, ou seja}

suprimindo _|ℜ|2_{. Portanto ﬁca provado que}

h∆A2_ih∆B2_{i ≥ |ℜ}+1 2ihCi|

2

≥ |1₂hC_i|2 (2.85)

ou ainda que

∆A∆B _≥ 1

2|hCi| (2.86)

Que é a rela¸cão de incerteza de Heisenberg. Esta rela¸cão assegura que ao se medir com precisão máxima o valor esperado de A desconhece-se completamente o valor esperado do operador B e vice-versa. Isto é, é imposs´ıvel medir, com precisão máxima, os valores esperados de A e B simultaneamente. Isso quer dizer que se medirmos a posi¸cão, por exemplo, de um elétron um milhão de vezes sob as mesmas condi¸cões, a cada medi¸cão obteremos um resultado diverso dos anteriores. Para extrair uma informa¸cão útil do sis-tema, tiramos a média das nossas medida e descrevemos os nossos resultados em termos estat´ısicos.

Exemplo: Prove a desigualdade ∆Q∆P _≥ ¯h₂.

Demonstra¸c˜ao: para provar a desigualdade basta considerar A = Q e B = P, onde

(33)

da eq(2.50) o comutador [Q, P] = i¯h, ent˜ao C = ¯h. Substituindo tudo isto na eq(2.86) teremos

∆Q∆P _≥ ¯h

2 (2.87)

Ou seja, se observador medir com precisão máxima a posi¸cãoqda part´ıcula, ele desconhece complemente o valor do momento linearpda mesma nesta posi¸cão. É claro que a rec´ıproca é verdadeira.

Mais a frente vamos poder voltar a este assunto quando estivermos discutindo as proje¸c˜oes do estado _|ψ_i nas bases _|q_i e _|p_i.

2.3.1 Pacote de incerteza m´ınima

´

E interessante estudar em que estado ocorre a m´ınima incerteza para um par de vari´aveis canonicamente conjugadas.

A incerteza m´ınima ocorre quando temos a igualdade na eq(2.87) i. e.

∆Q∆P = ¯h 2

Condi¸c˜ao de igualdade:

|φ′_i=λ_|φ_i

∆B_|ψ0i=λ∆A|ψ0i (2.88)

e

ℜ= 1 2

D

ψ0|[∆A,∆B]+|ψ0

E

= 0 (2.89)

onde λ´e uma constante arbitr´aria a ser determinada substituindo a eq(2.88) na eq(2.89) vamos ter

hψ0|∆A∆B|ψ0i+hψ0|∆B∆A|ψ0i= 0 ⇒

D

ψ0|λ∆A2|ψ0

E

+Dψ0|λ⋆∆A2|ψ0

E

= 0 _⇒ (2.90)

(λ+λ⋆)_h∆A2_i= 0 _⇒

(

como _h∆A2_{i 6}_{= 0}

ent˜ao (λ+λ⋆_{) = 0} (2.91)

onde _h∆A2_i₌_h_ψ

0|∆A2|ψ0i Logo

λ⋆ =₋λ (2.92)

(34)

(λ₋λ⋆)_h∆A2_i=i_hC_i (2.93)

substituindo a eq(2.92) na eq(2.93)

(λ+λ)_h∆A2_i= 2_h∆A2_i=i_hC_i _⇒

λ= ihCi

2_h∆A2_i (2.94)

Consideremos o caso particular onde A=Q eB =P. Da eq(2.50)QP ₋P Q=i¯h11

⇒ C = ¯h11

Substituindo λ na eq(2.88) vamos ter

∆P_|ψ0i=λ∆Q|ψ0i (2.95)

Na representa¸c˜ao de coordenadas _{|q_i}a eq(2.95) ﬁca

hq_|∆P_|ψ0i=λhq|∆Q|ψ0i=hq|(P − hPi)|ψ0i=λhq|(Q− hQi)|ψ0i (2.96)

ou

(h¯

i d

dq − hPi)hq|ψ0i=λ(q− hQi)hq|ψ0i ⇒ (2.97)

esta equa¸c˜ao pode ser reescrita do seguinte modo

(¯h

i d

dq − hPi)ψ0(q) = ih¯

2_h∆q2_i(q− hQi)ψ0(q) (2.98)

onde λ = i¯h

2h∆q2_i eψ0(q) = hq|ψ0i

reescrevendo a eq(2.98)

d dq −

i

¯

hhPi

!

ψ0(q) = −

(q_{− h}Q_i)

2_h∆q2_i ψ0(q) (2.99)

ou ainda

d ψ0(q)

dq = −

(q_{− h}Q_i) 2_h∆q2_i +

i

¯

hhPi

!

ψ0(q) (2.100)

integrando a eq(2.100) teremos:

ψ0(q) =

1

[2π_h∆q2_i_]1₄ exp

"

−(q− hQi)

2

4_h∆q2_i +

i

¯

hhPi(q− hQi)

#