PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PUC / SP
Acylena Coelho Costa
Geometria Analítica no Espaço:
Análise das Organizações Matemática e Didática em Materiais
Didáticos
DOUTORADO EM EDUCAÇÃO MATEMÁTICA
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PUC / SP
Acylena Coelho Costa
Geometria Analítica no Espaço:
Análise das Organizações Matemática e Didática em Materiais
Didáticos
São Paulo
2015
Tese apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo como exigência parcial para obtenção do título
de DOUTOR EM EDUCAÇÃO
Banca Examinadora
________________________________
________________________________
________________________________
________________________________
Autorizo, exclusivamente para fins acadêmicos e científicos, a reprodução total ou parcial desta Tese por processos de fotocopiadoras ou eletrônicos.
AGRADECIMENTOS
Agradeço a Deus, por sua infinita misericórdia em minha vida.
Ao meu esposo, Carlos, que sempre incentivou meu desenvolvimento profissional.
Ao Professor Doutor Saddo Ag Almouloud, orientador dessa pesquisa, pelo incentivo, amizade, ensinamentos e competência de sempre. Aos professores doutores Maria José Ferreira da Silva, Angelita Minetto Araújo e Marco Aurélio Kalinke, Celina Aparecida Almeida Pereira Abar que aceitaram participar da Banca Examinadora e contribuíram com este trabalho.
Aos professores do Programa de Pós-Graduação em Educação Matemática da PUC-SP, pelos valiosos conhecimentos.
Aos meus amigos do DINTER UEPA-PUC/SP pelos momentos compartilhados nessa trajetória. Ao professor Doutor Pedro Franco de Sá pelo incentivo ao DINTER UEPA-PUC/SP.
Ninguém ignora tudo. Ninguém sabe tudo. Todos nós sabemos alguma coisa. Todos nós ignoramos alguma coisa. Por isso aprendemos sempre.
RESUMO
A presente pesquisa tem como objetivo analisar como os autores de livros didáticos organizaram as atividades propostas no que se refere ao estudo da Reta e do Plano para o ensino da Geometria Analítica no Espaço. As análises dos livros didáticos fundamentaram-se essencialmente na Teoria Antropológica do Didático (TAD), quanto às praxeologias, propostas por Chevallard (1999) e nas variáveis didáticas para o ensino da Geometria Analítica no Espaço estabelecidas por Lebeau (2009). Com base no referencial teórico adotado realizamos uma investigação de caráter qualitativo do tipo documental, partindo de um levantamento bibliográfico em quatro livros didáticos de Geometria Analítica destinados ao ensino superior. A metodologia adotada em nossa pesquisa foi subsidiada na metodologia de análise de manuais desenvolvida por Chaachoua (2014a) analisando nos livros didáticos os seguintes aspectos: momento da edição, representatividade, estrutura, análise ecológica e análise praxeológica. Em relação a análise praxeológica identificamos seis tipos de tarefas presentes nos manuais analisados, a saber: determinar a equação da reta no espaço, determinar a condição de paralelismo de retas no espaço, determinar a condição de alinhamento de pontos no espaço, apresentar a equação do plano no espaço como uma propriedade da ortogonalidade, determinar um plano caracterizado por duas retas secantes e caracterizar algebricamente o paralelogramo. Dentre os resultados encontrados é possível inferir que os autores privilegiam uma modelização algébrica dos objetos matemáticos, bem como as técnicas adotadas pelos mesmos encontram-se situadas no campo da Álgebra Linear e da Geometria Analítica.
ABSTRACT
This research aims to analyze how the authors of textbooks organized the activities proposed in relation to the study of Line and Planning for the teaching of Analytic Geometry in Space. Analyses of textbooks substantiate mainly on Anthropological Theory of the Didactic (TAD), with regard to praxeologias proposed by Chevallard (1999) and in didactic variables for the teaching of Analytic Geometry in Space established by Lebeau (2009). Based on the theoretical framework adopted we conducted a qualitative investigation of documentary type, based on a literature review on four textbooks Analytic Geometry devoted to higher education. The methodology used in our research was supported in manual analysis methodology developed by Chaachoua (2014a) analyzing the textbooks the following: time of writing, representation, structure, ecological analysis and praxeological analysis. For regards the praxeological analysis identified six types present in the analyzed manual tasks, namely to: determine the equation of the line in space, determining the straight condition of parallelism in space, to determine the alignment condition of points in space, present plane equation in space as a property of orthogonality, determine a plan characterized by two intersecting lines and characterize algebraically the parallelogram. Among the findings it can be inferred that the authors favor an algebraic modeling of mathematical objects, as well as the techniques adopted by them are situated in the field of Linear Algebra and Analytic Geometry.
LISTA DOS QUADROS
LISTA DAS FIGURAS
Figura 1: Representação de um cubo ...22
Figura 2: Representação do plano dado um ponto e um vetor normal ...35
Figura 3: Representação do plano como conjunto de retas perpendiculares ...36
Figura 4: Representação do plano como superfície regular ...37
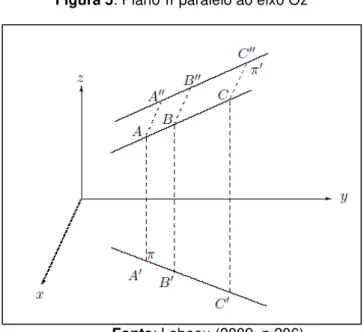
Figura 5: Plano π paralelo ao eixo Oz ...39
Figura 6: Representação do plano como superfície regular ...40
Figura 7: Conjunto de retas perpendiculares a uma reta dada d...47
Figura 8: Caracterização do plano Oyz ...48
Figura 9: Interseções de curvas com planos ...48
Figura 10: Conjunto de retas paralelas ...49
Figura 11: Projeção sobre o plano paralelamente a uma reta ...51
Figura 12: Projeções de pontos de uma curva ...52
Figura 13: Projeção de pontos sobre o plano OXY ...53
Figura 14: Quarto vértice do paralelogramo construído sobre O, A e B ...56
Figura 15: Quatro pontos dados A, B, C e D (ou suas projeções) ...60
Figura 16: Os pontos M, N e P e suas projeções no plano ...62
Figura 17: Retas paralelas d1 e d2 ...63
Figura 18: Capa do livro de Luiz Mauro Rocha ...71
Figura 19: Capa do livro Waldyr Muniz Oliva ...71
Figura 20: Capa do livro de Paulo Boulos e Ivan Camargo ...72
Figura 21: Capa do livro de Steinbruch e Paulo Winterle ...72
Figura 22: Prefácio de LD1...76
Figura 23: Prefácio de LD2...76
Figura 24: Prefácio de LD3...77
Figura 25: Prefácio de LD4...77
Figura 26: Equação vetorial da reta em LD2 ...83
Figura 27: Equação vetorial da reta em LD3 ...84
Figura 28: Equação vetorial da reta em LD4 ...84
Figura 29: Escrita de equações paramétricas de reta em LD2...85
Figura 30: Determinação da equação de uma reta em LD4 ...85
Figura 31: Solução do exercício da figura 30 ...86
Figura 32: Posição de retas e planos em LD1...87
Figura 33: Paralelismo de retas em LD3 ...88
Figura 34: Condição de paralelismo de duas retas em LD4 ...88
Figura 35: Posição relativa de retas em LD3...89
Figura 36: Resolução da questão da figura 35 ...89
Figura 37: Condição para que três pontos estejam alinhados em LD4 ...90
Figura 38: Exemplo de uso da técnica 2 em LD3 ...91
Figura 39: Exemplo de utilização das técnicas 1 e 2 em LD4 ...91
Figura 40: Condição de alinhamento de pontos em LD4 ...92
Figura 41: Determinação do plano em LD1 ...93
Figura 42: Equação do plano em LD2 ...94
Figura 43: Equação geral de plano em LD3 ...95
Figura 44: Equação geral do plano em LD4 ...96
Figura 45: Equações paramétricas do plano em LD3 ...97
Figura 46: Primeira resolução em LD3 ...98
Figura 47: Determinação da equação geral de um plano em LD4 ...98
Figura 49: Tarefas sobre equação geral do plano em LD4 ...99
Figura 50: Outras propostas de determinação de equação geral do plano em LD4 ...100
Figura 51: Postulado da determinação do plano em LD1 ...101
Figura 52: Abordagem vetorial em LD4 ...102
Figura 53: Determinação da equação vetorial do plano em LD2 ...102
SUMÁRIO
INTRODUÇÃO ... 15
CAPÍTULO 1: ESTUDOS PRELIMINARES ... 19
1.1 Pesquisas sobre o Ensino da Geometria Analítica ... 19
1.2 Pesquisas envolvendo a TAD e a Geometria Analítica ... 30
1.3.1 O Plano ... 35
1.3.2 A Reta ... 38
CAPÍTULO 2: FUNDAMENTOS TEÓRICOS DA PESQUISA ... 41
2.1. A Teoria Antropológica do Didático (TAD) ... 41
2.1.1 Os objetos ostensivos e não ostensivos ... 44
2.2.Variáveis Didáticas na perspectiva de Lebeau (2009) ... 46
2.2.1.Começar pelo plano? ... 46
2.2.2.Começar pela reta? ... 50
2.2.3. Passar da reta ao plano. ... 53
2.2.4. Paralelogramo, paralelismo e translação. ... 56
2.2.5. Os pressupostos geométricos. ... 62
2.2.6. Ostensivos e modos de pensar. ... 63
CAPÍTULO 3: ABORDAGEM METODOLÓGICA ... 69
3.1. Caracterização da pesquisa ... 69
3.2 A escolha dos livros didáticos ... 70
3.3. Metodologia de análise dos manuais ... 72
CAPÍTULO 4: ANÁLISES DOS RESULTADOS ... 75
4.1. Momento da edição ... 75
4.2. Representatividade ... 75
4.3. Estrutura ... 77
4.3.1. Apresentação do livro LD1 ... 78
4.3.2. Apresentação do livro LD2 ... 79
4.3.3. Apresentação do livro LD3 ... 79
4.3.4. Apresentação do livro LD4 ... 80
4.4. Análise ecológica ... 81
4.5. Análise praxeológica ... 82
4.5.1. Tipo de Tarefa (T1): Determinar a equação da reta no espaço ... 83
4.5.2 Tipos de Tarefa (T2): Determinar a condição de paralelismo de retas no espaço. ... 86
4.5.4. Tipo de tarefa (T4): Determinar a equação do plano no espaço
como uma propriedade da ortogonalidade. ... 92
4.5.5. Tipo de tarefa (T5): Determinar um plano caracterizado por duas
retas secantes. ... 100
4.5.6. Tipo de tarefa (T6): Caracterizar algebricamente o paralelogramo.
... 101
CONSIDERAÇÕES E PERSPECTIVAS FUTURAS ... 105
INTRODUÇÃO
Como professora do curso de Licenciatura em Matemática, há 12 anos, ministrando por 4 anos a disciplina Geometria Analítica, percebemos, em diferentes momentos, as dificuldades que os alunos apresentam nos conteúdos envolvendo tal disciplina, mesmo quando já estudaram esses conteúdos no Ensino Médio.
Ao verificarmos as dificuldades dos alunos em relação aos objetos de estudo da Geometria Analítica, principalmente ao lidar com diferentes registros (algébrico, gráfico e linguagem natural), nossa preocupação enquanto pesquisadora, foi investigar tais dificuldades relacionando-as à formação de professores de Matemática. Também percebemos na Geometria Analítica um campo relevante de pesquisa, pois relaciona duas áreas da Matemática, a Álgebra e a Geometria.
A Geometria Analítica, enquanto disciplina, representa um forte alicerce no currículo do curso de Licenciatura em Matemática, pois encontra-se presente em disciplinas como o Cálculo Diferencial e Integral, Álgebra Linear, Geometria Euclidiana, Física e Análise Matemática. Além disso, percebemos a relevância da disciplina Geometria Analítica por encontrar-se presente em outros cursos superiores, tais como Engenharias, Arquitetura, Licenciatura em Física e outros.
Ao iniciamos o curso de Doutorado em Educação Matemática por meio de um projeto de doutorado interinstitucional (DINTER) entre a Universidade do Estado do Pará (UEPA) e a Pontifícia Universidade Católica de São Paulo (PUCSP), no ano de 2010, passamos a integrar o grupo de pesquisa Processo de Ensino e Aprendizagem em Matemática – PEAMAT. Nesse grupo, despertamos nosso interesse pelas discussões envolvendo a Teoria Antropológica do Didático de Chevallard (1991), pois identificamos a sua importância para a análise da prática docente em instituições de ensino.
Geometria Analítica no Espaço, em livros didáticos, uma vez que percebemos poucas pesquisas no campo da Educação Matemática discutindo tal problemática no ensino superior.
Para a realização dessa pesquisa direcionamos o foco para análise de materiais didáticos1 no que se refere ao conteúdo de Geometria Analítica, no ensino superior. Ao trilharmos nos estudos de nosso campo investigativo percebemos que deveríamos centrar no estudo da Reta e do Plano no espaço no intuito de analisar a abordagem feita pelos autores dos livros didáticos adotados em Cursos de Licenciatura em Matemática em diferentes períodos. Os referenciais teóricos que subsidiaram tais análises foram a Teoria Antropológica do Didático (TAD) de Yves Chevallard (1999) e os estudos acerca das variáveis didáticas envolvidas no ensino da Geometria Analítica no Espaço desenvolvido por Catherine Lebeau (2009). Trataremos sobre os principais aspectos dessas teorias ao longo de nosso trabalho.
A opção por analisar livros didáticos se deu por entendermos que estes representam uma importante ferramenta para o professor, pois retratam uma forma de comunicação entre o professor e o aluno. Além disso, o livro didático foi instituído historicamente como um dos instrumentos para o ensino e para a aprendizagem, conforme explicita Núñez (2003).
Na visão de Lopes (2000) o livro didático tem uma importante representatividade tanto para o professor, como para o aluno. No que se refere ao professor, o autor aponta que o livro didático apresenta-se como o complemento de sua formação acadêmica, além de ser o apoio na prática escolar devido às condições de trabalho enfrentadas. Por sua vez, o aluno enxerga o livro didático como um reforço para a aprendizagem, como também o recurso para encarar o processo de avaliação.
Constitui-se como propósito dessa pesquisa contribuir com o ensino de Geometria Analítica, tendo a convicção de que esse tópico da Matemática é fundamental para os estudos em Geometria. Para tanto, pretendemos nesse trabalho de tese responder ao seguinte questionamento:
• Quais organizações matemática e didática podem estar presentes em livros didáticos para o ensino superior no que se refere ao estudo da Reta e do Plano no Espaço?
A proposta, em nossa pesquisa, é analisar as organizações didática e matemática utilizadas na apresentação dos conteúdos sobre Reta e Plano no Espaço.
Nosso objetivo é analisar como os autores de livros didáticos organizaram as atividades propostas em relação ao estudo da Reta e do Plano a partir das variáveis didáticas desenvolvidas por Lebeau (2009) para o ensino da Geometria Analítica no Espaço.
Para tanto, visamos:
• Caracterizar as organizações didáticas e matemáticas presentes em livros didáticos quanto ao estudo em Geometria Analítica no Espaço.
• Comparar os tipos de tarefas presentes nos manuais analisados com as variáveis didáticas apontadas por Lebeau (2009) para o estudo em Geometria Analítica no Espaço.
Para alcançar tais objetivos, analisamos livros didáticos publicados no período do Movimento da Matemática Moderna estabelecendo a metodologia de análise de manuais didáticos proposta por Chaachoua (2014a).
A seguir apresentaremos a estrutura desse trabalho de tese, destacando cada um de seus capítulos.
No capítulo 1, apresentamos os estudos preliminares que possibilitaram direcionar uma investigação em relação a temática desenvolvida. Realizamos primeiramente um levantamento de pesquisas que contribuíram para os processos de ensino e de aprendizagem de Geometria Analítica. A seguir, descrevemos a respeito da importância de uma análise acerca do livro didático e suas contribuições em relação ao saber dentro de uma instituição didática. E finalizamos esse capítulo fazendo um estudo do objeto matemático o qual servirá de apoio teórico matemático, de maneira a permitir o suporte necessário para essa pesquisa.
Didático de Chevallard (1999) que estuda as organizações praxeológicas (didática e matemática) pensadas para os processos de ensino e de aprendizagem de organizações matemáticas. Apresentamos ainda aspectos significativos sobre o estudo realizado por Lebeau (2009), do qual interessamo-nos pelas variáveis didáticas apontadas por essa pesquisadora em relação ao estudo de Geometria Analítica no Espaço, especificamente no que se refere a Reta e Plano.
No capítulo 3 discorremos sobre a metodologia adotada em nossa pesquisa, a qual encontra-se subsidiada na metodologia de análise de manuais desenvolvida por Chaachoua (2014a) que destaca nos livros analisados os seguintes aspectos: momento da edição, representatividade, estrutura, análise ecológica e análise praxeológica.
Em relação ao capítulo 4 apresentamos nossa análise praxeológica destacando os tipos de tarefas encontradas nos livros analisados.
CAPÍTULO 1: ESTUDOS PRELIMINARES
______________________________________________________Neste primeiro capítulo descrevemos os estudos preliminares que permitiram direcionar nossa pesquisa sobre a temática desenvolvida. Inicialmente destacamos as pesquisas que contribuíram para os processos de ensino e de aprendizagem da Geometria Analítica. Em seguida relatamos a importância de se realizar investigações sobre livros didáticos. Para finalizar, apresentamos um estudo do objeto matemático, o qual servirá de apoio para nossa pesquisa.
Esse capítulo mostra-se relevante para nosso trabalho, pois apresenta contribuições do âmbito da Educação Matemática, auxiliando dessa forma a sintetizar nossa problemática de pesquisa. Realizamos nesse capítulo um levantamento em relação aos problemas existentes em torno do tema proposto, os resultados alcançados pelos pesquisadores e as sugestões apontadas pelos mesmos em relação ao ensino da Geometria Analítica e das investigações em torno dos livros didáticos.
1.1 Pesquisas sobre o Ensino da Geometria Analítica
Destacamos nesse momento pesquisas em Geometria Analítica, desenvolvidas na área da Educação Matemática, em diferentes níveis de ensino, pela dificuldade de encontrarmos estudos destinados ao ensino superior. A realização dessa análise é relevante, pois dessa forma demonstra a pouca ênfase aos trabalhos em Geometria Analítica no Espaço. A busca por tais pesquisas ocorreu por meio da consulta ao banco de teses e dissertações da Capes, além de banco de teses de Instituições educacionais de nível superior tanto no Brasil, como no exterior, além de sites de busca nacionais e internacionais utilizando palavras-chave, tais como: Geometria Analítica, Geometria Analítica no Espaço, Reta no Espaço.
Analítica, por meio de atividades de resolução de problemas envolvendo ponto, reta e distâncias privilegiando o processo de construção dos conceitos matemáticos.
Para a realização das atividades, a turma investigada foi dividida em grupos e trabalhou em horário regular de aula, totalizando aproximadamente vinte horas-aula. No que se refere ao procedimento didático, as atividades foram desenvolvidas de forma orientada e estimulada criando-se condições que possibilitassem o envolvimento do aluno na busca de soluções alternativas para a resolução dos problemas apresentados.
Dentre as atividades elaboradas por Sidericoudes (1998) para o micromundo da Geometria Analítica, podemos destacar como exemplo a situação representada no quadro 1:
Quadro 1: Atividades elaboradas para o micromundo da Geometria Analítica
Fonte: Sidericoudes (1998, p. 5)
Com base nos resultados alcançados a autora pôde inferir que o ambiente favoreceu a realização das atividades pelos alunos da forma que eles consideraram ser a mais adequada. A liberdade de representação da linguagem Logo fez com que os alunos se sentissem seguros na resolução dos problemas aplicados. Além disso, os conteúdos de Geometria Analítica trabalhados durante as atividades aplicadas foram manuseados e compreendidos pelos alunos, possibilitando aos mesmos a “aprenderam Matemática”, “fazendo Matemática” (SIDERICOUDES, 1998).
compreensão de outros conceitos da Geometria Analítica, desenvolvidos em momentos anteriores à atividade proposta.
A proposta apresentada por Sidericoudes (1998) demonstra a preocupação da pesquisadora em elaborar uma atividade na qual o aluno participe do processo de construção dos conceitos de Geometria Analítica, uma vez que no ensino tradicional o conteúdo é abordado apresentando-se primeiramente os conceitos e depois solicitando a resolução de exercícios normalmente extraídos de um livro didático.
Ao analisarmos o trabalho de Sidericoudes (1998) percebemos o uso de softwares viabiliza a compreensão dos conceitos de Geometria Analítica, mas de acordo com pesquisas na área da Educação Matemática é necessário também observar as abordagens presentes nos livros didáticos utilizados pelos professores. Assim, diferentemente dessa autora, dedicamo-nos a investigar livros didáticos utilizados no ensino superior no que se refere ao estudo da Reta e do Plano no Espaço.
A pesquisa realizada por Osta (1990) teve como intuito estudar a possibilidade de recuperar durante o ensino de Geometria Analítica, a relação entre padrões espaciais e sua modelagem, por meio de representações gráficas. Tal relação se manifesta por meio da estruturação do objeto, e a construção de uma ordem espacial ao longo de cada uma das principais direções do espaço.
Osta (1990) testou suas atividades com alunos do ensino secundário por três vezes em uma oficina de informática, na região de Grenoble. Cada experimento foi realizado em duas sessões de duas horas cada, sendo tal experimento realizado com oito alunos que foram solicitados a trabalhar em pares, cada par com um computador. Para recolher as informações, a autora utilizou como instrumento de coleta de dados notas de observadores (um observador por par), áudio-gravações e arquivos de computador gravados, contendo desenhos produzidos pelos alunos
Figura 1: Representação de um cubo
Fonte: Osta (1990, p. 28)
A proposta apresentada pela pesquisadora consistia na realização de projetos para a construção de cubos utilizando ferramentas gráficas simples e chegando o mais próximo possível da construção feita em um ambiente de lápis e papel.
As análises dos dados coletados, objetivou identificar a relação entre as concepções dos estudantes e a situação vivenciada. Tais situações referem-se ao problema da interação entre alunos e computador e às interações entre os alunos (trabalho em pares promove conflito sócio cognitivo e a necessidade de argumento).
Após a análise dos resultados, Osta (1990) conclui que o computador pode desempenhar um papel importante para o ensino, a saber: “ele permite a construção de situações-problema nas quais a validação de trabalho dos alunos é interna à situação pela implementação de meios de controle ... os alunos podem decidir se a sua construção de um componente é correta ou não” (Tradução nossa, p.47). A pesquisadora também levanta a questão das escolhas didáticas feitas pelo professor, o qual tem uma ampla gama de escolhas que podem promover um processo de aprendizagem controlado.
Concordamos com Osta (1990) quando aponta sobre as escolhas didáticas que o professor possui para realizar o processo de aprendizagem, mas por vezes, recorre unicamente ao livro didático. Por essa razão, nossa pesquisa sobre análise de manuais didáticos de Geometria Analítica no Espaço pode contribuir no âmbito do ensino.
dinâmica, com o intuito de favorecer a formação de futuros professores de Matemática. Para nortear sua pesquisa Richit (2006) se preocupou em responder a seguinte questão: Como trabalhar com projetos em Geometria Analítica, usando software de geometria dinâmica, visando a favorecer a formação de futuros professores de Matemática?
Para obter os dados para sua pesquisa Richit (2006) investigou seis alunos em Regime Especial de Recuperação na disciplina de Geometria Analítica do Curso de Matemática da Unesp de Rio Claro, os quais foram agrupados em duplas e trabalharam durante nove sessões (3 horas cada) na elaboração de atividades didáticas de Geometria Analítica. A pesquisadora procurou promover conversas durante os encontros no intuito de saber como os licenciandos avaliavam a estratégia de trabalho adotada na investigação no que se refere à formação tecnológica e específica. As atividades elaboradas constituíram-se nos projetos de cada dupla, as quais foram pensadas como uma forma de promover a formação tecnológica, específica e pedagógica dos futuros professores de Matemática.
Nos resultados encontrados a partir dessa pesquisa, pode-se observar as indicações dos alunos investigados acerca da necessidade de se colocar o futuro professor, durante a sua formação, em contato com os recursos tecnológicos disponíveis, preparando-o para enfrentar os desafios de sua profissão, além de estimular o desenvolvimento de habilidades de uso pedagógico destes recursos, o que contribuirá com o processo de construção do conhecimento desse futuro docente.
Ao analisar a intervenção realizada, a autora citada inferiu que o uso do software, como o Geometricks, favoreceu a visualização de conceitos e propriedades que foram tratados nas atividades desenvolvidas pelos alunos. Tal pesquisadora também sustenta que tais atividades propiciaram a compreensão de conceitos e estimularam a investigação matemática, contribuindo na construção de saberes matemáticos.
desenvolvimento de competências de uso pedagógico das mídias informáticas, assim como permitem ampliar o conhecimento do recurso que está sendo utilizado” (p.14). A autora também acredita que o trabalho com projetos em Matemática ou em outra disciplina pode ser realizado com atividades distintas das que foram desenvolvidas no estudo realizado, como por exemplo, a elaboração de campanhas de conscientização, jornais escolares, peças de teatro, exposições de pesquisas ou trabalhos realizados na escola, feiras sobre assuntos disciplinares etc., de modo que este material seja repassado à comunidade.
A investigação realizada por Richit (2006) chamou nossa atenção pelo fato da autora se preocupar com o desenvolvimento de projetos em Geometria Analítica, para favorecer a formação de futuros professores de Matemática. Assim, constatamos a pouca ênfase que tem sido dada às pesquisas em Geometria Analítica no Espaço e, por conseguinte, nossa pesquisa segue um caminho oportuno para tal abordagem.
No estudo realizado por Bernard e Thoaldo (2009) são apresentados diferentes cenários utilizando o software de geometria dinâmica Cabri-Géomètre como ferramenta para o ensino e a aprendizagem da Matemática em Cursos de Engenharia de uma universidade no estado do Paraná, os quais poderão ser utilizados para o ensino a distância. Os autores mostram a possibilidade da obtenção de medidas deáreas e volumes de poliedros irregulares em tempo real utilizando a “Macro Construção” do Cabri (LABORDE, 1999, apud BERNARD E THOALDO, 2009), que possibilita a obtenção dos valores procurados apenas com os vértices da figura. Apresenta-se, também, um cálculo de medidas de áreas no espaço pela generalização do Teorema de Pitágoras.
Dentre os objetivos apontados para realização dessa pesquisa, podemos destacar que os autores pretendiam:
a) Participar de forma fundamentada com uma contribuição aos processos de ensino e deaprendizagem da Matemática e de sua integração nas conexões entre o sistema escolar e social na área da Matemática (CARRETERO, 1997, apud BERNARD E THOALDO, 2009);
c) Conduzir o aluno a resolver problemas geométricos por um enfoque que lhe permita conjecturar, modelar, experimentar, exemplificar, generalizar e verificar (MASON, 1982, apud BERNARD E THOALDO, 2009);
d) Utilizar a geometria intuitiva e a dedutiva que, juntas, devem contribuir para o aprimoramento do processo de aprendizagem em Matemática, não meramente pela ilustração geométrica, mas, sobretudo, pela validação da construção numa dada Teoria Geométrica (MARIOTTI, 1999, apud BERNARD E THOALDO, 2009);
e) Possibilitar as soluções gráficas e analíticas simultâneas em tempo real (BERNARD, 2001, apud BERNARD E THOALDO, 2009).
f) Proporcionar um enfoque construtivista aos processos de ensino e de aprendizagem (BODEM, 1999, apud BERNARD E THOALDO, 2009).
Para realização de sua pesquisa, Bernard e Thoaldo (2009) selecionaram alguns problemas métricos que dão enfoque especial aos métodos geométricos cujas soluções podem ser encontradas adotando-se uma abordagem que relaciona a geometria intuitiva e a dedutiva. Os problemas foram aplicados para turmas dos Cursos de Licenciatura em Matemática e Engenharia Ambiental que estavam cursando a disciplina Geometria Analítica, totalizando oitenta alunos. Segundo os autores, os alunos que participaram do experimento comprovaram um melhor desempenho e aproveitamento superior aos estudantes de anos anteriores.
Bernard e Thoaldo (2009) constataram que a geometria dinâmica pode promover a ligação entre a Álgebra e a Geometria e contribuir significativamente para a aprendizagem em matemática. Os resultados obtidos on-line permitiram inferir que o enfoque computacional proporcionado pela Geometria Dinâmica configura-se como uma alternativa didática para os processos de ensino e de aprendizagem da Matemática, além de atuar como agente de motivação e desenvolvimento do raciocínio lógico-espacial.
de teoremas e sem dúvida atuar como agente de motivação e desenvolvimento do raciocínio lógico.
O trabalho de pesquisa realizado por Colpo et al (2009) tem como intuito relatar a prática pedagógica realizada numa escola da rede estadual de Santiago (RS), com uma turma do 3º ano do Ensino Médio. Os autores elaboraram sequências de atividades fundamentadas nos princípios da Engenharia Didática, considerando atividades que conduzissem os alunos a experimentar, interpretar, visualizar, induzir, conjeturar, abstrair e generalizar os conceitos de Geometria Analítica, surgindo naturalmente daí o processo de argumentação e dedução das leis.
A aplicação das sequências de ensino ocorreu no laboratório de informática da escola investigada, com um total de quatorze horas/aula, distribuídas em cinco aulas semanais. Com base nos protocolos de pesquisa, os autores constataram que os recursos utilizados para o desenvolvimento das aulas, bem como as explicações ministradas pelos pesquisadores contribuíram para a motivação e aprendizagem significativa dos alunos em relação aos conceitos trabalhados de Geometria Analítica.
Nesse sentido, Colpo et al (2009) entendem que é possível explorar diversos outros conteúdos matemáticos com auxílio das novas tecnologias, ganhando-se tempo, criando-se motivação e aumentando-se o nível de compreensão dos alunos. No entanto, os autores alertam que o ensino com o uso dos recursos tecnológicos somente terá significado se o professor estiver preparado para elaborar um planejamento que explore ao máximo os conteúdos programáticos.
A pesquisa de Lebeau (2009) se propõe a investigar sobre o ensino e aprendizagem da Geometria Analítica tridimensional no ensino secundário refletindo tanto sobre questões epistemológicas quanto didáticas.
Lebeau (2009) realiza uma análise da transposição didática que permite explicar a inversão didática que consiste em ensinar a Geometria Analítica como um subproduto da Álgebra Linear. Em sua análise a autora destaca os seguintes aspectos:
1. Existe uma ruptura com o empirismo, com base nos contrastes entre as abordagens de Euclides e Hilbert: os pontos, retas e planos não são apenas especificados, segundo Hilbert, pelos axiomas que experimentam as relações entre eles, tal como “dois pontos determinam uma e somente uma reta”. Mas, segundo Euclides, as definições que são esperadas, levam em conta, de um modo empírico, a natureza dos objetos sobre os quais se trabalha.
2. O projeto de prolongar a Geometria axiomática para englobar o cálculo de coordenadas: na Geometria sintética é interessante ir adicionando os axiomas ou teoremas puramente geométricos que permitem incorporar de maneira coerente os sistemas de coordenadas. Por isso está longe de ser uma especificação geométrica da Álgebra Linear em que os primeiros objetos são vetores, os espaços vetoriais e o produto escalar como forma simétrica bilinear positiva.
Anglo-saxônica, uma ruptura com as experiências sensíveis e acesso aos espaços abstratos).
4. Uma inversão didática ao ensinar a Geometria como sendo um produto da álgebra linear: ao invés de ensinar a Geometria de maneira sintética e analítica para deduzir gradativamente os elementos que serão constituídos na Álgebra Linear, como ocorreu historicamente, se começa a ensinar pela Álgebra Linear para vir depois a Geometria como sendo uma de suas especificações.
5. Característica da engenharia didática: a reforma no ensino da Geometria permite estabelecer pontos entre o ensino secundário e o ensino superior, tais como: um modelo de Geometria para o “espaço físico”, uma ordenação dedutiva local, a questão do formalismo, um projeto no âmbito da Geometria Euclidiana, uma validação sócio construtivista do formalismo algébrico e o ensino da Geometria Analítica tridimensional insere-se em uma praxeologia do tipo “modelização” e rompe com a transposição habitual.
tecnológico justificando a modelização utilizada, como também analisa em que os ostensivos mobilizados são emblemáticos de um ou outro modo de pensar.
A partir dessa reflexão a pesquisadora coloca as seguintes questões para os alunos:
Questão 1: Que representação, no espaço, o conjunto de pontos incluindo as coordenadas (x, y, z) verificam a equação = − + 3 ? Qualquer ponto verifica a equação? Justifique sua resposta.
Questão 2: O que representa a equação = ² ? Questão 3: E a equação = ² ?
Questão 4: E a equação = ²+ ² ?
(LEBEAU, 2009, p. 254-255 - Tradução nossa).
Os resultados encontrados por Lebeau (2009) apontam que a maioria dos alunos interpretaram as questões 1 como sendo a equação de uma reta e a questão 2 foi interpretado como a equação de uma parábola no plano do sistema de eixos Oxy. A pesquisadora verificou a dificuldade dos alunos em organizar suas ideias de maneira racional e lógica, afirmando que a cota z não existe. Outra dificuldade encontrada por Lebeau (2009) refere-se à equação = +
, a qual, para alguns alunos, não está associada a equação canônica de um círculo no plano Oxy.
Em nossa pesquisa, nos referenciamos às variáveis didáticas apontadas pela pesquisadora citada por acreditarmos que apresenta aspectos que melhor se adaptam as análises das organizações matemática e didática presentes nos materiais didáticos que investigamos.
Em vista disso, acreditamos ser necessário e concludente a realização de uma investigação que contemple a Geometria Analítica no Espaço, abordando aspectos didáticos referentes ao ensino da Reta e do Plano e que caminhe para uma análise das organizações matemática e didática que podem se fazer presentes em livros didáticos destinados ao ensino superior.
1.2 Pesquisas envolvendo a TAD e a Geometria Analítica
Nessa parte de nossos estudos apresentamos um levantamento de pesquisas que se dedicaram a investigar o ensino de Geometria Analítica, utilizando a TAD como referencial teórico, bem como quais conclusões foram alcançadas e ainda que sugestões foram apontadas por tais investigadores. Ao realizarmos um levantamento dessas pesquisas no Banco de teses e dissertações da Capes, bem como anais de eventos de Educação Matemática, periódicos, dentre outros, nos deparamos com dois trabalhos contemplando a temática em questão. No que segue apresentamos os trabalhos encontrados.
A pesquisa desenvolvida pela autora teve como objrtivo analisar de que forma os autores de materiais didáticos para o Ensino Médio organizaram as tarefas propostas envolvendo provas e demonstrações sobre o conteúdo de Geometria Analítica Plana. A opção da autora em realizar uma investigação do livro didático se deu pelo fato da mesma atuar na Rede pública Estadual de Ensino e ter em mãos um material de apoio (Caderno do Professor) como um recurso de ensino elaborado por autores dentre os quais alguns são da área da Eduação Matemática.
As bases teóricas que subsidiaram as análises dos resultados encontrados na pesquisa de Varella (2010) foram a Teoria Antropológica do Didático de Yves Chevallard (1999), quanto aos conceitos de organização praxeológica e a tipologia de provas de Nicolas Balacheff (1988).
Após definir os materiais didáticos a serem analisados, Varella (2010) buscou analisar quais organizações didática e matemática presentes nestes materias no que se refere ao estudo da equação da Reta em Geometria Analítica. As análises da autora foram norteadas por quatro questões, concernentes ao estudo de provas e demonstrações e apresentando pelo menos uma tarefa a ser realizada tendo por justificativa as técnicas escolhidas pelos autores, as quais poderão ser mobilizadas pelos alunos:
• Questão 1: Qual a abordagem utilizada pelo autor para introdução ao conteúdo Geometria Analítica?
Tarefa 1: Apresentar parte introdutória à Geometria Analítica. • Questão 2: Como os conceitos matemáticos que antecedem o
estudo da Equaçãoda Reta são apresentados?
Tarefa 1: Identificar quais conceitos são trabalhados precedentes ao estudo da equação da Reta.
Tarefa 2: Identificar as abordagens utilizadas para descrever esses conceitos.
• Questão 3: Na introdução dos conceitos que antecedem o Estudo da equação da Reta são utilizados os termos propriedades, teorema, prova ou mesmo é feita alguma diferenciação entre eles? Tarefa 1: Identificar a utilização dos termos nas tarefas executadas e propostas.
Tarefa 2: Identificar se é apresentada alguma diferenciação entre os termos utilizados pelo método axiomático-dedutivo.
• Questão 4: As tarefas propostas, voltadas ao estudo da Equação da Reta, apresentam demonstrações ou provas?
Tarefa 1: Identificar as tarefas propostas para o estudo da equação da Reta.
Tarefa 2: Identificar, por meio das tarefas, a utilização de provas ou demonstrações.
diferentes registros de representação, tais como algébricos, figurais ou textuais por meio de exemplos dentro ou fora do contexto matemático.
Quanto ao estudo da equação da reta, Varella (2010) observou que todos os materiais apresentam pelo menos uma das formas de representação da reta: equação geral, equação reduzida, equação paramétrica e equação segmentária. Ao analisar as tarefas executadas pelos autores das coleções analisadas no que referentes à equação da reta, a autora identificou apenas uma atividade que utilizava o termo “analisar se” e destaca que esse tipo de tarefa torna-se interessante em relação à análise da resposta encontrada, pois possibilita ao aluno oportunidades de explorar, conjecturar, reformular, explicar e validar suas resoluções.
Varella (2010) conclui, diante das abordagens realizadas, que existe uma ausência de definição para os termos que constituem o método dedutivo, assim como falta clareza na organização Matemática ao se demonstrar um teorema. A autora também identificou que, na maioria dos livros didáticos analisados, não está explícito se uma relação representa uma propriedade, um teorema ou deduz apenas uma fórmula.
O segundo trabalho que encontramos foi de Andrade (2012). Em sua tese o autor demonstra uma preocupação com as organizações matemáticas propostas para o ensino médio em relação a Geometria Analítica Plana e aponta que tais organizações apresentam conexões internas reduzidas ou mesmo nenhuma, além da ausência de conexões com outros tópicos da Matemática.
Em relação as conexões internas, o autor observa que as organizações matemáticas apresentam praxeologias pontuais, tais como calcular a distância entre dois pontos e calcular o módulo de um vetor, em diferentes momentos do ensino, aparentemente, sem qualquer conexão, ainda que utilizem a mesma técnica, decorrente do Teorema de Pitágoras como tecnologia.
Andrade (2012) encontrou na Teoria Antropológica do Didático, especificamente na noção de Tarefas Fundamentais, os subsídios necessários para analisar e desenvolver organizações matemática e didática para os estudos de Geometria Analítica Plana. Dentre as Tarefas Fundamentais eleitas pelo pesquisador para desenvolver os momentos didáticos de um processo de estudo de Geometria Analítica Plana, destacam-se as seguintes tarefas:
• Tipo de Tarefa Fundamental 2: calcular a distância entre dois pontos. • Tipo de Tarefa Fundamental 3: encontrar a equação do segmento de reta.
Essas tarefas, apontadas por Andrade (2012), foram evidenciadas com base nas análises das organizações matemáticas propostas em livros didáticos, como também no levantamento histórico e epistemológico da Geometria Analítica presente na obra de René Descartes e permitiram ao autor perceber a potencialidade de Tarefas Fundamentais na Geometria Analítica. A partir dessas investigações, o autor aponta que o problema da desarticulação entre os conteúdos ocorre também em outros níveis de ensino, além do ensino médio, mencionando que tal problema ocorre também no nível superior, como entre a Geometria Sintética e a Geometria Analítica e ainda entre áreas como a álgebra e a geometria.
Ao analisar a proposta curricular brasileira em relação a Geometria, Andrade (2012) verifica que essa área da Matemática encontra-se estabelecida nos setores da Geometria Plana, Geometria Espacial, Geometria Métrica e Geometria Analítica. Em relação a Geometria Analítica, o autor destaca que a mesma é caracterizada pelo “método cartesiano” sustentada pelas técnicas da Álgebra Linear e no ensino básico tem se reduzido a “um simples transporte gráfico de pontos e curvas, um modo de reconhecer as formas das seções cônicas a partir de equações expressadas de maneiras mais ou menos normais” (Ibid, p. 97).
Dentre os tipos de tarefas para o estudo da Geometria Analítica no Plano, a comunidade investigada por Andrade (2012), após a apresentação das práticas destacou como importante: localizar pontos no plano, determinar a distância entre dois pontos, escrever a equação da reta, determinar a medida de um segmento a partir de outros segmentos.
A construção de organizações praxeológicas para a Geometria Analítica Plana, adotada pela comunidade de prática envolvida na pesquisa de Andrade (2012) mostrou-se árdua e complexa, apresentando alguns conflitos de relações pessoais com as novas relações institucionais com saberes nas organizações didáticas com saberes. Também ficou evidente nessa comunidade, que é tarefa do professor “construir uma organização a partir de recortes de organizações matemáticas presentes nos livros-textos do ensino básico”. (Ibid, p.162)
A partir da leitura dessas pesquisas foi possível perceber os problemas que existem em relação ao ensino de Geometria Analítica nos diferentes níveis de ensino, como também em relação ao ambiente em que se desenvolve. Tais investigações mostraram-se relevantes para nortear o desenvolvimento de nosso trabalho, em particular as que apresentam relação direta com o tema de nossa pesquisa, a saber: Lebeau (2009) por subsidiar nosso trabalho em relação às variáveis didáticas que possibilitaram analisar as diferentes articulações possíveis da Geometria Analítica no Espaço e Andrade (2012) por contribuir com sua pesquisa em relação ao referencial teórico apoiado nos parâmetros da TAD, apontando o papel funcional dos tipos de tarefas nas organizações matemática e didática de Geometria Analítica Plana.
Vale ainda ressaltar que a partir desses estudos preliminares foi possível constatar que apesar de encontrarmos estudos sobre a Geometria Analítica não constatamos pesquisas que tratassem sobre uma análise praxeológica referente à Geometria Analítica no Espaço como nos propomos a desenvolver. Desse modo, nos sentimos motivados a realizar este trabalho no intuito de colaborar com as pesquisas em Educação Matemática.
1.3 Estudo do Objeto Matemático
Por meio da apresentação dos conceitos referentes ao estudo da Geometria Analítica no Espaço temos a intenção de fazer um levantamento do objeto matemático, especificamente da Reta e do Plano, por meio de sua organização formal, conforme as indicações apontadas por Lebeau (2009). Tal estudo servirá de apoio em nossas análises no que se refere à descrição das tarefas apontadas nos materiais analisados.
1.3.1 O Plano
Como mencionado anteriormente, seguiremos as recomendações de Lebeau (2009) para abordagem do Plano no Espaço
Uma estratégia clássica, como designado por Lebeau (2009), para caracterizar o Plano, consiste em apresentar a equação + + + = 0 como uma propriedade da ortogonalidade. Desse modo, pode-se trabalhar uma equação do plano a partir de um ponto dado e de um vetor normal não nulo (cf. Figura 2).
Figura 2: Representação do plano dado um ponto e um vetor normal
FONTE: Lebeau (2009, p. 191)
Essa caracterização que conduz à equação cartesiana do plano pode ser demonstrada do seguinte modo:
Hipótese: seja P um ponto de coordenadas ( , , ) e um vetor normal não nulo.
Um ponto M qualquer de coordenadas ( , , ) pertence ao plano se, e
somente se, os vetores e são ortogonais. Por conseguinte: ∈ ↔ ⟘
↔ ( − , − , − ) ⟘( , , )
↔ − + − + − = 0
↔ + + − − − = 0
↔ + + + = 0 Pois, , , , , , são conhecidos por hipótese.
Conclusão: a equação + + + = 0 é uma equação cartesiana do plano .
Esta propriedade, sendo condição necessária e suficiente, caracteriza qualquer plano a partir de retas perpendiculares a uma reta dada, ou de modo mais preciso, os vetores ortogonais a uma vetor dado, o produto escalar nulo é condição necessária e suficiente para exprimir a ortogonalidade (LEBEAU, 2009).
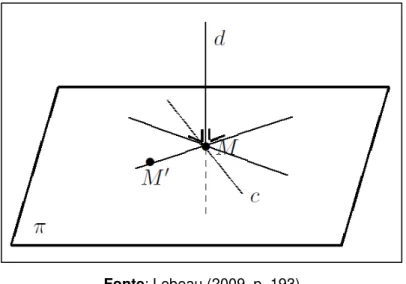
Outra estratégia para abordar o Plano, de acordo com a indicação de Lebeau (2009) é caracterizá-lo como um conjunto de retas perpendiculares a uma reta dada (Figura 3), em um de seus pontos .
Figura 3: Representação do plano como conjunto de retas perpendiculares
Fonte: Lebeau (2009, p.193)
e perpendicular a todas as retas do plano passando por qualquer ponto pertencendo a . Consequentemente, as retas ′ e são perpendiculares em e ′ pertencentes ao conjunto . Todo ponto de pertence, portanto, à uma reta de .
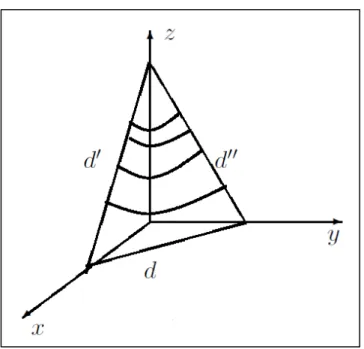
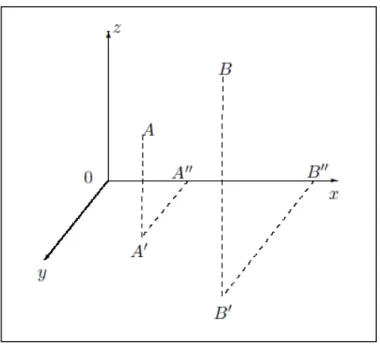
A abordagem do Plano também pode ser conduzida pela concepção desse objeto geométrico como uma superfície regular. Lebeau (2009) sugere que haja um questionamento inicial do tipo: “o que representa, no espaço, o
conjunto de pontos cujas coordenadas verificam a equação ! + 3 + − 2 =
0?” (p.194).
Uma das estratégias de resolução para essa questão é anular cada
variável da equação ! + 3 + − 2 = 0, interpretando a equação obtida como
uma reta do plano de coordenadas. Dessa maneira, ao considerar = 0, tem-se 3 + − 2 = 0 como a equação de uma reta d’ em xOy, ao considerar = 0, tem-se ! + 3 − 2 = 0 como a equação da reta d’ no plano xOz e ao considerar
= 0, tem-se ! + − 2 = 0 como a equação de d’’ no plano yOz. Portanto, é possível concluir que estamos lidando com um plano (Figura 4).
Figura 4: Representação do plano como superfície regular
Fonte: Lebeau (2009, p.194)
pressuposto que as equações paramétricas das retas já tenham sido objeto de uma institucionalização, pode-se dizer que:
Se k e k’ representam os parâmetros reais, as equações paramétricas das retas OA e BC são da forma:
Reta OA:# = $= $ %% = $ %
ou = $&
Reta BC:' == ((+ $+ $′(*( ((− − )))) = (+ $*( (− ))
ou = + + $′(+ − ,)
As retas serão secantes se, e só se, o sistema $& = + + $′(+ − ,) é compatível em $, $′ e possui uma única solução.
1.3.2 A Reta
Uma forma de abordar a Reta no Espaço, consiste em projetar os pontos sobre os planos de coordenadas, como aponta Lebeau (2009), verificando se suas projeções se encontram alinhadas e determinando se estes pontos também estão alinhados. Essa abordagem possibilita determinar dois tipos de caracterização das retas: a equação paramétrica e a equação cartesiana.
Assim, se considerarmos três pontos &, + e , cujas diferenças entre as coordenadas são proporcionais. Essa hipótese se exprime pela seguinte igualdade:
' ))− − %% = $(= $( ((− − %%)) )− % = $( (− %)
sendo k um número real.
Figura 5: Plano π paralelo ao eixo Oz
Fonte: Lebeau (2009, p.206)
Pode-se ainda realizar uma argumentação precedente na qual se aponta a interpretação em termos do plano paralelo a um eixo representado por uma equação do primeiro grau em , e no qual o coeficiente de uma variável é nulo.
O alinhamento das projeções &′, +′ e ,′ sobre o plano xOy pode ser estabelecido por meio de uma equação do tipo os + + = 0. Esta equação equivale a equação de um plano paralelo ao eixo Oz contendo &, + e ,′. Assim, por um lado, os pontos &′, +′ e ,′ estão alinhados e, de outra parte, a reta &&′ as retas ++′ e ,,′, bem como ao eixo Oz (pela definição de projeção paralela). Da mesma forma, se os pontos &′′, +′′ e ,′′ encontram-se alinhados, então a equação da reta que se compreende é da forma ′ + ′ + ′ = 0. Isto faz de um plano paralelo ao eixo Ox incluindo igualmente os pontos &, + e ,. Assim a intersecção de dois planos está alinhada se os dois planos são secantes.
Portanto, o alinhamento das projeções dos pontos iniciais no plano de coordenadas é traduzido pela escrita cartesiana a partir da proporcionalidade das diferenças de suas coordenadas e sendo da forma: + + = 0 e ′ +
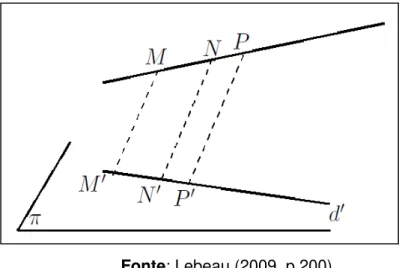
Outra forma de abordar a Reta é considerando três pontos alinhados , -e -e suas proj-eçõ-es *, -′ e ′ sobre um plano qualquer paralelamente a uma reta (Figura 6). Se a reta - é paralela à , as projeções são confundidas e assim pode-se chamar igualmente de alinhamento. Se os pontos , - e estão em , o resultado é trivial.
Figura 6: Representação do plano como superfície regular
Fonte: Lebeau (2009, p.200)
CAPÍTULO 2: FUNDAMENTOS TEÓRICOS DA PESQUISA
_______________________________________________________________
Nesse capítulo, destacamos a base teórica que norteou nossa pesquisa. Abordamos primeiramente a TAD com base nas ideias propostas por Chevallard (1999). Elucidamos em seguida as variáveis didáticas apontadas por Lebeau (2009) para o ensino da Geometria Analítica no Espaço.
2.1. A Teoria Antropológica do Didático (TAD)
No âmbito da didática da Matemática a TAD tem uma contribuição significativa, pois como afirma Almouloud (2007), tal teoria representa uma evolução do conceito de transposição didática2, bem como estuda as organizações praxeológicas didáticas planejadas para o ensino e a aprendizagem de organizações matemáticas. Tal praxeologia representa o produto de uma construção social e tem como finalidade específica, o estudo da Matemática.
Essa teoria busca estudar o homem diante do saber matemático, especificamente quando se depara com situações matemáticas. Assim, Chevallard (1999) utiliza o termo antropológico para situar o estudo da Matemática no interior do conjunto de atividades humanas e de instituições sociais. E é designada uma teoria do didático, pois é um estudo do objeto de estudo da didática.
A TAD mostra-se um instrumento relevante para analisar as práticas docentes e o estudo da Matemática em termos de praxeologias (organizações). Chevallard (1999) associa dois tipos de praxeologias para o saber matemático, a saber: a organização matemática (OM) e a organização didática (OD), isto é, as organizações dos conteúdos (o modo como é feita essa construção) e as organizações de ensino (a Matemática que é possível ser construída para desenvolvê-la em sala de aula).
2 Chevallard (1999, p.39) apresenta a definição de transposição didática como sendo: Um conteúdo do saber que tenha sido designado como saber a ensinar, sofre por conseguinte, um conjunto de transformações adaptativas que irão torná-lo apto a tomar lugar entre os objetos de ensino. O ‘trabalho’ que de um objeto de saber a ensinar faz um objeto de ensino é designado
Assim, entende-se que cada atividade matemática possui uma organização didática correspondente e que os conteúdos matemáticos, o conjunto de objetos matemáticos a serem trabalhados em sala de aula, apresentam uma forma específica de abordagem sendo necessário que o sujeito reorganize seus conceitos e mobilize seus saberes a respeito.
A palavra praxeologia é constituída por dois termos gregos, práxis (prática) e logos (razão), os quais encontram-se integrados, Chevallard; Bosch; Gascón (2001) explicam que, “como dois lados de uma moeda, não há práxis sem logos, mas também não há logos sem práxis” (p. 251). Portanto, as praxeologias podem ser descritas por meio dos componentes tarefa e técnica, referindo-se ao saber-fazer, e à tecnologia e teoria, as quais constituem o saber. Chevallard (1991) apresenta notações próprias para identificar cada uma dessas componentes praxeológicas da seguinte forma: tarefa pelo símbolo (t), tipos de tarefas pelo símbolo (T), técnica pelo símbolo (ô), tecnologia pelo símbolo (θ) e teoria pelo símbolo (Θ). De acordo com o autor, a tarefa faz parte de um conjunto mais amplo designado de tipos de tarefas, pois t∈T. O conjunto de técnicas, tecnologias e teorias organizadas para um certo tipo de tarefa é chamado de Organização Praxeológica.
Nesse sentido a tarefa é uma atividade específica, que Chevallard (1999) define como uma ação em que para executá-la, alguns conhecimentos serão mobilizados. Podemos citar como exemplo de tarefa, a seguinte situação em Geometria Analítica:
Tipo de tarefa (T): Calcular a distância entre dois pontos.
Tarefa (t): Calcular a distância entre os pontos A=(7, 3, 4) e B=(1, 0, 6).
representa o procedimento adotado para solucionar uma determinada tarefa (t) de certo tipo de tarefa (T).
Nesse sentido, uma técnica não representa uma decisão aleatória, pois não se usa qualquer técnica para resolver uma tarefa. Conforme a TAD, a técnica para resolver uma dada tarefa não é única, mas a escolha de uma técnica sempre vem acompanhada de uma justificativa. Assim, existe um conhecimento matemático para justificar a sua aplicação naquela tarefa e não em outra, e também existe um conhecimento didático que justifica a escolha daquela técnica ao invés de outra que produziria o mesmo resultado matemático. Tais conhecimentos, matemático e didático, devem explicar a razão para ela funcionar naquele caso específico e por quais motivos ela seria a técnica mais indicada. No exemplo citado anteriormente podemos usar como técnica:
Técnica (ô): Utilizar a fórmula d(A,B)= .( − ! )² + ( − ! )² + ( − ! )² para calcular a distância entre dois
pontos. Segundo os dados apresentados na questão ! = 7 1 = 1; ! = 3 1 = 0 e ! = 4 1 = 6. Logo, a distância entre os pontos A e B será .(7 − 1) + (3 − 0)² + (4 − 6)² = √49 = 7
Para o exemplo mencionado acima, definimos uma técnica (ô) na realização dessa tarefa, no entanto, toda técnica precisa ser justificada, isto é, um campo teórico para fundamentá-la. A esse bloco, constituído por um tipo de tarefa e uma técnica, Chevallard (1999) designa de bloco prático-teórico e pode ser identificado como um saber-fazer. Esse saber-fazer não se apresenta de forma isolada, pois toda técnica exige, pelo menos, uma justificativa, quer dizer, exige um “discurso lógico” (logos) que lhe sustenta, denominado de tecnologia (θ).
Considerando o exemplo citado e a técnica usada para resolução dessa tarefa, é possível justificá-la por meio da fórmula da distância entre dois pontos e das propriedades das operações aritméticas.
Por outro lado, a tecnologia (θ) exige uma justificativa em um nível superior que Chevallard (1999) denomina de teoria (Θ). A este bloco, referente ao papel que a tecnologia e a teoria possui em relação à técnica, Chevallard (1999) denomina de bloco tecnológico-teórico (θ/Θ), pois está relacionado com o “saber”. Como exemplo desse bloco podemos considerar os campos da Matemática, tais como: Geometria, Geometria Analítica e Álgebra.
Na perspectiva da TAD o componente mais amplo considerado em uma praxeologia é a teoria que transmite a ideia de generalidade, abstração. Sales (2010) indica que pode ser equivalente a um contemplar o cenário em busca das causas, dos objetivos e dos porquês.
A luz da TAD muitas vezes o que propomos como tecnologia pode ser considerado como a própria teoria. Mas, fica evidente, que essa alteração de posição depende da complexidade da tarefa e do nível de ensino a que foi destinada.
Observamos então, que uma organização didática não é determinada por uma ação isolada do professor, pois os fatores sociais e estruturais da disciplina influenciam fortemente na ação do professor no momento em que ele decide a organização didática que orientará a atividade proposta. Também é possível notar que a atitude do estudante mediante as atividades de estudo, sofre influência desses fatores.
Refletindo sobre as ideias da TAD recordamos que a teoria sugere um modelo de estudo da atividade matemática. Tal atividade consiste em “manipular” os objetos matemáticos, ostensivos ou não-ostensivos, e designa-se praxeologia. Uma praxeologia é composta de duas partes com dimensões distintas, a saber: a prática e a razão.
2.1.1 Os objetos ostensivos e não ostensivos
(1999, apud ALMOULOUD, 2007) ainstituir uma dicotomia fundamental que os diferencia em dois tipos: objetos ostensivos e objetos não-ostensivos.
A atividade matemática, segundo a TAD, se realiza mediante uma pluralidade de registros (escrito, gráfico, verbal, gestual e material). Sendo a Matemática uma ciência essencialmente abstrata, seus elementos fundamentais ou conceitos, não são tangíveis senão pela mediação de signos. A TAD não atribui valor aos signos e não os classifica em mais ou menos apropriados. Uma figura, uma descrição verbal ou um gesto pode desempenhar o mesmo papel ou possuir o mesmo significado.
O termo ostensivo é original do latim (ostendere) e significa mostrar, apresentar, apelar aos sentidos. Os ostensivos são todos os objetos manipuláveis na execução de uma atividade matemática. Por sua vez, os não-ostensivos são objetos que existem de forma institucional, tais como as ideias, as instituições ou os conceitos e podem ser invocados mediante a manipulação adequada de certos ostensivos apropriados (ALMOULOUD, 2007).
Na execução de uma atividade humana, em particular a atividade matemática, existe uma relação entre objetos ostensivos e não-ostensivos. No campo da antropologia, Almouloud (2007) aponta que é possível dizer que “o cumprimento de toda tarefa envolve a manipulação de ostensivos regulados pelos não-ostensivos, fazendo com que os objetos ostensivos tornem-se a parte perceptível da atividade” (p.120).
2.2.Variáveis Didáticas na perspectiva de Lebeau (2009)
No estudo proposto por Lebeau (2009) para o ensino da Geometria Analítica no Espaço, a autora realiza uma análise de variáveis didáticas partindo de questionamentos tais como: Por onde começar? Pelas retas? Pelos planos? Pelas equações cartesianas ou pelas equações paramétricas? A autora revela que no âmbito da transposição didática habitual os professores começam indiferentemente pela reta ou pelo plano, o que torna possível as definições vetoriais dos objetos geométricos, com base em conhecimentos prévios referentes ao conceito de vetor. Assim, em suas análises, Lebeau (2009) decide partir do estudo dos eixos sobre o plano, depois com as retas e as estratégias que permitem determinar o plano a partir das retas e, em última análise, mostrar o papel fundamental da figura do paralelogramo, por um lado, e a concepção de translação por outro. Destacaremos a seguir as análises feitas pela autora.
2.2.1.Começar pelo plano?
A ideia de começar o estudo de Geometria Analítica pelo plano, aponta Lebeau (2009), parece absurda, pois o objeto plano pode ser considerado, a princípio, mais complexo que o objeto reta, pois depende do registro que é visto. O registro cartesiano, explicita a pesquisadora, parece dificilmente acessível no que concerne à reta do que quanto aos planos, uma vez que a reta é determinada por duas equações cartesianas do plano e a variedade de equações possíveis parece problemática para certos alunos, devido a interpretação que esta implica em termos de sistema e de interseção. Enquanto que o plano é determinado por somente uma equação que, se apresenta ostensivamente como o prolongamento de uma equação já reencontrada na Geometria Analítica do plano do tipo ax + by + c = 0, que pode representar tanto uma vantagem como uma desvantagem.
que faz abstração do conceito de vetor, assumindo que o produto escalar foi trabalhado analiticamente no contexto da ortogonalidade da reta.
Lebeau (2009) destaca ainda que um plano pode ser caracterizado como um conjunto de retas perpendiculares a uma reta dada d em um de seus pontos
M, conforme ilustrado na figura 7.
Figura 7: Conjunto de retas perpendiculares a uma reta dada d
Fonte: Lebeau (2009, p. 193)
A autora conclui que a aproximação de uma caracterização cartesiana do plano, via ortogonalidade de vetores, conduz a um questionamento: a definição de um objeto da Geometria Afim por meio de conceitos da Geometria Métrica e um trabalho prévio sobre o objeto plano demanda um custo cognitivo. Portanto, Lebeau (2009) aponta que não parece conveniente adotar esta caracterização do plano que se assenta sobre a ortogonalidade.
Em outra abordagem do plano, Lebeau (2009) sugere que o trabalho com os alunos inicie com a seguinte questão: “o que representa, no espaço, o
conjunto de pontos cujas coordenadas verificam a equação ! + 3 + − 2 =
0?
Tal abordagem, explicita a autora, pode conduzir os alunos a pensar em
anular cada variável da equação ! + 3 + − 2 = 0, interpretando a equação
assim obtida como uma reta do plano de coordenadas. A partir desse pensamento, considerando z=0 3 + − 2 = 0 seria a equação de uma reta d
Oxz e considerando x=0 ! + − 2 = 0 a equação de d’’ no plano Oyz. Portanto,
a partir da figura 8, os alunos podem concluir que estamos lidando com um plano. Figura 8: Caracterização do plano Oyz
FONTE: Lebeau (2009, p. 194)
Ainda sobre essa abordagem, Lebeau (2009) destaca que é possível o professor questionar os alunos se pode existir uma superfície curva cuja interseções como os três planos de coordenadas sejam retas, como sugerido na figura 9.
Figura 9: Interseções de curvas com planos
A autora explica que os alunos podem utilizar a estratégia de substituir a
coordenada z por 4 na equação ! + 3 + − 2 = 0, obtendo assim a equação 3 + = 0 que representa uma reta paralela a d. Com a mesma estratégia o aluno poderá substituir z por 3 e desse modo, obterá uma outra reta paralela a
d, o que pode convencê-lo de que a superfície não pode ser curva, pois se constitui de um conjunto de retas. Nesse momento, Lebeau (2009) ressalta que o professor poderá argumentar que uma folha de papel estriada de paralelas e curvas representa um conjunto de retas paralelas que não formam um plano, pois as retas paralelas não dependem de um reta dada. Para tal situação
deve-se proceder da deve-seguinte maneira: substituir z por k, na equação 3 + + !$ − 2 = 0 nos conduz a uma reta paralela a d com os pontos em que a cota é igual a k. Essa reta corta o plano Oxz no ponto (789
: , 0, $) e esse ponto de
coordenadas verifica a equação de reta d’. O professor pode concluir que estamos frente a um conjunto de retas paralelas contidas todas em um plano, conforme figura 10.
Figura 10: Conjunto de retas paralelas
Fonte: Lebeau (2009, p. 195)