The Plethysm Tehnique Applied to the
Classiation of Nulear States
J.A. Castilho Alaras
InstitutodeFsiaTeoria,UNESP,01405-900, S~aoPaulo,Brazil
J. Tambergs, T. Krasta,J.Ruza,
NulearResearh Center,LV-2169,Salaspils,Latvia
and O.Katkeviius
InstituteofTheoretialPhysis andAstronomy,2600Vilnius,Lithuania
Reeivedon7August,2001
Ashortsummaryofthetheoryofsymmetrigroupandsymmetrifuntionsneededtofollowthe
theoryofShurfuntionsandplethysmsispresented. Onethendenesplethysm,givesitsproperties
andpresentsaproedureforitsalulation. Finally,someapliationsinatomiphysisandnulear
struturearegiven.
I. Introdution
The plethysm operation was introdued by
Littlewood[14℄ in 1936 as a third type of Shur
funtion[5, 6℄ multipliation and only later on it has
reeivedthisname.
PlethysmsplayafundamentalroleinPhysis
when-everone appliesgrouptheoryand anleadto
remark-ablesimpliationin thetheoryofomplexspetra.
Although plethysms havebeen extensivelystudied
by matematiiansin thepast[12℄-[20℄and even
nowa-days,surprisingly,withrareexeptions[2,3,35,38℄this
powerfultehniquehasbeenunreognizedbyphysiists.
Themainreasonofthisworkistopresentthis
pow-erful tehnique to the theoretial physiists omunity
andshowhowitanbeveryuseful. Basiallyitsutility
reliesinthedeterminationofthebranhingrulesof
irre-duible representations (irreps) of aontinuous group
when onsidered as irreps of one of its subgroups, a
veryommonsituationwhenoneappliesgrouptheory,
in partiularinthelassiationofstatesofaphysial
systemofidentialpartiles.
II. Shur Funtions and Plethysms
Inthis setion wewill initially introduethe basi
notionsofthesymmetrigroupS(n)neededtothe
un-derstanding ofthe notationused in theplethysm
the-ory. Laterwewill dene plethysm, expose its
proper-omputeplethysms of a given degree exploiting these
generalresultsandproperties.
II.1 Basi Notions of Symmetri Group and
Shur Funtions
The symmetrigroupS(n) is thegroupof
permu-tationsofnobjetsandhasn!elements. Eahelement
isdenotedby
P=
1 2 3 ... n
p
1 p
2 p
3
... p
n
(1)
withthemeaningthattheelement1isreplaedbyp
1 ,
the element 2 by p
2
and so on, p
1 ;p
2 ;:::;p
n
being a
permutationof1;2;:::;n.
Apermutationthathanges mnobjetilialy
isalledileoflengthm. Permutationswiththesame
ilestruturebelongtothesameonjugationlass. By
thisreasonthelasses ofS(n)are labeledbythe ile
strutureoftheirelements. Inthisway,agenerilass
() is written as () (1 1
;2 2;
:::) with the meaning
thattheirelementshave
1
ilesoflength1,
2 iles
oflength2,andsoon.
A partition [℄ of n is a set of n integers [℄
[
1 ;
2 ;:::;
n
℄satisfyingtherelations
1
2
:::
n ;
with
1 +
2
+:::+
n
=n: (2)
Ingeneraloneomitsthe
i
expo-[2 2
1 3
℄[221110:::0℄. Wewilldenote byGreeklettera
generi partition and by latin letter a partiular one.
Asexample,[n℄[n0:::0℄,[p;q℄[p;q;0:::0℄.
Toagivenpartition[℄oneassoiatesaYoung
dia-gramthatonsistsinagurewith
1
boxesintherst
line,
2
in the seond, and soon. Due to this
assoi-ation, its is usual to refer to the
i
's as the rows of
[℄.
When one lls these diagrams with the numbers
1;2;:::;nin suh awaythat thenumbersin theboxes
growfrom left to right andfrom up to down theyare
alled standard (or regular) Young tableau. When in
thellingproessthenumbersintherowsonlynot
de-reasebeingallowedtorepeatbutintheolumnsthey
ontinue to grow, the tableau is alled strit-olumn
tableau.
Given thepartition [℄ =[
1 ;
2; :::;
p
;0;:::;0℄ one
denesitsonjugatepartitionby
[ e
℄=
p p
;(p 1) p
1 p
;:::;2 2 3
;1 1 2
: (3)
TheYoungdiagram of [ e
℄is obtainedfrom theoneof
[℄byinterhangingrowsbyolumns.
Given n quantities
1 ;
2 ;:::
n
it is possible to
dene three types of symmetri funtions built with
them[1℄: a
r ;h
r ands
r .
The funtions a
i
are those that appear in the
ex-pansionofthepolynomialwithroots
1 ;
2 ;:::
n as
n
Y
i=1
(x
i )=
n
X
r=0 ( )
r
a
r x
n r
(4)
Therstthreeofthem aregivenby
a
1 =
X
i
i ; a
2 =
X
i<j
i
j ; a
3 =
X
i<j<k
i
j
k ; (5)
that is, eah a
i
is thesum of all linearly independent
produtsofrquantitieswithoutrepeatedindies.
Thefuntions h
r
aredenedbytheexpansion
1
Q
n
i=1
(1
i x)
= 1
X
r=0 h
r x
r
; (6)
resultingthateahh
r
isthesumofalllinearly
indepen-dentprodutsofrquantitiesallowingforrepeatings.
Itfollowsfrom (4)-(6)thatthersth
r 'sare
h
0
= 1; h
1 =a
1 =
X
i
i ; h
2 =a
2
1 a
2 =
X
i
2
i +
X
i<j
i
j ;
h
3 = a
3 2a
1 a
2 +a
3
1 =
X
i<j<k
i
j
k +
X
i<j (
i
2
j +
2
i
j )+
X
i
3
i :
Thefuntions s
r
aredened asthesumsofther-produtsofthe's.e.,
s
r =
n
X
i=1 (
i )
r
: (7)
GivenamatrixAofdimensionnnonedenesitsimmanantjAj [℄
bytherelation
jAj [℄
= X
P
[℄
(P)a
1p
1 a
2p
2 :::a
np
n
; (8)
where [℄
(P)is theharaterof thepermutationP (withomponentsp
1 ;p
2 ;:::;p
n
)intheirrep[℄ofS(n).
Sineintheirrep[1 n
℄theharaterofagivenpermutationisitsparity,jAj [1
n
℄
isthedeterminantofA. Similarly,
jAj [n℄
isitspermanent.
TheShur funtionfg ofdegree r=
1 +
2 +
3
+:::+
n
in thequantities
1 ;:::;
n
isdened in termsof
immanantsas
fg= 1
r! jZ
r j
[℄
Z
r =
0
B
B
B
B
B
B
s
1
1 0 0 ... ... ... 0
s
2 s
1
2 0 ... ... ... 0
s
3 s
2 s
1
3 0 ... ... 0
... ... ... .. ... ... ... 0
s
r 1 s
r 2
... ... ... ... s
1 r-1
s
r s
r 1
... ... ... ... s
2 s
1 1
C
C
C
C
C
C
A
: (10)
ForthesymmetriandantisymmetripartitionstheShurfuntions assumeverysimpleexpressions,namely,
frg=h
r andf1
r
g=a
r
: (11)
Asexample,wegivebelowtheexpliitexpressionsoftheShurfuntions ofdegreer=3:
f3g = 1
6 (s
3
1 +3s
1 s
2 +2s
3 )=
X
i<j<k
i
j
k +
X
i<j (
i
2
j +
2
i
j )+
X
i
3
i h
3 ,
f21g = 1
3 (s
3
1 s
3 )=2
X
i<j<k
i
j
k +
X
i<j (
i
2
j +
2
i
j
), (12)
f1 3
g = 1
6 (s
3
1 3s
1 s
2 +2s
3 )=
X
i<j<k
i
j
k a
3 .
d
Usingthe expliitexpressions ofimmanantsin the
denitionoftheShurfuntiononeobtainstherelation
fg= 1
r! X
n()
[℄
()s 1
1 s
2
2
::: (13)
whih givesthefundamental link between Shur
fun-tions and haraters of the symmetri group. In the
equation above the sum is over the lasses ()
(1 1
;2 2
;:::) and n() is the numberelementsof lass
().
Shurfuntions ofdegreer 0
an be\multiplied"by
Shur funtions of degree r 00
in 3 dierent ways and
in eahof them the\produt"is expressedasalinear
ombinationof Shur funtions allof the samedegree
r 000
.
These3typesofmultipliationare:
1) Inner(or diret) produt: f 0
g f 00
g =
P
000
(f 0
gf 00
g!f 000
g)f 000
g,
2)Outer produt: f 0
gf 00
g= P
000
(f 0
gf 00
g!
f 000
g)f 000
g,
3) Plethysm: fgf 00
g= P
000
(fgf
00
g!
f 000
g)f 000
g,
where (:::) isa non-negativeintegerdenotingthe
multipliity of f 000
g in the expansion. Forlarity we
attahtoitanargumentdenotingthekindofoperation
thatproduedit.
Intheinner produtthedegreesof theShur
fun-tions involved are all equal, i.e., r 000
= r 0
= r 00
= n,
andthe expansionoeÆients aretheoeÆientsof
redutionofthe Kronekerprodutof S(n)irreps [ 0
℄
and[ 00
℄.
In the outer produt one has r 000
= r 0
+r 00
and
the oeÆients are obtained simply by making the
produtofaShurfuntioninvariables(x
1 ;x
2 ;:::;x
n 0
)
by another in variables (y
1 ;y
2 ;:::;y
n 00
) and expressing
it as a linear ombination of Shur funtions in
vari-ables(z
1 ;z
2 ;:::;z
n 000)
with z
i =x
i
for1 i n 0
and
z
n 0
+i =y
i
for1in 00
. Littlewoodobtaineda
proe-duretondtheoeÆientsoftheouterprodutknown
intheliteratureas\Littlewood's rules".
Onendsintheliterature[1℄,[3℄,[37℄tables ofouter
produtsforn 0
+n 00
=1;2;:::;14. Tradiionallysuh
ta-blesareorganizedasthetablegivenbelowforn 0
+n 00
=
5.
f5g f41g f32g f31 2
g f2 2
1g f21 3
g f1 5
g
f4gf1g 1 1 f1
4
gf1g
f31gf1g 1 1 1 f21
2
gf1g
f2 2
gf1g 1 1 f2
2
gf1g
f3gf2g 1 1 1 f1
3
gf1 2
g
f21gf2g 1 1 1 1 f21gf1
2
g
f1 3
gf2g 1 1 f3gf1
2
g
f1 5
g f21 3
g f2 2
1g f31 2
g f32g f41g f5g
The numbers in the internal part of the table
givethe multipliityof theShurfuntions f 000
gthat
appear in the deomposition of the outer produt
f 0
gf 00
gand theemptyboxesmean zero. The Shur
funtionsintheupperedgeorrespondtotheproduts
that appear inthe leftedgewhile theones ofthe
bot-tomedgeorrespondtotheprodutsthatappearinthe
rightedge.
Plethysmswillbeonsideredinthenextsubsetion.
II.2 InvariantMatries and Plethysms
LetA(a
ij
)beanonsingularmatrixofdimension
nnrepresentingthelinearinversibletransformation
AofonepointX inapointX 0
ofan-dimensional
ve-torspae. Intermsofoordinatesonehas
[X 0
℄=A[X℄ (14)
where [X℄ = [x
1; x
2 ;:::;x
n ℄
T
and [X 0
℄ =
[x 0
1 ;x
0
2 ;:::;x
0
n ℄
T
are olumn vetors in the oordinates
of X and X 0
. One an onstrut ( n+r-1
r
)
homoge-neousprodutsofdegreerin theoordinatesx
i ofX:
x r
1
1 x
r
2
2 :::x
rn
n ; r
i 0;
n
X
i=1 r
i
=r: (15)
Eahofthoseprodutstransforms,underthe
trans-formation A, into a linearombinationof themselves.
Dening aolumn vetor[X℄ r
whose omponentsare
those produts enumerated in an arbitrary way, its
transformedunderAanbewrittenas
([X℄ r
) 0
=A [r℄
[X℄ r
; (16)
what denesamatrixA [r℄
alledther-induedmatrix
of thematrixA . The elementsof A [r℄
arelearly
ho-mogeneuspolynomialsofdegreerintheomponentsof
A.
Makingthesameoperationwithanonsingularnn
matrixB oneobtainsB [r℄
. IfC=AB, thenitanbe
provedthat
C [r℄
=(AB) [r℄
=A [r℄
B [r℄
(17)
what means that the set of matries D [r℄
(A) A [r℄
isa( n+r-1
r
)-dimensionalrepresentationofthegroup
GL(n)ofthenonsingularmatriesofdimensionnn.
Asexample,onehasforr=2:
x 0
i x
0
j =
X
k ;l a
ik a
jl x
k x
l =
X
k (a
ik a
jk )x
2
k +
X
k <l (a
ik a
jl +a
il a
jk ) x
k x
l
(18)
whatimpliesin
A [2℄
(ij)(k k ) =a
ik a
jk
; ij; A [2℄
(ij)(k l) =a
ik a
jl +a
il a
jk ;
ij;k<l.
Forn=2andhoosingtheordering(x 2
1 ;x
1 x
2 ;x
2
2
)onehas
A [2℄
= 0
a
2
11
2a
11 a
12
a 2
12
a
11 a
21 (a
11 a
22 +a
12 a
21 ) a
12 a
22
a 2
21
2a
21 a
22
a 2
22 1
A
; n=2 . (19)
Itshouldbenotied thatthetraeofA [2℄
is
tr
A [2℄
=a 2
11 +a
2
22 +a
11 a
22 +a
12 a
21 =
2
1 +
2
2 +
1
2 =h
2
=f2g();
wheref2g()istheShurfuntion f2gomputedwiththeeigenvaluesofA.
Foranyothernonsingular22matriesB;C ;D;:::oneanonstruttheirseondinduedmatriesB [2℄
;C [2℄
;D [2℄
;:::
asthematries whose omponentsare thesame polynomialsof degree2of A in whih nowthevariables are the
orrespondingelementsofmatriesB;C ;D;:::. Itisimmediateto prove,byhandalulation,that
A [2℄
B [2℄
=(AB) [2℄
; 8A;B; 22
whatagreeswithEq.(17). Letustakenowr(<n)opiesofthevetorX andbuildthe( n
r
)determinants
d
(e1e2:::ep) =
x
(1)
e1 x
(2)
e1
::: x (r)
e1
x (1)
e
2 x
(2)
e
2
::: x (r)
e
2
::: ::: ::: :::
x (1)
er x
(2)
er
::: x (r)
er
; 1e
1 <e
2
<:::<e
r
If eah X (s)
is transformedby the sametransformation A, these determinants will transform linearly among
themselvesbytherelation
[d℄ 0
=A (r)
[d℄ (21)
where[d℄istheolumnvetorwhoseomponentsarethed
(e
1 e
2 :::e
r )
enumeratedin anarbitraryway. Relation(21)
denes thematrixA [r℄
, therth ompound matrixofA. It followsfrom this denitionthat thematrixelementsof
A (r)
aretheminorsofdegreeroftheoriginalmatrixA.
IfC=AB,thenoneanalsodemonstratethat
C (r)
=(AB) (r)
=A (r)
B (r)
. (22)
Asexample,for r=2onehas
d
eiej 0
=
x
(1)
e
i x
(2)
e
i
x (1)
ej x
(2)
ej
=
P
k a
eik x
(1)
k P
k a
eik x
(2)
k
P
l a
ejl x
(1)
l P
l a
ejl x
(2)
l
=
= X
k ;l
a
e
i k
x (1)
k a
e
i k
x (2)
k
a
e
j l
x (1)
l a
e
j l
x (2)
l
=
X
k <l
a
ik a
jk
a
il a
jl
d
e
k e
l .
Then,forn=2onehas
A (2)
=a
11 a
22 a
12 a
21
=det( A) , n=2. (23)
For n=3,withtheorderingd
12 ;d
13 ;d
23
onehas
A (2)
= 0
a
11 a
22 a
12 a
21 a
11 a
23 a
13 a
21 a
11 a
23 a
13 a
23
a
11 a
32 a
12 a
31 a
11 a
33 a
13 a
31 a
12 a
33 a
13 a
32
a
21 a
32 a
22 a
31 a
21 a
33 a
23 a
31 a
22 a
33 a
23 a
32 1
A
; n=3. (24)
d
IfC=ABthen,againbyhandalulation,onean
provethat
C (2)
=(AB) (2)
=A (2)
B (2)
. (25)
The r-indued and r-ompound matries are
par-tiular asesofinvariant matrieswhosedenition are
givenin thefollowing.
Let T(A)be a matrixwhose elementsare
polyno-mials t
ij
havingasvariablesthematrixelementsofA.
LetT(B)beamatrixbuiltwiththesamepolynomials
ofT(A)nowin thematrixelementsofB. If
T(A)T(B)=T(AB) (26)
foranynonsingularnnmatriesA;Bthenthematrix
T(A)isalledainvariantmatrixofA.
Itfollowsfrom (26)that,onethesetof
polynomi-alst
ij
is xed,the setof matries D T
(A)T(A)is a
representationofGL(n).
Atrivialaseis the1-induedmatrix. Inthis ase
one has t
ij = a
ij and A
[1℄
A. As it is known, the
traeofAisthesumofitseigenvalues
i
,that is,
tr(A)= X
i
i =a
1
()=f1g() (27)
wheref1g()istheShurfuntionf1galulatedwith
theeigenvaluesofA. Thiswillbe,bydenition,D [1℄
.
SinetheKronekerprodutoftworepresentations
isalsoarepresentationandtheprodutoftwo
polyno-mialsisalsoapolynomial,itfollowsthatthekroneker
produtof twoinvariant matries is also an invariant
matrix.
Littlewood[1℄ showedthatif the produtof two
in-variant matriesis reduible, thenit will betotally
re-duible. Thisallowsus toobtainnewirreps by taking
multiple Kroneker produts of the irrep D [1℄
and
re-dutingthembysimilaritytransformations.
As asake of example, let us take n = p = 2. In
thisaseonehasA [2℄
andA (2)
givenby(19)and(23).
WritingAAintheform
AA= 0
B
B
a
11 a
11 a
11 a
12 a
12 a
11 a
12 a
12
a
11 a
21 a
11 a
22 a
12 a
21 a
12 a
22
a
21 a
11 a
21 a
12 a
22 a
11 a
22 a
12
a
21 a
21 a
21 a
22 a
22 a
21 a
22 a
22 1
C
C
A
M 1
(AA)M = 0
B
B
a
2
11
2a
11 a
12
a 2
12
0
a
11 a
21 a
11 a
22 +a
12 a
21 a
12 a
22
0
a 2
21
2a
21 a
22
a 2
22
0
0 0 0 a
11 a
22 a
12 a
21 1
C
C
A
= A
[2℄
+A (2)
d
with
M= 0
B
B
1 0 0 0
0 1 0 1
0 1 0 1
0 0 1 0
1
C
C
A .
Thisshowsthat,forn=2,A [1℄
A [1℄
redues into
A [2℄
+A (2)
.
Forr=2and anynonehas( n+2-1
2
)+( n
2 )=
n 2
. Sinetr(AA)=(tr(A)) 2
thisdrivesustosuppose
that
A [1℄
A [1℄
=A [2℄
+A (2)
for any n, what turns out to be true sine the
Kro-nekerprodut of twomatries anbedeomposed in
asymmetriandanantisymmetripartrelativetothe
omponentsoftherstandseondfatormatries.
An analogous analysis an be done for the
r-Kronekerprodut M M:::M . Based in this
analysis,Shur[4℄demonstrated that\If Ais annn
matrix, there are asmany irreduible invariant
matri-es ofA of degreer asarethe partitionsof r withno
morethannpartsandthetraeofthemaretheShur
funtionsofdegreerintheeigenvaluesofA."
Those irreduible matries anthen be labeled by
thepossiblepartitionsofrinnomorethannparts.In
thisnotationonewritesA (r)
A [1
r
℄
. Clearly,forr>n
onlytheirrepswithuptonrowsarerealizable.
The details of theeetiveonstrution ofan
irre-duible invariantmatrixorrespondingtoagiven
par-titionanbefoundin Refs[8℄,[14℄.
Using theomponentsoftheShur funtionsto
la-beltheGL(n) irreps,theaboveresultshowsthat
\ The GL(n) irreps an be labeled by
[m
1n ;m
2n ;:::;m
nn
℄wherethem
in
satisfytherelations
m
in m
i+1n
;1inandthetraeofeahelement
A of GL(n) is theShur funtion fm
1n ;m
2n ;:::;m
nn g
evaluatedwiththeeigenvaluesofA."
SinetheGL(n) irrepsdonotredue underthe
re-stritionGL(n)!U(n)thesameresultholdsforU(n).
LetT 0
andT 00
betworepresentationsofGL(n) by
invariantmatries. From(26)itfollowsthat
T 00
(T 0
(AB))=(T 00
(T 0
(A))(T 00
(T 0
(B)). (28)
Sinetheprodutoftwopolynomialsisalsoa
poly-nomial, it follows that any invariant matrix of an
in-variant matrixis also an invariantmatrix of the
orig-inal matrixandtherefore anbeexpressed asadiret
sumofirreduibleinvariantmatries. Thisallowsusto
write
[A [℄
℄ [℄
= X
A
[℄
: (29)
Letusdenotebyr
;r
er
thedegreesof[℄;[℄and
[℄. SineA [℄
isobtainedbytheredutionof ther
-pleKronekerprodutofAand,byitsturn,[A [℄
℄ [℄
is
obtainedreduingther
-pleKronekerprodutofA [℄
itfollowsthattheirrepsthatappearintheRHSof(29)
havedegreer
=r
r
.
Sinethetraeofanirreduibleinvariantmatrixis
equal to the Shur funtion of the orreponding
par-tition, Eq.(29) allows us to stablish a orrespondene
fgfgbetweentwoShurfuntions fgofdegrees
r
andr
withShurfuntionsfgofdegreer
r
given
by
fgfg= X
fg; (30)
wheretheoeÆients
aregivenby(29).
This orrespondene was desovered by
Littlewood[14℄andlaterwasnamed plethysm.
Theplethysmoperationhastheproperties[3℄,[2℄,
fg(fgfg) = fgfgfgfg, (32)
(fg+fg)fg = X
0
00
(f 0
gf 00
g!fg)(fgf 0
g)
(fgff 00
g). (33)
(fg fg)fg = X
0
00
( ) r
00
(f 0
gf 00
g!fg)(fgf 0
g)
(fgf ~
00
g) (34)
fg(fgfg) = (fgfg)(fgfg) (35)
(fgfg)fg = X
0
00
(f 0
gf 00
g!fg)(fgf 0
g)
(fgf 00
g) (36)
(fgfg) T
= (
f e
gfg; forr
even,
f e
gfeg; forr
odd.
(37)
Thesumin Eq.(33)inludestheasesf 0
g=f0g1,f 00
g=fgand f 0
g=fg,f 00
g=f0g1. Symilarly
in Eqs(34)and(36). Also,r 00
andr
are thedegreesoff 00
gand fg.
InEq.(37)weusedthenotation
"
X
i a
i f
(i) g
#
T
= X
i a
i f
e
(i)
g; (38)
d
where a
i
are numerialfators, f
(i)
gShur funtions
andf e
(i)
gtheironjugate.
Thereisalsoadimensionformula[2℄,[3℄,[33℄
d
fgfg
X
(fgfg!fg)d
[℄ =
(rs)!
(r!) s
s! (d
[℄ )
s
d
[℄ ,
(39)
where randsarethedegreesof[℄and[℄ andd
[℄ is
thedimensionoftheirrep[℄ ofS(degreeof[℄).
Up to now we haveseen plethysms of Shur
fun-tions of GL(n). Onean obtain plethysms of
ontin-uous subgroups G of GL(n) simply by expressing the
irreduible haratersofGintermsofShurfuntions
and then omputing the plethysm of Shur funtions.
If neessary,theresultan bere-expressedin termsof
theirreduibleharatersofG. Thiswillbedonewhen
wewill onsidertheappliations.
IntheaseofG=S(n),anitesubgroupofGL(n)
of great importane in thestudy ofsystems of
identi-al partiles,thisproessinvolvestheoneptofinner
plethysm whih weshallonsiderinthefollowing.
As we have seen previously, the inner produt
fgfg of two Shur funtions of the same degree
r orresponds to the Kroneker produt of two irreps
[℄ and [℄ of S(r). The asefgfg anbe
anal-ysedin itssymmetriandantisymmetrionstituents.
TheKronekerprodutMMofamatrixMbyitself
deomposesas
MM :
=M [2℄
uM [1
2
℄
: (40)
Taking by M the matrix that represents a given
permutation of S(n) in the irrep [℄, orrepondently,
theexpressionfgfganbeanalizedintwoparts,
denoted byfgf2gand fgf1 2
g. The operation
denoted by the symbol is alled inner plethysm[13℄
andwillbedened inthefollowing.
LetM
i
beamatrixofageneri permutation P
i of
S(n)and [℄
(P
i
)itstrae. Thentheinvariantmatrix
ofM
i
assoiatedtothepartition[℄,thatis,M [℄
i ,also
representsthe elementP
i
and itstraeisaompound
harater,say,
tr(M [℄
i )=
X
G
[℄
(P
i
) . (41)
Onedenes fgfg, theinner plethysm of
par-titions fg and fg of degrees n and m, as a linear
ombination of partitions fgof degree n with
oeÆ-ientsgivenbyEq.(41),that is,
fgfg= X
G
Notiethat although thedegreeof partitions [℄ and [℄ is n, there is norestrition onerningthe degreeof
partition[℄ .
Theinnerplethysmshavepropertiesanalogoustothoseofplethysms,roughlyhangingouterprodutsofShur
funtionsbyinnerproduts,thatis,
(fgfg)fg = fg(fgfg) ;
fg(fg+fg) = fgfg+fgfg ;
(fg+fg)fg = X
(fgfg!fg)(fgfg)(fgfg),
fg(fgfg) = (fgfg)(fgfg) ; (43)
(fgfg)fg = X
(fgfg!fg)(fgfg)(fgfg).
III. Plethysms Calulation
In[3℄onendsthefollowingexpressionforalulationofplethysm:
f 0
gf 00
g= X
( 00
) n
00
( 00
)
r 00
!
[ 00
℄
( 00
)(S 00
1 )
00
1
(S 00
2 )
00
2
:::(S 00
n 00
)
00
n 00
, (44)
where
r 0
andr 00
arethef 0
gandf 00
gdegrees,( 00
)=(1
00
1
;2
00
2
;:::) aretheS(r 00
)lassesandn 00
( 00
)theirnumberof
elements,
S 00
i =
X
[℄
ir 0
fg
in 0
X
( 0
) n
0
( 0
)
r 0
!
[ 0
℄
( 0
) [℄
ir 0
(
0 (
0
)) , (45)
0 (
0
)istheS(ir 0
)lasswith 0
1
ilesoflength1, 0
2
iles oflength2,et.
TheShurfuntionsf 000
g,havingdegreer 000
=r 0
r 00
,whihenterintheplethysmareobtainedafterreduing
theouter produtsof Shur funtions inside theS 00
i
. For smallvalues ofr 000
it is possibleto onstrutplethysms
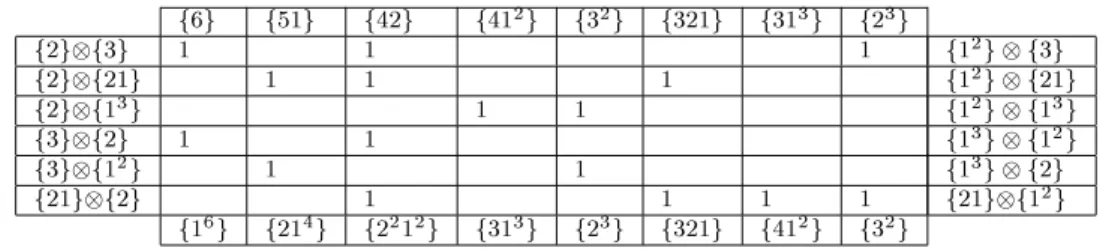
tables with thesameorganizationof thetables of outer produts. Onehas, asanexample, forr 000
=6 thetable
below
f6g f51g f42g f41 2
g f3 2
g f321g f31 3
g f2 3
g
f2gf3g 1 1 1 f1
2
gf3g
f2gf21g 1 1 1 f1
2
gf21g
f2gf1 3
g 1 1 f1
2
gf1 3
g
f3gf2g 1 1 f1
3
gf1 2
g
f3gf1 2
g 1 1 f1
3
gf2g
f21gf2g 1 1 1 1 f21gf1
2
g
f1 6
g f21 4
g f2 2
1 2
g f31 3
g f2 3
g f321g f41 2
g f3 2
g
TableII:AllplethysmsthatprodueShurfuntionsofdegree6.
In[3℄oneanndplethysmstablesforr 000
upto10. Ibrahin[15℄,[16℄publishedtableswithr 000
=12;14and15.
Notiethatsuhtablesexist onlyforr 000
nonprime. Partialtables werepublishedin [2℄and[21℄.
Forgreatvaluesofr 000
theuseof(44)isunpratial,thentheneedforalternativeformulas. Forsomepartiular
asesof f 0
gandf 00
gthereexistexpliit(oralmost)formulaseasytouse. Theyarethefollowing:
fgf1g = f1gfg=fg; (46)
fgf0g = f0g; f0gfg=Æ
fg;frg
f0g; (47)
frgf2g = [r=2℄
X
frgf1 2
g =
[(r+1)=2℄
X
i=1
f2r (2i 1);(2i 1)g; (49)
f2gfrg = X
fg
even
; (50)
f1 2
gfrg = X
^
fg
even
; (51)
f1 r
gf2g = f1 2r
g+ [r=2℄
X
i=1 f2
2i
;1 2r 4i
g ,r even, (52)
f1 r
gf1 2
g = f1 2r
g+ [r=2℄
X
i=1 f2
2i
;1 2r 4i
g , rodd (53)
f1 r
gf1 2
g =
[(r+1)=2℄
X
i=1 f2
2i 1
;1
2r 2(2i 1)
g ,r even, (54)
f1 r
gf2g =
[(r+1)=2℄
X
i=1 f2
2i 1
;1
2r 2(2i 1)
g , r odd, (55)
d
Eq.(46) follows from plethysms denition while
Eq.(47) is set for onsisteny. In Eq.(50), fg
even
meanspartitionof 2rwithalllineseven. Eqs.(54)and
(55)followfromEqs.(48)and(49)byonjugation[see
Eq.(37).℄.
In [21℄ there are formulas for the alulation of
plethysms fgfg when both Shur funtions are
symmetrior/andantisymmetri. Toexplainthem we
needthefollowingdenition: ak-borderstripofagiven
Youngdiagram [℄isasequeneofk squaresin whih
the rst of them is the last one of therst line of [℄
andthenextsquaretoagivenoneistheonebelowit,
ifitexists, ortheonetoitsleft,otherwise.
For example,the3-borderstrips of [41 2
℄;[321℄ and
[2 2
1 2
℄arethesquareswiththesymbolin thegures
below,respetively:
,
,
.
Whenfgandfgarebothsymmetri,one has
fngfmg= 1
m m
X
k =1 fng(x
k
)(fngfm kg); m1; (56)
with
fng(x k
)= X
C
n;k ;
fg: (57)
In(57)thefgareallShurfuntionsofdegreenk. TheoeÆientsC
n;k ;
areobtainedfromtheYoungdiagram
assoiatedto fgremoving,in sequene,nk-borderstrips. Ifin allstepstheresultingdiagramberegularthen
C
n;k ; =( )
l
(58)
withl=(numberoflines in the k-border strips) n. Ifin anystep theresultingdiagram be notregular, then
C
n;k ;
=0. Asexample,fromtheguresaboveonehas
C
2;3;f41 2
g =( )
4 2
=1; C
2;3;f321g =( )
5 2
= 1; C
2;3;f2 2
1 2
g =0.
TheoeÆientC
2;3;f2 2
1 2
g
iszerobeauseafterremovingtherst3-borderstriptheresultingdiagramorresponds
Eq.(56)allowsoneto relate theplethysm of twosymmetriShur funtions with theplethysms of symmetri
Shur funtions of smaller degrees. In this way, using fngf1g fng as starting point oneomputes all the
plethysmsoftypefngfmg.
Usingtheresult
f1 m
g=( ) m+1
fmg+ m 1
X
k =1 ( )
k +1
fkgf1 m k
g; m1 (59)
andEqs.(32)oneobtains
fngf1 m
g=( ) m+1
fngfmg+ m 1
X
k =1 ( )
k +1
(fngfkg)(fngf1 m k
g) (60)
f1 n
gf1 m
g=( ) m+1
f1 n
gfmg+ m 1
X
k =1 ( )
k +1
(f1 n
gfkg)(f1 n
gf1 m k
g) (61)
Forf1 n
gfmgoneuses
f1 n
gfmg= (
[fngfmg℄ T
; forneven,
[fngf1 m
g℄ T
; fornodd.
(62)
In this way, using (56) and (60)-(62) one omputes plethysms with both Shur funtions symmetri and/or
antisymmetri.
Theasesinwhihfgfghasalosedandsimpleexpressionallowustoompute,using(32)and(35)relations
alsolosedfortheorrespondingplethysms. Inthisway,from
fpgfqg= q
X
i=0
fp+q i;ig; pq (63)
oneobtainsfp;qg=fpgfqg fp+1;q 1g. Fromthisequation,using (32),(35)anditeratingoneobtains
fgfp;qg= q
X
i=0 ( )
i
(fgfp+ig)(fgfq ig); (64)
whatallowsustoexpressaplethysmwithatwo-rowShurfuntionatrightintermsofplethysmswithsymmetri
Shur funtionsatright.
Inananalogousway,from
f1 p
gf1 q
g= q
X
i=0 f2
q i
;1 p q+2i
g; pq; (65)
oneobtains
fgf2 q
;1 p q
g=(fgf1 p
g)(fgf1 q
g fgf1 p+1
g)(fgf1 q 1
g; (66)
what expressaplethysmwithatwo-olumnShur funtionat rightin termsofplethysmswith one-olumnShur
funtionsat right.
An analogousproedureisusedtoomputeplethysmswithShurfuntionsatleftwithmixedsymmetryusing
(33),(35)and(36). Dueto themoreomplexnatureoftheseequationsasomparedwiththatforShurfuntions
totherightthealulationis moreompliated.
WhenthedegreenoftheShurfuntion atleftisaompoundintegeroneanusethetablesofplethysmswith
naldegreentoobtainrelationsingeneralsimplerthantheonehereexposed. Asexample,fromf2gf1 2
g=f31g
oneobtains
f31gfg=(f2gf1 2
g)fg=f2g(f1 2
gfg)
andalsof21 2
gfgbyonjugation.
A veryommon situation whih arrisesin
applia-tionsiswhenoneneedstoomputeplethysmsofasame
Shurfuntionbymany(sometimesall)Shurfuntions
of agivendegreeto theright.[This is the aseof the
appliation that we will makein Setion 4.℄ For suh
aseswepresentthefollowingalgorithmthatallowsto
ompute,in abuildupway,allplethysmsfgfg
m
with fg a xed Shur funtion and fg
m
all Shur
funtions of degreem, one the plethysms fgfmg
andfgfg
m 0,
withm 0
<mhavealreadybeen
om-puted:
1) Find all partitions of m and order them in
de-sending order of their omponents read from left to
right;
2) For eah partition fg = f
1 ;
2 ;:::;
t
;0;:::;0g
performtheouterprodut
f
1 ;
2 ;:::;
t 1 gf
t
g,ordertheirrepsin theredution
asinitem(1),thenuseEqs.(32)toobtaintheequation
fgfg = (fgf
1 ;
2 ;:::;
t 1
g)(fgf
t g)
X
f 0
gfg (f
1 ;
2 ;:::;
t 1 gf
t g!f
0
g)fgf 0
g (67)
d
wherethesymbolmeanspreeding,followingthe
or-deringin item1).
Sinef
1 ;
2 ;:::;
t 1
gandf
t
ghavesmallerdegree
than fg, the plethysms fgf
1 ;
2 ;:::;
t 1 g and
fgf
t
ghavealreadybeenomputedintheindution
proess. Ontheotherhand,theplethysmsfgf 0
g
alsohavebeenomputedsinef 0
gpreedesfg.
As an example of the proedure suggested above,
welistbelowthesequeneofequations[obtainedfrom
Table I℄ that allows us to ompute fgfg for all
Shurfuntionsfgwithdegree5,onefgf5gand
theplethysmswithtotaldegreelessthan5r
beknown.
fgf5g = input,
fgf41g = (fgf4g)fg fgf5g;
fgf32g = (fgf3g)(fgf2g) fgf5g fgf41g;
fgf31 2
g = (fgf31g)fg fgf41g fgf32g;
fgf2 2
1g = (fgf2 2
g)fg fgf32g; (68)
fgf21 3
g = (fgf1 2
g(fgf2g) fgf31 2
g;
fgf1 5
g = (fgf1 3
g)(fgf1 2
g fgf21 3
g fgf2 2
1g:
d
Sinefngf5goneobtainsfrom(56),weuseitto
obtainallthe plethysms fngfgof degreenm. For
seuritysake,wereommendtomakeadimensiontest
using(39)forallnewplethysmobtained.
IV. Appliations
Inappliations of grouptheory to problems of
nu-learandatomi spetrosopywearefrequentlyledto
onsider thedeomposition ofharatersof irrepsofa
thoseofoneofitssubgroup. Thesubgroupanalsoat
over a n-dimensional vetor spae but in a restrited
way. It analso be the diret produt of twogroups
thatatovern
1 -andn
2
-dimensionalvetorsubspaes
of the original spae. As example, Sp(4` +2) !
SU(2)R (2`+1);R (2`+1) ! R (3);R (6) ! R (5)
andGL(2)!R (3)havemanyappliations inthe
the-oryofomplexspetra[WewillusethenotationU for
unitary,O fororthogonal, R=O +
=SO for
unimodu-larorthogonalorrotation,SpforsympletiandGLfor
asimpleandompletesolutiontothisproblem.
This solutionisbasedinthetheorem[2℄
If under the restrition G!H the harater [1℄
of group Gdeomposesas
[1℄ =( ) +( ) +:::+ ( ! ) (69)
thentheharater[℄ ofGdeomposesintothe
har-aters() of H aording to the haraters ontained
inthe plethysm
[ ( )+( ) +:::+ ( ! ) ℄[℄ : (70)
Thisplethysmanbeobtainedexpressingthe
har-aters of G and H in terms of haraters of GL(n),
omputingtheresultingplethysmsofGL(n)haraters
andre-expressingtheresultintermsofharatersofH
in ordertoobtainthenal result.
Using theassoiation irrep $ harater this
theo-remgivesustheoeÆientsoftheredutionoftheirrep
[℄ of Gin thediret sumofirreps() ofH.
Let us onsider now some illustrative examples of
the apppliationsof thetheorem. To this end welist
belowthe deomposition of the harater [1℄ ofG in
termsofharaters[2℄() ofH:
U(n) ! U(n-1): f1g=f1g+f0g;
U(4`+2) ! SU(2)O +
(2`+1): f1g=[ 1
2 ℄
0
(1);
O +
(8`+4) ! SU(2)Sp(4`+2): (1)=[ 1
2 ℄
0
<1>;
Sp(4`+2) ! SU(2)R (2`+1): <1>=[ 1
2 ℄
0
(1);
O +
(2`+1) ! O +
(3): (1)=(`);
O +
(6) ! O
+
(5): (1)=(1)+(0);
GL(2) ! O
+
(3): f1g=(3);
U(n) ! O(n): f1g=(1);
U
ST
(6) ! U
S
(3)U
T
(3): f1g=f1g
S f0g
T +f0g
S f1g
T ;
U(nm) ! U(n)U(m) f1g=f1g
0
f1g 00
:
(71)
Bytheabovetheorem andthe rstline of (71), in order toobtain theU(n 1) irrepsontainedin theU(n)
irrepfgwemustevaluatetheplethysm
(f1g+f0g)fg = X
0
00
(f 0
gf 00
g!fg)(f1gf 0
g)(f0gf 00
g
= X
0
n 00
(f 0
gfn 00
g!fg)f 0
g (72)
d
whereusewasmadeof(33),(46)and(47). From
Little-wood's rules,theShur funtionsf 0
gthat anouple
with somesymmetri Shur funtion fn 00
gtogivefg
aretheonesthatsatisfy
1
0
1
::::
n 1
0
n 1
n
: (73)
Usingthisresultin Eq.(72)oneseesthatunderthe
restritionU(n)U(n 1)onehastheredution
fg= X
0
f 0
g (74)
in whihthef 0
garealltheU(n 1)irrepssatisfying
Eq.(73).
These arethe wellknownin-betweeness onditions
introduedbyGelfand[34℄inthelabelingofbasisstates
ofU(n)irreps.
Inthelastlineof(71)onehastheaseofaredution
ofanirrepofaunitarygroupintoirrepsofitssubgroup
whih is adiret produt of onegroupating in aset
ofvariablesbyanotherthatatsintheremainingones.
Inthisaseonehastheplethysm
(f1g 0
f1g 00
)fg = X
0
00
(f 0
gf 00
g!fg)(f1g 0
f
0
g)(f1g 00
f
00
g=
X
0 00 (f
0
gf 00
g ! fg)f
0
gf 00
Theinnerprodutf 0
gf 00
gintheRHSof(75)
re-quiresthattheirrepsf 0
gandf 00
gthatappearinthe
redutionoffghaveboththesamedegreeastheone
offg. Thisresulthasanimportantroleinappliation
to Nulear Physisin the treatment ofthe spin-isopin
part of a system of nuleons. In this ase the basis
funtionsarelabeledbythehainofsubgroups
U(4)U(2)
spin U(2)
isospin.
Using (75)it followsthat theredutionof anirrep
fgofU(4)intoirrepsfgfgof U(2)U(2)isgiven
by
fg=
X
(fgfg!fg)fg
spin fg
isospin
. (76)
Theorrespondenewithtotalspinandisospin isgivenby
S = 1
2 (
1
2 ); T =
1
2 (
1
2 );
1 +
2 =
1 +
2
=n . (77)
Inthe treatmentof systemsof idential partiles, in (75)one uses fg=fng for bosons and fg=f1 n
gfor
fermions. Forthese aseonehas
(f1g 0
f1g 00
)fng = X
fg
0
fg 00
;
(f1g 0
f1g 00
)f1 n
g = X
fg
0
f e
g 00
;
from whatfollowstheredution
fng ! X
fg
0
fg 00
; r
0 =r
00 =n; (78)
f1 n
g !
X
fg
0
f e
g 00
; r
0
=r
00
=n; (79)
wherewehaveusedthenotationfg 0
andfg 00
todenotepartitionswithnomorethann 0
andn 00
rows,respetively.
Consider,asanotherexample,theredutionoftheirrepf1 n
gU(4`+2)intoirrepsofSU(2)O +
(2`+1). Using
(70)and(71)oneshouldrstomputetheplethysm([1=2℄ 0
(1))f1 n
g. UsingtheisomorphismbetweenSU(2)and
GL(2)wetake[1=2℄ 0
=f1g. Using(34),
(f 0
gf 00
g!fng)=Æ
f 00
g;f 0
g
, (f 0
gf 00
g!f1 n
g)=Æ
f 00
g;fe
0
g
(80)
and(46),itfollowsthat
(f1g 0
f1g)f1 n
g = X
0
00
(fg 0
fg
00
!f1 n
g)(f1g 0
fg
0
)
(f1gfg 00
) = X
fg
0
f e
g 00
, (81)
where fgarepartitions ofn. Sinefgmustbeexpressedin termsofGL(2) irreps,onlytheirrepsfgoftype
fp;qgwithp+q=nontribute. Suhirrepsareexpressedin termsofSU(2)irrepsas[(p q)=2℄. Onehasthen,
f1 n
g! h
n
2 i
f1 p
g+
X
p>q1; p+q=n
1
2 (p q)
f2 q
;1 p q
g (82)
where f1 p
gandf2 q
;1 p q
gmustbeexpressedintermsofO +
(7) irreps. Asanexample,forn=3,onehas
f1 3
g!
3
2
0
f111g+
1
2
0
f210g=
3
2
0
[111℄+
1
2
0
where useismadeof (84)[givenbelow℄to expressthe
U(7)irrepsintermsoftheones ofO +
(7).
In ases in whih [1 ℄ = (1), due to property
(46), the theorem gives a trivial identity being of no
use. It is what happens, for example, in the
redu-tion U(n) ! O(n). For this ase one has the known
result[1,2,3℄:
\TheharaterfgofU(n)deomposesintoO(n)
haraters( 00
)bytherelation
fg= X
00
"
X
0
(f 0
gf 00
g!fg) #
( 00
) (84)
where the sum is made in the irreps f 0
g with even
omponents. " Forexample,
f0g = (0); f1g=(1); f2g=(2)+(0);
f311g = (311)+(21)+(111):
UsingatableofredutionU(n)!O(n)[Onesuh
a table an be found, for instane, in Ref.[3℄. ℄ one
anobtaintheinverseresult: toexpresstheharaters
of an O(n) irrep () in terms of U(n) irreps fg. A
generalproedure toexpresstheharatersofO(n)in
termsofthoseofU(n)isgivenin Ref.[9℄
Theplethysmtehniqueanbeapplied in the
var-ious versions of the Interating Boson Model(IBM)
whih haveaveryrih algebrai struture. For
exam-ple, in IBM-4 oneneedsthebranhing rulefor the
re-dutionofirrepsfgofU
ST
(6)intoirrepsfgfgofthe
semi-diretprodutU
S (t)U
T
(3) ofU
S
(t) byU
T (3).
Thisredutionisobtainedusingthe9thlineofEq.(71).
ProeedingsymilarlytotheaseU(nm)U(n)U(m)
oneobtainsforthisredutiontheresult
fg
ST =
X
fg
S fg
T (fg
S fg
T !fg
ST )fg
S fg
T ;
(85)
fg
S
andfg
T
beingU(3)irreps.
IV.1 Apliationin Nulear Struture
Inthetraditionalnonrelativistitreatmentthe
nu-leus isonsidered asasystem ofA fermions, the
nu-leons, with spin and isospin 1=2 and 3 spatial
de-greesoffreedominteratingthroughone-andtwo-body
fores. Thebound statesofsuhsystemaredesribed
by totallyantisymmetri wavefuntions sineits
on-stituentsarefermions.
TheintrodutionofJaobivetors
!
i =
1
p
i(i+1) 0
i
X
j=1 !
r
j i
!
r
i+1 1
A
; i=1;2;:::;A 1 , (86)
!
A =
1
p
A A
X
j=1 !
r
j
(87)
allowsustoremovetheenterofmassandfousattentiononlytotherelativemotiondesribedbythetranslationally
invariantJaobyvetors !
1 ;
!
2 ;:::;
!
A 1.
Todesribetheboundstatesofsuhsystemwewilluseasbasisthebasisfuntionsofirrep[1 7(A 1)
℄ofU(7(A
1))U (r)
(3(A 1))U (s)
(4(A 1)):Thespin-isospinpartisdesribedusingthehain
U (s)
(4(A 1)) U
(ST)
(4) U
(s)
(A 1)
[ [
U (S)
(2)U (T)
(2) O
(s)
(A 1)
[
S (s)
(A)
(88)
whilethespaepartisdesribedby
U (r)
(3(A 1) U(3) U
(r)
(A 1)
[ [
O +
(3) O
(r)
(A 1)
[
S (r)
(A) :
Itfollowsthentheinterestin studyingthe
branh-ingrulesofirrepsofhainsofkind
U(A 1)O(A 1)S(A): (90)
Thisnotationis abit misleadingsineitmayraise
the question:how is it possible that the permutation
group of A objets may be a subgroup of a
transfor-mation group of a smaller number A 1 of objets?
The answer is that the objets are not the same. In
U(A 1) and O(A 1) we onsider the radial
om-ponents of the A 1 translationally invariant Jaobi
vetors(86)whileinS (r)
(A)theobjetsare theradial
omponentsofthepositionvetors !
r
i
. Apermutation
ofthepositionvetors !
r
i
turnsouttobeaorthogonal
transformation of the translationally invariant Jaobi
vetorandthereforeonehasO (r)
(A 1)S (r)
(A).
Sine the basis funtions of the irrep fg of
U (r)
(3(A 1))arefuntions onlyoftheoordinatesof
therstA 1Jaobivetors,fghastobesymmetri.
Wethen write fg =fEg . Sine the wavefuntions
ofthep-dimensionalharmoniosillatorarrytheirrep
fEgofU(p), it isusual to assoiateE to the
ongu-rationenergyofthenulearstateswhosespaepartis
desribedbywavefuntionslabeledbythehain(89).
This assoiation allows us to stablish a link with
the harmoni osillator shell model. The basis
fun-tionsoftheirrepfEgouldalternativelybelabeledby
thehainofsubroups
U(3(A 1))U (1)
(3)U (2)
(3):::U (A 1)
(3) (91)
d
inwhiheahlinkU (i)
(3)atsonlyinthe3oordinates
of the Jaoby vetor !
i
. Inthis ase theirreps
asso-iated to those U (i)
(3) would be all symmetri [E (i)
℄
and their basis funtions would beeigenstates of
har-moniosillatorswithenergyE (i)
=(E (i)
+3=2)~!and
itwouldresult
E = A 1
X
i=1 E
(i)
: (92)
Thenumberoflinearlyindependentwavefuntions
of the 3-dimensional harmoni osillator with energy
E=(E+3=2)~!isequaltothedimensionoftheirrep
fEgofU(3)givenby
dim
fEg =
1
2
(E+1)(E+2). (93)
Inthisway,byPaulipriniple,intheEshellonean
putatmost4dim
fEg
=2(E+1)(E+2)nuleons. The
minimalongurationenergyis obtainedbyllingthe
shellsE =0(s);E=1(p);E =2(s d);:::;E
0
1and
puttingtheremainingn
0
nuleonsintherstpartially
lledshellE
0
. Thellledshells(ore)will ontain
n
ore (E
0 )=
E
0 1
X
E=0
2(E+1)(E+2)= 2
3 E
0 (E
0 +1)(E
0
+2) (94)
nuleons. This equationallowsoneto nd, foragiven A, thevalueof E
0
astheoneforwhihn
ore (E
0
)A
n
ore (E
0
+1). Thenwewillhave
E
min =
E0 1
X
E=0 4Edim
fEg +E
0 (A A
ore (E
0 ))=E
0 A
1
6 E
0 (E
0 +1)(E
0 +2)(E
0
+3). (95)
d
Ouraimis tolabelthestatesofasystemofA
nu-leons with minimal onguration energy E = E
min
with the labels given by the unitary hain (89). This
labellinghasbeenextensivelyused in ourappliations
oftheRestritedDynamisModel[39℄.
The U(3(A 1)) irreps are labeled by E . For
1 A 4 one has E
0
= 0 and E = 0. For A 5
we put E = E
min
obtained by use of Eqs.(94) and
fE
1 ;E
2 ;E
3
gthat,aordingto(78)mustsatisfy
E
1 +E
2 +E
3
=E . (96)
Also,for (78),the U (r)
(A 1)irreps arethe same
of U(3), that is, fE
1 ;E
2 ;E
3
g . Eq.(84) give us the
O (r)
(A 1) irreps ontained in the U (r)
(A 1)
ir-repfE
1 ;E
2 ;E
3
g. Oneof them isby sure(E
1 ;E
2 ;E
3 )
and onlythis orrespondsto states ofminimal
ong-uration energy. This x us the O (r)
(A 1) irrep as
that of U (r)
(A 1) . It still remains the restrition
O (r)
(A 1)!S (r)
(A).
TheU (r)
(A 1)irrepsfE
1 ;E
2 ;E
3
garealltheones
that satisfy (96) . The Pauli priniple, however,
im-poses an additional restrition. The treatment of the
spin-isospin partby theWigner supermultiplet model
impliesthat theS (s)
(A)irrep[ e
℄musthaveat most4
lines,that is,
[ ~
℄=[ ~
1 ;
~
2 ;
~
3 ;
~
4
℄ : (97)
ThereforetheS (r)
(A)irrep[℄,beingitsonjugate,
musthaveatmost4olumns.
Wewill see in the following thebranhing rules in
thehainU(A 1)S(A). Theredutionofirrepsin
thehainO(A 1)S(A)isobtainedbyrst
express-ingtheO(A 1)haratersintermsofthoseofU(A 1)
and,after,makingtheredutionU(A 1)!S(A)of
theresultingU(A 1)irreps.
The S(A) irrepsontainedin the redutionof the
U(A 1) irrepf 0
g aregiven by theexpansionof the
innerplethysmfA 1;1gf 0
gintermsofS(A)irreps
[Refs.[13,38℄℄:
fA 1;1gf 0
g= X
00
V
0
00[A r
00
; 00
1 ;
00
2 ;:::;
00
A 1
℄ (98)
wherer 00
= P
i
00
i
isthedegreeofU(A 1)irrepf 00
g.
ToobtainthemultipliityoeÆientsV
0
00
thatappearin(98)oneneedsrsttodenetheoperators b
D and b
D
whihatonU(A 1)irreps
Theoperator b
D(fg) isdenedbyitsationoveranirrepf 0
g:
b
D(fg)f 0
g= X
00
(fgf 00
g!f 0
g)f 00
g. (99)
Asexample, b
D(f2g)f31g=f2g+f1 2
g.
FromthepropertiesoftheouterprodutofShurfuntions,itfollowsthattheoperators b
Dsatisfytherelations:
b
D(f 0
g) b
D(f 00
g) = b
D(f 0
gf 00
g), (100)
b
D(f 0
g)+ b
D(f 00
g) = b
D(f 0
g+f 00
g). (101)
Theoperator b
D isdened intermof b
Dby
b
D =
1
X
t2=0 X
t
2 1
X
t3=0 X
t
3 :::
1
X
j
2 =0
1
X
j
3 =0
:::(fg
t2 fg
t3 :::)(
b
D(f2gfg
t2 )
( b
D(f3gf
t
3 g):::(
b
D(f2gfj
2 g)(
b
D(f3gfj
3
g)::: . (102)
Thefj
2 g;fj
3
g;::: aresymmetriShurfuntions andthefg
t
2 ;fg
t
3
;:::aregeneralShurfuntions ofdegrees
t
2 ;t
3 ;::: .
Denotingby r;r 0
and r 00
the degreesof fg;f 0
gand f 00
g onesees from (99) that the Shur funtions f 00
g
produedby b
D(fg)whenatingin f 0
ghavedegreesr 00
=r 0
r. Siner 00
mustbenonnegative, thislimitsthe
sumsin t
2 ;t
3
;:::when b
D atsin anirrepf 0
g.
Byproperty(101)itfollowsthat
b
D(fkgfg
t
k ) =
b
D X
00
(fkgfg
t
k !f
00
g)f 00
g !
=
X
00
(fkgfg
t
k
! f
00
g) b
D(f 00
for eah plethysmthat appearsin (102) . After, byuseof (100), theprodut of b
D 'sis onverted into asingle b
D
withargumentequaltotheprodutoftheShurfuntionsofeahfator. MakingtheouterprodutoftheseShur
funtions andusingagain(101)onean rewrite b
D in aformlinearized inthe b
D'sandintheShurfuntions:
b
D= X
0
00
C
0
00f
0
g b
D(f 00
g) (103)
theC
0
00
beingonlynumerialoeÆients.
Inthelinearized formof b
D oneangatherthetermswhose b
D'sargumentshavethesamedegree,thatis,
b
D= 1
X
i=0 2
4 X
fgi X
00
C
00
fgi f
00
g !
b
D(fg
i )
3
5
1
X
i=0 Æ
i
. (104)
When b
D atsoverf 0
goneobtains
b
Df 0
g= 1
X
i=0 Æ
i f
0
g= 1
X
i=0 2
4 X
fg
i X
00
C
00
fg
i f
00
g !
b
D(fg
i )f
0
g 3
5
. (105)
d
Using(99),performingtheouterproduts,and
ol-leting similartermsoneobtainsalinearexpressionin
theShurfuntions
b
Df 0
g= X
00
V
0
00
f 00
g. (106)
This nal redution gives us the irreps f 00
g and
thenumerialoeÆientsV
0
00
whihappearin (98).
Thef 00
g'sgivetheS(A)irreps[A r 00
; 00
1 ;
00
2 ;:::;
00
A ℄
presentintheredutionofU(A 1)irrepf 0
gandthe
V 'saretheirmultipliities.
From theproeduredesribedabove,toobtainthe
Æ
1
'sgivenin(104)theonlyt
k andj
k
in(102)that
on-tributeforÆ
i
arethesolutionsbynonnegativeintegers
oftheequation
1
X
k =2 k(t
k +j
k
)=i. (107)
Fori=0onlyonesolutionexists,t
k =j
k
=0,and
therefore,Æ
1
=0. Fori=1thereis nosolution,then
Æ
1
=0. Fori=2;3and4thefollowingresultsfollow:
Æ
2
= (f0g+f1g) b
D(f2g), Æ
3
=(f0g+f1g) b
D (f3g),
Æ
4
= (2f0g+2f1g+f2g) b
D (f4g)+(f1g+f1 2
g) b
D(f31g)+
+(f0g+f1g+f2g) b
D (f2 2
g).
Fromthedenitionof the b
D 0
sitfollowsthatÆ
i f
0
g=0whenthedegreeoff 0
gis lessthaniand, therefore,
itresultsthat
b
Df 0
g
r =(Æ
0 +Æ
1
+:::+Æ
r )f
0
g
r
(108)
for aShur funtion of degreer. With theÆ 'slisted aboveoneanomputetheredution U(n 1) !S(n)for
irrepsofdegreelessorequalto4:
f0g = [n℄ ,
f1g = [n 1;1℄,
f2g = [n 2;2℄+[n 1;1℄+[n℄ ,
f1 2
g = [n 2;1 2
℄,
f3g = [n 3;3℄+[n 2;2℄+[n 2;1 2
℄+2[n 1;1℄+[n℄,
f1 3
g = [n 3;1 3
℄, (109)
f4g = 2[n℄+3[n 1;1℄+3[n 2;2℄+[n 2;1 2
℄+[n 3;3℄
+[n 3;2;1℄+[n 4;4℄,
f31g = 2[n 1;1℄+2[n 2;2℄+3[n 2;1 2
℄+[n 3;3℄+[n 3;2;1℄
+[n 3;1 3
℄+[n 4;3;1℄,
f2 2
g = [n℄+[n 1;1℄+2[n 2;2℄+[n 3;3℄+[n 3;2;1;℄+[n 4;2 2
℄,
f21 2
g = [n 2;1 2
℄+[n 3;2;1℄+[n 3;1 3
℄+[n 4;2;1 2
℄,
f1 4
g = [n 4;1 4
℄.
d
Usinga table of redution U(n)O(n) [Ref.[3℄℄,
oneanexpress,bysubtrations,theharatersofO(n)
intermsofthoseofU(n).
In Refs.[3, 38℄ there is a table of the redution
O(n 1) S(n) for ( 0
) of degree no more than 7
andwithnomorethan3rows.
The expansion(104) of b
D in terms of Æ
i
allowsus
to ompute all the S(A) irreps [ 00
℄ ontained in the
U(A 1)irrepf 0
g. Forgreatvaluesofr
0
thisproess
istoomuhlaborious.
InappliationsinNulear Physisonehasthatthe
U(A 1) irreps of interestare, aording to (96),the
ones with no morethan 3 rows, that is, those of the
formf 0
g=fE
1 ;E
2 ;E
3
g. Besides,Paulipriniple
im-poses that the only physially aeptable S(A) irreps
arethoseoftheform
[℄=[4 k4
;3 k3
;2 k2
;1 k1
℄ (110)
with
4k
4 +3k
3 +2k
2 +k
1
=A. (111)
The k
i
are interpreted[36℄ as the number of spae
levelsoupyedby1;2;3;and 4nuleons,respetively.
Fromnowonwewillrestritourselvestotheasesof
interest in Nulear Physis, that is, theones in whih
the U(A 1) irreps f 0
g are also U(3) irreps
satisfy-ing Eq.(96)and the S(A) irreps[℄ satisfy(110) This
means that f 0
g has at most 3 rows and [℄ at most
4 olumns. These restritions, as will be seen below,
simplify enormouslythealulations.
Havinginmindtheserestritions,letus ndwhih
t
k 'sandj
k
'sinEq.(102)maygiveaontribution. When
applyingthelinearizedform[Eq.(103)℄of b
DtoaShur
funtion fg (A)
E
of U(A 1) one has, using Eqs. (99)
and(103),
b
Dfg (A)
E =
X
0
00
C
0
00
X
(f
00
gfg!fg (A)
E )
X
000
(f 0
gfg!f 000
g)f 000
g
(112)
ByEq.(98)theShurfuntionsf 000
gwillgiveS(A)irreps
[℄=[A r
000;
000
1 ;
000
2 ;:::;
000
A 1
℄. (113)
[Herewereallthatr
denotesthedegreeofageneralShurfuntionfg.℄
Sinefg (A)
E
hasat most3rows,theouterprodutf 00
gfggivesanonzeroontributiononlywhenbothf 00
g
andfghaveatmost3rows,i.e.
f 00
g=f 00
1 ;
00
2 ;
00
3
g and fg=f
1 ;
2 ;
3
g. (114)
Sinef 00
gisaomponentoftheredution
(f2gfg
t
2
)(f2gfj
2
g)(f3gfg
t
3
)(f3gfj
3 g):::,
onlyontributetheomponentsinfkgfg
tk
andfkgfj
k
gwithnomorethan3rows.
Wethenintroduethenotationfmg _
fgtodenotewhat weallareduedplethysm:
fmg _
In our appliations to Nulear Physis the only
plethysms that one needsto ompute arethe redued
ones. Thesehavemuhlessomponentsthanthe
om-pleteplethysms,whatmakestheomputeralulations
feasible.
Therulesofouterprodutaresuhthatifoneofits
fatorshasmorethanprows,thesameourswithall
the Shur funtions in its redution. Due to that, all
the plethysms properties here presented, but Eq.(39),
applytoreduedplethysms.
ComputeralulationsusingEq.(60)showthat
fkg _
f1 m
g=0; form>(k+1)(k+2)=2. (116)
Fromthisresultoneprovesthat
fkg _
fg = 0forShurfuntions fgwithmorethan
m=(k+1)(k+2)=2 rows. (117)
d
Inorder to produeaphysially aeptable
ontri-bution,theShurfuntionsf 0
ginEq.(112)whenouter
multiplyedbyfgmustgive,byEq.(98)and (110),in
itsredutionaShurfuntionwithat most4olumns.
Bytherulesofouterprodut,itfollowsthatbothf 0
g
andfgmusthavethisproperty:
f ~
0
g=f
0
1 ;
0
2 ;
0
3 ;
0
4
g; f~g=f
1 ;
2 ;
3 ;
4
g: (118)
Sinef 0
gisatermoftheredutionoff
t2 gf
t3 g:::,
itfollowsthat alsothefg
tk
musthavethis property.
This implies that among the redued plethysms
fkg _
fg
tk
thatappearinEq(102),onlythoseinwhih
thelengthofthefg
tk
'srowsdonotexeed4mustbe
onsidered.
The analysis of degrees of the Shur funtions in
Eq.(112)givesfurther informations:
r
00 +r
=E; r
0+r
=r
000 . (119)
FromEq.(113)and(110)onehas
A r
000
4. (120)
CombiningEq.(119)and(120)itfollowsthat
ir
00
r
0
E A+4 (121)
what setsanupperbound ini:
i
max
=E A+4. (122)
FromEq.(114)and(118)oneonludesthat
r
12. (123)
This resulttogetherwiththerstofEqs.(119) implies
that
r 00
E 12. (124)
CombiningEq.(102)and(103)onehas
r
0
= X
k =2 t
k ; r
00
= X
k =2 k(t
k +j
k
) (125)
andtherefore
i= X
k =2 [k(t
k +j
k ) t
k ℄=t
2 +
X
k =2 k(t
k +1 +j
k
): (126)
Fromthese equationsoneonludesthat
i X
k =2 t
k
(127)
and
i= X
k =2 t
k )
t
2
=i; t
3 =t
4
=:::=0;
j
2 =j
3
=:::=0:
(128)
Eq.(127),ombinedwithEq.(125)and(124)gives
E 12r
00
2i (129)
fromwhih oneonludesthat
2iE 12. (130)
Thisgivesalowerboundto i:
i
min =
E+1
2
6. (131)
Summarizing: givenE andA,thet
k
'sandj
k 'sin
Eq.(102)appliedtofg (A)
E
thatmaygivephysially
a-eptableS(A)irrepsareobtainedfollowingthe2steps:
1)takeiintherange
E+1
2)foreahiin thisrange,nd thenonnegative
in-tegersj
k andt
k
thatsatisfy
t
2 +
P
k =2 k(t
k +1 +j
k )=i,
P
k =2 k(t
k +j
k )=r
00
,
(133)
wherer
00
mustbein therangegivenbyEq.(129).
Theseonditionsreduesdrastiallythenumberof
j
k
'sandj
k
'sthatmayontributeandalsotheirvalues,
beingvalidforanyvalueofAandEE
min .
One the t
k
's and j
k
's that have a hane to
ontribute are determined, one omputes the redued
plethysmsassoiatedto themandontinuesthe
alu-lations.
In any physial appliation one starts by
examin-ing rst the ase E = E
min
, so it deserves a speial
attention.
Forp nulei(5A16)onehasE
0
=1and,
a-ordingtoEq.(95),E
min
=A 4. InthisaseEq.(132)
givesonlythevalue0fori,andbyEq.(133)onehas
t
2 =t
3
=:::=0; j
2 =j
3
=:::=0 (p nulei).
(134)
Therefore
b
Dfg (A)
A 4 $fg
(A)
A 4
(135)
where here,andin thefollowing,thesymbol$means
that one onsiders in the RHS only those Shur
fun-tionsthatproduephysiallyaeptable S(A)irreps.
Then, byEq(98), for p-nulei in ground
ongura-tion,onehastheU(A 1)S(A)redution
fg (A)
A 4 $[4;
1 ;
2 ;
3
℄ p nulei (136)
with
1 +
2 +
3
=A 4 and
i
4 . (137)
InAppendix Aonelists theredutionU(A 1)
S(A) for p nulei in ground onguration. One
ob-serves that the results present the symmetry under
partile-holeexhangeintheopenshell:
A $ A=n
ore +n
0
A; (138)
(p E
1 E
2
; qE
2 E
3
)$(p;q)=(q;p): (139)
Forthisshellthese symmetryrelationsread as
A $ A=20 A
[℄
h
4; (0)
1 ;
(0)
2 ;
(0)
3 i
!
= h
4;4 (0)
3
;4 (0)
2
;4 (0)
1 i
. (140)
For(s d)-nulei(17A40), E
0
=2and E
min
=2A 20. Eq.(132)givesagainonlyonesolutionfori:
i=i
min =i
max
=A 16. (s d)-nulei (141)
Sinei=i
max
,byEq.(128)onehastheresult
t
2
=A 16; t
3 =t
4
=:::=0; j
2 =j
3
=:::=0(s d) nulei (142)
andtherefore
b
Dfg (A)
2A 20 $
X
fgA
16 fg
A 16 b
D(f2g _
fg
A 16 )fg
(A)
2A 20 =
X
fgA
16 fg
A 16
X
fg2(A
16) (f2g
_
fg
A 16 !fg
2(A 16) )
b
D(fg
2(A 16) )fg
(A)
2A 20
; (143)
for(s d) nulei.
Theonlyreduedplethysmsthatoneneedstoompute,forthewholeshell,aref2g _
fg
m
withm=1;2;:::;24.
Asseenpreviously,onlyontribute theShurfuntions fg
A 16
withno morethan(2+1)(2+2)=2 =6rows
andnomorethan4olumns.
Whenatingonfg (A)
2A 20
,theoperator b
D(fg
2(A 16)
)gives,byEqs.(114),(123)
b
D(fg
2(A 16) )fg
(A)
$(fg
2(A 16) f4
3
g!fg (A)
)f4 3