Dynami Saling in Vaany-Mediated Disordering
B. Shmittmann,R.K.P. Zia,and Wannapong Triampo
Departmentof PhysisandCenter
forStohastiProesses inSieneandEngineering,
VirginiaTeh,Blaksburg,V.A.24061-0435,USA
Reeived1November1999
Weonsiderthedisorderingdynamisofaninteratingbinaryalloy withasmalladmixtureof
va-anieswhihmediateatom-atomexhanges. Startingfromaperfetlyphase-segregatedstate,the
systemisrapidlyheatedtoatemperatureinthedisorderedphase. Asuitabledisorderparameter,
namely,thenumberofbrokenbonds,ismonitoredasafuntionoftime. UsingMonteCarlo
simula-tionsandaoarse-grainedeldtheory,weshowthatthelatestagesofthisproessexhibitdynami
saling, haraterizedby asetof saling funtionsand exponents. Wedisussthe universality of
theseexponentsandommentonsomesubtletiesintheearlystagesofthedisorderingproess.
I Introdution
The dynamis of binary alloys, undergoingmixing or
segregation proesses, is a venerable problem in the
physisand materials siene ommunities [1℄. Muh
interest has foused speially on the dynamis of
phase ordering and domain growth, following arapid
quenh below the oexistene urve. Starting from
an initial non-equilibrium onguration, the system
evolvestowardsitsnalequilibriumstate,givingriseto
fundamental questions in both disiplines. Cruialto
metallurgy,thedomainmorphologyisintimatelylinked
to strutural stability while statistial physis fouses
ontheuniversal,self-similaraspetsofitstemporal
evo-lution, manifested in harateristi growth exponents
anddynami saling.
A key ingredientin thestudy of these proessesis
the mehanismby whih twopartiles exhange
posi-tions. Fromtheviewpointofmodellingandsimulation
purposes, diret partile-partile exhanges obviously
lead to the simplest odes and oarse-grained
equa-tions. Moreover, invoking universality, it is expeted
that thedetails ofthe mirosopimehanismsdonot
aet large-wavelength, long-time properties, suh as
growth exponents and universal saling funtions. In
this spirit, Kawasaki dynamis and the Cahn-Hilliard
equation havebeen extensivelyused to desribephase
orderingin binaryalloys. However,inmostrealsolids,
mirosopiatom-atomexhangesanbemediatedby
avarietyofproesses[2℄,withdiretexhangesplaying
arathersmallrolesinesterihindranetendstoreate
large energybarriers. The mostommon mehanisms
terstitialsites. Forthesereasons,alloyshaveoftenbeen
modelled by three-state models [3℄ whose dynamis is
ontrolledbyatom-vaanyexhanges, withdiret
ex-hangesbeingompletely forbidden. Twoproblemsin
partiularhaveattrated onsiderableattention: rst,
theeetofvaaniesonphaseseparationanddomain
growth[4, 5℄,andseond,theirroleinatomi
interdif-fusion[6,7℄. Anumberof studieshavealsoaddressed
vaany-mediatedorderinginavarietyof
antiferromag-neti alloys [8℄, as well as surfae modes of unstable
dropletsinastablevaporphase[9℄.
In this review, we will desribe a third aspet of
defet-mediated dynamis, namely, the \inverse" of
the phase ordering problem. Instead of studying the
growth of order in response to a sudden temperature
derease (a \quenh"), we fous on thedisordering of
anitesystem, following arapidinreasein
tempera-ture. Starting with azero-temperatureferromagneti
onguration,i.e., aperfetlyphase-segregatedsystem
with sharp interfaes, we monitor how the interfaes
\roughen"and how partiles of one speies are
trans-ported into regions dominated by the other speies.
Clearly,ifthenaltemperatureissuÆientlyhigh,the
interfaes will eventually dissolve ompletely, leaving
us with ahomogeneous nal state. Several questions
emerge quite naturally: Are there harateristi time
sales on whih the disordering takes plae, and how
dotheydepend onsystemsize,temperatureandother
ontrolparameters? Howdoloal density prolesand
orrelationfuntions evolvewithtime? Are thereany
saling regimes, and what are the appropriate saling
ponents?
Inthefollowing,weaddresssomeofthesequestions
inasimplemodelfordefet-mediatedinterfae
destru-tion and bulk disordering. We onsider a symmetri
(Ising-like)binary alloyofAandBatoms whih is
di-luted by a very small number of vaanies (defets),
reetingtheminutevaanyonentrations(ofthe
or-derof10 5
)found inmostreal systems. Followingan
upquenh from zeroto anite temperatureT, the
va-anies at as \atalysts" for the disordering proess,
exhangingwithneighboringpartilesaordingtothe
usual energetis of the(dilute) Ising model. The
par-tilesthemselvesformapassivebakgroundwhose
dy-namisisslavedtothedefetmotion. Thus,thissystem
orrespondstoarealmaterialinwhihthe
harateris-titimesaleforvaanydiusionismuhfasterthan
the ordinarybulk diusion time. While vaanies are
typiallydistributed uniformlyin thebulk,ertain
de-fetsmayprefertoaumulateattheinterfaes. Thus,
the number of defets is not neessarily extensive in
systemsize.
While we allow for some variation in the vaany
number, weonsider equal onentrationsof A and B
atoms. Thus, our work forms a natural omplement
totheonlyotherstudy[10℄ofvaany-mediated
disor-dering in the literature. There, the alloy omposition
is hosen highly asymmetri: 95%of A atoms versus
only5%fortheBspeies,withasinglevaany. Thus,
the A atoms form a matrix for a B-preipitate. The
alloyisrstequilibratedataverylowtemperature,so
that small lusters of Batoms are present. It is then
rapidlyheated to ahighertemperature,andthe
num-berandsizeofBlustersaremonitored. Threedierent
senariosareobserved,dependingonwhetherthenal
temperatureisbelowthemisibilitygap,abovethe
mis-ibilitygapbutbelowT
,oraboveT
. Intherstase,
the preipitates remain ompat. They dissolve
par-tiallyatrst,butthenequilibrateagainbyoarsening.
In the seond ase, the preipitates also remain
om-patbuteventuallydissolveompletely,mostlythrough
\evaporation" from their surfaes. In the third ase,
thelustersdeomposerapidly(\explode")intoalarge
numberofsmallfragmentswhihthendisappear
diu-sively.
Theomplete orpartial mixingoftwomaterialsat
an interfae plays a key role in many physial
pro-esses, suh as orrosion or erosion phenomena [11℄.
We mention just two appliations with huge
tehno-logial potential for devie fabriation. The rst
on-erns nanowire ething by eletron beam lithography
[12℄: Ifathinlmofplatinumisdeposited onasilion
wafer, interdiusion of Pt and Si produes a mixing
a onventional eletron beam, siliides, suh as Pt
2 Si
and PtSi, form. The unexposed platinum an
subse-quently be ethed away, leaving onduting nanosale
struturesbehind. Theseondexampleonerns
meso-sopisuperlattiestrutures, onsistingofalternating
magnetiand nonmagnetimetalli layers. If adjaent
magnetilayersoupleantiferromagnetially,the
appli-ationofalargeuniformmagnetieldtotheselayered
struturesresultsingiantmagnetoresistane[13℄.
How-ever,theperformaneofthesedeviesrequirespreisely
engineeredlayerthiknessesandinterfaes,andanbe
signiantly aeted by disorder [14℄, inluding
inter-diusionorinterfaialutuations.
While motivated by these appliations, our study
an only form a baseline here, for further work on
morerealistimodels. However,italsohassomerather
fundamental impliations. First, it serves as a
test-ing ground for a basi problem in statistial physis,
namely,howasystemapproahesitsnalsteadystate,
startingfromaninitialnon-stationaryonguration. A
seond viewof ourstudyaddressestheeet ofa
ran-domwalkeronitsbakgroundmedium. Eahmoveofa
vaanyrearrangesthebakgroundatomsslightly,
leav-ing a trail behind like ahild runningaross asandy
beah.Inthesimplestase,thewalkerispurely
Brown-ian. Inourlanguage,thisorrespondsto anupquenh
to innite temperature, T = 1, where energy
barri-ersare ompletely irrelevant. Inthis ase, there is no
feedbak from the bakground to the loal motion of
the vaany. Nevertheless, eah displaed atom
dis-plays its own intriguing dynamis (mainly in d = 2)
[16,17℄. Tostudytheolletivebehavioroftheatoms,
[18℄exploredalattielledwithjusttwospeiesof
(in-distinguishable)partiles. Beyondthissimpleaseisa
systemheated to nitetemperatures. Sine the
bak-groundaetsthevaanythroughtheloalenergetis
assoiatedwith the nextmove, no exatsolutionsare
known. Instead,progressreliesmainlyonsimulations.
The key result of our study is the observation
of three distint temporal regimes, separated by two
rossovertimes, provided thenal temperature is not
too lose to T
. The intermediate and late stages of
the disordering proess exhibit dynami saling, with
harateristiexponentsandsaling funtionsthatare
omputedanalytially. Forthesystemsizesonsidered
here, a lear breakdown of these saling forms is
ob-served for temperatures within about10% of T
. We
arguethat this ourswhen theorrelationlength
be-omes omparableto thesystemsize. Inontrast, the
earlystage ofthedisorderingproessonsists of
trodue our model and dene an appropriate
\disor-der" parameter. We then review the purely diusive
ase, orresponding to T = 1 [18℄. Simulation
re-sultsfortwo-dimensiononalsystemsandanexatly
sol-uble mean-eld theory in general dimension are
dis-ussed. In Setion IV, we present a number of new
results, onerning upquenhes to nite temperatures
wherepartile-partileinterationsomeintoplay. We
onludewithsomeommentsontheeetofexternal
elds, upquenhestotemperaturesT <T
,anddetails
onerninginterfaialdestrutionin theearlystages.
II The Model
In thissetion, wedesribethedilute Ising model
un-derlyingourMonteCarlosimulations. It isdened on
a two-dimensional (d=2) square lattieof dimension
LL,withsitesdenotedbyapairofintegers,r(x;y).
The boundary onditions are fully periodi in all
di-retions. Tomodel thetwo speies of partiles, blak
(\spinup")andwhite(\spindown",displayedasgray
in thegures), andthevaanies,weintrodueaspin
variable
r
ateahsitewhihantakethreevalues:+1
( 1)ifthesiteisoupiedbyablak(white)partile,
and
r
=0 if it is empty. Multiple oupany is
for-bidden. The numbersof blak(N +
)and white (N )
partiles are onserved and dier by at most 1. The
number of vaanies,M, is muh smaller: M N +
.
In fat, most of our simulations will be restrited to
M =1,tomodeltheminutevaanyonentrationsin
real systems. In our analyti work, we will also
on-sider amoregeneralase,where M is allowed tovary
with system size aordingto M /L
. Dierent
val-ues of thevaany number exponent 2[0;d℄will be
disussed. Clearly,thesinglevaanyaseorresponds
to =0.
The partiles and vaanies interat with one
an-otheraordingtoadilute Isingmodel:
H [
r ℄= J
X
hr;r 0
i
r
r 0
(1)
withaferromagneti,nearest-neighborouplingJ >0.
Sinethedilutionissosmall,thebehaviorofthesystem
is that of the ordinary (non-dilute) two-dimensional
Ising model. Thus, it has a phase transition, from
a disordered to a phase-segregated phase, at the
On-sagerritialtemperature,T
=2:267:::J=k
B
[19℄. The
groundstateisdoublydegenerate. Itonsistsofastrip
of blakandastripof whitepartiles,eahllinghalf
thesystem,separatedbytwoplanarinterfaesrunning
parallel toalattieaxis. Sinethepartile-partile
in-terationsareferromagneti,thefewvaanies
aumu-Next,weturn to thedynamisofthemodel. Only
partile-holeexhangesareallowedandperformedwith
the usual Metropolis [20℄ rate: min f1;exp( H )g,
where H is the energy dierene of the system
be-foreand after the jump, and = 1=(k
B
T) is the
in-versetemperature. Theinitialongurationofthe
sys-tem is perfetly phase-segregated, with twointerfaes
hosen to lie along the x-axis. The vaanies are
lo-atedat random positions along oneof theinterfaes.
Sinethis istehnially azero-temperature
ongura-tion,whilethedynamisoursattemperatureT >0,
thevaanies will movearound, disorderingthe
inter-faes and, ifT >T
, dissolving themeventually. The
nal steady state is an equilibrium state of the usual
two-dimensional Ising model. Therefore, many of its
propertiesareexatlyknown[21℄.
In our simulations, the system sizes range from
L =30 to 60. The nal temperatureT, measuredin
units of the Onsager temperature T
, varied between
1:1T
andinnity. Ourdataareaveragesover10 2
to10 4
realizations(orruns)dependingonthedesiredquality
of the data. The time unit is one Monte Carlo step
(MCS)whihorrespondstoMattemptedpartile-hole
exhanges. All systems investigated equilibrate after
about10 8
MCS.
Tomonitortheevolutionofthesystem,wemeasure
a\disorderparameter",denedastheaveragenumber
of blak and white nearest-neighbor pairs, A(L;t), as
a funtion of (Monte Carlo) time t. This quantity is
easilyrelatedtotheIsingenergy,
A(L;t)= d
2 L
d
+ 1
2J
h H i+O(L
) (2)
wherehidenotestheongurationalaverageoverruns.
The orretion is due to the vaanies and remains
muh smaller than the two leading terms. More
de-tailedinformationisarriedbytheloalholeand
mag-netizationdensities,dened respetivelyas
(r;t)
Æ
r ;0
(r;t) h
r
i (3)
TheKroneker-Æ ensuresthatlattiesiter isoupied
by thevaany. Non-zerovaluesof (r;t) indiate an
exessofwhiteorblakpartilesatlattiesiter,whih
isobviouslyasensitivemeasureofthedisordering
pro-ess. Thefulltimedependeneofthesedensitiesanin
generalonlybeomputedwithinamean-eldapproah.
However,their stationary forms are easily foundfrom
III Brownian Vaanies: T = 1
InthisSetion, wefousonthesimplestase,namely,
upquenhestoinnitetemperature. Asaonsequene,
the nearest-neighbor oupling J plays no role at all,
andallattemptedpartile-holeexhangesareexeuted
withunitrate. Thus,thevaaniesperformaBrownian
randomwalk,regardlessoftheirloalenvironment. We
rstsummarizeoursimulationresultswhihsuggestthe
keyto themean-eldanalysis,namely,aseparationof
time sales. We thenintrodueasuitableset of
expo-nentsand saling formsand showthat thelate stages
ofthedisorderingproessdisplaydynamisaling.
Fi-nally,weturntoamean-eldtheoryandomputethese
exponentsandsalingfuntions analytially.
III.1 Simulation Results
To illustrate the gradual destrution of the
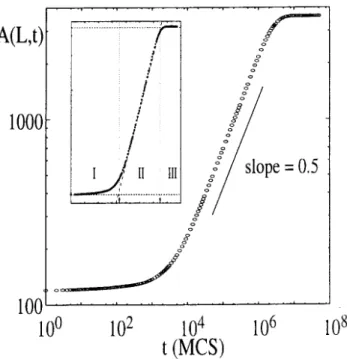
inter-faesand thedisorderingofthebulk,Fig.1showsthe
evolution of a typial onguration, in a6060
sys-tem with a single vaany (whih is represented by a
whitesquare in the gures). At t =0,the vaanyis
loated at the interfaein the enter whih begins to
break upslowly. Eventually, the seond interfaealso
beomesaeted,asmoreandmorepartilesare
trans-portedinto regions ofopposite olor,until the system
nallydisordersompletely. Forlaterreferene,wenote
that the lasttwoongurations,at 10 7
and 10 8
MCS,
are both already fully random. The disordering
pro-essislearlyreetedinthenumberofbrokenbonds:
A(60;t), shown in Fig. 2,inreases from its minimum
ofO(L)fortheinitialongurationat t=0,toO(L 2
)
forthefullyequilibratedsystematt=10 7
. Onelearly
distinguishesthreeregimes,shownshematiallyinthe
inset: anearly regime(I), theintermediate,orsaling,
regime(II),andnallyalate orsaturationregime(III)
in whih thesystemhaseetivelyreahedthesteady
state. Trakingthemotionofthevaany,thephysial
origin of these three regimes is easily identied. For
early times (regime I), thevaanyis still loalized in
theviinityofitsstartingpoint,farfromtheboundaries
ofthesystem. AfteratimeofO(L 2
),however,the
va-anyhasexplored thewholesystemandis eetively
equilibrated. Thismarkstheonsetoftheintermediate
regime. Thepartiledistribution isstillstrongly
inho-mogeneoushereanddoesnotequilibrate untilthe
sys-tem enters thesaturation regime. We emphasizethat
the seond and third regimes emerge only in a nite
system. In aninnitesystem, regime I persists for all
times. Someaspets willbebrieysummarized in the
onludingremarks.
Figure 1. Sequene ofsnapshots showing thedisordering proess ofa 6060 system withT =1. The blak and gray
squaresrepresentthetwotypesofpartiles(=1)andthewhitesquaredenotesthevaany(=0). Theongurations
Figure2.Plotofthetotalnumberofbrokenbonds,A(L;t)
vs t, for L =60 and T = 1. It shows the emergene of
anearlyregime(I),anintermediate,orsaling,regime(II),
andalateorsaturationregime(III).Thestraightreferene
line hasslope0:5.
Ourkeyobservationisthat,independentof
dimen-sion, Regimes II and III exhibit dynami saling. To
haraterizethisbehavior,weintrodueasetof
expo-nents: First,thesaturationvalueofAsaleswith
sys-temsize aordingto lim
t!1
A(L;t)A
sat
(L)L
.
Seond, in the intermediate regime, A(L;t) grows as
A(L;t) L
t
. Finally, the two rossover times
(\early" and \late") sale as t
e L
z
e
, and t
l
L
z
l
.
Thus, the intermediate-to-late time rossover an be
summarized bythesalingform
A(L;t)L
f(t=t
l
) (4)
with asaling funtion f whih satises f(x) 'onst
forx1,andf(x)x
forx1(butlargeenough
to fall within Regime II). The onsisteny ondition
A(L;t
l )'A
sat
(L)yieldsthesaling law
+z
l
=: (5)
Duetothepreseneofthenovelexponent,(5)diers
fromthefamiliarz =whihontrolssurfaegrowth
in,e.g.,theEdwards-Wilkinson[23℄ orKPZ[24℄
mod-els.
We rst onsider a single vaany, in d = 2. For
this ase, the data give = 20:1, = 0:50:06,
z
e
=20:2, z
l
= 40:2, and = 00:1. Clearly,
these exponents satisfy the saling law(5). Exellent
data ollapse is obtained by plotting A(L;t)=L
ver-sus t=L zl
, shown in Fig.3for arangeof systemsizes.
providedtheirnumberremainsonstant asthesystem
size L is varied, orrespondingto avaanyexponent
=0. Wenotebrieythat theexponent isrequired
here to aomplish good data ollapse in dimensions
greaterthan2.
Figure3. Thesaling plotof A(L;t)=L 2
vst=L 4
for L =
30 60withT =1. Thestraightreferene linehasslope
0:5.
Another natural ase is = d 1, orresponding
to a situation where the defets are initially \frozen"
atthe interfaes,andtheir numbersales withthe
in-terfaial area. Suh asenario ould our in surfae
atalysisor in welding. Sine our data are restrited
to d = 2, we examine the ase = 1, i.e., M / L.
Here,thedataollapseonlyif(i)urvesorresponding
todierentsystemsizesareshiftedbyanM-dependent
fatoralongthelnt-axis,and(ii)thelaterossover
ex-ponenttakesonthenewvaluez
l
=30:2,whileand
remain unhanged. This behaviorsuggeststhat the
exponent dependsnon-trivially on. For=1,the
data are onsistentwith = 1=2, sothat the saling
form (4)still holds and thesaling law (5) issatised
withthemodiedexponentz
l .
This onludesthe disussionof oursimulation
re-sults. We now turn to an analyti desription of the
disorderingproess.
III.2 Mean-Field Theory
As a rst step, we summarize the exatly known
resultsfor theinitial ongurationand thenal, fully
fullyperiodiboundaryonditions. Theinitialvalueof
thedisorderparameterisgivenbythenumberof
bro-kenbondsarossthetwoinitial,atinterfaesbetween
blakandwhitepartiles: A(L;t=0)=2L d 1
+O(M).
The saturation value, A
sat (L) = d 2 L 2d =(L d 1)
fol-lows easily from thefat that thenal steady stateis
ompletelyrandomfortheBrownianvaanyasewith
T =1. Thus,weanreadotheexatresult=d.
Toproeed further,we deriveaset of equationsof
motion, for the oarse-grained loal hole and partile
densities. Starting from the mirosopimaster
equa-tion, we an easily obtain evolution equations for the
disretedensities, (r;t) and (r;t). Sinethere isno
feedbak from the partile bakground, the equation
for(r;t)isompletely independentof (r;t). In
on-trast,themotionofthepartilesisslavedtothatofthe
vaany, so that the equation for (r;t) is inherently
nonlinearandontainstwo-pointfuntionsoftheform
r 0 Æ r ;0
. Here, amean-eldassumption isrequired,
totrunatetheseaverages. Finally,wetakethe
ontin-uumlimit,bylettingthelattieonstantvanishatxed
systemsizeL. Forsimpliity,weusethesamenotation
fordisretedensitiesandtheirontinuousounterparts.
Theposition vetorr(x
1; ::::;x
d
) denotesapoint in
thehyperube L=2x
i
+L=2,i=1;2;:::;d,with
volumeV L d
. Wealsoretain thesymbolt fortime,
sineMonteCarlotimeanditsoarse-grained
ounter-partdier onlyby asalefator. After somesuitable
resalings,weobtainthedesiredmean-eldequations:
t
(r;t) = r 2
(r;t)
t
(r;t) = (r;t)r 2
(r;t) (r;t)r 2
(r;t):(6)
Thesimplediusionequationforreetsthe
Brown-ian randomwalk ofthe vaanies. Themagnetization
density obeysabalane equation: therstterm
re-etsagain,providedavaanyisinitiallypresentand
a partile \diuses" in from a neighboring site. The
seondtermaountsforaloss,duetoapartile
jump-ingtoavaantnearest-neighborsite. Similarequations
havebeendisussedintheontextofbiaseddiusionof
twospeies[25℄andvaany-mediatedinterdiusion[7℄.
Note that both equations take the form of ontinuity
equations,duetotheonservationlawsonthepartile
numbers. Thetwodensitiesare normalized,aording
to R
V
(r;t) =M, and R
V
(r;t) =0. Givenfully
pe-riodiboundaryonditions,theseequationshavetobe
supplementedwith appropriate initialonditions. For
our simulations, we hoose (r;0) = M
L d 1
Æ(y) where
y x
d
, and (r;0) =2(y) 1. Thenal stateis, of
ourse,trivial: (r;1)
o
=M=V,and (r;1)=0.
Tosolvefortheholeandmagnetizationdensities,we
Monte Carlodata,intheequations(6). Thehole
den-sity,withadiusionoeÆientofO(1),relaxesrapidly
to the nal value M=V. Byontrast, the
magnetiza-tion densityis essentially slavedto (r;t) and relaxes
withadiusion\oeÆient"ofO(1=V). Thehole
den-sity spreads diusively and reahes the boundaries of
the systemafter a time of O(L 2
), marking theend of
theearlyregime. Thus,weidentifytheearly rossover
time t
e /L
2
andread o z
e
=2. Forlatertimes, the
vaaniesareuniformlydistributed overthesystem,so
thatmaybereplaedbyitsstationaryvalue,
o =
M
V .
Insertingthisintotheequationfor resultsinasimple
diusionequation t = o r 2 (7)
with adiusion oeÆientM=V. Its solution,subjet
totheinitialandfullyperiodiboundaryonditions,is
easilyfound:
(r;t)= 4 1 X n=1 sin[2(2n 1)y=L℄ 2n 1 e t(2n 1) 2 ; (8)
where 4 2
o =L
2
. Of ourse, (r;t) depends on y
only, reeting the homogeneityof initial and
bound-ary onditions in the d 1 transverse diretions. We
also note that, while this form is exat, it onverges
rapidly only for late times, t 1, orresponding
to the saturation regime. There, the prole is
har-moni with a rapidly deaying amplitude: (r;t) '
4
sin[2y=L℄e t
. Below,wewillpresentanequivalent
formwith goodonvergeneintheoppositelimit.
To desribethe simulation results,weneed an
ex-pression for the disorder parameter A. Realling its
onnetion to the average Ising energy, Eqn (2), we
invoke the ontinuum limit of the latter [26℄, hH i =
dJ R
V (r;t)
2
,whihisorretuptosurfaetermsof
O(1=L d 1
). Thus,weobtain
A(L;t)= d 2 V Z V (r;t) 2 d d r : (9)
We note that this form is manifestly extensive.
Moreover,sinesurfaeterms havebeen dropped, the
initialvalueofAisnowsimply0.
Thetimeevolutionofthisquantityfollowsfrom(8):
A(L;t)= d
2
V [1 S(2t)℄ ; (10)
where S() 8 2 P 1 1 e (2n 1) 2 =(2n 1) 2 . Sine
S(0) = 1 and S(1) = 0, we verify that A does
take on the orret initial and nal values. It is also
and the saling variable t=t
l
with t. This suggests
to dene the late rossover time as t
l
1=.
Col-leting the dependene on system size, we identify
t
l / L
2
=
o = L
d+2
. Hene, we read o z
l =
d+2 forthe saling exponent whih ontrols the
late rossovertime. Thus, t 1marks the
satura-tion regime where Eqn (4) onverges well, exhibiting
asimpleexponentialapproahto thesaturationvalue:
A(L;t)= d
2 V
1 8
2
e 2t
+O(e 4t
)
.
In ontrast, the intermediate regime (II)
orre-sponds to t 1. To apture the time dependene
here, we re-express the innite sum via a Poisson
re-summation [27℄. The keyadvantageofthis proedure
istoonvertasumwithrapidonvergeneinonelimit
(t1)intoanequivalentsumwithgoodonvergene
in theopposite (t1)limit. Deferring tehnial
de-tailstoanAppendix,weintrodueu
m
m=
p
8tand
arriveat
A(L;t)' 2d
3=2
V p
2t (
1+2 1
X
m=1 ( 1)
m
e u
2
m
u
m
1
2 ;u
2
m
)
(11)
d
where (;)denotestheinompleteGammafuntion.
In this form, the sum over m is suppressed for small
t. Thus, A(L;t) /V p
2t /L d
p
Mt=L 2+d
, yielding
the remaining indies, namely = 1
2
independent of
dimension,and = 1
2
(d+ 2). Itisstraightforward
tohekthatourexponentssatisfythesalingrelation
(5). Intwodimensions,ourtheorypreditsz
l
=4and
=0for =0,while z
l
=3and = 1
2
for =1,in
ompleteagreementwiththeMonte Carlodata.
Sine the full magnetization prole ontains more
detailed informationthan thedisorderparameter,one
might also be interested in its form for early times,
t 1. A similar Poisson resummation, of Eqn (8),
resultsin
(r;t)=erf
~ y
2 p
t
+ 1
X
m=1 ( 1)
m
erf
~ y+m
2 p
t
+erf
~
y m
2 p
t
; (12)
d
where y~ 2y=L. For t 1, this form still reets
the sharpness of the initial -funtion whih is only
gradually\washedout".
Thisonludesourdisussionofthemean-eld
the-ory, for the Brownian vaany ase. We note briey
that ourresultsremainunhanged(up toatrivial
am-plitude)ifperiodiboundaryonditionsarereplaedby
reetingones. Weshould alsoreiteratethatourfous
hererestsontheintermediateandlateregimes. Afull
mirosopitreatmentoftheearlyregimeisbeyondthe
sopeofthispaper. Forthebenetofthereader,
how-ever,a short summary is provided in the onlusions.
Instead,weturn totheroleofinterations.
IV The eet of interations:
T
< T < 1
When the nal temperature of the system is nite,
T < 1, the full Hamiltonian, Eqn (1), omes into
play when a vaany attempts to move. In
parti-walk,sinethejumpratesnowarryinformationabout
the loal environment, i.e., the distribution of blak
andwhitepartiles aroundtheoriginatingand
reeiv-ing site. Thus, a feedbak loop between vaany and
bakgroundisestablished,instarkontrasttothease
T = 1. One might expet that this has signiant
onsequenes for prolesand disorder parameter, and
thatdynami saling exponentsmight bemodied. It
is immediately obvious that we should distinguish
-naltemperaturesaboveritialityfromthosebelow. In
the former ase, the nal steady-state ongurations
arestillhomogeneous,eveniforrelationsbeomemore
notieable. Inthelatterase,however,theequilibrium
stateitselfisphase-separated,sothattheonlyeetof
thevaaniesis to\soften"theinitial interfaes. This
aspet of vaany-indued disordering should be
par-tiulary interestingin twodimensions, whereIsing
in-terfaesareknownto berough[28℄. There,the
vaan-iesmustmediate boththedevelopmentofan
\intrin-siinterfaialwidth" and theemergene oflarge-sale
wanderingsof the interfae[29℄. Certainly, weexpet
dif-vs. globaldisorder.
InthisSetion,wefousonnaltemperaturesabove
ritiality: T
<T <1,andasinglevaany, M=1.
Startingwithasetoftypialevolutionpitures,we
in-vestigatethedynamisalingpropertiesofthedisorder
parameter. Sinetheequationsofmotionnowbeome
highly nonlinear,wehavenot beenableto solvethem
exatly. Thus,weoeronlyafewommentsin
onlu-sion.
Fig. 4 shows the evolution of a typial
ongura-tion, in a 6060 system with a single vaany at
T =1:5T
. Notethat theMC timesarethesameasin
Fig. 1. Again, we observethe gradual, yet eventually
omplete, destrution oftheinterfaes. Inomparison
with Fig. 1, however, two obvious dierenes emerge:
First, the system takes longer to reah the nal
sta-tionary state. Seond, the nal onguration shows
learevideneofafiniteorrelationlength. Both
fea-turesareinduedbytheinterations. Inpartiular,the
disordering proess is sloweddown sinethe breaking
of bonds is energetially ostly. At a more
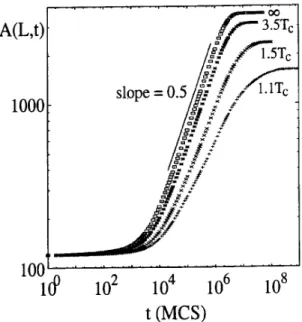
quantita-tive level, this is doumented by Fig. 5 whih shows
the disorderparameter,fora 6060systemand
sev-eraltemperatures. Oneobservesthatthelaterossover
timeshiftstolatertimesasthetemperaturedereases.
Inontrast,theearlyrossovertimeappearstobeless
aeted. Also,thesaturationvalueofthedisorder
pa-rameterdereases. However,beingessentiallytheIsing
energy, it remains extensive, with aT-dependent
am-plitude.
Figure 4. Sequene ofsnapshots showing thedisordering proess ofa 6060 system withT =1. The blak and gray
squaresrepresentthetwotypesofpartiles(=1)andthewhitesquaredenotesthevaany(=0). Theongurations
werereordedafter0;10 4
;10 5
;10 6
;10 7
and10 8
MCS.
Itisnaturaltoaskwhetherthesalingformsfound
in theprevioussetionstillhold. InFig.6,wepresent
the saling plots for the disorder parameter, i.e., we
show A(L;t)=L d
plotted vs. t=L 4
. Eah graph
orre-spondstoadierenttemperature: T=3:5T
(Fig.6a),
T =1:5T
(Fig.6b),andT =1:1T
(Fig.6). Fousing
onFig.6a,itisquiteevidentthatthedataollapsejust
as wellfor T =3:5T
as for T =1 (f. Fig.3). The
three temporal regimesare wellseparatedand easyto
distinguish. In the intermediate regime, the disorder
parameterfollowsthe t 1=2
power law, overmorethan
threedeades. Thus,thedataatthistemperaturestill
obey thesaling form (4), with the sameset of
expo-nents. However, for thenext temperature, T =1:5T
(Fig. 6b), the rangeof perfet data ollapsebeginsto
shrink: theurveforthesmallestsystemsize (L=30)
mergesnotieablylaterthaninFig.6a. Also,thepower
lawnolongerpersistsoversuhawideregion,andthe
exponent beomesmorediÆulttodetermine. Still,
thelargersystemsizesollapseratherwell,sothatthere
is still a well-dened saling funtion even if its form
appearstohange. Finally,Fig.6 showsthedatafor
T =1:1T
: here, the imposed saling form manifestly
Figure5. A(L;t)vstforL=60withT =1,3:5T
,1:5T
and1:1T
.
Figure 6. The saling plot of A(L;t)=L 2
vs t=L 4
for
L = 30 60 with (a) T = 3:5T, (b) T = 1:5T and
() T =1:1T. Thestraightreferenelineshaveslope0:5.
Weonludethat,fortemperaturesnottooloseto
the ritial temperature T
, the dynami saling form
of the purely diusive ase, Eqn (4), still holds. In
two dimensions, we identify the saturation exponent
=2and, forasingle vaany, thelate rossover
ex-ponent z
l
= 4. The saling funtion itself, however,
developsmoreurvatureintheintermediateregime,so
that itbeomesmorediÆultto extrat apure power
law, t
. One might be tempted to t the data to a
pure power law, resulting in a temperature-dependent
exponent, notieably smallerthan0:5. However, we
believe that there is littlephysial support for suh a
drasti hange in saling properties, espeially in the
disorderedphase of theIsing model. Instead,we
on-jeturethat =1=2isstillvalidbutthatT-dependent
orretions-to-saling beginto play astrongerrole. In
support, we heked that the data for T = 1:5T
,
in the earlier part of regime II, an be well tted
by a power law with an exponential orretion, i.e.,
A(L;t)=L 2
/ t 1=2
1+
1
(T)exp[
2 (T)t=L
4
℄ . This
form is gleaned from Eqn (11), by keeping the
lead-ing and rst sub-leading term but allowing for two
temperature-dependenttparameters
1
(T)and
2 (T).
Of ourse, we should antiipate signiant hanges in
thesaling behaviorupon entering the ritial region.
Sine1:1T
is\atthedoorstep"ofthelatter,some
pre-ursorssuhasaninreasedorrelationlengthbeginto
maketheirinuene felt.
Inthefollowing,weomment brieyon some
ana-lytiresults. First,weaneasilyhekthatthe
satura-tionvalues, A
sat
(L), are onsistent with exatresults
forthetwo-dimensionalIsingvalue. Table1showsthis
omparisonfora6060systemwithasinglevaany,
atseveral temperatures. A MC
sat
isthemeasured
satura-tionvalueofthedisorderparameter. A TH
sat
isalulated
on the basis of Eqn (2), where h H i is the exat bulk
value forthe average energy of theusual Ising model
[21℄. Theeetofthevaanyhasbeennegleted. The
agreementisverygood, within thestatistialerrorsof
our data. The disrepanies are of ourse largest for
thelast olumn,withT losestto T
.
Finally, sine hH i, and therefore A
sat
(L), are
ex-tensive,westillhavean exat valueforthesaturation
exponent=d.
The time-dependene of the disorder parameter
poses a muh more diÆult problem. It is of ourse
possibleto obtainthe temperature-dependent
general-izationofEqns(6),byaveragingthemirosopi
mas-ter equation, followed by a mean-eld approximation
anda naive ontinuumlimit. Foradynamis slightly
dierentfrom ours,this proedure wasfollowedin [5℄.
However,these equations are no longer easily soluble:
First,both ofthemareinherentlynonlinear,dueto
in-terations. Seond,theequationfortheloalhole
den-sity, (r;t), no longer deouples from the
magnetiza-tion (r;t), sine the bakground feeds bak into the
motion of the vaany. Thus, it is notapparent how
alean timesale separationouldemerge from these
equations. As a onsequene, we are redued to
nu-merialsolutionsorapproximate tehniques,suh asa
hightemperatureexpansion.Preliminaryresults,based
onthelatter,providesomesupportfor ouronjeture
that=1=2isstillvalidandthatlarger
orretions-to-salingareresponsiblefortheurvature inthe saling
funtion[30℄.
Tosummarizethissetionbriey,ourdataindiate
that,fortemperaturesnottoolosetotheritial
tem-perature T
, the dynami saling form of the purely
diusive ase still holds, even though
orretions-to-salingbeomemorenotieable. Inontrast,forTnear
Table1. Comparison ofexatand measuredvaluesof
the saturateddisorderparameter for several
tempera-tures.
T=T
1 3:5 1:5 1:1
A TH
sat
3600:0 3134:6 2367:0 1602:9
A MC
sat
3598:6 3134:0 2368:9 1615:7
V Conluding Remarks
To summarize, we have analyzed the vaany-driven
disorderingproessof aninitiallyphasesegregated
bi-narysystem,whihis rapidlyheatedtoatemperature
Taboveritiality. Thenumberofvaaniessaleswith
systemsize asL
, where thevaanyexponent is a
parameter. To quantify the evolution of the system,
wemeasure thenumberof brokenbonds,A(L;t),as a
funtion of time. This \disorderparameter" allowsus
toidentifythreetemporalregimes,distinguishedbythe
distributionof thevaaniesthroughthe system. Our
keyresultisthat thelatestagesofthisproessexhibit
dynamisaling. Asetofexponentsfz
e ;z
l
;;;gan
bedened,haraterizing,respetively,thesystemsize
dependeneoftworossovertimes,thenalsaturation
value of the disorder parameter, and its amplitude in
the intermediate regime. The temporal growth of A
during the latter regime is aptured by the exponent
. Ifthenal temperatureis innite,i.e.,T =1,the
motionof the vaanies is a simpleBrownianrandom
walk, and allindies anbe omputedanalytially, in
exellent agreement with the data. In partiular, we
ndthatthetypialtimesalet
l L
z
l
,whihontrols
the rossoverbetween inreasing disorder and
satura-tion,issetbyz
l
=2+d ,andthus depends
expli-itlyonboththespaeandvaanydimensionalities,d
and . Measurements of z
l
an therefore provide
in-formationaboutthevaanydistributionin asample.
In the most familiar ase, standard vaany diusion
insolids, thenumberofvaaniesisextensive(=d),
sothat thewell-knownresultz
l
=2isreprodued[2℄.
In ontrast, in two dimensions we nd z
l
= 4 for a
single vaany ( = 0) and z
l
= 3 if the defets are
generated at the initial interfae. For nite
tempera-ture T >
1:5T
, we observe that these saling forms
still hold. Eventhough interpartile interations now
play a role, orrelations in the system are still
short-ranged, so that the vaany still performs a random
walkifviewedonalengthsalewhihexeedsthe
or-relation length, (T). As T approahes T
, however,
(T)reahesO(L)sothatthesimplerandomwalk
se-nariomust breakdown. Inoursimulations,signiant
deviationsfrom thehigh-temperaturesaling form
ap-pearalreadyforT =1:1T
,where(T)'6,inunitsof
thelattiespaing [21℄.
All the investigations above are foused on
up-ofthisprojetistosetthenaltemperaturebelow
rit-iality. Needless to say,new questions and interesting
phenomena an be expeted. In partiular, the nal
equilibrium state is still phase separated, so that all
theinterfaialpropertiesomeintoplay. Withasingle
vaanyinanite system,theremaybeafurther
sep-arationof time sales. Weexpetthat, soon after the
early stage,the\intrinsi"densityproleof the
inter-fae anbebuilt. Atthis point,theinterfaialwidth,
w,ismostlikelyontrolledby. Ontheotherhand,at
suÆiently long times, the apillary waveswill surely
make their presene felt. In the d = 2 ase, the
in-terfae is alwaysrough, so that we analwaysexpet
the latter rossover to our. How, and if, w(;L;t)
sales will beof great interest. Besides dynamis and
timesales, weouldstudy theequilibrium probability
prole of the vaany, i.e., where the vaany spends
most of its time. In ase more than one vaany is
present, this prole should map into a density prole
forthevaanies. In eitherase,weexpetthe
vaan-ies tobetrapped,toagreaterorlesserextent,at the
interfae. Now,ifmoreandmorevaaniesareaddedto
thesystem,theinterfaeproleshouldbealtered,sine
apreponderaneof vaaniesmaysigniantlymodify
theinterfaialenergy. Ford=3Isingmodels,thereare
further interestingphenomena, assoiatedwith
rough-eningtransitions. Giventhatinterfaialenergiesshould
depend on vaany onentrations, how the loations
(if notthenature) of suh transitionsare aetedis a
naturalquestion. Finally,itwouldbeextremely
inter-esting to study thedynami ontentof these systems,
suhassalingpropertieswhen theupquenhis setat
arougheningtemperature.
We onlude with a few remarks on related
prob-lems. It is obviously interesting to test the range of
universalityofthehigh-temperaturesalingforms,with
respetto hangesin theboundaryonditionsand the
mirosopi dynamis. Returningto T =1, wehave
investigatedseveralases. First,replaing periodi by
reetingboundaryonditionshangesonlytrivial
am-plitudes. Amoresigniantmodiationistheaddition
ofabiasE,suhasagravitationaloreletrield[31℄:
if allpartiles arryequalharge while thevaanyis
neutral, vaanymovesalong aseleted diretion will
be suppressed. In this ase, the boundary onditions
determinethenature oftheresultingsteadystate. For
reetingboundaryonditions,itisdesribedbya
sim-ple Boltzmann fator, inorporatingagravitationalor
an eletrostati potential. Here, a new saling
vari-able,LE, emergeswhih haraterizesthe
poten-tial dierene between opposing boundaries. In
on-trast, in the periodi ase the steady state is a
non-equilibrium one. Moreover, it is translation-invariant,
so that all dependene on E disappears in asuitably
hosen o-moving frame! Remarkably, however, these
sal-exponentsfz
e ;z
l
;;;g[31℄.
Finally, weshould add afew remarkson theearly
regime. As pointed out above, for an innite system
withasinglevaany,thisistheonlyregime. First,
no-tiethatonlythephenomenonofinterfaialdestrution
is relevant,sinebulkdisorderingwould takeinnitely
long times. Next, onsidering the eetive range of a
Brownian walker,it is learthat the size of the
disor-dered region grows at mostwith t 1=2
. In moredetail,
we see that there are two distint types of disorder.
Loosely,wewilllabelthem\transverse"and
\longitudi-nal." Thersttypeisassoiatedwithamonolayer-like
disorder from the initially sharp interfae, spreading
from where thevaanybeganits journey. In
partiu-lar, eah time thevaany rossesthe planeat a new
loation, a partile is moved into the \wrong" phase.
Thus,wemayexpettransversedisordertospreadlike
t 1=2
. Theseond typeisameasureofthewidth ofthe
interfaialprole. For thisto our,thevaanymust
\arry" e.g., a blak partile deeper and deeper into
the seaof white ones. Thus, thereturnprobabilityof
the walkerplays aruial role. Only in d = 2is this
probabilitybothrelevantandnon-trivial. Applyingthe
well-known resultsof random walks[22℄, wend that
\longitudinal"disordergrowsas(lnt) 1=2
[17℄.
Eventhoughourmodelisverysimple,itformsthe
basisforthedesriptionofalargevarietyofrelated
sys-tems. Moreover,itistrulygratifyingthatonsiderable
analytiprogressispossibleforaproblemthatisboth
nonlinear and time-dependent. Work is in progressto
probetheeetofutuationsonthestrutural
deom-positionproessat amoremirosopilevel[32℄.
Aknowledgments
The authors gratefully aknowledge fruitful
ol-laborations with T. Aspelmeier, G. Korniss, and Z.
Torozkai. We also thank J. Beauvais, M. Grant, T.
Newman,S. RednerandB.Taggartforhelpful
disus-sions. ThisworkwassupportedinpartbytheNational
Siene Foundation through the Division of Materials
Researh.
Appendix: Poisson resummation
InthisAppendix,weaddafewdetailsofthePoisson
resummationproedure. OurstartingpointisEquation
(10). Droppingtheonstantprefator,wefousonthe
expressioninthebrakets,witht:
F()1 8 2 1 X n=1 e (2n 1) 2 =(2n 1) 2 (13)
This sum onvergesrapidly in the limit ! 1. We
seek a form whih onverges equallywell in the limit
! 0. We rst reast this sum in terms of a muh
simplerone,namely,
S() 1 X n=1 e (n) 2 : (14)
We begin by noting that P 1 1 1=(2n 1) 2 = 2 =8 so that
F() = 8 2 1 X n=1 1 e (2n 1) 2 (2n 1) 2 = 8 2 Z 1 0 ds 1 X n=1 e (2n 1) 2 s (15)
Itiseasytoreognizethesuminthisexpressionasthe
\odd"termsinS(),with= p
s. Thissuggeststhat
weshould reastS() intheform
S() = 1 X n=1 e (2n) 2 + 1 X n=1 e ((2n 1)) 2 S e ()+S
o ()
where the \even" terms just reprodue S(), via
S
e
()=S(2). Summarizingsofar,weobtain
F() 8 2 Z 1 0 dsS o ( p s) = 8 2 Z 1 0 ds h S( p s) S(2 p s ) i (16)
Thus, it is suÆient for us to resum S(). We reall
the Poisson resummation formula [27℄, for a funtion
f(x) , dened on 0 x < 1 with lim
x!1
f(x) = 0
and R
1
0
dxf(x)nite:
1
2 f(0)+
1
X
n=1
f(n)= 1
"
1
2 ~
f(0)+ 1 X m=1 ~ f( 2m ) # (17) where ~
f is theFourierosinetransformoff:
~
f()2 Z
1
0
dxf(x)os(x):
FromEqns(14),weanimmediatelyreado f(x)=exp( x 2
)forourasewhene
~ p
Thus,weobtain
S()= 1
2 +
1 (
p
2 +
p
1
X
m=1 e
(m=) 2
)
(18)
Clearly,the originalform ofS(), Eq. (14)onvergesrapidlyforlarge, whilethealternate form presentedhere
onvergesrapidlyfor!0. InsertingourresultintoEq. (16)andperformingtheintegrationresultsin
F()= 4
3=2
p
(
1+2 1
X
m=1 ( 1)
m
e u
2
m
u
m (
1
2 ;u
m )
)
(19)
whereu
m
m=
p
8t. Thisleadsimmediately toourresultforthedisorderparameter,Eq. (11).
ThePoissonresummationofthemagnetizationprole,Eq.(8),isalittlemoreinvolved,butfollowsananalogous
seriesofsteps. Inthisase,theproblemanbereduedto resumming
(~y;) 1
X
n=1
sin(ny)~
n e
n 2
;
wherey~2y=L,sineweanrewrite
(r;t)= 4
(~y;) 1
2
(2~y;4)
:
Theresummationleadsto
(~y;)= ~ y
2 +
2 erf
~ y
2 p
+
2 1
X
m=1
erf
~ y+2m
2 p
+erf
~
y 2m
2 p
sothat wenallyarriveat Eq. (12).
d
Referenes
[1℄ J.D.Gunton,M.SanMiguelandP.S.Sahni,in: Phase
TransitionsandCritialPhenomena,Vol.8,editedby.
C. Domb and J.L. Lebowitz (Aademi, New York,
1983); H. Furukawa, Adv. Phys. 34, 703 (1985); K.
Binder,Rep.Prog.Phys.50,783(1987),andin: Phase
Transitions of Materials, edited by R.W. Cahn, P.
Haasen and E.J. Kramer (VCH, Weinheim, 1991); J.
S.Langer, inSolids far from Equilibriumg, edited by
C.Godrehe(CambridgeUniversityPress,1992);A.J.
Bray,Adv.Phys.43,357(1994).
[2℄ See,e.g.,W.D.Callister Jr.,MaterialSieneand
En-gineering: AnIntrodution(Wiley,1994).
[3℄ M.Blume,V.J.EmeryandR.B.GriÆths,Phys.Rev.
A4, 1071 (1971);R.B.Potts,Pro. Camb.Phil. So.
48, 106 (1952); F.Y. Wu, Rev. Mod. Phys. 54, 235
(1982).
[4℄ K.YaldramandK.Binder,Atametall.mater.39,707
(1991),J.Stat.Phys.62,161(1991)andZ.Phys.B82,
405 (1991); K. Yaldram, G.K. Khalil and A. Sadiq,
SolidStateComm.87, 1045 (1993); P.Fratzland O.
Penrose,Phys.Rev.B50,3477(1994)andPhys.Rev.
B55,R6101(1997).
[5℄ S.Puri,Phys.Rev.E 55,1752 (1997);S.PuriandR.
Sharma,Phys.Rev.E57,1873(1998).
[6℄ K.W.Kehr,K.Binder, andS.M. Reulein,Phys.Rev.
[7℄ S.Alexander,Y.Rabin,andR.Zeitak,J.Chem.Phys.
95,2012 (1991).
[8℄ O.G.MouritsenandP.J.Shah,Phys.Rev.B40,11445
(1989); P.J.Shah and O.G. Mouritsen, Phys.Rev. B
41, 7003 (1990); E.Vivesand A. Planes, Phys.Rev.
Lett.68,812(1992)andPhys.Rev.B47,2557(1993);
C.Frontera,E.Vives,andA.Planes,Phys.Rev.B48,
9321 (1993); C.Frontera,E. Vives,T.Castan andA.
Planes,Phys.Rev.B51,11369(1995)andPhys.Rev.
B55,212(1997);M.Porta,C.Frontera,E.Vives,and
T.Castan,Phys.Rev.B56,5261(1997);C.Frontera
andE.Vives,Phys.Rev.B59,11121(1999);M.Porta,
E.Vives,andT.Castan,Phys.Rev.B60,3920(1999).
[9℄ M.PlappandJ.-F.Gouyet,Phys.Rev.Lett.78,4970
(1997).
[10℄ I.
Zizak,P.Fratzl, andO.Penrose, Phys.Rev.B55,
12121(1997).
[11℄ H-F.MengandE.D.G.Cohen,Phys.Rev.E51,3417
(1995); J.Krug and P.Meakin, Phys.Rev. Lett. 66,
703(1991);R.Cuerno,H.A.Makse, S.Tomassone,S.
HarringtonandH.E.Stanley,Phys.Rev.Lett.75,4464
(1995) andreferenestherein; S.G.Cororan,in
Pro-eedingsoftheEletrohemialSoiety,Symposiumon
CritialFatorsinLoalizedCorrosionIII,500(1999).
Gau-[13℄ M. N.Baibih, J.M. Broto, A.Fert, F.Nguyen Van
Dau,F.Petro,P.Etienne,G.Creuzet,A.Friederih,
andJ.Chazelas,Phys.Rev.Lett. 61,2472 (1988);G.
Binash, P. Grunberg, F. Saurenbah, and W. Zinn,
Phys.Rev.B39,4828(1989).
[14℄ S. Sanvito, C.J. Lambert, and J.H. Jeerson,
ond-mat/9903381(1999).
[15℄ Y.Ohno,Y.KawaiandS.Takeda,Phys.Rev.B,59,
2694 (1999).
[16℄ M. J.A.M.Brummelhuisand H.J.Hilhorst,J.Stat.
Phys. 53, 249 (1988). See also Z. Torozkai, Int. J.
Mod.Phys.B11,3343(1997).
[17℄ R.K.P. Zia and Z. Torozkai, J. Phys. A 31, 9667
(1998).
[18℄ Z. Torozkai, G.Korniss, B. Shmittmannand R.K.
P.Zia,Europhys.Lett.40,281(1997).
[19℄ L.Onsager,Phys.Rev.65,117(1944).
[20℄ N. Metropolis, A.W. Rosenbluth, M.M. Rosenbluth,
A.H. Teller, and E. Teller, J. Chem. Phys. 21, 1087
(1953).
[21℄ B.M. MCoy and T.T. Wu, The Two-Dimensional
Ising Model(HarvardUniversityPress,1973).
[22℄ B. D. Hughes, Random Walks and Random
Environ-ments, Vol. 1: Random Walks (Clarendon Press,
Ox-ford,1995).
[23℄ S.T. Chui and J.D. Weeks, Phys.Rev. Lett. 40, 733
(1978);S.F.EdwardsandD.R.Wilkinson,Pro.Roy.
So.London,Ser.A381,17(1982).
[24℄ M. Kardar, G. Parisi, and Y.-C. Zhang, Phys. Rev.
Lett.56,889(1986).
[25℄ B.Shmittmann,K.Hwang,andR.K.P.Zia,Europhys.
Lett.19,19(1992).
[26℄ D.J.Amit,Field Theory, TheRenormalizationGroup
andCritialPhenomena(WorldSienti,1984).
[27℄ D.S. Jones, The Theory of Generalised Funtions
(CambridgeUniversityPress,1982).
[28℄ H. vanBeijeren and I. Nolden, in Struture and
Dy-namis of Surfaes II, edited by W. Shommers and
P. von Blankenhagen; Vol. 43 of Topis in Current
Physis(SpringerVerlag,Berlin,1987).
[29℄ J.S. Rowlinson and B. Widom, Moleular Theory of
Capillarity(OxfordUniversityPress, 1982).
[30℄ B.Shmittmann,unpublished.
[31℄ W. Triampo, T. Aspelmeier, and B. Shmittmann,
ond-mat/9910275(1999).
[32℄ T. Aspelmeier, B. Shmittmann, W. Triampo and