Programação não Linear no Ensino Secundário

(1)

Universidade de Tr´

as-os-Montes e Alto Douro

Programa¸c˜

ao N˜

ao Linear

no

Ensino Secund´

ario

Dissertação de Mestrado em Ensino da Matemática

Catarina Meireles Rodrigues Ribeiro Gon¸calves

(2)

Este trabalho foi expressamente elaborado com vista à obten¸cão do grau de mestre em Ensino da Matemática de acordo com o disposto no decreto-lei 216/92 de 13 de Outubro.

A orienta¸cão deste trabalho foi levado a cabo pelo Professor João Lu´ıs Honório Matias.

(3)

Aos meus Pais, `

A minha Irm˜a, e Ao Dani...

(4)

Gostaria de agradecer:

Ao Professor Doutor João Lu´ıs Honório Matias, meu ori-entador, por todas as sugestões, cr´ıticas pertinentes e ensi-namentos ministrados, pela disponibilidade, apoio e incentivo que sempre me manifestou durante todo este per´ıodo;

Aos meus pais, irm˜a e namorado pelo seu imenso est´ımulo, for¸ca, apoio, por toda a sua paciˆencia e por sempre acredita-rem em mim;

`

A Professora e Colega, Rute Bar˜ao, pela ajuda e disponibili-dade que manifestou;

A todos o meu

(5)

Resumo

O trabalho que se apresenta, intitulado Programa¸cão Não Linear no Ensino Secundário, foi realizado no âmbito do Mestrado de Ensino de Matemática, da Universidade de Trás-os-Montes e Alto Douro (UTAD).

O que se pretende com este trabalho, é estudar uma poss´ıvel forma de alargar o horizonte matemático dos alunos do Ensino Secundário, através da introdu¸cão do tema Programa¸cão Não Linear no seu curriculum. Uma vez que o tema da Programa¸cão Linear é já um dos assuntos inseridos nos Programas Oficiais do Ensino Secundário, pretende-se assim, inves-tigar e reflectir de que forma os seus conteúdos podem ser aproveitados e utilizados para introduzir o novo tema.

Desta forma, o presente trabalho encontra-se dividido em cinco partes fundamentais, a saber: Programa¸cão Linear no Ensino Secundário; Problemas de Optimiza¸cão Não Lineares; Métodos de Pesquisa Directa; Sugestão de Apresenta¸cão do Tema ”Programa¸cão Não Linear No Ensino Secundário”; Conclusões e Trabalho Futuro.

Come¸cou por se elaborar uma pesquisa sobre os Programas Oficiais do Ensino Secundário que visou fazer um levantamento sobre os conteúdos que já são abordados e que poderiam servir de base à inser¸cão do tema da Programa¸cão Não Linear.

Após a devida justifica¸cão do tema a este n´ıvel de ensino, elaborou-se uma caracteriza¸cão pormenorizada dos Problemas de Optimiza¸cão Não Lineares, a qual, devido à vastidão do tema e aos conhecimentos adquiridos pelos alunos, foi limitada a problemas não lineares sem restri¸cões.

Os Métodos de Pesquisa Directa apresentados bem como a sua caracteriza¸cão, descri¸cão e condi¸cões de aplicabilidade a determinadas situa¸cões foram, para o caso de fun¸cões unidi-mensionais, os métodos da Seçcão Dourada e o de Davies, Swann e Campey (DSC), e para o caso de fun¸cões multidimensionais os métodos de Nelder-Mead, de Powell e de Pesquisa

(6)

Resumo vi em Padrão. A apresenta¸cão dos algoritmos dos diferentes métodos bem como da sua repre-senta¸cão recorrendo a fluxogramas, pretendeu ser um meio facilitador da compreensão do funcionamento dos diferentes métodos.

Na sugestão de apresenta¸cão do tema da Programa¸cão Não Linear para um poss´ıvel manual escolar para alunos do Ensino Secundário, come¸cou-se por introduzir o tema as-sim como os conceitos com ele relacionados, passando para a explica¸cão dos métodos da Seçcão Dourada, de DSC e de Nelder-Mead com exemplos ilustrativos e elucidativos destes conceitos. É também realizada a exemplifica¸cão da sua aplica¸cão em diferentes fun¸cões e apresentada uma ficha de trabalho para que os alunos possam verificar a aplicabilidade dos novos conteúdos e para que possam testar os conhecimentos adquiridos.

Palavras-chave: Programa¸cão Não Linear, Optimiza¸cão, Métodos de Pesquisa Directa, Ensino da Programa¸cão Não Linear.

(7)

Abstract

The following research entitled, Non Linear Programation on Secondary Education, was done for the Master Degree in Mathematics Teaching, in University of Tr´as-os-Montes e Alto Douro (UTAD).

The aim of the research was to study the possibility of widening the mathematical pers-pective of pupils in Secondary Education through the introduction of the subject Nonlinear Programation in their curriculum. Since the subject of Linear Programation is already in the Official Programs of Secondary School Education, the intention was to study and reflect upon the way knowledge can be used to introduce the new subject.

Therefore, the present work is divided into five chapters: Linear Programming in Se-condary Education; Non Linear Optimisation Problems; Direct Search Methods; A Possible Way to Present the Subject ”Nonlinear Programming In Secondary School Education”; Con-clusions and Future Work.

The starting point was a study about the Official Programs of Secondary Education, which aim was to collect the subjects taught and which could be useful to introduce the theme of Nonlinear Programation.

After justifying the theme at this teaching level, a detailed description of Non-Linear Optimisation was produced, limited to non-linear problems without constrains due to the extension of the theme and the knowledge acquired by pupils.

Direct Search Methods figured, their description and applicability conditions were in some specific situations were, in case of unidimensional functions, the Golden Section (GS) and the Davies, Swann and Campey (DSC) methods, and in case of multidimensional functions, the Nelder-Mead (NM), the Powell and the Pattern Search methods. The presentation of the algorithms of different methods and their illustration by flow charts, was meant to be a way of simplifying understanding and their functioning.

(8)

Abstract viii In the chapter ”Nonlinear Programming In Secondary School Education”, we started to introduce the subject and the concepts related were introduced, followed by the explanation of GS, DSC and NM methods with some examples. An exemplification of their application in different function and inserted a worksheet with the purpose of verifying the acquisition of new concepts and test the knowledge acquired.

Keywords: Nonlinear Programming, Optimisation, Direct Search Methods, Education of Nonlinear Programming.

(9)

´Indice

Resumo . . . v

Abstract . . . vii

´Indice de Tabelas . . . xi

´Indice de Figuras . . . xii

1 Introdu¸c˜ao 1 1.1 Finalidade do estudo . . . 1

1.2 Pertinˆencia do estudo . . . 2

1.3 Organiza¸c˜ao do estudo . . . 3

2 Programa¸cão Linear no Ensino Secundário 5 2.1 As Indica¸cões dos Programas Oficiais . . . 5

2.2 A Introdu¸cão da Programa¸cão Não Linear no Ensino Secundário . . . 7

3 Problemas de Optimiza¸cão Não Lineares 11 3.1 Caracteriza¸cão . . . 11

3.2 Condi¸c˜oes de existˆencia de um m´ınimo . . . 14

3.3 Problemas de optimiza¸c˜ao sem restri¸c˜oes . . . 16

3.3.1 Caso unidimensional . . . 16

3.3.2 Caso multidimensional . . . 18

3.4 Optimiza¸c˜ao N˜ao Linear . . . 20

4 M´etodos de Pesquisa Directa 22 4.1 Introdu¸c˜ao . . . 22

4.2 Pesquisa Unidimensional . . . 24

4.2.1 Pesquisa de Davies, Swann e Campey . . . 24

4.2.2 Método da Seçcão Dourada . . . 27 ix

(10)

´Indice x

4.3 Pesquisa Multidimensional . . . 30

4.3.1 M´etodo de Nelder-Mead . . . 31

4.3.2 Um Algoritmo de Nelder-Mead . . . 32

4.3.3 M´etodo de Powell . . . 36

4.3.4 M´etodo de Pesquisa em Padr˜ao . . . 39

Algoritmo do M´etodo de Pesquisa em Padr˜ao . . . 40

5 Sugestão de Apresenta¸cão do Tema ”Programa¸cão Não Linear No Ensino Secundário” 43 5.1 Introdu¸cão à Programa¸cão Não Linear . . . 43

5.2 Os Conceitos . . . 44

5.3 Os M´etodos . . . 45

5.3.1 M´etodo de DSC . . . 45

5.3.2 Método da Seçcão Dourada . . . 47

5.3.3 M´etodo de Nelder-Mead . . . 51

6 Conclus˜oes e Trabalho Futuro 54 6.1 Conclus˜oes . . . 54

6.2 Trabalho Futuro . . . 57

Bibliografia 58 A Algoritmos 61 A.1 Algoritmo de Davies, Swann e Campey . . . 61

Algoritmo de Davies, Swann e Campey . . . 61

A.2 Algoritmo da Sec¸c˜ao Dourada . . . 62

Algoritmo da Sec¸c˜ao Dourada . . . 62

A.3 Algoritmo de Nelder-Mead . . . 62

Algoritmo de Nelder-Mead . . . 62

A.4 Algoritmo de Powell (B´asico) . . . 63

A.5 Algoritmo de Pesquisa em Padr˜ao . . . 64

(11)

´Indice de Tabelas

3.1 Caracter´ısticas da fun¸c˜ao objectivo . . . 13

3.2 Caracter´ısticas das restri¸c˜oes . . . 14

4.1 Exemplo de aplica¸c˜ao do algoritmo de DSC(x0 = 1, δ = 0.1) . . . . 26

4.2 Exemplo de aplica¸c˜ao do algoritmo de DSC(x0 = 2.4, δ = 0.01) . . . . 26

4.3 Exemplo de aplica¸c˜ao do algoritmo de DSC(x0 = 2.4, δ = −0.01) . . . . 27

(12)

´Indice de Figuras

3.1 Representa¸cão de um m´ınimo e de um máximo de uma fun¸cão . . . 12

3.2 Tipos de minimizantes para o caso unidimensional . . . 15

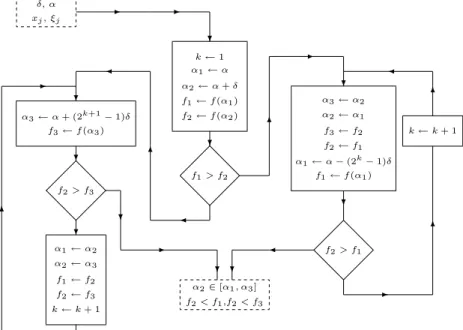
4.1 Fluxograma do algoritmo de Davies-Swann-Campey . . . 25

4.2 Esbo¸co do gr´afico de f (x) = (x − 2)2 _{. . . .} ₂₆

4.3 Raz˜ao de Ouro . . . 28

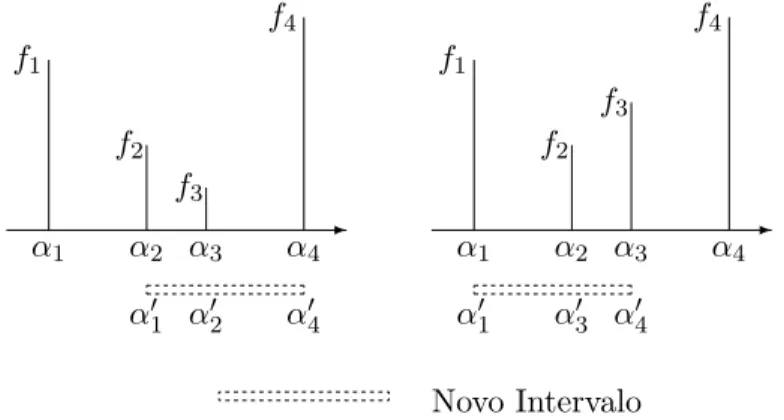
4.4 Escolha do sub-intervalo que cont´em o m´ınimo . . . 29

4.5 Fluxograma do método da seçcão dourada . . . 30

4.6 Simplex original e outros pontos auxiliares . . . 35

4.7 Fluxograma do algoritmo de Nelder Mead . . . 36

4.8 Evolu¸c˜ao do m´etodo de Powell . . . 38

4.9 Fluxograma do algoritmo de Powell (B´asico) . . . 38

4.10 Evolu¸cão do mótodo de Pesquisa em Padrão . . . 41

5.1 Representa¸cão gráfica de uma fun¸cão cúbica . . . 46

5.2 Aplica¸c˜ao do m´etodo de DSC . . . 46

5.3 Aplica¸cão do método da Seçcão Dourada . . . 48

5.4 Ficha de Aplica¸cão dos Métodos de DSC e Seçcão Dourada (pág.1) . . . 49

5.5 Ficha de Aplica¸cão dos Métodos de DSC e Seçcão Dourada (pág.2) . . . 50

5.6 Parabol´oide El´ıptico . . . 52

5.7 Curvas de N´ıvel de f (x, y) = 4 × (x − 5)2 _{+ (y − 6)}2 _{. . . .} ₅₃

5.8 Representa¸c˜ao do comportamento do Algoritmo de Neldel-Mead . . . 53

(13)

Cap´ıtulo 1

Introdu¸c˜

ao

Neste Cap´ıtulo ´e feita a introdu¸c˜ao deste trabalho, descrevendo-se os objectivos, bem como a estrutura do mesmo.

1.1 Finalidade do estudo

O interesse neste estudo surgiu duma alian¸ca entre a paixão pelo Ensino e pela Ma-temática. De facto a ideia de que existe uma separa¸cão entre a Matemática que é leccio-nada aos nossos alunos e aquela que se ”utiliza”a um n´ıvel superior, funcionou como uma motiva¸cão para o desenvolvimento deste trabalho. Tal havia já ocorrido no trabalho de Seminário inserido na parte curricular do Mestrado em Ensino da Matemática, no qual se elaborou um estudo sobre ”Introdu¸cão à Geometria Fractal”, tendo sido apresentada uma proposta de utiliza¸cão da Matemática numa forma mais avan¸cada para introduzir, de uma forma mais apelativa e atraente, as Sucessões e os conceitos a elas ligados.

Desta forma, tentando novamente estabelecer uma liga¸cão entre conceitos e métodos que exigem todo o rigor matemático e a capacidade de abstraçcão de alunos com idades compre-endidas entre os 15 e os 18 anos, e tendo em conta a constante actualiza¸cão dos programas oficiais do ensino secundário, surgiu o trabalho que se apresenta intitulado: Programa¸cão

N˜ao Linear no Ensino Secund´ario.

O desenvolvimento deste trabalho efectuou-se em duas fases que não podem ser delimita-das. Foi feito um levantamento sobre os conteúdos abordados nos actuais programas oficiais do ensino secundário, com o objectivo de estudar a viabilidade da introdu¸cão do novo tema

Programa¸cão Não Linear. Sendo já a Programa¸cão Linear um conteúdo programático do

En-sino Secundário, procedeu-se a um levantamento bibliográfico e a um estudo alargado sobre o tema da Programa¸cão Não Linear bem como à melhor forma de fazer a sua apresenta¸cão.

(14)

1. Introdu¸c˜ao 2 Para esta investiga¸c˜ao foram delineados os seguintes objectivos:

1. Apresentar uma proposta de inser¸cão do tema Programa¸cão Não Linear no Programa Oficial do Ensino Secundário.

2. Motivar os alunos para uma visualiza¸cão matemática da realidade através do estudo de problemas de optimiza¸cão, fazendo-os sentir a limita¸cão das fun¸cões lineares para a sua tradu¸cão.

3. Verificar em que medida as novas tecnologias possibilitam, a alunos do Ensino Se-cundário, o contacto com temas que exigem maior capacidade de abstraçcão, possibi-litando quer a consolida¸cão de competências quer um alargamento do seu racioc´ınio lógico-dedutivo.

1.2 Pertinˆ

encia do estudo

As transforma¸cões das quais a sociedade é alvo permanente, fazem com que surja uma nova visão da Matemática e se actualize a consciência da sua importância na vida dos cidadãos. As novas orienta¸cões sobre o que deve ser e no que se deve focar o ensino da Matemática, aliados ao modo como se processa a aprendizagem, vão suscitando cada vez mais interesse, nomeadamente das entidades nacionais responsáveis pelo emanar das directrizes para a lecciona¸cão dos conteúdos, determinando a insatisfa¸cão e o questionar dos temas abordados, ao mesmo tempo que se vão colocando novos desafios.

Descobrir o que o aluno pensa e os processos complexos de pensamento que desenvol-veu perante uma dada situa¸cão problemática, o desenvolvimento das novas tecnologias que fazem com que as técnicas de cálculo assumam menor importância e significado, o desejo de desenvolver no aluno a capacidade de enfrentar novas situa¸cões, a capacidade de inves-tiga¸cão, explora¸cão, comunica¸cão de ideias matemáticas e o estabelecimento de rela¸cões da Matemática com a realidade, são consideradas como indispensáveis numa educa¸cão para a Matemática e para a vida, fazendo com que nos apercebamos da necessidade de actualiza¸cão dos conteúdos abordados ao momento.

`

A medida que se alarga o campo de observa¸cão dos nossos alunos, queremos que eles se apercebam que as ferramentas matemáticas das quais são já conhecedores, vão-se tornando

(15)

1. Introdu¸cão 3 insuficientes para elaborar modelos explicativos de determinados fenómenos do quotidiano. A insatisfa¸cão é uma semente que deve ser colocada em cada aluno para que o ”porquê”passe a fazer parte do seu vocabulário incutindo-lhes a prática da investiga¸cão e a consciencializa¸cão de que há sempre mais a aprender.

A constante mudan¸ca e actualiza¸cão dos curr´ıculos programáticos do ensino em Portugal foi um dos principais impulsos para o desenvolvimento deste trabalho. A pertinência e a utilidade de conteúdos matemáticos como a programa¸cão linear, fizeram já com que estes fossem inclu´ıdos nos programas oficiais do ensino secundário.

A jornada escolar dos nossos alunos, está cada vez mais associada às novas tecnologias, nas quais o computador desempenha um papel fundamental, nomeadamente com a utiliza¸cão de folhas de cálculo nas quais permitem, por exemplo, realizar experiências ou estudar sistemas complexos de outro modo não poss´ıvel. O instrumento ”computador”, desempenha um papel cada vez mais relevante e impulsionador do desenvolvimento das ciências permitindo simular cenários virtuais ou leis de natureza essencialmente algor´ıtmicas. No campo do ensino, o seu uso simplifica, muitas vezes, processos que realizados de outra forma seriam morosos e desencorajariam grande parte dos alunos. Tendo em conta este facto, e dele tentando tirar vantagem, surge o principal objectivo deste trabalho que é mostrar que, com conceitos básicos que se leccionam actualmente, poderá ser introduzido um outro tema, o da Programa¸cão Não

Linear.

1.3 Organiza¸c˜

ao do estudo

Após este cap´ıtulo o trabalho apresentado foi estruturado em cinco partes principais. As-sim, no Cap´ıtulo 2 apresenta-se o que actualmente é leccionado no ensino secundário sobre Programa¸cão Linear. Num primeiro ponto, são abordadas as indica¸cões dos Programas Ofi-ciais, onde são descritos os conteúdos ligados à Programa¸cão Linear bem como os diferentes momentos do ensino secundário em que são ministrados. Num segundo ponto, é descrita a pertinência do tema da Programa¸cão Não Linear e a importância da sua introdu¸cão no en-sino secundário. É ainda realizada uma s´ıntese dos métodos de pesquisa directa escolhidos e que serão abordados com profundidade neste trabalho que, tendo em conta uma perspectiva construtiva da aprendizagem são: o Método da Seçcão Dourada (SD), o Método de Davies,

(16)

1. Introdu¸cão 4 Swann e Campey (DSC), o Método de Powell, e o Método de Nelder-Mead, sendo os últimos dois usados no caso de fun¸cões multidimensionais.

No Cap´ıtulo 3, são apresentados os Problemas de Optimiza¸cão Não Lineares. Num primeiro ponto, é feita a sua caracteriza¸cão e descri¸cão das designa¸cões e termos que lhes estão associados. Neste ponto é descrito o objectivo da optimiza¸cão e os seus diversos tipos de problemas, assim como a sua utilidade em diversos dom´ınios tais como a Engenharia, a Economia ou a Medicina. São ainda enunciadas as condi¸cões necessárias e suficientes para a existência de um m´ınimo, para fun¸cões uni e multidimensionais. Por último é apresentada a

Programa¸cão Não Linear, dos quais serão abordados apenas problemas sem restri¸cões, por

se tratar de um trabalho de apresenta¸c˜ao do temas com vista a ser inserido no curr´ıculo do ensino secund´ario.

No quarto Cap´ıtulo é feita a descri¸cão dos métodos de pesquisa directa utilizados, para o caso unidimensional, onde se inserem os métodos de pesquisa de Davies, Swann e Campey e o da Seçcão Dourada, e para o caso multidimensional, os métodos de Nelder-Mead, o de Powell e o método de Pesquisa em Padrão. São também descritos os algoritmos de cada um dos métodos. Esta descri¸cão é dirigida a dois tipos de ”público”: aos detentores de um saber cient´ıfico caracter´ıstico da Matemática e àqueles que, embora não o possuam, poderão tomar conhecimento de como opera cada algoritmo. Os algoritmos propriamente ditos podem ser encontrados no Anexo A.

O Cap´ıtulo 5 foi reservado para a apresenta¸c˜ao de uma proposta do tema Programa¸c˜ao

N˜ao Linear no Ensino Secund´ario, num poss´ıvel manual escolar direccionado a alunos deste

n´ıvel de ensino. Nesta parte do trabalho, pretende-se dar a conhecer o tema, apresentando os conceitos a ele ligados, as descri¸cões dos métodos de pesquisa directa seleccionados para serem leccionados, assim como, uma ficha de trabalho onde poderão ser praticados e aplicados os conhecimentos adquiridos.

No final deste trabalho estão reunidas as conclusões que se obtiveram da elabora¸cão do mesmo. De acordo com os objectivos definidos, foi deixada uma reflexão sobre o desenrolar do trabalho e da escolha de determinados caminhos na sua execu¸cão. Foi também deixada uma proposta de encaminhamento para um trabalho futuro que venha no seu seguimento.

(17)

Cap´ıtulo 2

Programa¸c˜

ao Linear no Ensino

Secund´

ario

Neste cap´ıtulo é apresentado o que nos programas oficiais do Ensino Secundário se encontra relativamente ao tema da Pro-grama¸cão Linear e de que forma é que tais conteúdos poderão ser ”aproveitados”para leccionar um novo tema, o da Programa¸cão

N˜ao Linear.

Apresenta-se também um parecer que pretende ser justificativo para a inser¸cão do tema da Programa¸cão Não Linear no curr´ıculo escolar dos alunos do Ensino Secundário.

2.1 As Indica¸c˜

oes dos Programas Oficiais

A constante evolu¸cão dos programas oficiais do ensino, e em particular do ensino se-cundário, faz com que deixem de ser enfatizados determinados temas e, por outro lado, cres¸ca a importância de outros. Isto acontece nos programas de Matemática, nomeada-mente, e verifica-se com o tema da Programa¸cão Linear, em concreto.

A estima¸cão e o cálculo de extremos de fun¸cões sobre os gráficos e as tabelas das mesmas, são já uma forma de, logo no 10o _{ano, os estudantes lidarem com problemas de optimiza¸cão.}

No 11o _{ano faz-se uma primeira referência à programa¸cão linear utilizando conceitos}

aprendidos no 10o _{ano e que poder˜ao vir a ser aprofundados. Este dom´ınio est´a inserido no}

Tema I - Geometria no Plano e no Espa¸co II e a justifica¸cão para a sua inser¸cão no Ensino secundário é a de que ”A programa¸cão linear vai permitir ao estudante aplicar na

resolu¸c˜ao de problemas de extrema simplicidade e utilidade (e que se apresentam hoje no dom´ınio da Economia) conceitos apreendidos no 10o _{e ampliados no 11}o _{”[21, p´ag.4].}

´

E também a este n´ıvel de ensino que é introduzido o cálculo diferencial e a taxa de varia¸cão média pretendendo-se ”... que os estudantes recordem propriedades das fun¸cões

(18)

2. Programa¸c˜ao Linear no Ensino Secund´ario 6

e aprendam intuitivamente o conceito de taxa de varia¸cão de preferência num contexto de modela¸cão matemática”[21, pág.5].

Dando continuidade aos conte´udos ministrados no 11o _{ano, o tema II do programa oficial}

continua a abordar o cálculo diferencial [22, pág.4]. São também introduzidos os problemas de optimiza¸cão que, ”... devem ser escolhidos de modo a que um estudante trabalhe de uma

forma tão completa quanto poss´ıvel a modela¸cão. É uma boa oportunidade para discutir com os estudantes o processo de modela¸cão matemática e a sua importância no mundo actual ”[22,

p´ag.6].

No programa oficial de 11o _{ou 12}o _{de Matemática B são introduzidos movimentos não}

lineares, taxa de varia¸cão e fun¸cões racionais. ”A no¸cão de fun¸cão atravessa o curr´ıculo

de Matemática e permite estabelecer liga¸cão entre vários conteúdos (Aritmética e Fun¸cões, ´

Algebra e Fun¸cões, Geometria e Fun¸cões, Estat´ıstica, Probabilidades e Fun¸cões.) A tec-nologia propicia boas abordagens para resolver problemas e influencia o tipo de questões a investigar. Os estudantes usam calculadoras gráficas para apoiar as resolu¸cões e as suas investiga¸cões mas poderão, sempre que poss´ıvel, recorrer também aos computadores, utilizar folhas de cálculo, programas de gráficos ou de geometria dinâmica. O recurso à tecnologia torna poss´ıvel a investiga¸cão e a conjectura sobre um maior número de exemplos”[23, pág.3].

No tema IV, Problemas de Optimiza¸cão, fazem parte do programa aplica¸cões das taxas de varia¸cão bem como a programa¸cão linear, como ferramenta de planeamento e gestão.

Situa¸cões realistas simples, com constrangimentos de produ¸cão ou outros que podem ser modelados por inequa¸cões lineares servem para delimitar um pol´ıgono convexo que dá informa¸cão completa sobre as quantidades poss´ıveis para cada produto.

Os conteúdos matemáticos utilizados são simples e acess´ıveis e as representa¸cões gráficas apuradas (dom´ınios planos) e tabelas, são bons instrumentos que ajudam a interpretar a si-tua¸cão, as condi¸cões impostas a uma produ¸cão ou uma cadeia de produ¸cão, armazenamento, distribui¸cão, etc..

Os problemas colocados apresentam os constrangimentos caracter´ısticos de cada situa¸cão e um objectivo (máximo ou m´ınimo de uma fun¸cão) a ser alcan¸cado com o maior êxito nas condi¸cões existentes. Pretende-se familiarizar os estudantes com situa¸cões de gestão e desenvolver competências para tomar boas decisões em termos de planeamento (da produ¸cão, por exemplo) que podem ter a ver com maximizar lucros, minimizar custos ou consumos,

(19)

2. Programa¸c˜ao Linear no Ensino Secund´ario 7 etc.

Na aula de Matemática poder-se-ão tratar problemas simples com caracter´ısticas idênticas. Assim cada exemplo tratará de maximizar ou minimizar uma determinada quantidade (fun¸cão objectivo) tendo em conta certas limita¸cões ou constrangimentos (restri¸cões do problema).

Se houver tempo, os estudantes podem mesmo ser colocados perante a necessidade de tomar decisões sobre novos procedimentos que alterem as condi¸cões de fabrico (o pol´ıgono das restri¸cões) de modo a responder a novos desafios ou a obter melhorias, com vantagem sobre o peso dos investimentos, nos máximos ou m´ınimos da fun¸cão objectivo. No fundo, trata-se de colocar aos estudantes situa¸cões de trabalho em que seja marcante a utilidade do planeamento e benéfica a colabora¸cão da matemática na tomada de boas decisões em situa¸cões da vida real. Pretende-se que os estudantes sejam capazes de:

- Reconhecer que diferentes situa¸c˜oes podem ser descritas pelo mesmo modelo Ma-tem´atico;

- Resolver num´erica e graficamente problemas simples de programa¸c˜ao linear;

- Reconhecer o contributo da matemática para a tomada de decisões, assim como as suas limita¸cões.[24, pág.6-8].

Nos manuais escolares consultados, nomeadamente [2], [8] e [9], s˜ao encontradas diferentes abordagens, com mais ou menos pormenor, do tema Programa¸c˜ao Linear.

2.2 A Introdu¸c˜

ao da Programa¸c˜

ao N˜

ao Linear no

En-sino Secund´

ario

Como justificar a inser¸cão do tema no curr´ıculo de aprendizagens dos nossos alunos? Para que o processo educativo se revele frut´ıfero, o qual pretende ser gradual e progressivo, deve ainda ser tido em conta que a capacidade de aquisi¸cão e assimila¸cão de conhecimen-tos/conteúdos por parte de alunos mais jovens é muito vasta, sendo ainda maior quando impulsionada por uma motiva¸cão adequada, preferencialmente participativa e construtiva, onde o aluno desempenha um papel activo na constru¸cão do seu próprio conhecimento.

A actual estrutura¸cão dos Programas Oficiais do Ensino Secundário faz com que, logo a partir do 10o _{ano, os alunos comecem a conviver com o estudo das fun¸cões fazendo estima¸cão}

(20)

2. Programa¸cão Linear no Ensino Secundário 8 e cálculo de extremos sobre as mesmas. Esta forma de trabalhar com problemas de opti-miza¸cão é ainda muito embrionária, pois este estudo é feito sem o recurso a ferramentas que lhes permitam ”rentabilizar”o seu trabalho, nomeadamente o recurso às derivadas de uma fun¸cão, conceito que é apenas introduzido no 11o _ano.

De facto, o conhecimento da derivada de uma fun¸cão não vai facilitar, inevitavelmente, o trabalho com todo o tipo de fun¸cão. Na realidade existem diversos tipos de fun¸cões em problemas de optimiza¸cão nos quais, devido à especificidade das expressões envolvidas, o recurso ao cálculo anal´ıtico das suas derivadas tornaria o problema interminável, ou insolúvel, quer em termos de tempo quer em esfor¸co computacional realizado, e sem qualquer n´ıvel de praticidade. Refira-se o caso de fun¸cões descont´ınuas, ou não deriváveis, ou ainda aquelas em que o cálculo da derivada ou derivadas, viria a aumentar a complexidade e o esfor¸co necessários. É, desta forma, relevante a utiliza¸cão de problemas de optimiza¸cão sem que se fa¸ca uso das derivadas das fun¸cões envolvidas.

Os métodos de pesquisa directa, não recorrem ao cálculo das derivadas para localizarem o extremo da fun¸cão. Nalguns casos nem necessário é a verifica¸cão da sua continuidade.

Assim, sabendo que os conceitos básicos ligados à optimiza¸cão são já leccionados e co-nhecidos pelos alunos ao n´ıvel do 10o _{ano, nomeadamente conceitos como os de m´ınimo,}

máximo, maximizante, minimizante, extremo ou fun¸cão objectivo, poderão ser aproveitados para introduzir um novo tema no primeiro ano de ensino secundário: o tema da Programa¸cão Não Linear. Devido à vastidão do tema e aos conhecimentos dos alunos, limitar-nos-emos aos problemas de optimiza¸cão não linear sem restri¸cões.

A introdu¸cão deste tema permitirá aos alunos alargar o dom´ınio de observa¸cão e de aplicabilidade da Matemática na vida prática, bem como alargar o conceito de fun¸cão per-cebendo a sua importância no estudo de diversas situa¸cões quotidianas, nomeadamente o de fun¸cões de várias variáveis, isto é, dotá-los de algum ”poder”que lhes confira autonomia de trabalho num campo mais diversificado de situa¸cões.

Tudo isto poderá ser efectuado de acordo com as orienta¸cões pedagógicas, onde se refere o facto de ser fundamental a cria¸cão de ambientes de trabalho com condi¸cões ideais para que os alunos possam formular hipóteses, conjecturar e experimentar adquirindo, com a experiência maior esp´ırito cr´ıtico e auto-confian¸ca.

(21)

ma-2. Programa¸cão Linear no Ensino Secundário 9 temáticas as quais se iniciam com a escolha de um problema real, seguindo-se a formula¸cão de hipóteses sobre ele. Após a tradu¸cão do problema real por um modelo matemático, é necessário tentar resolvê-lo utilizando as técnicas matemáticas dispon´ıveis. Uma vez encon-trada a solu¸cão, tem de ser implementada e comparada com a realidade para testar o seu ajustamento. Poder-se-á ainda proceder à elabora¸cão de um relatório onde constem as prin-cipais conclusões explicativas da situa¸cão e que sirvam, entre outras, para prever, conjecturar ou decidir em rela¸cão aos elementos intervenientes.

Desta forma, será proporcionado aos alunos um primeiro contacto e um breve aprofunda-mento a este novo tema pertinente e actual, contribuindo assim para o desenvolviaprofunda-mento do racioc´ınio matemático, interligando conhecimentos em muitas actividades de investiga¸cão, poss´ıveis de serem desenvolvidas, neste grau de ensino. As actividades já referidas, bem como outras que possam ser planeadas, de forma individual e colectiva, quer sejam a resolu¸cão de fichas, pequenos relatórios, monografias..., contribuirão para estimular a comunica¸cão matemática, fundamental na forma¸cão de estudantes.

As calculadoras e computadores, poderão e deverão funcionar como auxiliares educativos, bem como outros recursos tecnológicos, pelas suas potencialidades de explora¸cão e pesquisa, recupera¸cão e desenvolvimento.

A parábola ou mesmo uma fun¸cão cúbica, quando utilizadas para definirem dom´ınios planos, tema leccionado no 10o _{ano de escolaridade, podem ser uma boa ferramenta}

intro-dutória do tema da programa¸cão não linear, uma vez que analiticamente são descritas por expressões não lineares.

Para a apresenta¸cão do tema da programa¸cão não linear, e após um estudo aprofundado, foram escolhidos quatro métodos de pesquisa directa, subdivididos em dois grupos: os que fazem uma procura unidimensional como o Método da Seçcão Dourada (SD) e o Método de Davies, Swann e Campey (DSC), e os que fazem conjuga¸cão de direcçcões de modo a chegar mais rapidamente à solu¸cão pretendida como o Método de Powell e o Método de Nelder-Mead, estes no caso espec´ıfico de fun¸cões de várias variáveis.

Para uma aquisi¸cão de conhecimento progressiva e construtiva, come¸camos pela apre-senta¸cão dos métodos de DSC e SD em IR, no estudo e determina¸cão de extremos da fun¸cão não linear. Seguidamente passaremos para IRn_{, onde utilizaremos o método de Powell para}

(22)

2. Programa¸cão Linear no Ensino Secundário 10 mesmo através do método de Nelder-Mead.

Nunca será demasiado referir que, apenas serão abordados problemas não lineares, sem restri¸cões, tendo em aten¸cão o carácter introdutório deste trabalho, entre outros aspectos.

(23)

Cap´ıtulo 3

Problemas de Optimiza¸c˜

ao N˜

ao

Lineares

Neste cap´ıtulo é feita uma apresenta¸cão das caracter´ısticas dos problemas de Optimiza¸cão Não Lineares, em que consistem e das suas propriedades, quer para o caso de fun¸cões unidimensionais quer para o caso de fun¸cões multidimensionais.

Devido à vastidão do tema, ao objectivo deste trabalho e ao seu público alvo, apenas se apresentam problemas não lineares sem restri¸cões.

3.1 Caracteriza¸c˜

ao

Um problema de optimiza¸cão é caracterizado por um conjunto de variáveis independentes ou parâmetros, onde se incluem muitas vezes condi¸cões ou restri¸cões que definem valores aceitáveis das variáveis. Uma outra componente essencial de um problema de optimiza¸cão é uma fun¸cão, chamada fun¸cão objectivo. A solu¸cão de um problema de optimiza¸cão é um conjunto de valores permitidos para as variáveis, e para os quais a fun¸cão objectivo assume um valor ”óptimo”. Em Matemática, optimiza¸cão envolve normalmente maximizar ou minimizar. Problemas de diversas áreas como a Engenharia, a Economia, a Medicina ou a Estat´ıstica, podem ser colocados em termos de optimiza¸cão. Modelos matemáticos são muita vezes desenvolvidos com o objectivo de analisar e compreender fenómenos complexos. A optimiza¸cão é muito usada para determinar a forma e as caracter´ısticas do modelo que mais se aproximam da realidade, ou do problema em questão.

Ao longo deste trabalho serão estudados problemas de minimiza¸cão, o que faz com que se torne essencial definir uma forma geral para este tipo de problema. Em termos matemáticos, poder-se-á definir um problema de minimiza¸cão da seguinte forma:

(24)

3. Problemas de Optimiza¸c˜ao N˜ao Lineares 12 minimizar x∈IRn f (x) sujeito a ci(x) = 0, i = 1, 2, . . . , q ci(x) ≥ 0, i = q + 1, . . . , t, (3.1)

onde a fun¸cão objectivo, f , é uma fun¸cão real de variáveis reais x = (x1, x2, ..., xn)T, sujeitas

às condi¸cões reais, ci(x) = 0 que representam restri¸cões de igualdade para i = 1, 2, ..., q, e

ci(x) ≥ 0 que representam as desigualdades para i = q + 1, ..., t.

Existem também problemas com apenas alguns dos tipos de restri¸cões referidos e ainda problemas sem qualquer tipo de restri¸cão, assumindo neste caso a forma:

minimizar

x∈IRn f (x) (3.2)

Sendo o problema formulado em (3.1) um problema de minimiza¸cão, esta formula¸cão não é restritiva pois qualquer problema de optimiza¸cão pode ser colocado nesta forma. Em particular, um problema de maximiza¸cão pode ser resolvido com a implementa¸cão de um método que calcule m´ınimos de fun¸cões uma vez que

max f (x) = −min[−f (x)]

e o valor de x, onde f atinge o seu m´aximo ´e o mesmo onde −f atinge o seu m´ınimo.

Figura 3.1: Representa¸cão de um m´ınimo e de um máximo de uma fun¸cão

Ao ponto x∗_{chama-se maximizante ou minimizante consoante a formula¸c˜ao do problema.}

Um ponto x que verifica as fun¸cões de restri¸cão do problema, chama-se ponto admiss´ıvel. Ao conjunto de todos os pontos admiss´ıveis chama-se região admiss´ıvel podendo ser repre-sentado por

C = {x ∈ IRn _{: c}

(25)

3. Problemas de Optimiza¸cão Não Lineares 13 Apesar da grande maioria dos problemas de optimiza¸cão poderem ser expressos na forma (3.1), a existência de uma forma padrão e de toda generalidade que ela possa representar, não significa que as diferen¸cas dos diversos problemas possam ser ignoradas. Quando um problema nos é apresentado, é normalmente vantajoso determinar as caracter´ısticas especiais que vão permitir uma resolu¸cão mais eficiente do mesmo. Por exemplo, poderá ser poss´ıvel omitir testes para situa¸cões que não ocorram, ou evitar recalcular quantidades que não variam. Sabendo que a classifica¸cão ideal por categorias ou classes não existe, ou pelo menos não será exacta para todas as circunstâncias, será, todavia, conveniente classificar os problemas de optimiza¸cão de uma maneira não muito r´ıgida mas rigorosa, sem cair em exageros de considerar cada problema como único ou como uma classe separada. A distin¸cão mais óbvia entre problemas de optimiza¸cão envolve as poss´ıveis varia¸cões nas caracter´ısticas matemáticas da fun¸cão objectivo e das restri¸cões do problema. Por exemplo, estas poderão nalguns casos, possuir sucessivas derivadas cont´ınuas em todo o seu dom´ınio, ou por outro lado serem descont´ınuas; o problema de optimiza¸cão poderá possuir uma forma simples com as suas propriedades matemáticas bem compreendidas, ou pelo contrário, o seu cálculo computacional envolver e necessitar da solu¸cão de vários e complexos subproblemas.

As tabelas 3.1 e 3.2 indicam uma classifica¸cão t´ıpica de problemas de optimiza¸cão baseada na natureza matemática das expressões e para os quais existem algoritmos espec´ıficos.

Propriedades de f (x) Fun¸c˜ao unidimensional Fun¸c˜ao linear

Soma de quadrados de fun¸cões lineares Fun¸cão quadrática

Soma de quadrados de fun¸cões não lineares Fun¸cão diferenciável não linear

Fun¸cão não linear definida por ramos Fun¸cão descont´ınua não linear

Tabela 3.1: Caracter´ısticas da fun¸c˜ao objectivo

Outros factores podem também ser usados para distinguir problemas de optimiza¸cão. A dimensão do problema é um desses factores, podendo ser usado para distinguir problemas de optimiza¸cão, e afecta tanto o armazenamento como o esfor¸co computacional necessário

(26)

3. Problemas de Optimiza¸c˜ao N˜ao Lineares 14 Propriedades de ci(x)

Sem restri¸cões Limites simples Fun¸cões lineares Fun¸cões não lineares

Fun¸cões lineares definidas por ramos Fun¸cões diferenciáveis não lineares Fun¸cões não lineares definidas por ramos Fun¸cões descont´ınuas não lineares

Tabela 3.2: Caracter´ısticas das restri¸c˜oes

para obter a solu¸cão, fazendo com que técnicas eficientes para um problema com poucas variáveis, não se adeqúem a problemas com centenas ou milhares de variáveis. Embora a defini¸cão de ”dimensão do problema”não seja absoluta e não esteja convencionado a partir de que número de variáreis o problema é considerado de grande dimensão, a adequa¸cão dos métodos está também dependente do tipo de sistema computacional a utilizar.

´

E ainda de salientar que a aplica¸cão dos diferentes métodos de optimiza¸cão pode exigir requisitos especiais sem os quais a obten¸cão da solu¸cão não será poss´ıvel. Neste trabalho serão apenas utilizados e descritos, alguns métodos de pesquisa directa ou seja, métodos que não recorrem à informa¸cão proveniente das derivadas das fun¸cões envolvidas, directa ou indirectamente.

3.2 Condi¸c˜

oes de existˆ

encia de um m´ınimo

O principal objectivo em optimiza¸cão é a determina¸cão do vector x∗ _{onde a fun¸cão}

objectivo f atinge o seu valor m´ınimo. Será então conveniente definir os vários tipos de m´ınimo que poderão ocorrer.

Defini¸c˜ao 3.1. Ao conjunto de todos os pontos do hiperplano situados a uma distˆancia

inferior a δ de um ponto dado a , chama-se bola aberta de centro em a e raio δ , representando-se por B(a, δ).

Defini¸c˜ao 3.2. Seja f : IRn −→ IR uma fun¸cão dada e D um subconjunto de IRn. Diz-se que x∗ _{é um minimizante local forte sobre D se e só se existe ε > 0 tal que B(x}∗_{, ε) ⊂ D}

e

(27)

3. Problemas de Optimiza¸cão Não Lineares 15 Defini¸c˜ao 3.3. Seja f : IRn _{−→ IR uma fun¸cão dada e D um subconjunto de IR}n_{. Diz-se}

que x∗ _{´e um minimizante local fraco sobre D se e s´o se existe ε > 0 tal que B(x}∗_{, ε) ⊂ D}

e

f (x∗) ≤ f (x), ∀x ∈ B(x∗, ε).

Virtualmente, com a utiliza¸cão de métodos numéricos para resolu¸cão de problemas de minimiza¸cão, obtêm-se estimativas de m´ınimos locais. Contudo muitas vezes são necessários m´ınimos globais de uma fun¸cão, sobre um determinado conjunto, assim:

Defini¸c˜ao 3.4. Seja f : IRn −→ IR uma fun¸cão dada e D um subconjunto de IRn. Diz-se que x∗ _{é um minimizante global forte sobre D se e só se}

f (x∗_{) < f (x),} _{∀x ∈ D com x 6= x}∗_.

Se o problema abordado possuir restri¸cões, as defini¸cões anteriores poderão ainda ser válidas, bastando para tal, exigir que x∗ _{seja um ponto admiss´ıvel do problema, e do mesmo}

modo, que B(x∗_{, ε) e D sejam conjuntos de pontos admiss´ıveis do problema, por outras}

palavras, que x∗_{, B(x}∗_{, ε) e D pertencem e estejam contidos na regi˜ao admiss´ıvel.}

De uma maneira geral, para a grande maioria dos problemas de optimiza¸cão, não é poss´ıvel determinar um m´ınimo global. Porém este facto raramente é um impedimento para a obten¸cão de uma solu¸cão satisfatória de problemas práticos. Na Figura 3.2 apresentam-se alguns dos tipos de minimizantes referidos anteriormente, para o caso unidimensional.

Figura 3.2: Tipos de minimizantes para o caso unidimensional

Para o caso geral de problemas não lineares sem restri¸cões, poderão não existir estes tipos de m´ınimos. Por exemplo, se considerarmos a fun¸cão f (x) = x3_{, esta não é inferiormente}

(28)

3. Problemas de Optimiza¸cão Não Lineares 16 limitada. E mesmo em casos em que a fun¸cão é inferiormente limitada, como é o caso da fun¸cão f (x) = ex_{, o seu m´ınimo encontra-se no infinito.}

O interesse na abordagem das condi¸cões de optimalidade surge por se pretender verificar se um determinado ponto é óptimo, e porque as propriedades de um ponto óptimo poderão sugerir algoritmos para obter uma solu¸cão. Para tal, as defini¸cões dos diferentes tipos de m´ınimos atrás descritas, não são satisfatórios. Se fossem usadas para verificar a optimalidade, seria necessário avaliar f para um conjunto infinito de pontos admiss´ıveis, numa vizinhan¸ca de qualquer poss´ıvel solu¸cão, dando origem a um inaceitável esfor¸co computacional.

Por tal razão, são apresentados de seguida, condi¸cões necessárias e suficientes de existência de m´ınimos, ultrapassando assim os problemas antes definidos. Convém, no entanto, ressal-var tais condi¸cões, apesar da sua inegável utilidade, da´ı a sua inclusão neste trabalho, não serão utilizadas, uma vez que apenas serão objecto de estudo e implementa¸cão nos métodos e algoritmos, sem recurso à utiliza¸cão de derivadas, directa ou indirectamente.

3.3 Problemas de optimiza¸c˜

ao sem restri¸c˜

oes

3.3.1 Caso unidimensional

O problema mais simples que se pode considerar em optimiza¸cão é o da minimiza¸cão sem restri¸cões de uma fun¸cão, f , unidimensional, ou seja da forma do problema considerado em (3.1) tomando n = 1:

minimizar

x∈IR f (x)

Embora se venham a utilizar posteriormente técnicas de pesquisa directa sem qualquer recurso a cálculo de derivadas, não se deverão excluir outras propriedades das fun¸cões do problema a minimizar. Se essas propriedades são, por exemplo, a continuidade e diferenci-abilidade, então poderão ser utilizadas na constru¸cão, melhoria ou percep¸cão de algoritmos para a determina¸cão do óptimo e para permitir definir condi¸cões necessárias e suficientes, para identificar o(s) ponto(s) óptimo(s), como será agora o caso.

(29)

3. Problemas de Optimiza¸cão Não Lineares 17 Admitindo, que f é de classe C2_{, e que existe um minimizante local de f num ponto}

finito, x∗_{, então as duas condi¸cões seguintes terão de ser verificadas.}

Condi¸c˜oes necess´arias para a

existˆencia de um m´ınimo de uma fun¸c˜ao unidimensional

f0_(x∗_{) = 0} _(3.4)

f00_(x∗_{) ≥ 0} _(3.5)

A condi¸cão (3.4) é conhecida por condi¸cão de primeira ordem, podendo ser provada por absurdo, veja-se em [16, pág.9]. Genericamente, poder-se-á afirmar que a referida condi¸cão define os pontos de estacionaridade da fun¸cão f .

A condi¸cão (3.4) define os pontos estacionários da fun¸cão f .

Se um ponto é minimizante de uma fun¸cão continuamente diferenciável, então ele é ponto de estacionaridade dessa fun¸cão. O rec´ıproco não é no entanto verdade, pois um ponto pode ser ponto de estacionaridade e não ser um minimizante. Um maximizante local, por exem-plo, também tem primeira derivada nula. Mesmo não sendo maximizante ou minimizante, existem outros pontos que anulam a primeira derivada e que se chamam pontos de inflexão de f (x), como é o caso da fun¸cão f (x) = x3_{, em que na origem não possui maximizante nem}

minimizante e no entanto f0_{(0) = 0.}

A segunda condi¸cão apresentada, (3.5), diz-se condi¸cão de segunda ordem, e pode ser também demonstrada por absurdo, veja-se em [16, pág.9].

As condi¸cões necessárias (3.4) e (3.5) são muito utilizadas para mostrar que um dado ponto não é um minimizante, contudo, seria útil determinar condi¸cões suficientes que garan-tissem que um certo ponto é minimizante.

Condi¸c˜oes suficientes para a

f0_(x∗_{) = 0} _(3.6)

f00(x∗) > 0 (3.7)

A condi¸cão (3.6) já foi indicada uma vez que é uma das condi¸cões necessárias para a existência de m´ınimo, condi¸cão (3.4). Se (3.7) se verificar, uma vez que se admite a

(30)

3. Problemas de Optimiza¸cão Não Lineares 18 continuidade de f00_{, f}00_(x∗ _{+ h) será estritamente positiva para todo o |h| suficientemente}

pequeno.

Escolhendo |h| correctamente, e atendendo ao desenvolvimento em s´erie de Taylor de

f (x∗_{+ h) em torno de x}∗_{, at´e ordem dois, ou seja,}

f (x∗+ h) = f (x∗) + f0(x∗)h +1 2f

00_(x∗_{+ θh}2₎ _(3.8)

para algum θ ∈ [0, 1]. Por (3.6) f0_(x∗_{) anula-se, vindo}

f (x∗_{+ h) = f (x}∗_{) + f}00_(x∗_{+ θh}2

) (3.9)

ou seja f (x∗_{) + h) > f (x}∗_{) pois f}00_(x∗_{+ θh > 0 e atendendo `a defini¸c˜ao (3.2) de m´ınimo}

local, est´a provado, uma vez que f (x∗_{, h) > f (x}∗_).

3.3.2 Caso multidimensional

Nesta seçcão, consideremos um problema de minimiza¸cão sem restri¸cões para o caso de uma fun¸cão objectivo multidimensional, ou seja, um problema da forma:

minimizar

x∈IRn f (x) (3.10)

Admitindo que f (x) ´a continuamente diferenci´avel, a derivada parcial de f (x) em ordem a xi(i = 1, 2, ..., n) representa-se por:

∂f (x) ∂xi

Ao vector que possui como componentes as n derivadas parciais da fun¸c˜ao f (x), chama-mos vector gradiente de f , e representa-se por g(x) ou ∇f (x),

g(x) = µ ∂f (x) ∂x1 ,∂f (x) ∂x2 , ...,∂f (x) ∂xn ¶_T (3.11) De modo semelhante, as segundas derivadas parciais s˜ao representadas por:

∂2_f ∂xi∂xj para i 6= j e ∂ 2_f ∂x2 i para i = j

(31)

3. Problemas de Optimiza¸c˜ao N˜ao Lineares 19 Obtemos assim n2 _{derivadas parciais,} n2_+n

2 derivadas parciais distintas, formando com

elas uma matriz quadrada, sim´etrica e de ordem n, conhecida por matriz Hessiana de f (x), representada por ∇2_{f (x) ou G(x),} G(x) =             ∂2_f ∂x2 1 ∂2_f ∂x1∂x2 . . . ∂2_f ∂x1∂xn ∂2_f ∂x2∂x1 ∂2_f ∂x2 2 . . . ∂2_f ∂x2∂xn ... ... . .. ... ∂2_f ∂xn∂x1 ∂2_f ∂xn∂x2 . . . ∂2_f ∂x2 n             . (3.12)

Quando a matriz Hessiana da fun¸cão f (x) for constante, a fun¸cão objectivo f (x) é quadrática. De facto, se as segundas derivadas são constantes, integrando duas vezes G, obtém-se uma expressão quadrática , da forma:

f (x) = 1

2x

T_{Gx + c}T_{x + b}

com c ∈ IRn e b ∈ IR.

Comecemos agora por apresentar as condi¸cões necessárias para a existência de m´ınimo, tal como foi feito para o caso de fun¸cões unidimensionais.

Condi¸c˜oes necess´arias para a

existˆencia de um m´ınimo de uma fun¸c˜ao multidimensional

kg(x∗_{)k = 0 e} _(3.13)

G(x∗_{)´e semi-definida positiva} _(3.14)

A condi¸cão (3.13) verifica-se também para os pontos x∗ _{onde a fun¸cão objectivo atinge}

um m´aximo. `A semelhan¸ca do caso unidimensional, se existir um ponto x∗_{, para o qual o}

vector gradiente de f (x) se anula não sendo máximo ou m´ınimo, então ele é denominado ponto de descanso ou ponto de sela.

(32)

3. Problemas de Optimiza¸cão Não Lineares 20 Condi¸cões suficientes para a

kg(x∗)k = 0 e (3.15)

G(x∗_{)´e definida positiva} _(3.16)

As demonstra¸c˜oes das condi¸c˜oes anteriores podem ser encontradas por exemplo em [1] ou [19].

3.4 Optimiza¸c˜

ao N˜

ao Linear

Tendo em conta a forma geral apresentada em 3.1, se alguma das fun¸cões envolvidas no problema for não linear nas variáveis, então estaremos perante um problema conhecido por

problema de optimiza¸c˜ao n˜ao linear.

Restri¸cões em parâmetros ou nas variáveis independentes, podem fazer com que estas assumam apenas um número finito de valores, como por exemplo em problemas de op-timiza¸cão discreta. Outras caracter´ısticas e propriedades dos problemas de opop-timiza¸cão, como por exemplo a sua dimensão, vão influenciar a respectiva resolu¸cão do problema Neste último caso as dificuldades surgem quando a dimensão do problema ultrapassa a capacidade do sistema de cálculo, ou seja, a quantidade de dados e parâmetros é tão extensa que a memória de funcionamento do sistema de cálculo poderá ser insuficiente.

De um modo geral, um aumento do número de variáveis em problemas semelhantes, poderá aumentar significativamente a complexidade e dificuldade.

Outro aspecto a ter em conta é a forma das restri¸cões, forma esta que terá uma enorme influência na complexidade do problema de optimiza¸cão. Normalmente existe um aumento muito pequeno, na dificuldade de obten¸cão de solu¸cão, quando se passa de um problema sem restri¸cões para outro com restri¸cões do tipo limites simples nas variáveis. Da mesma forma, a generalidade dos problemas com restri¸cões lineares nas variáveis são mais dif´ıceis de resolver do que aqueles que só possuem restri¸cões do tipo limites simples, e a presen¸ca de restri¸cões não lineares aumenta a dificuldade de obten¸cão da solu¸cão.

A diferenciabilidade é, provavelmente, a propriedade mais importante de um problema no que diz respeito à facilidade de optimiza¸cão, importância que se revela na aplica¸cão de algoritmos baseados na informa¸cão relativa ao valor da fun¸cão e das suas derivadas,

(33)

3. Problemas de Optimiza¸cão Não Lineares 21 permitindo deduzir o comportamento da mesma. Se as fun¸cões do problema são duas vezes continuamente diferenciáveis (o que admitiremos salvo excep¸cões devidamente indicadas), aumenta a eficiência de um algoritmo para localizar a solu¸cão, quando comparada com os casos em que as fun¸cões de problemas são não diferenciáveis.

A maioria do software de optimiza¸cão é, desta forma, concebido para resolver problemas cujas fun¸cões sejam continuamente diferenciáveis, podendo ser seleccionados diferentes algo-ritmos, dependendo da informa¸cão dispon´ıvel relativa às derivadas ou do custo relativo de cálculo de certas quantidade, por exemplo. Os algoritmos tendem a ficar mais eficiente e robustos, quanto mais informa¸cão lhes é fornecida.

As condi¸cões de optimalidade são outra razão pelo interesse na diferenciabilidade de um problema de optimiza¸cão. Para se poder verificar se um determinado ponto é óptimo, as defini¸cões 3.2 e 3.3 de minimizantes locais forte e fracos não são satisfatórias, pois seria ne-cessário avaliar a fun¸cão objectivo num número infinito de poss´ıveis pontos, numa vizinhan¸ca de qualquer solu¸cão proposta. Ainda que esse processo fosse levado a cabo por poderosas máquinas digitais, apenas uma finita quantidade de pontos seria considerada e com esfor¸co computacional totalmente inaceitável. Todavia, se a fun¸cão objectivo e as restri¸cões do pro-blema tiverem algumas propriedades de suavidade, é poss´ıvel utilizar outro critério, mais prático, de condi¸cões que caracterizam um m´ınimo, nomeadamente utilizando as condi¸cões (3.6) e (3.7) ou (3.15) e (3.16) ou equivalentes.

Rematando o que se tem vindo a descrever, os problemas de optimiza¸cão caracterizam-se pelo tipo de fun¸cão objectivo e pelas caracter´ısticas das restri¸cões que lhe estão associadas, podendo estas ser do tipo linear ou não linear e, cada uma delas ainda ser subdividida em restri¸cões de igualdade e restri¸cões de desigualdade. Uma vez que este trabalho está a ser desenvolvido com vista a apresentar um projecto de introdu¸cão da programa¸cão não linear no ensino secundário, serão apenas abordados com mais profundidade os problemas de opti-miza¸cão não linear sem restri¸cões, recorrendo a métodos de pesquisa directa, atendendo ao grau de ensino a que se destina e aos conhecimentos cient´ıficos já adquiridos pelos estudantes.

(34)

Cap´ıtulo 4

M´

etodos de Pesquisa Directa

Neste cap´ıtulo são apresentados alguns Métodos de Pesquisa Directa e feita a sua caracteriza¸cão, descri¸cão e condi¸cões de aplica¸cão a determinadas situa¸cões. Para o caso de fun¸cões unidimensionais são distinguidos o método da Seçcão Dourada e o método de Davies, Swann e Campey (DSC). Para o caso de fun¸cões multidimensionais distinguem-se, neste trabalho os métodos de Nelder-Mead, de Powell e de Pesquisa em Padrão. Como meio de facilitar a compreensão do funcionamento dos di-ferentes métodos, serão apresentados os algoritmos bem como a sua representa¸cão por meio de fluxogramas.

4.1 Introdu¸c˜

ao

Para muitas fun¸cões que resultam de aplica¸cões da optimiza¸cão, industriais, económicas, cient´ıficas e outras, é muito dif´ıcil, senão mesmo imposs´ıvel calcular analiticamente as de-rivadas. Em muitas situa¸cões da via real surgem problemas cujo processo de optimiza¸cão, já de si complicado, possui limita¸cões, nomeadamente, a sua formula¸cão matemática dema-siado complexa, ou a falta dela. São exemplos desta última situa¸cão, os casos em que os dados do problema são fornecidos por uma tabela de valores ou estão relacionados com a medi¸cão de alguma grandeza f´ısica, não havendo nenhum modelo matemático. Ainda que a fun¸cão que se pretende optimizar seja definida por uma fórmula matemática, as suas deri-vadas podem ser desconhecidas, ou mesmo inexistentes, em todo o dom´ınio de interesse ou em pontos chave desse dom´ınio, situa¸cões estas que ocorrem muito mais frequentemente em problemas práticos de optimiza¸cão do que se possa pensar. Torna-se, desta forma, essencial utilizar métodos de optimiza¸cão em que o cálculo das derivadas ou mesmo a verifica¸cão da sua existência não seja necessário.

Para problemas de minimiza¸cão não lineares, existem duas grandes classes de métodos: os métodos dos gradientes e os métodos de pesquisa directa. Normalmente aplicáveis a fun¸cões

(35)

4. Métodos de Pesquisa Directa 23 cont´ınuas, os primeiros aproximam a fun¸cão f por outra fun¸cão mais simples, que será pos-teriormente analisada para se determinar o seu m´ınimo. As fun¸cões de aproxima¸cão são, em geral, polinomiais de grau baixo. Os métodos de procura directa partem de um intervalo que contém o m´ınimo ou de uma aproxima¸cão inicial e têm como objectivo a sua determina¸cão, calculando e comparando os valores de f em diversos pontos. A principal particularidade que distingue estes métodos dos restantes, reside no facto de estes poderem ser aplicados à resolu¸cão de qualquer problema, desde que a fun¸cão objectivo seja unimodal num intervalo que contém o m´ınimo. Esta diferen¸ca básica pode parecer pouco importante mas por vezes é limitativa. Imagine-se o caso em que o problema possui uma fun¸cão objectivo descont´ınua, com derivadas descont´ınuas, ou mesmo inexistentes, ou ainda, o caso em que a expressão da fun¸cão é demasiado complexa e o cálculo das derivadas parciais está fora de questão. O caso extremo é aquele em que a expressão da fun¸cão objectivo não é conhecida, sendo os seus valores obtidos pela medi¸cão de alguma grandeza f´ısica. Por exemplo o comprimento de uma pe¸ca produzida por uma máquina, que vê o seu produto influenciado por diversos factores variáveis, é uma quantidade que não é poss´ıvel derivar pela inexistência do modelo matemático.

As técnicas mais utilizadas na optimiza¸cão de fun¸cões sem restri¸cões nas variáveis, tendo em conta apenas os valores da fun¸cão objectivo, sem estimar nem utilizar os valores das suas derivadas, podem ser, de uma maneira geral, agrupadas em três principais classes:

- aquelas que pesquisam ao longo de direçcões e deslocamentos pré-definidos;

- aquelas que utilizam uma pesquisa unidimensional ao longo de direçcões pré-definidas; - aquelas que utilizam um conjunto determinado de pontos, em cada itera¸cão.

Em geral nos métodos de pesquisa directa, os iterandos são gerados, tendo como base apenas valores da fun¸cão objectivo. Nestes métodos não se usam os valores da fun¸cão para construir aproxima¸cões ao vector dos gradientes nem sequer se usa o gradiente como direçcão de pesquisa dos iterandos. Existem dois grandes grupos nos métodos de pesquisa directa: os que modificam as direçcões de pesquisa no final de cada itera¸cão e os que usam direçcões fixas ao longo do processo iterativo. São exemplos dos primeiros o método de Nelder-Mead [18] e o de Powell [20] e da segunda classe, os mais conhecidos são o método de Hooke e Jeeves[10] e o de pesquisa em padrão.

(36)

4. M´etodos de Pesquisa Directa 24 Comecemos por analisar o problema com a seguinte forma

minimizar

x∈IRn f (x) (4.1)

com f uma fun¸c˜ao gen´erica, da qual apenas se assume a continuidade numa vizinhan¸ca do minimizante, x∗_.

4.2 Pesquisa Unidimensional

4.2.1 Pesquisa de Davies, Swann e Campey

O método de DSC, deve o seu nome aos autores, e consiste num algoritmo de procura ao longo de uma direçcão. Resumidamente pode-se explicar que partindo de uma estimativa

x de x∗_{, procura-se um escalar α, ao longo de uma direc¸c˜ao ξ previamente conhecida, que}

minimiza localmente f (x + αξ), isto é, α = arg (min f (α)) ≡ arg (min f (x + αξ)). Com estas mudan¸cas de variável alteramos o processo da procura do m´ınimo de um problema, à procura do m´ınimo sobre uma única direçcão. Se no caso unidimensional, a direçcão é única, já tal não acontece num problema de n variéveis, em que o algoritmo teria de ser repetido no m´ınimo n vezes, uma vez sobre cada uma das n direçcões que se adoptassem para a referida pesquisa. Em qualquer dos casos como se explicará posteriormente, tornar-se-á porventura necessário, repetir todo o processo. O algoritmo de DSC baseia-se assim, para o cálculo deste escalar, na compara¸cão dos valores da fun¸cão f (α), em determinados pontos obtidos a partir de uma aproxima¸cão inicial de α e tendo como base um passo inicial

δ. Valores de espa¸camento m´ultiplos de δ, sendo cada um duplo ao anterior, v˜ao sendo

sucessivamente adicionados aos pontos calculados para obter novos pontos, sempre que a fun¸cão estiver a diminuir. O processo pára quando for encontrado um ponto cujo valor da fun¸cão seja superior ao valor da fun¸cão no ponto anterior, estando o m´ınimo encaixado entre estes últimos pontos. A procura pode também ser feita no sentido negativo, se a fun¸cão for crescente à direita no ponto inicial e decrescente à sua esquerda, segundo a direçcão e sentido de ξ. Em qualquer dos casos anteriores,os três últimos pontos de pesquisa definem dois intervalos que no seu todo contêm o minimizante procurado.

Resumindo, come¸cando numa estimativa inicial, x0, do minimizante x∗, avan¸ca-se ou

(37)

4. Métodos de Pesquisa Directa 25 nas condi¸cões desejadas, isto é, que contenha o minimizante. Posteriormente pode-se voltar a aplicar o algoritmo de DSC, come¸cando agora com uma outra estimativa x obtida no intervalo anterior, e novo tamanho do passo, δ, menor que o anterior.

Assim, após conhecida uma direçcão de procura, escolhido um ponto de partida e o tamanho do passo a utilizar, o algoritmo vai calculando os valores da fun¸cão nos novos pontos obtidos a partir dos pontos anteriores. Sempre que o valor da fun¸cão no novo ponto obtido estiver a diminuir, a direçcão (sentido)de procura do m´ınimo é mantida, e duplicado o valor do passo a utilizar no cálculo do novo ponto. Se a dado momento o valor da fun¸cão aumentar relactivamente ao ponto anterior, pára-se. O processo repetir-se-à até que a amplitude do intervalo onde se encontra o m´ınimo seja tão pequena quanto se queira.

A única excep¸cão, verifica-se na primeira itera¸cão, em que se o valor da fun¸cão aumentar aquando da progressão no sentido positivo, far-se-á a pesquisa no sentido contrário.

δ, α x_j, ξ_j - -? k ← 1 α1← α α2← α + δ f1← f (α1) f2← f (α2) ? f1> f2 ¾ 6 ¾ ? α3← α + (2k+1− 1)δ f3← f (α3) ? f2> f3 ? α1← α2 α2← α3 f1← f2 f2← f3 k ← k + 1 ¾ 6 -? -? 6 -? α3← α2 α2← α1 f3← f2 f2← f1 α1← α − (2k− 1)δ f1← f (α1) ? f2> f1 -6 k ← k + 1 6 ¾ ¾ ? α2∈ [α1, α3] f2< f1,f2< f3

Figura 4.1: Fluxograma do algoritmo de Davies-Swann-Campey

Após identifica¸cão do intervalo que contenha o minimizante, poder-se-á escolher um valor do seu interior, como a melhor estimativa obtida, servindo ainda como ponto de partida para uma nova aplica¸cão do algoritmo. Nesta situa¸cão poder-se-á optar por simplesmente se escolher o ponto com menor valor da fun¸cão, de entre os calculados, ou escolher entre este último e o ponto médio do intervalo, segundo o mesmo critério. Alguns autores utilizam uma outra abordagem que consiste em determinar o polinómio de segundo grau, que interpola os últimos pontos calculados, após o que se calcula a abcissa do respectivo vértice, adoptando-a

(38)

4. Métodos de Pesquisa Directa 26 como a estimativa procurada. Na Figura (4.1) é apresentado o algoritmo de DSC, sob uma forma gráfica.

Consideremos o seguinte exemplo, de uma fun¸cão quadrática, descrita analiticamente por: y = f (x) = (x − 2)2_{, cuja representa¸cão gráfica é apresentada na Figura 4.2.}

Figura 4.2: Esbo¸co do gr´afico de f (x) = (x − 2)2

Embora saibamos que admite como m´ınimo global o ponto (2,0), considere-se a aplica¸c˜ao do m´etodo de DSC ao problema

min

x∈IR (x − 2)

2

(4.2) com a aproxima¸c˜ao inicial de x0 = 1 e tamanho do passo δ = 0, 1. Apresentam-se na

Tabela 4.1 os respectivos c´alculos.

i Deslocamento x f (x) 0 0 1 1 1 0,1 1,1 0,81 2 0,3 1,3 0,49 3 0,7 1,7 0,09 4 1,5 2,5 0,25

Tabela 4.1: Exemplo de aplica¸c˜ao do algoritmo de DSC(x0 = 1, δ = 0.1)

Pela an´alise dos valores, conclui-se que o minimizante estar´a entre 1, 3 e 2, 5 ou de outra forma x∗ _{∈ [1, 3; 2, 5].}

i Deslocamento x f (x)

0 0 2,4 0,16

1 0,01 2,41 0,1681

Tabela 4.2: Exemplo de aplica¸c˜ao do algoritmo de DSC(x0 = 2.4, δ = 0.01)

Para ilustrar completamente o algoritmo, imagine-se agora que, continuando a aplica¸c˜ao do mesmo, repetimos a metodologia para uma nova itera¸c˜ao, com x0 = 2, 4 e δ = 0, 01.

(39)

4. Métodos de Pesquisa Directa 27 Obter-se-iam os resultados apresentados na Tabela 4.2, onde se constata um aumento do valor de f (x), logo no primeiro valor calculado. Tal facto, indica-nos que se terá de pesquisar no sentido contrário ao efectuado.

Este processo ´e ilustrado na Tabela 4.3, tendo sido utilizados deslocamentos negativos, por forma a se obter o pretendido, vindo x∗ _{∈ [1, 77; 2, 25].}

i Deslocamento x f (x) 0 0 2,4 0,16 1 -0,01 2,39 0,1521 2 -0,02 2,37 0,1369 3 -0,04 2,33 0,1089 4 -0,08 2,25 0,0625 5 -0,16 2,09 0,0081 6 -0,32 1,77 0,0520

Tabela 4.3: Exemplo de aplica¸c˜ao do algoritmo de DSC(x0 = 2.4, δ = −0.01)

Os valores iniciais foram escolhidos de forma intencional, de modo a evidenciar o com-portamento do algoritmo.

4.2.2 M´

etodo da Sec¸c˜

ao Dourada

O algoritmo da seçcão dourada tem como objectivo o refinamento de um intervalo que contém o m´ınimo de uma fun¸cão unidimensional, ou segundo uma única direçcão.

A diferen¸ca principal relativamente ao algoritmo de DSC, reside nas condi¸c˜oes iniciais. No algoritmo anterior era indicada uma estimativa inicial, a partir da qual se procurava um intervalo que contivesse o m´ınimo a estimar.

O algoritmo da seçcão dourada (SD), inicia-se com duas estimativas, os limites inferior e superior de um intervalo, suficientemente amplo, que contenha o m´ınimo pretendido. Nesse intervalo a fun¸cão deve ser unimodal, isto é, possuir um único m´ınimo, aquele que se pretende estimar. O esfor¸co é então todo dirigido no sentido da diminui¸cão da amplitude do intervalo, contendo sempre o m´ınimo, escolhendo novos limites, de tal forma que o novo intervalo esteja contido no anterior. O processo estará conclu´ıdo, quando se obtiver um intervalo cuja amplitude seja inferior a uma precisão pré-definida. Este método, tem por base a razão de ouro, utilizada da forma a seguir descrita.

(40)

4. Métodos de Pesquisa Directa 28 Imagine-se um ponto P , pertencente ao segmento de recta, [AB], ponto P esse, não coincidente com o ponto médio do segmento [AB]. Para facilitar, tome-se P mais próximo de A do que de B.

Se o ponto considerado fosse Q, que está mais próximo de B do que de A, o resultado seria o mesmo. Convém no entanto, referir que ambos os pontos, P e Q, são os únicos que verificam as propriedades a seguir apresentadas.

Admita-se que a razão entre os comprimentos dos segmentos [AB] e [PB] é igual à razão entre os comprimentos de [PB] e [AP], e é constante, representada por τ , como ilustrado na Figura 4.3. t -¾ r -¾ ¾ s -A P Q B t s

=

sr

= τ

Figura 4.3: Raz˜ao de Ouro

Assim, AB P B = P B AP = τ (4.3) e como AB = AP + P B, vem AP + P B P B = τ, simplificando, tem-se AP P B + 1 = τ mas, por (4.3), AP P B = 1 τ

originando uma equa¸c˜ao polinomial do segundo grau, 1

τ + 1 = τ

cujas solu¸c˜oes s˜ao τ = 1+√5 2 e τ =

1−√5 2 .

Ignorando a raiz negativa, a raz˜ao de ouro ´e dada por τ = 1+√5 2 .