Geometria Basica Aula1 Volume1

Aula 1 – No¸

c˜

oes elementares

Objetivos

• Criar os alicerces para que o aluno possa acompanhar todo o restante

da disciplina.

• Introduzir elementos primitivos e alguns axiomas b´asicos da Geometria

Euclidiana.

Introdu¸

c˜

ao

Geometria

Geometria significamedida da terra. A palavra

geometriavem do gregogeo, terra, emetrein, medir, que remonta `a origem da Geometria, nascida da necessidade pr´atica de medir o tamanho das propriedades agr´ıcolas. Desenvolveu-se, incialmente, no Egito, onde as cheias do rio Nilo cancelavam as divisas entre as glebas. As primeiras no¸c˜oes geom´etricas surgiram quando o homem teve necessidade de realizar medidas; como por exemplo, comparar distˆancias e determinar dimens˜oes de corpos que estavam `a sua volta. Mas o que se tem de mais interessante ao se estudar a hist´oria, ´e que os primeiros passos no estudo da Geometria foram dados com base numa hip´otese falsa: acreditava-se que a Terra era plana. Todas as pesquisas foram feitas segundo essa cren¸ca, mas isso n˜ao impediu o desenvolvimento da Geometria.

“O estudo profundo da natureza ´e a mais fecunda fonte de descobertas matem´aticas”

Joseph Fourier (1768-1830)

Os elementos b´asicos do estudo da Geometria s˜ao as id´eias de ponto,

retae plano. No nosso dia-a-dia usamos essas palavras em diversas ocasi˜oes, e com diversos significados diferentes, tais como:

- A que ponto chegamos!

- Estamos na reta final do trabalho.

- Eu tenho um plano!

Sob o ponto de vista da Geometria, no entanto, essas palavras tˆem sig-nificados muito espec´ıficos. Contudo, apesar de serem conceitos importantes e intuitivos, s˜ao dif´ıceis de definir. Tente dar uma defini¸c˜ao de um deles:

- O que ´e reta?

- ´E uma “coisa” que n˜ao ´e curva.

- O que ´e curva?

- Ah, ´e uma “coisa” que n˜ao ´e reta. Opa!

O ponto, a reta e o plano n˜ao existem no mundo real, s˜ao instrumentos que usamos para modelar a natureza. Um gr˜ao de areia, uma vareta ou um tampo de mesa nos d˜ao a id´eia de ponto, reta e plano, mas nunca vimos um gr˜ao de areia que n˜ao tenha volume (mesmo pequeno), uma vareta que n˜ao tenha espessura e se prolongue indefinidamente, ou um tampo de mesa que se prolongue em todas as dire¸c˜oes...

Podemos, por´em, imaginar esses elementos e estudar suas proprieda-des. Indo mais al´em, podemos imaginar partes desses elementos (semi-retas, segmentos, semiplanos, etc.), composi¸c˜oes dessas partes (ˆangulos, triˆangulos, circunferˆencias, etc.) e estudar suas propriedades.

Fig. 2: Elementos do mundo real na Geometria.

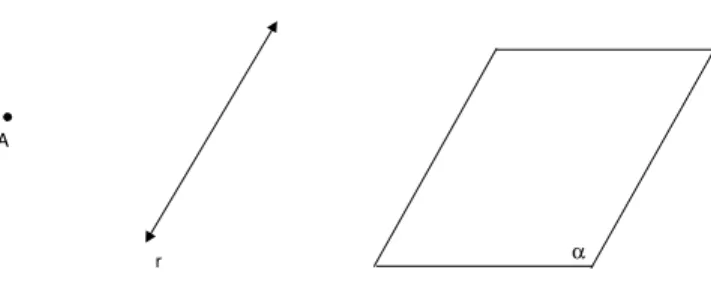
Em nosso estudo da Geometria, n˜ao definiremos ponto, reta e plano: esses ser˜ao elementos primitivos. Usaremos letras mai´usculas (A,B, C, etc.) para designar pontos, letras min´usculas (a, b, c, etc.) para designar retas, e letras do alfabeto grego (α, β, γ, etc.) para designar planos.

Veja na figura 3 como ser˜ao representados no papel os elementos pri-mitivos ponto, reta e plano.

A

r α

Fig. 3: Ponto, reta e plano representados no papel.

Para evoluir em nosso estudo da Geometria Euclidiana precisamos es-tabelecer algumas rela¸c˜oes entre os elementos primitivos, rela¸c˜oes que cha-maremos de axiomas. Axiomas s˜ao verdades primitivas, aceitas a priori, e que refletem propriedades observ´aveis dos objetos do mundo real que esta-mos modelando. Mais a frente vocˆe entender´a mais sobre o significado dos axiomas.

A partir dos elementos primitivos, ponto, reta e plano e das verda-des intuitivas, os axiomas, usamos argumentos logicamente consistentes para decidirmos se novas propriedades s˜ao verdadeiras ou falsas.

Justamente porque pontos, retas e planos s˜ao modelos abstratos do mundo real e os axiomas verdades auto-evidentes, ´e importante sermos ex-tremamente criteriosos na escolha dos axiomas. Eles devem, a princ´ıpio, serem de f´acil aceita¸c˜ao como verdades evidentes.

Felizmente, estamos estudando uma disciplina que tem mais de 2.400 anos de existˆencia. A fase criativa mais importante da Geometria Euclidiana ocorreu no s´eculo IV a.C., onde foram enunciados a quase totalidade dos axiomas na impressionante obra “Os Elementos” de Euclides.

Exemplo 1

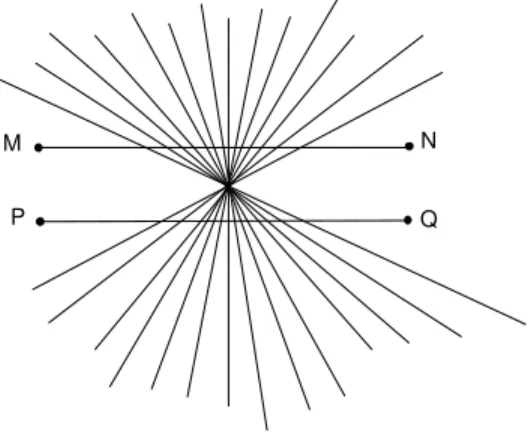
Observe a figura 4 e responda se as linhas que ligam M a N e P a Q s˜ao linhas retas.

M N

P Q

Fig. 4: Ilus˜ao de ´otica?

Exemplo 2

Na figura 5, qual das linhas ´e maior: a horizontal ou a vertical ?

Confira as respostas com sua r´egua.

Fig. 5: Qual ´e a maior linha?

Bom, se por um lado n˜ao podemos confiar apenas no bom senso e na intui¸c˜ao, por outro lado eles s˜ao muito importantes.

Como j´a lhe contamos, o estudo da Geometria come¸ca por admitir como propriedades verdadeiras apenas algumas afirma¸c˜oes simples, chamadas

axiomas ou postulados, que s˜ao bastante intuitivas. A partir dos axiomas ´e poss´ıvel provar (ou demonstrar) outras afirma¸c˜oes. A essas afirma¸c˜oes, que ser˜ao provadas, daremos o nome de proposi¸c˜oes ou teoremas. O que entendemos por provarficar´a mais claro ao longo do curso.

Veja, a seguir, alguns dos axiomas da Geometria plana, chamados

axiomas de incidˆencia:

Axiomas de incidˆencia:

• Existem infinitos pontos no plano.

• Por dois pontos distintos (ou seja, diferentes) passa uma ´unica

reta.

• Dada uma reta, existem infinitos pontos pertencentes a ela, e

infinitos pontos fora dela.

´

E correto afirmar que o

plano´e constitu´ıdo de pontos e que as retas s˜ao subconjuntos de pontos do plano.

Axioma

Chama-seaxiomaou

postuladotoda afirma¸c˜ao aceita sem demonstra¸c˜ao.

Usando a forma de representar utilizada na figura 3, podemos repre-sentar esses axiomas no papel. ´E claro que n˜ao podemos desenhar infinitos pontos, mas, ao buscar colocar as id´eias no papel, desenvolvemos nossa vis˜ao geom´etrica.

Para indicar que um ponto est´a em uma reta, plano, etc., usaremos o s´ımbolo ∈ (pertence). Assim a express˜ao A ∈ r significa que o ponto A

pertence `a reta r, ou est´a na reta r. Nesse caso, diz-se tamb´em que r passa pelo pontoA. A reta que passa pelos pontosA e B ser´a denotada por ←AB→. Para indicar que uma reta est´a contida em um plano, usaremos o s´ımbolo⊂.

Assim a express˜aor ⊂α significa que a retar est´a contida no plano α.

B

A

C

Fig. 6: A_,B_eC_{s˜ao pontos n˜ao-colineares.}

O segundo axioma acima diz que, dados dois pontos distintos A e B, sempre existe uma (´unica) reta que passa pelos dois. Se forem dados trˆes pontos, ao inv´es de dois, pode ser que n˜ao exista uma reta que passe pelos trˆes, como ´e o caso dos pontos A, B e C na figura 6. Pontos A, B, C como tais s˜ao chamados de pontos n˜ao-colineares.

M´etodo dedutivo

O m´etodo deprovar(ou demonstrar) resultados a partir de axiomas utilizando apenas o racioc´ınio l´ogico ´e chamadom´etodo dedutivoe ´

e atribu´ıdo aos gregos. Atrav´es dele, os gregos levaram a Geometria a um est´agio bem avan¸cado.

Geometria Euclidiana

Vocˆe deve ter observado que os axiomas anteriores parecem bastante razo´aveis, no sentido de que parecem verdadeiros e indiscut´ıveis. Justamente por causarem essa impress˜ao, foram escolhidos como axiomas. A busca de axiomas, no entanto, n˜ao foi sempre uma tarefa f´acil. Em diversos momentos da Hist´oria, os geˆometras (e tamb´em outros grupos de matem´aticos) tiveram discuss˜oes acaloradas sobre esse assunto.

Na leitura desta primeira aula, n˜ao se preocupe em fixar ou decorar axiomas. O mais importante, por enquanto, ´e formar uma boa id´eia de ponto, reta e plano e do que est´a sendo dito a respeito deles. Ao ler os axiomas, procure desenhar figuras, fazer imagens mentais, discutir com outras pessoas e se convencer de que fazem sentido.

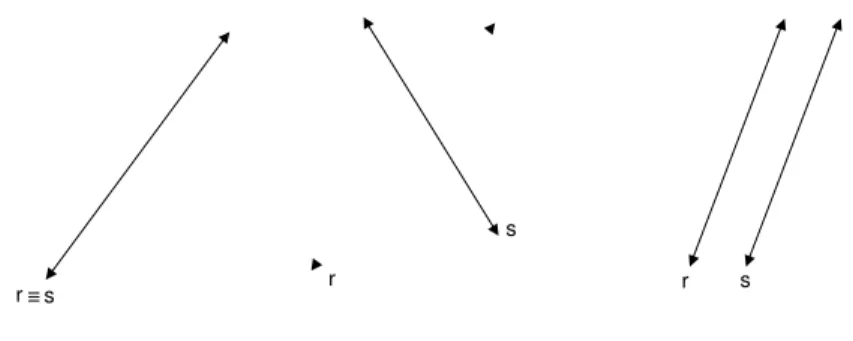
Dadas duas retas no plano, h´a trˆes possibilidades: elas se intersectam em um ´unico ponto (retas concorrentes), elas n˜ao se intersectam (retas para-lelas) ou elas tˆem todos os pontos em comum (retas coincidentes). Observe na figura 7 esses trˆes casos.

r s r

s

r s

Fig. 7: Retas coincidentes, retas concorrentes e retas paralelas.

• Retas paralelas: Nenhum ponto em comum.

• Retas concorrentes: Apenas um ponto em comum.

• Retas coincidentes: Mais de um ponto em comum.

Segmentos de reta, semi-retas e semiplanos

Euclides de Alexandria

325-265 (?) a.C.

Matem´atico grego. ´E um dos mais famosos matem´aticos da antig¨uidade. N˜ao se sabe ao certo o local e nem as datas de seu nascimento e de sua morte, e quase nada se sabe sobre sua vida. ´E poss´ıvel que tenha recebido ensinamentos dos primeiros disc´ıpulos de Plat˜ao. A ´

unica certeza ´e que fundou em Alexandria, durante o reinado de Ptolomeu I (323 a.C.-285 a.C.), a primeira escola de Matem´atica. No tempo de Euclides (cerca de 300 a.C.), a Geometria alcan¸cou um est´agio bem avan¸cado. Do conhecimento acumulado, Euclides compilouOs elementos, um dos mais not´aveis livros j´a escritos. Al´em de ser uma exposi¸c˜ao sistem´atica da Geometria elementar,Os Elementostamb´em contˆem tudo que era conhecido na ´

epoca sobre Teoria dos N´umeros. Consulte: http://www-groups.dcs. st-nd.ac.uk/~history/ Mathematicians/Euclid. html

Defini¸c˜ao 1 (Pontos colineares)

Se um determinado conjunto de pontos est´a contido em uma mesma reta, dizemos que esses pontos s˜ao colineares.

Nosso objetivo, agora, ´e introduzir a no¸c˜ao de ordem para pontos de uma mesma reta. Para isso, considere uma reta r e sobre ela trˆes pontos distintosA, B eC (veja figura 8). Observe que o pontoB encontra-se entre

A e C. Al´em disso, existem outros pontos entre A e C (al´em de B); s´o n˜ao est˜ao destacados na figura e n˜ao designamos letras para eles. Existem tamb´em pontos que n˜ao est˜ao entreA e C.

A B

C r

Fig. 8: BentreAeC.

Esses fatos s˜ao bastante intuitivos e fazem parte do que chamamos

axiomas de ordem:

Axiomas de ordem:

• Dados trˆes pontos colineares e distintos dois a dois, um deles,

e apenas um, est´a entre os outros dois.

• Dados dois pontos distintos A e B, existe sempre um ponto C

que est´a entreAeB, e um pontoDtal queAest´a entreDeB.

Enfatizamos que a no¸c˜ao de ordem ´e para pontos que est˜ao sobre uma mesma reta. Assim, quando dizemos queB est´a entreA e C, em particular, estamos afirmando que A, B e C s˜ao colineares e diferentes. Al´em disso, dizer queB est´a entre A eC ´e o mesmo que dizer queB est´a entre C e A.

Defini¸c˜ao 2 (Segmento de reta)

Chamamos segmento de reta AB ao conjunto formado por A, B e todos os pontos que est˜ao entre A e B, ou seja, o “peda¸co” da reta que come¸ca em

A e termina em B (ou que come¸ca em B e termina em A). Veja a figura 9.

Dizer que os pontosA,Be

C_{s˜ao distintos dois a dois}

significa queA6=B_,A6=C

eB6=C_.

A

B

Fig. 9: Segmento de retaAB.

Com o intuito de definir outros elementos importantes para nosso es-tudo (semiplano e semi-reta), introduzimos mais um axioma:

• Uma retardo planoαsepara o conjunto dos pontos desse plano

que n˜ao pertencem a r em dois conjuntos, α′ e α′′

, tais que:

− α′ e α′′ s˜ao disjuntos (n˜ao tˆem elementos em comum).

− Se A ∈ α′ e B ∈ α′′, ent˜ao AB intersecta r (o segmento

AB e a retar tˆem um elemento em comum).

− SeAeB est˜ao ambos emα′ (ou emα′′), ent˜ao o segmento

AB n˜ao intersecta a retar.

Defini¸c˜ao 3 (Semiplano)

Os conjuntos α′ e α′′ referidos anteriormente s˜ao chamados semiplanos de-terminados pela retar.

Na figura 10,AeBpertencem a um mesmo semiplano, pois o segmento

AB n˜ao intersectar. Dizemos que Ae B est˜ao em um mesmo lado de r. Os pontos C e D est˜ao em semiplanos opostos, pois CD intersecta r. Dizemos queC e D est˜ao em lados opostos der.

A

B

C

D

r

Fig. 10:AeBpertecem a um mesmo semiplano. CeDest˜ao em semiplanos opostos.

Da mesma forma, um ponto pertencente a uma reta separa essa reta em dois conjuntos. Mais precisamente, se A est´a entre B e C e r ´e a reta que cont´em esses trˆes pontos, o pontoAsepara a retarem duas partes, uma contendo o pontoB e outra contendo o ponto C.

Defini¸c˜ao 4 (Semi-reta)

As partes da reta, referidas acima, s˜ao chamadas semi-retas determinadas pelo ponto A.

A semi-reta que cont´em o ponto B ´e denotada por −→AB (veja a figura 11), e a que cont´em o pontoC ´e denotada por −→AC. Dizemos que a semi-reta

−→

AC ´e oposta `a semi-reta −→AB (e vice-versa).

A

B

C

Fig. 11: Semi-retas

→

→

As nota¸c˜oes utilizadas para semi-reta e para reta s˜ao bastante sugestivas. A seta em apenas uma dire¸c˜ao em

−→

ABsignifica que a semi-reta tem come¸co e n˜ao tem fim. A seta nas duas dire¸c˜oes em

←→

ABsignifica que a reta n˜ao tem come¸co nem fim.

Defini¸c˜ao 5 (ˆAngulo) ˆ

Angulo ´e uma figura formada por duas semi-retas distintas e n˜ao-opostas com a mesma origem.

Se−→ABe−→AC s˜ao semi-retas definindo um ˆangulo, diz-se queA´e ov´ertice

do ˆangulo. Para designar esse ˆangulo, usa-se a nota¸c˜ao BACˆ , ou apenas ˆA, se n˜ao houver mais de um ˆangulo sendo considerado com v´ertice emA. As semi-retas −→AB e −→AC s˜ao os lados do ˆangulo.

A

B

C

Defini¸c˜ao 6 (Interior de um ˆangulo)

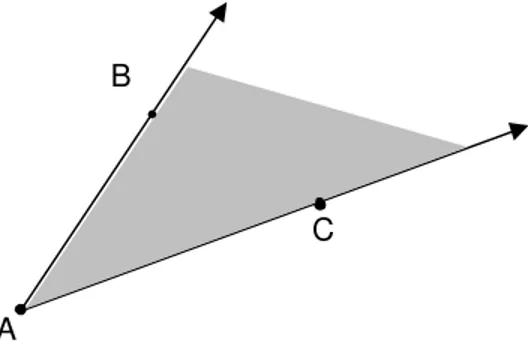
Dado um ˆangulo BACˆ , define-se o interior de BACˆ como o conjunto de todos os pontos que pertencem `a interse¸c˜ao entre o semiplano determinado por ←AB→ que cont´em C e o semiplano determinado por ←AC→ que cont´em B. (Veja a figura 13).

A

B

C

Fig. 13: Interior do ˆanguloBACˆ _.

Resumo

Nessa aula vocˆe aprendeu...

• Que ponto, reta e plano s˜ao elementos primitivos da Geometria

Eucli-diana.

• Que axioma ou postulado ´e uma afirma¸c˜ao aceita sem prova.

• O enunciado de alguns axiomas.

• As defini¸c˜oes de ˆangulo, segmento de reta, semiplano, semi-reta e

inte-rior de um ˆangulo.

Exerc´ıcios

1. Retorne ao in´ıcio do texto da aula e releia apenas os axiomas.

2. Diga se cada uma das afirma¸c˜oes abaixo ´e verdadeira ou falsa.

• Por um ponto passam infinitas retas.

• Por trˆes pontos dados passa uma reta.

• Quatro pontos dados, todos distintos, determinam duas retas.

• Se dois pontos distintos A e B pertencem `as retas r e s, ent˜ao

r =s.

• Duas retas distintas que tˆem um ponto em comum s˜ao

concorren-tes.

• Quatro pontos distintos, sendo apenas trˆes deles colineares,

deter-minam quatro retas.

3. Dados trˆes pontos distintos de uma reta, quantos segmentos distintos eles determinam?

4. Dados dois pontos distintos A e B, quantos segmentos h´a com extre-midades A e B? Quantos segmentos h´a que passam pelos pontos A e

B?

5. Fa¸ca um desenho onde constem pontos A, B, C, D eE, e retas r e s, satisfazendo ao mesmo tempo os itens a seguir:

• r e s n˜ao s˜ao coincidentes,

• A∈r e A∈s,

• B ∈r eC ∈r,

• B e C est˜ao em semiplanos opostos com respeito as,

• D e E est˜ao em semiplanos opostos com respeito a r, e nenhum

dos dois pontos pertence a s.

Existem v´arios desenhos poss´ıveis com essas propriedades. Entretanto, todos tˆem algumas coisas em comum. Por exemplo, em todos os de-senhos poss´ıveis, r e s n˜ao s˜ao paralelas, e se vocˆe tra¸car a reta ←DE→, esta ser´a concorrente com r. Se←DE→ser´a concorrente ou n˜ao coms, vai depender do desenho que vocˆe fizer. Desenhe as duas possibilidades.

6. Desenhe dois segmentos ABe CD tais que a interse¸c˜ao deAB eCD ´e o conjunto vazio, mas ←AB→ e ←CD→tˆem um ponto em comum.

7. Desenhe dois segmentos ABe CD tais que a interse¸c˜ao deAB eCD ´e o conjunto vazio, mas ←AB→=←CD→.