Open Formulações matemáticas para o problema de de lotes com penalidades por atraso

CENTRO DE INFORM ´

ATICA

PROGRAMA DE P ´

OS-GRADUA ¸

C ˜

AO EM INFORM ´

ATICA

KATYANNE FARIAS DE ARA´

UJO

FORMULA ¸

C ˜

OES MATEM ´

ATICAS PARA O PROBLEMA DE SEQUENCIAMENTO

DE LOTES COM PENALIDADES POR ATRASO

FORMULA ¸

C ˜

OES MATEM ´

ATICAS PARA O PROBLEMA DE SEQUENCIAMENTO

DE LOTES COM PENALIDADES POR ATRASO

Disserta¸c˜ao apresentada ao Programa de

P´os-Gradua¸c˜ao em Inform´atica do

Cen-tro de Inform´atica da Universidade

Fe-deral da Para´ıba, como requisito parcial

para obten¸c˜ao do Grau de Mestre em

In-form´atica.

Orientador: Prof. Dr. Anand Subramanian

A663f Araújo, Katyanne Farias de.

Formulações matemáticas para o problema de

sequenciamento de lotes com penalidades por atraso /

Katyanne Farias de Araújo.- João Pessoa, 2016.

190f. : il.

Orientador: Anand Subramanian

Dissertação (Mestrado) - UFPB/CI

1. Informática. 2. Processamento em lotes.

3. Sequenciamento. 4. Atraso ponderado. 5. Formulação

matemática.

la force sans la justice est tyrannique.”

Ao professor e “coorientador” Artur Pessoa, por todo conhecimento transmitido e

pela aten¸c˜ao fornecida ao longo do desenvolvimento deste trabalho.

Ao professor Anand Subramanian, pela orienta¸c˜ao e pelos conhecimentos

transmi-tidos ao longo da minha trajet´oria acadˆemica.

A minha fam´ılia, em especial a minha m˜ae Angela Farias, meu tio ´

Alvaro Farias e

minha irm˜a Kelyanne Farias, pelo apoio, compreens˜ao e s´abios conselhos.

O problema de sequenciamento de lotes da produ¸c˜ao em uma m´aquina,

compro-vadamente tido como

N P

-dif´ıcil, consiste na defini¸c˜ao do agrupamento de tarefas em lotes

e da sequˆencia em que estes ser˜ao processados em uma m´aquina. Cada tarefa est´a

asso-ciada a uma data de libera¸c˜ao, um tempo de processamento, uma data de entrega, um

n´ıvel de prioridade em rela¸c˜ao `as demais, e um tamanho. A m´aquina ´e capaz de processar

um conjunto de tarefas (lote) simultaneamente, contanto que a soma dos tamanhos das

tarefas pertencentes ao referido lote respeite a capacidade da m´aquina. Cada tarefa deve

ser processada apenas uma vez e somente um lote ´e processado por vez na m´aquina. Neste

trabalho, considera-se como objetivo a minimiza¸c˜ao do total de atrasos ponderados, onde

o atraso de uma tarefa ´e igual ao seu tempo de t´ermino menos a sua data de entrega,

caso o processamento da tarefa seja finalizado ap´os a sua data da entrega e, portanto, em

atraso, e ´e igual a zero, caso contr´ario. Na literatura, este problema ´e geralmente

referen-ciado como 1

|

batch, r

, s

, compt

|

P

w

T

. Quando todas as tarefas est˜ao dispon´ıveis para

serem processadas no instante de tempo zero, o problema ´e usualmente representado por

1

_|

batch, s

, compt

|

P

w

T

. Estes s˜ao problemas ainda pouco investigados na literatura

e, al´em disso, abordam uma grande quantidade de variantes. Existem poucos trabalhos

envolvendo a aplica¸c˜ao de m´etodos exatos para a resolu¸c˜ao de ambos. Apenas uma

for-mula¸c˜ao matem´atica foi identificada na literatura para estes problemas. Dessa forma,

quatro formula¸c˜oes matem´aticas com vari´aveis indexadas no tempo foram desenvolvidas

para resolver os problemas mencionados anteriormente, das quais uma ´e capaz de tratar de

ambos os problemas. Os resultados alcan¸cados por meio dos modelos desenvolvidos foram

comparados entre si e com os resultados do modelo dispon´ıvel na literatura. Tais

resulta-dos computacionais demonstram que dois resulta-dos modelos propostos obtiveram desempenho

superior tanto em termos de qualidade da solu¸c˜ao, em especial em rela¸c˜ao aos limites

in-feriores alcan¸cados, quanto em n´

umeros de n´os abertos e quantidade de solu¸c˜oes ´otimas

comprovadas.

The problem of scheduling on a single machine, proven to be

N P

-hard, consists of

defining the job grouping in batches and of the sequence in which these batches will be

processed on a machine. Each job is associated with a release date, a processing time, a

due date, a priority level in relation to the others and a size. The machine is able to process

a group of jobs (batch) simultaneously, provided that the sum of the job sizes belonging to

the referred batch does not exceed the machine capacity. Each job must be processed only

once and only one batch is processed at a time on the machine. In this work, we consider

the objective as the minimization of total weighted tardiness, where the tardiness of a job

is the difference between its completion time and its due date, in case the job processing

is finished after its due date and hence is late, or equals zero, otherwise. In the literature,

this problem is usually referred to as 1

|

batch, r

, s

, compt

|

P

w

T

. When all jobs are

available to be processed at time zero, the problem is usually represented as 1

_|

batch, s

,

compt

|

P

w

T

. These problems are still poorly explored in the literature and in addition,

cover a large number of variant forms. There are few studies involving the application of

exact methods for solving both. Only one mathematical formulation was identified in the

literature for these problems. Hence, four time-indexed formulations were developed to

solve the aforementioned problems, one of which is capable of dealing with both problems.

The results achieved by the developed models were compared between themselves and with

the results of the model available in the literature. These computational results reveal that

two of the proposed models obtained higher performance both in terms of quality of the

solution, particularly regarding the achieved lower bounds, and in numbers of open nodes

and of proven optimal solutions.

SUM ´

ARIO

1

INTRODU ¸

C ˜

AO

15

1.1

DEFINI ¸

C ˜

AO DO TEMA . . . .

15

1.2

JUSTIFICATIVA . . . .

19

1.3

OBJETIVOS . . . .

21

1.3.1

Objetivo Geral . . . .

21

1.3.2

Objetivos Espec´ıficos . . . .

21

1.4

ESTRUTURA DO TRABALHO . . . .

22

2

FUNDAMENTA ¸

C ˜

AO TE ´

ORICA E DESCRI ¸

C ˜

AO DO PROBLEMA

23

2.1

ESCALONAMENTO DA PRODU ¸

C ˜

AO . . . .

23

2.1.1

Configura¸c˜ao da(s) M´aquina(s) . . . .

25

2.1.2

Caracter´ısticas das Tarefas . . . .

26

2.1.3

Fun¸c˜ao Objetivo . . . .

28

2.2

PROBLEMA ABORDADO . . . .

29

3

TRABALHOS RELACIONADOS

32

3.1

FAM´ILIAS DE TAREFAS COMPAT´IVEIS

. . . .

32

3.1.1

Tamanhos de Tarefas Idˆenticos . . . .

33

3.1.2

Tamanhos de Tarefas Distintos . . . .

41

3.1.3

Capacidade Ilimitada . . . .

46

3.2

FAM´ILIAS DE TAREFAS INCOMPAT´IVEIS . . . .

49

3.2.1

Tamanhos de Tarefas Idˆenticos . . . .

50

3.2.2

Tamanhos de Tarefas Distintos . . . .

53

3.2.3

Capacidade Ilimitada . . . .

55

4

ASPECTOS METODOL ´

OGICOS

58

4.1

Formula¸c˜ao Matem´atica I (Chou e Wang, 2008) . . . .

59

4.4

Formula¸c˜ao Matem´atica IV . . . .

64

4.5

Formula¸c˜ao Matem´atica V . . . .

66

5

RESULTADOS

72

5.1

Grupo de Instˆancias . . . .

73

5.2

Resultados do Problema 1

|

batch, r

, s

, compt

|

P

w

T

. . . .

74

5.2.1

Capacidade da M´aquina Igual a 20 . . . .

75

5.2.2

Capacidade da M´aquina Igual a 40 . . . .

80

5.2.3

S´ıntese dos Resultados de 1

_|

batch, r

, s

, compt

|

P

w

T

. . . .

81

5.3

Resultados do Problema 1

|

batch, s

, compt

|

P

w

T

. . . .

86

5.3.1

Capacidade da M´aquina Igual a 20 . . . .

86

5.3.2

Capacidade da M´aquina Igual a 40 . . . .

91

5.3.3

S´ıntese dos Resultados de 1

_|

batch, s

, compt

|

P

w

T

. . . .

95

6

CONCLUS ˜

AO

97

A Apˆ

endice

110

A.1 Resultados por instˆancia do 1

|

batch, r

, s

, compt

|

P

w

T

. . . 110

A.1.1 Capacidade igual a 20 . . . 110

A.1.2 Capacidade igual a 40 . . . 126

A.2 Resultados por instˆancia do 1

_|

batch, s

, compt

|

P

w

T

. . . 142

A.2.1 Capacidade igual a 20 . . . 142

1.1

Exemplo de uma solu¸c˜ao do 1

_|

batch, r

, s

, compt

|

P

w

T

. . . .

18

4.1

Representa¸c˜ao de uma solu¸c˜ao vi´avel . . . .

67

4.2

Solu¸c˜oes vi´aveis utilizando

F.IV

_{. . . .}

₆₇

4.3

Representa¸c˜ao de solu¸c˜oes vi´aveis . . . .

70

LISTA DE TABELAS

1.1

Exemplo de uma instˆancia do 1

_|

batch, r

, s

, compt

|

P

w

T

. . . .

17

3.1

Resumo dos trabalhos com

compt,

Q < n,

s

=

cte,

∀

j

∈

J

. . . .

41

3.2

Resumo dos trabalhos com

compt,

Q < n,

s

distintos,

∀

j

∈

J

. . . .

47

3.3

Resumo dos trabalhos com

compt

e

Q

_≥

n

. . . .

49

3.4

Resumo dos trabalhos com

incompt,

Q < n

e

s

=

cte,

∀

j

∈

J

. . . .

53

3.5

Resumo dos trabalhos com

incompt,

Q < n,

s

distintos,

∀

j

∈

J

. . . .

55

3.6

Resumo dos trabalhos com

incompt

e

Q

_≥

n

. . . .

57

4.1

Dados do exemplo . . . .

66

5.1

Distribui¸c˜ao dos Parˆametros . . . .

73

5.2

Grupos de instˆancias por configura¸c˜ao . . . .

73

5.3

Resultados de instˆancias“pequenas”para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 20 . . . .

77

5.4

Resultados de instˆancias “m´edias” para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 20 . . . .

78

5.5

Resultados de instˆancias “grandes” para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 20 . . . .

79

5.6

Resultados de instˆancias“pequenas”para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 40 . . . .

82

5.7

Resultados de instˆancias “m´edias” para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 40 . . . .

83

5.8

Resultados de instˆancias “grandes” para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 40 . . . .

84

5.9

M´edias por tamanho de instˆancia para 1

|

batch, r

, s

, compt

|

P

w

T

. . . .

85

20 . . . .

89

5.12 Resultados de instˆancias “grandes” para 1

|

batch, s

, compt

|

P

w

T

, com

Q

= 20 . . . .

90

5.13 Resultados de instˆancias “pequenas” para 1

|

batch, s

, compt

|

P

w

T

, com

Q

= 40 . . . .

92

5.14 Resultados de instˆancias “m´edias” para 1

|

batch, s

, compt

|

P

w

T

, com

Q

=

40 . . . .

93

5.15 Resultados de instˆancias “grandes” para 1

|

batch, s

, compt

|

P

w

T

, com

Q

= 40 . . . .

94

5.16 M´edias por tamanho de instˆancia para 1

|

batch, s

, compt

|

P

w

T

. . . .

96

A.1 Resultados de

_F

1 para 1

_|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 20 . . . 110

A.2 Resultados de

F

2 para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 20 . . . 118

A.3 Resultados de

_F

4 para 1

_|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 20 . . . 119

A.4 Resultados de

F

1 para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 40 . . . 126

A.5 Resultados de

_F

2 para 1

_|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 40 . . . 134

A.6 Resultados de

F

4 para 1

|

batch, r

, s

, compt

|

P

w

T

, com

Q

= 40 . . . 135

A.7 Resultados de

_F

1 para 1

_|

batch, s

, compt

|

P

w

T

, com

Q

= 20 . . . 142

A.8 Resultados de

F

3 para 1

|

batch, s

, compt

|

P

w

T

, com

Q

= 20 . . . 150

A.9 Resultados de

_F

4 para 1

_|

batch, s

, compt

|

P

w

T

, com

Q

= 20 . . . 153

A.10 Resultados de

F

5 para 1

|

batch, s

, compt

|

P

w

T

, com

Q

= 20 . . . 159

A.11 Resultados de

_F

1 para 1

_|

batch, s

, compt

|

P

w

T

, com

Q

= 40 . . . 168

A.12 Resultados de

F

3 para 1

|

batch, s

, compt

|

P

w

T

, com

Q

= 40 . . . 176

A.13 Resultados de

_F

4 para 1

_|

batch, s

, compt

|

P

w

T

, com

Q

= 40 . . . 177

LISTA DE ABREVIA ¸

C ˜

OES

ACO

Ant Colony Optimization

AG

Algoritmo Gen´etico

ARB

Attribute Ratio of Batch

BATC

Batch Apparent Tardiness Cost

ATC

Apparent Tardiness Cost

BFF

Batch First-Fit

B&B

Branch-and-Bound

B&P

Branch-and-Price

DH

Decomposition Heuristic

EDD

Earliest Due Date

FF

First Fit

FBLPT

Full Batch Largest Processing Time

GC

Gera¸c˜ao de Colunas

ILS

Iterated Local Search

JIT

Just-In-Time

LB

Lower Bound

LPT

Longest Processing Time

MBS

Minimum Batch Sized

MARB

Minimum Attribute Ratio of Batch

OC

Otimiza¸c˜ao Combinat´oria

PO

Pesquisa Operacional

PD

Programa¸c˜ao Dinˆamica

PI

Programa¸c˜ao Inteira

PIM

Programa¸c˜ao Inteira Mista

PSH

Pairwise Swapping Heuristic

PLI

Programa¸c˜ao Linear Inteira

PLIM

Programa¸c˜ao Linear Inteira Mista

PBR

Population-Based Reasoning

RL

Relaxa¸c˜ao Linear

1.1 DEFINI ¸

C ˜

AO DO TEMA

O escalonamento da produ¸c˜ao ´e um problema de Otimiza¸c˜ao Combinat´oria (OC)

amplamente estudado na literatura. Trata-se da aloca¸c˜ao de atividades a recursos,

po-dendo se referir, segundo Pinedo (2008), a decolagens e aterrizagens em uma pista de um

aeroporto, enfermeiras em setores do hospital, aloca¸c˜ao de opera¸c˜oes de um processo de

produ¸c˜ao a m´aquinas, entre outros. Quando apenas um recurso ´e considerado, como por

exemplo a utiliza¸c˜ao de exatamente uma m´aquina, alguns autores denominam o problema

de

sequenciamento

da produ¸c˜ao.

Dentre os principais problemas de escalonamento estudados, est˜ao:

job shop

,

flow

shop

,

open shop

, sequenciamento em uma m´aquina, escalonamento em m´aquinas paralelas,

entre outros. Alguns desses problemas s˜ao descritos brevemente na Se¸c˜ao 2.1. A

depen-der das caracter´ısticas do sistema produtivo, particularidades s˜ao inclu´ıdas ao problema

considerado e, consequentemente, s˜ao identificadas diversas variantes. Uma caracter´ıstica

poss´ıvel de ser considerada ´e a penalidade por atraso, com a imposi¸c˜ao de prioridades

distintas para cada tarefa/atividade.

O problema de sequenciamento da produ¸c˜ao com penalidades por atraso pode ser

definido da seguinte forma: sendo

J

=

_{

1, ..., n

_}

o conjunto de

n

tarefas a serem processadas

em uma m´aquina, de modo que apenas uma tarefa pode ser processada por vez. Cada

tarefa possui um determinado tempo de processamento

p

, um certo n´ıvel de prioridade

w

e uma data de entrega

d

. Al´em disso, pode-se considerar um tempo de in´ıcio

r

a

a sequˆencia que minimize o total de atrasos ponderados, onde o atraso de uma tarefa ´e

igual ao seu tempo de t´ermino menos a data de entrega, caso essa tarefa termine de ser

processada ap´os a sua data de entrega, e ´e igual a zero caso contr´ario. Dessa forma, s˜ao

definidos os tempos de in´ıcio de processamento de cada tarefa, obtendo a ordem em que as

tarefas ser˜ao executadas. Em problemas de sequenciamento, diversos objetivos podem ser

considerados, como a minimiza¸c˜ao do tempo de t´ermino da ´

ultima tarefa (

makespan

), a

minimiza¸c˜ao do n´

umero de tarefas completadas ap´os seu prazo de entrega, a minimiza¸c˜ao

da soma dos atrasos das tarefas, etc.

Buscando reduzir os custos da produ¸c˜ao, uma segunda caracter´ıstica pode ser

in-corporada ao problema. Trata-se do processamento simultˆaneo de um conjunto de tarefas

em uma m´aquina, denominado lote, o qual geralmente torna mais barato e/ou r´apido o

processamento da totalidade das tarefas. Uma descri¸c˜ao do processamento em lotes ´e

encontrada em Pinedo (2008). Desse modo, cada tarefa

j

_∈

J

possui um tamanho

s

e

o conjunto de tarefas processadas simultaneamente n˜ao deve exceder a capacidade

Q

da

m´aquina, ou seja, a soma dos

s

das tarefas processadas no lote deve ser menor ou igual `a

Q.

De acordo com Potts e Kovalyov (2000), todas as tarefas pertencentes a um

deter-minado lote iniciam e concluem seu processamento no mesmo instante de tempo. Portanto,

o tempo de processamento

p(B

) de um lote

i

´e igual ao maior tempo de processamento

dentre o de todas as tarefas pertencentes ao lote, pois uma tarefa s´o se torna dispon´ıvel

quando o processamento de todas as tarefas do lote ao qual ela pertence for finalizado. Da

mesma forma, a data de libera¸c˜ao

r(B

) de um lote ´e igual a maior dentre as das tarefas

do referido lote, j´a que as tarefas alocadas em um determinado lote n˜ao podem iniciar o

processamento simultaneamente sem que isso seja permitido para todas elas.

S´o ´e permitido processar um lote por vez na m´aquina. Sendo assim, seu tempo

de t´ermino ´e definido como sendo

C(B

) =

max

{

r(B

);

C(B

}

+

p(B

). Logo, uma

tarefa

j

pertencente ao lote

i

possui como tempo de t´ermino

C

=

C(B

). O atraso dessa

tarefa ´e definido como sendo

T

=

max

{

C

−

d

; 0

}

. Quando o objetivo considerado ´e a

desse problema ´e determinar os lotes de tarefas e sequenci´a-los, visando a minimiza¸c˜ao do

P

w

T

.

Neste problema, restri¸c˜oes adicionais podem ser consideradas definindo conjuntos

de tarefas as quais podem ser processadas simultaneamente, denominados fam´ılias de

tare-fas. Tarefas pertencentes a fam´ılias distintas s˜ao ditas incompat´ıveis. Como exposto por

M¨onch et al (2011), nesta configura¸c˜ao, apenas as tarefas que pertencem `a mesma fam´ılia

podem ser processadas simultaneamente, contanto que respeite a capacidade m´axima da

m´aquina. Entretanto, a existˆencia de tarefas incompat´ıveis e a determina¸c˜ao de fam´ılias de

tarefas n˜ao s˜ao consideradas no problema tratado neste trabalho. A caracter´ıstica de

in-compatibilidade de tarefas em fam´ılias distintas ´e normalmente referenciada como

incompt,

enquanto que a inexistˆencia de incompatibilidade de tarefas ´e indicado por

compt.

Este trabalho aborda o problema de sequenciamento de lotes em uma m´aquina,

com tarefas compat´ıveis, tamanhos de tarefas distintos e a existˆencia de datas de libera¸c˜ao

diferentes de zero, visando minimizar o atraso ponderado total. Dessa forma, segundo a

nomenclatura proposta por Graham et al (1979), o problema abordado neste trabalho pode

ser representado por 1

_|

batch, r

, s

, compt

|

P

w

T

. Visando tornar mais claro o

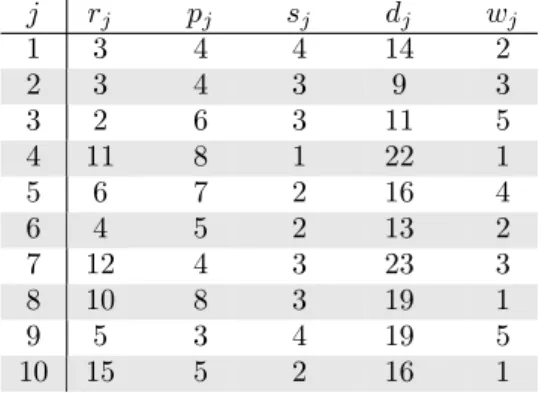
entendi-mento deste problema, ´e apresentada na Tabela 1.1 uma instˆancia pequena, com apenas

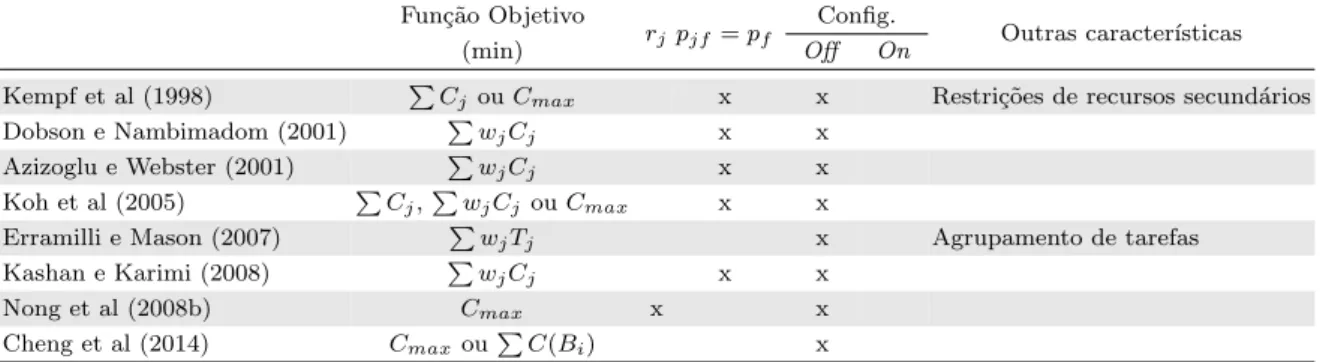
10 tarefas, em que a capacidade da m´aquina ´e igual a 10. A Figura 1.1 ilustra uma solu¸c˜ao

vi´avel desta instˆancia, em que as tarefas est˜ao agrupadas e sequenciadas em 3 lotes.

Tabela 1.1: Exemplo de uma instˆancia do 1

_|

batch, r

, s

, compt

|

P

w

T

j

r

p

s

d

w

1

3

4

4

14

2

2

3

4

3

9

3

3

2

6

3

11

5

4

11

8

1

22

1

5

6

7

2

16

4

6

4

5

2

13

2

7

12

4

3

23

3

8

10

8

3

19

1

9

5

3

4

19

5

10

15

5

2

16

1

Figura 1.1: Exemplo de uma solu¸c˜ao do 1

_|

batch, r

, s

, compt

|

P

w

T

semelhante, a data de libera¸c˜ao de um lote ´e a maior dentre as das tarefas que fazem parte

do lote. Logo,

r(B1) = 4,

r(B2) = 6 e

r(B3) = 15. Consequentemente, o primeiro lote

finalizar´a seu processamento em

C(B1) = 10, o segundo lote em

C(B2) = 17 e, por fim, o

tempo de t´ermino do ´

ultimo lote ´e igual a

C(B3) = 25.

Como as tarefas de um determinado lote se tornam dispon´ıveis apenas quando o

processamento do lote for finalizado, o tempo de t´ermino de uma tarefa ´e igual ao tempo

de t´ermino do lote no qual a tarefa est´a alocada. Tendo em vista que, neste trabalho,

considera-se como fun¸c˜ao objetivo a minimiza¸c˜ao do atraso ponderado total, na solu¸c˜ao

vi´avel apresentada, o valor da fun¸c˜ao objetivo ´e dado por:

P

1≤j≤10

w

(max

{

C

−

d

,

0

}

),

ou ainda, 2(max

{

17

−

14,

0

}

) + 3(max

{

10

−

9,

0

}

) + 5(max

{

10

−

11,

0

}

) + 1(max

{

25

−

22,

0

}

) + 4(max

{

17

−

16,

0

}

) + 2(max

{

10

−

13,

0

}

) + 3(max

{

25

−

23,

0

}

) + 1(max

{

25

−

19,

0

}

) + 5(max

{

17

−

19,

0

}

) + 1(max

{

25

−

16,

0

}

). O custo desta solu¸c˜ao ´e, portanto, igual

a 37.

Os autores destacam que para determinar uma solu¸c˜ao ´otima, pode-se enumerar todas as

poss´ıveis solu¸c˜oes; entretanto, para instˆancias de tamanho moderado, um n´

umero elevado

de solu¸c˜oes pode inviabilizar sua enumera¸c˜ao completa.

Em problemas de minimiza¸c˜ao, a solu¸c˜ao ´otima ser´a dada pela escolha das vari´aveis

que forne¸ca o menor valor poss´ıvel para a fun¸c˜ao objetivo, de forma que as restri¸c˜oes n˜ao

sejam violadas. Nestes m´etodos, limites inferiores e superiores podem ser obtidos quando

utilizado um crit´erio de parada, como por exemplo um intervalo de tempo m´aximo de

execu¸c˜ao, e a execu¸c˜ao do modelo ´e interrompida sem que tenha sido necessariamente

encontrada uma solu¸c˜ao comprovadamente ´otima.

Este trabalho prop˜oe diferentes formula¸c˜oes matem´aticas para o problema de

se-quenciamento de lotes com penalidades por atraso, considerando datas de libera¸c˜ao,

tama-nhos diferentes de tarefas e tendo como objetivo minimizar a soma dos atrasos ponderados.

1.2 JUSTIFICATIVA

´

E not´avel o impacto do sequenciamento da produ¸c˜ao, tanto nos sistemas de

manufa-tura quanto de servi¸cos, e sua influˆencia direta no prazo de entrega acordado com os clientes

e no custo final dos produtos. Consequentemente, encontrar solu¸c˜oes eficientes para os

problemas de sequenciamento constitui um importante diferencial econˆomico. Tendo em

vista o exposto, ´e cada vez mais comum a aplica¸c˜ao de t´ecnicas modernas de

gerenci-amento para a resolu¸c˜ao desses problemas. Somado a isso, a utiliza¸c˜ao de ferramentas

computacionais no aux´ılio `a tomada de decis˜ao podem garantir e facilitar a obten¸c˜ao em

tempo h´abil de solu¸c˜oes satisfat´orias.

dos materiais a serem processados; entre outros.

A fabrica¸c˜ao de itens em grande quantidade e/ou a existˆencia de etapas iguais na

produ¸c˜ao de itens distintos tornam poss´ıvel a realiza¸c˜ao de atividades da fabrica¸c˜ao por

meio de lotes de produ¸c˜ao. A fabrica¸c˜ao de lotes gera, normalmente, uma redu¸c˜ao do

custo e do tempo total de processamento, quando comparado a fabrica¸c˜ao individual de

itens. Um dos problemas que motivou o estudo acerca do sequenciamento de lotes da

produ¸c˜ao diz respeito `a fabrica¸c˜ao de semicondutores, especificamente no sequenciamento

da etapa de queima no forno. A fase final da produ¸c˜ao de circuitos integrados ´e a opera¸c˜ao

de queima, na qual os

chips

s˜ao alocados em placas e, em seguida, estas s˜ao colocadas em

um forno e expostas a altas temperaturas. O objetivo da opera¸c˜ao de queima ´e sujeitar os

chips

ao estresse t´ermico por um longo per´ıodo de tempo, a fim de visualizar os defeitos

latentes. Esse problema e algumas de suas variantes foram abordados por Uzsoy et al

(1992, 1994).

Outro exemplo pr´atico se refere ao problema de entrega com um ´

unico ve´ıculo, como

descrito em Ikura e Gimple (1986). Apenas um ve´ıculo ´e usado para transportar itens

(tare-fas) de um local de coleta A para um ponto de entrega B. Os itens chegam dinamicamente

no ponto A em hor´arios fixos, ou seja, com datas de libera¸c˜ao pr´e-determinadas, possuindo

cada item uma data ideal para ser entregue no ponto B. O ve´ıculo tem uma capacidade

referente ao n´

umero m´aximo de itens que podem ser transportados por vez e um intervalo

de tempo fixo ´e necess´ario para realizar o percurso de ida e volta entre A e B. A finalidade

´e determinar os itens transportados em cada percurso e a sequˆencia de viagens do ve´ıculo,

visando minimizar o tempo de t´ermino.

De acordo com Lopez e Roubellat (2008), alguns desses problemas pertencem `a

classe

_{N P}

-dif´ıcil e, apesar de ser relativamente simples formular problemas como esse,

nem sempre ´e poss´ıvel resolver instˆancias de dimens˜oes maiores por meio de m´etodos

exatos. O problema de sequenciamento de lotes da produ¸c˜ao abordado neste trabalho ´e

considerado

N P

-dif´ıcil, por incluir como caso especial o problema 1

|

batch, compt

|

P

w

T

,

exatos desenvolvidos para a resolu¸c˜ao desse problema.

Por esse motivo, optou-se por elaborar diferentes modelos matem´aticos

relativa-mente eficientes, com o intuito de resolver instˆancias de pequeno porte, bem como

determi-nar limites inferiores para instˆancias maiores. Com base no exposto, esse trabalho pretende

desenvolver formula¸c˜oes matem´aticas para o problema 1

_|

batch, r

, s

, compt

|

P

w

T

.

1.3 OBJETIVOS

1.3.1 Objetivo Geral

Desenvolver diferentes formula¸c˜oes matem´aticas para o problema de

sequencia-mento de lotes em uma m´aquina, com fam´ılia de produtos compat´ıveis, tamanhos de

tarefas distintos e datas de libera¸c˜ao, com o objetivo de minimizar o atraso ponderado

total.

1.3.2 Objetivos Espec´ıficos

•

Realizar revis˜ao da literatura sobre o problema abordado, englobando trabalhos que

consideram restri¸c˜oes de fam´ılias de tarefas incompat´ıveis.

•

Identificar instˆancias dispon´ıveis na literatura.

•

Identificar formula¸c˜oes matem´aticas existentes na literatura para o problema tratado.

•

Desenvolver formula¸c˜oes matem´aticas distintas.

•

Implementar e validar as formula¸c˜oes propostas.

•

Implementar formula¸c˜oes matem´aticas dispon´ıveis na literatura, em caso de

consi-dera¸c˜ao de instˆancias diferentes.

•

Comparar os resultados obtidos pelas formula¸c˜oes desenvolvidas entre os mesmos,

como tamb´em com os resultados dispon´ıveis ou obtidos por formula¸c˜oes existentes

na literatura.

1.4 ESTRUTURA DO TRABALHO

Neste cap´ıtulo s˜ao apresentados alguns conceitos e defini¸c˜oes relacionados ao

pro-blema de escalonamento da produ¸c˜ao. Em seguida, s˜ao especificadas as caracter´ısticas do

problema abordado neste trabalho.

2.1 ESCALONAMENTO DA PRODU ¸

C ˜

AO

De acordo com Pinedo (2009), um sistema de manufatura pode conter uma

varie-dade de fatores, como por exemplo: o n´

umero de recursos ou m´aquinas existente;

carac-ter´ısticas particulares de cada um dos recursos; o tipo de material processado no sistema;

restri¸c˜oes inerentes `a capacidade de processamento; entre tantos outros. Dada a enorme

quantidade de fatores poss´ıveis de serem considerados, existe um grande n´

umero de

vari-antes do problema de escalonamento da produ¸c˜ao. Em um processo de manufatura, os

recursos podem ser referenciados como “m´aquinas”, e as atividades realizadas em uma

m´aquina s˜ao tidas como “tarefas”.

•

Tempo de processamento

p

, ou seja, o tempo que a tarefa

j

necessita permanecer

na m´aquina

k. Quando apenas uma m´aquina est´a dispon´ıvel para o processamento

das tarefas, ou quando o tempo de processamento de uma tarefa n˜ao depende da

m´aquina, o ´ındice

k

´e omitido.

•

Data de libera¸c˜ao (em inglˆes

release date

)

r

da tarefa

j, referente ao instante de

tempo a partir do qual a tarefa

j

est´a dispon´ıvel para ser processada no sistema.

•

Data de entrega

d

da tarefa

j, a qual diz respeito, por exemplo, ao prazo de conclus˜ao

definido junto ao cliente.

•

Data de vencimento ¯

d

da tarefa

j, isto ´e, o prazo acordado com o cliente que deve

ser obrigatoriamente cumprido.

•

Peso ou penalidade

w

, tido como um fator de prioridade da tarefa

j

em rela¸c˜ao `as

demais. Esse dado pode tamb´em ser entendido como o custo proporcional ao tempo

em que a tarefa

j

permaneceu no sistema.

Os dados listados acima s˜ao chamados dados est´aticos, pois s˜ao independentes da

sequˆencia. Por outro lado, de acordo com o mesmo autor, quando os dados n˜ao s˜ao

fixos a princ´ıpio e dependem do sequenciamento, denominam-se dados dinˆamicos. Dois

importantes dados dinˆamicos para esse tipo de problema s˜ao:

•

Tempo de in´ıcio

S

, ou seja, o instante de tempo em que a tarefa

j

come¸ca a ser

processada na m´aquina

k. Desconsiderando o ´ındice

k, tem-se um tempo de in´ıcio

que independe da m´aquina.

•

Tempo de t´ermino

C

, que se refere ao momento em que a tarefa

j

finaliza seu

processamento na m´aquina

k. Da mesma forma que o item anterior, para o tempo

de t´ermino independente da m´aquina, basta omitir o ´ındice

k.

processamento ou restri¸c˜oes, podendo conter nenhuma, uma ou m´

ultiplas entradas. Por

fim,

γ

descreve o objetivo a ser minimizado ou maximizado com apenas uma entrada. As

principais configura¸c˜oes poss´ıveis de cada um dos campos s˜ao descritas a seguir.

2.1.1 Configura¸c˜ao da(s) M´aquina(s)

Segundo Pinedo (2008), as configura¸c˜oes

α

normalmente utilizadas no que se refere

`as m´aquinas s˜ao:

•

Uma m´aquina (1), em que apenas uma m´aquina est´a dispon´ıvel para processar todas

as tarefas. Trata-se do caso mais simples da configura¸c˜ao

α, sendo este um caso

especial dos ambientes descritos a seguir.

•

M´aquinas paralelas idˆenticas (P m), em que est˜ao dispon´ıveis

m

m´aquinas idˆenticas

em paralelo e, portanto, o tempo de processamento de uma tarefa

j

em qualquer

uma das

m

m´aquinas ´e o mesmo. Dessa forma, uma tarefa

j

pode ser processada

em qualquer uma das

m

m´aquinas ou em um subconjunto

M

pr´e-determinado.

•

M´aquinas paralelas uniformes (Qm), ou seja, um ambiente com

m

m´aquinas em

paralelo que possuem diferentes fatores de velocidade

v

para cada m´aquina

k.

Por-tanto, o tempo

p

da tarefa

j

na m´aquina

k

´e dado por

p

/v

. Quando os fatores

de velocidade s˜ao iguais para todas as m´aquinas, tem-se o ambiente anterior.

•

M´aquinas paralelas n˜ao relacionadas (Rm), onde existem

m

m´aquinas diferentes em

paralelo. Trata-se de uma generaliza¸c˜ao do ambiente anterior, onde a velocidade de

processamento depende da m´aquina e da tarefa (v

). Logo, o tempo de

processa-mento

p

da tarefa

j

na m´aquina

k

´e igual a

p

/v

. Se o fator de velocidade das

m´aquinas independe das tarefas, tem-se o caso anterior.

•

Job shop

(Jm), com

m

m´aquinas e cada uma das

n

tarefas possuindo sua pr´opria

rota predeterminada. Destaca-se a existˆencia de dois casos: quando cada tarefa visita

cada uma das

m

m´aquinas no m´aximo uma vez; e quando uma tarefa pode visitar

cada m´aquina mais de uma vez, ou seja, ´e permitida a existˆencia de recircula¸c˜ao

(rcrc).

•

Open shop

(Om), onde existem

m

m´aquinas e cada tarefa

j

tem que ser processada

em todas as m´aquinas. Entretanto, alguns dos tempos de processamento podem ser

iguais `a zero. Nesse ambiente, n˜ao h´a restri¸c˜oes em rela¸c˜ao `a sequˆencia em que uma

tarefa ´e processada nas

m

m´aquinas, sendo poss´ıvel que cada tarefa possua uma

sequˆencia distinta das demais.

2.1.2 Caracter´ısticas das Tarefas

As caracter´ısticas relacionadas ao processamento das tarefas s˜ao especificadas no

campo

β. Como dito anteriormente, ´e poss´ıvel que exista nenhuma, uma ou m´

ultiplas

ca-racter´ısticas descritas neste campo. Dentre as caca-racter´ısticas expostas por Pinedo (2008),

est˜ao:

•

Data de libera¸c˜ao da tarefa

j

(r

), onde s´o ´e permitido que a tarefa

j

inicie seu

processamento ap´os o instante de tempo

r

. Caso este item n˜ao apare¸ca em

β, as

tarefas podem come¸car a ser processadas a qualquer momento. Por outro lado, as

datas de entrega n˜ao s˜ao especificadas, pois sua existˆencia ´e facilmente identificada

a partir da fun¸c˜ao objetivo considerada.

•

Preemp¸c˜ao (pmtn), a qual ocorre quando o processamento da tarefa pode ser

inter-rompido na m´aquina e retomado ap´os um certo tempo na mesma m´aquina ou em

outra. Se essa condi¸c˜ao n˜ao for permitida pelo sistema, n˜ao constar´a no campo

β.

tem no m´aximo uma sucessora, referindo a estas restri¸c˜oes como

intree

; e no caso

em que cada tarefa possui no m´aximo uma antecessora, sendo chamado de

outtree

.

•

Tempo de

setup

dependente da sequˆencia (s

), isto ´e, um tempo de prepara¸c˜ao entre

o processamento da tarefa

h

seguido da tarefa

j. Note que

s0

se refere ao tempo

de

setup

quando o item

j

´e o primeiro da sequˆencia; e

s

o tempo de prepara¸c˜ao

ap´os o t´ermino do processamento da tarefa

h, quando esta ´e a ´

ultima da sequˆencia.

Se o

setup

depende da m´aquina em que os itens est˜ao sendo processados, o ´ındice

k

´e inclu´ıdo (s

). O

setup

pode tamb´em independer da sequˆencia e da m´aquina,

significando um tempo de preparo padr˜ao por tarefa dado por

s

.

•

Fam´ılias de tarefas (f mls), que ocorre quando as

n

tarefas s˜ao particionadas em

F

fam´ılias. As tarefas de uma mesma fam´ılia podem ter diferentes tempos de

processa-mento, entretanto elas s˜ao processadas uma em seguida de outra sem a necessidade

de um tempo de

setup

entre as duas. Por outro lado, quando tarefas sucessivas

per-tencem a fam´ılias distintas, a execu¸c˜ao de um

setup

´e possivelmente necess´aria, o

qual pode ser dependente das fam´ılias de ambas as tarefas, de apenas uma, ou pode

ser um tempo de prepara¸c˜ao constante.

•

Processamento em lotes (batch), que ocorre quando uma m´aquina processa um

con-junto de tarefas (lote), de forma que a capacidade da m´aquina seja respeitada. Nesse

caso, para cada lote

i

do conjunto

B

de lotes, as tarefas pertencentes `a

i

s´o podem

iniciar seu processamento quando este for permitido para todas elas, e uma tarefa ´e

considerada finalizada apenas ap´os a finaliza¸c˜ao do processamento de todas as tarefas

do referido lote.

Diversos autores, como M¨onch et al (2011) e Xu et al (2012), apresentam dois tipos

de m´aquinas de processamento em lotes: sequencial (s

−

batch), em que as tarefas de um

lote s˜ao processadas em sequˆencia e o tempo de processamento do lote ´e igual `a soma de

todos os tempos de processamento das tarefas que fazem parte deste lote; e em paralelo (p

−

batch), onde a m´aquina ´e capaz de processar todas as tarefas de um lote simultaneamente,

das tarefas do referido lote. O problema estudado neste trabalho envolve a configura¸c˜ao

p

₋

batch, sendo comumente referenciada apenas como

batch. Caso uma m´aquina

s

₋

batch

seja considera, esta ser´a indicada explicitamente. Algumas particularidades normalmente

especificadas nos trabalhos dispon´ıveis na literatura que adotam esta caracter´ıstica em

problemas de sequenciamento s˜ao descritas a seguir.

•

A capacidade da m´aquina pode ser ilimitada ou limitada. No primeiro caso, todas

as

n

tarefas podem ser processadas ao mesmo tempo. Quando a capacidade da

m´aquina ´e limitada, s˜ao abordados em geral dois casos: quando a m´aquina ´e capaz

de processar um n´

umero m´aximo

Q

de tarefas, onde cada tarefa utiliza a mesma

fra¸c˜ao de capacidade da m´aquina; e quando cada tarefa possui um tamanho

s

, com

a soma dos tamanhos das tarefas de um lote sendo menor que a capacidade

Q

da

m´aquina.

•

Todas as tarefas podem ainda ser compat´ıveis (compt) entre si e, portanto, serem

processadas em um mesmo lote. Quando consideradas fam´ılias de tarefas, aquelas

pertencentes a fam´ılias diferentes s˜ao incompat´ıveis (incompt) e, nesse caso, podem

ser processadas apenas em lotes diferentes.

2.1.3 Fun¸c˜ao Objetivo

A fun¸c˜ao objetivo do problema ´e descrita no ´

ultimo campo de classifica¸c˜ao (γ)

apresentado por Graham et al (1979). As principais fun¸c˜oes objetivo adotadas para o

problema de escalonamento descritas em Pinedo (2008) s˜ao apresentadas a seguir, sendo

todas fun¸c˜oes de minimiza¸c˜ao.

•

Makespan

(C

), definido como o tempo de t´ermino da ´

ultima tarefa, ou seja,

max(C1, C2, ..., C

). Geralmente, essa fun¸c˜ao objetivo fornece uma boa utiliza¸c˜ao

das m´aquinas.

•

Soma ponderada dos tempos de t´ermino (

P

w

C

). A soma dos tempos de t´ermino

´e tamb´em referenciada como o tempo de fluxo. Quando todas as tarefas possuem o

mesmo n´ıvel de prioridade, tem-se como fun¸c˜ao objetivo

P

•

M´aximo

lateness

(L

), o qual ´e definido para uma dada tarefa

j

como

C

−

d

,

podendo representar o atraso ou a antecipa¸c˜ao da tarefa em quest˜ao. O m´aximo

lateness

´e dado por max(L1, L2, ..., L

), sendo essa fun¸c˜ao objetivo equivalente a

minimizar a pior data de entrega dado o cronograma.

•

Atraso ponderado total (

P

w

T

), onde

T

= max(L

,

0), podendo assumir apenas

valores positivos. Supondo que cada tarefa tenha o mesmo peso, obt´em-se a fun¸c˜ao

objetivo de minimiza¸c˜ao do atraso total (

P

T

).

•

Total do n´

umero ponderado de tarefas em atraso (

P

w

U

), sendo

U

igual a 1

quando

C

> d

, e 0 caso contr´ario. Obt´em-se o

P

U

quando os pesos das tarefas

s˜ao considerados iguais.

•

Total ponderado de antecipa¸c˜oes (

P

w

E

). A antecipa¸c˜ao

E

da tarefa

j

ocorre

quando a tarefa ´e conclu´ıda antes do prazo de entrega, ou seja, quando

C

< d

.

Dessa forma,

E

= max(d

−

C

,

0). Quando a prioridade de todas as tarefas ´e a

mesma, tem-se o

P

E

.

•

Soma dos atrasos e antecipa¸c˜oes ponderados (

P

w

j

E

+

P

w

T

). Essa ´e uma

im-portante medida quando utilizada a filosofia

Just in Time

(JIT), em que o ideal seria

a conclus˜ao da tarefa exatamente no prazo de entrega, sendo a fun¸c˜ao penalizada

quando a tarefa ´e conclu´ıda com um tempo de antecipa¸c˜ao ou de atraso. Quando

n˜ao s˜ao considerados pesos das tarefas, tem-se a fun¸c˜ao objetivo de minimiza¸c˜ao das

antecipa¸c˜oes e atrasos, dada por

P

E

+

P

T

.

2.2 PROBLEMA ABORDADO

Este trabalho trata do problema de sequenciamento de tarefas compat´ıveis com

penalidades por atraso em uma m´aquina de processamento em lotes, considerando datas

de libera¸c˜ao e tamanhos distintos das tarefas. Segundo a nomenclatura proposta por

Graham et al (1979), este problema ´e representado como 1

_|

batch, r

, s

, compt

|

P

w

T

.

•

Apenas uma m´aquina est´a dispon´ıvel para o processamento do conjunto de tarefas

J, tratando-se portanto de um problema de sequenciamento da produ¸c˜ao.

•

Cada tarefa

j

possui os seguintes dados: uma data de libera¸c˜ao

r

; um tempo de

processamento

p

; uma data de entrega

d

; um tamanho

s

; e um n´ıvel de prioridade

w

.

•

Cada tarefa

j

´e processada apenas uma vez na m´aquina, e n˜ao existem restri¸c˜oes

quanto a precedˆencias.

•

A m´aquina ´e capaz de processar um subconjunto de tarefas simultaneamente, ao

qual dar-se o nome de lote, sendo limitada por sua capacidade

Q. Isto ´e, a soma

dos tamanhos associados `as tarefas processadas em conjunto n˜ao pode exceder a

capacidade da m´aquina, e portanto, deve ser menor ou igual `a

Q.

•

Preemp¸c˜oes n˜ao s˜ao permitidas. Quando o processamento de um lote for iniciado,

ele deve ser conclu´ıdo sem que haja interrup¸c˜ao. Al´em disso, apenas um lote pode

ser processado por vez na m´aquina.

•

O tempo de processamento de um lote

p(B

) ´e dado pelo maior tempo de

processa-mento dentre as tarefas alocadas no referido lote.

•

A data de libera¸c˜ao de um lote

r(B

) ´e a maior dentre as datas de libera¸c˜ao do

referido lote.

•

O tempo de t´ermino de um lote

C(B

) ´e o maior valor entre a data de libera¸c˜ao do

lote e o tempo de t´ermino do lote anterior, somado ao tempo de processamento do

lote atual. Ou seja,

C(B

) = max

{

r(B

), C

(B

}

+

p(B

).

•

Como o processamento de uma tarefa s´o ´e considerado finalizado quando todas as

tarefas do lote ao qual ela pertence foram finalizadas, o tempo de t´ermino de uma

tarefa

j

_∈

J

alocada ao lote

i, ou seja,

C

, ´e igual `a

C(B

).

•

O objetivo adotado ´e o de minimiza¸c˜ao do atraso ponderado total. O atraso de uma

tarefa

j

_∈

J

assume apenas valores positivos, sendo definido como a diferen¸ca entre

o instante de tempo em que seu processamento foi finalizado e sua data de entrega,

ou seja,

T

= max

{

C

−

d

,

0

}

. Dessa forma, o atraso ponderado de uma tarefa

j

´e dado por

w

T

, onde

w

pode representar a prioridade da tarefa

j

em rela¸c˜ao `as

demais. A fun¸c˜ao objetivo considerada pode ser escrita como

P

O problema de sequenciamento de lotes pode ser classificado de duas formas: com

incompatibilidade de fam´ılias de tarefas e com tarefas compat´ıveis. No primeiro caso,

tarefas de fam´ılias diferentes n˜ao podem ser processadas no mesmo lote, o que ´e permitido

quando as tarefas s˜ao todas compat´ıveis. Neste cap´ıtulo s˜ao descritos os principais

traba-lhos encontrados na literatura referentes a ambos os casos. N˜ao est˜ao descritos trabatraba-lhos

envolvendo m´

ultiplas m´aquinas e tempos de

setup

, j´a que estas caracter´ısticas n˜ao s˜ao

consideradas no problema estudado neste trabalho.

Os trabalhos Potts e Kovalyov (2000), M¨onch et al (2011) e Mathirajan e Sivakumar

(2006) trazem uma descri¸c˜ao do problema de sequenciamento de lotes, assim como uma

revis˜ao dos trabalhos encontrados na literatura.

3.1 FAM´ILIAS DE TAREFAS COMPAT´IVEIS

O problema de sequenciamento de lotes em uma m´aquina com tarefas compat´ıveis

pode ainda ser classificado segundo a capacidade da m´aquina, em capacidade finita (Q < n)

ou infinita (Q

_≥

n). Quando a capacidade ´e tida como finita, s˜ao abordados na literatura

dois casos: com tamanhos idˆenticos de tarefas; e com tamanhos de tarefas distintos. Neste

´

de processar um n´

umero m´aximo de tarefas simultaneamente.

As subse¸c˜oes a seguir apresentam, respectivamente, os trabalhos envolvendo

tama-nhos de tarefas idˆenticos, tamatama-nhos distintos de tarefas e capacidade ilimitada da m´aquina.

3.1.1 Tamanhos de Tarefas Idˆenticos

Alguns autores, tais como Li et al (2015), Xu et al (2012) e Mathirajan et al (2010),

consideram o trabalho de Ikura e Gimple (1986) como um dos primeiros a tratarem do

problema abordado. Os autores consideraram tamanhos idˆenticos e tempo de

processa-mento dos lotes constante, com o objetivo de minimizar o tempo de t´ermino final. Algumas

simplifica¸c˜oes foram assumidas nesse trabalho. A primeira ocorre quando n˜ao s˜ao

consi-deradas datas de entrega, e nesse caso, foi proposto o algoritmo

First-Only-Empty

, com

o primeiro lote parcialmente vazio e os demais completos, o que resulta em um m´ınimo

n´

umero de lotes. A segunda ocorre quando as tarefas s˜ao idˆenticas e, nesse caso, ´e poss´ıvel

atribuir as datas de entrega `as tarefas na ordem em que elas chegam, fazendo com que as

datas de libera¸c˜ao sejam proporcionais `as de entrega (r

< r

, d

< d

); para esse caso foi

proposto o algoritmo

Greedy-Adjusted-Bunching

, que utiliza o procedimento guloso

Greedy

Bunching

, o qual tenta colocar a m´axima quantidade de tarefas poss´ıvel em um lote, desde

que a data de entrega da pr´oxima tarefa seja atendida.

espera foi investigado em fun¸c˜ao de dois parˆametros: coeficiente de varia¸c˜ao do tempo de

chegada e intensidade do tr´afego.

Lee et al (1992) apresentaram algoritmos baseados em Programa¸c˜ao Dinˆamica (PD)

que minimizam v´arias medidas de desempenho, entre elas o atraso m´aximo e o n´

umero

de tarefas em atraso. No caso do atraso m´aximo, assumiram que todos os tempos de

processamento s˜ao iguais e que as datas de libera¸c˜ao e de entrega s˜ao proporcionais.

Avaliaram tamb´em para essa fun¸c˜ao objetivo o caso em que n˜ao h´a datas de libera¸c˜ao e os

tempos de processamento e datas de entrega s˜ao proporcionais. Para quando a finalidade ´e

minimizar o n´

umero de tarefas em atraso, foram propostos dois algoritmos: o primeiro com

tempos de processamento das tarefas iguais; o segundo considerando que as tarefas est˜ao

dispon´ıveis no instante de tempo zero, com tempos de processamento e datas de entrega

proporcionais. Al´em disso, propuseram heur´ısticas para o caso de m´aquinas paralelas, com

o objetivo de minimizar o

makespan

e o m´aximo

lateness

.

Os problemas de minimiza¸c˜ao do tempo de t´ermino total em uma m´aquina e em

m´aquinas paralelas foram resolvidos por Chandru et al (1993a). Os autores propuseram

um algoritmo

Branch-and-Bound

(B&B) para o primeiro caso e uma heur´ıstica nomeada

Greedy Ratio

para ambos. Li e Lee (1997) abordaram o problema de minimiza¸c˜ao do

atraso m´aximo e de minimiza¸c˜ao do n´

umero de tarefas em atraso. Os autores mostraram

que o 1/r

, batch/T

e o 1/r

, batch/

P

U

, com

r

< r

implicando em

d

< d

, s˜ao

problemas do tipo

_{N P}

-dif´ıcil. Quando os tempos de processamento tamb´em s˜ao

conside-rados proporcionais em conjunto com as datas de libera¸c˜ao e de entrega, pode-se resolvˆe-lo

em tempo polinomial. Foram desenvolvidos para esse caso dois algoritmos baseados em

PD, um para cada fun¸c˜ao objetivo.

com tarefas de tamanhos idˆenticos, tempo de processamento do lote constante e datas de

libera¸c˜ao. Al´em dos objetivos descritos anteriormente, os autores consideraram, para esse

problema, a minimiza¸c˜ao do

makespan

. Por fim, descreveram o caso em que o tempo de

processamento de um lote ´e o maior dentre os tempos de processamento das tarefas que

fazem parte do mesmo.

Para a minimiza¸c˜ao do total dos tempos de t´ermino ponderados, Uzsoy e Yang

(1997) apresentaram um algoritmo B&B, bem como limites inferiores e condi¸c˜oes de

do-minˆancia. Al´em disso, desenvolveram heur´ısticas para esse problema. A primeira delas

procura manter a m´aquina com uso m´aximo em rela¸c˜ao `a sua capacidade sempre que

houver tarefas em espera para serem processadas. A segunda heur´ıstica ´e baseada no

algo-ritmo proposto por Chandru et al (1993a), com os lotes formados por tarefas consecutivas.

Entretanto, quando consideradas prioridades distintas das tarefas, essa ´

ultima propriedade

pode ser violada. Dessa forma, outras heur´ısticas foram propostas para tentar corrigir essa

viola¸c˜ao, as quais geram um lote considerando os demais ainda n˜ao sequenciados.

o n´

umero ponderado de tarefas em atraso e minimizar a soma dos atrasos ponderados s˜ao

problemas

_{N P}

-dif´ıceis. Para o caso em que a capacidade ´e limitada, foi proposto um

al-goritmo de PD para a minimiza¸c˜ao do tempo de t´ermino total, al´em de um alal-goritmo para

o caso em que o n´

umero de tempos de processamento distintos ´e conhecido. Provaram

tamb´em que quando a fun¸c˜ao objetivo ´e baseada nas datas de entrega, o problema ´e tido

como

N P

-dif´ıcil. Por fim, mostraram que uma fun¸c˜ao de custo regular arbitr´aria pode ser

minimizada em tempo polinomial para um n´

umero fixo de lotes.

Qi e Tu (1999) propuseram um algoritmo baseado de PD de tempo polinomial para o

problema de minimiza¸c˜ao do total de atraso e antecipa¸c˜ao, com o tempo de processamento

por lote constante. Entretanto, segundos os autores, o algoritmo proposto n˜ao apresentou

bom desempenho devido `a quantidade de mem´oria utilizada. Um segundo algoritmo

tam-b´em baseado em PD foi, ent˜ao, desenvolvido, com tempo de resolu¸c˜ao pseudo-polinomial.

Por fim, foi analisado o problema de minimiza¸c˜ao dos atrasos e antecipa¸c˜oes ponderados,

considerando datas de libera¸c˜ao e datas de entrega proporcionais e tarefas com janelas de

tempo referente `as datas de entrega.

O problema de minimiza¸c˜ao do

makespan

considerando datas de libera¸c˜ao foi tratado

por Lee e Uzsoy (1999). Os autores mostraram que casos especiais desse problema podem

ser resolvidos em tempo polinomial e pseudo-polinomial e propuseram heur´ısticas para o

problema geral abordado. Liu e Yu (2000) mostraram que esse mesmo problema ´e

N P

-dif´ıcil, mesmo quando s˜ao considerados apenas dois poss´ıveis valores de datas de libera¸c˜ao.

Al´em disso, propuseram um algoritmo pseudo-polinomial baseado em PD para quando o

n´

umero de datas de libera¸c˜ao ´e conhecido. Desenvolveram tamb´em uma heur´ıstica gulosa

para o problema geral, onde opta-se por sequenciar a tarefa vi´avel de maior tempo de

processamento, respeitando a capacidade da m´aquina na forma¸c˜ao de lotes.

Baptiste (2000) abordou o problema de sequenciamento de lotes com tempo

cons-tante de processamento das tarefas e a existˆencia de datas de libera¸c˜ao. Dois tipos de

m´aquinas de processamento de lotes foram considerados:

s

₋

batch, com tempo de

setup

constante entre o processamento de lotes; e

p

₋

batch, sem a existˆencia de tempos de

setup

.

O autor mostrou para ambos os casos que, quando utilizadas fun¸c˜oes objetivo

ordered

ou

que podem ser transformadas nestas, as quais s˜ao, dentre outras caracter´ısticas, fun¸c˜oes

n˜ao decrescentes, o problema pode ser resolvido em tempo polinomial por meio de uma

PD.

Zhang et al (2001a) estudaram o problema de minimiza¸c˜ao do

makespan

em uma

configura¸c˜ao

online

, considerando datas de libera¸c˜ao. Diferente da configura¸c˜ao

offline

normalmente utilizada, no problema de sequenciamento

online

, as tarefas chegam ao longo

do tempo e, portanto, o conjunto de tarefas n˜ao ´e conhecido a priori e suas caracter´ısticas

s˜ao fornecidas quando chegam no sistema. Duas situa¸c˜oes foram avaliadas: quando a

capacidade ´e ilimitada; e quando a capacidade ´e limitada e existem apenas dois valores

poss´ıveis de datas de libera¸c˜ao. Os algoritmos propostos para os dois casos possuem a raz˜ao

de pior caso igual `a (

√

5 + 1)/2. Esses algoritmos foram generalizados para o caso geral,

possuindo uma raz˜ao de pior caso igual `a 2. Por fim, os autores estudaram o problema de

sequenciamento de lotes em m´aquinas paralelas com capacidades ilimitadas.

Um m´etodo considerando datas de libera¸c˜ao para a minimiza¸c˜ao do m´aximo

late-ness

foi apresentado por Wang e Uzsoy (2002). Os autores identificaram a possibilidade

de gera¸c˜ao de lotes com datas de entrega vi´aveis dada uma sequˆencia de tarefas, com base

em um algoritmo de PD proposto por Lee et al (1992). Em seguida, apresentaram um

Algoritmo Gen´etico (AG), com a jun¸c˜ao da referida PD com uma codifica¸c˜ao aleat´oria de

chaves proposta por Bean (1994).

´

ultimo. Al´em disso, consideraram o problema de configura¸c˜ao

online

, onde as datas de

libera¸c˜ao s˜ao desconhecidas at´e que sejam processadas. Para esse ´

ultimo caso, um limite

inferior para a raz˜ao de qualquer algoritmo de aproxima¸c˜ao com capacidade maior que

1 foi apresentado, al´em de ter sido mostrado que esse limite ´e apertado para quando a

capacidade ´e ilimitada.

Poon e Zhang (2004) propuseram v´arios algoritmos para casos especiais a partir

de modifica¸c˜oes em algoritmos dispon´ıveis na literatura baseados em PD, considerando

datas de libera¸c˜ao, com o objetivo de minimizar o

makespan

. Para o caso em que existe

um n´

umero

t

de valores poss´ıveis de datas de libera¸c˜ao e todos os dados s˜ao n´

umeros

inteiros, foi proposto um algoritmo com tempo de execu¸c˜ao

O(n(QR

)

(2/t)

), onde

R

´e igual a diferen¸ca entre a maior e a menor data de libera¸c˜ao. Para o caso com

u

poss´ıveis valores de tempos de processamento e

t

datas de libera¸c˜ao, foi proposto um

algoritmo com tempo de execu¸c˜ao da ordem de

O(nlogt

+

u

_Q

_t

_{logt). Al´em disso,}

foram desenvolvidos algoritmos mais eficientes para quando

t

= 2 e

u

= 1. Os autores

apresentaram tamb´em um algoritmo com tempo de execu¸c˜ao O(nlogn) para o problema

com capacidade ilimitada.

Deng et al (2005) desenvolveram esquemas de aproxima¸c˜ao em tempo polinomial

para o problema de minimiza¸c˜ao do tempo total de t´ermino, considerando datas de

libera-¸c˜ao, para os seguintes casos: quando todas as tarefas s˜ao ditas curtas, ou seja, seu tempo

de processamento ´e menor que um determinado limite; quando existe um n´

umero pequeno

de tarefas; e quando tarefas de tempos de processamento maiores s˜ao adiadas. M¨onch et al

(2006) abordaram o problema de minimiza¸c˜ao do atraso e antecipa¸c˜ao total, considerando

uma restri¸c˜ao de atraso m´aximo. Os autores apresentaram, para esse problema, v´arias

heur´ısticas de duas fases. Algumas delas n˜ao consideram, na primeira fase, a restri¸c˜ao

de atraso m´aximo permitido, sendo a sequˆencia modificada, se necess´ario, para satisfazer

essa restri¸c˜ao. Tais heur´ısticas s˜ao baseadas em AG e regras de dominˆancia das solu¸c˜oes

´otimas.

minimiza¸c˜ao do atraso total, os autores provaram ser este um problema

N P

-dif´ıcil, mesmo

quando a capacidade da m´aquina ´e de apenas duas tarefas, al´em de terem desenvolvido um

algoritmo pseudo-polinomial para um caso especial desse problema. Propuseram tamb´em

um algoritmo pseudo-polinomial para o problema de minimiza¸c˜ao do n´

umero ponderado

de tarefas em atraso, tido como

_{N P}

-dif´ıcil.

Liu et al (2009) estudaram o problema de minimiza¸c˜ao simultˆanea de dois

obje-tivos, com tempos constantes de processamento das tarefas. Foram propostos neste

tra-balho v´arios algoritmos de tempo polinomial que fornecem solu¸c˜oes ´otimas para diferentes

combina¸c˜oes de objetivos, seja na minimiza¸c˜ao de um objetivo em primeiro lugar, seguido

da minimiza¸c˜ao de um segundo objetivo, ou a partir da considera¸c˜ao de pesos dos dois

objetivos, com a minimiza¸c˜ao da soma ponderada dos mesmos.

Li et al (2009) estudaram o problema de maximizar o n´

umero de tarefas antecipadas,

com tempos de processamento iguais a um, configura¸c˜ao

online

e aquisi¸c˜ao das informa¸c˜oes

antecipada por um determinado intervalo de tempo. Neste trabalho, foi proposto um

algoritmo

online

guloso com uma melhor raz˜ao de pior caso poss´ıvel, de 1/min

_{

n, Q

+ 1

_}

.

A partir desta conclus˜ao, os autores mostraram que a capacidade de previs˜ao ´e in´

util

quando o intervalo de tempo referente `a previs˜ao ´e menor que 1. Quando esse intervalo ´e

maior ou igual a 1 e menor que 2, foram propostos limites superiores com raz˜ao de pior

caso de 39/100 para quando a capacidade ´e ilimitada e 2/3 para capacidade limitada, al´em

de terem sido desenvolvidos, para esses dois casos, algoritmos

online

com raz˜ao de pior

caso igual a 1/4 e 1/5, respectivamente.

O mesmo problema que o abordado no trabalho anterior foi tratado por Lu et al

(2009). Um algoritmo de tempo polinomial baseado em PD foi proposto para quando

todas as tarefas possuem a mesma data de libera¸c˜ao. Um algoritmo tamb´em baseado em

PD, entretanto de tempo pseudo-polinomial, foi desenvolvido para quando o n´

umero de

valores distintos de datas de libera¸c˜ao ´e conhecido. Por fim, foi proposto um algoritmo

de aproxima¸c˜ao e um esquema de aproxima¸c˜ao de tempo polinomial para o caso geral do

referido problema.

He et al (2015) consideraram a possibilidade de rejei¸c˜ao de tarefas e, para quando

a capacidade da m´aquina ´e considerada ilimitada, foram inclu´ıdas datas de libera¸c˜ao.

Inicialmente, os autores abordaram o problema de minimiza¸c˜ao do

makespan

sujeito a

restri¸c˜ao de que o custo total de rejei¸c˜oes ´e limitado. Em seguida, estudaram o problema

de minimiza¸c˜ao do custo total de rejei¸c˜oes com a restri¸c˜ao de que o

makespan

deve respeitar

um determinado limite. Para o primeiro caso, foi proposto um algoritmo de aproxima¸c˜ao

para o caso com capacidade finita, como tamb´em para quando a capacidade ´e infinita.

J´a para ambos os casos, foram desenvolvidos algoritmos baseados em PD e esquemas de

aproxima¸c˜ao de tempo polinomial, tanto para quando a capacidade ´e limitada, como para

quando a capacidade ´e ilimitada.