PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PUC/SP
Ednaldo José Leandro
Saberes mobilizados por professores quando o
foco são as provas matemáticas: Um estudo de caso
DOUTORADO EM EDUCAÇÃO MATEMÁTICA
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PUC/SP
Ednaldo José Leandro
Saberes mobilizados por professores quando o
foco são as provas matemáticas: Um estudo de caso
Tese apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para obtenção do título de Doutor em Educação Matemática sob a orientação da Professora Doutora Ana Lúcia Manrique.
Banca Examinadora
________________________________________
________________________________________
________________________________________
________________________________________
Autorizo, exclusivamente para fins acadêmicos e científicos, a reprodução total ou parcial desta Tese por processos de fotocopiadoras ou eletrônicos.
A minha família,
de maneira especial a minha esposa Márcia,
minha mãe Edite, meus filhos Eduardo Augusto,
AGRADECIMENTOS
À CAPES, pelo apoio parcial com a bolsa flexibilizada.
À minha orientadora Professora Doutora Ana Lúcia Manrique por sua orientação e apoio em todo este trabalho.
Aos professores Doutores Adair Mendes Nacarato, Antonio Brolezzi, Celi Aparecida Espasandin Lopes e Saddo Ag
Almouloud, pela participação na banca e sugestões essenciais para o andamento desta pesquisa.
Aos professores do programa e colegas pela amizade e companheirismo.
À minha Família pela paciência e apoio durante esta trajetória.
RESUMO
Por meio de um levantamento realizado junto a cinco professores da rede municipal de ensino de São Paulo, realizou-se um estudo sobre saberes mobilizados por eles, quando o foco são as provas matemáticas no Ensino Fundamental. O texto retrata as motivações e os obstáculos encontrados pelos docentes ao desenvolverem em sala de aula assuntos relacionados às provas matemáticas, bem como suas funções e tipologias almejadas. Para o desenvolvimento da pesquisa, utilizou-se o estudo de caso e, como referencial teórico, os seguintes trabalhos: Tardif, sobre os saberes docentes; as tipologias e funções das provas matemáticas, de Balacheff e de Villiers, respectivamente. Foram utilizados os seguintes instrumentos para a coleta de dados: observação direta, anotações de campo, entrevistas, atividades e questionário. Os resultados obtidos apontam para a mobilização de alguns saberes, quais sejam: Curriculares, Experienciais e Disciplinares. Constatou-se ainda que os professores percebem a elaboração das provas matemáticas como um processo, considerando-as um importante elemento para fazer os alunos desenvolverem o hábito de apresentar justificativas para suas elaborações. Saber realizar uma prova foi apontado como uma habilidade relevante a ser adquirida não só para a matemática, como também para a vida do aprendiz após a escola, além de ser uma oportunidade para perceberem a estrutura, a beleza e as conexões das ideias matemáticas. As produções das provas matemáticas, elaboradas pelos discentes, são identificadas pelos professores como sendo predominantemente pragmáticas, nesse nível de ensino, e utilizadas com a função de explicar e, consequentemente, de convencer.
ABSTRACT
Through a study conducted with five teachers of municipal schools of São Paulo, a survey was carried out which knowledge is mobilized by them, when the focus is on mathematical proofs in elementary school. The text portrays the motivations and obstacles encountered by teachers in developing classroom issues related to mathematical proofs, as well as its functions and typologies aimed. For the development of the research, we used the case study and theoretical reference, the following works: Tardif, on teacher knowledge, the types and functions of mathematical proofs of Balacheff and de Villiers, respectively. The following instruments were used to collect data: direct observation, field notes, interviews, and survey activities. The results point to the mobilization of some knowledge, namely: Curriculum, Experiential and Disciplinary. It was also found that teachers perceive the development of mathematical proofs as a process, considering them an important element to make students develop the habit of presenting justifications for their elaborations. Knowing to do an exam was pointed as a skill to be acquired relevant not only for mathematics, but also for the life of apprentice after school, besides being an opportunity to realize the structure, beauty and connections of mathematical ideas. The productions of mathematical proofs, prepared by students, are identified by teachers as being predominantly pragmatic, at this level of education, and used to explain the function and hence to convince.
SUMÁRIO
APRESENTAÇÃO ... 1
CAPÍTULO I ... 3
CONSIDERAÇÕES INICIAIS ... 3
1.1 Impressões anteriores... 3
1.2 Professores e Provas Matemáticas ... 4
1.3 Proposta ... 9
1.4 Questão de pesquisa ... 10
CAPÍTULO II ... 13
ESTUDOS PRELIMINARES ... 13
2.1 Histórico ... 13
2.1.1 Matemática pragmática ... 13
2.1.2 Influência social grega ... 15
2.1.3 Geometrias não euclidianas ... 21
2.1.4 Reestruturação axiomática ... 25
2.2 Educação Matemática... 28
2.3 Provas Matemáticas ... 31
CAPÍTULO III ... 39
REFERENCIAL TEÓRICO... 39
3.1 Saberes ... 39
3.2 Provas matemáticas: Funções e tipologias ... 50
CAPÍTULO IV ... 57
METODOLOGIA DE PESQUISA ... 57
4.1 Objetivos da pesquisa ... 57
4.2 Pesquisa Qualitativa ... 58
4.3 Estudo de Caso ... 59
4.5 Escolha e caracterização da escola ... 69
4.6 Caracterização dos professores ... 71
CAPÍTULO V ... 73
DESCRIÇÃO DOS DADOS ... 73
5.1 Contato inicial ... 74
5.2 Descrição do questionário inicial ... 83
5.3 Encontros ... 87
5.3.1 Primeiro encontro ... 87
5.3.2 Segundo encontro ... 97
5.3.3 Terceiro encontro ... 103
5.3.4 Quarto encontro ... 112
5.3.5 Quinto encontro ... 118
5.4 Entrevista pessoal ... 125
5.5 Instrução ao Sósia ... 133
CAPÍTULO VI ... 143
ANÁLISE DOS DADOS ... 143
6.1 Saberes disciplinares ... 144
6.2 Saberes curriculares ... 148
6.3 Saberes experienciais ... 153
6.4 Saberes da Formação profissional ... 163
6.5 Finalizando ... 164
CONSIDERAÇÕES FINAIS ... 169
BIBLIOGRAFIA ... 173
APÊNDICES ... 179
LISTA DE QUADRO
Quadro 1 - Segunda questão dissertativa do concurso da SEESP 2007. .. 5
Quadro 2 – Os saberes dos professores ... 45
Quadro 3 – Métodos utilizados para coleta de dados utilizados ... 68
Quadro 4 – Atividades para exploração do ângulo inscrito na circunferência ... 135
Quadro 5 – Instrução do primeiro caso abordagem genérica ... 137
Quadro 6 – Instrução do segundo caso abordagem genérica ... 138
Quadro 7 – Instrução do terceiro caso abordagem genérica ... 138
Quadro 8 - Recorte da instrução ao sósia - primeiro caso. Abordagem utilizando valores concretos especulando a relação existente entre a medida do arco AC e o ângulo Bˆ. ... 159
LISTA DE FIGURAS
Figura 1 - Circunferência ... 18
Figura 2 - Comparação de segmentos múltiplos ... 18
Figura 3 – Comparação de segmentos não múltiplos ... 19
Figura 4: a)Modelo Esférico e b) Círculos máximos ... 23
Figura 5 - Prova realizada pelo Grupo 1 a atividade 5 ... 118
Figura 6 - Prova realizada pelo Grupo 2 a atividade 5 ... 119
1
APRESENTAÇÃO
Durante o mestrado, sentimos falta de uma pesquisa voltada aos saberes docentes dos professores de matemática quanto à argumentação e às provas matemáticas na Educação Básica, pela importância atribuída a eles, na condução do processo de ensino-aprendizagem dessas questões.
As pesquisas na época mostravam que os alunos não sentiam a necessidade de elaborarem provas matemáticas (Healy e Hoyles, 2000), enquanto outras (Pietropaolo, 2005) sinalizavam para a importância da inclusão das provas matemáticas nas aulas de Matemática desde o Ensino Fundamental.
Propomos, então, ao Programa de Pós-Graduação em Educação Matemática da PUCSP, um projeto de pesquisa para elaboração de um levantamento dos saberes mobilizados pelos professores, quando o foco são as provas matemáticas no Ensino Fundamental. No programa, escolhemos participar do grupo de pesquisa Professor de Matemática: formação, profissão, saberes e trabalho docente, quando surgiu a oportunidade de pôr em andamento esta pesquisa, em uma escola da rede municipal de ensino, da Cidade de São Paulo.
No primeiro capítulo apresentamos as justificativas e motivações que nos levaram a pesquisar o tema proposto, tendo nosso contato com os professores da Educação Básica durante o mestrado nos instigado a saber mais sobre os saberes mobilizados por esses docentes quanto à exploração das provas matemáticas no Ensino Fundamental.
No segundo capítulo, apresentamos episódios históricos que demonstram nosso ponto de vista, quanto à influência social na construção das provas matemáticas, o que foi importante para a ampliação da própria concepção que tínhamos desse tipo de prova e de seu papel na Educação Básica.
2
Balacheff (1987, 2000) quanto às tipologias de provas e De Villiers (1993) quanto às funções atribuídas às provas matemáticas. A discussão teórica nos revelaram pistas e permitiram reflexões sobre o caminho a perseguir para alcançar os objetivos propostos.
Reservamos o quarto capítulo para apresentar a metodologia adotada para a coleta e análise dos dados. Como buscamos compreender, explorar acontecimentos e contextos complexos, escolhemos o estudo de caso, indicado para essas situações. Esse procedimento possibilitou criar um planejamento para a coleta de dados.
No quinto capítulo, apresentamos uma descrição dos diversos momentos utilizados para a coleta de dados. Tais momentos ocorreram nos horários coletivos em uma escola da rede de ensino do município de São Paulo, contando com a participação de cinco professores licenciados em matemática, identificados como: Carlos, Fausto, Givaldo, Jorge e Marcelo.
No sexto capítulo, elaboramos uma análise dos dados, como base nas ações discursivas apresentadas, coletivamente ou individualmente pelos professores, conforme Tardif (2006), nos diversos momentos da coleta de dados.
3
CAPÍTULO I
CONSIDERAÇÕES INICIAIS
Neste capítulo apresentamos nosso objetivo de pesquisa e o caminho percorrido para a elaboração da questão de pesquisa que está centrado nos saberes mobilizados pelos professores de matemática quando o foco são as provas matemáticas no Ensino Fundamental.
1.1 Impressões anteriores
Durante o mestrado, participamos da primeira fase do projeto Argumentação e Provas na Matemática Escolar (AProvaME), iniciado em agosto de 2005 com duração de 24 meses, realizado pelo Programa de Estudos de Pós-Graduados em Educação Matemática da PUC-SP, com Coordenação da professora Doutora Siobhan Victoria Healy. Esse projeto realizou um mapeamento das concepções sobre argumentação e provas matemáticas1 de estudantes brasileiros da 8ª série do
ensino fundamental e 1ª série do ensino médio, com aproximadamente 2000 estudantes, na faixa etária entre 14 e 16 anos. Com esse fim, foram elaborados dois questionários: um de álgebra e outro de geometria, com base no trabalho de Healy e Hoyles (1998) na Inglaterra e já utilizado em outros países como França, Taiwan, Israel e Austrália.
Os questionários compreenderam questões que buscaram avaliar em que medida os estudantes aceitam evidências empíricas como prova; distinguem evidências empíricas de argumentos matematicamente válidos; compreendem o
1 U
tilizamos o termo “prova” com o significado de apresentar razões que possam ser aceitas dentro
de um sistema de validação comum aos interlocutores. O termo “demonstração” é utilizado como um
4
domínio de validade de uma prova e se são capazes de construir argumentos válidos. Os questionários foram estruturados e organizados em dois blocos, a saber:
- Avaliação de vários argumentos apresentados como provas de uma dada afirmação, e
- Construção de provas e argumentos.
Em nossa dissertação de mestrado (Leandro, 2006), elaboramos uma análise quantitativa e outra qualitativa dos dados obtidos em questões que abordam o fatorial, inserido no questionário de álgebra do referido projeto. Ainda, identificamos que nossos alunos não têm o hábito de apresentar provas, tampouco justificativas para as respostas elaboradas, resultado não muito diferente dos apontados pela literatura internacional (Healy e Hoyles, 2000). Embora exista uma literatura consistente apontando a importância da argumentação e provas matemáticas em sala de aula, sua abordagem parece não fazer parte do nosso cotidiano escolar.
Constatamos a falta de hábito dos alunos em apresentarem justificativas para suas respostas, sendo a simples solicitação de justificativa, motivo alegado por alguns, para terem deixado as questões em branco. (LEANDRO, 2006, p.88).
Apesar do foco principal da nossa dissertação, na época, não ter sido o conhecimento dos professores de matemática sobre o tema, não pudemos deixar de perceber a falta de uma literatura acadêmica brasileira tratando dos conhecimentos dos docentes, atuantes na Educação Básica, com relação ao tema. Por isso, em maio de 2006, resolvemos estender aos professores a aplicação dos questionários trabalhados anteriormente com os alunos. Para esse novo momento contamos com a participação de docentes de duas escolas, uma municipal e outra estadual, cujos discentes haviam participado da pesquisa inicial. Os dados obtidos mostraram grande dificuldade dos docentes em relação à argumentação e provas matemáticas, sendo o desempenho deles não muito diferente do apresentado pelos alunos.
1.2 Professores e Provas Matemáticas
5
tema da argumentação e provas matemáticas, percebemos não ter sido uma hábito abordar de forma sistemática esse tema em sala de aula.
Nas leituras realizadas, focadas nas provas matemáticas, encontramos a geometria como um campo fértil para a abordagem da argumentação e provas matemáticas na Educação Básica e na formação de professores devido a seu potencial de exploração, conjecturas, visualização, exploração e descoberta dos conceitos matemáticos nela oferecidos, sendo potencializado, quando aliado aos recursos tecnológicos existentes, como os softwares de geometria dinâmica devido ao seu poder de manipulação. Acreditávamos, assim, encontrar um professor desta disciplina com mais familiaridade com a argumentação e provas matemáticas nessa área especifica da matemática.
No entanto, deparamos com professores em sala de aula com várias queixas e dificuldades, por exemplo, em um encontro realizado em uma Delegacia de Ensino da Grande São Paulo, entre professores de matemática da rede pública estadual de ensino, muitos mostraram a falta de prática com problemas envolvendo demonstrações geométricas. Uma das indagações levantadas pelos professores no encontro foi à questão dissertativa abordada no concurso público para professor da rede Estadual de Ensino do Estado de São Paulo 2007, cujo enunciado apresentamos a seguir:
QUESTÃO 2
Um livro de matemática definiu paralelogramo como sendo um quadrilátero cujos lados opostos são paralelos. Um professor questiona seus alunos a darem outras possíveis definições de paralelogramo e obtém deles as seguintes respostas:
1. É um quadrilátero convexo cujos lados opostos são congruentes. 2. É um quadrilátero convexo cujos ângulos opostos são congruentes. 3. É um quadrilátero cujas diagonais se cortam no ponto médio.
4. É um quadrilátero que possui um par de lados opostos paralelos e congruentes.
5. É um quadrilátero que possui um par de lados opostos paralelos e um par de ângulos opostos congruentes.
6. É um quadrilátero que possui um par de lados opostos paralelos e o outro par de lados opostos congruentes.
a) Demonstre que as quatro primeiras respostas são equivalentes à definição dada no livro.
b) As afirmações (5) e (6) estão corretas? Justifique?
6
A maioria dos professores classificou a questão como muito difícil2, com a
qual não conseguiram elaborar uma resolução. E os presentes ao encontro alegaram não ter apresentado resposta à questão e queriam discuti-la, mesmo meses após a realização do concurso, pois ainda não tinham clareza das respostas esperadas.
Nas reflexões para futuros estudos, em nossas conclusões no mestrado (LEANDRO, 2006), indicamos que a realização de uma pesquisa voltada aos saberes dos professores de matemática quanto à argumentação e provas matemáticas poderia fornecer um quadro mais significativo, pois os dados que obtivemos dos professores não foram os desejáveis e sabemos que os alunos retratam seus professores, que retratam sua formação acadêmica que, por sua vez, refletem os sistemas de ensino.
Acreditamos que, o domínio e prática do professor de matemática, faça parte de qualquer solução apresentada para uma mudança na realidade que encontramos na Educação Básica, no que concerne a uma efetiva inserção das argumentações e provas matemáticas na prática docente em todos os níveis escolares, pois é o professor que vai explicitar a necessidade e os significados do tema com seus alunos e, ainda, conduzir todo o processo.
Para um avanço nas provas matemáticas na Educação Básica, o professor tem um papel primordial. No entanto, ele apresenta dificuldades na operacionalização do tema, como sinalizaram alguns professores dos encontros em que participamos durante nossa trajetória no mestrado.
Em levantamento realizado em 2008 no banco de teses da capes, periódicos e no jornal: International Newsletter on the Teaching and Learning of Mathematical Proof, cujo site é www.lettredelapreuve.it3, dedicado exclusivamente a publicações sobre provas matemáticas, poucas foram as pesquisas encontradas com o foco nos
2 Tanto que a Revista do Professor de Matemática. Número 64, 3° Quadrimestre, p.28-34,
abordou o tema a pedido de muitos leitores.
3 Editeurs: Maria-Alessandra Mariotti & Bettina Pedemonte English Editor : Virginia Warfield,
7
saberes e práticas docentes quanto as provas matemáticas. Além desses trabalhos, encontramos o projeto AProvaME, segunda fase, que também elaborou um trabalho com professores, os trabalhos de Pais e Freitas (1999) e Knuth (2002).
O projeto AProvaME investigou em sua segunda fase em que medida a participação dos professores nos grupos colaborativos contribuíram para apropriação de novas perspectivas sobre o ensino e aprendizagem de provas matemáticas em sala de aula, conforme Jahn, Healy e Pitta Coelho (2007). O trabalho coletivo mostrou contribuições, mas não para todos os professores, identificando-se ao final do processo professores ainda com dúvidas sobre a possibilidade ou viabilidade de um ensino efetivo das provas matemáticas no nível da Educação Básica, no contexto atual brasileiro.
Cabe ressaltar que esses professores, vinte e sete no total, eram todos mestrandos no Programa de Estudos de Pós-Graduação em Educação Matemática da PUCSP, tendo inclusive já participado e discutido muito sobre a literatura existente da argumentação e provas matemáticas na primeira fase do projeto, bem como domínio satisfatório dos recursos de informática utilizados para a elaboração dos cenários, tais como: Cabri e Excel, adquiridos em disciplinas do mestrado.
Pais e Freitas (1999), ao trabalharem com a geometria dedutiva tiveram como sujeitos professores de matemática das séries finais do ensino fundamental da rede pública do sul do país. Com isso puderam acessar o discurso dos próprios professores sobre o ensino da geometria dedutiva e explorar o significado atribuído por esses ao conhecimento geométrico e, ainda, os procedimentos de prova e argumentação.
8
[...] esta pesquisa revelou que a maioria dos professores pesquisados não tem uma visão da importância lógico-dedutiva e, consequentemente, retorna-se às questões essenciais que estruturam o atual processo de formação de professores. (p.69).
As recomendações do National Council of Teachers of Mathematics – NCTM (2000) indicam de forma mais enfática, o desenvolvimento na educação escolar do raciocínio e da construção de argumentações e provas matemáticas, aplicados nos mais diversos contextos, além de competências, tais como:
(a) reconhecer o raciocínio e a prova matemática como aspectos essenciais da matemática;
(b) formular e investigar conjecturas matemáticas;
(c) produzir e avaliar argumentos e provas matemáticas; e
(d) selecionar e usar vários tipos de raciocínio e provas (NCTM, 2000, p.80).
Knuth (2002) acompanhou as discussões do ensino das argumentações e provas matemáticas nas escolas americanas e após o tema ganhar maior espaço no currículo americano, principalmente depois do NCTM(2000), resolveu desenvolver uma investigação buscando responder uma questão primordial nessa nova realidade, que se impõem com as novas recomendações: Os professores estão preparados para por em prática as novas recomendações curriculares com relação às provas matemáticas? Teve por objeto de estudo as concepções de provas matemáticas de 18 professores da Educação Básica americana, concluiu que para esses docentes a primeira função atribuída às provas é a de verificação dos resultados, se aproximando das concepções obtidas por Pais e Freitas (1999). A segunda como estímulo a autonomia dos alunos, ou seja, para que esses desenvolvam a confiança necessária para validar as próprias afirmações, assim como a de seus pares.
9
O autor ainda indica a Educação Matemática como responsável em prover a ampliação das concepções das provas matemáticas dos futuros professores, possibilitando a eles um maior envolvimento em experiências e reflexões com argumentações e provas matemáticas, não podendo ter uma formação limitada do tema. O autor acredita que dificilmente os alunos alcancem as recomendações elaboradas pelo NCTM (2000) no cenário pesquisado.
Com o exposto, nos questionamos sobre a preparação dos professores de matemática para conduzir satisfatoriamente a argumentação e provas matemáticas em sala de aula, no nível desejável pelas pesquisas recentes e documentos oficiais, percebemos a necessidade de mais pesquisas com o foco nos professores quanto às provas matemática, para obtermos um quadro real dos conhecimentos e saberes mobilizados por eles sobre o tema.
1.3 Proposta
Propusemos, então, elaborar uma pesquisa para obter um levantamento dos saberes mobilizados por professores atuantes nas escolas da rede pública na Educação Básica, quando o ponto central são as provas matemáticas. Um levantamento realizado diretamente na escola, com professores em atividade, permitirá traçar um quadro mais significativo da situação dos saberes mobilizados por esses professores, uma vez que as pesquisas envolvendo as provas matemáticas encontradas em nossa revisão bibliográfica contemplaram apenas os futuros professores, em fase de formação inicial, ou com professores de matemática em sua fase de busca de conhecimento, motivados, participando de cursos de pós-graduação ou de aperfeiçoamento espontaneamente, mesmo fora do horário de serviço e em ambientes muitas vezes controlados, e esse número ainda ser pouco expressivo quando comparado ao total de professores de matemática na rede de ensino.
10
objetivo possibilitar a reflexão sobre a prática docente, favorecer o intercâmbio de experiências e promover o aperfeiçoamento individual e coletivo dos educadores quanto à prática docente, lugar e momento mais do que adequados para o desenvolvimento da nossa pesquisa. Nacarato (2005) aponta a escola e o trabalho coletivo/colaborativo como instância do desenvolvimento dos professores, exatamente, por proporcionar condição permanente de formação, troca de experiências e busca de soluções para temas que emergem no contexto escolar.
Nesses espaços acompanhamos e investigamos os saberes mobilizados pelos professores quando as provas matemáticas são o tema da discussão, pois acreditamos que para uma cultura de provas matemáticas ocupar um lugar na realidade escolar, deverá primeiramente ser prática e domínio dos professores.
1.4 Questão de pesquisa
Nossa pesquisa teve como objetivo elaborar um levantamento dos saberes mobilizados por professores de matemática do Ensino Fundamental quando o foco são as provas matemáticas. Além das funções e tipologias de provas exploradas pelos professores.
Objetivo geral:
– Levantar os saberes mobilizados por professores de matemática do Ensino Fundamental quando o foco são as provas matemáticas.
Este estudo se desenvolveu em uma única escola pertencente à rede municipal de ensino de São Paulo e foram realizados encontros com professores de matemática dessa escola nos espaços e horários de trabalhos coletivos nela existentes, com a intenção de colocar em discussão o tema de pesquisa, buscando coletar dados para análise.
Objetivos específicos:
11
– Acompanhar e analisar as discussões entre os professores visando os saberes por eles mobilizados quando o foco são as provas matemáticas no Ensino Fundamental.
– Identificar as motivações ou obstáculos para o trabalho das provas matemática em sala de aula.
13
CAPÍTULO II
ESTUDOS PRELIMINARES
Neste capítulo abordamos algumas leituras e reflexões realizadas no caminho elaborado para a nossa pesquisa. Assim, apresentamos episódios históricos das provas matemáticas, pois conceitos matemáticos foram diretamente influenciados pelas culturas e cenários desenhados durante seu percurso de desenvolvimento e as provas matemáticas não seguiram um caminho diferente.
Abordamos ainda fatos da constituição da Educação Matemática e uma visão dos estudos das provas matemáticas realizada nessa área.
2.1 Histórico
Não buscamos aqui traçar uma gênese histórica da demonstração matemática, já realizada por Arsac (1987). Buscamos apresentar três momentos com episódios que mostram a tendência cultural no status e rigor das provas matemáticas ao longo da história. São eles:
1) A matemática pragmática, em que as provas eram obtidas pela verificação direta dos resultados.
2) A matemática axiomática, formulada no período grego.
3) A descoberta das geometrias não euclidianas, que desencadeou uma nova reestruturação das provas.
2.1.1 Matemática pragmática
14
Grécia no séc. V a.C., no entanto, a matemática tem suas origens em tempos que nem historiadores se arriscam a dar um palpite.
Noções primitivas relacionadas com os conceitos de número, grandeza e forma podem ser encontradas nos primeiros tempos da raça humana, e vislumbre de noções matemáticas se encontra em formas de vida que podem datar de milhões de anos antes da humanidade. (Boyer, 1974, p.1).
Nas civilizações babilônica e egípcia encontramos trabalhos matemáticos que chegaram até nosso tempo, devido aos materiais utilizados para registro por esses povos, como argila, pedras e papiros, que resistiram à ação do tempo, ainda tendo grande influência nos conhecimentos matemáticos desses povos os aspectos geográficos. A egípcia era isolada, enquanto a babilônica tinha um maior contato com outros povos favorecendo o intercâmbio de informações, tanto que na civilização babilônica encontramos um nível de conhecimento matemático maior que na egípcia.
De outros povos também importantes na antiguidade, como a chinesa e indiana não dispomos de materiais devido à fragilidade temporal dos materiais utilizados por esses para registros, como: casca de árvores e bambu.
Da matemática egípcia da antiguidade destaca-se o Papiro de Rhind, também conhecido como Papiro de Ahmes, por ter sido copiado pelo escriba Ahmes em 1650 a.C.. Nele encontramos 87 problemas matemáticos.
Os problemas egípcios descritos até agora são de tipo digamos, aritmético, mas há outros que merecem a designação de algébricos. Não se referem a objetos concretos, específicos, como pães e cerveja, nem exigem operações entre números conhecidos. Em vez disso, pedem o que equivale a soluções de equações lineares, da forma x + ax = b ou x + ax + bx = c, onde a, b e c são conhecidos e x é desconhecido (BOYER, 1974, p. 12).
Os egípcios provavam seus cálculos empiricamente, sendo para eles o suficiente a verificação dos resultados para que uma prova matemática pudesse ser aceita.
15
na resolução de problemas práticos, sendo a certeza dos cálculos, a prova, realizada pela verificação dos resultados. Visão diferente da grega como verificaremos a seguir.
2.1.2 Influência social grega
Boyer (1974, p.35) e Eves (1995, p.25) apontam Tales de Mileto (c. 600 a.C.) como o primeiro matemático preocupado com a demonstração. Para Tales, “a questão primordial não é o que sabemos, mas como sabemos” (Boyer, 1974, p.33). É atribuída a Tales a demonstração do diâmetro da circunferência, divisão do círculo em partes iguais; todo o ângulo inscrito numa semicircunferência é um ângulo reto e, ainda, que dois ângulos opostos pelo vértice são iguais.
A preocupação de como podemos ter certeza se um raciocínio é correto ou não, levou muitos outros matemáticos a trabalharem no tema na antiguidade, como: Parmênides (c. 450 a.C.), cuja teoria gerou muita polêmica, principalmente os paradoxos do seu discípulo Zenão de Eléia (c. 450-a. C.).
Em um mundo onde o que conhecemos é sabido graças primeiramente aos sentidos, deveríamos a ele utilizar como meio de verificar se um raciocínio é válido ou não, devendo ainda desconfiar dos objetos que não são possíveis alcançar por meio desses. No entanto, Platão (427-347 a.C. aprox.) nos ensina que as coisas que observamos com nossos sentidos não são verdadeiras. Na realidade, para esse filósofo, o que vemos são apenas imagens distorcidas da verdade, pelas imperfeições dos nossos sentidos, sendo as únicas verdades aquelas concebidas pela razão. Para ele, o mundo sensível é imperfeito, logo, as ideias matemáticas não podem ser concebidas nesse mundo.
Platão refuta, assim, o empirismo, nascendo o realismo platônico em que os objetos matemáticos são abstratos, possuindo uma existência própria fora do tempo e do espaço da experiência sensível ou mental. A nós caberíamos apenas descobri-los. Platão influenciou toda a matemática discutindo seus fundamentos, esclarecendo algumas definições e reorganizando hipóteses.
16
construiu uma sofisticada teoria dos argumentos, cujo núcleo é a caracterização e análise do chamado silogismo. Além disso, foi autor de vários livros (Categorias, Analíticos I, Analíticos II, o Peri Hermeneias (interpretação), Tópicos e Refutação de argumentos sofistas), que seriam editados por Andrônico de Rodes no século I d.C. e que receberam posteriormente o nome de Organon (Fonseca Filho, 2007).
Um exemplo clássico de raciocínio baseado em premissas e conclusões da Lógica Aristotélica, conhecido como silogismos, é:
Premissa 1: Todo homem é mortal Premissa 2: Sócrates é homem Conclusão: Logo Sócrates é mortal.
É atribuída a Aristóteles a criação da Lógica Matemática, sendo dado por ele um grande passo para orientar o pensamento.
Os matemáticos procuraram abordar a Matemática pelo raciocínio dedutivo e assim lhe conferir um fundamento sólido, alcançando sua estrutura axiomática conhecida atualmente, no qual a influência da intuição e ambiguidades ficassem de fora, já que poderiam produzir paradoxos na teoria. Mesmo causando problemas, polêmicas e mal-estar à comunidade matemática ao longo dos séculos, a intuição se mostrou importante como desafio à mente humana na busca de soluções para os problemas apresentados, sendo responsável direta por grandes avanços, ao desenvolver, ampliar e criar novas áreas em toda a matemática e nas ciências em geral.
17
Aquiles aposta corrida com uma tartaruga que sai com vantagem e é argumentado que Aquiles por mais depressa que corra, não pode alcançar a tartaruga, por mais devagar que ela caminhe. Pois, quando Aquiles chegar à posição inicial da tartaruga, ela já terá avançado um pouco; e quando Aquiles cobrir essa distância, a tartaruga terá avançado um pouco mais. E o processo continua indefinidamente, com o resultado que Aquiles nunca pode alcançar a lenta tartaruga.
Mas, sabemos que em um determinado instante o corredor Aquiles alcança e ultrapassa a tartaruga. O apelo ao infinitamente pequeno, subdivisão infinita do espaço ou tempo, sempre foi polêmico e por esse motivo os matemáticos preferiam não recorrer a essas noções, evitando embaraços como os apresentados por Zenão.
Nossa intuição pode nos levar a contradições, principalmente com recorrência ao infinitamente pequeno ou grande, o que ocasiona uma aceitação de resultados que parecem corretos, mas que produzem alguma contradição. É importante salientar que dissemos que a intuição pode nos levar a contradições, mas isso não necessariamente ocorre, como podemos verificar no exemplo a seguir:
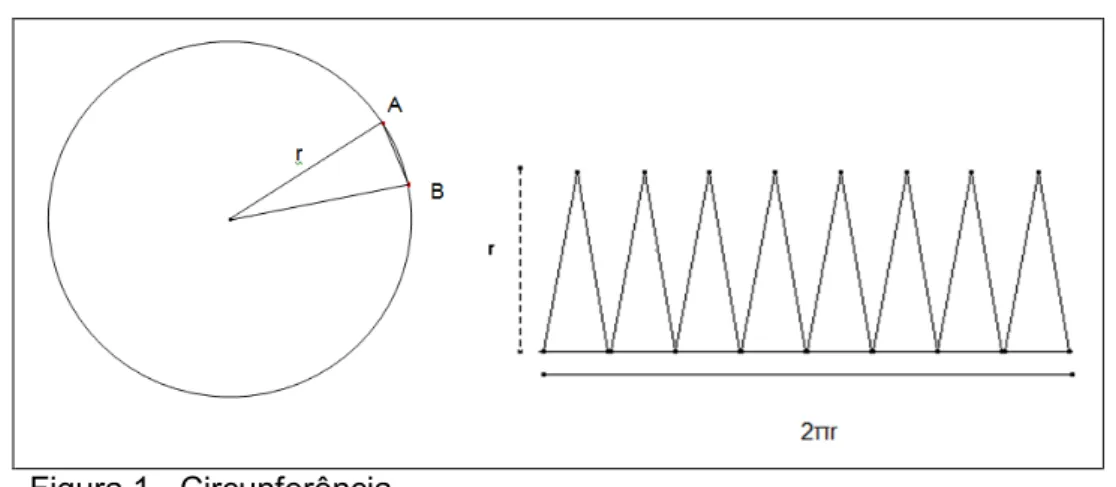
Na Educação Básica é utilizada uma abordagem para deduzir a fórmula da medida da área de uma circunferência de raio r. Ideia explorada nos materiais utilizados pela rede estadual (SÃO PAULO, 2008a, p.27).
18
Figura 1 - Circunferência
Contudo, o problema da comparação de dois segmentos utilizados pelos gregos ilustra como nossa intuição pode nos enganar. Nos tempos de Pitágoras de Samos (586-500 a.C. aprox.), pensava-se que os números racionais fossem suficientes para comparar segmentos de reta. Isto se mostrou incorreto, abalando muito a filosofia pitagórica.
Os Gregos utilizaram o seguinte método:
Para comparar os segmentos e. , Figura 2, percebemos que isso é possível e nos basta usar a medida como a unidade, pois o segmento é
um múltiplo do segmento , ou que o segmento pode ser subdividido em 3 segmentos, de comprimento igual ao de .
Figura 2 - Comparação de segmentos múltiplos
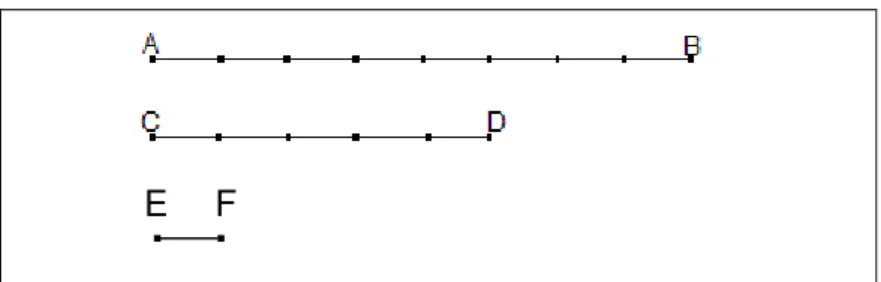
Quando a subdivisão dos segmentos não é possível em um primeiro momento, ou seja, um não é múltiplo do outro, tentamos obter um segmento menor (submúltiplo) que sirva de unidade para ambos. Vejamos os segmentos e , Figura 3.
AB CD
CD AB
CD AB
CD
19
Figura 3 – Comparação de segmentos não múltiplos
Como o segmento CD não pode ser a unidade, pois AB não é múltiplo de CD, obtemos outro segmento menor como unidade.
O segmento será a nova unidade, e caberá cinco vezes em e 8 em
.
Refletindo, podemos chegar, precipitadamente, à conclusão que sempre é possível obter uma unidade menor que possa servir de unidade comum a dois segmentos quaisquer. Dessa forma, os dois segmentos seriam sempre comensuráveis. Entretanto, nem sempre isso é possível e os próprios Pitagóricos, seguidores da filosofia de Pitágoras, descobriram que no caso da comparação de dois segmentos (lado de um quadrado e sua diagonal) não é possível encontrar um “tal segmento” que sirva de unidade para ambos os segmentos, por menor que se imagine este terceiro – mesmo que nossa intuição diga que é possível e por menor que possamos imaginá-lo: pequeno, muito pequeno, pequeníssimo, não é. Dizemos, então, serem segmentos incomensuráveis, surgindo daí o conceito de número irracional.
A descoberta da incomensurabilidade é, apontada por Arsac (1987), como responsável direta pela origem do surgimento das provas matemática, concepção internalista.
Como exemplo, vamos construir a prova matemática clássica da
irracionalidade do número . A medida da diagonal de um quadrado com lado medido uma unidade, não é um número racional, a qual se poderá acompanhar sem muitos problemas, já que sua abordagem é bem conhecida e, até mesmo, sugerida no ensino fundamental. A seguir demonstraremos que não é um número racional por meio da demonstração por absurdo dada por Aristóteles (384-322 a. c.).
EF
EF CD
AB
2
20
Demonstração clássica da irracionalidade da 2, explorado nos cadernos utilizado pela rede estadual de ensino da (SÃO PAULO, 2008b, p. 15).
A não pode ser representada por um número racional, ou seja, não pode ser um número escrito na forma , com p e q Z, inteiros, com q≠0. No entanto, vamos supor, por absurdo, que: x= é racional, logo existem dois números inteiros p e q Z, primos entre si, tais que (isto é, suponhamos a
fração escrita na forma irredutível. Então, x² =2. Logo, , e p² é um número par, pois p² = 2q². E consequentemente p também é par (porque se fosse ímpar seria do tipo p=2k+1, para algum número inteiro k e então seria ímpar). Se p é um número par, existe um inteiro k’ tal que p=2k’ e assim 2 2 2 2
' 2 2
'
4k q q k . Então, q seria par (porque q² é par, pelo mesmo raciocínio anterior para p² ), o que é absurdo visto que p e q são primos entre si. Em outras palavras: Como supomos que era um número racional irredutível e chegamos à conclusão que tanto p como q são pares, logo são divisíveis, no mínimo por 2, concluímos que tal número não existe, estando à hipótese inicial errada, então não é um número racional.
A civilização grega, situada como o berço da demonstração matemática e influenciada por sua cultura, foi a que mais contribuiu para a matemática do ponto de vista racional. Ao transpor o empirismo e alcançar o dedutivo, colaborou para a sistematização e estruturação dos conhecimentos matemáticos acumulados, estabelecendo assim a verdade e a certeza, pela primeira vez na história da matemática, à luz de noções abstratas, em detrimento ao apoio intuitivo.
O maior exemplo disso foi dado por Euclides (c. 300 a.C.), em sua obra “Os Elementos”. Euclides alcançou o auge da organização sequencial grega dos conhecimentos matemáticos, conseguindo obter outros conceitos matemáticos mediante regras estabelecidas, partido de termos básicos denominados axiomas. O
2 q p 2 q p x q p 2 2 q p
2 1
2 4 2 4 1 4
2
12
21
poder do método dedutivo da matemática formaliza sistematicamente o saber geométrico conhecido, iniciando aqui um modelo de rigor matemático que teve um longo período de duração.
Euclides, talvez, criou sua obra como um livro texto, mas, mesmo que não o tenha sido, foi assim utilizado, tendo grande influência para a Matemática e, também, para a Educação Matemática. O seu inovador método axiomático ou dedutivo consistia em admitir como verdadeiras certas proposições (mais ou menos evidentes - axiomas ou postulados). A partir delas, por meio de um encadeamento lógico, chegar às proposições mais gerais (chamadas teoremas). Euclides pedia para que o leitor aceitasse os cinco postulados a seguir:
1. Uma linha reta pode ser traçada de um ponto para outro qualquer. 2. Qualquer segmento finito de reta pode ser prolongado indefinidamente para constituir uma reta.
3. Dados um ponto qualquer e uma distância qualquer pode-se traçar um círculo de centro naquele ponto e raio igual à dada distância.
4. Todos os ângulos retos são iguais entre si.
5. Por um ponto não contido em uma reta dada pode ser traçada uma e apenas uma reta paralela à reta dada.
Cada teorema que surgia em seu sistema lógico era consequência direta dos postulados ou dos teoremas já deduzidos a partir desses.
O quinto postulado é conhecido como o postulado das paralelas e provocou a discussão de novas geometrias, que abordaremos em seguida.
2.1.3 Geometrias não euclidianas
Esses postulados utilizados por Euclides foram considerados durante séculos como fruto de uma intuição clara e distinta. Hoje, sabe-se que os seus postulados eram insuficientes e suas definições imprecisas, porém toda obra de Euclides serviu de inspiração e avanços em toda a Matemática.
22
geometria, pois acreditavam que este postulado fosse independente dos outros quatro não obtendo sucesso.
As tentativas de prová-lo terminaram somente no século XIX, quando o matemático alemão Karl Friedrich Gauss (1777-1855) convenceu-se da não demonstrabilidade desse postulado e a possibilidade da construção de sistemas geométricos não euclidianos. Assim, nascem as Geometrias Não-Euclidianas, com esforços simultâneos de Gauss, Janos Bolyai (1802-1860), Nikolai Ivanovitch Lobatchewski (1792-1856) e Bernhard Riemann (1826-1866), que com trabalhos independentes constroem novas geometrias (as Geometrias Não-Euclidianas), na quais o postulado das paralelas não vale mais, confirmando-se, assim, que o Postulado das Paralelas era realmente independente dos demais.
Apresentamos dois modelos de Geometrias Não Euclidianas:
Geometria de Lobatchevsky ou Geometria Hiperbólica – esse modelo é creditado independentemente a Nicolai Lobachevski e János Bólyai. Nela é possível criar o plano hiperbólico, que é interpretado no espaço tridimensional euclidiano por uma superfície denominada parabolóide hiperbólico, estabelecendo que por um ponto exterior a uma reta podemos traçar uma infinidade de paralelas a esta reta.
Geometria Riemanniana ou Geometria Elíptica ou Esférica – creditada a Bernhard Riemann, o plano elíptico é interpretado no espaço quadridimencional por uma superfície semelhante à esfera estabelecendo que por um ponto exterior a uma reta não podemos traçar nenhuma paralela a esta reta.
23
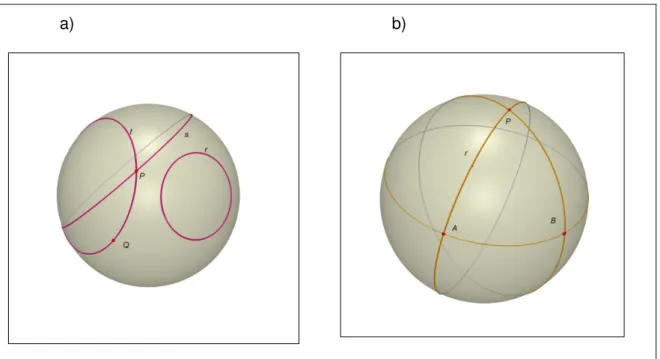
a) b)
Figura 4: a)Modelo Esférico e b) Círculos máximos
Podemos, ainda, especulando o modelo, Figura 4(b), considerarmos como retas apenas os círculos máximos. Percebemos, assim, que não será possível traçar por nenhum ponto fora da reta r, uma reta paralela a esta. Percebemos também que a soma dos ângulos internos de um triângulo será maior que 180°(a prova de que a soma dos ângulos de um triângulo é igual a 180° é consequência direta da unicidade das paralelas), observe o triângulo APB no plano no nosso plano esférico.
Uma das preocupações constantes dos matemáticos é a de construir um modelo axiomático para a matemática, deixando-a livre de qualquer contradição, pois, se o conhecimento matemático fosse construído sobre alicerces que gerassem contradições, poder-se-ia ruir todo o edifício matemático construído sobre eles. Dessa forma, se inicia uma nova corrida social para reestruturar as ideias quanto ao rigor matemático.
Após o período da verdade inquestionável, inaugura-se na matemática um período de busca a certeza matemática, um novo rigor. Correntes tinham como objetivo reformular as ideias de demonstração e um novo sentido para esse termo.
24
e Karl Weierstrass (1815 -1897), que passaram da geometria à aritmética como fundamento para a matemática. Esse movimento ficou conhecido como aritmetização e é nele que começa a se formar um novo modelo de rigor matemático.
No final do próprio século XIX os estudos da Lógica Matemática deram passos gigantescos para formalizar os fundamentos da matemática. Entre os matemáticos e filósofos que mais contribuíram para os avanços destacaram-se: Gottlob Frege (1848-1925), cujas obras principais datam de 1879 e 1893, contribuiu com a criação do cálculo de predicados dando forma ao conceito de demonstração formal, sendo utilizado como base na matemática os conceitos aritméticos e não mais as noções geométricas gregas.
Giuseppe Peano (1858-1932), um dos pioneiros na lógica matemática e na axiomatização da matemática, responsável pela axiomatização da aritmética em 1899. Axiomas de Peano:
1) Zero é um número;
2) O sucessor de um número é um número; 3) Zero não é sucessor de nenhum outro número; 4) Não existem dois números com o mesmo sucessor e 5) Indução matemática.
Bertrand Russel (1872-1970) e Alfred Whitehead (1861-1970) na obra “Principia Mathematica” procuraram desenvolver o projeto do logicismo, isto é, a redução da matemática à lógica. David Hilbert (1862–1943) com seu enfoque formalista, além de Sofás Lie (1842-1899); Felix Klein (1849-1925); Henry Poincaré (1854-1912); Dery Lebesgue (1875-1941) e L.E.J. Brouwer (1881-1961).
25
...como o barbeiro da cidade que barbeia todos aqueles, e somente aqueles, que não barbeiam a si mesmo. O barbeiro está ou não incluído no conjunto daqueles que barbeiam a si mesmo? (BOYER, 1974, p. 449).
Se o barbeiro não se barbeia, ele está no conjunto das pessoas que não barbeiam a si mesmo; logo ele poderia fazer a própria barba. No entanto, no momento em que começa a fazê-la quebra a regra, pois estará barbeando a alguém que faz a própria barba.
2.1.4 Reestruturação axiomática
Em meio a essas controvérsias do sistema lógico, Hanna (1995, p.42) descreve que três escolas famosas surgiram, ou seja, grupos sociais com suas particularidades para dar conta das novas teorias matemáticas que aparecem ao final do século XIX, onde a visão platonista não mais se sustentava, mantendo cada uma desses grupos visões diferentes sobre o papel da demonstração em matemática e ainda sobre os critérios de sua validade.
Essas escolas buscaram leis lógicas que forneciam ou que pudessem fornecer um mecanismo de crenças absolutamente confiáveis, filosofia absolutista4. Tais mecanismos teriam a função de validar os novos resultados para serem incorporados ao conjunto daqueles já aceitos como válidos, influenciando a concepção da matemática é sua evolução. São elas:
LOGICISMO: com origens em Aristóteles e as contribuições dos logicistas: Bertrand Russell, Gottlob Frege e Alfred Whitehead, defenderam que a Matemática era um ramo da Lógica, sendo as leis da aritmética reduzidas às leis lógicas. Ao utilizar as regras de inferências lógicas, pretendiam reduzir todos os conceitos matemáticos a conceitos lógicos e demonstrar todas as verdades matemáticas a partir dos axiomas. Desse modo se distanciaram das concepções empíricas e intuitivas.
4 O conhecimento matemático consiste de verdades seguras e incontestáveis.
26
INTUICIONISMO: nascida por volta de 1908, o topólogo holandês L.E.J. Brouwer negava o infinito atual e defendia que a Matemática teria de ser desenvolvida apenas por métodos construtivos finitos sobre a sequência dos números naturais, dada intuitivamente, ou seja, que existe uma intuição primitiva dos números naturais.
FORMALISMO: Na tentativa de provar a consistência da matemática pretendiam organizá-la numa estrututra lógica e axiomática, restrigindo-a à manipulação de simbolos, sem sentido e significado. Seu defensor mais radical foi David Hilbert (1862–1943) que em 1900 provou a consistência interna da geometria elementar. Hilbert criou a obra Fundamentos da Geometria (1899) para uma nova axiomatização para a geometria euclidiana e propôs, ainda , construir um formalismo matemático do qual seria extinto qualquer tipo de significado. Na demonstração, teríamos sua consistência de forma absoluta e para toda e qualquer proposição da matemática haveria uma maneira formal de se declará-la falsa ou verdadeira.
O objetivo de minha teoria é estabelecer de uma vez por todas a certeza dos métodos matemáticos... O estado atual das coisas, em que nos chocamos com os paradoxos, é intolerável. Imaginem as definições e os métodos dedutivos que todos aprendem, ensinam e usam em matemática, os paradigmas de verdade e de certeza, conduzindo a absurdos! Se o pensamento matemático é defeituoso,
onde acharemos verdade e certeza?
(DAVID HILBERT apud DAVIS & HERSH, 1996, p. 315-316).
O grupo de matemáticos franceses Nicolas Bourbaki é um bom exemplo da influência do formalismo. Esse grupo teve grande influência no ensino da matemática nos níveis mais elementares no advento do Movimento da Matemática Moderna (1960).
Essas novas correntes filosóficas trouxeram novas maneiras de enxergar a natureza da matemática e, consequentemente, a sua relação com a verdade e com a certeza dentro da comunidade que vai avaliar. No entanto, não ficaram imunes às controvérsias e argumentos paradoxais. Por exemplo, o paradoxo de Russell atacou a definição de número de Frege, causando abalos no programa logicista.
27
Gödel (1906-1978) em 1931, ficou demonstrado a incompletude de todo sistema axiomático expressivo o suficiente para conter a teoria dos números. Provou-se que não há e nem poderia haver um sistema formal, no qual se pudesse expressar toda a aritmética, como sonhava Hilbert, e que satisfizesse todas as exigências de consistência do programa formalista, ficando mais distante o sonho do rigor absoluto (COURANT & ROBBINS, 2000, p. 106-107).
Mesmo com os problemas, certezas e incertezas no que foi exposto, até o momento, houve uma evolução da Matemática surpreendente. Desde os tempos de Tales de Mileto aos dias atuais, a Matemática e seus processos de validação conseguiram um extraordinário avanço. Podemos dizer que, atualmente, o rigor matemático profissional é estruturado, possuindo uma linguagem universal e confiável, embora ainda existam polêmicas, como as entre formalistas, logicistas e intuicionistas, ou da validação ou não de demonstrações utilizando computadores, como na conjectura das quatro cores, que foi verificada com a utilização desses por W. Haken e K. Appel, em 1976.
A matemática está em uma constante evolução e “todas as pedras encontradas”, como o todo não ser maior que uma parte (teoria dos conjuntos), colaboraram para o fortalecimento de suas estruturas dando-lhe uma precisão, não encontrada em nenhuma outra área do conhecimento humano, mesmo sabendo das limitações de qualquer uma das visões matemáticas adotadas.
A complexidade associada à demonstração matemática formal atual cria dificuldades imensas às demais pessoas. Quando perguntado a Hilbert se os 23 problemas, por ele anunciados, no 2° Congresso Internacional de Matemáticos realizado em Paris em 1900, estavam todos solucionados, teria ele respondido:
Uma teoria matemática não pode ser considerada completa enquanto não for possível torná-la tão clara a ponto de poder ser explicada ao primeiro homem que se encontre na rua. (YANDELL, 2002).
28
e compreensão dentro de uma coerência e validação escolar, percebidas como culturalmente determinada e não apenas um acúmulo de conhecimento.
Pelo exposto, podemos observar que a prova matemática pode apresentar significados distintos, em função da época e cultura, mesmo em um cenário social específico. Além disso, a depender da noção de prova adotada por uma comunidade em dado instante, podem ocorrer pontos de controvérsias a respeito da validade dos processos utilizados. O consenso é obtido após influencias, debates e negociações, que conduzem à construção de um modelo aceito por essa comunidade, podendo inclusive, como relatam Harel e Sowder (2007):
[...] Variar de indivíduo para indivíduo, de contexto para contexto, de civilização para civilização e, dentro da mesma civilização, de geração para geração, pois utilizam dois processos: persuadir e convencer que são processos subjetivos. (p.808).
Com o exposto queremos compartilhar com o leitor a nossa visão das provas como uma verdadeira prática social, passando por revisões e reestruturações.
2.2 Educação Matemática
Durante o desenvolvimento desta pesquisa tivemos que nos posicionar em muitos campos e temas, não apenas para nós mesmos, como também para os que nos rodeavam. Dessa forma, nossas leituras convergiram ao histórico e temas de estudos da Educação Matemática.
Educação Matemática, o que estuda? Quais as suas preocupações? Todos concordam que a Educação Matemática tem como objetivo final a melhoria do ensino e da aprendizagem da matemática em todos os níveis.
«Educação matemática» deve ser interpretada como significando todo o campo das ideias e atividades humanas que afeta, ou poderia afetar, a aprendizagem da matemática5. (Barwell, 2011, p.
contracapa, tradução nossa).
5 «Mathematics education» should be interpreted to mean the whole field of human ideas and
29
As preocupações com a compreensão, transmissão, natureza e construção do conhecimento matemático vem de tempos antigos. No diálogo de Mênon de Platão, encontramos conceitos matemáticos utilizados para o ensino (Platão, 1962). No entanto, como comenta D‟ambrósio (2004, p.13):
[...] somente a partir das três grandes revoluções da modernidade –
a Revolução Industrial (1767), a Revolução Americana (1776) e a
Revolução Francesa (1789) – que as preocupações com a educação
matemática da juventude começam a tomar corpo.
A consolidação da Educação Matemática ocorre apenas em 1908 durante a realização, em Roma, do Quarto Congresso Internacional de Matemáticos, com a criação da Comissão Internacional de Educação Matemática (International Commission on the Teaching of Mathematics, posteriormente conhecida como International Commission on Mathematical Instruction - ICMI).
Pouco material foi produzido pela Educação Matemática durante seus primeiros anos, exceto algumas compilações de dados, mas conseguiu formular suas próprias questões de pesquisa e abordagens teóricas encontrando sua identidade. As disciplinas que mais tiveram influência sobre as investigações em Educação Matemática realizadas desde a sua origem foram a Matemática e suas reformas e a Psicologia, com seus estudos voltados aos processos mentais ocorridos durante a atividade matemática.
Ao longo da sua história a Educação Matemática desenvolveu um campo próprio de investigação com um grande número de pesquisas realizadas de modo intencional e sistemático com um corpo teórico sustentado, desenvolvido por um corpo de profissionais dedicados a área, sendo reconhecida pelas contribuições ao ensino e aprendizagem da matemática resultante das pesquisas desenvolvidas, não só pela sociedade, como também por toda comunidade científica.
30
A investigação em Educação Matemática para Ernest (1994, p. 72-73) objetiva a melhoria do ensino e da aprendizagem da matemática com práticas investigativas envolvendo:
- O ensino e a aprendizagem da matemática em todos os seus níveis (Educação Básica e Universitária), dentro ou fora da escola;
- Os materiais utilizados para o ensino e aprendizagem em matemática em todos os níveis;
- A formação dos professores em seus diversos níveis;
- A investigação em todos os níveis.
Tendo em vista serem reflexivas as investigações na Educação Matemática, Ernest (1997, p.75) distinguiu dois tipos de objetivos nas investigações. Os objetivos primários são aqueles fenômenos diretamente relacionados com o ensino e aprendizagem da matemática e, por isso, recebem uma maior atenção principal das pesquisas realizadas:
- A natureza da matemática e do conhecimento matemático escolar. - A aprendizagem da matemática.
- As metas e objetivos do ensino da matemática e da escolarização. - O ensino da matemática, incluindo os métodos e abordagens utilizados.
- O conjunto de textos, materiais, ajudas e recursos eletrônicos utilizados.
- Os contextos sociais e humanos do ensino e aprendizagem da matemática em toda a sua complexidade.
- As interações e relações entre todos os itens anteriores. (tradução nossa).
E os objetivos secundários, cujo estudo é a própria Educação Matemática, são também importantes, não podendo ser negligenciados. Segundo o autor:
- A natureza do conhecimento em educação matemática: conceitos, teorias, resultados, literatura, propósito e função.
31
- As instituições sociais de educação matemática: pessoas, lugares, instituições (universidades, escolas, centros de pesquisa), conferências, organizações, redes, revistas, e outros, e suas relações com os contextos sociais. (p.75, tradução nossa).
A seguir focaremos nas pesquisas realizadas quanto ao ensino e aprendizagem das provas matemáticas. Encontramos na Educação Matemática vários trabalhos desenvolvidos apontando caminhos e também muito a ser feito e esclarecido.
2.3Provas Matemáticas
Ao longo do desenvolvimento da Educação Matemática diversas pesquisas associadas às provas matemáticas têm sido realizadas. Tanto que Reid e Knipping (2010) ao perceber o grande número de trabalho sobre o tema resolveram elaborar um livro com uma síntese da literatura existente.
No Brasil, temos como referência o grupo Processo de Ensino e Aprendizagem em Matemática – PEAMAT, pertencente ao Programa de Pós-Graduação em Educação Matemática da PUCSP, coordenado pelo Prof. Dr. Saddo Ag Almouloud, orientador de dezenas de dissertações e teses sobre as provas matemáticas.
Essas pesquisas têm explorado os mais diversos aspectos das provas, inclusive o seu ensino-aprendizagem na Educação Básica, mesmo que essas estejam longe da definição formal de prova matemática, ou seja, prova formal de uma proposição é uma cadeia de deduções lógicas que levam à proposição de um conjunto base de axiomas.
Para os matemáticos a prova formal é a única maneira de termos certeza da validez de uma conjectura, sendo, portanto, utilizada como um método de verificação, descobrimento e comunicação, devido a sua precisão, por não permitir ambiguidades. No entanto, está disponível apenas para aqueles familiarizados com sua linguagem e gramática.
32
dos métodos demonstrativos utilizados e reconhecidos por sua comunidade. Para isso, buscam ler e entender as provas formais elaboradas e identificam as técnicas utilizadas como: Método direto, redução ao absurdo-indireto, construtivos, contraexemplo, com o objetivo de que, no final do processo de formação, possam com a experiência adquirida, engenhosidade, intuição e criatividade desenvolverem e comunicarem suas próprias provas.
Mesmo assim, encontramos trabalhos que apontam dificuldades com relação ao tema também nesse nível, em grande parte atribuída à complexidade das provas matemáticas utilizadas no contexto profissional matemático. Constatamos, desse modo, não ser a abordagem realizada no nível superior a mais apropriada para o ensino e aprendizagem das provas matemáticas na Educação Básica.
Na formação de professores muito se tem pesquisado para possibilitar uma abordagem mais significativa das provas matemáticas, convergindo para um aspecto mais crítico em vez de técnico. Garnica (1995) ao buscar o significado atribuído à prova rigorosa nas Licenciaturas em Matemática, se concentrou na formação de professores e encontrou duas categorias quanto à importância da prova formal na formação do docente, geradas por duas leituras distintas: A técnica fundada na prática cientifica da matemática, e o estabelecimento da crítica como ponto de vista a ser defendido pela Educação Matemática.
33
[...] a prova deve fazer parte da formação dos alunos da Educação Básica, desde que o significado a ela atribuído seja ampliado e que se caracterize por um processo de busca, de questionamento, de conjecturas, de contra-exemplos, de refutação, de aplicação e de comunicação e não com o sentido formalista que a caracterizou nos currículos praticados em outros períodos. (Pietropaolo, 2005, p. 212).
Essas pesquisas apontam um caminho de formação inicial dos professores de matemática quanto às provas matemáticas, tendo com foco a preparação dos futuros professores para enfrentarem os desafios em sala de aula, possibilitando uma abordagem mais próxima das indicadas na literatura atual e documentos oficiais.
[...] resolver situações-problema, sabendo validar estratégias e resultados, desenvolvendo formas de raciocínio e processos, como intuição, indução, dedução, analogia, estimativa, e utilizando conceitos e procedimentos matemáticos, bem como instrumentos tecnológicos disponíveis; (PCN, 1998, p. 48, grifo nosso).
Para a matemática escolar na Educação Básica encontramos vários objetivos presentes nos parâmetros, orientações, materiais, artigos, entre outros. Os Parâmetros Curriculares Nacionais para o Ensino Fundamental (PCN) indicam desafios como a seleção de conteúdos para alcançar os objetivos traçados, como sua relevância social e desafio intelectual para o aluno, precisando o professor estar preparado. O texto ressalta ainda que:
Embora nos Parâmetros a Lógica não se constitua como um assunto a ser tratado explicitamente, alguns de seus princípios podem e devem ser integrados aos conteúdos, desde os ciclos iniciais, uma vez que ela é inerente à Matemática. No contexto da construção do conhecimento matemático é ela que permite a compreensão dos processos; é ela que possibilita o desenvolvimento da capacidade de argumentar e de fazer conjecturas e generalizações, bem como o da capacidade de justificar por meio de uma demonstração formal. (PCN, 1998, p. 49).
34
[...] um conjunto de processos mentais complexos através dos quais se obtêm novas proposições (conhecimento novo) a partir de proposições conhecidas ou assumidas (conhecimento prévio). É frequente considerar-se que a obtenção dessas novas proposições se faz através do raciocínio dedutivo, esquematizável na forma «Se A então B» (simbolicamente, A ⇒ B). A uma sequência de deduções, do tipo A ⇒ B ⇒ . . . ⇒ Z, chama-se demonstração. A demonstração é, por isso, central ao raciocínio tipicamente matemático.
As provas matemáticas são defendidas como uma importante atividade matemática escolar, devendo ser uma preocupação em todos os níveis de ensino, como um meio essencial na compreensão matemática e importante característica dos métodos científicos. Para isso é primordial ser valorizada e reconhecida tanto pelos educadores matemáticos em sala de aula, como pelas pessoas encarregadas de traçar as políticas educacionais, para que o tema venha a ser abordado na Educação Básica e os alunos se apropriem do tema.
Estudos realizados defendem as provas matemáticas em todos os níveis, começando com uma rica prática de argumentação e justificativas em defesa de suas conjecturas e afirmações no ambiente escolar, obtidas durante um processo de investigação. Torna-se importante explorar, ainda, as funções e níveis das provas elaboradas nas diversas etapas da escolarização para uma convergência para tipos de provas mais bem elaboradas.
Demonstrar e argumentar, como processos, têm muitos aspectos comuns, tanto do ponto de vista epistemológico como cognitivo, apesar de existirem diferenças significativas entre demonstração e argumentação como produtos socialmente situados. (DOUEK, 1998 apud LOUREIRO, 2002, p.112 ).
Na Educação Matemática a argumentação é compreendida como apresentação de razões, argumentos para uma proposição matemática, e utiliza uma forma em que prevalece o raciocínio de caráter explicativo/justificativo, com o intuito de convencer um auditório a aceitar ou recusar essa preposição, mesmo considerando outros elementos na argumentação o que predomina é o uso da linguagem natural.
35
prevalência de estudos que veem a demonstração incluída na argumentação e é com ela que concordamos. Por exemplo, Boero (1999) defende uma continuidade entre a argumentação e a demonstração matemática, sendo esta vista como produtiva e inevitável, mesmo com toda a sua complexidade, quando observada de maneira ampla nos processos de ensino e aprendizagem.
Outros autores, Balacheff (1999) e Duval (1993), centralizando a comunicação e estruturas internas dos raciocínios envolvidos, defendem a existência de uma ruptura entre a argumentação e a demonstração, sendo a demonstração vista mais por sua ligação à lógica formal, de forma impessoal e isolada de qualquer contexto, divergindo, desse modo, da argumentação que é situada e usa a linguagem natural, dependente da opinião, adesão e da persuasão.
As pesquisas encontradas em Educação Matemática com foco no ensino e aprendizagem das provas matemáticas são abordadas em várias frentes de pesquisas:
- Didática, estudos focados no papel das provas no currículo de matemática e os estudos que buscam possíveis abordagens para o trabalho com elas em contextos de ensino e aprendizagem, por exemplo, o trabalho de Hanna (2001).
Hanna (2001) defende, entre outras funções presentes nas provas matemáticas, a utilização das explicativas como sendo as mais adequadas e pertinentes ao contexto escolar. Indicando a geometria como a área da matemática com maior potencialidade de exploração de atividades com essa função.
- Epistemológica, estudos focados no status dos objetos matemáticos, suas propriedade e relações que são colocados em jogo nos processos de provas matemáticas, por exemplo, o trabalho de Balacheff (1987) que estabelece níveis de provas elaboradas, estabelecendo ainda um marco teórico para avaliar e avançar nos tipos de provas elaboradas pelos alunos.