Cependant, dans le cas d'une propagation dans un conduit en régime transitoire et en présence d'un courant porteur uniforme, plusieurs études ont montré que cette méthode. Cette deuxième partie de la thèse traite de la résolution numérique par une méthode des éléments finis de l'équation de Galbrun en régime harmonique et dans un domaine borné.

Descriptions du mouvement d’un fluide
Repr´ esentation de Lagrange
Dans ce chapitre, l'équation de propagation dite de Galbrun est établie sur la base du système d'équations de la mécanique des fluides. La représentation mixte Lagrange-Euler des perturbations et l'introduction de la variable lagrangienne de déplacement conduisent enfin.
Repr´ esentation d’Euler
Equations de conservation pour un fluide parfait en ´ ´ evolution adiabatique
Dans ce cas, on obtient l'équation de conservation de la quantité de mouvement des fluides parfaits. L'application de la première loi de la thermodynamique (cf. [69], section IV.3.1.) conduit à l'équation de conservation de l'énergie suivante pour tout sous-domaine Ω(t) de D(t) .
Equation d’´ ´ etat
Cette dernière relation permet d'établir l'équation d'équilibre de l'entropie à partir de l'équation (1.8). Un écoulement fluide parfait en évolution adiabatique est donc isentropique, ce qui signifie que l'entropie reste constante le long du trajet des particules.
Syst` eme des ´ equations de la m´ ecanique des fluides parfaits en ´ evolution adiabatique
Changement de variables Euler-Lagrange
Syst` eme des ´ equations de la m´ ecanique des fluides parfaits en ´ evolution adiabatique
Perturbations des ´ equations de conservation en repr´ esentation mixte
Perturbations des ´ equations en variables de Lagrange
Par conséquent, à partir de l'égalité (1.35), le développement du premier ordre suivant pour le déplacement lagrangien suit. Un développement de Taylor du premier ordre en ε autour de l'état non perturbé donne : p(a, t)e − pe0(a, t) = ε.

Passage en repr´ esentation mixte
La perturbation lagrangienne de l'entropie reste donc constante le long des trajectoires des particules fluides. La linéarisation du premier ordre et la représentation mixte de l'égalité (1.38) conduisent à la relation suivante pour la perturbation de vitesse lagrangienne du premier ordre.
Retour en repr´ esentation d’Euler
Equation dite de Galbrun
Enfin, la relation (1.63) à partir des égalités et (1.60) permet d'exprimer les perturbations eulériennes de densité, de vitesse et de pression en fonction de la perturbation du déplacement lagrangien4, celle-ci joue alors le rôle d'un potentiel vecteur de champ de perturbation : . 1.68) Il apparaît que lorsque les grandeurs caractéristiques du courant porteur sont constantes dans l'espace, les perturbations lagrangiennes et eulériennes du premier ordre sont identifiées.
Remarques sur le mod` ele
Notes bibliographiques
En formulant l'hypothèse d'un écoulement de fluide isentropique parfait, Hayes [85] utilise une représentation mixte et un décalage lagrangien pour déterminer la densité lagrangienne associée aux perturbations du problème linéarisé (Section 8, Eq. (57)), ce qui donne une équation très proche de l'équation de Galbrun (Eq. (58 )). Dans ce chapitre, la résolution numérique de l'équation de Galbrun en écoulement stationnaire subsonique et en régime harmonique est étudiée.
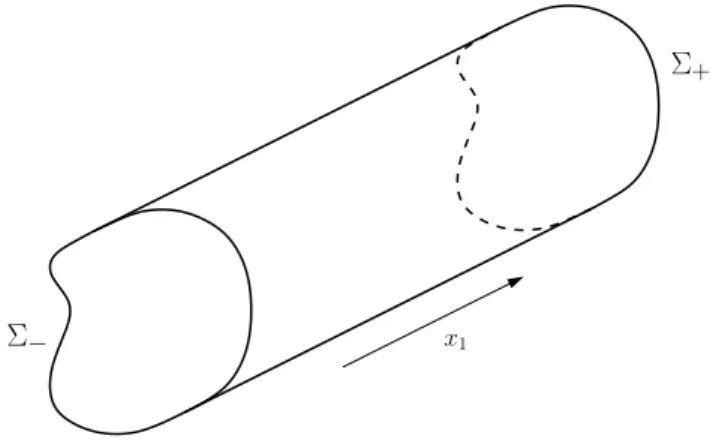
Un cas mod` ele : le probl` eme sans ´ ecoulement
Analogie avec l’´ electromagn´ etisme
Néanmoins, la discrétisation de ce problème d'électromagnétisme par éléments finis dans le nœud est possible, mais il est nécessaire de le "régulariser" au préalable. Une méthode d'éléments finis nodaux conformes dans l'espace H1(Ω) converge alors vers la solution du problème régularisé si celui-ci est bien énoncé.
La m´ ethode de r´ egularisation
Notons cependant que cette approche du problème n'est plus valable lorsque le domaine Ω a des singularités géométriques, telles que des sommets ou des arêtes rentrants [50]. Dans ce cas, la solution du problème régularisé converge vers une solution qui n'est pas à divergence nulle et n'est donc pas le problème physique d'origine7.
R´ egularisation en ´ ecoulement uniforme
Une ´ equation pour le rotationnel du d´ eplacement
Formulation variationnelle du probl` eme r´ egularis´ e
Théorème 2.2 Si s ≥1, le problème (2.26) admet une solution unique, sauf peut-être pour un ensemble discret de valeurs k=k(M, s) (fini sur tout compact C). La dépendance de l'opérateur compact à k étant polynomiale et donc analytique, le problème peut aisément être placé dans le cadre du théorème de Steinberg (Théorème B.37).
Equivalence
Enfin, si seule la régularisation du problème est envisagée pour sa solution, c'est que l'approche par éléments finis mixtes ne semble pas envisageable. D'une part, les différents éléments finis déjà introduits par Raviart et Thomas [137] ou N'ed'elec ne permettent pas de discrétiser les opérateurs associés aux termes de convection de l'équation, il faut donc développer d'éventuels éléments ad hoc.
Convergence et estimations d’erreur
Lemme 2.4 Si les formes sesquilinéaires ah(·,·) forment une famille stable, alors les problèmes approchés (2.31) sont bien posés. Pour les problèmes abordés dans cette thèse, la forme sesquilinéaire qui interfère avec la formulation variationnelle définit un opérateur qui n'est qu'à un pas de la perturbation compacte de l'opérateur coercitif.
Discr´ etisation du probl` eme par ´ el´ ements finis
Après avoir construit la matrice et le deuxième membre du système linéaire en ajoutant les matrices et les vecteurs élémentaires calculés dans chacun des éléments du triangle, on peut procéder à une pseudo-élimination des conditions aux limites. Il est également possible d'éliminer les lignes et les colonnes de la matrice dont les indices correspondent à ces degrés de liberté.
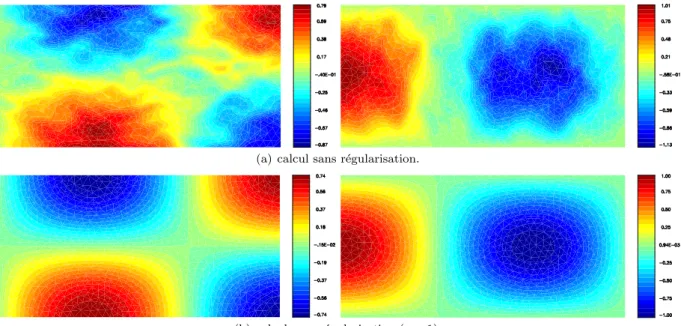
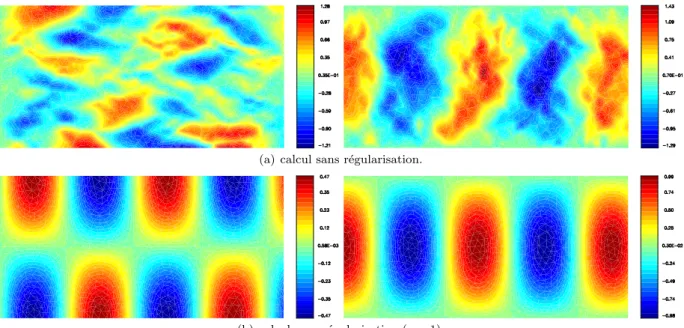
R´ esultats num´ eriques
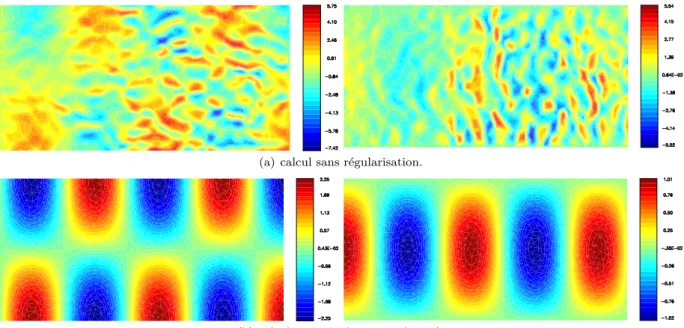
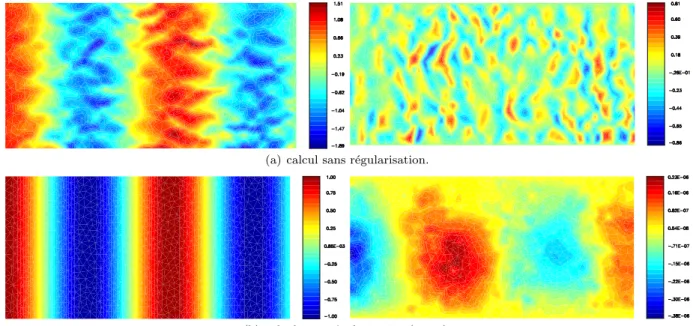
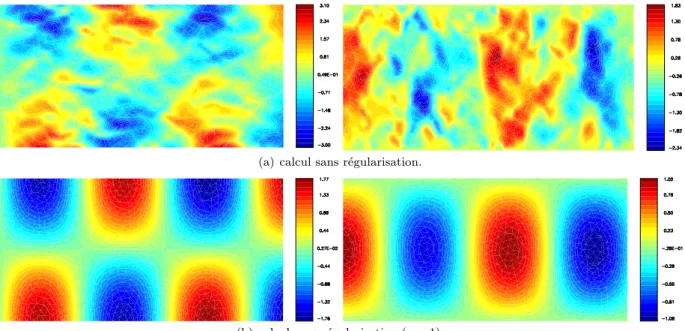
2.4 – Isovaleurs des composantes de la partie réelle de l'eldu de déplacement pour la propagation d'un mode aval d'indice n= 1, k= 7,7 et M = 0 (composante gauche u1, composante droite u2) . 2.7 – Isovaleurs des composantes de la partie réelle du champ de déplacementu pour la propagation d'un mode hydrodynamique, k= 2 et M = 0,3 (à gauche composante u1, à droite composante u2).
Quelques remarques
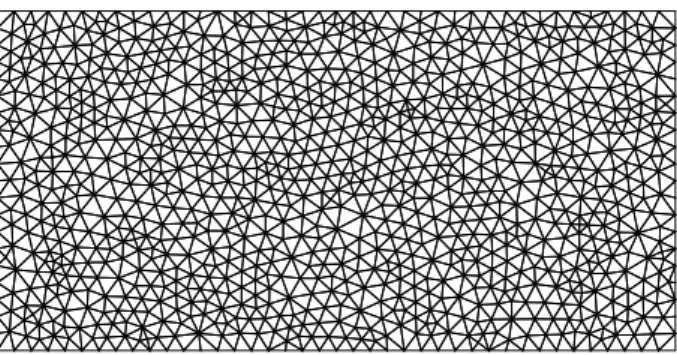
Effets du maillage
Dans [29] Boffie et al étudient le problème régularisé dans des domaines non convexes au moyen d'éléments finis nodaux. Il est donc possible de discrétiser le problème régularisé par la méthode des éléments finis même si le domaine n'est pas convexe.

G´ en´ eralit´ es
Nous étudions d'abord un écoulement uniforme par morceaux, qui présente donc une (ou plusieurs) discontinuité(s) et constitue peut-être l'exemple le plus simple d'écoulement de cisaillement. On traite alors le cas d'un écoulement cisaillé d'un fluide parfaitement compressible dont le profil de vitesse ne présente aucune discontinuité.
Ecoulement cisaill´ ´ e discontinu
- Description du probl` eme
- Quelques observations pr´ eliminaires
- Le probl` eme r´ egularis´ e
- Position math´ ematique du probl` eme
- Application
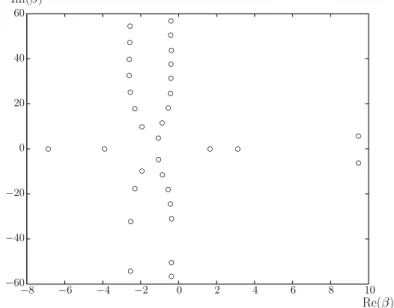
La suite de la démonstration est alors relativement différente selon que la vitesse du courant porteur est nulle d'un côté ou de l'autre de l'interface Γ ou non. Pour conclure cette description, notons que ces deux modes sont limités à la proximité de l'interface.
Ecoulement cisaill´ ´ e “r´ egulier”
- Equation diff´ ´ erentielle pour le rotationnel du d´ eplacement
- R´ esolution de l’´ equation diff´ erentielle
- Etude du probl` ´ eme r´ egularis´ e
- Quelques r´ eflexions
In particular, PMLs have been used for the time-domain solution of the linearized Euler equations that model acoustic propagation in the presence of a current. A modal analysis shows that these layers "match perfectly". In addition, they are absorbing, except for classical PMLs in the presence of so-called opposite upstream modes.
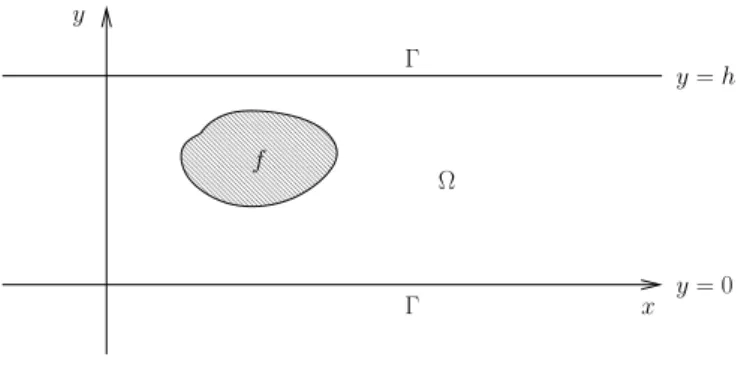
The physical and the mathematical models
The problem in the infinite duct
This change of variable corresponds to the similarity applied to the axial wavenumbers of the modes. But in the presence of current, the transformation sends the inverse upstream modes into the "bad" part of the complex plane, leading to the instabilities observed in the time domain.
Reduction to a bounded domain
The number of propagating modes is an increasing function of the Mach number M, which is assumed to be positive. The fact that f is compactly supported in Ωbs clearly shows that the problems (4.10) and are equivalent in the sense of the following proposition.
Well posedness
After establishing exact boundary conditions that are satisfied byp, we can now define a problem in the bounded domain Ωb: findp∈H1(Ωb) such that. In what follows, we assume that the problem is well-posed, which means that (4.15) is satisfied.
The PML model
Modal analysis of B´ erenger’s model in a waveguide
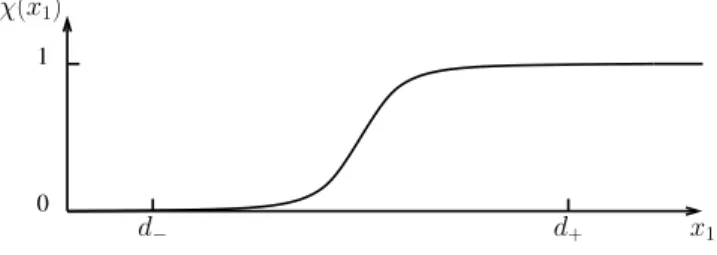
For modal analysis in waveguides, we now assume that α(x) is a constant in Ω\Ωb, which we still denote by α for simplicity. For any α, the interface between the PML and the physical domain is completely transparent, and we will see that if α is well chosen, the transmitted waves decay exponentially in the layer.
The new PML formulation for the convected Helmholtz equation
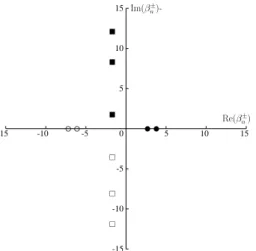
This leads us to conclude that the PML model does not produce unstable (i.e., growing exponentially in the layer) modes if all axial wavenumbers βn,α for the propagating downstream (resp., upstream) modes are strictly in the upper (resp., lower ) half of the complex plane. Other choices for λ would require further constraints on α to ensure that the βn's associated with volatile modes also remain on the "right side" of the complex plane (see Fig. 4.6).
PML truncation. Error estimates
Truncation of the absorbing layer and well posedness
Reduction to a problem posed in Ω b
The key idea for reformulating the problem as a problem posed in Ωb is to write an exact boundary condition satisfied by the solution on the boundaries Σ±. Using the Dirichlet boundary condition on the external layer boundary ΣL+, the solution can be written as.
Convergence and error estimates
Note that the estimate (4.49) also proves that convergence holds when the layer length Lis fixed and |α| tends to 0. More precisely, for a given value of the argument θ of the coefficient α, the accuracy deteriorates as it approaches a cutoff wavenumber (see Figure 4.8).
Varying coefficients
Numerical results
The no inverse upstream mode case
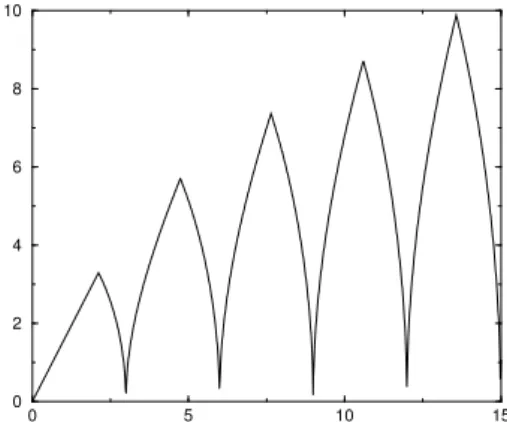
To this end, the inverse of the logarithm of the relative error in H1(Ωb) norm is plotted as a function of the inverse of|α|for both PML models. The exponential convergence of the method, which can be deduced from the slope of curves in Figure 4.13, agrees satisfactorily with the estimate given by theory for both PML models, since the two curves coincide for this case.
The inverse upstream mode case
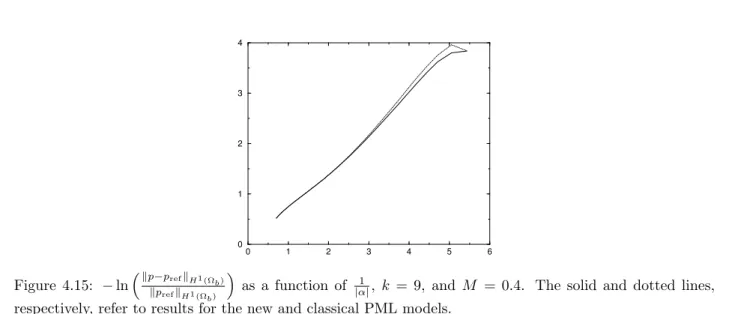
As can be seen by zooming into Figure 4.14, the relative error curves again have a minimum plateau for both PML models. To conclude, Figures 4.16 and 4.17 respectively show the solutions for the new and classic models, the value |α| for this case it corresponds to the smallest curve in Figure 4.14.
Some practical remarks on the use of PMLs for time-harmonic problems
This time the size of the plateau is smaller for the classical PML and the error for this model has a rather erratic behavior for small values of |α|. A good choice of the parameters of the absorbent layer makes it possible to choose the outgoing solution to the problem.
Conclusion
On considère le problème de la propagation en écoulement uniforme, de vitesse subsonique v0, dans un conduit infini à parois rigides. Pour le problème bidimensionnel que nous voulons traiter, les conditions de régularité sont suffisantes.
Le cas dissipatif
- Principe d’absorption limite
- Etude du probl` ´ eme dissipatif
- Convergence vers un probl` eme limite
- Extension du principe ` a d’autres ´ ecoulements
Nous pouvons maintenant énoncer le résultat de convergence pour le problème (5.8). Théorème 5.8 La solution ϕh du problème (5.9) converge vers la fonction ϕh dans H2(Ωb) lorsqu'elle tend vers 0.
![Fig. 5.1 – R´ eponse lin´ earis´ ee ϕ(x, t) dans l’espace libre ` a un ´ etat initial localis´ e en espace ϕ(x, 0) pour diff´ erents types d’´ ecoulement (d’apr` es Huerre et Rossi [96]).](https://thumb-eu.123doks.com/thumbv2/1bibliocom/460892.67618/113.892.308.603.408.971/eponse-espace-initial-localis-espace-erents-ecoulement-huerre.webp)
Probl` eme avec couches absorbantes parfaitement adapt´ ees
Position du probl` eme
Le module de cette fonction décroît exponentiellement avec la distance dans la coque, d'après les hypothèses (5.17) en α. Cependant, le module de cette fonction diminue de façon exponentielle avec la distance à la couche absorbante.
Etude du probl` ´ eme variationnel
Théorème 5.13 Si le nombre complexe α vérifie les conditions (5.17) dans les couches d'absorption, le problème variationnel (5.21) appartient à l'alternative de Fredholm. Alors il existe une constante strictement positive L1, de sorte que le problème (5.21) admet une unique solution si L≥L1.
Convergence et estimations d’erreurs
En utilisant la forme ψ∞, on peut déterminer explicitement la fonction ζ, solution du problème :. et que nous recherchons également sous une certaine forme. Nous devons maintenant évaluer la différence L−uL pour prouver la convergence de la méthode.
R´ esultats num´ eriques
Propagation de modes dans un conduit
Fig.5.3 – Erreur relative sur la norme H1(Ωb)2 en fonction de |α| pour la propagation des modes acoustiques vers l'aval, k= 8 et M = 0,4. Nous avons reproduit les simulations précédentes pour une couche de longueur égale à 25% de la taille du domaine Ωb.
Rayonnement d’une source acoustique
Un moyen simple de traiter un cas "général" de manière assez satisfaisante consiste à envisager d'utiliser des couches beaucoup plus grandes que d'habitude.
Rayonnement d’une source tourbillonaire
L'application du même modèle à l'équation de Galbrun ajustée a prouvé que la prise en compte d'un terme source. On reconnaît dans la première ligne le membre gauche de l'équation de Galbrun (A.13).

Espaces de Hilbert
D´ efinitions
Cette annexe présente quelques définitions et résultats classiques d'analyse de fonctions, ainsi que des notions de théorie spectrale des opérateurs dans les espaces de Hilbert, qui peuvent ou non être utilisées dans nos études et sont nécessaires à leur bonne compréhension. Pour les preuves et plus de détails nous renvoyons le lecteur intéressé à Br´ezis [37] et Dautray et Lions [55, 56] pour les définitions et les résultats généraux Eraux, Kato [99], Schechter [141] ou encore Edmunds et Evans [60 ] pour la théorie spectrale en particulier.
Dual topologique d’un espace de Hilbert
Théorème B.6 (Théorème de représentation de Riesz-Fr´echet) Soit E0 le dual topologique d'un espace de Hilbert E et d'un élément de E0.
Formulations faibles
G´ en´ eralit´ es sur les espaces de Sobolev
Si la limite ∂Ω est régulière, on a aussi que l'injection de Hm+1(Ω) dans Hm(Ω) est compacte. L'inégalité précédente est valable dès que l'ouvert est borné dans une direction de l'espace.
Lemme de Lax-Milgram
Théorème B.16 (Théorème de compacité de Rellich) Si Ω est un ouvert fini de Rn, alors l'injection de H0m+1(Ω) dans H0m(Ω) est compacte, pour tout m∈ NOT. On appelle traces d'ordre j (j∈N) de u sur le bord ∂Ω l'application linéaire γj définie par :. γm−1u) défini sur D(Ω) et à valeurs dans D(∂Ω)m se prolonge avec la densité en une application linéaire continue surjective de Hm(Ω) sur Qm−1.
Th´ eorie des op´ erateurs
- Op´ erateurs born´ es
- Op´ erateurs compacts
- Op´ erateurs auto-adjoints
- Th´ eor` eme de Steinberg
Cette géométrie étant séparable, l'étude des modes guidés consiste à rechercher, pour une pulsation ω1 donnée, des solutions non nulles de l'équation de Galbrun homogène de la forme. La vitesse de groupe ∂ω∂β est identifiée à la vitesse de transport d'énergie dans le tuyau à parois rigides.

Modes en ´ ecoulement uniforme par morceaux
Solution de l’´ equation homog` ene
1 Le terme source de l'équation (D.1) est donc qualifié car issu de la partie rotation, c'est-à-dire g= rotf, de la source de perturbationf dans l'équation de Galbrun.
Fonctions de Green
Solution g´ en´ erale de l’´ equation diff´ erentielle
R´ esolution en domaine born´ e
R´ esolution en domaine non born´ e
Il est donc possible de déterminer analytiquement ψ= rotξ, la solution de l'équation différentielle (11), à partir de ses données (supposées régulières) en Γ0 et ΓL. En conclusion, pour le problème considéré (flux uniforme et champ rectangulaire) nous avons obtenu une formulation mathématique de l'équation de Galbrun qui se prête à une discrétisation par éléments finis nodaux.