On the approximate analytical solution of a problem of optimization in the field of immobilized enzymes

On the approximate analytical solution of a problem of

optimization in the field of immobilized enzymes

by F. XAVIER MALCATA

Escola Superior de Biotecnologia, Universidade Catolica Portuguesa, Rua Dr Antonio Bernardino de Almeida, 4200 Porto, Portugal

(Received 3 January 1989)

The problem of optimizing the thickness of a microporous slab containing an immobilized enzyme is addressed, using an economic criterion as the objective function. The steady-state material balance to the substrate as transported by diffusion and depleted by a biochemical reaction following classical Michaëlis-Menten kinetics within the pellet is obtained. Taking advantage of a number of algebraic manipulations and mathematical artefacts, one is able to solve the resulting second-order, non-linear differential equation by an analytical method, provided that an upper error bound for the solution in the order of 5 per cent is acceptable. The validity of the approximation is tested, and useful applications are reported.

1. Introduction

Enzymes are proteins with enhanced catalytic properties due to their power of specific activation [1]. As proteins, enzymes consist of a linear chain of amino acid residues bonded via peptide linkages. As catalysts, enzymes affect the rate of biochemical reactions without themselves appearing as either reactants or products of the global reaction, and without being consumed within reasonable time scales. Being highly specific, enzymes act only upon some bonds of some substrates, thus accelerating chemical reactions without formation of by-products. Furthermore, enzymes are able to function in dilute aqueous solutions under very mild conditions of temperature, pH and ionic strength [2]. These characteristics have emphasized the industrial use of enzymes to bring about a number of relevant chemical reactions within the food, pharmaceutical, and cleaning fields.

Immobilization of an enzyme on or within an insoluble solid matrix means that the enzyme has been confined or localized so that it can be re-used continuously [3]. There are several reasons why immobilization may be desirable: no enzyme is allowed to leave the reactor in the outlet solution (which avoids the need of extra enzyme makeup, or of enzyme removal from the product where it might play the role of an impurity); longer retention of catalytic activity is possible (so the enzyme becomes intrinsically more stable and less sensitive to thermal denaturation); and the control of the chemical process becomes more feasible and accurate (thus eliminating unwanted variability and making it easier to meet the required product specifi-cations). These characteristics make immobilized enzyme technology attractive if a very large throughput is required and/or the enzymes involved are expensive. Three notable examples of industrial processes that employ immobilized enzyme catalysts are the production of high fructose corn syrups from corn starch, the manufacture of L-amino acids by resolution of racemic amino acid mixtures, and the manufacture of semi-synthetic penicillins [3].

0020-739X/91 $3.00 © 1991 Taylor & Francis Ltd.

178 F. X. Malcata

Many methods are available for enzyme immobilization. Enzymes are typically immobilized on the internal surfaces of porous supports, or entrapped in matrices through which a substrate can diffuse. In such systems, calculation of the observed rate of substrate disappearance requires evaluation of the concentration profile of substrate within the pellet [3]. Fick's law of diffusion can in principle be applied [4], provided that the effective diffusivity is known. This parameter accounts for the fact that some of the particle cross-section is occupied by solid and hence not available for diffusive transport, and the pore network is complex and entangled so diffusion occurs only in allowed, frequently changing directions [5]. On the other hand, the kinetic equation describing the biochemical reaction occurring within the pellet must be taken into account; this is usually done via the utilization of the classical Michaelis-Menten model [6], where the order of the reaction on the substrate concentration increases gradually from zero (for high substrate concentrations) up to unity (for low substrate concentrations).

A number of shapes for the pellets where the enzymes can be immobilized are commercially available, the slab-shaped type being particularly easy to manufacture and model. The development of a design methodology for optimal slab thickness in heterogeneous, catalytic biochemical reactors is, then, undoubtedly both of academic interest and commercial significance.

2. Problem formulation

Consider a control volume accounted for by a porous solid supporting an immobilized enzyme, whose pores are completely filled with a liquid solution containing the reacting substrate. A chemical reaction following Michaelis-Menten kinetics takes place within this porous pellet, with a 1:1 stoichiometry [7]. This stoichiometry, coupled to the assumption that the solvent is virtually stagnant, leads to a null molar average velocity, which is characteristic of an equimolar counter diffusional process. The solute becomes available to the active sites inside the pellet via a molar diffusion flux arising from a concentration gradient across the particle. The physical medium is assumed to behave isotropically with respect to the global mass density and to the resistance offered to the molecular transport of solute within the pellet. The resistance to mass transfer of the liquid film surrounding the pellet is considered negligible when compared with the intraparticle resistance. The average pore size is taken as sufficiently low so that the external forced convection past the pellet does not penetrate the pore network, and thus has no appreciable effect on the intraparticle concentration profile [8]. The solution containing the substrate is assumed to behave ideally, so no volume change of mixing occurs. Steady-state conditions of operation have been reached. The process of diffusion and homo-geneous reaction can then be described [9—12] by

where C denotes the concentration of substrate, Detf is the effective diffusivity of

substrate within the pellet, vm is the maximum rate, and Km is the Michaelis-Menten

constant. In the case of a constant cross-sectional area, sealed-edge, catalyst slab of half-thickness L in the direction of solute flow (the tf-direction), fairly small when

compared with the other characteristic dimensions of the slab, the problem becomes virtually unidimensional. Equation (1) can, thus, be simplified to

(2)

dx2 Dcft Km

A set of physically meaningful boundary conditions can be written as

*=0, ^ = 0 (3)

dx

arising from the symmetry condition at the centre plane of the slab [9], and

x = L, C=CS (4)

where the subscript V stands for the conditions prevailing at the surface of the slab. An analytical solution of equation (2) coupled to equations (3) and (4) has not been reported to date [13], so a numerical method is required. Since one is dealing with a double boundary value problem, an iterative procedure is in general needed [14]; the integration is then performed through the construction of a concentration profile from the initial point, given by equation (3), as many times as needed for convergence be achieved to the final condition, equation (4). This method may be cumbersome to implement and somewhat susceptible to cumulative errors because a higher-order derivative exists; furthermore, no general conclusions can be drawn out for the problem because each time the parameters are changed the numerical procedure has to be restarted and carried over once more.

An interesting alternative approach can, nonetheless, be devised after a careful inspection of equation (2). In fact, no explict functional dependence on variable x exists; the independent variable can, therefore, be changed from x to C [13,15] through the definition of the auxiliary dependent variable <D

* = £ (5)

dx

Application of the chain rule of differentiation to equation (5) and use of the result in equation (2) eventually gives

d*=v^_^_

dC Dc(fKm + C K

Equation (3) is now directly replaced by an equivalent boundary condition, namely

C=CC, <D = 0 (7) where the subscript c denotes the conditions on the symmetry plane of the slab. Adequate integration of equation (6) coupled to equation (7) leads to

A suitable variable normalization is now apparent, according to

C* = !+-£-

(9)

180 F. X. Malcata

which leads to the logical definition of the following dimensionless parameter

\

KD ' ( 1 0 )

usually known as the Thiele modulus [5]. Using equations (9) and (10) in equation (8), and recalling equations (4) and (5), one finally converts the differential equation to quadratures, namely

where C* is the current independent variable of interest. An artefact is now possible with respect to the evaluation of the above integral. In fact, the integral term in equation (11) can be partitioned into two integrals, and a new dummy variable of integration can be defined according to

(12) thus leading to

Th{C*) =

HI

I

[2[C*[exp(C)-l]-C]]1/2

Expansion of the exponential term in equation (13) as a McLaurin series [15], and truncation after the quadratic term yields

Th(C*) <z 77*app(C*) = [2[C* - C* - In (Cf/C*)]]1/2

i:

The integral in equation (14) can be obtained as a finite combination of elementary functions, provided that a Chebyshev change of variable of the third kind is performed [16,17] according to

After integration, (14) finally becomes

TKPP(C*) = [2[C* - C* - In (C?/C*)]] ^

^

V C*ln(C* T *

?-i>

An estimate of the error implicit in the foregoing approximation can be obtained by numerically integrating equation (13) by a trapezoidal rule, with a total number of

mesh-points equal to Nmt tot, each one being located in the ^-dimension according to

the formula

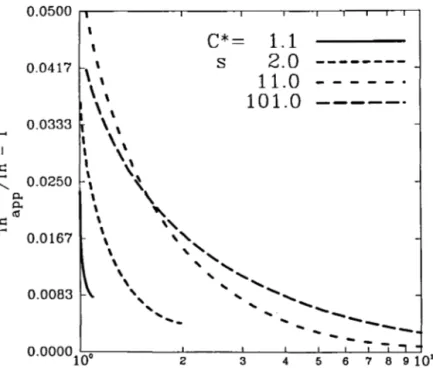
(17) The fractional error of the approximation can be depicted in Figure 1 for a few levels of parameter C*.

When dealing with a chemical process aimed at the manufacture of a high-value chemical compound via an enzyme-catalyzed biochemical route using fixed-bed reactor technology, the choice of the thickness of the slab can be obtained as a compromise between the market price of the product and the capital cost of the pellet. This statement can be mathematically expressed via

— t

-2ALV

where Vn is the overall net profit associated with the operation of the reactor over the

entire service life of the enzyme, A is the cross-sectional area of the catalyst slab, Vp is

the molar market price of the product, Vc is the volumetric market cost of the

supported enzyme, and te is the service life of the supported enzyme. Equation (18) is

equivalent to the dimensionless form

V*=Ma [C* - C* - In (C*IC*)]1/2 - ^ 2 Th (19) 0.0500 0.0417 0.0333 i E-0.0250 IX a, (0 0.0167 0.0083 0.0000 6 7 8 9 10'

Figure 1. Fractional error of the approximation used to compute Th, (Thapp~Th)ITh,

plotted as a continuous function of C* for various values of C*.

182 F. X. Malcata

where Ma is a dimensionless economic parameter defined as

Ma= eff —p_!H_l

and the dimensionless net profit is obtained from

V ./«

V*=-(20)

(21) Differentiating equation (19) with respect to'C*, and setting the outcoming result equal to zero, one obtains

M . . . . [C*-C*o p t-ln(C*/C*o p t)]''2

C*o p t-1

V

In

2(C*

-l)

C*opt\n(C*IC*opt)

2(C*

-l) V'

C*

2j2{C*opt-1 +ln (C*/C*op,))

— 11 V'2

(22)

After the optimum value C*opt for C* is found via equation (22) for any given Ma,

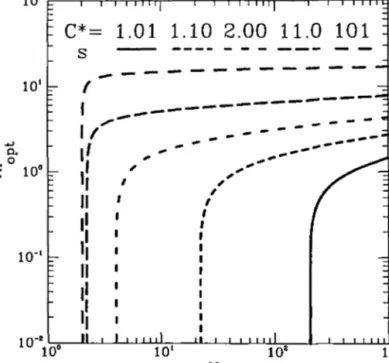
equation (16) can be used to obtain the corresponding value for Thopi as depicted in

Figure 2. The calculation of the optimum value of the slab thickness is now apparent from equation (10).

3. Discussion

The traditional approach to the optimal design of the thickness of slab-shaped pellets catalyzing simple biochemical reactions is based on the calculation of an effectiveness factor for the Michaelis-Menten, rectangular hyperbola-type kinetic expression [18,19]. A dimensionless parameter containing the Michaelis-Menten kinetic constant appears to play an important role in such an analysis. The alternative approach reported in this communication replaces that parameter by a dimension-less concentration of substrate at the centre of the slab; this fact arises naturally from the strategy followed during the integration of the differential mass balance to the substrate within the pellet. Although introduced during the analysis in a way similar to a boundary condition, C* is not truly required to specify any integration constant;

C* turns out to be the actual, physically meaningful, independent variable in the

optimization procedure.

The expansion of the exponential function in equation (13) as a power series presents obvious advantages relative to the expansion of the logarithmic function in equation (11). In fact the former possesses an infinite radius of convergence, whereas the latter has a considerably narrow, finite radius of convergence; thus, the expansion actually employed leads to more general and powerful results.

The solution of equation (11) is accomplished at the expense of an approximating function. The integrand of this equation possesses a singularity at the lower limit of

10' 10' T-10" ^ 10" 10' I I I

: C* =

\

s

r

f~

w

: II

ii:

! II '

Mi

1.01 1.10 2.00 11.0 101 :

^ ..

-*

Figure 2. Plot of the values for Th^vv leading to the optimal economic design Thopt versus the

economic parameter Ma for various values of Cf.

integration which gives a major c o n t r i b u t i o n to t h e value of t h e integral. T h e use of t h e approximating function avoids numerical integration, w h i c h in this case m i g h t be a notoriously e r r o r - p r o n e process if n o special precautions are taken in o r d e r to deal with t h e aforementioned singularity. T h e approximation used consists of expanding t h e exponential function in such a way as t o b e c o m e exact at t h e lower limit of integration. I n order to obtain an estimate of t h e error associated with t h e approximation, the numerical integration of equation (13) was accomplished via a trapezoidal rule, using a criteriously defined spacing for t h e m e s h - p o i n t s as introduced in equation (17). T h e particular spacing formula employed clusters t h e points near t h e lower b o u n d a r y , w h e r e t h e singularity is m o r e likely to affect t h e mathematical behaviour of t h e function. O w i n g to t h e finite n a t u r e of the h a r d w a r e available for automatic calculus, integration can only be numerically started at a positive value of S, t h e lower b o u n d a r y condition. T h e optimal 8 to be used, as well as t h e total n u m b e r of m e s h points required were found by a trial-and-error p r o c e d u r e , aiming at reaching t h e best c o m p r o m i s e between low C P U time and high intrinsic mathematical accuracy; a double-precision m e t h o d o l o g y was necessary in order to release partly the constraint of additive error d u r i n g t h e iterative numerical evaluation of t h e integral. T h e percentual error does not exceed t h e 5 per cent level in t h e range of physical interest. L a r g e r values for C* lead to a monotonically decreasing fractional error for t h e approximation. As Cf increases, the fractional error t e n d s to b e c o m e m o r e sluggish with Cf, with t h e worst situation being achieved at an intermediate range of t h e dimensionless surface concentration (about 1 1 0 ) . T h e highest interest lies on t h e case of having C * ^ 2 0 , because this corresponds t o t h e physiological level w h e r e m o s t enzymes exhibit t h e best operating characteristics (i.e. Ct~-Km leads to t h e largest efficiency coupled to t h e highest

184 F. X. Malcata

control feasibility [1]). It is remarkable to note that the approximation resulting from the truncation of the series expansion of the exponential function about zero after the quadratic term always yields consistently positive deviations in the computation of the Thiele modulus. Therefore, a conservative approach results, which makes the approximation developed robust to inadequacies during modelling and/or inaccuracies in the estimation of the parameters relevant for the operation.

As the value of the product of the reaction increases with respect to the cost of the supported enzyme, the optimal concentration of substrate at the centre of the slab decreases, and the corresponding Thiele modulus increases (see Figure 2). This analysis is valid on the assumption that the substrate concentration on the surface of the slab is known and kept constant, as is the case of a continuous stirred tank reactor with the slabs suspended in the solution of substrate. If a fixed bed reactor is to be used, then the substrate concentration is expected to decrease along the reactor as the conversion level increases downstream; in this case, a non-uniform profile of slab thicknesses along the reactor coordinate based on the results plotted in Figure 2 should be considered for maximum net profit if it is feasible to do so. If not, then a weighted average of the values obtained for the optimal slab thickness according to the procedure outlined previously should be used instead.

The shape of the Thopt versus Ma plot shows a steep bend in a narrow range of

values for parameter Ma, located at lower levels of Ma as C* gets larger. In the remainder of the scale, the behaviour approaches either a vertical or a horizontal linear asymptote, for lower and higher values of Ma, respectively. In general, the optimum Thiele moduli do not change appreciably with Ma at high values for Ma, this finding being especially true under the condition of high dimensionless surface concentrations. This is equivalent to saying that the actual value of Ma is not too important for the selection of the optimum slab thickness in the diffusional regime. When the kinetic regime (low Th) is reached, however, the optimal slab thickness becomes extremely sensitive to the economic parameter. The analysis reported here can then be ascribed a high value provided that its results are used as a designing tool for the industrial biochemical practice.

References

[1] WHITAKER, J . R . , 1972, Principles of Enzymology for the Food Sciences (New York: Marcel Dekker).

[2] LEHNINGER, A. L., 1982, Principles of Biochemistry (New York: Worth).

[3] BAILEY, J. E., and OLLIS, D . F., 1986, Biochemical Engineering Fundamentals (New York: McGraw-Hill).

[4] GEANKOPOLIS, C. J., 1983, Transport Processes and Unit Operations (Boston: Allyn and Bacon).

[5] H I L L , C. G., 1977, An Introduction to Chemical Engineering Kinetics and Reactor Design (New York: Wiley).

[6] MICHAËLIS, L., and MENTEN, M. L., 1913, Biochem. Z., 49, 333.

[7] SEGEL, I. H., 1975, Enzyme Kinetics -- Behavior and Analysis of Rapid Equilibrium and

Steady-State Enzyme Systems (New York: Wiley).

[8] N I R , A., and PISMEN, L. M., 1977, Chem. Engng. Sci., 32, 35.

[9] BIRD, R. B., STEWART, W. E., and LIGHTFOOT, E. N., 1960, Transport Phenomena

(New York: Wiley).

[10] DANCKWERTS, P. V., 1951, Trans. Faraday Soc., 47, 1014.

[11] CRANK, J., 1956, The Mathematics of Diffusion (Oxford: Oxford University Press). [12] ARIS, R., 1975, The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts

(Oxford: Clarendon Press).

[13] BOAS, M. L., 1983, Mathematical Methods in the Physical Sciences (New York: Wiley). [14] KREYSZIG, E., 1979, Advanced Engineering Mathematics (New York: Wiley).

[15] STEPHENSON, G., 1973, Mathematical Methods for Science Students (London: Longman). [16] PISKOUNOV, N., 1980, Differential and Integral Calculus (Moscow: MIR).

[17] BARANENKOV, G., DEMIDOVITCH, B., EFIMENKO, V., FROLOV, S., KOGAN, S., LUNTZ, G., PORSNEVA, E., SHOSTAK, R., SITCHEVA, E., and YANPOLSKI, A., 1977, Problems of

Mathematical Analysis (Moscow: MIR).

[18] HOUGEN, O., 1961, Ind. Eng. Chem., 53, 509.

[19] BISCHOFF, K. B., 1965, American Institute of Chemical Engineering Journal, 11, 351.