Duarte Chambel Ribeiro
Licenciado em MatemáticaCoherent presentation for the hypoplactic
monoid of rank
n
Dissertação para obtenção do Grau de Mestre em
Matemática
Orientador: António José Mesquita da Cunha Machado Malheiro, Professor Auxiliar, Faculdade de Ciências e Tecnolo-gia da Universidade Nova de Lisboa
Coherent presentation for the hypoplactic monoid of rankn
Copyright © Duarte Chambel Ribeiro, Faculdade de Ciências e Tecnologia, Universidade NOVA de Lisboa.
A c k n o w l e d g e m e n t s
I would like to thank my thesis advisor Professor António Malheiro. His enthusiasm to introduce me to new and interesting subjects, going back to when I was in my last year of my bachelor’s studies, were key to shaping my choice in pursuing the study of Pure Mathematics, and, in particular, Semigroup Theory, as my career. His guidance during my master’s studies helped me to achieve a strong grasp of the fundamental concepts and results which are the foundation of my thesis. His patience and effort in successively
reviewing my work were the reason I was able to complete my thesis in such a short amount of time, even with several setbacks and difficulties. In this way, I give my sincere
gratitude to Professor António for helping me secure a better future in the demanding world of Mathematics Investigation.
I would also like to thank my thesis co-advisor Investigator Alan J. Cain for his guidance during my master’s studies, for also successively reviewing my work and for always being available to help me with LATEXproblems, which, due to the fact that I only recently started using LATEX, would frequently arise.
I would like to thank the Departamento de Matemática da Faculdade de Ciências e Tecnologia da Universidade Nova de Lisboa, and, in particular, the President of the Departamento de Matemática, Professor Vítor Hugo Fernandes, for not only being the person responsible for the blooming of my interest in Pure Algebra, but also for the opportunity he provided for me to be a teaching assistant these last two semesters. I feel deeply indebted to him for all his support and dearly thank him for such. I also acknowledge all other professors of the Departamento de Matemática, both those under whom I studied and those who I met in the many Mathematics divulgation activities organized by the Departamento de Matemática. I thank them all for their support and for showing me the beautiful world of Mathematics.
I would like to thank all my friends, in particular, the members of my band Sopas de Chavalo Cansado, Bruno, Daniel, and Cláudio, for sharing with me the most wonderful artistic activity in the world, playing music with a serious attitude, and my friends in the Núcleo de Jogos da FCT, for tolerating my cringeworthy verbal wit and spontaneous Military History lessons and keeping me company during my master’s studies, on which I felt particularly lonely. I also thank all others friends, whom I will not name here, for fear of forgetting anyone.
and encouragement, both in my academic life and my private life. Without them, I wouldn’t have been able to choose this arduous path of life, so beautiful, yet so harsh.
Finally, I would like to thank Sofia. I give her my love.
A b s t r a c t
In this thesis, we construct a coherent presentation for the hypoplactic monoid of rank
n and characterize the confluence diagrams associated with it, then we use the theory of quasi-Kashiwara operators and quasi-crystal graphs to prove that all confluence dia-grams can be obtained from those diadia-grams whose vertices are highest-weight words. To do so, we first give a complete rewriting system for the hypoplactic monoid of rank n, then, using an extension of the Knuth–Bendix completion procedure called the homotopi-cal completion procedure, we compute the previously mentioned coherent presentation, which, from a viewpoint of Monoidal Category Theory, gives us a family of generators of the relations amongst the relations. These coherent presentations are used for representa-tions of monoids and are particularly useful to describe acrepresenta-tions of monoids on categories. The theoretical background is given without proof, since the main purpose of this thesis is to present new results.
R e s u m o
Nesta tese, construímos uma apresentação coerente para o monóide hipopláctico de carac-terísticane caracterizamos os diagramas de confluência associados, utilizando depois a Teoria dos operadores quasi-Kashiwara e dos grafos quasi-cristais para provar que todos os diagramas de confluência podem ser obtidos dos diagramas cujos vértices são pala-vras de maior peso. De forma a realizar esta tarefa, construímos primeiro um sistema de reescrita completo para o monóide hipopláctico de característicane depois, utilizando o procedimento de completude homotópica, uma extensão do procedimento de comple-tude de Knuth–Bendix, computamos a apresentação coerente atrás referida, que, dum ponto de vista de Teoria de Categorias Monoidais, nos dá uma família de geradores das relações entre as relações. Estas apresentações coerentes são usadas para representações de monóides e são particularmente úteis para descrever ações de monóides em categorias. A fundamentação teórica é dada sem demonstrações, dado que o principal objetivo desta tese é apresentar novos resultados.
C o n t e n t s
1 Introduction 1
2 Introduction to Combinatorial Semigroup Theory 5
2.1 Basic concepts and results on Semigroup Theory . . . 5
2.2 Alphabets, Presentations and Rewriting Systems . . . 7
2.3 Graphs . . . 11
2.4 Homotopy relations, finite derivation type and coherent presentations . . 13
3 The plactic monoid 17
3.1 The plactic monoid, Young tableaux and insertion . . . 17
3.2 Kashiwara operators and the crystal graph . . . 20
3.3 Properties of the crystal graph . . . 22
3.4 Column presentation and complete rewriting system for the plactic monoid of rankn . . . 24
3.5 Coherent presentation for the plactic monoid of rankn. . . 25
4 The hypoplactic monoid 27
4.1 The hypoplactic monoid, quasi-ribbon tableaux and insertion . . . 27
4.2 Quasi-Kashiwara operators and the quasi-crystal graph . . . 31
4.3 Properties of the quasi-crystal graph . . . 32
5 Coherent presentation for the hypoplactic monoid of ranknand
characteri-zation of the confluence diagrams 35
5.1 Column presentation and complete rewriting system for the hypoplactic monoid of rankn . . . 35
5.2 Coherent presentation for the hypoplactic monoid of ranknand charac-terization of the confluence diagrams . . . 38
C
h
a
p
t
e
r
1
I n t r o d u c t i o n
In Semigroup and Monoid Theory, one of the most interesting and widely-studied prob-lems is the word problem, first introduced in Group Theory by M. Dehn [7]. Given a presentationhA|Rifor a monoidM, whereAis an alphabet andRis a rewriting system, we can formulate the word problem in the following way: foru, v∈A∗, decide ifu↔∗
Rv,
where↔∗R is the Thue congruence generated byR. IfR is finite and complete, then
the word problem is solved using the "normal form algorithm", that is, foru, v∈A∗, we compute normal formsu0andv0foruandv, respectively, then we conclude thatu↔∗Rv
if and only ifu0=v0. The property of having solvable word problem is invariant for any finite presentation defining the same monoid, however the property of having a finite and complete rewriting system is not invariable under monoid presentations.
In [24], C. Squier, along with F. Otto and Y. Kobayashi, introduced the concept of finite derivation type(FDT), a combinatorial property of presentations of monoids, and showed that if a monoid is presented by a finite complete rewriting system, then it is FDT. This property is also an invariant property of finite monoid presentations. Squier’s theory has recently been further developed by Guiraud, Malbos and Mimram [9], using the language of strict monoidal categories and higher-dimensional variations of them. In this paper, they introduce the concept ofcoherent presentationand give an extension of the Knuth–Bendix completion procedure, called the homotopical completion procedure, that allows one to obtain a coherent presentation from a noetherian rewriting system for the monoid being studied.
C H A P T E R 1 . I N T R O D U C T I O N
plactic monoid of rank n placn and from it, in [10], a coherent presentation for placn was computed. The plactic monoid can also be defined using the theory of Kashiwara operators and the crystal graph [13]. A similar structure, the hypoplactic monoid, studied in depth by Novelli [19], initially defined using either the hypoplactic relations or ribbon tableaux and Krob–Thibon’s algorithm, was also defined using the theory of quasi-Kashiwara operators and the quasi-crystal graph in [3].
The main purpose of this thesis is the construction of a coherent presentation for the hypoplactic monoid of ranknand the characterization of the confluence diagrams associated with it, using the theory of quasi-Kashiwara operators and quasi-crystal graphs to reduce the number of relevant diagrams. Given the significant extent of the theoretical background and the fact that this thesis presents new results, we have chosen to give the background without proof, otherwise the thesis would be exceedingly large compared to the new content presented. However, we give several definitions which, while not used directly in the obtained results, are fundamental to understand the concepts we deal with and the tools used.
In Chapter2, we give the theoretical background, in Combinatorial Semigroup Theory, needed to reach the definitions ofFDTand coherent presentations, and related results. In Section2.1, we present fundamental Semigroup Theory concepts and results. In Section
2.2, we recall the concepts of presentations and rewriting systems and other important concepts and results of Combinatorial Semigroup Theory. In Section2.3, we present basic definitions and theorems regarding graphs. In Section2.4, we finally present the concepts ofFDTand coherent presentation and give the homotopical completion procedure, which will be the main tool used to construct a coherent presentation for hypon.
In Chapter3, we start by giving some background on the plactic monoid, including two possible definitions, one via the Knuth relations, the other via Young tableaux and Schensted’s algorithm, and the Robinson–Schensted–Knuth correspondence. Afterwards, we introduce the Kashiwara operators and the crystal graph, restricted to the context of placn, and use them to give another definition of placn. We also give some important prop-erties of the crystal graph and its interaction with the combinatorics of Young tableaux. Then, we give a finite complete rewriting system on the column alphabet, which gives us a presentation of placnfrom which we compute a coherent presentation for placn, us-ing the homotopical completion procedure. We also characterize the related confluence diagrams.
Chapter4mirrors the first three Sections of Chapter3, since we first give some back-ground on the hypoplactic monoid, including two possible definitions, one via the hy-poplactic relations, the other via quasi-ribbon tableaux and the Krob–Thibon algorithm, and an analogue of the Robinson–Schensted–Knuth correspondence. Then, we introduce the quasi-Kashiwara operators and the quasi-crystal graph, restricted to the context of hypon, and use them to give another definition of hypon. Afterwards, we present some important properties of the quasi-crystal graph and its interaction with the combinatorics of quasi-ribbon tableaux, which are used in the final results of this thesis.
Finally, in Chapter5, we present new results and their respective proofs. We first give a complete rewriting system, on the alphabetAn, for hypo
C
h
a
p
t
e
r
2
I n t r o d u c t i o n t o C o m b i n a t o r i a l S e m i g r o u p
T h e o r y
This chapter contains the basic concepts and theorems that will be used throughout this thesis. It mostly follows Chapter 1 of [18], except for Section2.4, which follows [9] and [10]. In the first section, we present basic definitions and results on Semigroup Theory. We follow with a section onpresentationsandstring rewriting systems. In the next section, we present basic definitions and results on graphs. Finally, we introduce the concept ofcoherent presentation, using the language of Combinatorial Semigroup Theory. This concept and related results expand on the theory developed by C. Squier in the late 1980’s and early 1990’s and were first introduced in [9], using the language of strict monoidal categories and higher-dimensional variations of them.
2.1
Basic concepts and results on Semigroup Theory
In this section, we will present concepts and results from fundamental Semigroup Theory, necessary for the understanding of this thesis. These and other fundamental results can be found in [12]. Some definitions regarding partial orders and admissible relations are taken from [2].
LetSbe a non-empty set and let·be a binary operation onS, that is, a mapping from
S×S intoS. We will refer to·as multiplication and, forx, y∈S, we representx·y, the image of the pair (x, y) by·, simply byxy.
The pair (S,·) is asemigroupif·is an associative binary operation onS. Instead of (S,·), we usually write justS. Letx1, . . . , xn(n∈N) be elements ofS, then, we can writex1· · ·xn without any ambiguity, as a consequence of the associative property.
C H A P T E R 2 . I N T R O D U C T I O N TO COM B I N ATO R I A L S E M I G R O U P T H E O RY
Given a semigroup (S,·), it is always possible to extend it to obtain a monoid (S1,∗): If (S,·) is already a monoid, then (S,·) = (S1,∗); otherwise, we add an element 1<S , take
S1:=S∪ {1}, and define∗in the following way: Forx, y∈S,x∗y=x·y,x∗1 =x,1∗x=x
and 1∗1 = 1.
LetM be a monoid and letx∈M. We sayxhas aninverseif there exists an elementx′
inM such thatxx′=x′x= 1M. If every element ofMhas an inverse, we sayM is agroup. Given semigroups S andT, we say T is asubsemigroup ofS ifT ⊆S andt1, t2 ∈T
implies thatt1t2∈T. IfT is a subsemigroup ofS, and is also a monoid, thenT is called a submonoid; If T is also a group, then T is called asubgroup. Note that S need not necessarily be a monoid, and that, even ifS is a monoid, then the identities ofS andT
need not coincide.
Let A be a non-empty subset of a semigroup S and let Abe the collection of all subsemigroups ofSthat containA. The intersectionTT∈AcontainsAand not only is a
subsemigroup ofS, it is also the least subsemigroup ofS containingA. It is called the subsemigroup ofSgenerated byA, and is denoted byhAi. IfS=hAi, then we say thatSis generated byA(or thatAgeneratesS), and the elements ofAare calledgeneratorsofS. If
Ais a finite set that generatesS, we say thatS is afinitely generated semigroup.
We can also define thesubmonoid of a monoidM generated byAin a similar manner: LetAbe the collection of all submonoids ofM that containA∪ {1M}. The intersection
T
T∈Acontains A and not only is a submonoid of M, it is also the least submonoid of
M with identity 1M containingA. It is called thesubmonoid ofS generated byA, and is denoted byhAi. Similarly, ifM=hAi, then we say thatMisgenerated byAas a monoid(or thatAgeneratesM as a monoid), and the elements ofAare calledgeneratorsofM. IfAis a finite set that generatesM, we say thatM is afinitely generated monoid.
Letρ⊆S×Sbe a binary relation onS. We say thatρis:
• reflexiveifx ρ x, for allx∈S;
• symmetricifx ρ y theny ρ x, for allx, y∈S;
• anti-symmetricifx ρ y andy ρ xthenx=y, for allx, y∈S;
• transitiveifx ρ yandy ρ zthenx ρ z, for allx, y, z∈S.
Ifρis reflexive, symmetric and transitive, it is said to be anequivalence relation. An equivalence relation onSpartitions the setSintoequivalence classes, such that each class only contains elementsρ-related to one another.
Ifρis reflexive, anti-symmetric and transitive, it is said to be a(strict) partial order. The most common symbols used for partial orders are≤,, and⊑. We writex < yto denote that x≤y andx,y. Alinear order is a strict partial order such that eitherx < y, x =y or x > y, forx, y ∈S. We say that a partial order iswell-founded if there is no infinite chain of the formx1> x2> . . ., forxi∈S, i∈N. A linear and well-founded order is called
2 . 2 . A L P H A B E T S , P R E S E N TAT I O N S A N D R E W R I T I N G S YS T E M S
a well-ordering. We say that< isadmissibleif, for all x, y, u, v ∈S, wheneverx < y then
uxv < uyv.
An equivalence relationρonSis said to beright (left) compatibleifa ρ bimpliesax ρ bx
(a ρ b ⇒xa ρ xb), for anya, b, x∈S. Ifρ is both left and right compatible, it is called a congruence.
LetS, T be semigroups. A mappingφ:S→T fromStoT is called ahomomorphismif, for anyx, y∈S,we haveφ(xy) =φ(x)φ(y). A homomorphismφis called amonomorphism orisomorphismif it is, respectively, injective or bijective. If there exists an isomorphism
φ:S→T, we say thatSandT areisomorphicand writeST.
Letφ:S→T be a homomorphism between semigroupsSandT. Then,φinduces a congruence onS, called thekernelofφ, denoted by kerφand given by
kerφ={(x, y)∈S×S|φ(x) =φ(y)}.
LetS be a semigroup andρa congruence onS. Consider the quotient set ofS byρ, denoted byS/ρ. For anyx∈S, let [x]ρbe theρ-class ofx, that is, [x]ρ={y∈S|y ρ x}. We define a multiplication onS/ρin the following way: Forx, y∈S, [x]ρ[y]ρ:= [xy]ρ. With this multiplication, the quotient setS/ρis a semigroup and is called thequotientofS by
ρ. Furthermore, the natural mappingρ♮:S→S/ρ, given byx7→[x]ρ, for anyx∈S, is an epimorphism.
The following well known result can be found in [11, Theorem 5.4].
Theorem 2.1.1. Letφ:S →T be a homomorphism between semigroups and letρbe a
con-gruence onSsuch thatρ⊆kerφ. Then, there exists a homomorphismψ:S/ρ→T such that ψ◦ρ♮=φ. Moreover,ψis injective if and only ifρ= kerφ.
LetMbe a monoid andXa non-empty set. A mappingχ:M×X→X is said to be aleft actionofMonX if it satisfies the equalitiesχ(m1, χ(m2, x)) =χ(m1m2, x) andχ(1M, x) =x, for allm1, m2∈M, x∈X. We also say thatM acts on X on the leftand we usually represent the elementχ(m, x) bym·x, which allows us to rewrite the previous equalities in the formm1·(m2·x) = (m1m2)·xand 1M·x=x. Similarly, we can define aright actionof a monoid on a set. We say that a monoidM acts ona setX (or that there exists anaction ofM onX), if there exists simultaneously a left and a right action ofM onX satisfying the following equality, called the compatible property: (m1·x)·m2=m1·(x·m2) for any
m1, m2∈M, x∈X. Note that every monoid acts on itself by multiplication, both on the left and on the right.
2.2
Alphabets, Presentations and Rewriting Systems
C H A P T E R 2 . I N T R O D U C T I O N TO COM B I N ATO R I A L S E M I G R O U P T H E O RY
LetAbe a non-empty set, which we will refer to as analphabet. The elements ofA are calledlettersand finite sequences of letters are calledwordsover the alphabetA. The lengthof a wordwis the number of letters that formwand is denoted by|w|. Fora∈A, the number of times the elementaappears in a word wis denoted by|w|a. The empty sequence is called theempty word, has length zero and is denoted byε. For any two words
u, v overA, we writeu=vif they are equal as words.
Supposew=w1. . . wk is a word overA, withw1, . . . , wk ∈A. For 1≤i≤j ≤k, we say
wi· · ·wj is afactorofw. (Note that a factor must be made up of consecutive letters.) For
i1, . . . , im∈ {1, . . . , k}such thati1<· · ·< im, we say thatwi1· · ·wimis asubsequenceofw. (Note that a subsequence may not be necessarily made up of consecutive letters, unlike a factor.) The set of all non-empty words overAis denoted by A+, and the set of all words over A, including the empty word, is denoted byA∗. When equipped with the binary operation of concatenation of words,A+forms a semigroup, called thefree semigroup over A, andA∗forms a monoid, with the empty word as the identity element, and is called the free monoid overA.
Throughout this text, we will considerAto be the set of natural numbers viewed as an infinite ordered alphabet: A={1<2<3<· · · }. Also, forn∈N, we will denote byAnthe set of the firstnnatural numbers viewed as a finite ordered alphabet:A
n={1<2<· · ·< n}. Aweak compositionαis a finite sequence (α1, . . . , αm) with terms inN∪ {0}. The terms
αh up to the last non-zero terms of the sequence are the parts of α. The length ofα, denoted byl(α), is the number of its parts. Theweightofα, denoted by|α|, is the sum of its parts, that is,|α|=α1+· · ·+αm. For example ifα= (0,1,3,0,2,0) thenl(α) = 5 and |α| = 6. We shall identify weak compositions whose parts are the same, that is, weak compositions which only differ in a tail of terms 0.
Acompositionis a weak composition whose parts are exclusively inN. For a composi-tionα= (α1, . . . , αl(α)), let us denote byD(α) the set{α1, α1+α2, . . . , α1+· · ·+αl(α)−1}.
We say that a non-increasing finite sequence λ = (λ1, . . . , λm) with terms in N is a
partition. Note that a partition is a particular kind of weak composition, thus, we define and denote thelengthandweightofλin the exact same way as before.
We now define the weight function (not to be confused with the weight of a weak composition), which informally is the function that counts the number of times each element appears in a word. More formally, it is defined by
wt :A∗→(N∪ {0})A, w7→(|w|1,|w|2, . . .).
Since words are finite sequences, then wt(·) has an infinite tail of elements 0, thus we only consider its prefix up to the last non-zero term. Hence wt(·) is a weak composition. We compare weights using the following order:
(α1, α2, . . .)≤(β1, β2, . . .)⇔ k X
i=1
αi≤ k X
i=1
βi,
for anyk∈N.
2 . 2 . A L P H A B E T S , P R E S E N TAT I O N S A N D R E W R I T I N G S YS T E M S
When wt(w1)<wt(w2), for wordsw1, w2∈A∗, we say thatw1haslower weightthanw2 (and thatw2hashigher weightthanw1).
We now relate alphabets with semigroups and introduce notions that allow us to apply combinatorial results to Semigroup Theory.
Proposition 2.2.1. LetMbe a monoid. For any alphabetAand any mappingθ:A→S, there is a unique extension ofθ to a homomorphism from A∗ intoM, also denoted by θ, defined by θ(a1· · ·an) = (θa1)· · ·(θan), for anya1, . . . , an ∈ A. The image of this homomorphism is the submonoid ofM generated byθ(A), and this submonoid is equal toM if and only ifθis surjective.
Amonoid presentationPis a pairhA|Risuch thatRis a binary relation in the free monoid over the alphabetA. The setRis know as arewriting systemand its elements as rewriting rules. We say thatPis finite if bothAandRare finite.
LetRbe a rewriting system overA∗. We define a binary relation→RonA∗, called a single-step reduction, in the following way: For anyu, v∈A∗,
u→Rv⇔(u=w1r+1w2)∧(v=w1r−1w2),
for some (r+1, r−1)∈ Randw1, w2 ∈A∗. We denote the transitive and reflexive closure of→R by →∗R, and the equivalence relation that→R induces by ↔∗R. Note that this
equivalence relation is in fact the smallest congruence on the free monoidA∗that contains R, called theThue congruencegenerated byR.
We sayRis:
• noetherian if there is no infinite descending chain w1 →Rw2 →R · · ·, with wn ∈
A+, n∈N;
• confluentif, foru, w1, w2∈A∗, wheneveru →∗
Rw1 andu → ∗
Rw2then there exists
v∈A∗such thatw1→∗
Rv andw2→∗Rv;
• locally confluentif, foru, w1, w2∈A∗, wheneveru →Rw1andu→Rw2 then there
existsv∈A∗such thatw
1→∗Rvandw2→ ∗ Rv.
IfRis both noetherian and confluent, it is calledcomplete.
Letu∈A∗. If there is no wordv∈A∗such thatu→Rv, we say thatu isirreducible. If
u, v∈A∗are such thatu↔∗
Rvandvis irreducible, we sayvis anormal formforu.
The next results are consequences of Lemma 1.1.10, Corollary 1.1.8, and Theorem 1.1.12, respectively, in [2].
Proposition 2.2.2. LetRbe a noetherian rewriting system on an alphabetA. Then, for every
u∈A∗,uhas at least one normal form.
Proposition 2.2.3. LetRbe a confluent rewriting system on an alphabetA. Then, for every
C H A P T E R 2 . I N T R O D U C T I O N TO COM B I N ATO R I A L S E M I G R O U P T H E O RY
Corollary 2.2.4. LetRbe a complete rewriting system on an alphabet A. Then, for every
u∈A∗,uhas a unique normal form.
Letu, v∈A∗. The wordsu andvare said tooverlapif, up to symmetry, one of the two following cases occur:
(i) vis a factor ofu, that is, there exista, c∈A∗such thatu=avc; or
(ii) u overlaps withv on the left, that is, there exist wordsa, b, cover the alphabet A, withbnon-empty, such thatu=abandv=bc.
Furthermore, if both u andv are left sides of rewriting rules inR, that is, there exist
u′, v′ ∈ A∗such that (u, u′),(v, v′)∈R, then in case (i) and if wheneveraandcare both empty, thenu′ ,v′, then the pair of words{u′, av′c}is called acritical pair. In case (ii) we say thatuc=avis anoverlap ambiguityofRand the pair{u′c, av′}is also acritical pairof R.
We say that a critical pair{u, v}ofRisresolvedif there existsw∈A∗such thatu→∗
Rw
andv→∗Rw.
The following result follows from [1, Corollary 6.2.5] and [2, Theorem 1.1.13].
Proposition 2.2.5. LetRbe a noetherian rewriting system on an alphabetA. The following conditions are equivalent:
• Ris confluent;
• Ris locally confluent;
• All critical pairs ofRare resolved.
Note that, by Proposition 1.5.10 in [12], given a rewriting systemRon an alphabet Aand wordsu, v∈A∗, we haveu↔∗
Rv if and only if there is a finite sequence of words
w0, . . . , wn∈A∗, n∈Nsuch thatw0=u, wn=v and eitherwi→Rwi+1orwi ←Rwi+1, for
alli= 1, . . . , n−1.
Proposition 2.2.6([2, Theorem 2.2.4]). LetRbe a rewriting system on an alphabetA. Then, the following two statements are equivalent:
• Ris noetherian;
• There exists an admissible well-founded partial order<onA∗that is compatible withR (in the sense thatv < ufor each rule(u, v)∈R).
Definition 2.2.7(The length-plus-lexicographic order [2, Definition 2.2.2(d)]). We define thelength-plus-lexicographic order, denoted by<lenlex, induced by the natural order onA in the following way: Letu=u1· · ·uk, v=v1· · ·vl be words inA∗. Then,
u <lenlexv ⇔ (k < l) ∨
k=l ∧ (∃i)ui< vi ∧ (∀j < i)(uj=vj)
.
2 . 3 . G R A P H S
It is easy to see that the length-plus-lexicographic order is an admissible well-ordering, thus, it is an admissible well-founded partial order onA∗. If a rewriting systemRonA is compatible with the length-plus-lexicographic order, then it is noetherian.
The quotient of the free monoidA∗by the Thue congruence↔∗
Ris called themonoid defined bythe presentation P=hA|Riand is denoted byM(P). Consider the natural mapping ρ : A→ M(P), a 7→ [a]
↔∗
R. The homomorphism extension of ρ to
A+ is an epimorphism fromA∗ontoM(P), by Proposition2.2.1, henceρ(A) generatesM(P). By this reason, the elements ofAare called thegenerating symbols. If there is no ambiguity, it is usual to identify a word on Awith its corresponding congruence class ofM(P), hence we identify the generating symbols with the generators ofM(P) andAwith the generating set ofM(P).
Letu, v∈A∗. Ifu↔∗
Rv, we say thatuandvrepresent the same element ofM(P) and
denote it byu≡Rv. We also say thatM(P)satisfies the relationu≡v. Since, by definition,
M(P) satisfies all relations inR, a rewriting rule (r+1, r−1) is also called adefining relation and written in the formr+1≡r−1.
LetM be a monoid andρ:A→M a mapping from AtoM. If its homomorphism extension is an epimorphism fromA∗ontoM, we call the alphabetAagenerating set for
M. Also, if↔∗R= kerρ, for a rewriting systemR, we say thatM isdefined byP=hA|Ri.
In this case, due to Theorem 2.1.1, there exists an isomorphism ψ :M(P) →M such that ψ◦φ =ρ, where φ:A∗→M(P) is the natural homomorphism. More generally, a monoidM is said to bedefined bya monoid presentationP=hA|RiifM andM(P) are isomorphic. It is also possible to identify elements ofA∗with elements ofM, by extending the identification presented above, under the mappingρ. Ifρ(u)≡ρ(v), we say thatM
satisfiesthe relationu≡v, foru, v∈A∗.
To define the notions of semigroup presentation and of semigroup S(P) defined by P=hA| Ri, just replace A∗ with A+, in the definitions given above. For most of the text, we will work mostly with monoid presentations, and we shall refer to them just as presentations, as long as there is no confusion with semigroup presentations.
2.3
Graphs
In this section we will present some basic definitions and theorems regarding graphs, according to Serre [22].
An(oriented) graphis a quintupleΓ= (V , E, ι, τ,−1), whereV =V(Γ) is the (non-empty) set of vertices, E =E(Γ) is the set ofedges, andι:E →V andτ :E →V are mappings, respectively called theinitialandterminal mapping. Givene∈E, the verticesιeandτeare respectively know as thestartandendofe, and are collectively known as theextremities ofe. Orientation on the graph is given by theinverse mapping−1:E→E, a mapping that satisfies, for alle∈E,e,e−1,ι(e−1) =τ(e),τ(e−1) =ι(e) and (e−1)−1=e.
C H A P T E R 2 . I N T R O D U C T I O N TO COM B I N ATO R I A L S E M I G R O U P T H E O RY
p hasn elements, we sayphaslengthnand writel(p) =n. We also extend the notions of start, end and extremities to paths, by definingιp:=ιe1andτp:=τen. If, for vertices
u, v ∈V,ιp =uandτp=v (orιp =vandτp=u), we saypjoinsu andv. We say a path
pisclosedifιp=τp. We define theinverse pathofpas the pathen−1· · ·e−11and denote it byp−1. For eachv∈V, we define anempty path1v with no edges, such thatι1v=τ1v =v
and 1−1 v = 1v.
Definition 2.3.1. Given a presentationP=hA| Ri, define a unique graph associated toP, denoted byΓ(P). Its set of vertices is the free monoid A∗(or the free semigroup A+), and the edges are quadruples of the form e= (w1, r+1=r
−1, ǫ, w2), wherew1, w2 ∈ A∗,(r+1, r−1)∈Randǫ=±1.
The initial and terminal vertices and the inverse mapping are defined, respectively, by
ιe=w1rǫw2, τe=w1r−ǫw2ande−1= (w1, r+1=r−1,−ǫ, w2). We say that an edge is positive ifǫ= +1 and negative otherwise. Also, for each wordw∈A∗, there is an empty path 1w with no edges.
Note that, given any wordsu, v∈A∗, we haveu→Rvif and only if there is a positive edgeeofΓ(P) such thatιe=uandτe=v. Thus, we haveu↔∗
Rv if and only if there is a
path inΓ(P) that joinsuandv.
LetΓ= (V , E, ι, τ,−1) be a graph and letMbe a monoid. We say thatMacts on the left of the graphΓifM acts on the left of the setsV andE, respectively, and, for anym∈M, e∈E, we haveι(m·e) =m·ιe, τ(m·e) =m·τeand (m·e)−1=m·e−1. We can extend this action to paths in the following way: given edgese1, . . . , en∈Eandm∈M, forp=e1. . . en, we define
m·p:= (m·e1)· · ·(m·en). We define aright action of MonΓin a similar way. We say that
M actsonΓifM simultaneously acts on the left and on the right onΓand if both actions on the set of vertices and on the set of edges are compatible.
Definition 2.3.2. The concatenation product inA∗induces natural left and right actions ofA∗on Γ(P), in the following way: For anyx, y∈A∗ and any vertexw∈A∗, we define
x·w=xwandw·y=wy; and for any edgee= (u, r, ǫ, v), we definex·e= (xu, r, ǫ, v) and
e·y= (u, r, ǫ, vy). Both actions are compatible, thusA∗acts onΓ(P).
LetΓ = (V , E, ι, τ,−1) be a graph. LetV0 be a subset of V andE0 be a subset of E. The quintupleΓ0 = (V0, E0, ι, τ,−1) is a subgraphofΓ if, for alle ∈E0, we have e−1 ∈ E0 and ιe, τe ∈ V0. If E0 is the set of all edges of Γ with both extremities in V0, that is,
E0={e∈E|ιe, τe∈V0}, then the subgraph ofΓdefined byV0andE0is known as thefull subgraphdefined byV0and denoted byΓV0.
We say a graphΓ= (V , E, ι, τ,−1) isconnectedif any two vertices in it are joined by a path. It is easy to see that the binary relation onV, defined byubeing related tovif and only if there is a path starting inuand ending inv, foru, v∈V, is in fact an equivalence relation. The full subgraphs whose vertex sets are the equivalence classes of this relation are known as theconnected componentsofΓ.
2 . 4 . H OM O TO P Y R E L AT I O N S , F I N I T E D E R I VAT I O N T Y P E A N D CO H E R E N T P R E S E N TAT I O N S
Remark2.3.3. LetP=hA|Ri. Recalling Definition2.3.1, each congruence class of↔∗
Ris
a connected component of the graphΓ(P). Thus the set of elements of the monoidM(P) (or the semigroupS(P)) is in bijection with the set of the connected componentsπ
0(Γ(P)) ofΓ(P).
LetΓ1 andΓ2 be graphs. Amapping of graphs φ fromΓ1 toΓ2is a pair of mappings
φV :V(Γ
1)→V(Γ2) andφE :E(Γ1)→E(Γ2), such that, for alle∈E,φE(e) is a path onΓ2 starting atφV(ιe) and ending atφV(τe), andφE(e−1) = (φE(e))−1. As long as there is no confusion, we shall write bothφV andφE asφ. This map can be extended to paths by definingφ(1v) := 1φ(v), for allv∈V(Γ
1), andφ(p) =φ(e1)· · ·φ(en), for a non-empty path
p=e1. . . en, withn∈N.
2.4
Homotopy relations, finite derivation type and coherent
presentations
In this section, we will present three important concepts: the concept ofhomotopy rela-tionsand the concept offinite derivation type (FDT), a finiteness property of semigroup presentations, first introduced by C. Squier in the 1990’s and further studied by F. Otto and Y. Kobayashi (see [24]), and the concept ofcoherent presentation, which, as we have said before, were first introduced in [9], using the language of strict monoidal categories and higher-dimensional variations of them.
LetP=hA|Ribe a finite monoid presentation and letΓ(P) be the graph associated with it. Consider the setsPΓ(P)of all paths inΓ(P) andP(2)Γ(P)of all ordered pairs of paths inΓ(P) which have a common start and a common end. An equivalence relation ∼onP(2)Γ(P)is called ahomotopy relationif it satisfies the following conditions:
(H1) For any edgese1ande2ofΓ(P), we have
(e1·ιe2)(τe1·e2)∼(ιe1·e2)(e1·τe2).
(H2) Ifp∼q, then, for anyx, y∈A∗, we havex·p·y∼x·q·y;
(H3) Ifp, q1, q2, r∈P
Γ(P)are such thatτp=ιq1=ιq2,τq1=τq2=ιr andq1∼q2, then
pq1r∼pq2r;
(H4) Ifp∈PΓ(P), thenpp−1∼1ιp.
Notice that the collection of all homotopy relations on the set of paths inΓ(P) is closed under arbitrary intersection, and thatP(2)Γ(P)is itself a homotopy relation. Thus, for any subsetX⊆P(2)Γ(P), there is a unique smallest homotopy relation∼Xon the set of paths inΓ(P) that containsX, called thehomotopy relation generated byX.
C H A P T E R 2 . I N T R O D U C T I O N TO COM B I N ATO R I A L S E M I G R O U P T H E O RY
Theorem 2.4.1([24, Theorem 4.3]). LetP
1andP2 be finite monoid presentations defining the same monoid. Then,P
1is of FDT if and only ifP2is of FDT.
Thus, havingFDT is an invariant property of finitely presented monoids, hence it makes sense to refer toFDTmonoids.
Recall the notion of critical pair of a rewriting system given in Section2.2. Lete1, e2 be positive edges inΓ(P), withιe1=ιe2, for a presentationP=hA|Ri. We say the pair (e1, e2) is a critical pair of edgesif the left-hand sides of the underlying rewriting rules overlap and lead to a critical pair. Aresolutionof a critical pair of edges (e1, e2) is a pair of paths (p1, p2) such thatιp1=τe1, ιp2=τe2, τp1=τp2and all edges of bothp1andp2are positive. For any resolvable critical pair (e1, e2), fix a resolution (p1, p2). Denote byBthe set
n
(e1p1, e2p2)|(e1, e2)is a critical pair ofR, and{p1, p2}is the corresponding resolution o
.
(2.4.1)
Theorem 2.4.2([24, Theorem 5.2]). LetP=hA|Ribe a presentation, whereRis a complete rewriting system, and letΓ(P)be the graph associated with it. LetB⊆P(2)Γ(P)be defined as above. Then,BgeneratesP(2)Γ(P)as a homotopy relation.
Observe that ifRif finite, thenBis also finite, thusPis ofFDT.
Theorem 2.4.3([24, Theorem 5.3]). LetM be a finitely presented monoid. LetP=hA|Ri be a presentation, whereRis a finite complete rewriting system. IfM is presented byP, then
M is FDT.
Now, we are able to introduce some definitions, first given by [9], but presented here using the language of Combinatorial Semigroup Theory.
An extended presentation of a monoidM is a pairhP| Ci, where P=hA| Ri is a presentation ofM, Ris a rewriting system and Cis a subset ofP(2)Γ(P)in which the pairs are oriented, that is, it is an analogue of a string-rewriting system for paths, with the restriction that the paths in each pair have the same start and end. We can also write an extended presentation as a triplehA|R| Ci. An extended presentation isfiniteif both Pand Care finite.
Acoherent presentationis an extended presentation such that CgeneratesP(2)Γ(P). Thus, if a monoidM admits a finite coherent presentation, it isFDT.
In the remaining of this section we provide tools to be able to construct coherent pre-sentations. LetP=hA|Ribe a presentation. The following four types of transformations ofhA|Riare calledelementary Tietze transformations:
(T1) -Add a generator: Forw∈A∗anda<A, addatoAand (w, a) toR;
(T2) -Delete a generator: Fora∈Aandw∈(A\ {a})∗such thatw→Ra,
1. removeafromA;
2 . 4 . H OM O TO P Y R E L AT I O N S , F I N I T E D E R I VAT I O N T Y P E A N D CO H E R E N T P R E S E N TAT I O N S
2. remove (w, a) fromR;
3. for any (u, v)∈R, replace any factoraofuandvbyw;
(T3) -Add a relation: Foru, v∈A∗such thatu→∗Rvbut (u, v)<R, add (u, v) toR;
(T4) -Delete a relation: Foru, v∈A∗such thatu→∗R′v, whereR′ =R\ {(u, v)}, remove
(u, v) fromR.
We say that a (finite)Tietze transformationis a (finite) sequence of elementary Tietze transformations.
In [8], a corresponding notion of Tietze transformations was introduced for extended presentations. Let hA|R| Cibe an extended presentation. The following six types of transformations ofhA|R| Ciare calledelementary Tietze transformations:
(T1∗) -Add a generator: Forw∈A∗anda<A, addatoAand (w, a) toR;
(T2∗) -Delete a generator: Fora∈Aandw∈(A\ {a})∗such thatw→Ra,
1. removeafromA;
2. remove (w, a) fromR;
3. for any (u, v)∈R, replace any factoraofuandvbyw;
4. for any (f , g)∈ C, remove any occurrence of (w, a) inf andg;
5. for any (f , g)∈ C, replace any occurrence of a rule (u, v) inf andgby the rule (u′, v′), whereu orvhave a factoraand (u′, v′) is obtained by replacingainu
andvbyw;
(T3∗) -Add a relation: Foru, v∈A∗such thatu→∗
Rvbut (u, v)<R,
1. add (u, v) toR;
2. add (f , g) toC, wheref = (u, v) andg= (u, w), forw∈A∗\{v}such thatu→Rw andw→∗Rv;
(T4∗) -Delete a relation: Foru, v∈A∗such thatu→∗
R′v, whereR′ =R\ {(u, v)},
1. remove (u, v) fromR;
2. for any (f , g)∈ C, remove any occurrence of (u, v) inf andg;
(T5∗) -Add a pair of paths: Forf ∼Cgbut (f , g)< C, add (f , g) to C;
(T6∗) -Delete a pair of paths: For (f , g) ∈ Csuch thatf ∼C′ g, where C′ = C\ {(f , g)}, remove (f , g) from C.
C H A P T E R 2 . I N T R O D U C T I O N TO COM B I N ATO R I A L S E M I G R O U P T H E O RY
Theorem 2.4.4([8, Theorem 2.1.3]). The monoids presented by two (finite) extended pre-sentations are isomorphic if, and only if, there exists a (finite) Tietze transformation between them.
Thus, if a monoidMis presented byP=hA|Ri, whereRis a noetherian rewriting system, we can build a coherent presentation forM: We start with the extended presen-tationhP| Ci, where Cis the empty set. Then, for each critical pair of edges (e1, e2) of hP| Ci,
• if (e1, e2) admits a resolution, fix one resolution (p1, p2), then add (e1p1, e2p2) to C;
• otherwise, sinceRis noetherian, bothτe1andτe2have normal forms. Letu1, u2∈ A∗ be those normal forms, let p1 be the path from τe1 to u1 andp2 be the path from τe2 tou2. Let< be the admissible well-founded partial order on A∗ that is compatible withR(see2.2.6).
– Ifv < u, add (u1, u2) toR. Lete3be the edge with startu1 and endu2. Add (e1p1e3, e2p2) to C.
– Otherwise add (u2, u1) toR. Lete4be the edge with startu2and endu1. Add (e1p1, e2p2e4) to C.
This procedure is called thehomotopical completion procedureand can be seen in much greater detail in [9]. The main feature of this homotopical completion procedure is that extends the Knuth–Bendix completion procedure (see for instance [2, Subsection 2.4]) into a tool for computing coherent presentations, by keeping track of homotopy generators created when adding new rules. Note that, in general, the procedure is not guaranteed to terminate.
In particular, ifRis a complete rewriting system, then we can construct a coherent presentation forM in the following way: By Theorem2.4.2, we consider the subset Cof
P(2)Γ(P)as defined by (2.4.1). Thus, the extended presentationhP| Ciis a coherent presentation forM. Note that, sinceRis a complete rewriting system, to obtainhP| Ci fromP=hA|Ri, we apply a Tietze transformation toPthat consists only in elementary Tietze transformations of type (T5∗).
C
h
a
p
t
e
r
3
T h e p l a c t i c m o n o i d
In this chapter, we shall discuss three possible ways to define the plactic monoid: via generators and relations,tableaux and insertion, andcrystals, and also the interaction of the crystal structure with the combinatorics of Young tableaux (following [3]). We shall also present a finite complete rewriting system for the plactic monoid of rankn, from which a convergent presentation for it can be computed (following [4] and [10]).
3.1
The plactic monoid, Young tableaux and insertion
Consider the ordered alphabetA={1<2< . . .}. Theplactic monoid, denoted by plac, is presented byhA|Rplaci, whereRplacis the set of relations of the form
(cab, acb) witha≤b < c; (bca, bac) witha < b≤c ,
known as theKnuth relations.
Letn∈Nand consider the finite ordered alphabetA
n={1<2<· · ·< n}. Theplactic
monoidof rankn, denoted by placn, is presented byhAn|Rplaci, where in this case the set of defining relationsRplacis naturally restricted toA∗
n×A∗n.
We now proceed to introduce Young tableaux and related concepts, and then present an equivalent definition of the plactic monoid using these tools.
C H A P T E R 3 . T H E P L AC T I C M O N O I D
column shape. For example, the Young diagram of shape (4,3,2) is
. (3.1.1)
AYoung tableauis a Young diagram filled with symbols fromAsuch that entries in each row are non-decreasing from left to right, and entries in each column are (strictly) increasing from top to bottom. For example, a Young tableau of shape (4,3,2) is
1 2 2 5 2 3 6 4 5
. (3.1.2)
A Young tableau of shape (1,1, . . . ,1) is called acolumn.
Astandard Young tableauof shapeλ is a Young tableau with entries from{1, . . . ,|λ|} such that each symbol appears exactly once, entries in each row are increasing from left to right, and entries in each column are increasing from top to bottom. For example, a standard Young tableau of shape (4,3,2) is
1 3 5 6 2 7 8 4 9
(3.1.3)
A tabloid is a grid of cells, filled with symbols from A, obtained by concatenating columns, such that entries in each column are strictly increasing from top to bottom. Compared to a tableau, there is no restriction on the relative heights of columns, nor is there a condition on the order of entries in a row. Note that a tableau is a special case of a tabloid and that the shape of a tabloid cannot in general be expressed using a partition. An example of a tabloid is
5 3 4 1 2 4 5 8 6 7
9
. (3.1.4)
Letw=w1· · ·wkbe a word inA∗, withw
i∈A, fori= 1, . . . , k. We saywis arow wordif
wi≤wi+1for alli= 1, . . . , k−1. We saywis acolumn wordifwi> wi+1for alli= 1, . . . , k−1. The column reading C(T) of a tabloid T is the word in A∗ obtained by reading its columns from left to right, and reading each column from bottom to top. For exam-ple, the column reading of (3.1.2) is 421 532 62 5 and the column reading of (3.1.4) is 5 643 9754 1 82.
Letw∈A∗. Note that every word overA∗has a factorization into maximal decreasing factors. Letw(1)· · ·w(k) be such a factorization of w. Let Toid(w) be the tabloid whose
h-th column has height|w(h)|and is filled with the symbols ofw(h), forh= 1, . . . , k. Then,
C(Toid(w)) = w. Ifw is the column reading of a Young tableauT, it is called atableau word. By definition, it is immediate thatwis a tableau word if and only if Toid(w) is a
3 . 1 . T H E P L AC T I C M O N O I D , YO U N G TA B L E AU X A N D I N S E R T I O N
Young tableau. Thus, we conclude that not every word inA∗is a tableau word. Also note that the column reading of a column matches the definition of a column word, and the column reading of a row matches the definition of a row word.
We will now see how the plactic monoid can be defined using Young tableaux, by introducing an insertion algorithm that computes a (unique) Young tableauP(w) from a wordw∈A∗.
Algorithm 3.1.1(Schensted’s algorithm).
Input: A Young tableauT and a symbola∈A. Output: A Young tableauT ←a.
Method:
• Ifais greater than or equal to every entry in the topmost row ofT, addaas an entry at the rightmost end of the topmost row ofT and output the resulting tableau.
• Otherwise, letz be the leftmost entry in the top row of T that is strictly greater thana. Replacezbyain the topmost row and recursively insertzinto the tableau formed by the rows ofT below the topmost (note that the recursion may end with an insertion into an ‘empty row’ below the existing rows ofT).
Let w = w1· · ·wk be a word in A∗. By applying the algorithm iteratively, we can compute a unique Young tableau P(w): Starting with the empty word, we iteratively insert the symbolsw1, . . . , wk∈Ain order. After inserting the last symbol, we obtain the tableauP(w1· · ·wk). This algorithm also allows us to compute a standard Young tableau
Q(w), in the following way:
Algorithm 3.1.2.
Input: A wordw=w1· · ·wk, wherewi∈A, fori= 1, . . . , k.
Output: A Young tableauP(w) and a standard Young tableauQ(w).
Method: Start with an empty Young tableauP0and an empty standard Young tableau
Q0. For eachi= 1, . . . , k, insert the symbolwi intoPi−1 as per Algorithm3.1.1; letPi be the resulting Young tableau. Add a cell filled withi to the standard tableauxQi−1in the same place as the unique cell that lies inPibut not inPi−1; letQibe the resulting standard Young tableau. OutputPk forP(w) andQkforQ(w).
The mapw7→P(w), Q(w) is the well known Robinson–Schensted–Knuth correspon-dence, that is, a bijection between words in A∗and pairs consisting of a Young tableau over Aand a standard Young tableau of the same shape (For more information on the subject, see [17, Subsection 5.3]). For example, the sequence of pairs (Pi, Qi) produced during the application of Algorithm3.1.2to the word 3231 is:
(,), ( 3 , 1 ), 2
3 , 1 2
!
, 2 3
C H A P T E R 3 . T H E P L AC T I C M O N O I D
ThusP(3231) = 1 3 2 3
andQ(3231) = 1 3 2 4
.
The following result states the key combinatorial facts about tableaux:
Theorem 3.1.3([17, Theorem 5.1.1]). Letw∈A∗. The number of columns inP(w)is equal to the length of the longest non-decreasing subsequence inw. The number of rows inP(w)is equal to the length of the longest decreasing subsequence inw.
Thus, we are now able to present an alternative definition of the plactic monoid in terms of tableaux. Define≡placin the following way: For wordsu, v∈A∗,
u≡placv⇔P(u) =P(v).
Using this definition, it follows that≡plac is in fact a congruence onA∗(see [14]). Thus, the plactic monoid is the factor monoid A∗/ ≡
plac. The congruence≡plac, known as the
plactic congruence, naturally restricts to a congruence onA∗
n, and hence the plactic monoid of ranknis the factor monoidA∗
n/≡plac.
Note that ifwis a tableau word, then w=C(P(w)) and Toid(w) =P(w). Hence the tableau words inA∗(respectively,A∗
n) form a set of normal forms, called a cross-section, for plac (respectively, placn).
3.2
Kashiwara operators and the crystal graph
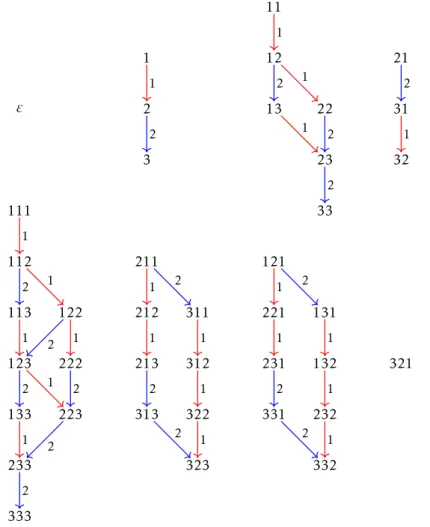
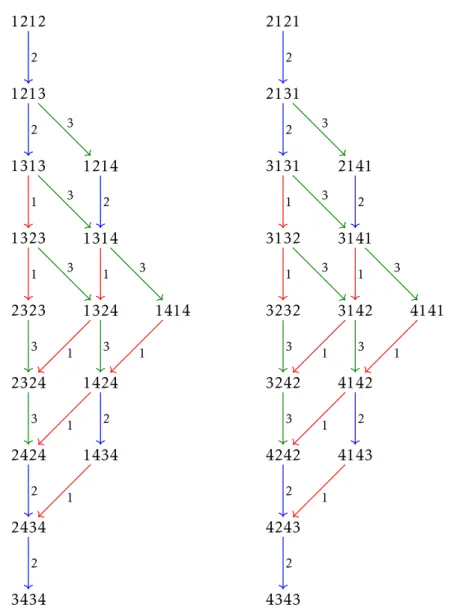
We will now introduce the concepts of crystal graphs and Kashiwara operators, in the context of placn. For a more general introduction to crystal bases, see [6].
TheKashiwara operatorse˜i and ˜fi, withi ∈ {1, . . . , n−1}, are partially defined opera-tors on A∗
n. They are described in a combinatorial way using the bracketing rule. The definitions of ˜eiand ˜fi start from thecrystal basisfor placn, which will form a connected component of the crystal graph:
1 1 2 2 3 3 . . . n−2 n−1 n−1 n.
Each operator ˜fi is defined so that it replaces a symbola with the end symbol of a directed edge labelled by i whenever such an edge starts at a, and each operator ˜ei is defined so that it replaces a symbolawith the start symbol of a directed edge labelled by
i whenever such an edge ends ata:
a i f˜i(a); e˜i(a) i a.
3 . 2 . K A S H I WA R A O P E R ATO R S A N D T H E C RYS TA L G R A P H
Thus, by looking at the crystal basis given before, we have that:
• ˜ei(i+ 1) =i, ˜ei(j) is undefined forj,i+ 1;
• ˜fi(i) =i+ 1, ˜fi(j) is undefined forj,i.
This definition is extended toA∗
n\Anby the recursion:
˜
ei(uv) =
˜
ei(u)v if ˜ǫi(u)>φ˜i(u);
ue˜i(v) if ˜ǫi(u)≤φ˜i(u),
˜
fi(uv) = ˜
fi(u)v if ˜ǫi(u)≥φ˜i(u);
uf˜i(v) if ˜ǫi(u)<φ˜i(u),
where ˜ǫiand ˜φi are auxiliary maps defined by
˜
ǫi(w) = max n
k∈N∪ {0} |e˜i· · ·e˜i |{z} ktimes
(w) is definedo
˜
φi(w) = max n
k∈N∪ {0} |f˜i· · ·f˜i |{z} ktimes
(w) is definedo.
Note that the definitions of ˜ei and ˜fi are not circular, since they depend, via ˜ǫi and ˜
φi, only on ˜ei and ˜fi applied to strictly shorter words. The recursion stops when ˜ei and ˜fi are applied to single letters, since we have already defined these applications by using the crystal basis. Also note that, although not immediate, it is possible to see that these operators are not only well-defined, but are also mutually inverse whenever they are defined, that is, if ˜ei(w) is defined, thenw= ˜fi(˜ei(w)) (and if ˜fi(w) is defined, then
w= ˜ei( ˜fi(w))).
Thecrystal graphfor placn, denoted byΓ(plac
n), is the directed labelled graph with vertex setA∗
nand, foru, v∈A∗n, an edge fromu tov labelled byi if and only ifu = ˜fi(v) (or, equivalently, ˜ei(u) =v). Note that the operators ˜ei and ˜fipreserve length. Therefore, since there are finitely many words in A∗
n of each length, each connected component in the crystal graph is finite. For anyw∈A∗
n, denote the connected component ofΓ(placn) that contains the vertexwbyΓ(plac
n, w).
Acrystal isomorphismbetween two connected components is a weight-preserving la-belled digraph isomorphism. In other words, if a mapθ:Γ(plac
n, u)→Γ(placn, v) verifies the following properties, then it is called a crystal isomorphism:
• θis bijective;
• wt(θ(w)) = wt(w), for allu∈Γ(plac n, u);
• For allw, w′ ∈Γ(plac
n, u), there is an edgeu i vif and only if there is an edge