Critial Phenomena in Gravitational
Collapse: The Studies So Far
Anzhong Wang
Departamento deFsiaTeoria,
UniversidadedoEstadodoRiodeJaneiro,
RuaS~aoFranisoXavier524,Maraan~a, 20550-013,RiodeJaneiro,RJ,Brazil
Reeivedon22February,2001
Studies of blak hole formation from gravitational ollapse have revealed interesting non-linear
phenomenaat thethresholdofblakhole formation. Inpartiular,in1993 Choptuikstudiedthe
ollapseofamasslesssalareldwithspherialsymmetryandfoundsomebehaviour,whihisquite
similartotheritial phenomenawell-knowninStatistialMehanisandQuantum FieldTheory.
Universality and ehoing of the ritial solutionand power-law saling of the blak hole masses
havegivenrisetothenameCritialPhenomenainGravitationalCollapse. Choptuik'sresultswere
soononrmedbothnumeriallyandsemi-analytially,andhaveextendedtovariousothermatter
elds. Inthispaper,weshallgiveabriefintrodution tothisfasinatingandrelatively newarea,
andprovideanupdatedpubliationlist. Ananalytial\toy"modelofritialollapseispresented,
andsomeurrentinvestigationsaregiven.
I Introdution
Gravitationalollapseofarealistibodyhasbeenone
ofthe mostimportantandthornysubjets inGeneral
Relativity (GR) sine the veryearly times of GR [1℄.
The ollapse generallyhas four kinds of possible nal
states. The rstis simplythe haltof theproess in a
self-sustainedobjet,suhas,stars. Theseondisthe
dispersion of the ollapsing objet and nally leaves
behind a at spaetime. The third is the formation
of blak holeswith outgoinggravitationaland matter
radiation, while the fourth is the formation of naked
singularities. For the last ase, however, the osmi
ensorshiphypothesis[2℄delaresthatthesenaked
sin-gularitiesdonotourin Nature.
DuetothemathematialomplexityoftheEinstein
eldequations,wearefrequentlyforedtoimposesome
symmetriesonthe onernedsystemin orderto make
theproblemtratable. Spaetimeswithspherial
sym-metryareoneoftheases. Inpartiular,gravitational
ollapseofaminimally oupledmasslesssalareld in
suh spaetimes wasstudied both analytially[3℄ and
numerially[4℄, and somefundamental theorems were
established. Quitereentlythisproblemhasfurther
at-tratedattention, due to Choptuik'sdisoveryof
rit-ialphenomena that were hitherto unknown[5℄. As a
matteroffat,itissoattrativethatCritial
Phenom-enain GravitationalCollapse hasalreadybeenavery
establishedsub-areainGR,andseveralomprehensive
reviewartilesalreadyexist[6, 7,8,9,10,11, 12, 13℄.
Inthispaper,asummaryofaninvitedtalkgivenat
the XXI Brazilian National Meeting on Partiles and
Fields,weshallrstbrieyreviewthesubjetandgive
an updatedlist of publiation in this area,whih will
bedonein Se. II.Then, in Se. III,weshallpresent
ananalyti\toy"modelofaollapsingmasslesssalar
eld. Theword\toy"modelheremeansthatthemodel
doesn'treally representritialollapse, sinethe
per-turbationsoftheorresponding\ritial"solutionhave
morethan one unstablemode. However, itdoeshave
allthemainfeaturesofritialollapse. Sinesofar,no
anyritialsolutionisknownexpliitlyinaloseform,
thistoymodelstillservesasagoodillustrationto
rit-ialphenomenaingravitationalollapse. Thepaperis
losedbySe. IV,inwhihsomeurrentinvestigations
in thisfasinatingareaaregiven.
II Critial phenomena in
gravi-tational ollapse
Startingwithspherialspaetimes,
ds 2
=
2
(t;r)dt 2
+a 2
(t;r)dr 2
+r 2
d 2
; (1)
where d d 2
+sin 2
d' 2
, and fx
g = ft;r;;'g
aretheusualspherialoordinates,Choptuik[5℄
inves-tigatedgravitationalollapseofamasslesssalareld,
,whihsatisestheEinstein-salareldequations, R = ; ; ;
2 = 0; (2)
whereR
denotestheRiitensor,[8G= 4
℄isthe
gravitationalouplingonstant,()
;
=()=x ; 2 g r r
, and r
denotes the ovariant derivative.
One an initial smooth onguration of the massless
salareldisgiven,theseequationsuniquelydetermine
thelaterevolutionofthespaetimeandthesalareld
[3℄. Let the initial distribution of the massless salar
eldbeparameterizedsmoothlybyaparameterpthat
haraterizesthestrengthoftheinitialonditions,suh
thattheollapseofthesalareldwiththeinitialdata
p >p
forms ablakhole, while the onewith p<p
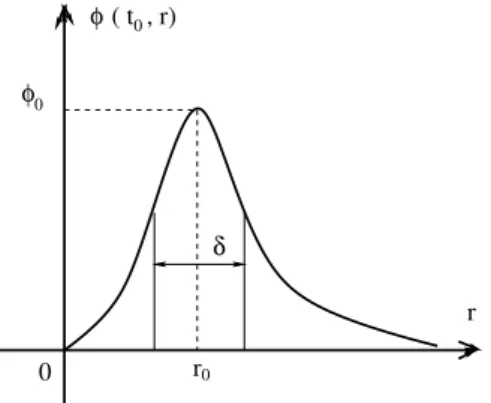
doesnot. Asimpleexampleisthegaussiandistribution
ofthemasslesssalareld
(t
0 ;r)=
0 r r 0 3 exp r r 0 Æ q ; (3) where t 0
denotes the initial time of the ollapse, and
0 ; r
0
; Æ,and qareonstants[SeeFig. 1℄.
φ
r
0
r
φ
( t , r)
0
0
0
δ
Figure 1. The initial onguration of the massless salar
eld att=t
0
givenby Eq.(3)inthe text. It atually
rep-resents a ollapsing spherial shell, made of the massless
salar eld,withitsthiknessÆandentralizingatthe
ra-diusr=r
0 .
0
representstheamplitudeofthewavepaket.
Inthisase,Choptuik foundthattheparameterpan
beanyofthefourparameters,
p=f
0 ; r
0
; q; Æg; (4)
that is,xinganythree ofthefour parameters,for
ex-ample,r
0
; Æandq,andleavingonly
0
hange,weshall
obtain a familyof initial data, S[
0
℄. For this family
of initialdata Choptuikfoundthat there existsa
rit-ial value
0
suh that when
0 >
0
theollapse
al-waysformsblakholes,andwhen
0 <
0
themassless
salar eld rst ollapses, then disperses to spaelike
innity,andnallyleavesaatspaetimebehind
with-outforminganykindofspaetimesingularities. When
0 0 + 0 , where 0
is verysmall,after ertain
theritial one (
0 =
0
). But, at the veryend, the
ollapsewillsuddenlyruns awayfrom theritialone,
by either forming blak holesordispersingto innity,
dependingonthesignsof
0
. Choptuikfoundthatfor
theongurationofEq.(3)therearefourdierent
fam-ilies ofinitial data, S[
0 ℄; S[r
0
℄; S[Æ℄ and S[q℄, whih
allexhibit theabovebehaviour.
In addition to these four, Choptuik also studied
many others and found that for all the families that
behaveasabove,the so-alledgenerismooth families
of initial data, all the ritial solutions are idential,
or in another word, universal. Moreover, the ritial
solutionisalsoperiodi, thatis,
A
(;)=A
(; +4); (5)
whereA =f ;a ; g,and =ln t r 0
; =ln r t 0
(); (6)
withr
0
beingadimensionfulonstant,and
0
()a
pe-riodiotherwisearbitraryfuntionwithperiod4. The
onstant4isadimensionless onstant,whihwas
nu-meriallydeterminedas43:447.
Yet,near theritialsolutionbut withp>p
, the
massofblakholestakesthesalingform
M
BH
=K(p p
)
; (7)
where K is a family-dependent onstant, but is
an-otherdimensionless universalonstant,whihwas
nu-meriallydeterminedas0:37.
Universalityandehoingoftheritialsolutionand
power-lawsaling of theblakhole masseshave given
riseto the name Critial Phenomena in Gravitational
Collapse.
Choptuik's results were soon onrmed by several
independent studies both numerial [14℄ and
semi-analytial[15℄,andhavebeenextendedtoothermatter
elds,suhas,
Axisymmetrigravitationalwaves[16℄;
Perfetuids with theequation of statep=k,
where p denotes the pressure of the uid and
theenergydensity,andkisaonstant[17,18℄;
Quantum blak holeformation in 2-dimensional
spaetimes[19℄;
Non-linear -models in two dimensional target
spae[20℄;
Masslesssalareldin Brans-Diketheory[21℄;
SU(2)Yang-Millseld [22℄;
Gravitationallyollapsingprimordialdensity
u-tuations intheradiationdominatedphaseofthe
earlyUniverse [25℄;
SU(2)Skyrmeeld [26℄;
The ollapse of ollisionless matter of the
Einstein-Vlasovequations[27, 28℄;
Topologial domain walls interating with blak
holes[29℄;
Thegravitationalollapseofmasslesssalareld
in higherdimensional spaetimes[30℄;
Non-linear -models in three dimensional target
spae[31℄;
GravitationalollapseinTensor-Multi-Salarand
Non-linearGravityTheories[32℄;
Bosonstars[33℄;
Massless salar eld oupled with the
osmo-logialonstantin (2+1)-dimensionalspaetimes
[34℄.
In review of all these studies, nowthe followingis
lear:
(a) In general the ritial solution and the two
di-mensionlessonstants4andareuniversalonly
withrespettothesamemattereld,andusually
are matter-dependent. Forexample, forthe
ol-lapseoftheSU(2)Yang-Mills eld,itwasfound
[22℄ that 4 0:74 and 0:2, while in the
aseofmasslesssalareld,Choptuikfoundthat
43:447and0:37.
(b) The ritial solutions an have disrete
self-similarity(DSS)[35℄orontinuousself-similarity
(CSS) [36℄, or none of them, depending on the
mattereldsandregionsoftheinitialdataspae.
So far, in all the ases where the ritial
solu-tioneither hasDSS orCSS,blakholesform
al-ways startingwith zeromass,and taketheform
ofEq.(7),theso-alledTypeII ollapse,whilein
theasesinwhihtheritialsolutionhasneither
DSSnorCSS,theformationalwaysturnsonwith
amass gap,theso-alled TypeI ollapse,
orre-sponding, respetively, to the seond- and
rst-order phase transitions in Statistial Mehanis
[37℄.
() The universality of the ritial solution and the
exponent now arewell understood in termsof
perturbations ofritial solutions[18℄, whilethe
one of 4 still remains somewhat of a mystery.
Theformeris loselyrelatedtothefat thatthe
perturbationsoftheritialsolutionhasonlyone
unstable mode. This propertynowis onsidered
asthemain riterionforasolutionto beritial
Tounderstandthe lastpropertybetter,letus
on-sider the phase spae, that is, onsider GR as an
innite-dimensional dynami system. If we make a
(3+1) split of the spaetime, for example, following
the Arnowitt, Deser, and Misner (ADM)
deomposi-tion,wewillndthatthedynamiquantitieswillbethe
indued spatial three metri, the extrinsi urvature,
and the matter distribution. Then, the phase spae
will onsist of all the possible three metris, extrinsi
urvature, andongurationsofthematterelds. For
the aseof masslesssalareld,from theno-hair
the-oremofblakholes[38℄,weknowthat theonlystable
blakholesolutionoftheEinstein-salareldequations
is the Shwarzshild blak holewith aonstant
mass-less salar eld. Exept for this blak hole, another
stable stateis theMinkowskianspaetime. Ofourse,
wealsoknowthattheollapseofamasslesssalareld
an form naked singularities,too, but so farwedon't
know if they are stable or not [1℄. At this point, we
shall adopt thepointof viewof theosmi ensorship
onjeture [2℄, and assume that they are not stable.
Otherwise, theremayexist twomoreritialsolutions
thatseparate,respetively,blakholesfromnaked
sin-gularities,andatspaetimesfromnakedsingularities.
However,thisdoesn'taetourfollowingdisussionsif
weare restrited onlyto theboundary betweenblak
holesandatspaetimes,andtheanalysisanbeeasily
extended tootherboundaries.
p*
p > p*
*
A
S
S[p]
Flat
Space-Times
Black
Holes
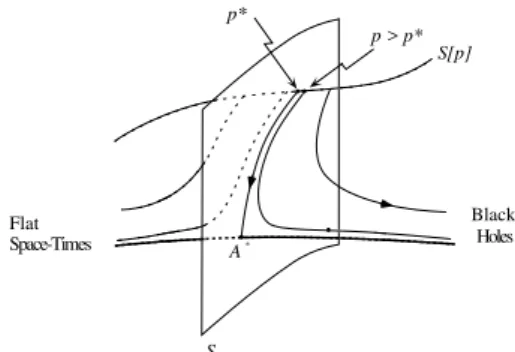
Figure 2. The phase spae of the dynami system of the
Einstein-salar eld equations. Thehypersurfae S is the
ritial surfae of odimension one, whih separates the
basin of blak holes from the basinof at spaetimes. A
generismoothfamilyofinitialdataS[p℄alwayspassesthe
twobasins at the ritial point p = p
onthe ritial
hy-persurfae. All the initial data on the hypersurfae will
ollapseto theritial solutionA
that isaxedpoint on
the hypersurfae whenit has CSS anda xed ylewhen
it hasDSS.Alldetails ofinitial dataare soonwashedout
during theollapsingproess,andthe ollapsewithinitial
dataneartheritialpointwillbeverysimilartothe
riti-alollapse. Thissimilarityanbelastalmosttothexed
point A
,whereby theoneunstablemodesuddenlydraws
the ollapse eitherto form blak hole or a atspaetime,
dependingonwhetherp>p
orp<p
.
theatspaetimeswithdierentonstantvaluesofthe
salareld,areattrativexedpoints,whileinsidethe
basinofblakholes,theShwarzshildblakholeswith
dierent masses are the attrating xed points. The
boundary between the two attrative basins is alled
the ritial surfae, and the ritial solution always
lies on it. Sine it has only one unstable mode, this
surfae must be a hypersurfae of odimension one,
that is, one dimension less than the original
innite-dimensional phasespae. Bydenition, aphase spae
trajetoryneverleavesthishypersurfae,ifitisinitially
onit,butapproahestotheritialsolution,whihisa
xed point onthishypersurfaeifthe ritialsolution
isontinuousself-similar,oraxedyleiftheritial
solution is disrete self-similar [13℄. Within the
om-plete phase spae, the ritial solutionis anattrator
of odimension one, i.e., it has an innite number of
deayingperturbation modestangentialtothe ritial
hypersurfaeandasinglegrowingmodeperpendiular
tothehypersurfae. Anytrajetorybeginningnearthe
ritialhypersurfae,butnotneessarilynearthe
riti-alpoint(oryleintheDSSase),rstmovesparallel
to thehypersurfaeand goesdownalmost to the
rit-ial point (or yle), then is suddenly drawn away by
thesingleunstablemodeintheperpendiulardiretion,
andnallyendsupatoneofthexedpoints,byeither
formingablakholeoraatspaetime. Duringthe
dy-namiproess,alldetailsoftheinitialdataarequikly
washed away, exept for the distane from the blak
hole threshold. Therefore, for the both super-ritial
(p>p
)andsub-ritial(p<p
)ollapse,thereexists
adomain,p
4ppp
+4p,inthephasespae,
in whihtheollapseisverysimilar totheritialone
during ertainperiodoftimes[SeeFig.2℄.
III Critial ollapse of massless
salar eld: an analyti Toy
model
Inthissetion,weshallpresentalassofanalyti
solu-tionsoftheEinstein-salareldequations,whih
repre-sentsgravitationalollapseofawavepaketonsisting
ofmasslesssalareld[39℄. Thislassofsolutionswas
rst disovered by Roberts [40℄ and later studied by
severalauthors in the ontext of ritialollapse [41℄.
Asweshallshowbelow,thesesolutionspossessmostof
thefeaturesofritialphenomena,althoughtheydon't
exatlyrepresentritialollapse,beausethesolution
thatseparatestheformationofblakholesfromthatof
atspaetimeshasmorethanoneunstablemode[42℄.
It is exatly in this sense, we refer these solutions as
representinga\toy"modelofritialollapse.
TheRobertssolutionsaregivenby[40℄
ds 2
= G(u;v)dudv+r 2
(u;v)d 2
; (8)
whereuandv representtwonulloordinates,interms
ofwhihthe metrioeÆientsandthe orresponding
masslesssalareld are given,respetively,by
r(u;v) = 1
2 u
2
2uv+4b
2 v
2
1=2
;
G(u;v) = 1; (9)
(u;v) = 1
p
2 ln
(u v) (1 4b
2 )
1=2
v
(u v)+(1 4b
2 )
1=2
v
;(10)
where b
2
is an arbitrary onstant. Note that the
no-tations used here losely follow the ones used in [39℄
butslightlydierentfrom theones used in[40℄. From
Eq.(9)itanbeeasilyshownthat theloalmass
fun-tion[43℄ isgivenby
m(u;v) r
2 1 r
; r
; g
=
(1 4b
2 )uv
8r
; (11)
whih is zero onthe hypersurfaev =0 and negative
for u; v < 0. Thus, to have a physially reasonable
spaetimeweneedto restrittheabovesolutionsvalid
onlyin theregionu0; v0. Sinethemassiszero
onthehypersurfaev=0,wemayjointheabove
solu-tionsarossthehypersurfaev=0withaMinkowskian
spaetime. Asshownin[39℄,thisispossibleifthe
met-riintheregionv0takestheformofEq.(8)butwith
themetrioeÆientsandthemasslesssalareld
be-inggivenby
r(u;v) = a(v) 1
2
u a(0);
G(u;r) = 2a 0
(v); =0; (v<0); (12)
wherea(v)isanarbitraryfuntionsubjettoa 0
(v)>0
and a 0
(0) = 1=2, and a prime denotes the ordinary
dierentiationwithrespet totheindiatedargument.
Forsuha mathing, itanbeshownthat the
hyper-surfae v = 0 is free of any kind of matter and
rep-resentsa boundary surfae [44℄. The region v < 0 is
Minkowskian[SeeFig.3℄.
Ontheotherhand,fromEqs.(9)and(10)itanbe
alsoshownthatthespaetimeintheregionu<0;v>0
represents a ollapsing massless salar wave. When
b
2
<0, thesalarwaveollapsesinto aspaetime
sin-gularityonthehypersurfaeu= [(1 4b
2 )
1=2
1℄v,
whihispreeded byanapparenthorizonat u=4b
2 v.
Thus,theorrespondingsolutionsrepresentthe
forma-tionof blak holes. When b
2
= 0, the singularity
o-inides with the apparent horizon on the null
hyper-surfaeu =0. When0 < b
2
<1=4, it an beshown
that the massless salar eld rst ollapses and then
dispersesintoinnity,withoutformingblakholes,but
instead,leavesaMinkowskianspaetimebehind,whih
nowisrepresentedbytheregion,u;v>0,inwhihthe
metritakestheform ofEq.(8),butwith
G(u;v) = 4b 1=2
b 0
(u); r=b 1=2
(u;v) = 1 p 2 ln
1+(1 4b
2 )
1=2
1 (1 4b
2 )
1=2
;
(0<b
2
<1=4; u;v>0); (13)
where b(u)is anarbitraryfuntion,subjetto b 0
(u)>
0;b 0
(0)=1=(4b 1=2
2
). Oneanshow that the
hypersur-faeu=0;v>0isalsofreeofanykindofmatterand
representsaboundarysurfae.
Vaidya
u
v
0
v
φ
M
4
0
Figure 3. The spaetime inthe (u; v)-plane. Theregion
v<0isMinkowskian,whiletheregionu0; v0
repre-sentsgravitationalollapseofthemassless salareld. (a)
When b2 < 0, the salar wave ollapses into a spaetime
singularity at u = [(1 4b
2 )
1=2
1℄v <0, whihis
pre-ededby anapparenthorizon loatedat u= 4jb
2 jv <0.
(b)Whenb
2
=0,the spaetimesingularity oinideswith
the apparent horizon on u = 0 whih is null. () When
0 <b2 < 1=4, the massless salar eld rst ollapses and
thendispersesintoinnity,andnallyleavesaMinkowskian
spaetimebehindintheregionu; v>0.
Inthe ase b
2
< 0, where blak holes are formed,
Eq.(11)showsthatontheapparenthorizonu= 4jb
2 jv
themassbeomesunboundedasv!+1. Inorderto
haveblak holeswith nite mass, we shall follow [39℄
rsttoutthespaetimealongthehypersurfaev=v
0
and then join the region 0 v v
0
with an
asymp-totiallyatregion. Tomodeltheout-goingradiation
of themasslesssalareld, weshall hoose theregion
vv
0
asdesribedbytheVaidyasolution[45℄,
ds 2 = 1 2m(U) r dU 2
+2dUdr+r 2
d 2
;
(vv
0
); (14)
where U is the Eddington retarded time, whih is in
generalthefuntionofuappearinginEq.(8),andm(U)
istheloalmassoftheout-goingVaidyadust. The
or-respondingenergy-momentumtensorisgivenby
T + = 2 r 2 dm(U) dU Æ U Æ U
; (vv
0
): (15)
The hypersurfae v = v
0
in the oordinates fx
g =
fU; r; ; 'gisgivenby
dU(r)
=
2r
; (vv
0
): (16)
Then, itanbeshown thatthejuntion onditionson
thehypersurfaev=v
0
require
M(r) m(U)j
v=v0 = 1 r h p(4p 2 +r 2 ) 1=2 2p 2 i ; v 0 = 4p 2 p ; (17)
wherepistheintegrationonstant,and
p (1 4b 2 ) 1=2 4 v 0 : (18)
Forthedetails, we referreaders to [39℄. Sine for the
abovemathing,thehypersurfaev=v
0
isfreeof
mat-ter,thefuntion M(r)representsthetotalmassofthe
ollapsing wavepaket lledin theregion 0v v
0 .
Atthepastnullinnity,Eq.(17)showsthat
M(r!+1)=p; (19)
that is, theparameterpinthepresentaserepresents
thetotalinitialmassofthemasslesssalarwavepaket
withwhihitstartstoollapse.
As r ! 0 +
, from Eq.(17) we an see that M(r)
behavesas
M(r)! (
+1; p>p
,
0; p=p
,
1; p<p
.
(20)
M (r)
(a)
f = r/2
(b)
(c)
0
p
r
AH
r
*
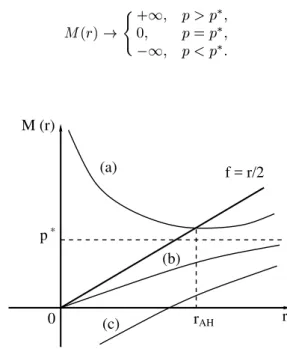
Figure 4. The mass M(r) of ollapsing spherial shell.
The line (a) orresponds to the ase where p > p
, in
whih a blak hole is formed, and its mass is given by
MBH = M(rAH). The line (b) orresponds to the ase
where p = p
, while the line () orresponds to the ase
wherep<p
.
On the other hand, it is well-known that the
ap-parent horizon at r =2M(r)of the out-goingVaidya
Thus, by omparing the mass M(r) with r=2 we an
tellwhethertheollapseformsablakholeornot,
M(r) r
2 =
(
4p
2
+r 2
4r 2
[p+(4p
2
+r 2
)℄ )
1=2
h
4(p 2
p
2
) r 2
i
: (21)
Clearly,onlywhenp>p
,thesalareldandthenull
shell willollapseinside theeventhorizonat
r
AH =2(p
2
p
2
) 1=2
: (22)
r = 0
A H
EH
φ
Vaid.
M
0
v
0
4
(a)
M
0
v
r = 0
Vaid.
4
0
φ
(b)
M
M
0
v
4
0
4
Vaid.
0
φ
(c)
Figure 5. The orresponding Penrose diagrams. (a) The
asewherep>p
,inwhihablakholeis formed,andits
mass is givenby MBH = M(rAH). (b)It orrespondsto
thease where p=p
,inwhih thespaetime singularity
beomesnull andoinideswiththeapparent horizon. ()
Itorrespondstotheasewherep<p
,inwhihno
spae-timesingularityisformed,instead,whenthewavepaketof
themasslesssalareldollapsestothehypersurfaeu=0,
allofitsmasshasbeenradiatedawayandnothingisleftto
ollapse, so thespaetime intheregion u; v0beomes
Minkowskian.
Whenp=p
,M(r)=r=2ispossibleonlyattheorigin,
r=0,where azero-masssingularityis formed. Thus,
thesolutionwith p=p
representsthe\ritial"
solu-tionthat separatesthesuperritialsolutions(p>p
)
from the subritial ones (p < p
). In the subritial
ase, M(r) is always less than r=2, and the ollapse
neverforms ablakhole[f. Fig.4℄.
In the subritial ase, the region u;v > 0should
be replaed by the Minkowskian solution (13). As
shown above, the mathing aross the hypersurfae
u=0; 0vv
0
issmooth,i.e.,nomatterappearson
it. Toshowthatitisalsotheaseonthehypersurfae
u=0; vv
0
,whihseparatestheVaidyasolution(14)
from theMinkowskianone(13),werst makethe
o-ordinatetransformationU =U(u),andthen writethe
metri(14)intermsofu. Usingtheresultsobtainedin
[46℄,oneanshowthatto haveasmoothmathingwe
havetoimpose theondition
U 0
(0)= 1
(4b
2 )
1=2
; (23)
Clearly,byproperlyhoosingthe funtion-dependene
of U(u), the rst ondition (23) an be always
satis-ed. Ontheotherhand,fromEqs.(9)and(17)onean
showthatthelastonditionisalsosatisedidentially.
Therefore, themathing of the Vaidyasolutionto the
Minkowskianonearossthehypersurfaeu=0; vv
0
isalwayspossibleforp<p
. Theorresponding
Pen-rose diagram for eah of the three asesare shown in
Fig. 5.
Ontheapparenthorizonr=r
AH
,thetotalmassof
thesalarwavepaket isgivenby
M
BH =
1
2 r
AH
=K(p p
) 1=2
; (25)
where K (p+p
) 1=2
. The above expression shows
that theblakholemass takesapower-lawform with
its exponent =0:5, whih is dierentfrom theDSS
ase, where Choptuik found 0:37. As we
men-tionedpreviously,theabovesolutionsdon'treally
rep-resent ritial ollapse, beause the \ritial" solution
given above has more than one unstable modes [42℄.
Therefore, the dierent value of obtained here does
not means any ontridition to Choptuik's numerial
results.
IV Current Investigations
As Critial Phenomena in gravitational ollapse is a
rathernewareainGR,therearemanyopenproblems.
Inthefollowingweshallmentionsomeofthem.
A. The eets of angular momentumin ritial
ollapse
As we know, the angular momentum plays avery
signiantroleinblakholephysis,andallthe
realis-tibodies,suhas,neutronstars,havenon-zeroangular
momentum. Thus,itisveryimportanttostudythe
ef-fetsofangularmomentumonritialollapse. Sofar,
all the studies of ritial phenomena in gravitational
ollapse havebeenrestrited to spherialase, exept
for the works of Abrahams and Evans [16℄ and
Alu-bierreet al. [47℄. In[16℄ the authors studied the
ol-lapseof axisymmetri purely gravitationalwaves,and
found the type II ritial ollapse. However, in this
studythetotalangularmomentumisstillzero. In[47℄
theollapseofpureBrilltypegravitationalwavesin3D
Numerial Relativity wasstudied and the ritial
am-plitudeforblakholeformationwasdetermined.
How-ever,duetotheomplexityoftheproblem,nosuÆient
evideneforritialollapsewasobserved.
In addition to the above, Gundlah and his
o-workers [48℄ studied the problem using non-spherial
perturbations, and in partiular found that all the
modes of non-spherial perturbations of the massless
salar eld studied initially by Chpotuik are stable,
the spherial ase may remain ritial even in
non-spherial ase. He also found that small angular
mo-mentumalsotakesasalingformneartheritialpoint
but with adierentexponent. Besides, Rein, Rendall
andShaeer[27℄studiedthespherialollapseof
ol-lisionlessmatterthatonsistsofounter-rotating
parti-les,andfoundthatonlyTypeIritialollapse. This
result was further onrmed by Olabarrieta quite
re-ently[28℄.
Movingfromspheriallysymmetriaseto
axisym-metrione,theproblembeomesmuhmathematially
involved, and very sophistiated (numerial)
meth-ods are needed. Choptuik, Hirshmann and Liebling,
among others, havebeenworking on this problem
re-ently [49℄, and are expeted to report their results
soon.
B. The quantumeets on ritialollapse
Critialphenomena areatuallyphenomena in the
stronggravitationaleld regime,and Quantum eets
should be very important for the formation of blak
holeswithverysmallmass. ChibaandSiino[50℄
stud-iedthisproblem andshowedthattheQuantumeets
maydestroythetypeIIritialphenomena,whileAyal
andPiran[51℄ showedthattheydon't,butrathershift
theritialvaluep
. However,sineinbothofthetwo
asesthe Quantum eetive energy-momentumtensor
(EMT)wastakenfromtwo-dimensionaltoymodel,the
onsisteneofsuhanEMTwiththefour-dimensional
gravitational ollapse is still an open question.
Re-ently,Bradyand Ottewill[52℄alulatedtheeetive
EMTofaonformallyoupledsalareld onthexed
bakgroundoftheritialsolutionsoftheperfetuid
with the equationof state p=k in four-dimensional
spherial spaetimes, and found that when k < 0:53,
the Quantum eets destroy the type II ritial
phe-nomena, whilewhen k >0:53 theiralulationsbreak
down,andadenitiveonlusionisstill absent.
C.Theappliationofrenormalizationgroup
the-ory to ritialollapse
The Renormalization Group Theory has ahieved
great suess in the studies of ritial phenomena in
StatistialMehanis[37℄,andseveralauthors,
inlud-ingArgyres[53℄,andKoike,HaraandAdahi[18℄,have
pointedoutthatthetimeevolutionneartheritial
so-lution ingravitationalollapsemayalso beonsidered
as arenormalizationgroupow onthe phasespaeof
initial data. As a matter of fat, the analysis of the
phasespaegivenin theIntrodutionexatlyfollowed
this idea. However, this analysis is valid onlyin
self-similar spaetimes. Inorder toobtainafull
renormal-ization group, one needs to generalize them to
arbi-traryspaetimes,whih isturnedoutnottrivial,as in
ar-initial stepsto thisdiretion,but asuessful
applia-tion of the Renormalization Group Theory to ritial
ollapsestillremainsasanopenquestion.
Besides the above mentioned problems many
oth-ers are also under the urrent investigations, suh as,
ndingmoremattereldsthatexhibitritialollapse,
inludinguniversallasses;applyingtheanalysisof
per-turbations of blak holes to ritial solutions;
under-standingitsphysialoriginoftheonstant4[55℄;
nd-ing somepossibleastrophysialobservationsof ritial
phenomena,andsoon. Inpartiular,itwasknownfor
alongtime that theollapseof neutronstarsexhibits
thetypeIritialphenomena[56℄. Animportant
ques-tionisthat: DoesthistypeIritialollapsehaveany
observationalonsequene?
Forfurtherreferenesofritialphenomenain
grav-itationalollapse,wewouldliketoreferthereadersto
thereviewartiles[6,7,8,9,10,11,12, 13℄.
Aknowledgments
The author would like to express his gratitude to
M.W. Choptuik, S.L. Liebling, J. Pullin, and W.M.
Suenforvaluabledisussionsandsuggestionsinritial
ollapse. Hewouldalsolikeverymuhtothankhis
ol-laboratorsinthisarea,C.F.C.Brandt,R.-G.Cai,E.W.
Hirshmann,L.-M.Lin,H.P.deOliveira,J.F.Villasda
Roha, N.O. Santos, and Y.M. Wu. Thenanial
as-sistanefromCNPqis gratefullyaknowledged.
Referenes
[1℄ P.S.Joshi, GlobalAspets inGravitationand
Cosmol-ogy (Clarendon Press, Oxford, 1993); \Gravitational
Collapse: TheStorysofar,"gr-q/0006101.
[2℄ R.Penrose,Riv.NuovoCimento1,252(1969).
[3℄ D. Christodoulou, Commun. Math. Phys. 105, 337
(1986);ibid.106,587(1986);ibid.109,591(1987);ibid.
109,613(1987);Commun.PureAppl.math.XLIV,339
(1991); Ann. Math. 140, 607 (1994); ibid., 149, 183
(1999).
[4℄ D.S. Goldwirth and T. Piran, Phys. Rev. D36, 3575
(1987).
[5℄ M.W.Choptuik,\CritialBehaviourinMasslessSalar
Field Collapse," inApprohes to NumerialRelativity,
Proeedings of the International Workshop on
Numer-ial Relativity, Southampton, Deember, 1991, Edited
byRayd'Inverno;Phys.Rev.Lett.70,9(1993);M.W.
Choptuik,\CritialBehaviourinSalarFieldCollpase,"
inDeterministiChaosinGeneralRelativity,Editedby
D. Hobill etal. (Plenum Press, New York, 1994), pp.
155-175;M.W.Choptuik,E.W.Hirshmann,andS.L.
Liebling,Phys.Rev.D55,6014 (1997).
[6℄ A.M.AbrahamsandC.R.Evans,Gen.Relat.Grav.26,
379(1994).
[7℄ C. Gundlah, \Critial phenomena in gravitational
143, Institute ofMathematis, PolishAademy of
Si-ene (Banah Center Publiations), Warszawa 1997,
gr-q/9606023.
[8℄ P. Bizon, Ata Cosmologia 22, 81 (1996),
gr-q/9606060.
[9℄ J.Horne,\Critialbehaviorinblakholeollapse,"
Mat-tersofGravity7,14(1996),gr-q/9602001.
[10℄ M. W. Choptuik, \The (unstable) threshold of blak
hole formation," talk given at GR15, Pune, India, to
appearintheproeedings,gr-q/9803075.
[11℄ C. Gundlah, Adv. Theor. Math. Phys. 2 1 (1998),
gr-q/9712084.
[12℄ S.L. Liebling, J. Phys. PRAMANA (India), 55, 497
(2000),gr-q/0006005.
[13℄ C.Gundlah,\Critialphenomenaingravitational
ol-lapse,"gr-q/0001046.
[14℄ C.Gundlah,J.Pullin,andR.Prie, Phys.Rev.D49,
890(1994);D.Garnkle, Phys.Rev.D51,5558(1995);
R.S.HamadeandJ.M.Stewart,Class.QuantumGrav.
13,497 (1996), S.Hod and T.Piran,Phys.Rev.D55,
R440(1997).
[15℄ C.Gundlah,Phys.Rev.Lett.75,3214(1995); Phys.
Rev.D55,695(1997).
[16℄ A.M.AbrahamsandC.R.Evans,Phys.Rev.Lett.70,
2980(1993);Phys.Rev.D49,3998(1994).
[17℄ C.R.Evansand J.S.Coleman,Phys.Rev.Lett. 72,
1782(1994); D. Maison, Phys.Lett. B366,82 (1996);
M.Goliath,U.S.Nilsson,andC.Uggla,Class.Quantum
Grav. 15,2841 (1998);D.W. Neilsen andM.W.
Chop-tuik,ibid., 17, 733(2000); ibid., 17,761 (2000); B.J.
Carr,A.A.Coley,M.Goliath,U.S.Nilsson,andC.
Ug-gla,Phys.Rev.D61,081502(2000);C.Gundlah,
\Crit-ialgravitational ollapseofa perfetuidwithp=k:
Nonspherialperturbations,"gr-q/9906124.
[18℄ T.Koike,T.Hara,andS.Adahi,Phys.Rev.Lett.74,
5170(1995);Phys.Rev.D59,104008(1999).
[19℄ A.StromingerandL.Thorlaius,Phys.Rev.Lett.72,
1584 (1994); J.-G. Zhou, H.J.W. Muller-Kirsten, and
M.-Z.Yang,Phys.Rev.D51,R314(1995);Y.Peleg,S.
Bose,andL.Parker,ibid.,D55,R4525(1997);L.Parker
andY.Peleg,\QuantumMassGapattheThresholdof
BlakHoleFormationI&II,"inProeedingsofthe8th
MarelGrossmannMeetingonGR,Ed.T.Piran,22-27,
June, 1997, Jerusalem, Israel(WorldSienti, 1997),
pp.723-727.
[20℄ E.W. Hirshmannand D. M. Eardley, Phys.Rev.D
51,4198(1995);ibid.D52,5850(1995);ibid.D56,4696
(1997); D. M. Eardley, E. W. Hirshmann, and J. H.
Horne, ibid., D52, 5397 (1995); R. S. Hamade and J.
M. Stewart, Class. Quantum Grav. 13, 497 (1996); S.
Liebling,Phys.Rev.D58,084015 (1998).
[21℄ S.L. Liebling and M. W.Choptuik, Phys.Rev.Lett.
77,1424 (1996); S.L.Liebling, M.A. Thesis, The
Uni-versityofTexasatAustin,1995(unpublished).
[22℄ M.W.Choptuik,T.Chmajand P.Bizon,Phys.Rev.
Lett. 77, 424 (1996); C. Gundlah, Phys. Rev. D55,
6002 (1997); M. W. Choptuik, E. W. Hirshmann, R.
[23℄ C.GundlahandJ.M.Martn-Gara,Phys.Rev.D54,
7353-7360(1996);S.HodandT.Piran,ibid.,D55,3485
(1997).
[24℄ P.R.Brady,C.M.Chambers,S.M.C.V.Gonalves,
Phys.Rev.D56,6057(1997).
[25℄ J.C. Niemeyer and K. Jedamzik, Phys. Rev. Lett.
80, 5481 (1997); Phys. Rev. D59, 124013 (1999); J.
Yokoyama,ibid.,D58,083510(1998);K.Jedamzikand
J.C. Niemeyer, ibid., D59, 124014 (1999); A.M.Green
andA.R.Liddle,ibid.,D60,063509 (1999).
[26℄ P. Bizon and T. Chmaj,
Phys.Rev.D58,041501(1998),AtaPhys.Polon.B29,
1071 (1998),gr-q/9802002; \Remarkon formationof
olored blakholesviane tuning,"gr-q/9906070; P.
Bizon,T.Chmaj,andZ.Tabor,Phys.Rev.D59,104003
(1999).
[27℄ G.Rein, A. D. Rendall, and J.Shaeer, Phys. Rev.
D58,044007(1998).
[28℄ I.Olabarrieta,\CritialCollapseofCollisionless
mat-terinSpherialSymmetry,"gr-q/0012059.
[29℄ M. Christensen, V.P. Frolov, and A.L.Larsen, Phys.
Rev.D58,085005(1998);V.P.Frolov,A.L.Larsen,and
M.Christensen,ibid.,D59,125008(1999).
[30℄ D.Garnkle,C.Cutler,andG.C.Dunan,Phys.Rev.
D60,104007(1999).
[31℄ S.L.Liebling,Phys.Rev.D60,061502(1999);D.
Mai-sonandS.L.Liebling,Phys.Rev.Lett.83,5218(1999);
P. Bizon, \Equivariant Self-Similar wave Maps from
MinkowskiSpaetimeinto3-Sphere,"math-ph/9910026;
P. Bizon, T. Chmaj, and Z. Tabor, \Dispersion and
Collapse of Wave Maps," math-ph/9912009; P. Bizon
and A. Wasserman, \Self-Similar Spherially
Symmet-ri Wave Maps Coupled to Gravity," gr-q/0006034;
S.L. Liebling, E.W. Hirshmann, and J. Isenberg,
\Critial Phenomena in Non-linear Sigma Models,"
gr-q/9911020; S. Husa, C. Lehner, M. Purrer, J.
Thornburg, and P.C. Aihelburg, \Type II Critial
Collapse of a Self-Gravitating Non-linear -Model,"
gr-q/0002067.
[32℄ A.Z. Wang, \Critial Collapse in Salar-Tensor and
Non-linear Gravity Theories: A Universal Class,"
gr-q/9901044.
[33℄ S.H.HawleyandandM.W.Choptuik,Phys.Rev.D62,
104024(2000).
[34℄ Y.PelegandA.R.Steif,Phys.Rev.D51,R3992(1995);
D. Birminghan and S. Sen, Phys.Rev. Lett. 84, 1074
(2000); F.Pretorius and M. W.Choptuik, Phys. Rev.
D62, 104012 (2000); L.M. Burko, ibid., D62, 127503
(2000); D. Garnkle, D63, 044007 (2001); V. Husain
andM.Olivier,Class.QuantumGrav.18,L1(2001);G.
Clementand A.Fabbri,\Analytial Treatment of
Crit-ial Collapse in 2+1 Dimensional AdS Spaetimes,"
gr-q/0101073; D.Birminghan,\Choptuik Salingand
QuasinormalModesintheAdS=CFTCorrespondene,"
hep-th/0101194.
[35℄ Thedenitionofdisreteself-similaritywasrstgiven
by Gundlah in C. Gundlah Phys. Rev. D55, 695
[36℄ Solutions of the homotheti (or the rst kind)
self-similaritywererststudiedbyCahillandTaubin
Gen-eralRelativityforaperfetuid[A.H.CahillandM.E.
Taub, Commu. Math. Phys. 21, 1 (1971).℄, and later
Carter and Henriksen [B. Carter and R.N. Henriksen,
Ann. Physique Suppl. 14, 47 (1989)℄ generalized this
asetoamoregeneralone,theso-alledkinemati
self-similarity,whihinludestheself-similaritiesoftherst,
seond, and zeroth kinds. For details of the latter, we
refer readerstoA.A. Coley,Class.QuantumGrav. 14,
87(1997);P.M.BenoitandA.A.Coley,Class.Quantum
Grav.15,2397(1998),C.F.C.Brandt,L.-M.Lin,J.F.V.
da Roha, and A.Z. Wang, \Gravitational ollapse of
spherially symmetri perfet uid with kinemati
self-similarity,"preprint,gr-q/0105019(2001);toappearin
Inter.J.Mod.Phys.D.
[37℄ N. Goldenfeld, Letures on Phase Transitions and
theRenormalizationGroup(AddisonWesleyPublishing
Company, New York, 1992); J. M. Yeomans,
Statisti-alMehanisofPhase Transitions(OxfordUniversity
Press1992).
[38℄ J.D. Bekenstein, \Blak Holes: Classial
Proper-ties, Thermodynamis, and Heuristi Quantization,"
gr-q/9808028.
[39℄ A.Z.WangandH.P.deOliveira,Phys.Rev.D56,753
(1997).
[40℄ M.D.Roberts,Gen.Relativ.Grav.21,907(1989).
[41℄ P.R. Brady, Class. Quantum Grav. 11, 1255 (1994);
Phys.Rev.D51,4168(1995);Y.Oshiro,K.Nakamura,
andA.Tomimatsu,Prog.Theor.Phys.91,1265(1994);
L.M.Burko,Gen.Rel.Grav.29,259(1997);S.A.
Hay-ward,Class.QuantumGrav.17,4021(2000).
[42℄ A. V. Frolov, Phys.Rev. D56, 6433 (1997); ibid., D
59,104011(1999);ibid.,D61,084006(2000).
[43℄ E.PoissonandW.Israel,Phys.Rev.D41,1796(1990).
[44℄ W.Israel, NuovoCimento,B44, 1(1966); ibid.,B48,
463(E)(1967).
[45℄ P.C. Vaidya, Pro. Ind. Aad. Sienes, A33, 264
(1951).
[46℄ C. Barrabes and W. Israel, Phys. Rev. D43, 1129
(1991).
[47℄ M. Alubierre, G. Allen, B. Bruegmann, G.
Lanfer-mann,E.Seidel,W.M.Suen,andM.Tobias,Phys.Rev.
D61,041501(2000).
[48℄ C.Gundlah,Phys.Rev.D577075(1998);ibid.,D57,
7080 (1998); J. M. Martn-Gara and C. Gundlah,
ibid., D59, 064031 (1999); D. Garnkle, C. Gundlah,
andJ.M.Martn-Gara, ibid.,D59,104012(1999).
[49℄ Privateommuniations.
[50℄ T. Chiba and M. Siino, Mod. Phys. Lett. A12, 709
(1997).
[51℄ S.AyalandT.Piran,Phys.Rev.D56,4768 (1997).
[53℄ P.C. Argyres, inContributionsfrom the G1 Working
Group at theAPS Summer Study on Partileand
Nu-lear Astrophysis and Cosmology in the Next
Millen-nium,Snowmass,Colorado,June29-July14, 1994,p.
23,astro-ph/9412046.
[54℄ D. Garnkle, Phys. Rev. D56, R3169 (1997); D.
Garnkleand C.Gundlah,Class. QuantumGrav.16,
4111 (1999); D. Garnkle and K. Meyer, Phys. Rev.
D59,064003(1999).
[55℄ R.H.PrieandJ.Pullin,Phys.Rev.D54,3792(1996).
[56℄ B.K. Harrison, K.P. Thorne, M. Wakano, and J.A.
Wheeler,GravitationTheoryandGravitationalCollapse