Localização de campos em branas isotrópicas e anisotrópicas em seis dimensões

(1)

CENTRO DE CIˆENCIAS DEPARTAMENTO DE F´ISICA

PROGRAMA DE P ÓS-GRADUAÇ ÃO EM FÍSICA

LUIS JOS´

E SILVEIRA DE SOUSA

LOCALIZAC

¸ ˜

AO DE CAMPOS EM

BRANAS ISOTR ´

OPICAS E

ANISOTR ´

OPICAS EM SEIS DIMENS ˜

OES

(2)

LOCALIZAC

¸ ˜

AO DE CAMPOS EM

BRANAS ISOTR ´

OPICAS E

ANISOTR ´

OPICAS EM SEIS DIMENS ˜

OES

Tese de Doutorado apresentada ao Programa de Pós-Gradua¸cão em F´ısica da Universidade Federal do Ceará, como requisito parcial para a obten¸cão do T´ıtulo de Doutor em F´ısica.

´

Area de Concentra¸c˜ao: F´ısica da Mat´eria Condensada.

Orientador: Prof. Dr. Carlos Alberto Santos Almeida

(3)

LOCALIZAC

¸ ˜

AO DE CAMPOS EM

BRANAS ISOTR ´

OPICAS E

ANISOTR ´

OPICAS EM SEIS DIMENS ˜

OES

Tese de Doutorado apresentada ao Programa de Pós-Gradua¸cão em F´ısica da Universidade Federal do Ceará, como requisito parcial para a obten¸cão do T´ıtulo de Doutor em F´ısica.

´

Area de Concentra¸c˜ao: F´ısica da Mat´eria Condensada.

Aprovada em 07/2013

BANCA EXAMINADORA

Prof. Dr. Carlos Alberto Santos Almeida (Orientador) Universidade Federal do Cear´a (UFC)

Prof. Dr. Roberto Vinhaes Maluf Cavalcante Universidade Federal do Cear´a (UFC)

Prof. Dr. Wilami Teixeira da Cruz

Instituto Federal de Educa¸cão, Ciência e Tecnologia do Ceará (IFCE)

Prof. Dr. Carlos Alex Sousa da Silva

(4)

(5)

Biblioteca Setorial de F´ısica A000p Sousa, Luis Jos´e Silveira de .

Localiza¸cão de campos em branas isotrópicas e anisotrópicas em seis dimensões / Luis José Silveira de Sousa. – 2013.

106 p.;il.

Tese de Doutorado - Universidade Federal do Ceará, Departa-mento de F´ısica, Programa de Pós-Gradua¸cão em F´ısica, Centro de Ciências, Fortaleza, 2013.

´

Area de Concentra¸cão: F´ısica da Matéria Condensada Orienta¸cão: Prof. Dr. Carlos Alberto Santos Almeida

1. Mundo brana. 2. Ondas estacion´arias. 3. Localiza¸c˜ao de campos. 4. Anisotropia. 5. Campo fantasma. I.

(6)

A todos os meus familiares, especialmente pais e

irm˜as. `

A nova fam´ıla que ganhei ao vir para

Fortaleza. `

(7)

AGRADECIMENTOS

A Deus Uno e Trino.

A meus familiares: meus pais João e Maria, minhas irmãs Jaqueline e Concibida - minha pequena Carmelita. Aos tios, tias, primos e primas, afilhados, afilhadas, comadres, com-padres... a todos, emfim, pelo apoio e incentivo. Todos merecem ter o nome citado mas são tantos... Estão no meu cora¸cão.

`

A fam´ılia que me acolheu, me adotou por assim dizer. À D. Zenaide e S. Napoleão. Aos seus filhos, particularmente meu irmão Kilpatrick que acreditou em mim mais do que eu mesmo. Deus sabe o quanto lhes sou grato. Muito obrigado por tudo!

`

A minha namorada, Rafaela, por toda a ajuda, compreens˜ao, amizade, companheirismo, pela alegria, pela for¸ca, pelo apoio incessante... `A D. Irene pelo cuidado filial que tem tido para comigo. Eu lhes sou muito grato!

Aos professores e demais funcionários do Departamento de F´ısica da UFC, particular-mente ao meu orientador, professor Dr. Carlos Alberto pelas mais diversas li¸cões, pela paciência, confian¸ca e compreensão.

Aos meus amigos que sempre me incentivaram. Aos colegas do LASSCO, particularmente, os professores Wilami e Alex, companheiros dos tempos de UECE. Devo agradecê-los pelo incentivo para realiza¸cão da prova de admissão para o doutorado, no caso o Prof. Wil-ami, e ainda por participarem diretamente na minha forma¸cão, ambos, Wilami e Alex. É necessário agradecer também aos professores Euclides e Victor pelas várias vezes em que me auxiliaram na compreensão de vários assuntos da nossa área de estudos. Aos demais colegas: Diego, Davi, Julio, Samuel, Wagner, Ivan, Hudson, Aristeu, Maluf e Luciana também sou muito grato pelas mais variadas li¸cões de f´ısica e de vida. Desculpem se cometi a injusti¸ca de esquecer alguém. Tenho aprendido muito com vocês, meus caros.

(8)

Nesta tese propõe-se o estudo de mundos branas isotrópicos e anisotrópicos em seis di-mensões. No que concerne às branas anisotrópicas é realizada a extensão de cinco para seis dimensões de um modelo de mundo brana com solu¸cão de ondas gravitacionais esta-cionárias. Não há preocupa¸cão quanto ao estudo da cosmologia mas, principalmente, evidencia-se os mecanismos de localiza¸cão de campos em tais cenários. Em cinco di-mensões a brana é gerada por um campo do tipo fantasma, o qual não satisfaz as condi¸cões de energia. Por esta razão no modelo em seis dimensões aqui apresentado houve a pre-ocupa¸cão de que o mesmo seja gerado por matéria normal a

. No contexto de branas isotrópicas algumas solu¸cões relevantes foram obtidas. Particularmente, foi constru´ıda uma 4-brana como solu¸cão das equa¸cões de Einstein em seis dimensões, sendo que neste caso a dimensão compacta pertence à brana e deve ser considerada pequena o suficiente para que a membrana possa representar o universo vis´ıvel (compactifica¸cão h´ıbrida). Esta solu¸cão representa uma brana espessa o que generaliza modelos já presentes na literatura, como o defeito tipo corda, por exemplo. Nessa geometria foi realizada a localiza¸cão dos campos escalar, vetorial e fermiônico. Ainda no contexto de branas isotrópicas foi re-alizada a localiza¸cão do campo de Kalb-Ramond em um defeito tipo corda. No que se refere aos modelos de branas anisotrópicas propostos aqui b

, foi poss´ıvel generalizar o modelo de cinco para seis dimensões obtendo as seguintes solu¸cões: um modelo de brana espessa anisotrópica, o qual generaliza o modelo de brana espessa homogênea referido anteriormente; uma versão mais simples deste modelo, em que se considera uma 4-brana fina em seis dimensões e dois outros modelos de brana anisotrópica com solu¸cão de on-das estacionárias sendo um na presen¸ca de matéria não normal c

e um outro gerado por matéria normal, o que vem a ser o resultado principal desta tese. Nesta geometria foi poss´ıvel resolver o problema da hierarquia à maneira do que se obtém em modelos do tipo Randall-Sundrum. No que concerne à localiza¸cão de campos em branas anisotrópicas foram considerados os campos escalar e fermiônico na brana fina antes referida. A local-iza¸cão para ambos os campos foi realizada com sucesso.

Palavras-chave: Mundo brana. Ondas estacion´arias. Localiza¸c˜ao de campos. Anisotropia. Campo fantasma.

a

Chama-se matéria normal aquela que satisfaz as quatro condi¸cões clássicas de energia: condi¸cões nula, fraca, forte e dominante. Uma breve revisão neste assunto pode ser encontrada no apêndice.

b

Deve-se destacar que os modelos de branas anisotróicas considerados aqui, as quais são geradas por ondas gravitacionais estacionárias, não são os modelos mais comuns de branas anisotrópicas considerados na literatura.

c

(9)

ABSTRACT

This work describes isotropic and anisotropic braneworlds emphasizing the localization of fields in this scenarios. In spite of studding its cosmology, the approach consider the viability of field localization in such models. It is relevant to say that the anisotropic model presented here was first implemented in five dimensions. This solution was obtained in the presence of a phantom like scalar field, but this kind of matter do not satisfies the classical energy conditions. By this reason in the work proposed here it has been tried to obtain a standing wave braneworld solution in the presence of normal matter. In the context of isotropic braneworld it was found important solutions. Particularly, it was obtained a 4-brane as solution of a six dimensional Einstein gravitational theory with the feature that the compact dimension belongs to the brane (hybrid compactification). This solution, which represents a thick brane, generalizes some braneworld models in six dimensions, as the string-like defect. The localization of the scalar, vector and fermion fields was successfully performed. An other relevant result obtained in six dimensional isotropic braneworld was the study of localization of the tensor or Kalb-Ramond field in the string-like defect. In the context of anisotropic standing wave braneworld it was possible to generalizes the original five dimensional model to six dimensions. Particularly, the thick braneworld cited above was generalized for the case of an anisotropic thick brane. A simplified solution in the form of a thin brane was found and the study of localization for the scalar and fermions fields was implemented. This solution was obtained with a phantom like scalar as source similar to the solution found in five dimensions. Finally it has been found a solutions in the presence of not normal and normal matter. This last version satisfies the energy conditions and presents the possibility to solve the hierarchy problem in the same way that one solve it in Randall-Sundrum-like models.

(10)

1 Fator de warp - brana fina - e−2krc|ϕ| . . . . p. 26

2 Fator de warp - brana espessa - e−A(r)_. _{. . . .} _{p. 26}

3 Perfil do fator de warp e−A(r) _para _β _{= 1;}_a _{= 1 . . . .} _{p. 30}

4 Perfil de t0(r) = tθ(r) para v = −1 (linha cheia), e para v = 1 (linha

seccionada) . . . p. 31

5 Perfil de tr(r) para v = 1 (linha cheia), e para v =−1 (linha seccionada) p. 31

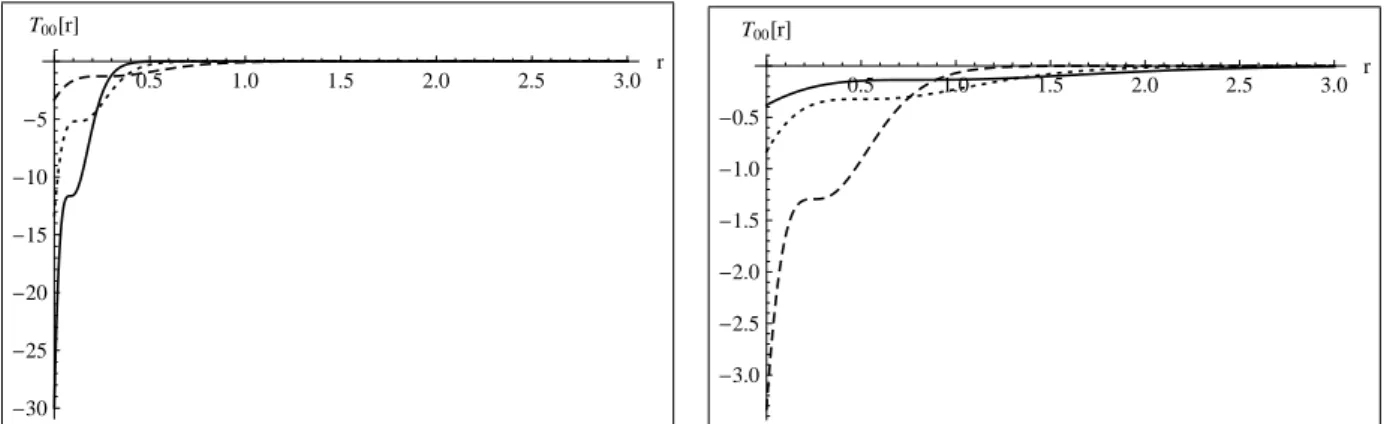
6 Perfil de _hTtti , a= 1, ω = 3,38 . . . p. 40

7 Perfil de _hTxxi , a= 1, ω = 3,38 . . . p. 40

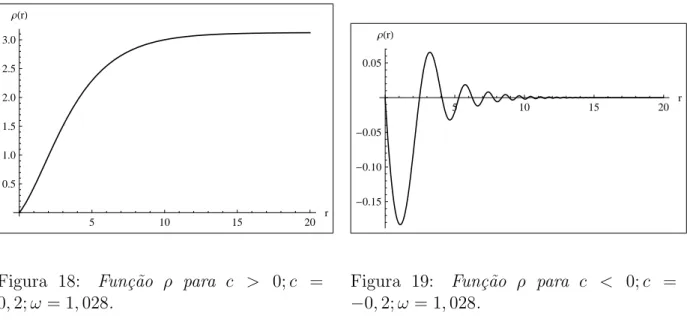
8 Perfil de ρ(r) para a = 1 e ω = 12,3 . . . p. 49

9 Perfil de ρ(r) para a = -1 e ω= 12,3 . . . p. 49

10 Perfil de _hT_i , ω = 5,76. A linha cheia representa _hTtti. A linha

sec-cionada representa _hTrri. A linha pontilhada representa hTxxi=hTyyi=

hTzzi=hTθθi. . . . p. 52

11 Perfil de _hT_i , ω = 9,09. A linha cheia representa _hTtti. A linha

sec-cionada representa _hTrri. A linha pontilhada representa hTxxi=hTyyi=

hTzzi=hTθθi. . . . p. 52

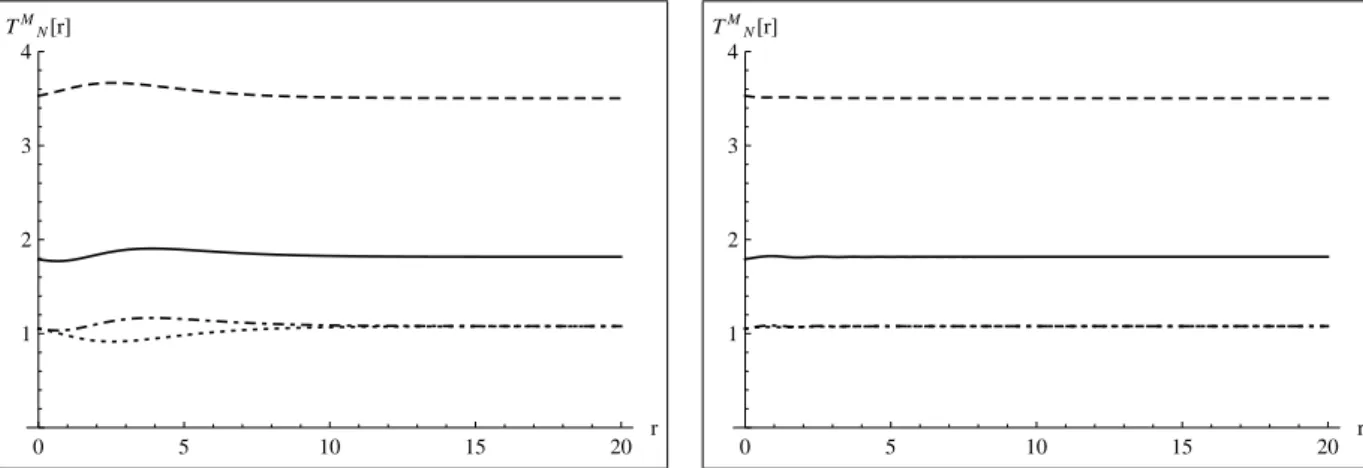
12 Perfil de _hT0i . ω = 5,76 e a = 1 para linha seccionada; ω = 11,52 e

a= 2 para linha pontilhada; ω = 17,28e a= 3 para linha cheia. . . . . p. 53

13 Perfil de _hT0i. ω = 5,76 e a = 1 para linha seccionada; ω = 2,88 e

a= 0,50 para linha pontilhada;ω = 1,92 e a = 0,33 para linha cheia. . p. 53

14 Perfil de _hR_i. ω = 5,76(linha seccionada), ω= 9,09(linha pontilhada),

ω = 12,3 (linha cheia) . . . p. 53

15 Perfil de _hR(4)_i_. _ω _{= 5}_,₇₆ _{(linha seccionada),} _ω _{= 9}_,₀₉ _(linha

(11)

17 Perfil de 3A′′₍_r_{) +} 3 2A′

2 _{. . . .} _{p. 56}

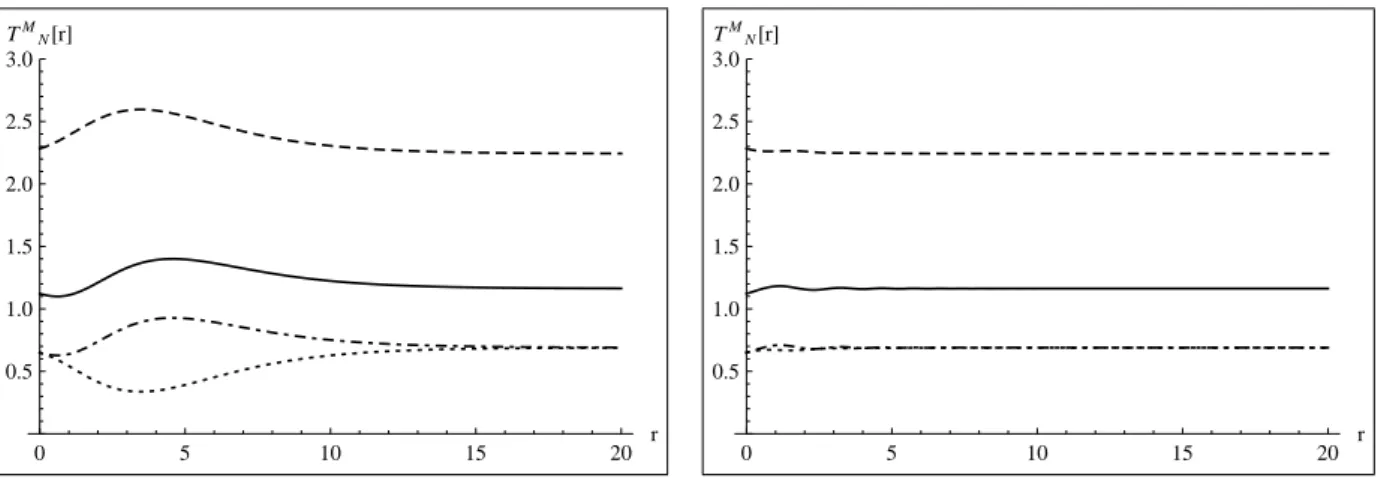
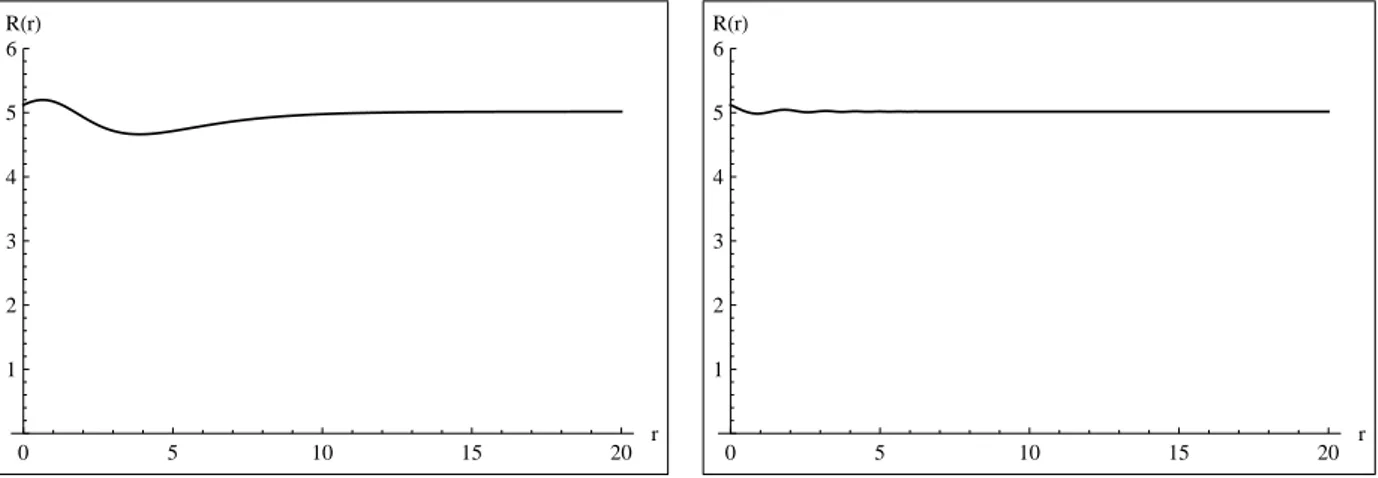
18 Fun¸c˜ao ρ para c >0;c= 0,2;ω = 1,028. . . p. 61

19 Fun¸c˜ao ρ para c <0;c=₋0,2;ω = 1,028. . . p. 61

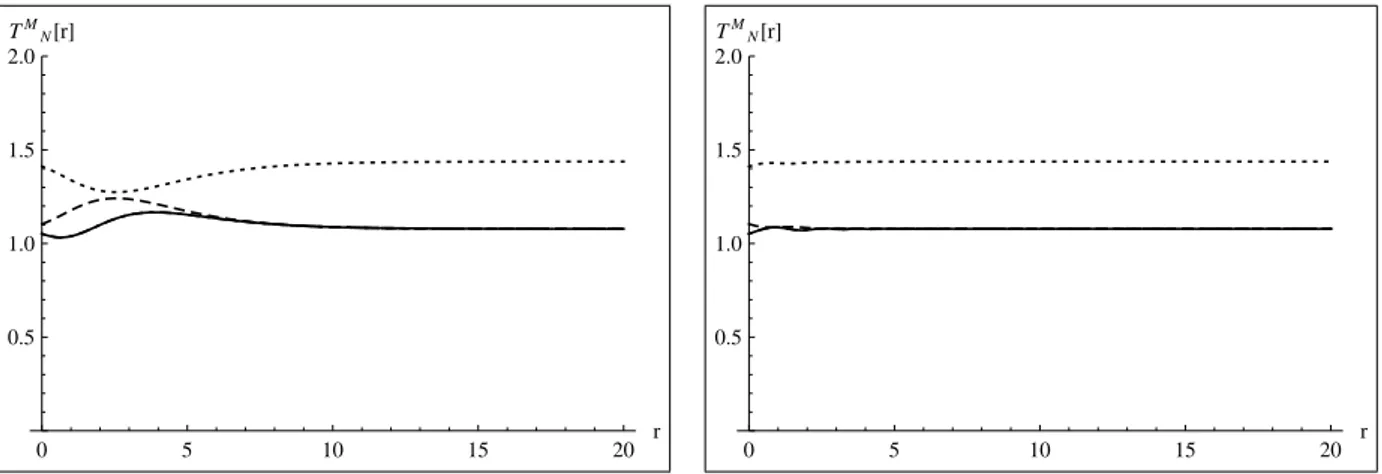
20 M´edia temporal das componentes n˜ao nulas de _hTM

N i para c > 0 (c =

0,250). Linha pontilhada: _hTt

ti. Linha pontilhada-seccionada: hTxxi = hTy

yi=hTzzi. Linha seccionada: hTrri Linha cheia: hTθθi. . . . p. 62

N i para c < 0 (c =

-0,250). Linha pontilhada: _hTt

N i para c > 0 (c =

N i para c < 0 (c =

24 M´edia temporal para o escalar de curvatura do bulk _hR6_i _para _{c >}_0. _{. .} _{p. 64}

25 M´edia temporal para o escalar de curvatura do bulk _hR6_i para c <0. . . p. 64

N i para c > 0 (c =

N i para c < 0 (c =

28 Perfil de V(r) para β = 2;a= 1 . . . p. 81

29 M´edia temporal da exponencial da fun¸c˜ao u, _hebu_i_para_b.C

1 =±1; a= 1

; ω= 12,3 . . . p. 87

30 M´edia temporal da exponencial da fun¸c˜ao u, _hebu_i_para_b.C

1 =±3; a= 1

; ω= 12,3. . . p. 87

31 Integral de e12ρ¯para b.C

(12)

1 INTRODUC¸ ˜AO p. 13

2 MUNDO BRANA DO TIPO RANDALL-SUNDRUM EM CINCO

E SEIS DIMENS ˜OES p. 19

2.1 Solu¸c˜oes em cinco dimens˜oes . . . p. 21

2.1.1 Solu¸c˜ao tipo bounce . . . p. 23

2.1.2 O modelo Randall-Sundrum (RS) . . . p. 24

2.2 Solu¸c˜oes em seis dimens˜oes . . . p. 27

2.2.1 Solu¸c˜ao do tipo brana espessa . . . p. 28

2.2.2 Defeito tipo corda . . . p. 31

3 SOLUÇ ÕES DE ONDAS ESTACION ÁRIAS PARA BRANAS ANISOTR ÓPICAS

p. 34

3.1 Brana gerada a partir de ondas gravitacionais estacion´arias em cinco

dimens˜oes . . . p. 37

3.2 Outras solu¸c˜oes . . . p. 41

3.3 Branas geradas a partir de ondas gravitacionais estacion´arias em seis

dimens˜oes . . . p. 43

3.3.1 Solu¸c˜ao do tipo brana fina . . . p. 46

3.3.2 Solu¸c˜ao do tipo brana espessa . . . p. 53

3.3.3 Brana gerada por ondas gravitacionais estacion´arias na presen¸ca

de uma fonte normal . . . p. 57

(13)

4.1.1 Localiza¸c˜ao do campo escalar em um defeito tipo corda . . . p. 68

4.1.2 Localiza¸c˜ao do campo vetorial no defeito tipo corda. . . p. 69

4.1.3 Localiza¸c˜ao do campo fermiˆonico em um defeito tipo corda . . . p. 72

4.1.4 Localiza¸c˜ao do campo de Kalb-Ramond em um defeito tipo corda p. 75

4.2 Localiza¸c˜ao de campo em uma brana espessa em seis dimens˜oes . . . . p. 79

4.2.1 Campo escalar . . . p. 79

4.2.2 Campo vetorial . . . p. 82

4.2.3 Campo fermiˆonico . . . p. 83

4.3 Localiza¸c˜ao de campos em uma brana gerada por ondas gravitacionais

estacion´arias . . . p. 84

4.3.1 Localiza¸c˜ao do campo escalar . . . p. 84

4.3.2 Localiza¸c˜ao do modo zero do campo fermiˆonico . . . p. 90

5 CONCLUS ˜OES E PERSPECTIVAS p. 93

6 APÊNDICE - CONDIÇ ÕES CL ÁSSICAS DE ENERGIA p. 98 6.1 Condi¸cão nula de energia - NEC . . . p. 98

6.2 Condi¸c˜ao fraca de energia - WEC . . . p. 99

6.3 Condi¸c˜ao forte de energia - SEC . . . p. 99

6.4 Condi¸c˜ao dominante de energia - DEC . . . p. 99

(14)

1 INTRODUC

¸ ˜

AO

Nos ´ultimos anos surgiram modelos de universo nos quais se considera que o mundo

em que vivemos est´a ’imerso’ em um universo com dimens˜oes extras chamadobulk. Den-tre esses modelos denominados de mundo brana (braneworld) destacam-se os que foram inicialmente propostos por Arkani-Hamed, Dimopoulos e Davili [1, 2, 3], conhecido sim-plesmente como modelo ADD e o modelo de Randall e Sundrum (RS), [4, 5], do qual

o trabalho aqui introduzido representa uma extensão. A razão principal de se estudar modelos com dimensão extra reside na possibilidade de explicar algumas dificuldades que surgem no Modelo Padrão, como o problema da hierarquia.

Um dos aspectos estudados nos diversos modelos de brana é a possibilidade de ”local-iza¸cão”de campo em um tal modelo. No cenário proposto originalmente por RS

assume-se que todos os campos estão limitados a assume-se propagar apenas na brana (ou membrana) enquanto que a gravidade é livre, por assim dizer, para se propagar em todo obulk. En-tretanto, assumir ,a priori, que todos os campos, a exce¸cão da gravidade, estão restritos a se mover apenas na brana não parece uma op¸cão suficientemente rigorosa. Por isso é

necessário buscar mecanismos teóricos de localiza¸cão de campo na membrana [6]. Em razão disso, a capacidade de um dado modelo de localizar campos é agora um parâmetro para classificá-lo (ou não) como potencial candidato a nosso universo 1 _{. ´}_{E vasta a} liter-atura sobre a localiza¸cão de campos em branas tanto em cinco, [4, 5, 6, 7, 8, 9], quanto

em seis dimens˜oes [10, 11, 12, 13, 14, 15, 16].

A maioria dos modelos de mundo brana presentes na literatura são estáticos, ho-mogêneos e isotrópicos. No entanto, apesar de que, em larga escala, nosso universo de fato se apresenta homogêneo e isotrópico, a teoria de Friedmann–Lemaˆıtre–Robertson–Walker (FLRW), que descreve o referido universo, não é capaz de explicar certas caracter´ısticas

do mesmo. Por exemplo: porque nosso universo é isotrópico hoje uma vez que ele deve ter sido anisotrópico em seu estágio inicial? Além disso, se na teoria de FLRW é

im-1

(15)

plementada uma perturba¸cão encontram-se novos modelos que seriam mais importantes em épocas iniciais do que o modelo FLRW, ou, dizendo de outra maneira, flutua¸cões estat´ısticas puras em FLRW não colapsam rápido o suficiente para formar as galáxias ob-servadas hoje [17]. Uma vez que os modelos de mundos branas pretendem descrever nosso

universo é razoável, pelo que foi dito acima, considerar modelos de branas anistrópicas. Encontram-se na literatura trabalhos nesta perspectiva [18, 19, 20, 21, 22, 23, 24, 25]. Nestes trabalhos o interesse maior reside em estudar a cosmologia de tais modelos (os quais são anisotrópicos, mas homogêneos) desconsiderando-se o estudo de localiza¸cão de

campos nesses cenários, na maioria dos casos. Excessão feita a alguns deles, particular-mente ao modelo de brana gerado a partir ondas gravitacionais estacionárias no qual os autores consideram a localiza¸cão de gravidade [18], campos escalar e tensorial [9], bosons [8] e fermions [26] . Este modelo em 5 dimensões representa uma generaliza¸cão de RS

para o caso em que a métrica é não estática e anisotrópica. Conforme citado acima, a localiza¸cão do modo zero de todos os campos do Modelo Padrão foi estudada neste cenário sendo considerada exitosa para todos a exce¸cão do campo fermiônico cuja fun¸cão de onda para o fermion direito é divergente.

Nesta tese objetiva-se estudar a localiza¸cão de campos em branas isotrópicas e anisotrópicas em seis dimensões. No que se refere às branas anisotrópicas, particularmente, houve a

preocupa¸cão em se construir um modelo que seja eficiente na localiza¸cão de campos e que resolva o problema da hierarquia. Para isso propõe-se uma generaliza¸cão para seis dimensões do modelo de Merab [18] tendo em vista não a cosmologia, mas o estudo da localiza¸cão de campos na referida geometria. Uma das principais dificuldades

apresen-tadas pelo modelo de ondas gravitacionais estacionárias referido acima consiste no fato de que a fonte é um campo escalar do tipo fantasma. Teorias com esse tipo de fonte via de regra apresentam dificuldades de estabilidade. No modelo de cinco dimensões já referido

o campo escalar do tipo fantasma é identificado com o escalar de Weyl. Sendo a teoria de Weyl estável, também será a teoria de brana com o campo escalar fantasma. Esta é a lógica seguida no trabalho já citado. No entanto, conforme será visto ao longo dessa tese, as componentes do tensor momento energia nessa teoria não satisfazem as condi¸cões de

energia (vide apêndice 6). Por isso procurou-se encontrar solu¸cões de ondas estacionárias, em seis dimensões, geradas por uma fonte de matéria que satisfa¸ca as condi¸cões clássicas de energia (vide apêndice 6). É importante observar que a afirma¸cão ”a solu¸cão de ondas estacionárias( ou a brana) é gerada por matéria normal”segue a afirma¸cão do modelo

(16)

Como será visto o modelo de Merab foi extendido para 6 dimensões e neste novo cenário a localiza¸cão do modo zero para os campos escalar e fermiônico foi obtida. In-teressante destacar que em cinco dimensões não foi poss´ıvel localizar o fermion direito, enquanto que em seis dimensões o estudo se mostrou exitoso. No que concerne às solu¸cões

na presen¸ca de matéria normal, as mesmas foram obtidas, embora tenha sido necessário considerar constante cosmológica anisotrópica nobulk, o que não vem a ser um absurdo tendo em vista que há modelos reais que consideram varia¸cão na constante cosmológica. Além disso obteve-se solu¸cão de onda gravitacional estacionária na presen¸ca de fonte

que satisfaz algumas das condi¸cões de energia, sem a necessidade de uma constante cos-mológica anisotrópica, o que vem a ser um avan¸co com rela¸cão ao modelo de Merab em cinco dimensões.

Ao longo do desenvolvimento desta tese foi realizado um estudo de revisão da bibli-ografia, como não poderia deixar de ser. Particularmente foram revisadas as solu¸cões das equa¸cões de Einstein em cinco e seis dimensões, no contexto de mundo brana, as quais

podem ser interpretadas como defeitos topológicos, mais precisamente, solu¸cão do tipo parede de dom´ınio e defeito tipo corda, respectivamente. Foram obtidas solu¸cões que cor-respondem a branas finas e espessas em ambos os casos. Neste contexto se deu o estudo de localiza¸cão de campos em branas isotrópicas, em seis dimensões. Estes estudos geraram

dois trabalhos que foram publicados no decorrer da tese e ser˜ao melhor detalhados nos cap´ıtulos espec´ıficos. A seguir a estrutura da tese ser´a apresentada.

Uma breve revisão da chamada f´ısica de dimensões extras, naquilo que se considera mais relevante para o desenvolvimento desta tese, é realizada no cap´ıtulo (2). No mesmo são apresentadas algumas solu¸cões que generalizam os modelos revisados. Na subse¸cão

(2.1.1) foi obtida a solu¸cão tipo kink para as equa¸cões de Einstein em cinco dimensões, tendo um campo escalar (kink) como fonte. Esta é uma solu¸cão já conhecida na liter-atura. Ela generaliza o modelo de RS para o caso de uma brana espessa. Este, por sua vez, é discutido na subse¸cão (2.1.2) do cap´ıtulo referido acima. Essa revisão geral

é importante para que se possa posicionar os resultados aqui obtidos diante do que já existe na literatura. Ainda no cap´ıtulo (2), na subse¸cão (2.2.1), descreve-se como obter uma 4-brana como solu¸cão das equa¸cões de Einstein em seis dimensões, sendo que neste caso a dimensão compacta pertence à brana e deve ser considerada pequena o suficiente

(17)

t´ıtulo ”Brane bounce-type configurations in a string-like scenario”. O cap´ıtulo é finalizado com a obten¸cão de um defeito tipo corda como solu¸cão das equa¸cões de Einstein em seis dimensões. Este modelo representa uma generaliza¸cão direta do modelo original de RS, para seis dimensões. Neste cenário foi realizado a localiza¸cão do campo de Kalb-Ramond,

complementando outros trabalhos que já tinham sido feito na localiza¸cão dos campos escalar, de gauge e fermiônicos, [6]. Os resultados da localiza¸cão do campo de Kalb-Ramond foram publicados também na PLB sob o t´ıtulo ”Tensor gauge field localization on a string-like defect”, [16].

O estudo das branas anisotrópicas, geradas por ondas estacionárias, se inicia no cap´ıtulo (3). Já na se¸cão (3.1) é discutido a solu¸cão de ondas gravitacionais estacionárias

para uma brana gerada a partir de um campo do tipo fantasma, [18], o qual é utilizado como referência para as solu¸cões de brana anisotrópicas aqui obtidas. O referido modelo generaliza o modelo RS pois que a presen¸ca dos fatores eu(r,t)_{, e}u(r,t)_{, e}−2u(r,t) _{diante das} variáves x, y e z, respectivamente, torna a métrica anisotrópica. Tal modelo consiste em uma solu¸cão para as equa¸cões de Einstein em cinco dimensões, tendo como fonte um campo do tipo fantasma, sendo a métrica anisotrópica, conforme já foi dito. Uma das di-ficuldades que este modelo apresenta é justamente o fato de a fonte ser um campo escalar do tipo fantasma, uma vez que teorias na presen¸ca de tais campos costumam apresentar

problemas de instabilidade. Para escapar dessas dificuldades a teoria é ”mergulhada”em um modelo de gravidade de Weyl em cinco dimensões. Pelo que foi poss´ıvel analisar mesmo nessas circunstâncias a teoria não satisfaz as condi¸cões de energia. Trata-se de solu¸cões na presen¸ca de uma fonte exótica (vide apêndice (6) para a defini¸cão de matéria

ex´otica).

Foi realizado um esfor¸co no sentido de obter outras solu¸cões, além da que foi obtida por Merab ([18]), ainda em cinco dimensõs. Na se¸cão (3.2) é apresentada uma solu¸cão de vácuo e uma solu¸cão na presen¸ca de uma constante cosmológica. No entanto em nenhum dos casos foi poss´ıvel obter solu¸cão do tipo onda gravitacional estacionária, embora tal

solu¸c˜ao exista em quatro dimens˜oes, [28].

A generaliza¸cão para seis dimensões do modelo de Merab é realizada na se¸cão (3.3). Foram obtidas solu¸cões que representam tanto brana fina quanto brana espessa. Além disso foi poss´ıvel obter solu¸cão na presen¸ca de matéria ”não normal”, que é bem menos ruim do que matéria exótica. Uma generaliza¸cão direta do modelo de Merab foi obtida

(18)

o modelo muito se assemelha ao de Merab, principalmente no que concerne a natureza exótica da fonte. Por outro lado, no que se refere a localiza¸cão de campos, se mostra mais eficiente. Os resultados aqui obtidos encontram-se em um trabalho submetido aoJournal of Physics G - JPG, [29] sob o t´ıtulo ”A 6D standing-wave Braneworld”. Além dessa

solu¸cão foi poss´ıvel generalizar tanto o modelo de 4-brana considerado na subse¸cão 2.2.1, como o próprio modelo obtido na subse¸cão (3.3.1), referido acima, através da obten¸cão de uma solu¸cão de brana espessa na presen¸ca de uma métrica anisotrópica. Esta solu¸cão se encontra na subse¸cão (3.3.2). Apesar de mais geral que as duas anteriores esta solu¸cão

está incompleta pois apenas se obteve o fator de warp e colocou-se a equa¸cão para a fun¸cão que representa a anisotropia em uma forma separável, de tal maneira que se possa ter uma solu¸cão do tipo onda estacionária. No entanto esta equa¸cão não foi resolvida e fica como perspectiva de trabalho futuro resolvê-la e estudá-la melhor. Por fim, na subse¸cão (3.3.3)

obteve-se uma solu¸cão do tipo onda estacionária na presen¸ca de uma fonte não normal (satisfaz a todas as condi¸cões de energia, a excessão da condi¸cão dominante). Todas as componentes da pressão como a densidade de energia para essa fonte são positivas. Além disso é poss´ıvel obter solu¸cão com fator de warp crescente ou decrescente. Apresenta

ainda a vantagem de resolver o problema da hierarquia, coisa que não é possivel no modelo original de Merab, bem como no modelo de seis dimensões apresentado em (3.3.1). No entanto a solu¸cão é gerada por matéria que, apesar de ter as componentes do tensor momento energia todas positivas e de satisfazer as condi¸cões NEC, WEK e NEC não

satisfaz a condi¸cão DEC, que seria suficiente para assegurar estabilidade. Por isso uma nova solu¸cão foi obtida desta vez satisfazedendo a todas as condi¸cões clássicas de energia acima referidas. Esta solu¸cão, no entanto, exige que a constante cosmológica assuma diferentes valores ao longo das coordenadas espaciais e temporal. Em outras palavras, a

constante cosmológica neste caso é anisotrópica e não homogênea. Estes resultados estão submetidos aoJournal of High Energy Physics - JHEP, com t´ıtulo ”A 6D standing-wave Braneworld in the presence of anormal matter source”, [30].

A localiza¸cão de campos é o objeto do cap´ıtulo (4) desta tese. Na se¸cão (4.1) foi considerado o estudo dos campos escalar (4.1.1), vetorial (4.1.2), fermiônico (4.1.3) e

tensorial (4.1.4). Os três primeiros são apresentados como uma revisão bibliográfica en-quanto que a localiza¸cão do campo tensorial (Kalb-Ramond), conforme foi dito, resultou em um trabalho recentemente publicado [16]. Nem todos os campos do modelo padrão foram considerados no modelo de brana anisotrópica, mas apenas os campos escalar e

(19)

para o caso da gravidade porque o resultado é semelhante ao que se obtém para o campo escalar. A localiza¸cão do campo escalar nesse modelo é obtida na subse¸cão (4.2.1). O resultado mostra que a localiza¸cão é poss´ıvel para o modo zero. Interessante notar que não há necessidade de intera¸cão adicional, além da gravitacional, para se obter localiza¸cão

do modo zero do campo escalar. No caso do campo vetorial também foi poss´ıvel obter a localiza¸cão (4.2.2), o mesmo acontecendo para o campo fermiônico (4.2.3). Para que fosse poss´ıvel este último resultado foi necessário alterar a derivada na equa¸cão de Dirac de tal forma a considerar um acoplamento m´ınimo, semelhante ao que acontece no caso

do defeito tipo corda. Na subse¸cão (4.3.1) considera-se a localiza¸cão do campo escalar na brana anisotrópica estudada na subse¸cão (3.3.1). Mais uma vez é poss´ıvel verificar a localiza¸cão do modo zero. Diferente do resultado obtido em [11] em que o campo escalar é localizado em um defeito tipo corda para um fator de warp que decresce

exponencial-mente, aqui obteve-se a localiza¸cão para um fator exponencialmente crescente. Por fim foi realizado o estudo da localiza¸cão do campo fermiônico neste mesmo cenário, 4.3.2. Foi poss´ıvel mostrar que há localiza¸cão do modo zero o que vem a ser um resultado destacável uma vez que em cinco dimensões não foi poss´ıvel obter tal resultado.

Conclusões do que já foi feito e perspectivas para o desenvolvimento futuro são apon-tadas no cap´ıtulo (5). O apêndice (6) traz uma breve descri¸cão das condi¸cões clássicas

(20)

2 MUNDO BRANA DO TIPO

RANDALL-SUNDRUM EM

CINCO E SEIS DIMENS ˜

OES

Por volta dos anos 20 surgiram as primeiras teorias que consideravam a existência de dimensões extras no universo, as denominadas teorias de Kaluza-Klein [31], nas quais o acréscimo de uma dimensão espacial extra no espa¸co-tempo quadridimensional tinha a pretensão de unificar eletromagnetismo e gravidade. Outras motiva¸cões existem para se

estudar teorias com dimensões extras como, por exemplo, a necessidade de se explicar a velocidade com que as estrelas orbitam o centro das galáxias (a massa necessária descon-hecida estaria oculta em dimensões espaciais extras) e o fato de a intera¸cão gravitacional se mostrar tão fraca em nosso planeta [32]. Nesse contexto, depois de um vazio de cerca de

60 anos, teorias com dimensões extras voltaram à literatura. In 1982 Akama[33] usou a dinâmica de vórtice de Nielsen-Olesen para localizar o nosso universo em uma membrana mergulhada em um espa¸co tempo de seis dimensões. Trabalhos semelhantes foram publi-cados em 1983 e 1985, por Rubakov e Shaposhnikov [34] e Visser [35], respectivamente. Os modelos ADD [1, 2, 3] e RS [4, 5] oferecem solu¸cões para o problema da hierarquia [36] e alternativas à compatifica¸cão do tipoKaluza-Klein.

Não é exagero dizer que os trabalhos de Randall e Sundrum são paradigmáticos no contexto de dimensões extras. Este trabalho que consiste em uma teoria de gravidade em 5 dimensões foi rapidamente estendido de forma a compreender mais dimensões. Par-ticularmente em seis dimensões alguns autores contribuiram em menos de um ano do

surgimento do modelo original, [6, 10, 37]. O modelo de RS é usado como referência de universo com dimensões extras do qual o mundo em que se passam os fenômenos descritos pela dita f´ısica do modelo padrão é uma membrana, ou simplesmente brana. O modelo proposto nesta tese, em seis dimensões, apresenta-se como uma generaliza¸cão do modelo

RS.

(21)

dimensões serão descritas. Também será estudado o modelo anisotrópico de Merab. Serão apresentados modelos em cinco e seis dimensões, por isso considerar-se-á inicialmente o seguinteansatz para a métrica em um espa¸co tempo D-dimensional

ds2 =gM NdxMdxN

=gµνdxµdxν + ˜gabdxadxb

=e−A(r)gˆµνdxµdxν −dr2−e−B(r)dΩ2n−1 (2.1)

onde M, N, ... denotam ´ındices do espa¸co tempo D-dimensional , µ, ν, ..., representam ´ındices na membrana p-dimensional ea, b, ...representam as n-dimensões espaciais extras. Como será visto, para alguns dos modelos considerados aqui, a parte da métrica que no

devido limite representa a brana, ˆgµνdxµdxν, e em alguns casos, a fun¸c˜ao que multiplica

a dimensão extra compacta conterão termos do tipo eu_{, e}−2u_{, e}−3u_{, onde} _u_{é uma fun¸cão}

que depende das variáveis r e t, u=u(r, t). Esta fun¸cão é que definirá a anisotropia nos modelos de branas com solu¸cão do tipo onda estacionária.

A a¸cão é dada em D-mimensões por

S =₋ 1 2κ2

D Z

dD_x√₋_g₍_R₋_{2Λ) +} Z

dD_x√₋_gL

m (2.2)

na qual κD representa a constante gravitacional D-dimensional , Λ ´e a constante

cos-mológica do bulk e Lm é a Lagrangiana de algum campo de matéria. Nesta tese será

usada, de maneira geral, a conven¸cão de sinais de Landau [38], conforme observado em Misner, Thorne e Wheeler [39]. Apenas nas subse¸cões (2.1.2) e (2.2.1) será utilizada a

m´etrica com assinatura (₋,+,+,+), por conveniˆencia, para seguir os trabalhos originais.

As equa¸cões de Einstein obtidas da varia¸cão da a¸cão (2.2) com rela¸cão ao tensor gM N

s˜ao dadas como segue

RM N −

1

2gM NR = ΛgM N+κ 2

DTM N (2.3)

onde o tensor TM N ´e definido por

TM N =

2

κ2 D

1 √

−g

δSm

δgM N (2.4)

e o tensor de Ricci ´e obtido pela contra¸c˜ao do tensor de curvatura,RM N =RM P NP , o qual

´e dado na forma tradicional

RP

(22)

onde a conexão da métrica também se expressa na forma já conhecida

ΓP_{M N} = 1 2g

P Q₍_∂

MgQN +∂NgQM −∂MgM N) (2.6)

e, finalmente, o escalar de curvatura ´e dado por R=gM N_R

M N.

A seguir serão analizadas solu¸cões para a métrica (2.1) que correspondem, respecti-vamente, a uma membrana do tipo parede de dom´ınio e ao modelo RS que é obtido desse como um caso limite. Apesar deste último ser a referência de mundo brana considerado

nesta tese não será apresentado como primeiro exemplo, como até parece mais didático, porque preferiu-se apresentar solu¸cões mais gerais para as equa¸cões de Einstein e destas extrair as solu¸cões particulares. É o oposto do desenvolvimento histórico, talvez, mas acredita-se que não trará preju´ızo à compreensão do leitor.

2.1 Solu¸c˜

oes em cinco dimens˜

oes

Nesta se¸cão serão apresentados dois tipos básicos de modelos de branas em cinco

dimensões. O primeiro deles é o modelo descripo por Kehagias [4]. Trata-se de uma geometria com brana espessa, caracterizada por um fator dewarp suave, cuja fonte é um kink. O segundo é o modelo RS. Os conceitos aqui apresentados são básicos e certamente

bastante conhecidos do leitor familiarizado com modelos de mundo brana. No entanto, tendo em vista que esta tese é devotada ao estudo de mundo brana (especificamente branas geradas por ondas gravitacionais) parece necessário apresentar esses conceitos. Encontrar solu¸cão de brana consiste em resolver as equa¸cões de Einstein para uma métrica

espec´ıfica, que possa ser separada de tal forma que se destaque a métrica da brana e a das dimensões extras, devendo a métrica da brana, no limite conveniente, coincidir com a métrica de Minkowski em um espa¸co-tempo quadridimensional. A fonte de matéria pode ser apresentada explicitamente como em Kehagias [4] e RS [4], por exemplo, ou

escrevendo-a de forma genérica como em Oda [6] e Ghergeta [10]. A métrica geral 2.1 é conveniente para os propósitos dessa tese, bastando para isso escolher n = 1 ou n = 2 para cinco e seis dimensões, respectivamente, além de acrescentar os termos que definem a anisotropia, quando for o caso. Para esta se¸cão assume-se n = 1, que corresponde ao caso de uma dimensão extra, portanto a métrica (2.1), sem anisotropia, é reescrita como

(23)

A presen¸ca do fator dewarp (o fator exponencial) na métrica acima merece ser destacada. A fun¸cão A depende apenas da dimensão extra r. Isso significa que uma vez fixada a posi¸cão da brana nobulk sua métrica será equivalente ouconforme a de Minkowski. Isso significa que na brana será válida a f´ısica do modelo padrão [40].

Isto posto é chegado o momento de se obter as componentes do tensor de Einstein para (2.7). Para esta métrica as únicas componentes não nulas da conexão (2.6) são

Γxrx = Γyry = Γzrz = Γtrt=−

1 2A

′

(r) (2.8)

e

Γr

xx = Γryy = Γrzz =−Γrtt =

1 2e

−A(r)_A′

(r) (2.9)

onde x, y, z, t são as componentes usuais do espa¸co tempo de Minkowski, r é a dimensão extra e a linha, ′, representa derivada com rela¸cão à coordenada extra. As componentes não nulas do tensor de Ricci, por sua vez, resultam

Rxx =Ryy =Rzz =−Rtt =

1 2e

−A(r)

−2A′2(r) +A′′(r), (2.10)

Rrr =−A ′₂

(r) + 2A′′(r). (2.11)

Para possibilitar o c´alculo do tensor de Einstein falta ainda o escalar de curvatura, o qual ´e dado a seguir

R = 5A′2(r)₋4A′′(r). (2.12)

Com isso o tensor de Einstein ´e dado por

Gxx =Gyy =Gzz =−Gtt =

3 2e

−A(r)_A′₂

(r)₋A′′(r), (2.13)

Grr=

3 2A

′₂

(r). (2.14)

(24)

2.1.1 Solu¸c˜

ao tipo

bounce

O t´ıtulo desta subse¸cão remete ao trabalho deKehagias que assim denomina a solu¸cão obtida. Outros autores diriam solu¸cão do tipo kink (por isso essa denomina¸cão tem sido

usada ao longo da tese) ou que a brana está localizada numa parede de dom´ınio ou ainda que é a própria parede de dom´ınio [41], [42]. A solu¸cão obtida aqui segue um caminho ligeiramente diferente do trabalho de Kehagias inclusive no que se refere à assinatura da métrica. Há também a diferen¸ca no fator de warp, pois no trabalho original a fun¸cão

A(r) é multiplicada por 2. Além disso há ausência de algumas constantes na defini¸cão do campo escalar utilizado aqui, em compara¸cão com o modelo original.

Depois dessas breves considera¸cões pode-se avan¸car para a solu¸cão das equa¸cões de Einstein. Considerando-se um campo escalar acoplado à gravidade o tensor momentum energia para tal configura¸cão é obtido a partir de (2.4)

TM N =∂MΦ∂NΦ−gM N

1 2∂

C_Φ_∂

CΦ +V(Φ)

, (2.15)

considerando-se que a Lagrangiana do campo escalar seja dada por

Lm =

1 2g

M N_∂

MΦ∂NΦ +V(Φ). (2.16)

Com isso as equa¸c˜oes de Einstein (2.14), (2.13) e (2.3), para Λ = 0, se resumem ao sistema a seguir:

3 2

A′2₍_r₎₋_A′′

(r)=κ2 5

1 2φ

′₂

+V(φ)

(2.17)

3 2A

′₂

(r) = κ2₅

3 2φ

′₂

+V(φ)

(2.18)

em que κ5 representa a constante gravitacional em cinco dimensões. A partir do sistema acima pode-se determinar a fun¸cão de warp A(r). Para isso subtrai-se (2.18) de (2.17) resultando na seguinte equa¸cão

A′′(r) =κ2₅φ′2. (2.19)

´

(25)

φ(r) = tanh(r) (2.20)

No caso em mãos, na presen¸ca de gravidade, admite-se uma solu¸cão do tipo kink (2.20), encontra-se o fator de warp e depois retorna-se às equa¸cões de Einstein (2.18), (2.17) e calcula-se o novo potencial. Portanto, para φ dado em (2.20) a solu¸cão de (2.19) é dada por

A(r) = 2 9κ

2

5log(cosh 2

(r)) + 1 9κ

2 5tanh

2

(r) (2.21)

para a qual A(0) = A′(0) = 0. A equa¸c˜ao para o potencial ´e obtida eliminando-se φ de (2.18) e (2.17)

V = 3 4κ2

5

3A′′(r)₋2A′2(r) (2.22)

A partir das derivadas de A dadas a seguir

A′(r) = ₋2 9κ

2

5tanh(r) tanh2(r)−3

; A′′(r) = 2 3κ

2

5 tanh2(r)−1

2

, (2.23)

substituindo-se em (2.22), usando (2.20) obtem-se para o potencial

V = 3 2

φ′2₋₁2₋ 2 27κ

2

5φ2 φ2−3

2

(2.24)

o qual reduz-se ao caso em que n˜ao h´a gravidade no limite κ2

5 → 0. Esta solu¸c˜ao

corre-sponde a uma membrana espessa que no limiter_{→ ∞}assume a forma do modelo RS, ou seja,e−A_∝_e−|r|_para _r _{→ ∞}_{. O fato de que esta solu¸cão é uma generaliza¸cão do modelo} RS será melhor discutido ao final deste cap´ıtulo. Como será visto na subse¸cão (2.2.1) este modelo foi generalizado para seis dimensões, tendo este resultado sido publicado na

revista Physics Letter B [27]. A seguir ser´a analizado o modelo RS.

2.1.2 O modelo Randall-Sundrum (RS)

Será apresentado aqui o modelo conhecido na literatura como RSI, [5]. A descri¸cão desse modelo exige a solu¸cão das equa¸cões de Einstein em 5 dimensões em um pro-cedimento semelhante ao que foi feito acima, embora os modelos apresentem algumas

diferen¸cas. A primeira delas que se deve destacar ´e a fonte que neste caso ´e dada por

T_{M N}(RSI) =₋ √

−G

4M3 Vvis √

−gvisgvisµνδ µ

MδνNδ(ϕ−π) +Vcom√−gcomgcomµν δ

µ

MδNνδ(ϕ)

(26)

em que os sub(super)escritovis, com referem-se, respectivamente, às branas vis´ıvel, com a qual identifica-se nosso universo quadridimensional, e companheira [40]. Esta fonte representa pois as branas e ϕ representa a dimensão extra que neste caso é compacta. A métrica no modelo RSI pode ser obtida de (2.7) fazendo-seA _≡2krc|ϕ|er≡rc2ϕem que

rc representa a distância entre as branas, também chamado de raio de compactifica¸cão.

Com essas modifica¸cões, usando-se aassinatura ₋+ ++, a métrica para o modelo RSI é dada por

ds2 =e−2krc|ϕ|η

µνdxµdxν +r2cdϕ2 (2.26)

onde k ´e uma constante e ηµν representa a m´etrica de Minkowski.

O modelo RSI, portanto, consiste em um espa¸co tempo com cinco dimens˜oes com duas 3-branas, uma das quais modela nosso universo, e uma dimens˜ao extra transversa a

estas, à qual da-se o nomeorbifold. Esta dimensão extra tem simetriaZ2 a qual possibilita a identifica¸cão entre (xµ_{, ϕ}_{) e (}_xµ_,₋_ϕ_{). A dimensão extra é angular e as duas 3-branas}

podem ser fixadas nos extremosϕ = 0 eϕ=π desta dimensão, além disso a geometria do bulk é anti de Sitter, (AdS5), [5, 40]. O modelo RSII pode ser obtido de RSI tomando-se o limite rc → ∞, [4]. Neste caso há apenas uma 3-brana presente e a dimensão extra é

n˜ao compacta.

Uma das razões do sucesso, por assim dizer, do modelo RS reside na sua viabilidade fenomenológica. Isto se reflete, por exemplo, na forma como este modelo apresenta uma solu¸cão simples para o problema da hierarquia. Além disso, uma vez que o fator de warp depende apenas da coordenada extra, a fixa¸cão da brana torna sua métrica conforme o

espa¸co de Minkowski, implicando em uma brana apta a suportar todos os campos do modelo padrão, uma vez que a métrica (2.26) é um caso particular da métrica mais geral (2.7). No entanto, a localiza¸cão de alguns campos exige a presen¸ca de campos auxiliares, como o dilaton, no setup de RS, fato que motivou a busca por modelos de branas mais

gerais que fossem capazes de localizar os campos do modelo padrão através da intera¸cão gravitacional, unicamente. Esta abordagem resumida do modelo RS é suficiente para o momento, outros aspectos serão discutidos em cap´ıtulos posteriores.

Antes de fechar este cap´ıtulo é interessante voltar à solu¸cão tipo kink encontrada na subse¸cão (2.1.1) e compará-la com o modelo RSI da subse¸cão (2.1.2) atual. O primeiro

(27)

-3 -2 -1 1 2 3 j 0.2

0.4 0.6 0.8 1.0

e-k rc¡j¥

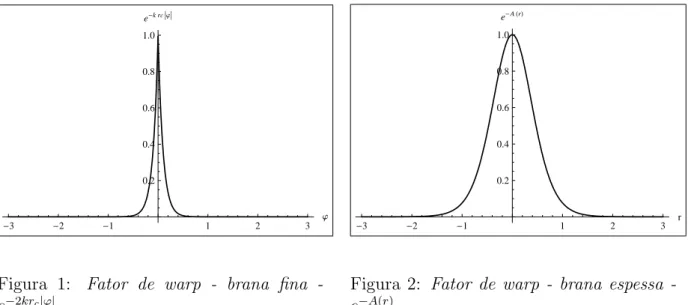
Figura 1: Fator de warp brana fina

-e−2krc|ϕ| .

-3 -2 -1 1 2 3

r 0.2

0.4 0.6 0.8 1.0

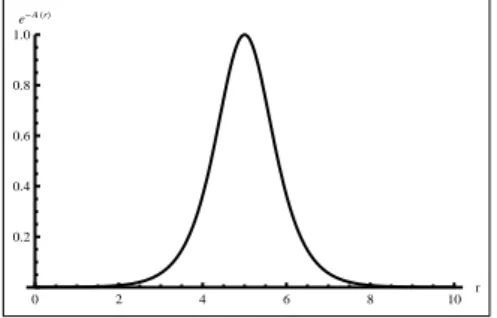
e-AHrL

Figura 2: Fator de warp brana espessa

-e−A(r)_.

der, condizente com e−A(r) _∝_e−|r| _{no limite} _r _{→ ∞} _{como já tinha sido dito antes. Dai} pode-se concluir que na solu¸cão tipo bounce, para regiões distantes da brana, o espa¸co tempo é anti de Sitter, como no caso RS, [43]. No entanto o primeiro modelo, em que a brana é espessa, não apresenta singularidade, sendo esta caracter´ıstica uma vantagem

com rela¸cão ao modelo RS. Além disso é mais real´ıstico um cenário em que a brana ou membrana tenha alguma espessura [44]. É importante explicar que entende-se por brana espessa uma estrutura que se espalhe pela dimensão extra de tal forma que sua influência

é percebida nas vizinhan¸cas da posi¸cão ao longo da referida dimensão, na qual a brana se localiza. Em cinco dimensões ela se assemelha à parede de dom´ınio ferromagnética [43].

As figuras (1, 2) revelam ainda que a exponencial da fun¸c˜aoA(r) tem o mesmo perfil

para r_{± → ∞} o que torna o fator de warp da solu¸c˜ao tipo bounce condizente com a

simetriaZ2. Por fim, a forma do fator de warp com um pico apenas emr = 0 demonstra que a geometria se localiza junto `a brana espessa ou parede de dom´ınio [43]. Esta solu¸c˜ao

é interessante também porque propicia a constru¸cão de modelos de brana relacionadas a defeitos topológicos.

Fica por aqui esta análise inicial de modelos de brana em 5 dimensões, os quais serão revisitados para que outros aspectos como a generaliza¸cão para modelos (anisotrópicos) obtidos a partir de ondas estacionárias e localiza¸cão de campos sejam estudados. Na

(28)

2.2 Solu¸c˜

oes em seis dimens˜

oes

A generaliza¸cão do modelo RS para seis dimensões aconteceu tão logo surgiu o modelo original [6, 10, 37]. O modelo aqui analizado parte da métrica (2.1) para o caso n = 2, ainda sem anisotropia, o que resulta

ds2 =e−A(r)gˆµνdxµdxν −dr2−R02e−B(r)dθ2 (2.27)

em queR2

0é uma constante e as coordenadasreθestão restritas aos respectivos intervalos: 0_≤r _{≤ ∞}, 0 _≤θ _≤2π. Este modelo, consistente com invariância de Poincaré em quatro dimensões foi estudado por varios autores em diferentes contextos. Para o escopo desta

tese é importante destacar que as equa¸cões de Einstein obtidas da métrica (2.27) podem ter como solu¸cão um defeito tipo corda [6, 10, 37] bem como uma 4-brana em um cenario com compactifica¸cão h´ıbrida, [45], por exemplo. Mais uma vez, a exemplo do que se passa em cinco dimensões, como foi visto na se¸cão 2.1, é poss´ıvel relacionar a brana com

um defeito topológico: parede de dom´ınio em cinco dimensões, defeito tipo corda em seis... Para a métrica dada acima, uma outra poss´ıvel solu¸cão do sistema de equa¸cões de Einstein é encontrada quando se admite a presen¸ca de um campo escalar no bulk, de forma semelhante ao que se obteve em 5 dimensões em que a solu¸cão é do tipo parede

de dom´ınio. Neste caso não se pode falar em parede de dom´ınio mas é ainda poss´ıvel a solu¸cão na forma de uma 4-brana em que a coordenada compacta reside na brana, correspondendo a uma compactifica¸cão h´ıbrida. A propósito a expressãocompactifica¸cão h´ıbridaé utilizada porKoley [45] para referir ao fato de a coordenada compacta pertencer

`a brana, diferente do defeito tipo corda, por exemplo, em que a dita coordenada faz parte do espa¸co extra.

´

E tempo de obter as equa¸cões de Einstein para a métrica (2.27). Para isso calcula-se inicialmente as componentes não nulas do s´ımbolo de Christoffel, (2.6), que neste caso são dadas por

Γx_rx = Γy_ry = Γz_rz = Γt_rt =₋1 2A

′

(r), (2.28)

Γr_xx = Γr_yy = Γr_zz =₋Γr_tt = 1 2e

−A(r)_A′

(r), (2.29)

e

Γr

θθ =

1 2R

2

0e−B(r)B ′

(r); Γθ

rθ =−

1 2B

′

(29)

Resumindo um pouco a quantidade de equa¸cões e suprimindo, portanto, as componentes do tensor de Ricci, uma vez que os cálculos muito se assemelham ao que se fez em cinco dimensões, pode-se exibir diretamente as componentes não nulas do tensor de Einstein

Gxx =Gyy =Gzz =−Gtt =

1 4e

−A(r)₆_A′₂

+ 3A′B′ +B′2₋2(3A′′+B′′) (2.31)

Grr =

3 2A

′₂

(r) +A′B′ (2.32)

Gθθ =

1 2R

2

0e−B(r)(5A ′₂

(r)₋4A′′) (2.33)

Assumindo-se para o tensor momentum energia a express˜ao (2.4) as equa¸c˜oes de Einstein (2.3), (2.31), (2.32) e (2.33) resultam, de forma geral1

1 4

6A′2+ 3A′B′ +B′2₋2(3A′′+B′′)=κ2₅

1 2φ

′₂

+V(φ)

+ Λ (2.34)

3 2A

′₂

(r) +A′B′ =κ2₅

3 2φ

′₂

+V(φ)

+ Λ (2.35)

e

1 2(5A

′₂

(r)₋4A′′) =κ2₅

1 2φ

′₂

+V(φ)

+ Λ (2.36)

as quais não diferem muito do que se obteve em cinco dimensões. No entanto no que se refere à localiza¸cão de campos e a estabilidade esta solu¸cão em seis dimensões se mostra mais vantajosa em rela¸cão à solu¸cão de cinco dimensões, como será visto. A seguir serão

ilustradas duas poss´ıveis solu¸cões para este sistema de equa¸cões. No primeiro caso a solu¸cão corresponde a uma 4-brana espessa e no segundo caso tem-se o correspondente do modelo RS em seis dimensões

2.2.1 Solu¸c˜

ao do tipo brana espessa

A brana obtida aqui como solu¸cão das equa¸cões de Einstein (2.34 - 2.36)pode ser clas-sificada como topologicamente não trivial, conforme classifica¸cão dada emDzhunushaliev [44] pois é gerada por um único campo escalar, conforme discutido acima. Para obter

uma solu¸cão do tipo 4-brana espessa admitir-se-á o caso especial em que A(r) = B(r). Com esta simplifica¸cão, a métrica (2.27) equivale a um defeito tipo corda local conforme

1

(30)

descri¸cão dada no trabalho de Oda [6], embora como será visto a solu¸cão encontrada aqui não seja um defeito topológico. Além disso, naquele artigo o autor optou pelo ansatz A(r) = cr, em que c é uma constante. Portanto o trabalho aqui representa uma generaliza¸cão daquele, sendo esta abordagem inédita na literatura, fato que justifica a

elabora¸c˜ao de um trabalho o qual foi publicado na revista Physics Letter B, sob o t´ıtulo ”Brane bounce-type configurations in a string-like scenario”, [27].

Para o caso A(r) = B(r) as equa¸c˜oes (2.31), (2.32) e (2.33) assumem a forma mais simples a seguir

1 2(5A

′₂

(r)₋4A′′) = ₋κ2₆

1 2φ

′₂

+V(φ)

−Λ (2.37)

5 2A

′₂

(r) =κ2₆

1 2φ

′₂

−V(φ)

−Λ. (2.38)

Resalve-se que neste caso preferiu-se usar a assinatura₋,+,+,+, que est´a de acordo com [27].

Estas equa¸cões, descontando-se a diferen¸ca de sinais em virtude da assinatura da métrica são as mesmas que se encontrou no caso da solu¸cão tipo bounce, quais sejam, (2.17) e (2.18), com diferen¸cas apenas nos fatores que multiplicam as derivadas de A. Portanto a solu¸cão para A(r) é a mesma que foi obtida para a solu¸cão do tipo parede de dom´ınio, (2.21), sendo o potencial também equivalente ao caso da solu¸cão em cinco dimensões, (2.24). Cabe, portanto, a pergunta: que tem esta solu¸cão a oferecer além do que já se obtem em cinco dimensões? Sem querer detalhar todos os pormenores da diferen¸ca que pode haver entre os dois modelos, para o escopo desta tese importa saber

que para determinados modelos nos quais a localiza¸cão de certos campos não é poss´ıvel em cinco dimensões, a simples generaliza¸cão destes para seis dimensões torna poss´ıvel a localiza¸cão . Um exemplo disso é a localiza¸cão do campo de gauge que só é poss´ıvel com a adi¸cão de um campo auxiliar na teoria, em cinco dimensões [43], entretanto pode ser

localizado em seis dimensões apenas através da intera¸cão gravitacional, como pode ser visto em Oda [6] e será revisto aqui no cap´ıtulo sobre localiza¸cão. Esta, portanto, é a principal razão do interesse em estudar o mesmo modelo em cinco o seis dimensões, neste trabalho.

Retornado às equa¸cões (2.37) e (2.38),φ representa o campo escalar que gera a brana, o qual será dado por

φ(r) =νtanh(ar), (2.39)

com a2 _≡ _λν2_/_{2. O potencial corresponde ao modelo} _λφ4_{, ou seja,} _V₍_φ_{) =} λ

(31)

Assim, a partir das equa¸cões (2.37) e (2.38) encontra-se para a fun¸cão A(r) a equa¸cão diferencialA′′

= κ26

4 φ ′₂

cuja solu¸c˜ao ´e

A(r) =βln cosh2(ar) + β 2 tanh

2₍_ar₎ _(2.40)

onde β = 1 3κ

2

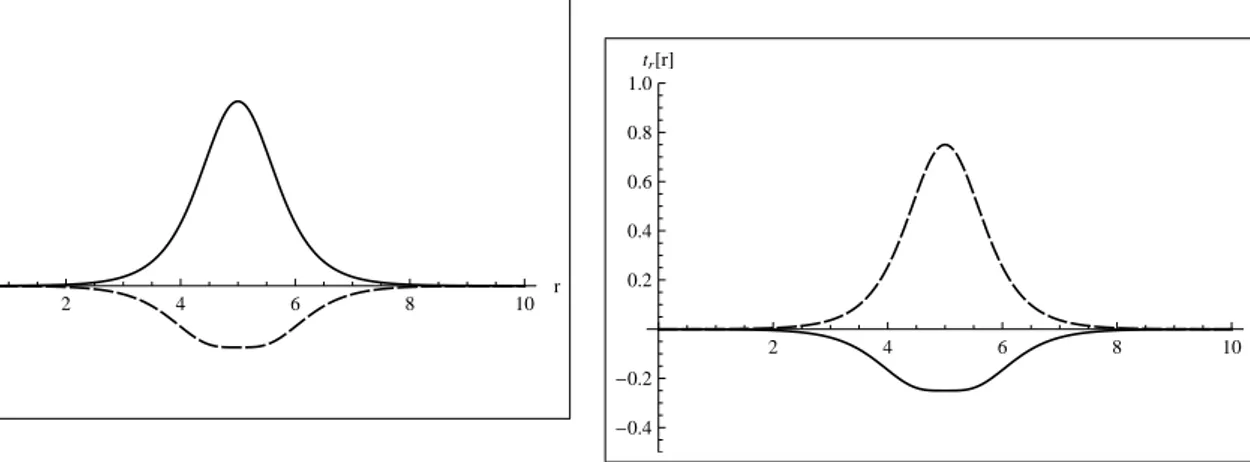
6ν2. Um perfil do fator de warp e−A(r) ´e dado na figura (3). O gr´afico se apresenta deslocado da origem, no entanto foi apenas para enaltecer visualmente que

representa uma brana com espessura não negligenciável. O mesmo apresenta um pico onde se localiza a brana, além disso é finito, ou seja e−A(r) _→ _{0 para} _r _{→ ∞}_{. Isto}

0 2 4 6 8 10 r 0.2

0.4 0.6 0.8 1.0

e-AHrL

Figura 3: Perfil do fator de warp e−A(r) _para _β _{= 1;}_a_{= 1}

assegura que a rela¸cão entre as escalas de Plank reduzidas em quatro (Mp) e seis (M6) dimensões dada a seguir é finita (2.41),

M_p2 = 2πM₆4

Z ∞

0

dre−3/2A(r), (2.41)

o que qualifica o modelo como potencial canditado a resolver o problema da hierarquia, o que vem a ser uma das razões, embora não a única, de se estudar modelos com dimensões

extras [10].

No que concerne `as condi¸c˜oes de energia pode ser observado a partir das componentes

t0, tr, tθ que dependendo dos valores das constantes presentes na defini¸c˜ao do campo

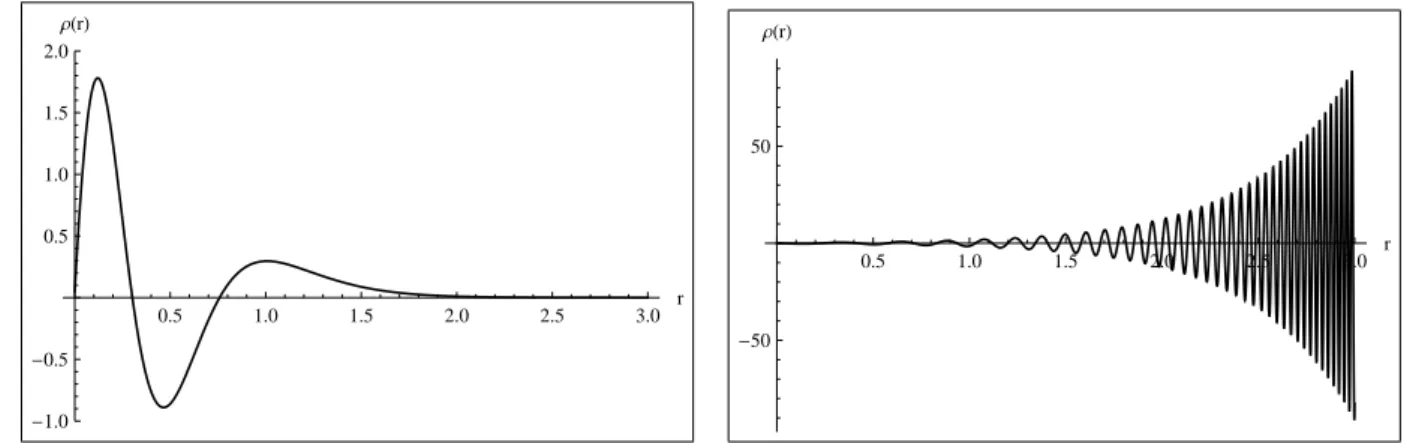
escalar, estas componentes podem ser positivas, assegurando a satisfa¸c˜ao das referidas condi¸c˜oes. Na figura 4 tem-se os perfis das componentest0(r) =tθ(r) e na figura 5 tem-se

a componente tr(r). Percebe-se que a depender dos valores escolhidos para v tais

com-ponentes podem ser positivas ou negativas. Por isso pode-se afirmar que a configura¸cão debounce assegura a satisfa¸cão das condi¸cões de energia, o que qualifica o modelo como fisicamente aceitável. Isto vem a ser um resultado destacável em compara¸cão com o

(32)

2 4 6 8 10 r

-0.4 -0.2 0.2 0.4 0.6 0.8 1.0

t0@rD

Figura 4: Perfil de t0(r) = tθ(r) para

v = ₋1 (linha cheia), e para v = 1 (linha seccionada)

2 4 6 8 10 r

-0.4 -0.2 0.2 0.4 0.6 0.8 1.0

tr@rD

Figura 5: Perfil de tr(r) para v = 1 (linha

cheia), e para v =₋1 (linha seccionada)

Quando for abordada a localiza¸cão de campos no cap´ıtulo (4) será realizada a lo-caliz¸cão dos campos escalar, de gauge e o campo fermiônico no modelo acima descrito. Não é poss´ıvel dizer que esta solu¸cão seja um defeito topológico pois sendo em seis

di-mensões ela teria de representar o defeito tipo corda para merecer tal denomina¸cão. No entanto, conforme revisão dada na próxima subse¸cão, a solu¸cão obtida acima poderia ser válida apenas em uma região exterior ao núcleo da brana exigindo-se que em seu interior fossem válidas as condi¸cões (2.46), as quais determinam um defeito tipo corda. Assim

seria poss´ıvel falar de um defeito tipo corda até mais realista do que a que se considera em Oda [6], que será revista a seguir. No entanto, preferiu-se assumir uma 4-brana em que a dimensão compacta é pequena o suficiente para que nela seja válida a f´ısica do modelo padrão [45].

2.2.2 Defeito tipo corda

Uma vez que o universo conhecido pode ser identificado com um defeito topológico, precisamente uma parede de dom´ınio, em um bulk com cinco dimensões, é natural inquirir sobre a possibilidade de outros defeitos topológicos em um bulk com mais dimensões extras poderem ser identificados com o universo do modelo padrão. Da´ı surgirem, por exemplo,

os modelos que consideram a existência de defeito tipo corda e monopolo em espa¸co-tempo com dois e três dimensões extras, respectivamente [37]. O interesse principal aqui reside na descri¸cão do defeito tipo corda uma vez que os estudos feitos aqui se restringem a modelos de brana em seis dimensões 2_{. Alguns dos primeiros trabalhos na tentativa de obter o}

2

(33)

que hoje se denomina defeito tipo corda em um bulk com duas dimensões espaciais extras foram realizados por [34, 37, 46, 47]. No que se refere ao estudo de localiza¸cão de campos em um defeito tipo corda Gherghetta [10], estudou o modo zero e os modos massivos para gravidade, Oda [6] estudou a localiza¸cão do modo zero para os campos escalar, vetorial e

fermiˆonicos de spin 1/2 e 3/2 al´em da gravidade; estudou ainda os modos massivos para os campos escalar e vetorial [12].

O estudo da localiza¸cão de fermions também foi realizado por Liu et al. [48]. A seguir é apresentada um defeito tipo corda como solu¸cão das equa¸cões de Einstein seguindo o desenvolvimento efetuado em [6]. A localiza¸cão do campo de Kalb-Ramond foi obtida ao longo do desenvolvimento desta tese e tal estudo se encontra publicado sob o t´ıtulo

”Tensor gauge field localization on a string-like defect”[16].

A métrica 2.27, como já foi dito, é compat´ıvel com um defeito tipo corda. Gherghetta [10] considera uma solu¸cão com uma 3-brana na origem da dimensão extra,r = 0, como será considerado aqui. Similar modelo é considerado por Oda [6]. Assumir-se-á para o tensor momentum energia o ansatz

Tνµ =δνµt0(r), Trr =tr(r), Tθθ =tθ(r) (2.42)

onde ti(i = o, r, θ) s˜ao fun¸c˜oes apenas de r, a coordenada radial. Este ansatz garante

simetria esférica. Para este cenário, no caso sem fonte (ti = 0), as equa¸cões de Einstein

para A=B =cr, sendo c uma constante, tˆem como solu¸c˜ao um defeito tipo corda local com

c2 = 2

5(−Λ) (2.43)

exigindo que se tenha Λ<0. Esta solu¸cão é facilmente obtida das equa¸cões (2.34), (2.35) e (2.36) substituindo-se as componentes do tensor energia momentum nestas equa¸cões pelo ansatz 2.42. Neste caso a solu¸cão para o fator de warp resulta e−cr_{, o que equivale, por}

assim dizer, a uma generaliza¸c˜ao do modelo RS para seis dimens˜oes. No caso tr = −tθ,

que representa uma quebra espontˆanea de simetria [6, 37] obtem-se como solu¸c˜ao um defeito tipo corda global

c1 =c− 8

pcκ

2

Dtθ (2.44)

c2 = 1

p(p+ 1)(−8Λ + 8κ 2

Dα)>0 (2.45)

onde A(r) =cr e B(r) = c1r.

(34)

sejam satisfeitas

e−12B(r)

′

|ǫ0 =−

δ

2π;

e−12B(0)

′

|ǫ0 = 1; e−B(ǫ) = 0 (2.46)

onde δ é o défice angular e ǫ é um pequeno raio contendo a brana. Estas condi¸cões de contorno não são de grande relevância quando se está interessado apenas na localiza¸cão de campo, [6].

Neste modelo também é poss´ıvel resolver o problema da hierarquia, como no caso do modelo RS em cinco dimensões. Além disso, ao contrário do que ocorre em cinco

dimensões, nesse caso não há necessidade de ajuste fino entre a constante cosmológica no bulk e a tensão na brana. Isto se deve ao fato de que no caso de cinco dimensões o espa¸co unidimensional na parede de dom´ınio é flat equanto que em seis dimensões o espa¸co bidimensional ao redor da corda cósmica pode ser curvo, [10].

Apesar desta solu¸cão ser um defeito tipo corda, na prática ela funciona como se fosse uma 4-brana tendo em vista que o fator que multiplica a dimensão extra compacta θ, é e−cr _ou _e−c1

r, portanto não obedece às condi¸cões (2.46). É neste sentido que se afir-mou que o modelo proposto na subse¸cão 2.2.1 pode ser modificado para comportar uma 3-brana que na linguagem desta subse¸cão corresponde a um defeito tipo corda local em quatro dimensões, mas tendo como solu¸cão externa o perfil de brana espessa lá

determi-nado. Um tal modelo uma vez construido seria, obviamente, uma generaliza¸c˜ao deste que descrevemos nesta subse¸c˜ao (2.2.2).

(35)

3 SOLUC

¸ ˜

OES DE ONDAS

ESTACION ´

ARIAS PARA

BRANAS ANISOTR ´

OPICAS

A suposi¸cão de que o universo conhecido é isotrópico, embora esteja de acordo com o que se observa em larga escala, deixa sem respostas algumas perguntas intrigantes e relevantes, tais como: porque nosso universo é isotrópico hoje uma vez que ele deve ter

sido anisotrópico em seu estágio inicial? A mais comum resposta dada pela cosmologia é que a expansão exponencial (infla¸cão) no universo primordial eliminaria a anisotropia. No entanto, tem sido mostrado que modelos real´ısticos de universo inflacionário têm ex-pansão aproximadamente, mas não exatamente exponencial [49]. Por outro lado

Watan-abe, Kanno e Soda mostraram que em um modelo com expansão aproximadamente expo-nencial persiste alguma anisotropia [50]. Além disso, se na teoria de Friedman-Lamaˆıtre-Robertson-Walker (FLRW), que descreve o universo conhecido é implementada uma per-turba¸cão encontram-se novos modelos que seriam mais importantes em épocas iniciais

do que o modelo FLRW, ou, dizendo de outra maneira, flutua¸cões estat´ısticas puras em FLRW não colapsam rápido o suficiente para formar as galáxias observadas hoje [17].

Se há razões para estudar anisotropia no universo, igualmente há razões para estudar modelos de branas anisotrópicas, uma vez que os modelos de brana têm todos a pretensão de representar o universo. Neste sentido é poss´ıvel encontrar uma gama variada de trabal-hos que descrevem mundo brana em cenários anisotrópicos, [18, 19, 20, 21, 22, 23, 24, 25].

Hoogen eIbanez [20] consideram um modelo de brana anisotrópico do tipo Bianchi II em que a fonte é uma combina¸cão de um fluido perfeito com um campo escalar minimamente acoplado, o qual é restrito a se propagar apenas na brana. Um dos resultados desse

(36)

De maneira geral a grande maioria dos estudos de brana anisotrópica estão interessado na cosmologia dos modelos, não há preocupa¸cão quanto ao estudo de localiza¸cão de campos, excessão feita ao trabalho de Merab [18] cuja extensão para seis dimensões será realizada neste cap´ıtulo. Este modelo, recente na literatura, descreve um cenário exótico em que a

brana é gerada por ondas gravitacionais estacionárias, sendo a fonte o campo escalar do tipo fantasma, ou seja, com um sinal negativo em frente ao termo cinético na Lagrangiana [8, 9, 18]. Como será visto aqui o modelo original já foi por nós generalizado, inclusive para seis dimensões, e se encontra submetido ao PRD sob o t´ıtulo ”A 6D standing-wave

Braneworld”, [29].

Para o estudo do modelo anisotr´opico considerado aqui inicia-se pela m´etrica que

generaliza aquela usada na se¸c˜ao (2.1), precisamente a m´etrica (2.7)

ds2 =eA(r) dt2₋eu(r,t)dx2₋eu(r,t)dy2₋e−2u(r,t)dz2

−dr2 (3.1)

ondeA(r) é uma fun¸cão que depende apenas de r eu=u(r, t) é a fun¸cão que determina a anisotropia e depende de t e r.

Nas expressões a seguir, o ponto representa derivada com rela¸cão ao tempo enquanto que a linha representa derivada com rela¸cão a variável extra r. Os termos não nulos da conexão para esta métrica são

Γx_tx = Γyty =

1 2u˙; Γ

z

tz =−u˙ (3.2)

Γx_rx = Γy_ry = 1 2(A

′

+u′); Γz_rz = 1 2(A

′

−2u′); Γt_rt= 1 2A

′

, (3.3)

Γt_xx = Γt_yy = 1 2e

u_u_˙_{; Γ}t

zz =−

1 2e

−2u_u_˙_; _(3.4)

e

Γr_xx = Γr_yy =₋1 2e

A+u₍_A′

+u′); Γr_zz =₋1 2e

A−2u₍_A′

−2u′); Γr_tt = 1 2e

A_A′

. (3.5)

A partir destes calculam-se as componentes n˜ao nulas do tensor de Ricci

Rxx =Ryy =−

1 2e

A+u₂_A′₂

+A′′₋e−Au¨+ 2A′u′ +u′′ (3.6)

Rzz =−

1 2e

A−2u₂_A′₂

(37)

Rtt =

1 2e

A₂_A′₂

+A′′₋3e−Au˙2 (3.8)

Rrt =−

3 2uu˙

′

(3.9)

Rrr =

1 2

−2A′2₋₄_A′′

−3u′2 _(3.10)

Enquanto isso o escalar de curvatura lˆe-se

R= 5A′2+ 4A′′+ 3 2

−e−Au˙2+u′2 (3.11)

Finalmente as equa¸c˜oes de Einstein resultam

Gxx =Gyy =

1 4e

A+u

6A′2+ 6A′′₋3e−Au˙2+ 2e−Au¨₋4A′u′+ 3u′2₋2u′′

=κ2₅Txx−gxxΛ (3.12)

Gzz =

1 4e

A−2u

6A′2+ 6A′′₋3e−Au˙2 ₋4e−Au¨+ 8A′u′ + 3u′2+ 4u′′

=κ2₅Tzz −gzzΛ (3.13)

Gtt =−

3 4e

A₂_A′₂

+ 2A′′+e−Au˙2+u′2=κ2₅Ttt−gttΛ (3.14)

Grt =−

3 2uu˙

′

=κ25Trt (3.15)

Grr=

3 4

2A′2₋e−Au˙2 ₋u′2=κ2₅Trr−grrΛ (3.16)

onde o tensor energia momentum n˜ao est´a determinado, em princ´ıpio. No entanto, pela

(38)

fantasma, em cinco dimens˜oes, ´e dado por

TM N =−∂MΦ∂NΦ +gM N

1 2∂

C_Φ_∂

CΦ +gM NV(Φ) (3.17)

o qual pode ser obtido da Lagrangeana geral para um campo fantasma, para a métrica com assinatura (+,₋,₋,₋,₋) [51] que é considerada nesta se¸cão

Lp =−gM N

1

2∇MΦ∇NΦ−V(Φ). (3.18)

A partir de (3.17), para o casoV(Φ) = 0 as equa¸c˜oes de Einstein (2.3) podem ser reescritas como

RM N =−κ25∂Mφ∂Nφ+

2

3gM NΛ (3.19)

cujas componentes n˜ao nulas s˜ao dadas por

Rxx =

2 3e

A+u_{Λ =}_R

yy (3.20)

Rzz =

2 3e

A−2u_Λ _(3.21)

Rtt =−κ25φ˙2− 2 3Λe

A _(3.22)

Rrt=−κ25φφ˙ ′

(3.23)

Rrr =−κ25φ ′₂

+2

3Λ (3.24)

A seguir serão apresentadas algumas solu¸cões para as equa¸cões de Einstein a come¸car

pelo modelo de Merab [18] que será discutido na próxima subse¸cão.

3.1 Brana gerada a partir de ondas gravitacionais

estacion´

arias em cinco dimens˜

oes

O modelo aqui descrito representa uma generaliza¸cão do modelo RS uma vez que apresenta anisotropia, mas no limite u _→ 0, no que se refere ao ansatz para a métrica, resulta igual ao modelo RS para A(r) = 2a_|r_|. A solu¸cão apresentada aqui segue aquela apresentada originalmente em [18], portanto considerar-se-á apenas ondas estacionárias

”se propagando para a direita”, ou seja, A(r) = 2ar. Com isso a m´etrica (3.1) assume a forma mais simples

ds2 =e2ar dt2₋eu(r,t)dx2₋eu(r,t)dy2₋e−2u(r,t)dz2