Lat. Am. j. solids struct. vol.10 número2

(1)

T hermomechanical

Buckling

of

T

emperature-dependent FGM Beams

1 INT RODUCT ION

Funct ionally graded mat erials, as a branch of new mat erials, have at t ract ed increasing at t en-t ion in recenen-t years. A survey in en-t he lien-t eraen-t ure reveals en-t he exisen-t ence of wealen-t h invesen-t igaen-t ions on analysis of funct ionally graded mat erial beams. Among t hem, K ang and Lee [1] present ed explicit expressions for deflect ion and rot at ion of an FGM cant ilever beam subject ed t o an end moment . Considering t he large deflect ion of t he beam, t hey report ed t hat an FGM beam can bear larger applied load t han a homogeneous beam. Free vibrat ion analysis of simply-support ed funct ionally graded mat erial beams is report ed by Aydogdu and T askin [2]. T hey

Y. Kiani a and M .R. Eslami b, * a_{Ph.D. St udent , Mechanical Engineering} De-part ment , Amirkabir Universit y of T echnology, 15914 T ehran, Iran.

b

Professor and Fellow of Academy of Sciences, Mechanical Engineering Depart ment , Amirkabir

Universit y of T echnology, T ehran 15914, Iran. T el: (+ 98-21) 6454-3416,

Fax: (+ 98-21) 6641-9736.

Received 11 Oct 2011 In revised form 13 Nov 2012

*

Aut hor email: eslami@aut .ac.ir Abstract

Buckling of beams made of functionally graded materials (FGM) under thermomechanical loading is analyzed herein. Properties of the const ituent s are considered t o be functions of t emperature and thickness coordinat e. T he derivation of the equations is based on the T imoshenko beam theory, where the effect of shear is includ-ed. It is assumed that the mechanical and thermal nonhomogene-ous properties of beam vary smoothly by dist ribution of the power law index across the thickness of the beam. The equilibrium and st abilit y equations for an FGM beam are derived and the exist -ence of bifurcat ion buckling is examined. The beam is assumed under three t ypes of thermal loadings; namely, the uniform t em-perature rise, heat conduction across the thickness, and linear distribut ion across the thickness. V arious t ypes of boundary condi-t ions are assumed for condi-the beam wicondi-th combinacondi-tion of roller, clamped, and simply-support ed edges. In each case of boundary condit ions and loading, closed form solutions for the critical buck-ling t emperature of the beam is present ed. The result s are com-pared with the isotropic homogeneous beams, that are reported in the literature, by reducing the result s of the functionally graded beam to the isot ropic homogeneous beam.

Keywords

(2)

Lat in American Journal of Solids and St ruct ures 10(2013) 223 – 246

used bot h exponent ial and power law form of mat erial propert ies dist ribut ion t o derive t he governing equat ions. T heir st udy includes four t ypes of displacement fields namely, t he classi-cal beam t heory, t he first order t heory, and t he parabolic and exponent ial shear deformat ion beam t heories. T hey concluded t hat , in comparison wit h t he classical beam t heory, ot her t hree t ypes of displacement fields accurat ely predict the nat ural frequencies. Nirvana et al. [3] obt ained analyt ical expressions for t hermo-elast ic analysis of t hree layered beams, when t he middle layer is made of FGMs. A unified met hod t o st udy t he dynamic and st at ic analysis of FGM T imoshenko beams is report ed by Li [4]. He derived a fourt h order different ial equat ion and linked t he ot her paramet ers of t he beam t o t he solut ion of fourt h order different ial equa-t ion. His sequa-t udy includes equa-t he simply supporequa-t ed and canequa-t ilever beams. T he sequa-t aequa-t ic and free vi-brat ion analysis of layered FGM beams based on a third order shear deformat ion beam t heo-ry is developed by Kapuria et al. [5]. A t wo nodes finit e element met hod is adopt ed t o solve t he coupled ordinary different ial equat ions.

(3)

first order shear deformat ion t heory of beams. T he derivat ion of t he equat ions is based on t he concept of neut ral surface, where t he numerical shooting met hod is used t o solve t he coupled nonlinear equat ions. T heir st udy concluded t hat when a clamped-clamped FGM beam is sub-ject ed t o uniform t hermal loading, it follows t he bifurcat ion-t ype buckling while t he simply-support ed beams do not . T his feat ure of FGM beams, however, is ignored in some of t he published works t hrough t he lit erat ure [9, 14, 15].

Kiani et al. [16,17] st udied t he eﬀect of applied act uat or volt age on t he crit ical buckling t emperat ure difference of FGM beams. It is report ed t hat t he effect of applied act uat or smart layers is somehow negligible on t hermal buckling cont rol. In an analyt ical st udy, Ma and Wang [18] analyzed t he nonlinear response of FGM beams wit h shear deformat ion effect s and obt ained t he exact closed-form solut ions for equilibrium pat h of t he beam. T his analyt ical st udy also proves t he import ance of t he boundary condit ions on t he beam equilibrium pat h. Fu and his co-aut hors [19] obt ained closed-form solut ions for t he free vibrat ion of t hermally loaded and t hermal equilibrium pat h of a t hin FGM beam wit h bot h edges clamped. In t his work t he t emperat ure dependency of t he const it uent s is also t aken int o account . A single t erm Rit z solut ion along wit h a finit e element formulat ion is developed by Anadrao et al. [20]. In t his work t he cases of a beam wit h bot h edges clamped and bot h edges simply-support ed are analyzed.

T he present work deals wit h t he buckling analysis of FGM beams subject ed t o t hermal or mechanical loadings. Various t ypes of boundary condit ions are assumed and t he exist ence of bifurcat ion t ype buckling in each case is examined. Based on t he concept of virt ual displace-ment s principle, t hree coupled different ial equat ions are obt ained as t he equilibrium equat ions. In equat hermal buckling analysis, equat he beam is under equat hree equat ypes of equat hermal loading disequat incequat -ly, and closed-form solut ions are obt ained t o evaluat e t he crit ical buckling t emperat ures/ loads .

2 FUNCT IONALLY GRADED T IM OSHENKO BEAM S

Consider a beam of funct ionally graded mat erial, where t he graded propert ies are assumed t o be t hrough t he t hickness direct ion. T he volume fractions of t he const it uent mat erials, which are assumed t o ceramic of volume V_c and met al of volume V_m , may be expressed using t he power law dist ribut ion as [21]

1 1,

2

k

c m c

z

V V V

h

 _



  _  __

  (1)

whereh is t he t hickness of t he beam and z is t he t hickness coordinat e measured from t he middle surface of t he beam h / 2 z h/ 2, k is t he power law index which has t he val-ue equal or great er t han zero. Variat ion of V_c wit h k and z / h is shown in Figure 1.

(4)

Figure 1 Distribution of ceramic volume fraction t hrough t he thickness for various power law indices

T he value of k equal t o zero represent s a fully ceramic beam



V_c 1



and k equal t o in-finit y represent s a fully met allic beam



V_c 0



. We assume t hat t he mechanical and t hermal propert ies of t he FGM beam are dist ribut ed based on Voigt 's rule [22]. T hus, t he propert y variat ion of a funct ionally graded mat erial using Eq. (1) is given by

( ) 1

2

k

m cm

z P z P P

h

 _



  __  ___ (2)

whereP_cm  P_c P_m, P_c and P_m are t he corresponding propert ies of t he met al and ceramic, respect ively. In t his analysis t he mat erial propert ies, such as Young's modulusE z( ), coeffi-cient of t hermal expansion ( )z and t hermal conduct ivit y K z( ) may be expressed by Eq. (2), whereas Poisson's rat io  is considered t o be const ant across t he t hickness [21].

3 GOVERNING EQUAT IONS

(5)

Figure 2 geometry and coordinate syst em of an FGM beam

T he analysis of beam is based on t he first order shear deformat ion beam t heory using t he T imoshenko assumpt ions. According t o t his t heory, t he displacement field of t he beam is assumed t o be [4]

( , )

u x z  u z

(3) ( , )

w x z w

whereu x z( , ) and w x z( , ) are displacement s of an arbit rary point of t he beam along t he x

and z-direct ions, respect ively. Here, u and w are t he displacement component s of middle surface and  is t he rot at ion of t he beam cross-sect ion, which are funct ions of x only. T he st rain-displacement relat ions for t he beam are given in t he form [11]

2 1 2

xx

u w

x x



 

 _ _

  _ __

 

 _ _

(4)

xz

u w z x

   

 

where_xx and _xz are t he axial and shear st rains. Subst it ut ing Eq. (3) int o Eq. (4) gives

2 1 2

xx

du dw d z dx dx dx

    __ ___ 

(5)

xz

dw dx

 

(6)







0



xx E xx T T

     (6)





2 1 xz xz E     

In Eqs. (6), _xx and _xz are t he axial and shear st resses, T₀is t he reference t emperat ure, and T is t he t emperat ure dist ribut ion t hrough t he beam. Eqs. (5) and (6) are combined t o give t he axial and shear st resses in t he beam in t erms of t he middle surface displacement s as





2 0 1 2 xx

du dw d

E z T T

dx dx dx

    _ _ _  _ _ _  _  _  __ __    __   (7)





2 1 xz E dw dx     _   _ __  ___

T he st ress result ant s of t he beam expressed in t erms of t he st resses t hrough t he t hickness, according t o t he T imoshenko beam t heory, are [8]

/ 2 / 2

h x _h xx

N  dz





_

/ 2

h

x _h xx

M z dz





_

(8)

/ 2 / 2

h xz s _h xz

Q K  dz





_

whereK_s is t he shear correct ion fact or. T he values of 5/ 6 or 2/ 12 are used as it s approx-imat e value for t he composit e and FGM beams wit h rect angular cross sect ion [12]. T he shear correct ion fact or is t aken as 2 _{/ 12}

s

K   for t he FGM beam in t his st udy.

Using Eqs. (2), (7), and (8) and not ing t hat u w, , and  are funct ions of x only, t he ex-pressions forN_x,M_x, and Q_xz are obt ained as

2 1 2 1 2 T x x

du dw d

N E E N

dx dx dx

  _ _{ }  _ _ _  _  _  __ __ __      2 2 3 1 2 T x x

du dw d

M E E M

dx dx dx

  _ _{ }  _ _ _  _  _  __ __ __   

(7)



1



2 1

s xz

E K dw Q dz    _   _  __   

whereE₁, E₂, and E₃ are st ret ching, coupling st ret ching-bending, and bending st iffnesses, respect ively, and T

x

N and T x

M are t hermal force and t hermal moment result ant s, which are calculat ed using t he following relat ions

/ 2

1 _{/ 2} ( )

1 h cm m h E E E z dz h E

k   _  _   __  __   



/ 2 2 2 / 2 1 1 ( )

2 2 2

h

cm h

E zE z dz h E

k k   _    __  ___  



/ 2 2 3 3 / 2

1 1 1 1

( )

12 3 2 4 4

h

m cm h

E z E z dz h E E

k k k



  _

 

  _  _   __

     



(10)





/ 2

0 / 2 ( ) ( )

h T

x _h

N E z z T T dz





_







/ 2

0 / 2 ( ) ( )

h T

x _h

M zE z z T T dz









Not e t hat t o find t he t hermal force and moment result ant s, t he t emperat ure dist ribut ion t hrough t he beam should be known.

T he equilibrium equat ions of an FGM beam may be obt ained t hrough t he st at ic version of virt ual displacement principle. According t o t his principle, since t he ext ernal load is absent , an equilibrium posit ion occurs when t he first variation of st rain energy funct ion vanishes. T hus, one may writ e





/ 2 / 2

0 / 2 / 2 0

L b h

xx xx s xz xz

b h

U K dzdydx

     

 



_{ }

_

  (11)

(8)

0

x

dN dx 

dMx Q_xz 0

dx  

(12)

2

2 0

xz x

dQ d w N

dx  _dx 

and t he boundary condit ions for each side of t he beam are

0 0

x

N  or u 

0 0

x

M  or  

(14)

0 0

xz x

dw

Q N or w

dx 

  

4 EXIST EN CE OF BIFURCAT ION T YPE BUCKLING

4.1 T hermal Loading

Consider a beam made of FGMs subject ed t o a t ransversely t emperat ure dist ribut ion. When t he axial deformat ion is prevent ed in t he beam, an applied t hermal loading may produce an axial load. Only perfect ly flat pre-buckling configurat ions are considered in t he present work, which lead t o bifurcat ion t ype buckling, ot herwise beam undergoes a unique and st able equi-librium pat h. Now, based on Eq. (9), in t he pre-buckling st at e, when beam is complet ely un-deformed, and bot h edges are immovable, t he generat ed pre-buckling force t hrough t he beam is equal t o

0

T

x x

N  N (14)

Here a subscript 0 is adopt ed t o indicat e t he pre-buckling st at e deformat ion. Also, ac-cording t o Eq. (9), an ext ra moment is produced t hrough t he beam which is equal t o

0

T

x x

M  M (15)

(9)

un-Lat in American Journal of Solids and St ruct ures 10(2013) 223 – 246

deformed when it is subject ed t o uniform t emperat ure rise, because t hermal moment vanishes t hrough t he beam. T herefore, bifurcat ion t ype buckling exist s for C C and C R FGM beams subject ed t o arbit rary t ransverse t hermal loading. T he same is t rue for t he isot ropic homogeneous beams subject ed t o uniform t emperat ure rise wit h arbit rary case of boundary conditions.

4.2 M echanical Loading in T hermal Field

Consider an FGM beam in t hermal field which is subject ed t o an in-plane axial loadP, and operat es in t hermal field. T he left side of t he beam is immovable, while t he right hand side is movable and undergoes an in-plane force P

When t he beam exhibit s t he bifurcat ion-t ype of buckling, it remains un-deformed in primary equilibrium pat h. Based t o t he first equilibrium equat ion, t he prebuckling force result -ant is equal t o

0 =

x

P N

b

 (16)

Based on t he definit ion of force result ant s, when t he lat eral deflect ion is ignored, t he in-duced mechanical moment due t o t he applied in-plane force is equal t o

2 2

0

1 1

= T T

x x x

E E

P

M N M

b E E

   (17)

T he exist ence of bifurcat ion t ype buckling depends on t he vanishing of t he ext ra bending moment in Eq. (17). In t he following general cases are st udied

C ase 1: For t he case when an FGM beam is subject ed t o axial load only, C C and

C R cases follow t he branching t ype of buckling. Ot herwise t he induced moment in Eq. (17) result s in t he init ial de_ﬂect ion.

C ase 2: For t he case of reduct ion of an FGM beam t o an isot ropic homogeneous one t hat

is subject ed t o uniform t emperat ure rise loading, M_x₀  0 and bifurcat ion occurs for any arbit rary case of out -of-plane boundary condit ions.

C ase 3: For t he case of reduct ion of an FGM beam t o an isot ropic homogeneous one t hat

is subject ed t o heat conduct ion across t he t hickness, ₀ T

x x

(10)

C ase 4: For t he case of an FGM beam t hat is subject ed t o arbit rary case of t hermal

load-ing in t he presence of axial in-plane load, M_x₀ is given by Eq. (17). Generally t his moment does not vanish and similar t o t he previous case only C C and C R end support s exhib-it t he bifurcat ion-t ype of buckling. In ot her combinat ions of edge support s, beam inexhib-it ially st art t o lat eral deflect ion at t he onset of t hermal loading.

5 ST ABILIT Y EQUAT IONS

T o derive t he st abilit y equat ions, t he adjacent -equilibrium crit erion is used. Assume t hat t he equilibrium st at e of a funct ionally graded beam in pre-buckling st at e is defined in t erms of t he displacement component su₀,w₀ and₀. T he displacement component s of a neighboring st able st at e differ byu₁,w₁ and₁ wit h respect t o t he equilibrium posit ion. T hus, t he t ot al displacement s of a neighboring st at e are [23]

0 1

u u u

0 1

w w w (18)  ₀₁

Similar t o t he displacement s, t he force and moment result ant s of a neighboring st at e may be relat ed t o t he st at e of equilibrium as

0 1

x x x

N N N

0 1

x x x

M  M M (19)

0 1

xz xz xz

Q Q Q

Here, st ress result ant s wit h subscript 1 represent t he linear part s of t he force and moment result ant increment s corresponding t ou₁, w₁and₁. T he st abilit y equat ions may be obt ained by subst it ut ing Eqs. (18) and (19) in Eq. (12). Upon subst it ut ion, t he t erms in t he result ing equat ions wit h subscript 0 sat isfy t he equilibrium conditions and t herefore drop out of t he equat ions. Also, t he non-linear t erms wit h subscript 1 are ignored because t hey are small compared t o t he linear t erms. T he remaining t erms form t he st abilit y equat ions as

2 2

1 1

1 ₂ 2 ₂ 0

d u d

E E

dx dx



(11)





2 2

1 1 1 1

2 ₂ 3 ₂ 1 0

2 1

s

d u d E K dw

E E dx dx dx     _  _   __  __

  

(20)





2 2

1 1 1 1

0

2 2 0

2 1

s

x

E K d d w d w N dx dx dx

   _  _      _    _ _

Combining Eqs. (20) by eliminat ing u₁ and ₁ provides an ordinary different ial equat ion in t erms of w₁ which is t he st abilit y equat ion of an FGM beam under t ransverse t hermal loadings

4 2

2

1 1

4 2

d w d w

dx  dx (21)

wit h





2 1 0

2

1 3 2 0

1 1 1 2 x x s E N E E E N

E K    _ _    _  _  __   (22)

T he st ress result ant s wit h subscript 1 are linear part s of result ant s t hat correspond t o t he neighboring st at e. Using Eqs. (9) and (18) t he expressions for,N_x₁, M_x₁and Q_xz₁ become

1 1

1 1 2

x

du d

N E E

dx dx



 

1 1

1 2 3

x

du d

M E E

dx dx



  (23)



1



1

1 1

2 1

s xz

E K dw Q dx    _  _  __  __   

When t emperat ure dist ribut ion t hrough t he beam is along t he t hickness direct ion only, t he paramet er  is const ant . In t his case t he exact solut ion of Eq. (2) is

 

1( ) 1sin 2cos 3 4

w x C x C x C x C (24)

(12)

 



 



1( )x S C1cos x C2sin x C3

       

 



 



2

1 1 2 5 6

1

( ) E cos sin

u x S C x C x C x C

E   

   

 





2 1 3 2

1 1 2 2 5

1

( ) ( ) sin cos

x

E E E

M x S C x C x E C

E

    

  

(25)



1





 





 



1( ) 1cos 2sin

2 1

s xz

E K

Q x  S  C x C x



  



1( ) 1 5

x

N x E C

Wit h





2 1 3 22

2 1

( )

1 2 1

s S

E E E E K

 

  



 

(26)

T he const ant s of int egrat ion C₁ t o C₆ are obt ained using t he boundary condit ions of t he beam. Also, t he paramet er  must be minimized t o find t he minimum value of N_x₀ associ-at ed wit h t he t hermal or mechanical buckling load. Five t ypes of boundary condit ions are assumed for t he FGM or homogeneous beam wit h combinat ion of t he roller, simply support -ed, and clamped edges. Boundary condit ions in each case are list ed in T able 1.

T able 1 Boundary conditions for FGM T imoshenko beams under t hermal loading. C indicat es clamped,

S shows simply-support ed and R is used for roller edge. For mechanical buckling case, u₁should be replaced by N_x₁

Edge support s B.Cs at x  0 B.Cs at x L

C C u1 w1 1  0 u1 w1 1 0

S S u1 w1 Mx1  0 u1 w1 Mx1  0

C S u1 w1 1  0 u1 w1 Mx1  0

C R u1 w1 1  0 1 1 xz1 x0 1 0

dw

u Q N

dx



   

S R u1 w1 Mx1  0 1 1 xz1 x0 1 0

dw

u Q N

dx



(13)

Let us consider a beam wit h bot h edges clamped under t hermal loading. Using Eqs. (24) and (25), t he const ant s C₁ t o C₆ must sat isfy t he syst em of equat ions

 

   

 

   

1 2 3 4 2 5 1

2 2 6

1 1

0 1 0 1 0 0

sin cos 1 0 0

0 1 0 0 0

cos sin 1 0 0 0

0 0 0 0 1

cos sin 0 0 1

C

L L L

C S

C

S L S L

C E

S

C E

E E C

S L S L L

E E              _  _  _{ }     _ _     _{ }_  _ _ __ _  __ _  __ _  _ _    _ _  _ __  _  _      __ _        _ _  _{ }_  __ _  __ __  _ _  _     0 0 0 0 0 0                                           (27)

T o have a nont rivial solut ion, t he det erminant of coefficient mat rix must be set equal t o zero, which yields

 



2 2 cos

 

   

sin



0

S  L  L LS  L  (28)

T he smallest posit ive value of  which sat isﬁes Eq. (28) is _min 6.28319

L

  . It can be seen

easily t hat for t he ot her t ypes of boundary condit ions, except C S case, t he nont rivial solu-t ion leads solu-t o an exacsolu-t paramesolu-t er for. Using an approximat e solut ion given in [24] for t he crit ical axial force of C S beams, t he crit ical force for an FGM T imoshenko beam wit h arbit rary boundary condit ions can be expressed as below

2 2 3 2 1 0, ₂ 3 2 2 1 1 1 1 x cr s E p E E L N E E q E E K L   _  _   _  _    _ _      _ _ __ __  __  ___ __ _    (29)

where p and q are const ant s depending upon t he boundary condit ions and are list ed in T able 2

T able 2 Constants of formula (29) which are related to boundary condit ions.

Paramet er C C S S C S S R C R

p 39.47842 9.86960 20.19077 2.46740 9.86960

(14)

When t he crit ical buckling force result ant is obt ained, in t he case of mechanical loading, t he t ot al compressive load may be evaluat ed by Eq. (16). For t he case of t hermal buckling analysis, however, t emperat ure profile should be known.

6 T YPES OF T HERM AL LOAD ING

6.1 Uniform temperature rise (UT R)

Consider a beam which is at reference t emperat ureT₀. When t he axial displacement is prevent ed, t he uniform t emperat ure may be raised t o T₀ T such t hat t he beam buckles. Subst it ut ing T₀  T int o Eq. (10) gives

=

1 2 1

T cm m m cm cm cm

x m m

E E E

N h T E

k k      _ _  _  __   __  

  (30)

Considering Eq. (30), t he crit ical buckling t emperat ure diﬀerence

∆

T

crUT R is expressed in

t he form

2

( , ) =

1

( , , ) 1 ( , )

UT R m

cr s p h F k L T h

G k q E k

K L                _ _     _ _ _   _{ }_      (31)

where = cm

m

E E

 and = cm

m  

 . Also, t he funct ionsE k( , ) ,F k( , ) , and G k( , , )  are

de-fined as

2 2 2

2

( 2)

1 ( , ) =

12 4( 1)( 2)( 3) 4( 1)( 2) ( 1 )

k k k

F k

k k k k k k

              

2 2 2

2 2

( 2)

1 ( , ) =

12( 1 ) 4( 2)( 3)( 1 ) 4( 2) ( 1 )

k k

E k

k k k k k k

 



  

 

 _ _

        

(32)

( , , ) = 1

1 2 1

G k

k k

  

    

(15)

Lat in American Journal of Solids and St ruct ures 10(2013) 223 – 246 6.2 Linear temperature distribution (LT D)

Consider a t hin FGM beam which t he t emperat ure in ceramic-rich and met al-rich surfaces are T_c andT_m, respect ively. T he t emperat ure dist ribut ion for t he given boundary condit ions is obt ained by solving t he heat conduct ion equat ion along t he beam t hickness. If t he beam t hickness is t hin enough, t he t emperat ure dist ribut ion is approximat ed linear t hrough t he t hickness. So t he t emperat ure as a funct ion of t hickness coordinat e z can be writt en in t he form

1

= ( )( )

2

m c m

z T T T T

h

   (33)

Subst it ut ing Eq. (33) int o Eq. (10) gives t he t hermal force as

0

= ( )

1 2 1

T cm m m cm cm cm

x m m m

E E E

N h T T E

k k       _  _  __   __     (34)

2 2 2 2

m m cm m m cm cm cm

E E E E

h T k k      _ _  _   __   __    

where  T T_c T_m. Combining Eqs. (29) and (34) gives t he ﬁnal form of t he crit ical buckling t emperat ure difference t hrough t he t hickness as

2 0 2 ( , ) ( , , ) = ( ) ( , , ) 1

( , , ) 1 ( , )

LT D m

cr m

s p h

F k

L G k

T T T

H k h

H k q E k

K L                    _ _       _ _ _       _ _ _       (35)

Here, t he funct ionsE k( , ) ,F k( , ) , and G k( , , )  are deﬁned in Eq. (32) and funct ion ( , , )

H k   is defined as given below

1 ( , , ) =

2 2 2 2

H k

k k

  

    

(16)

Lat in American Journal of Solids and St ruct ures 10(2013) 223 – 246 6.3 Nonlinear temperature distribution (NLT D)

Assume an FGM beam where t he t emperat ure in ceramic-rich and met al-rich surfaces are

c

T andT_m, respect ively. T he governing equat ion for t he st eady-st at e one-dimensional heat conduct ion equat ion, in t he absence of heat generat ion, becomes

( ) = 0

d dT K z dz dz  _  _  _     (37) ( ) = , ( ) =

2 c 2 m

h h

T T T  T

whereK z( ) is given by Eq. (2). Solving t his equat ion via polynomial series yields t he t em-perat ure dist ribut ion across t he beam t hickness as

1

= 0

( ) ( 1) 1

=

1 2

i ik

N i

c m cm

m

i m

T T K z

T T

D ik K h

  _ _{ } _      _     _ _ _ _ _  _ _ 



 (38) wit h = 0 ( 1) = 1 i N i cm i m K D ik K    __ __   _    



(39)

Here N is t he number of t erms which should be t aken int o account t o assure t he conver-gence of t he series. Evaluat ing T

x

N and solving for T gives t he crit ical bucking value of t he t emperat ure difference as

2 0 2 ( , ) ( , , ) = ( ) ( , , , ) 1

( , , , ) 1 ( , )

N LT D m

cr m

s p h

F k

L G k

T T T

I k h

I k q E k

(17)

In t his relat ion, = cm

m K

K

 and t he funct ion I k( , , , )   is defined as

 

0

1 1

( , , , ) =

1 2 2 2 2

i N

i I k

D ik ik ik k ik k

   

  



 _  _

 

 

 _      _



(41)

It should be point ed out t hat in each case of t hermal loading, an it erat ive process should be implement ed t o calculat e t he crit ical buckling t emperat ure difference. T o t his end, proper-t ies are evaluaproper-t ed aproper-t reference proper-t emperaproper-t ure and proper-t he criproper-t ical buckling proper-t emperaproper-t ure difference is calculat ed. Propert ies of t he const it uent s are t hen evaluat ed at t he current t emperat ure and again crit ical buckling t emperat ure difference is obt ained. T his process should be cont inued t o obt ain t he convergent crit ical buckling t emperat ure difference.

7 RESULT S AND DISCUSSION

Consider a ceramic-met al funct ionally graded beam. T he combinat ion of mat erials consist of Silicon-Nit ride as ceramic and st ainless st eel as met al. T he elast icit y modulus, t he t hermal expansion coefficient , and t he t hermal conduct ivit y coefficient for t hese const it uent s are high-ly dependent t o t he t emperat ure and t heir propert ies may be evaluat ed in any t emperat ure based on T oloukian model. Each propert y of t he const it uent s follow t he next dependency t o t he t emperat ure



1 2 3



0 1 1 2 3

( ) 1

P T P P T_  P T P T P T (42)

In t his equat ion T is measured in K elvin. T he const ant s P_iare unique for t he const it uent s and for t he const it uent s of t his st udy are given in T able 3. Poisson’s rat io for simplicit y is chosen as 0.28.

T able 3 Introduced coe_ﬃcients of Eq. (42)

c

E E_m _c _m K_c K_m

0

P 348.43e9 201.04e9 5.8723e6 12.33e6 13.723 15.379

1

P 3.070e4 3.079e4 9.095e4 8.086e4 1.032e3 1.264e3

2

P 2.16e7 6.534e7 0 0 5.466e7 2.092e6

3

(18)

T o validat e t he result s, t he effect of shear is plot t ed in Figure 3, for an isot ropic homoge-neous beam wit h t emperat ure independent mat erial propert ies. For t his purpose, t he result s are compared bet ween t he Euler and T imoshenko beam t heories. T he beam is under t he uni-form t emperat ure rise loading. Non-dimensional crit ical buckling t emperat ure is defined

by ₌ UT R₍ _/ ₎2

cr m Tcr L h

   . It is apparent t hat t he crit ical buckling t emperat ure for beams wit h L / h rat io more t han 50 is ident ical bet ween t he t wo t heories. But , for L/ h rat io less t han 50, t he difference bet ween t he t wo t heories become larger, and it will become more dif-ferent for L/ h values less t han 20. T he same graph is report ed in [8] based on t he numerical shoot ing met hod.

Figure 3 Effect of transverse shear on critical buckling t emperat ure difference

(19)

Lat in American Journal of Solids and St ruct ures 10(2013) 223 – 246 Figure 4 Effect s of power law index and t emperat ure dependency on T_cr

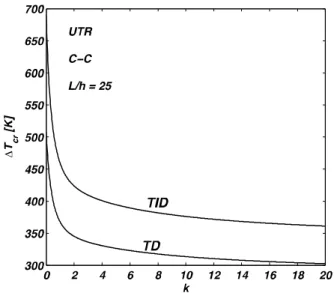
In Figure 5, t wo ot her cases of t hermal loadings are compared wit h respect t o each ot her. As seen in bot h of t hese cases, also, an increase in power law index result s in lower buckling t emperat ure. LT D case as an approximat e solut ion of t he NLT D case underest imat es t he crit ical buckling t emperat ures except for t he case of reduct ion of an FGM beam t o t he associ-at ed homogeneous cases. T his is expect ed since in t hese cases, t he exact solut ion of t he heassoci-at conduct ion equat ion is also linear.

Figure 5 Effect s of power law index on

cr

T

(20)

T he influence of boundary condit ions on buckling t emperat ure difference is plot t ed in Figure 6. T he uniform t emperat ure rise case of loading is assumed and propert ies are assumed t o be T D. T he case of a homogeneous beam is chosen. As expect ed, t he higher buckling t empera-t ure belongs empera-t o a beam wiempera-t h boempera-t h edges clamped and empera-t he lower one is associaempera-t ed empera-t o a beam wit h one side simply support ed and t he ot her one roller. T he crit ical buckling t emperat ure of

S Sand C Rcases are t he same.

Figure 6 Boundary conditions effect on T_cr

T he effect of uniform t emperat ure rise field on t he axial buckling load of C R and

C C beams is demonst rat ed in Figure 7. T he obt ained buckling loads are normalized by t he equat ion

2

3 12

T cr

cr _ref c

P L n

E bh

 , where E_cref is t he ceramic elast icit y module at reference t

(21)

Lat in American Journal of Solids and St ruct ures 10(2013) 223 – 246 Figure 7 Effect of t hermal environment on mechanical buckling of FGM beams

8 CON CLUSION

In t he present art icle, t he equilibrium and st abilit y equat ions for t he FGM beams wit h vari-ous t ypes of boundary condit ions are obt ained. T he derivat ion is based on t he T imoshenko beam t heory, wit h t he assumpt ion of power law composit ion for t he const it uent mat erial. T he buckling analysis under t hree t ypes of t hermal loadings is present ed. Also, t he mechanical buckling analysis under t hermal loads is st udied. Closed form solut ions are derived for t he crit ical t emperat ure/ load. It is concluded t hat :

1) T he C C and C R funct ionally graded beams exhibit t he bifurcat ion t ype buck-ling while t heS S, C S and S R FGM beams commence t o deflect wit h t he init iat ion of t hermal loading.

2) In each case of t hermal loading, t he crit ical buckling t emperat ure for FGM beams is lower t han fully ceramic beam but great er t han fully met allic beam.

(22)

4) T he crit ical buckling t emperat ure of C R and S S homogeneous beams are ident i-cal for st udied cases of t hermal loading, while S S andC R FGM beams reveal dif-ferent behaviors when are subject ed t o in-plane t hermal loading.

5) T he Euler beam t heory over-predict s t he crit ical t emperat ure of t hick beams, especially for h / L great er t han 0.05.

6) T emperat ure dependency of t he const it uent s has signi_ﬁcant e_ﬀect on crit ical buckling t emperat ure difference. T he value of T_cris overest imat ed when t he propert ies are as-sumed t o be independent of t emperat ure.

7) In each case of t hermal loading, t he T imoshenko beam t heory predict s lower values for crit ical buckling t emperat ure in comparison wit h t he Euler beam t heory.

Acknowledgment T he ﬁnancial support of t he Nat ional Elit e Foundat ion is grat efully acknowl-edged.

References

[1] K ang Y .A ., Li X .F., (2010) Large Deﬂections of a Non-linear Cantilever Functionally Graded Beam,

Journal of Reinforced Plastics and Composit es, 29: 1761-1774.

[2] Aydogdu M., T askin V., (2007) Free Vibration Analysis of Functionally Graded Beams with Simply Supported Edges. Mat erial and Design, 28: 1651-1656.

[3] Nirmala K ., Upadhyay P.C., Prucz, J., Lyons D., (2006), Thermo-elastic Stresses in Composite Beams with Functionally Graded Layer, Journal of Reinforced Plastics and Composit es, 25: 1241-1254.

[4] Li X .F., (2008) A Uniﬁed A pproach for Analyzing St atic and Dynamic Behaviors of Functionally Grad-ed Timoshenko and Euler–Bernoulli Beams, Journal of Sound and Vibration, 318: 1210-1229.

[5] K apuria S., Bhattacharyya M., Kumar A .N., (2008) Bending and Free V ibration Response of Layered Functionally Graded Beams: A Theoretical Model and Its Experimental Validation. Composite St

ruc-tures, 82: 390-402.

[6] Huang Y ., Li X .F., (2010) Buckling of Functionally Graded Circular Columns Including Shear Defor-mation. Materials and Design, 31: 3159-3166.

[7] Zhao F.Q., Wang Z., Liu, H., (2007) Thermal Post -buckling Analyses of Functionally Graded Material Rod. Applied Mathematics and Mechanics, 28: 59-67.

[8] Li S., Zhang J., Zhao Y ., (2006) Thermal Post -buckling of Functionally Graded Material Timoshenko Beams. Applied Mathematics and Mechanics, 27: 803-810.

[9] K iani Y ., Eslami M.R., (2010) Thermal buckling analysis of functionally graded material beams.

(23)

Lat in American Journal of Solids and St ruct ures 10(2013) 223 – 246 [10] Aydogdu M., (2008) Semi-inverse Method for Vibration and Buckling of Axially Funct ionally Graded

Beams. Journal of Reinforced Plast ics and Composit es, 27: 683-691.

[11] K e L.L., Yang J., Kitipornchai S., (2009) Postbuckling Analysis of Edge Cracked Functionally Graded T imoshenko Beams under End-shortening. Composit e Structures, 90: 152-160.

[12] K e L.L., Yang J., Kitipornchai S., Xiang Y., (2009) Flexural Vibration and Elastic Buckling of a Cracked Timoshenko Beam Made of Functionally Graded Materials. Mechanics of Advanced Materials

and Structures, 16: 488-502.

[13] Ma, L.S. and Lee, D.W. (2011) A Further Discussion of Nonlinear Mechanical Behavior for FGM Beams under In-plane Thermal Loading. Composite Structures, 93: 831-842

[14] Fallah, A. and Aghdam, M.M. (2012) Thermo-mechanical buckling and nonlinear free vibration analysis of funct ionally graded beams on nonlinear elastic foundation. Composites Part B: Engineering, 43: 1523-1530

[15] Wattanasakulpong N., Prusty B. G., K elly D. W., (2011) Thermal Buckling and Elastic Vibration of Third-order Shear Deformable Functionally Graded Beams, International Journal of Mechanical

Scienc-es, 53: 734-743

[16] K iani Y., Rezaei M., T aheri S., Eslami M. R., (2011) Thermo-elect rical buckling of piezoelectric func-tionally graded material Timoshenko beams, International Journal of Mechanics and Materials in

De-sign, 7 :185-197

[17] K iani Y., Taheri S., Eslami M. R., (2011) Thermal Buckling of Piezoelect ric Functionally Graded Mate-rial Beams, Journal of Thermal Stresses, 34 :835-850

[18] Ma L.S., Lee D. W., (2011) Exact solutions for nonlinear static responses of a shear deformable FGM beam under an in-plane thermal loading, European Journal of Mechanics A Solids, 31 :13-20

[19] Fu Y., Wang J., Mao Y ., (2012) Nonlinear analysis of buckling, free vibration and dynamic stability for the piezoelectric functionally graded beams in thermal environment, Applied Mathematical Modelling, 36 :4324-4340

[20] Anandrao K. S., Gupt a R. K ., Ramchandran P., Rao G. V ., (2010), Thermal post -buckling analysis of uniform slender functionally graded material beams, Structural Engineering and Mechanics, 36 :545-560

[21] Praveen, G.N. and Reddy, J.N. (1998) Nonlinear T ransient Thermoelastic Analysis of Funct ionally Graded Ceramic-Metal Plates. International Journal of Solids and Structures, 35: 4457-4476.

[22] Suresh, S. and Mortensen, A . (1998) Fundamentals of Functionally Graded Materials, IOM Communi-cations Ltd, London.

[23] Brush, D.O. and Almorth, B.O. (1975) Buckling of Bars, Plates, and Shells, McGraw-Hill, New York.

(24)