NILSON ALVES DA SILVA UMA SITUAÇÃO DIDÁTICA PARA ENSINO DE NÚMEROS COMPLEXOS COM FOCO EM ELETRICIDADE PELA VIA DA ENGENHARIA DIDÁTICA

(1)

INSTITUTO FEDERAL DO ESPÍRITO SANTO

MESTRADO PROFISSIONAL EM EDUCAÇÃO EM CIÊNCIAS E MATEMÁTICA

NILSON ALVES DA SILVA

UMA SITUAÇÃO DIDÁTICA PARA ENSINO DE NÚMEROS COMPLEXOS COM FOCO EM ELETRICIDADE PELA VIA DA ENGENHARIA DIDÁTICA

(2)

NILSON ALVES DA SILVA

UMA SITUAÇÃO DIDÁTICA PARA ENSINO DE NÚMEROS COMPLEXOS COM FOCO EM ELETRICIDADE PELA VIA DA ENGENHARIA DIDÁTICA

Dissertação apresentada ao Programa de Pós-Graduação em Educação em Ciências e Matemática do Instituto Federal do Espírito Santo, como requisito parcial para a obtenção do título de Mestre em Educação em Ciências e Matemática.

Orientadora: Profa_{. Dr}a_{. Maria Alice Veiga Ferreira de Souza.}

(3)

(Biblioteca Nilo Peçanha do Instituto Federal do Espírito Santo) S586s Silva, Nilson Alves da.

Uma situação didática para ensino de números complexos com foco em eletricidade pela via da engenharia didática / Nilson Alves da Silva. – 2016.

226 f. : il. ; 30 cm

Orientadora: Maria Alice Veiga Ferreira de Souza.

Dissertação (mestrado) – Instituto Federal do Espírito Santo, Programa de Pós-graduação em Educação em Ciências e Matemática, Vitória, 2016. 1. Matemática - Estudo e ensino. 2. Números complexos. 3. Eletricidade –

Estudo e ensino. 4. Didática. 5. Circuitos elétricos. 6. Matemática - Problemas, questões, exercícios. I. Souza, Maria Alice Veiga Ferreira de. II. Instituto Federal do Espírito Santo. III. Título.

(4)

(5)

(6)

(7)

(8)

AGRADECIMENTOS

Primeiramente quero agradecer a Deus, por tudo que Ele tem feito por mim;

À prof. Dr.ª Maria Alice Veiga Ferreira de Souza, pela orientação, paciência e consideração;

Aos colegas e professores que compõem o GEPEME, grupo de pesquisa, pelos momentos dos debates e estudos que trouxeram valiosas contribuições para a minha pesquisa;

Aos prof. Dr.Sc. Luciano Lessa Lorenzoni e Dr.Sc. Oscar Luiz Teixeira Resende pelas contribuições nas Bancas de Qualificação e Defesa, como Membro Interno do Instituto Federal do Espírito Santo;

Ao Prof. Dr. Ed. Wagner Marcelo Pommer que aceitou fazer parte dessa banca, como Membro Externo, e por seus estudos em Situação Didática e Engenharia Didática que serviram de base para o desenvolvimento da minha pesquisa;

Ao professor Edmar Thiengo, pelas contribuições na definição e entendimento sobre os aspectos metodológicos da pesquisa;

(9)

MINISTÉRIO DA EDUCAÇÃO

PROGRAMA DE PÓS - GRADUAÇÃO EM EDUCAÇÃO EM CIÊNCIAS E MATEMÁTICA

RESUMO

A motivação para o desenvolvimento desse trabalho surgiu em meio aos debates no Grupo de Estudo e Pesquisa em Modelagem Matemática e Educação Estatística do qual faço parte, onde estudou-se a teoria da Situação Didática e o método da Engenharia Didática. Foi elaborado um instrumento e investigado seu potencial didático por meio de uma Situação Didática que favoreceu o ensino de Números Complexos visando a aprendizagem em Eletricidade, via Engenharia Didática, uma vez que esse conteúdo matemático apresenta limitações na compreensão de alunos em circuitos elétricos de corrente alternada que, por sua vez, dependem diretamente do domínio e compreensão do conteúdo matemático de Números Complexos, comprometendo, assim, aquela aprendizagem. Geralmente, como alternativa, alguns professores recorrem ao uso da calculadora científica que já transformam as coordenadas retangulares dos números complexos em valores descritos na forma de um vetor com um ângulo, ou seja, a forma polar. O uso da calculadora assim empregada promove uma mecanização da aprendizagem não desejável, sobretudo porque os alunos, em geral, não atingem estágios desejados de compreensão para futura utilização em contextos outros. Nesse sentido, investigou-se meios didáticos de promover a necessária compreensão e domínio das operações com números complexos de modo não algoritmizado, visando uma apropriação do conteúdo de circuitos elétricos em corrente alternada. Em outras palavras, foi elaborada uma Situação Didática com uso de um instrumento didático, denominado Complex, que

favorecesse a produção de sentido sobre Números Complexos pela via da Engenharia Didática por alunos do curso técnico de Eletromecânica utilizando Resolução de Problemas. Trata-se de uma pesquisa qualitativa, pois envolve análise dos protocolos orais e escritos dos estudantes e, com respaldo quantitativo de seus desempenhos. Este trabalho contou com apoio teórico da Teoria das Situações Didáticas de G. Brousseau (1996), com aplicação desta situação por meio da Engenharia Didática proposta por M. Artigue (1996). O Complex

(10)

caracterizou como instrumento facilitador para a produção de sentido de Números Complexos aplicado a alunos de um curso básico de Eletricidade.

Palavras-chave: Números complexos. Eletricidade. Situação didática. Engenharia didática.

(11)

MINISTÉRIO DA EDUCAÇÃO

PROGRAMA DE PÓS - GRADUAÇÃO EM CIÊNCIAS E MATEMÁTICA

ABSTRACT

(12)

(13)

LISTA DE FIGURAS

Figura 1 - Representação Geométrica dos Números Complexos ... 40

Figura 2 - Giro do Número Complexo ao longo do círculo ... 41

Figura 3 - Transformação de Polar para Retangular... 42

Figura 4 - Circuito RL ... 43

Figura 5 - Circuito RC ... 43

Figura 6 - Circuito RLC ... 44

Figura 7 - Tabela Resumo das Impedâncias em Série ... 44

Figura 8 - Triângulo de Potência Complexa ... 45

Figura 9 - Exemplo de Cálculo de Potência Complexa ... 46

Figura 10 - Quadro Resumo da Potência Complexa ... 46

Figura 11 - Operação de mutiplicação no eixo real 1 x (-2)... 48

Figura 12 - Operação de mutiplicação no eixo real 1 x (-2) x (-2) ... 48

Figura 13 - Operação de multiplicação 1 x (-1) ... 49

Figura 14 - Operação de multiplicação 1 x (-1) x (-1) ... 49

Figura 15 - Operação de multiplicação 2 x (-1) x (-1) ... 49

Figura 16 - Representação geométrica de i = 1 ... 50

Figura 17 - Representação geométrica de 1 x 1 ... 50

Figura 18 - Representação do eixo real e imáginário ... 51

Figura 19 - Adição de dois Números Complexos na forma retangular... 52

Figura 20 - Operação de multiplicação (1 +1i) x 2 ... 52

Figura 21- Operação de multiplicação (3+1i) x i ... 53

Figura 22 - Operação de multiplicação na forma retangular e polar ... 54

Figura 23 - Matéria prima (matriz 21x21) utilizada no Complex. ... 62

Figura 24 - Montagem do transferidor sobre a matriz ... 62

Figura 25 - Cursores real (horizontal) e imaginário (vertical) – ambos verdes - ... 63

Figura 26 - Instrumento Didático - Complex ... 63

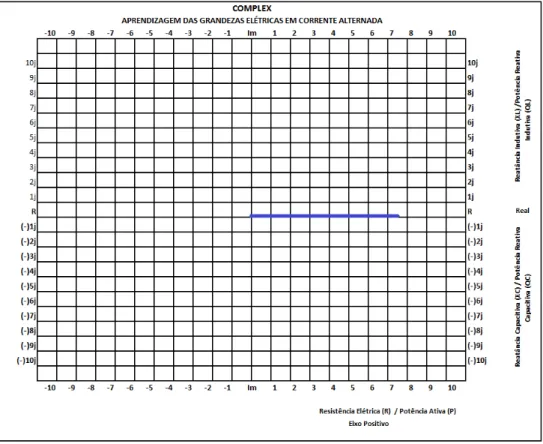
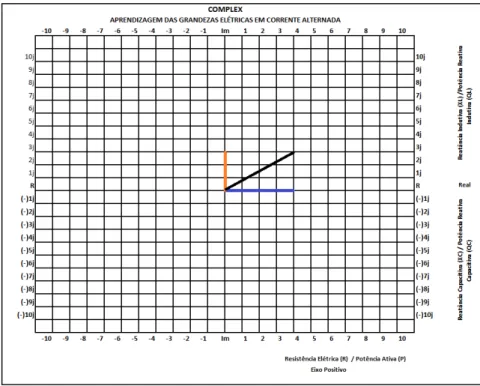
Figura 27 - Representação das coordenadas e grandezas do Complex... 64

Figura 28 - Representação do deslocamento no eixo - x (real) para direita ou esquerda ... 65

Figura 29 - Representação do deslocamento no eixo - y (imaginário) para cima ou baixo ... 66

(14)

Figura 31- Representação número real positivo ... 69

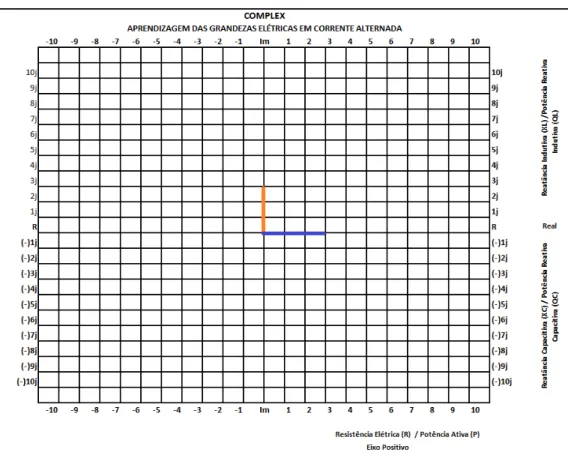
Figura 32 - Representação número imaginário positivo ... 70

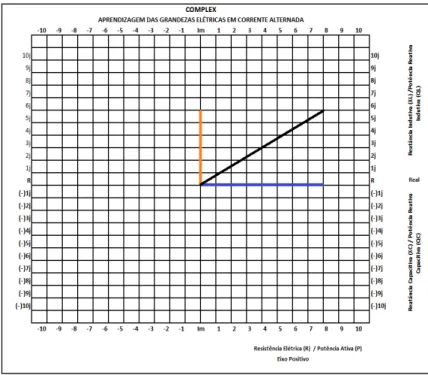
Figura 33 - Representação do módulo e ângulo do vetor resultante ... 71

Figura 34 - Modelo do Complex... 75

Figura 35 - Chuveiros elétricos... 76

Figura 36 - Complex aplicado ao Problema (P01-item b) ... 77

Figura 37 - Complex aplicado ao Problema (P01-item c) ... 78

Figura 38 - Componente elétrico ... 79

Figura 39 - Complex aplicado ao Problema (P02 – item c) ... 80

Figura 40 - Disjuntor termomagnético ... 82

Figura 41 - Complex aplicado ao Problema (P03 – item a) ... 82

Figura 42 - Complex aplicado ao Problema (P03 – item b) ... 83

Figura 43 - Distribuidor veicular ... 85

Figura 44 - Complex aplicado ao Problema (P04 – itens a e b) ... 86

Figura 46 - Transformador com núcleo de ferro ... 88

Figura 47 - Complex aplicado ao Problema (P05 – itens a, b e c) ... 89

Figura 48 - Geração de tensão trifásica ... 90

Figura 49 - Complex aplicado ao Problema (P06 – itens de a a f) ... 91

Figura 50 - Circuito RL em série ... 93

Figura 51 - Complex aplicado ao Problema (P07 – itens de a a d) ... 94

Figura 56 - O alto-falante ... 98

Figura 59 - Toróide com Galvanômetro... 102

Figura 61 - Distribuição dos Fios Condutores... 104

(15)

Figura 63 - Galvanômetro de Bobina Móvel ... 107

Figura 65 - Geradores elétricos em paralelo ... 109

Figura 66 - Complex Aplicado ao Problema (P13 – item a) ... 110

Figura 67 - Complex Aplicado ao Problema (P13 – item b) ... 110

Figura 68 - Motor Trifásico tipo Gaiola ... 112

Figura 69 - Complex aplicado ao Problema (P14 – item a) ... 113

Figura 71 - Banco de Capacitores ... 116

Figura 72 - Complex aplicado ao Problema (P15 – itens a, b e d) ... 116

Figura 73 - Leitura do P01 - Turma A ... 125

Figura 74 - Resposta do P01 - A1- Pontuação Máxima ... 126

Figura 75 - Resposta do P01 - A2 ... 127

Figura 77 - Resposta do P01- B3 ... 130

Figura 78 - Resposta do P02 - A3- item "a" ... 135

Figura 79 - Resposta do P02 - A1- item "b" e "c" ... 135

Figura 80 - Resposta do P02 - A5- Pontuação Máxima ... 136

Figura 81 - Resposta do P02 - C4, C5 - Erro nos Itens "b" e "c"... 138

Figura 83 - Resposta do P03 - B1 ... 143

Figura 86 - Resposta do P04 - C1 ... 149

(16)

Figura 96 - Representação no Complex da Soma dos vetores - item "c" ... 169

Figura 110 - Reaplicação do P03M ... 194

Figura 111 - Giro de 90° no Vetor resultante do P03M ... 195

Figura 112 - Representação do Vetor Resultante do P03M - A ... 197

Figura 113 - Representação do Giro de 90° do Vetor Resultante do P03M - A ... 197

Figura 114 - Momento do Giro de 90° do Vetor Resultante do P03M - B ... 199

(17)

LISTA DE TABELAS

Tabela 1 - Distribuição dos participantes por turma ... 56

Tabela 2 - Resumo do percurso metodológico: objetivos de pesquisa, temas, método, instrumentos, participantes e análise dos resultados ... 60

Tabela 3 - Quadro dos problemas propostos na Situação Didática. ... 73

Tabela 4 - Estratégias utilizadas em cada problema e em cada turma ... 121

Tabela 5 - Cumprimentos dos objetivos da pesquisa em cada problema e em cada turma .... 122

Tabela 6 - Pontuações obtidas por cada grupo em cada problema. ... 123

Tabela 7 - Pontuação em Valores Monetários por Turma/Grupos - P01 ... 133

(18)

SUMÁRIO

1 INTRODUÇÃO ... 19

1.1 OBJETIVOS DA PESQUISA ... 23

1.1.1 Geral ... 23

1.1.2 Específicos ... 23

2 FUNDAMENTAÇÃO TEÓRICA ... 24

2.1 SITUAÇÕES DIDÁTICAS ... 24

2.2 ENGENHARIA DIDÁTICA ... 27

2.3 O QUE É PROBLEMA ... 31

4 FUNDAMENTAÇÃO MATEMÁTICA DE NÚMEROS COMPLEXOS ... 37

4.1 UMA BREVE HISTÓRIA DOS NÚMEROS COMPLEXOS ... 37

4.2 DEFINIÇÃO ... 40

4.3 REPRESENTAÇÕES ALGÉBRICAS E TRIGONOMÉTRICAS ... 41

4.3.1 Forma retangular e Polar dos Números Complexos ... 41

4.4 APLICAÇÕES NA ELETRICIDADE ... 42

4.4.1 Impedância Complexa em Série ... 42

4.2 Circuito RL ... 43

4.4.3 Circuito RC ... 43

4.4.4 Circuito RLC ... 44

4.4.5 Quadro Resumo das Impedâncias em Série ... 44

4.4.6 Potência Complexa ... 45

4.4.7 Exemplo de Cálculo de Potência Complexa ... 45

4.4.8 Quadro Resumo da Potência Complexa ... 46

5 ABORDAGEM DE NÚMEROS COMPLEXOS POR ADRIEN DOUADY ... 48

5.1 CONCEITUAÇÃO DAS REPRESENTAÇÃO DOS NÚMEROS COMPLEXOS ... 48

5.2 OPERAÇÕES COM OS NÚMEROS COMPLEXOS ... 51

5.2.1 Adição de Números Complexos na forma algébrica(retangular) ... 51

(19)

5.3 REPRESENTAÇÃO DOS NÚMEROS COMPLEXOS COM MÓDULO E

ÂNGULO NA FORMA GEOMÉTRICA (POLAR) ... 53

6 PROCEDIMENTOS METODOLÓGICOS... 55

6.1 O AMBIENTE DE PESQUISA E OS PARTICIPANTES ... 55

6.2 CONSTRUÇÃO DE UM INSTRUMENTO DIDÁTICO (COMPLEX) PARA APRENDIZAGEM DE NÚMEROS COMPLEXOS ... 61

6.2.1 Objetivos e metas ... 61

6.2.2 Materiais utilizados no Complexe sua montagem ... 61

6.3 DIRETRIZES PARA A UTILIZAÇÃO DO COMPLEX ... 64

6.4 ANÁLISES PRELIMINARES E A PRIORI ... 71

6.4.1 Primeira seção da Situação Didática ... 74

6.4.2 Segunda seção da Situação Didática ... 84

6.4.3 Terceira seção da Situação Didática ... 92

6.4.4 Quarta seção da Situação Didática ... 101

6.4.5 Quinta seção da Situação Didática ... 108

7 RESULTADOS E ANÁLISES DOS DADOS: A ANÁLISE A POSTERIORI E CONCLUSÕES PARCIAIS ... 118

7.1 DESCRIÇÃO E CONFRONTO DA ANÁLISE A POSTERIORI E A PRIORI DO P01 - 1ª. SEÇÃO ... 124

(20)

P07 - 3ª. SEÇÃO ... 163

7.13 INSTITUCIONALIZAÇÃO ANTECEDENDO A 5ª SEÇÃO ... 191

8 PRODUTO DA INVESTIGAÇÃO ... 217

9 CONCLUSÕES ... 218

REFERÊNCIAS ... 221

APÊNDICE A - Termo de Autorização ... 224

APÊNDICE B - Termo de Consentimento Livre e Esclarecido ... 225

(21)

1 INTRODUÇÃO

O estudo da matemática no ensino médio constitui elemento fundamental para apropriação de conteúdos das diversas áreas das ciências, tais como: a biologia, a música, a química, a física e em especial, a eletricidade. É desejável que se desenvolva no aluno a capacidade de raciocínio, reflexão, análise e domínio dos conceitos matemáticos aplicando-os na solução de problemas. Ao longo dos anos constata-se o surgimento de novas realidades pedagógicas e o desenvolvimento de procedimentos metodológicos que têm contribuído para melhorar este processo de aprendizagem da matemática, a exemplo das pesquisas na área da Educação Matemática.

Em um retrospecto histórico, pode-se mencionar meios de aprendizagem da matemática desde o ensino tradicional com réguas e tabuadas, que tornavam a aprendizagem da matemática pouco atrativa para o aluno, até recursos modernos como softwares

matemáticos, que são ferramentas da tecnologia da informação mais dinâmicas e atrativas quando usadas de maneira não mecanizada.

Ao iniciar este Mestrado surgiu a oportunidade de estudar, pesquisar e propor um produto educacional que fosse um instrumento que pudesse contribuir para a aprendizagem de Números Complexos com ênfase na aplicação no curso Técnico de Eletromecânica. Os Números Complexos tem sido um "gargalo" para que o aluno compreenda e desenvolva técnicas de soluções de circuitos elétricos em corrente alternada, o que justifica a opção por esse contexto de investigação. Lendo diversas publicações que versam sobre o assunto, entre elas o artigo de Assemany e Harab (2013) intitulado, “Potencializando o ensino de

Números Complexos a partir da Abordagem Vetorial”, publicado no VII Congreso Iberoamericano de Educación Matemática. Esse artigo se propôs a mostrar, a partir do

(22)

Em uma perspectiva histórica, o artigo de Hellmich (1992) com título: Números Complexos - A história de 1 relata desdobramentos na linha do tempo dessa unidade imaginária, desde Cardano até Gauss e dá uma breve abordagem dos Números Complexos com a representação trigonométrica de De Moivre, e geométrica de Wessel e Argand.

Ainda na perspectiva histórica, Silva (2011), no artigo - Da Teoria à Prática: Uma Análise Histórica do Desenvolvimento Conceitual dos Números Complexos e suas Aplicações - faz um ensaio com o objetivo de apresentar a evolução temporal do conceito de Números Complexos, desde o surgimento de sua necessidade dentro do contexto matemático envolvido na época, até o início de sua formalização e aceitação.

Fontes e Muniz (2013), no seu artigo - Coordenadas Polares no Ensino Médio: Contribuições para o Ensino e Aprendizagem de Trigonometria e Números Complexos - realizaram uma abordagem teórica que permitiu a integração entre a Trigonometria e os Números Complexos. Destacaram que, apesar da sua relevância, o estudo dos Números Complexos é feito de forma rápida e sem sentido.

Mello (2015) na sua dissertação - O Ensino de Matemática e a Educação Profissional: A Aplicabilidade dos Números Complexos na Análise de Circuitos Elétricos, tem como objetivo avaliar a aplicabilidade de Números Complexos como estratégia de ensino com uso de análise de circuitos elétricos em corrente alternada, colocando à disposição do Técnico em Eletrotécnica, Mecatrônica, Eletromecânica, Telecomunicações, Automação Industrial e Eletrônica essa abordagem alternativa de análise.

A busca pela revisão literária apresentou ausência de trabalhos sobre Situação Didática aplicada a cursos técnicos e, em especial, focando assunto de Eletricidade. Dessa forma, o instrumento didático, Complex, desenvolvido como o Produto Educacional dessa pesquisa

parece ser um objeto útil para o ensino de Números Complexos com foco em Eletricidade. Como resultado, o Produto Educacional Complex acompanhado por um guia didático será

(23)

Em uma observação sobre o estudo dos Números Complexos relatado por professores que ministram esse conteúdo escolar, nota-se que predominam duas abordagens: uma de forma algébrica e outra geométrica. Porém, a abordagem mais utilizada pelos livros que tratam do ensino de análise de circuitos com corrente alternada é a algébrica. Acredita-se que as duas devam ser contempladas, uma vez que ambas são úteis para a compreensão dos conceitos de circuitos elétricos de corrente alternada, e, por esse motivo, serão valorizadas nesse trabalho.

Sobre esse tema, destacam-se as Orientações Educacionais Complementares aos Parâmetros Curriculares Nacionais (PCN+₎1_{, Brasil (2002), que salientam a importância da articulação} entre a álgebra e a geometria.

Ainda nessa direção,

[...] a possibilidade, na Matemática, de usar vários tipos de registros gráficos, algébricos, geométricos e outros, interfere de modo decisivo no aprendizado. A qualquer momento pode ser exigida uma troca de registro ou a mobilização simultânea de, pelo menos, dois tipos de registros (CALDEIRA, 2013 apud DUVAL, 2003, p.14).

No curso técnico de eletromecânica estuda-se em eletricidade, eletrônica e circuitos elétricos, inicialmente, as grandezas elétricas tensão e corrente elétrica. Considerando somente a natureza contínua da eletricidade, esta é descrita de forma polarizada (pólo positivo e negativo não variam ao longo do tempo). As diversas operações matemáticas envolvidas na resolução dos problemas de grandezas elétricas de natureza contínua são todas representadas no domínio dos números reais, e o desenvolvimento deste conteúdo programado flui conforme o planejamento esperado. Quando estas grandezas elétricas necessitam ser trabalhadas com a corrente na natureza alternada (a polarização positiva e negativa se alterna com uma frequência desejada), as operações matemáticas envolvidas necessitarão utilizar tanto o domínio real quanto o domínio imaginário.

É exatamente neste momento da aprendizagem que se observou, ao longo da trajetória como professor, que os alunos têm mais dificuldade epistemológica de se apropriar dos

(24)

conhecimentos das análises do circuito elétrico. A apropriação dos Números Complexos é fundamental para a compreensão e posterior condição de análise do comportamento dos componentes como capacitores, indutores, resistores e suas associações encontradas nos inúmeros circuitos elétricos.

A aprendizagem de operações matemáticas, no domínio imaginário, para compreensão dos componentes, será necessária para elaboração de soluções técnicas para muitos equipamentos e máquinas que fazem parte do ambiente industrial, como exemplo de aplicação desses conhecimentos. A competência necessária para o técnico eletricista depende em grande parte da sua capacidade de análise e de propor soluções diante das situações que surgem na execução das suas atividades profissionais.

No Grupo de Estudo e Pesquisa em Modelagem Matemática e Educação Estatística - GEPEME - foram estudadas as Situações Didáticas de G. Brousseau e, especialmente, o procedimento metodológico denominado de Engenharia Didática, proposto por M. Artigue para análise de situações baseadas na definição de problema estabelecido por Pólya, que se constituíram-se em opções teóricas e metodológicas que apoiarão a investigação. Ao debruçar-se sobre a Engenharia Didática, observou-se na teoria de Artigue uma linguagem com a qual houve uma identificação, ao constatar a possibilidade de uma atitude típica da Engenharia que possa se tornar um instrumento que contribua no processo de aprendizagem.

Essa pesquisa está em sintonia com os objetivos iniciais da Didática da Matemática Francesa que se reuniam para a concepção de objetos que pudessem ser utilizados como Recursos Didáticos para favorecer o aprendizado de matemática. Brousseau elaborou na sua Tese as Situações Didáticas e Artigue, a Engenharia Didática, como o método de viabilizá-las e validá-viabilizá-las. Nessa pesquisa foi feito esse resgate do objetivo original do grupo da Didática Matemática Francesa, através da construção de um Recurso Didático, o Complex,

(25)

Ressalta-se que a construção desse Recurso Didático, como Produto Educacional, foi possível pelo perfil do Programa do Mestrado Profissional do EDUCIMAT e toda a preocupação com a Formação Profissional do Professor.

A partir destas premissas e constatações, fez-se a proposição dos seguintes objetivos para o estudo.

1.1 OBJETIVOS DA PESQUISA

1.1.1 Geral

Construir e avaliar um instrumento didático em uma Situação Didática, que possa contribuir para a produção de sentido de Números Complexos e que vise conceitos básicos de Eletricidade por alunos do curso técnico de Eletromecânica.

1.1.2 Específicos

(1) Avaliar, qualitativamente, com respaldo quantitativo,a potencialidade da Situação Didática para o ensino de Números Complexos como meio para a construção de conceito básicos de Eletricidade e para a realização das operações matemáticas nesse âmbito;

(2) Identificar facilidades/dificuldades epistemológicas apresentadas pelos alunos da resolução de problemas propostos na Situação Didática;

(3) Verificar a aprendizagem de aspectos geométricos, associados aos algébricos, dos Números Complexos e suas operações com uso do instrumento didático.

(26)

2 FUNDAMENTAÇÃO TEÓRICA

2.1 SITUAÇÕES DIDÁTICAS

Brousseau (1996) considerava que as Situações Didáticas deveriam se situar na proposta construtivista e contemplar os processos adaptativos e de equilibração delineados por Piaget. Ele considera que Piaget não observou a particularidade da aprendizagem de cada conhecimento matemático ao considerar a estrutura formal e a função lógica como fundamentais. Para superar tais impedimentos, Brousseau (1996) propôs uma retomada do contexto de origem dos saberes e a importância do valor funcional das etapas que o saber percorre para ser elaborado. Nesse assunto, Gálvez (1996, p.32) destaca que Brousseau (1996) defende "a criação de Situações Didáticas que promovam o saber, a partir dos saberes definido culturalmente nos programas escolares".

É útil conhecer as principais características das Situações Didáticas em Brousseau (1996, p. 54) visando orientar as opções metodológicas desta investigação. Dessa forma, as Situações Didáticas:

a) devem levar os alunos a aceitara responsabilidade pelo fazer e pela organização da situação-problema, como um projeto pessoal;

b) são elaboradas para se obter certo conhecimento que é parcial ou totalmente possível de ser alcançado pelo aluno;

c) requerem que o aluno tome decisões, testem-nas e modifiquem-nas quando necessário para adequá-las à busca da resposta correta;

d) necessitam de uma estratégia de base disponibilizada pelo repertório de conhecimento dos alunos que permitam uma solução local ou uma situação parcial que inicie o desenvolvimento das atividades;

e) terão eficácia e viabilidade dependendo das variáveis didáticas de comando que o professor, convenientemente, deve escolher e utilizar nas concepções das atividades;

(27)

g) são elaboradas para que o aluno perceba que o novo conhecimento almejado é meio mais eficaz para encaminhar e resolver a situação;

h) permitem a construção do conhecimento, o que equivale à formação de sentido para o aluno.

Para Brousseau (1996a) a intencionalidade não revelada é outra característica que deve permear o milieu, de modo que o aluno não perceba os pressupostos didáticos que o professor gerencia

por meio da situação a-didática. O milieu está relacionado aos comportamentos que os alunos

revelam no funcionamento do meio. Ele deve ser planejado e organizado pelo professor/pesquisador para que a aprendizagem ocorra em uma interação feita de desequilíbrios, assimilações e acomodações (conforme propôs Piaget), permitindo ao aluno a reflexão sobre suas ações e retroações, impondo restrições através de regras que devem ser respeitadas. Deve possibilitar a interação autônoma do aluno em relação às situações que interage e em relação ao professor.

Pommer (2013) cita que, de acordo com Gálvez (1996), a teoria de Brousseau (1996a) esclarece a integração das dimensões epistemológicas, cognitivas e sociais no campo da Educação Matemática, permitindo compreender as interações sociais que ocorrem na sala de aula entre alunos e professores, as condições e a forma que o conhecimento matemático pode ser aprendido, sendo que o controle destas condições permitiria reproduzir e otimizar os processos de aquisição de conhecimento matemático escolar.

Para Brousseau (1996a), a Situação Didática é utilizada para descrever os modelos que retratam as atividades do professor e do aluno. A Situação Didática envolve todo contexto que cerca o aluno, nele incluídos o professor e o sistema educacional. A Situação é criada para ensinar um conteúdo ou controlar a sua aquisição. Abrange um meio material (peças de um jogo, um problema) cujo desenvolvimento pode produzir um efeito de ensino. Nesta perspectiva, a aprendizagem é alcançada pela adaptação do sujeito, que assimila o meio criado por essa situação, sem a intervenção do professor e os conhecimentos se manifestam como instrumentos de controle das situações.

(28)

formulação e Situação de validação. A Situação de ação consiste em escolher diretamente os estados do meio antagonista em função de suas próprias motivações. Esse meio antagonista ocorre quando o meio oferece a resistência adequada ao aluno. Se o meio antagonista for muito difícil, ou seja, se a distância entre os conhecimentos anteriores dos alunos e os ‘novos’

conhecimentos for grande, o meio não terá funcionalidade. Se o professor ajudar demais com informações que visem a diminuir esta distância, então a função antagonista do meio no problema cessará, e se instalará um meio aliado. O meio aliado prejudica a participação e responsabilização do aluno no processo de ensino-aprendizagem. Um meio adequado é aquele onde a distância entre o conhecimento almejado e o anterior seja alcançável, pelo menos em parte, através do esforço próprio do aluno, pois o aluno é o sujeito-pesquisador.

Assim, a aprendizagem é o processo em que os conhecimentos são modificados, esses conhecimentos permitem produzir e mudar essas antecipações. A Situação de formulação consiste na formulação de um conhecimento que corresponderia a uma capacidade do sujeito de retomá-lo. O meio que exigirá do sujeito o uso de uma formulação deve, então, envolver um outro sujeito, a quem o primeiro deverá comunicar uma informação. Na Situação de validação, os alunos organizam enunciados em demonstrações, constroem teorias e tanto aprendem a convencer os demais alunos como se deixarem convencer sem ceder a argumentos retóricos, à autoridade, à sedução, à soberba, a intimidações. O aluno não só deve comunicar uma informação, como também precisa afirmar que o que diz é verdadeiro dentro de um sistema determinado. Brousseau (1996a) ressalta que na perspectiva da teoria das situações, os alunos tornam-se reveladores das características das situações às quais reagem.

Para Gálvez (1996), na institucionalização, o professor procura não intervir diretamente nas três fases anteriores, limitando-se a orientações, quando julgar necessário, para evitar possíveis bloqueios. O professor reassume a ação, estabelecendo quais conhecimentos obtidos nas etapas anteriores são relevantes e quais são descartáveis, configurando o estatuto de objeto aos conhecimentos obtidos.

(29)

Desde as primeiras reuniões no IREM (Instituto de Investigação do Ensino de Matemática) as

discussões se dirigiram para a “[...] produção de conhecimento para controlar e produzir [...]

ações sobre o ensino” (GÁLVEZ, 1996, p. 26). Como um dos pesquisadores do IREM,

Brousseau contribuiu com o desenvolvimento da teoria das Situações Didáticas (1996). A visão dominante no campo da Educação era essencialmente cognitiva, devido a Piaget e colaboradores, que evidenciou o papel central da ação no desenvolvimento, a originalidade do pensamento matemático e as etapas de seu desenvolvimento nas crianças, mas não observou a particularidade da aprendizagem de cada conhecimento matemático ao considerar a estrutura formal e a função da lógica como fundamentais.

Reforça-se que na abordagem da Teoria da Situação Didática, Brousseau (1996) descreve que o seu objetivo é propiciar a reflexão sobre as relações entre os conteúdos do ensino e os métodos educacionais e, de modo mais amplo, abordar a didática como campo de pesquisa cujo objeto é a comunicação dos conhecimentos matemáticos e suas transformações.

2.2 ENGENHARIA DIDÁTICA

A Engenharia Didática surgiu como uma forma de concretizar as ideias e pressupostos de investigação da escola da Didática da Matemática Francesa. A ideia inicial dos estudiosos franceses era a criação de recursos e meios para aprimorar o trabalho em sala de aula, mas os estudos evoluíram para a estruturação em um quadro teórico mais amplo, o que possibilitou a concepção de situações de aprendizagem e também de referencial metodológico. A Engenharia Didática surgiu das discussões no IREM (Instituto de Investigação do Ensino de Matemática), na França, no final da década de 1960.

Esse método tem uma característica que se assemelha à função de um engenheiro na execução de seu trabalho. Artigue (1996) descreve que como método para a análise de Situações Didáticas, a Engenharia Didática foi concebida como um trabalho didático de modo análogo ao:

(30)

complexos que os objetos depurados na ciência e, portanto, a enfrentar [...] problemas que a ciência não quer ou não pode levar em conta (ARTIGUE, 1996, p.193).

Artigue (1996) descreve a Engenharia Didática como um processo empírico que objetiva conceber, realizar, observar e analisar as Situações Didáticas. A autora pondera que a Engenharia Didática possui dupla função, a qual pode ser compreendida como uma produção para o ensino tanto como uma metodologia de pesquisa qualitativa. O entendimento nessa pesquisa é da Engenharia Didática como um método para a aplicação e validação da Situação Didática aplicada através de Resolução de Problemas.

A Engenharia Didática se caracteriza por propor:

[...] uma seqüência de aula(s) concebida(s), organizada(s) e articulada(s) no tempo, de forma constante, por um professor-engenheiro para realizar um projeto de aprendizagem para certa população de alunos. No decurso das trocas entre professor e alunos, o projeto evolui sob as reações dos alunos e em função das escolhas e decisões do professor (MACHADO, 2002, p. 198, apud DOUADY,1993, p. 2).

A contribuição da Engenharia Didática para a sala de aula, como campo metodológico, diz respeito à possibilidade de prover a fundamentação teórica para que o professor conheça o significado e amplie o leque de opções, formando elo entre a teoria e a prática de sala de aula.

(31)

Pommer (2013) propôs uma investigação para revelar o potencial didático e epistemológico presente nas Equações Diofantinas Lineares, ao validar uma ferramenta de aprendizagem significativa. Propõem-se, também, que esta pesquisa caminha nesse sentido de verificar o potencial de uma intervenção didática que aborde os Números Complexos de maneira a gerar aprendizagem que favoreça a compreensão de Circuitos Elétricos em corrente alternada no Curso de Eletromecânica no IFES, o que supõe apreensão dos Números Complexos e suas operações.

A Engenharia Didática, por sua vez, como método descrito por Artigue (1996), compreende quatro fases: a primeira fase, das análises preliminares, a segunda fase, da concepção e da análise a priori, a terceira fase, da experimentação e a quarta e última fase, da análise a posteriori e validação. Artigue (1996) ressalta que as quatro fases não ocorrem de forma

linear e estanque. Ao contrário, a elaboração da Engenharia Didática necessita, em alguns momentos, da articulação, da antecipação e até da superposição dos elementos caracterizadores dessas quatro fases.

Na análise preliminar é realizada uma revisão bibliográfica envolvendo as condições e contextos presentes nos vários níveis de produção didática e no ambiente onde ocorrerá a pesquisa, bem como uma análise geral quanto aos aspectos histórico-epistemológicos dos assuntos do ensino a serem trabalhados e dos efeitos por eles provocados, da concepção, das dificuldades e obstáculos epistemológicos encontrados pelos alunos dentro deste contexto de ensino.

É nesta fase da Engenharia Didática que poder-se-á realizar o levantamento dos diversos obstáculos/facilidades a serem considerados e que permitir-se-á a análise dos fatores para a superação dos problemas observados na aprendizagem, em conformidade com os objetivos da pesquisa, viabilizando a etapa seguinte: a concepção da Situação Didática.

(32)

(professor/aluno/saber), que representam o entendimento da aplicação dessas grandezas como: no chuveiro, no funcionamento dos componentes elétricos, nos motores e painéis elétricos na indústria.

Na análise a priori, seu objetivo é:

[...] determinar de que forma permitem as escolhas efetuadas controlar os comportamentos dos alunos e o sentido desses comportamentos. Para isso, ela funda-se em hipóteses; será a validação destas hipóteses que estará, em princípio, indiretamente em jogo no confronto, operado na quarta fase, entre a análise a priori e a análise a posteriori (ARTIGUE, 1996, p. 205).

Para modelar a teoria das Situações Didáticas, Brousseau (1996a) propõe o sistema didático

stricto sensu ou triângulo didático, que comporta três elementos - o aluno, o professor e o

saber, partes constitutivas de uma relação dinâmica e complexa, a relação didática, que leva em consideração as interações entre professor e alunos (elementos humanos), mediadas pelo saber (elemento não-humano), que determina a forma como tais relações irão se desenvolver.

Artigue (1996) descreve que na análise a priori o aluno é o ator principal, sendo que o papel

do professor é recuperado no contrato didático2_{e nas situações de institucionalização. Os} alunos devem tomar as decisões que faltam para organizar a resolução do problema ou do jogo a ser proposto. A terceira fase da Engenharia Didática corresponde à experimentação. Consiste, basicamente, no desenvolvimento da aplicação da Engenharia Didática, concebida a um grupo de alunos, objetivando verificar as ponderações levantadas na análise a priori.

Segundo Machado (2002), é nessa fase da pesquisa que os seguintes itens devem estar estabelecidos: a explicitação dos objetivos e condições de realização da pesquisa e o quantitativo de alunos que participará da experimentação; o estabelecimento do contrato didático; a aplicação do instrumento de pesquisa (as Situações Didáticas estabelecidas); o registro das observações feitas durante a experimentação.

2_{é definido por Guy Brousseau como sendo a totalidade de comportamentos do docente esperados pelo aluno e}

(33)

Por último, a quarta fase, corresponde à análise a posteriori e validação. De acordo com

Artigue (1996), essa fase se baseia sobre o conjunto de dados obtidos ao longo da experimentação pelas observações do pesquisador, pelo registro sonoro ou através da produção escrita. Essa fase se caracteriza pelo tratamento dos dados colhidos e a confrontação com a análise a priori, permitindo a interpretação dos resultados e em que condições as

questões levantadas foram respondidas. Assim, é possível analisar se ocorrem e quais são as contribuições para a superação do problema, caracterizando a generalização local que permitirá a validação interna do objetivo da pesquisa.

2.3 O QUE É PROBLEMA

Esta pesquisa usou a definição de Problema, segundo a perspectiva de Pólya, sem, contudo, considerar os aspectos heurísticos da sua teoria. Para Pólya (1945, p.164), problemas de Matemática não são fáceis demais nem constituem simples problemas rotineiros. Exigem originalidade e engenho. São acompanhados de indicações que conduzem à solução, pela citação de uma frase adequada. Para um aluno atento, pronto a aproveitar sugestões, elas poderão revelar a idéia-chave da solução.

Souza e Guimarães (2015, p. 137), seguidores de Pólya, assumem que:

[...] resolver um problema significa buscar conscientemente alguma ação apropriada para atingir um objetivo claramente definido, mas não imediatamente atingível. Por outras palavras, estamos perante um problema quando nos confrontamos com uma questão que nos interessa responder ou resolver e não dispomos previamente de uma estratégia, pelo menos completamente definida, para o fazer. Resulta daqui assim que, por um lado, o que é um problema para alguns, pode não o ser para outros, por outro lado, que todo o problema encerra uma questão, embora, nem toda a questão constitua um problema. Se alguém possuir antecipadamente todos os meios para alcançar os fins delineados, não há que falar em problema, mas em exercício para esse alguém. Um exercício requer de um sujeito baixo investimento cognitivo, uma vez que já está de posse dos meios e mecanismos para o resolver, que apenas necessita de aplicar, mais ou menos directamente.

(34)

diferentes formas e tomando decisões, de modo que o processo de construção do conhecimento matemático efetivamente ocorra e, como consequência, haja a formação de sentido para o aluno.

Abrantes (1988), em seu artigo "Um (bom) problema(não) é (só)..." descreve os diversos tipos de problemas: dos tipos de palavras, de equacionar, de demonstrar, de descobrir, da vida real e de uma situação problemática. O autor diz que a proposta de colocar a resolução de problemas no primeiro plano da Matemática escolar tem sido apresentada com insistência há alguns anos por algumas das mais prestigiadas figuras e associações da Educação Matemática. Ele lembra que o reconhecimento de que a resolução de problemas é, afinal, o motor do desenvolvimento da Matemática e da atividade matemática, e a perspectiva de que um papel de relevância deve ser-lhe destinado na aprendizagem, não são ideias novas. Para o autor, a Matemática escolar parece ter assumido sempre a resolução de problemas como uma atividade complementar, paralela, geralmente destinada a estimular ou detectar alunos particularmente dotados, por vezes associada a propósitos de popularização da Matemática ou de motivação externa para o seu estudo. A resolução de problemas nunca terá sido assumida como o centro em volta do qual se processaria a aprendizagem da Matemática, a não ser em projetos isolados ou em estudos experimentais de ponta. Hoje o relançamento de propostas de valorização do papel da resolução de problemas nos currículos de Matemática é acompanhado de um esforço no sentido de um alargamento de perspectivas sobre o que é um problema e sobre o que é a resolução de problemas.

(35)

3 REVISÃO DE LITERATURA

Esse capítulo visa complementar a revisão de literatura iniciada na Introdução dessa dissertação. O trabalho de Assemany e Harab (2013), se propôs a mostrar pelo enfoque vetorial uma abordagem geométrica sobre Números Complexos no Ensino Médio. Concretamente, aplicaram seis atividades às turmas e concluíram que o enfoque geométrico permitiu que o ensino dos Números Complexos fosse significativo e útil dentro da matemática estudada.

Ainda na perspectiva histórica, Silva (2011), no artigo - Da Teoria à Prática: Uma Análise Histórica do Desenvolvimento Conceitual dos Números Complexos e suas Aplicações relata que as equações representavam uma formulação matemática para resolver um problema real, por isso não havia necessidade de aceitar ou levar em conta a resolução de radicais de números negativos. Enfatiza que a busca de uma solução para as equações de terceiro grau foi um passo decisivo para que os Números Complexos fossem aceitos e compreendidos pela comunidade científica. Destaca que a emergência dos Números Complexos foi decisiva na Itália do século XVI, quando dois personagens, Girolamo Cardano e Niccolò Fontana, protagonizaram uma solução para as equações do terceiro grau, a qual são válidas até hoje. O referido autor descreve, ainda, a trajetória do estudo dos Números Complexos ao longo dos séculos até sua aceitação pela comunidade específica com os trabalhos de um genial matemático alemão: Johann Carl Friedrich Gauss (1777–1855), conhecido como o príncipe dos matemáticos. Conclui seu artigo afirmando que:

[...] que qualquer estudante de tecnologia convive diariamente com a teoria dos números complexos. Eles aparecem no estudo de circuitos, na corrente e na tensão elétrica, na potência, na impedância, na equação de onda que rege o movimento dos elétrons, na equação de normalização que tem um papel importante na mecânica quântica, entre outras aplicações. Mas uma das mais belas aplicações dos números complexos remonta à sua representação gráfica e não ao formalismo de equações rigorosas. Ao representarmos simples equações de números complexos, utilizando o princípio computacional da recorrência e a moderna Teoria dos Fractais, obtemos figuras belíssimas, que parecem reproduzir fenômenos e formas da natureza, com todas as combinações possíveis entre simetria e caos (Silva 2011, p.89).

(36)

Complexos são tratados no meio educacional. Ele enfatiza o 'tratamento demasiadamente longo' da Trigonometria e a 'imperdoável ausência' de aplicações geométricas das operações entre Números Complexos, o que reforça o trabalho aqui desenvolvido.

Segundo Fontes e Muniz (2013, p.4),

Ao terminar o Ensino Fundamental, o aluno tem a nítida impressão de que não existem raízes quadradas de números negativos, mesmo que o professor tenha o cuidado de dizer que uma equação de 2º grau de discriminante negativo não possui raízes reais. Isso porque a palavra real, para ele, significa algo que existe, e não um elemento do conjunto dos números reais. Ao se defrontar com os Números Complexos, o aluno sente-se enganado. Como é que, de repente, aquilo que não existia simplesmente passou a existir? O conhecimento dos números reais, ao mesmo tempo em que é necessário para a compreensão dos Números Complexos, pode também se constituir um obstáculo para sua aprendizagem.

Dessa forma, o artigo propõe uma introdução ao sistema de coordenadas polares como elemento facilitador do ensino e da aprendizagem de Números Complexos e da Trigonometria, a fim de resgatar a importância gráfica para a compreensão dos Números Complexos.

(37)

serem instituições que oferecem cursos técnicos nos quais se ensina a disciplina de Eletricidade que trata da análise de circuitos elétricos em Corrente Alternada (CA).

Mello (2015) concluiu que os professores justificaram a não utilização do método por ele proposto devido às dificuldades de os alunos aprenderem por uma aprendizagem descontextualizada e não-significativa, ou seja, de um ensino mecanicista. Essa modalidade de ensino, por sua vez, repercute em uma aprendizagem que não é capaz de estabelecer conexões com outros conceitos ou mesmo servir de ancoradouro para novas aprendizagens. Isso se justifica pela resposta dos professores que apontam a dificuldade de os alunos compreenderem a aplicabilidade dos Números Complexos na análise dos circuitos elétricos.

Almeida (2013) na sua dissertação - Números Complexos para o Ensino Médio: Uma Abordagem Com História, Conceitos Básicos e Aplicações - apresentou uma proposta de ensino de Números Complexos por meio de resolução de problemas. O seu objetivo foi desenvolver um método de ensino que visou melhorar a abordagem dos Números Complexos no Ensino Médio. Para isso, propôs uma série de atividades, que conteve problemas resolvidos e comentados, distribuídos em três capítulos, em que aparecem, respectivamente, a história, conceitos básicos e aplicações dos Números Complexos à Geometria Plana.

Almeida (2013) concluiu que o assunto de Números Complexos pode ser ensinado no Ensino Médio abordando os reais fatos do seu surgimento, bem como podem ser exploradas suas aplicações. Afirma acreditar que qualquer aluno de Ensino Médio, que tenha conhecimentos básicos sobre geometria plana e analítica, é capaz de entender os problemas e soluções que foram propostos na sua pesquisa.

(38)

(39)

4 FUNDAMENTAÇÃO MATEMÁTICA DE NÚMEROS COMPLEXOS

4.1 UMA BREVE HISTÓRIA DOS NÚMEROS COMPLEXOS

A história contribui para esclarecer os movimentos e forças com que determinado conceito foi desenvolvido. É possível que o conhecimento sobre a dinâmica do surgimento de uma noção matemática possa produzir insights importantes que influenciem positivamente a didática dos

professores. Com isso em mente, reuni aspectos históricos acerca do surgimento dos Números Complexos visando dar substância e argumentações que venham proporcionar apoio ao lado das teorias por mim eleitas.

Para Boyer (2010), os Números Complexos surgiram com os matemáticos algebristas italianos do século XVI. Esses matemáticos não tinham esclarecido os conceitos dos números negativos irracionais. Até o século XIX, alguns matemáticos ainda discutiam a existência dos números negativos.

Cardano (1501) havia proposto um método para resolver a equação do terceiro grau utilizando operações com Números Complexos considerando-os como se fossem números reais. No entanto, quando a equação possuía três raízes, esse método não atendia e ele acabava trabalhando de modo equivalente com raízes de natureza diferentes (reais e imaginárias).

Bombelli (1526-1572), discípulo de Cardano, introduziu a quantidade "piu di meno", que corresponde à 1, e anunciou as operações com este número. No século XVI, os matemáticos começaram a usar os Números Complexos, aplicando as regras dos números reais, e ficavam escandalizados e declaravam sua não existência ou que eram inúteis. A crença de que se poderia aplicar aos Números Complexos as mesmas regras do cálculo com números reais levou, por vezes, a enganos.

(40)

Peter Rothe (?,1617), matemático de Nutemberg; em sua Arithmética Philosophica, de 1600. Ele afirma que uma equação tem no máximo tantas raízes quanto seu grau.

Além de Rothe, um dos primeiros matemáticos a se ocuparem com este teorema foi Albert Girard (1595-1632), em cujo livro L'Invention Nouvelle em Algèbre, 1629, lê-se que uma

equação algébrica completa de grau "n", possui "n" raízes.

René Descartes (1596,1650), em seu La Géométrie, aceita que uma equação tem tantas raízes

quanto seu grau, se forem admitidas raízes imaginárias. Descartes introduziu em seu livro a denominação números imaginários: "nem as raízes verdadeiras nem as falsas são sempre reais; por vezes elas são imaginárias". Para ele, enquanto as raízes negativas podem ser tornadas "reais" transformando a equação em outras cujas raízes são positivas, isto não pode ser feito com raízes complexas. Assim, para ele, essas raízes não são números.

D'Alembert mostrou, em 1747, que qualquer expressão algébrica de um Número Complexo a + b 1 é também um número da forma a - b 1. Expressão algébrica, para D'Alembert, incluía elevar um número complexo a uma potência complexa. Sua demonstração só não é correta para o caso (a + b 1) c + d 1_.

Em 1749, D'Alembert (1717-1783) apresentou a primeira tentativa de demonstração convincente desse teorema, que até hoje é conhecido como Teorema de D'Alembert. A demonstração de D'Alembert não mostra a existência de raízes da equação. Ele demonstra qual a forma das raízes, se elas existirem. O mérito do trabalho de D'Alembert foi o de divulgar os números complexos, pois nele encontra-se uma exposição da teoria dos Números Complexos e das funções complexas.

Euler (1707-1783), já no século XVIII, afirmou que 2 2= 4= 2, por analogia com

(41)

Ainda Boyer (2010) ressalta que com Euler, em 1749, as investigações atingiram outro nível. Em seu livro "Pesquisa sobre as Raízes Imaginárias de uma Equação", ele mostrou que, se a + b 1 é raiz de uma equação, então o mesmo acontece com a - 1. Ou seja, se uma equação tem uma raiz complexa, possui um fator da forma x2_{+ kx + r. Ele mostrou, em} seguida, que toda equação que possui grau ímpar tem pelo menos uma raiz real, e que uma equação de grau par ou não possui raízes reais ou possui pares de raízes complexas. Demonstrou, posteriormente, que todas as raízes não reais são da forma a + b 1. Para isso, foi necessário estudar as operações com Números Complexos, incluindo potências imaginárias, logaritmos de Números Complexos, funções trigonométricas de argumento complexo, entre outras maneiras.

No final do século XVIII, os matemáticos já se aventuravam a efetuar operações bem mais ousadas com Números Complexos. No entanto, uma indicação da posição ambígua mantida por eles em relação aos Números Complexos fica evidente pelo fato de que a Enciclopédia, organizada por D'Alembert e outros filósofos franceses, em seus artigos sobre Matemática mantém um silêncio prudente sobre estes números.

Laplace (1794-1827) atacou o problema de demonstrar o Teorema Fundamental de Álgebra, sem, contudo, conseguir uma prova aceitável. A primeira demonstração correta deve-se a Gauss (1777-1885), na qual utiliza propriedades topológicas da reta e do plano que não tinham sido ainda explicitadas em sua época. A demonstração de Gauss encontra-se em sua tese de doutoramento, de 1799. No trabalho, Gauss, além de apresentar sua demonstração, estuda as demonstrações precedentes de D'Alembert (1749), de Foncenet (1759) e de Lagrange (1772), todas elas insatisfatórias. Gauss ainda apresentou três novas demonstrações do Teorema Fundamental. Foi necessário o prestígio de Gauss para tornar conhecida e aceita a representação geométrica dos Números Complexos. Ele publicou suas ideias em 1831, referindo-se "a verdadeira metafísica das quantidades imaginárias"

(42)

operações com uma visão voltada para a Engenharia. Aqui, o número imaginário é representado pela letra j, apesar de nos livros de matemática serem representados pela letra i.

4.2 DEFINIÇÃO

No livro da coleção SCHAUM de Eletricidade Básica, Milton Gussow (2009) define que um Número Complexo z tem a forma x +j y, sendo x e y números reais e j a parte imaginária do

número (nos livros de matemática usa-se a letra i). Em um Número Complexo x + j y, o

primeiro termo, x, é denominado de parte real e o segundo, j y, é denominado de parte

imaginária.

Os Números Complexos podem ser representados por eixos perpendiculares, com um eixo representando a parte real (eixo das abscissas) e o outro a parte imaginária (eixo das ordenadas).

Figura 1- Representação Geométrica dos Números Complexos

Fonte: Eletricidade básica, Gussow (2009, p.400)

Operador j

Conforme a Figura 2, o número j multiplicado pelo vetor "a", j x a, significa uma mudança de

90° no vetor a no sentido anti-horário. o número j multiplicado duas vezes pelo vetor a, j x j

x a. Como, por definição j2 = -1, temos, = j2 x a = - a, o resultado é uma variação de 180° no

sentido anti-horário do vetor a. O número j multiplicado por ele mesmo três vezes, e, depois,

(43)

variação de 270° do vetor a. E ao multiplicarmos o número j quatro vezes pelo vetor a, temos j x j x j x j x a = j 2 x j2 x a = (-1) x (-1) x a = a, o vetor a dá um giro de uma volta de 360°,

voltando à origem.

Figura 2 - Giro do Número Complexo ao longo do círculo

4.3REPRESENTAÇÕES ALGÉBRICAS E TRIGONOMÉTRICAS

4.3.1 Forma retangular e Polar dos Números Complexos

Gussow (2009, p.400) mostra que o Número Complexo z = x + j y mostrado na figura 1

representa a sua forma retangular. Uma outra forma de representação é a forma polar que é expressa da forma:

z = z sendo z = módulo (ou argumento) de z e = ângulo de z em relação ao eixo real positivo.

da trigonometria temos que:

x = z cos (1)

y = z sen (2)

(44)

z 2_{= x}2_{+ y}2

z = (x2_{+ y}2) e = arc tg (y/x)

Para o exemplo da Figura 3:

x = 10 cos 30° = 10 (0,866) = 8,66 z = 8,66 + j 5

O exemplo da figura 3 ilustra a transformação de polar e retangular.

Figura 3 - Transformação de Polar para Retangular

4.4 APLICAÇÕES NA ELETRICIDADE

4.4.1 Impedância Complexa em Série

(45)

armazenar carga elétrica. A grandeza denominada impedância (Z) representa a soma vetorial destas grandezas. Os Circuitos RL, RC e RLC e o quadro resumo são representados pelas figuras 4, 5, 6 e 7.

4.2 Circuito RL

Figura 4 - Circuito RL

4.4.3 Circuito RC

Figura 5 - Circuito RC

(46)

4.4.4 Circuito RLC

Figura 6 - Circuito RLC

4.4.5 Quadro Resumo das Impedâncias em Série

Figura 7 - Tabela Resumo das Impedâncias em Série

(47)

4.4.6 Potência Complexa

O cálculo da potência complexa é possível com a utilização dos Números Complexos. As fórmulas básicas e a representação da potência complexa ativa P, reativa Q e aparente S, são mostradas no triângulo das potências na figura 8. A potência ativa representa aquela que executa o trabalho, no caso de um resistor. Ele produz o aquecimento e, nos casos dos motores, é responsável pelo giro do motor e a potência útil no seu eixo. A potência reativa é de natureza indutiva e/ou capacitiva armazenam energia provocam perdas e reduzem a potência ativa do circuito ou equipamento. A potência aparente é a soma vetorial das potências ativa e reativa.

Figura 8- Triângulo de Potência Complexa

4.4.7 Exemplo de Cálculo de Potência Complexa

(48)

Figura 9 - Exemplo de Cálculo de Potência Complexa

4.4.8 Quadro Resumo da Potência Complexa

Figura 10 - Quadro Resumo da Potência Complexa

(49)

(50)

5 ABORDAGEM DE NÚMEROS COMPLEXOS POR ADRIEN DOUADY

5.1 CONCEITUAÇÃO DAS REPRESENTAÇÃO DOS NÚMEROS COMPLEXOS

O matemático francês Adrien Douady (1935-2006) explica na sequência de figuras, de forma simples, os Números Complexos e a raiz quadrada dos números negativos. Para preservar o material original pesquisado nessa sequência de figuras foi mantido a letra "i" para representar o número imaginário. Na figura 11 um ponto de valor 1 do eixo dos números reias multiplicado por (-2) produz um giro de 180º e, como resultado, o valor de (-2). Porém, se o resultado for multiplicado por (-2), novamente teremos de continuar girando mais 180º e, com isso, teremos 1x(-2)x(-2) = 4, ou seja, o valor resultante de um giro total tem o seu módulo positivo. A figura 12 representa esta situação.

Figura 11- Operação de mutiplicação no eixo real 1 x (-2)

Fonte: https://www.youtube.com/watch?v=3Eben6cFZds Figura 12 - Operação de mutiplicação no eixo real 1 x (-2) x (-2)

(51)

Seguindo o mesmo raciocínio, Douady (1935-2006) mostra na figura 13 que se multiplicarmos o valor 1 por (-1) teremos de realizar um giro de 180º e o valor resultante será (-1). Se continuarmos a operação de multiplicação da resposta por (-1), novamente teremos um giro completo de 360º formando um círculo, e o resultado será positivo com valor 1, como mostrado na figura 14. Semelhantemente, ter-se-ía vários círculos repetindo a operação com os demais números do eixo real, como mostra a figura 15 com a operação com número 2.

Figura 13 - Operação de multiplicação 1 x (-1)

Fonte: https://www.youtube.com/watch?v=3Eben6cFZds

Figura 14 -Operação de multiplicação 1 x (-1) x (-1)

Figura 15 -Operação de multiplicação 2 x (-1) x (-1)

(52)

Douady3_{(1935-2006) mostra como Gauss (1777 - 1885), utilizando propriedades da reta e do} plano, conseguiu a demonstração correta dos Números Complexos e a representação do seu componente "imaginário" utilizando a representação geométrica dos Números Complexos.

Na figura 16, se for realizada a operação de multiplicação 1x (- 1), ter-se-á realizado no plano um giro de 90º, e este ponto passou a ser considerado o ponto "imaginário" do plano que têm valor de 1 e foi convencionado com a representação "i". A figura 17 mostra que se multiplicarmos novamente por 1, ter-se-á um giro completo de 180º e o resultando será o número real -1.

Figura 16 -Representação geométrica de i = 1

Figura 17 -Representação geométrica de 1 x 1

(53)

Dessa forma, ao traçar-se uma curva de 90º de cada ponto do eixo real pode-se definir os diversos pontos "imaginários" e, assim, foi definido por Gauss (1977-1885) como eixo dos números imaginários formando o gráfico cartesiano da figura 18. Logo, qualquer Número Complexo pode ser representado neste plano por um número com componente real e outro "imaginário".

Figura 18 -Representação do eixo real e imáginário

5.2 OPERAÇÕES COM OS NÚMEROS COMPLEXOS

5.2.1 Adição de Números Complexos na forma algébrica(retangular)

(54)

Figura 19 -Adição de dois Números Complexos na forma retangular

5.2.2 Multiplicação de Números Complexos na forma algébrica(retangular)

A figura 20 representa a multiplicação do Número Complexo (1 + 1i) por um Número Complexo com componente real igual 2 e componente imaginário zero, logo as coordenadas que representam o resultado dessa operação é representada por (2 +2i). Observa-se que se continuar multiplicando agora por 3, depois 4 e, assim sucessivamente, ter-se-á coordenadas que representam uma reta com ângulo de 45º, este entendimento é muito importante para a compreensão da outra forma de representação dos Números Complexos que será abordada mais à frente.

Figura 20 -Operação de multiplicação (1 +1i) x 2

(55)

A figura 21 representa a multiplicação do Número Complexo (3 + 1i) por um Número Complexo com componente real igual zero e componente imaginário 1i. Logo as coordenadas que representam o resultado dessa operação é representada por (-1 +3i). Observa-se que a coordenada (3 + 1i), que forma a figura de um retângulo com maior lado na horizontal, sofreu um giro de 90º, formando outro retângulo com coordenadas de (-1 + 3i) com maior lado na vertical. O entendimento da defasagem de 90º será muito importante para a aprendizagem de conceitos aplicados na eletricidade.

Figura 21-Operação de multiplicação (3+1i) x i

5.3 REPRESENTAÇÃO DOS NÚMEROS COMPLEXOS COM MÓDULO E ÂNGULONA FORMA GEOMÉTRICA (POLAR)