Aula 6 – Pol´ıgonos
Objetivos
• Introduzir o conceito de pol´ıgono.
• Estabelecer alguns resultados sobre paralelogramos.
Introdu¸
c˜
ao
Defini¸c˜ao 14
Chamamos de pol´ıgono uma figura plana formada por um n´umero finito de segmentos de reta tais que:
• Cada extremo de cada segmento ´e extremo de exatamente dois
segmentos;
• Os segmentos intersectam-se apenas nos extremos;
• Lados consecutivos n˜ao est˜ao contidos na mesma reta.
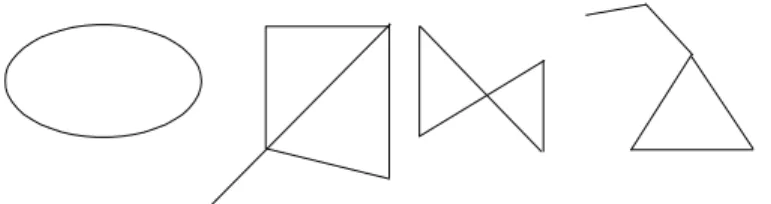
Veja alguns exemplos na figura 96.
Fig. 96: Exemplos de pol´ıgonos.
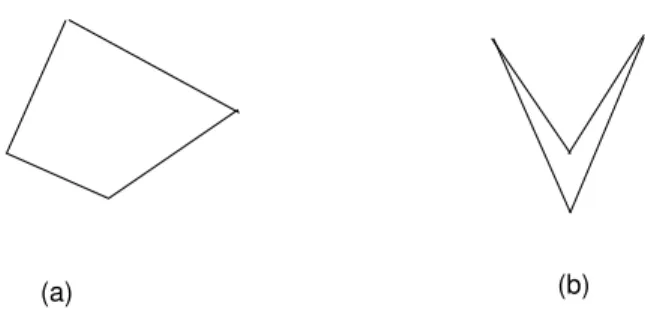
Na figura 97, vocˆe pode ver exemplos de outras figuras planas que n˜ao s˜ao pol´ıgonos (vocˆe deve dizer por que cada uma delas n˜ao satisfaz `a defini¸c˜ao de pol´ıgono).
Cada extremo de cada segmento ´e chamado v´ertice do pol´ıgono, e os segmentos s˜ao chamados lados do pol´ıgono. Um pol´ıgono divide o plano em duas regi˜oes, uma limitada e outra ilimitada. A regi˜ao limitada ´e chamada interior do pol´ıgono. Observe que n˜ao faz sentido falarmos de pol´ıgonos com somente um lado ou somente dois lados.
Defini¸c˜ao 15
Oper´ımetro de um pol´ıgono ´e a soma das medidas de seus lados.
Defini¸c˜ao 16
Uma diagonal ´e um segmento que liga dois v´ertices do pol´ıgono que n˜ao pertencem a um mesmo lado.
Defini¸c˜ao 17
Um pol´ıgono ´e ditoconvexose, dados dois pontos quaisquerAeB no interior do pol´ıgono, o segmento de reta AB est´a contido no interior do pol´ıgono.
Na figura 98, os pol´ıgonos (a) e (b) s˜ao convexos, enquanto o pol´ıgono (c) n˜ao ´e convexo.
A B
(a) (b) (c)
Fig. 98: (a) e (b) s˜ao convexos e (c) n˜ao ´e convexo.
Um triˆangulo (que ´e um pol´ıgono de trˆes lados) ´e sempre convexo. O mesmo n˜ao acontece com outros pol´ıgonos. Observe as figuras 98 e 99. Alguns pol´ıgonos com mais de trˆes lados tamb´em recebem nomes especiais.
Quadril´atero - pol´ıgono de quatro lados
Pent´agono - pol´ıgono de cinco lados
Hex´agono - pol´ıgono de seis lados
Hept´agono - pol´ıgono de sete lados
e assim sucessivamente.
(a) (b)
Fig. 99: a) Quadril´atero convexo. b) Quadril´atero n˜ao-convexo.
Alguns quadril´ateros recebem nomes especiais. Um paralelogramo ´e um quadril´atero que tem os lados opostos paralelos. Um retˆangulo ´e um quadril´atero com todos os ˆangulos retos. Umtrap´ezio´e um quadril´atero que possui um par de lados opostos paralelos, chamados de basesdo trap´ezio.
Vocˆe sabia que...
O Pent´agono (Minist´erio da Defesa dos EUA) tem esse nome porque o pr´edio que o abriga tem esse formato.
Segue da proposi¸c˜ao 9 que todo retˆangulo ´e um paralelogramo. Observe a figura 100.
(a) (b) (c)
Fig. 100: a) Paralelogramo. b) Retˆangulo. c) Trap´ezio.
Umlosango´e um paralelogramo que possui todos os seus lados congru-entes. Um quadrado ´e um retˆangulo que possui todos os lados congruentes. Veja a figura 101. Observe que todo quadrado ´e losango.
(a) (b)
Propriedades dos pol´ıgonos
Usando os fatos que j´a conhecemos a respeito de triˆangulos, podemos mostrar algumas propriedades de outras figuras planas, como veremos a se-guir e at´e o final desta aula.
Proposi¸c˜ao 11
Os lados opostos de um paralelogramo s˜ao congruentes.
Prova:
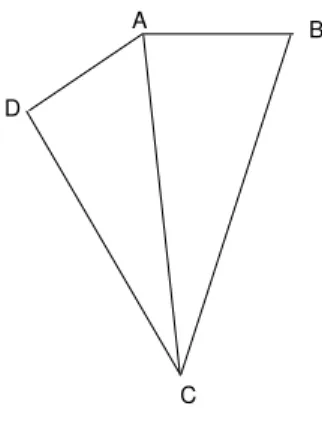
Considere um paralelogramo ABCD. Queremos mostrar que AB ≡
CD e BC ≡ AD. Para isso, vamos tra¸car a diagonal BD, e considerar os triˆangulos DAB e BCD. Veja a figura 102.
A B
C D
Fig. 102: Proposi¸c˜ao 11. A Matem´atica guarda uma
rela¸c˜ao com o esteticamente agrad´avel. Um exemplo disto encontra-se no chamadoretˆangulo ´aureo, utilizado na arquitetura e nas artes, h´a muito tempo. Um retˆangulo ´aureo ´e aquele no qual, ao se destacar um quadrado de lado igual ao menor lado do retˆangulo, obt´em-se um retˆangulo menor que guarda propor¸c˜ao com o retˆangulo original. Para construirmos um retˆangulo ´aureo, partimos de um quadrado (ABCD na figura). Localizamos o ponto m´edio (M) de um lado do quadrado e medimos a distˆancia deste at´e um de seus v´ertices mais distantes (comprimento deM B).
A B
C M D
QuadradoABCDe ponto m´edioM.
A essa medida somamos metade do lado do quadrado, obtendo, assim, o comprimento do retˆangulo
´ aureo.
A B
C
D M E
F
Retˆangulo ´aureo. Comprimento deM B´e igual ao comprimento de
M E.
Consulte: http://www.terravista.pt /Bi-lene/4331/geomcuriosidades.htm
Temos que as retas ←AB→ e ←CD→ s˜ao paralelas e que a reta que cont´em
BD´e transversal `as duas. De acordo com a proposi¸c˜ao 10, os ˆangulos ABDˆ
eCDBˆ s˜ao congruentes. Do mesmo modo, mudando o ponto de vista, como ←→
ADe←BC→s˜ao paralelas eBD←→´e transversal `as duas, os ˆangulosADBˆ eCBDˆ
s˜ao congruentes. O lado BD ´e comum aos dois triˆangulos considerados. Juntando essas informa¸c˜oes, conclu´ımos que, de acordo com o caso A.L.A., os triˆangulosADBeCBDs˜ao congruentes. Isso nos d´aAB≡CDeBC ≡AD.
Q.E.D.
Usando os mesmos argumentos utilizados na proposi¸c˜ao anterior, pode-se mostrar que os ˆangulos opostos de um paralelogramo s˜ao congruentes (veja o exerc´ıcio 9 desta aula).
De acordo com a defini¸c˜ao, para verificar se um dado quadril´atero ´e um paralelogramo, seria preciso constatar que os seus lados opostos s˜ao paralelos. As proposi¸c˜oes a seguir d˜ao outras maneiras de chegar a essa conclus˜ao.
Proposi¸c˜ao 12
Se um quadril´atero possui os lados opostos congruentes, ent˜ao ele ´e um pa-ralelogramo.
Prova:
Seja ABCD um quadril´atero tal queAB ≡CD e BC ≡ AD. Quere-mos Quere-mostrar que a reta←AB→´e paralela `a reta ←CD→e que a reta ←BC→´e paralela `a reta ←AD→. Para isso, vamos tra¸car o segmento BD, como na figura 103. Note que, de acordo com o caso L.L.L., os triˆangulos ABD e CDB s˜ao congruentes.
A B
C D
Fig. 103: Proposi¸c˜ao 12.
Da´ı conclu´ımos que os ˆangulos ABDˆ e CDBˆ s˜ao congruentes, como tamb´em s˜ao congruentes ADBˆ e CBDˆ . A reta ←BD→ ´e transversal `as retas ←→
AB e←CD→, e determina com elas ˆangulos alternos internos ABDˆ e CDBˆ .
De acordo com a proposi¸c˜ao 9, como esses ˆangulos s˜ao congruentes, podemos concluir que ←AB→ e ←CD→ s˜ao paralelas. Da mesma forma, como a reta←BD→tamb´em ´e transversal `as retas ←BC→e ←AD→, e forma com elas ˆangulos alternos internos ADBˆ e CBDˆ , pela mesma proposi¸c˜ao conclu´ımos que ←BC→
e←AD→s˜ao paralelas. Isso prova que ABCD´e de fato um paralelogramo.
Q.E.D.
Simetria num rosto
Simetria num rosto.
No desenho de Leonardo da Vinci representando um velho, o artista sobrepˆos ao esbo¸co um quadrado dividido em retˆangulos, alguns dos quais se aproximam do retˆangulo ´
aureo.
O retˆangulo ´aureo ´e considerado a forma geom´etrica mais agrad´avel `a vista.
Proposi¸c˜ao 13
Se um quadril´atero possui um par de lados opostos paralelos e congruentes, ent˜ao esse quadril´atero ´e um paralelogramo.
Prova:
Seja ABCD um tal quadril´atero, com os lados AB e CD paralelos e congruentes. Trace a diagonal BD (figura 104). Queremos provar que os ladosAD eBC s˜ao tamb´em paralelos. Observe que a reta←BD→´e transversal `as retas paralelas←AB→ e←CD→.
A B
C D
A
B
D
B
D
C
Segue da proposi¸c˜ao 10 que os ˆangulos alternos internos ABDˆ eCDBˆ
s˜ao congruentes. Pelo caso de congruˆencia L.A.L., os triˆangulosABDeCDB
s˜ao congruentes.
Como conseq¨uˆencia,ADBˆ eCBDˆ s˜ao congruentes. A reta←BD→tamb´em ´e transversal `as retas←AD→e←BC→. Com essas retas,←BD→forma ˆangulos alternos internos ADBˆ e CBDˆ ; usando a proposi¸c˜ao 9, segue que ←AD→ e ←BC→ s˜ao paralelas. Com isso, podemos concluir que ABCD ´e um paralelogramo.
Q.E.D.
Encerraremos esta aula apresentando um resultado sobre quadril´ateros convexos.
Proposi¸c˜ao 14
A soma dos ˆangulos internos de qualquer quadril´atero convexo ´e 360o
.
Prova:
SejaABCDum quadril´atero convexo; trace a diagonalAC(figura 105).
B A
C D
Fig. 105: Proposi¸c˜ao 14.
Note que a soma dos ˆangulos internos deABCD ´e a soma dos ˆangulos internos de ABC mais a soma dos ˆangulos internos de ADC. Mas a soma dos ˆangulos internos de qualquer triˆangulo ´e 180o
(veja a lei angular de Tales na Aula 5). Logo, a soma dos ˆangulos internos deABCD ´e 360o
Presen¸ca do retˆangulo ´aureo no Partenon
O Partenon de Atenas se encaixa quase perfeitamente no retˆangulo ´aureo, reconstituindo-se a c´upula retangular de sua fachada. Embora seja dotado de v´arias propor¸c˜oes geometricamente equilibradas, provavelmente seus construtores, no s´eculo V a.C., n˜ao tinham sen˜ao conhecimento intuitivo da propor¸c˜ao ´aurea.
A Lei Angular de Tales tamb´em permite calcular a soma dos ˆangulos internos de qualquer pol´ıgono convexo (veja exerc´ıcio 16 desta aula).
Resumo
Nesta aula vocˆe aprendeu...
• O que ´e um pol´ıgono.
• As defini¸c˜oes de paralelogramo, de retˆangulo, de trap´ezio, de losango e
de quadrado.
• Que os lados opostos de um paralelogramo s˜ao congruentes.
• Que um quadril´atero que tem os lados opostos congruentes ´e um
para-lelogramo.
• Que um quadril´atero que tem um par de lados opostos paralelos e
congruentes ´e um paralelogramo.
Exerc´ıcios
1. Diga se cada uma das afirma¸c˜oes abaixo ´e verdadeira ou falsa:
a) Todo quadrado ´e losango.
b) Todo losango ´e quadrado.
c) Se dois ˆangulos opostos de um quadril´atero s˜ao congruentes, ent˜ao esse quadril´atero ´e um paralelogramo.
d) Todo paralelogramo que tem dois lados adjacentes congruentes ´e losango.
2. Na figura 106,ABCD ´e um paralelogramo,m(AB) = 7cm, m(P C) = 3cm e os ˆangulos destacados s˜ao congruentes. Determine o per´ımetro do paralelogramo.
A
B C
D P
3. Na figura 107,ABCD´e um quadrado eABP ´e um triˆangulo equil´atero. DetermineADPˆ .
A B
C D
P
Fig. 107: Exerc´ıcio 3.
4. Na figura 108, ABCD ´e um quadrado. Prove que DEF ´e equil´atero.
15
15 o
o
A B C
D E
F
Fig. 108: Exerc´ıcio 4.
5. Prove que as diagonais de um paralelogramo intersectam-se em um ponto que ´e ponto m´edio de cada diagonal.
6. Na figura 109,ABCD´e um paralelogramo,m(AD) = 20cm,m(BQ) = 12cm e BF ≡BQ. Determine o per´ımetro desse paralelogramo.
A
B C
D
F Q
Fig. 109: Exerc´ıcio 6.
7. Na figura 110, ABC ´e retˆangulo de hipotenusa BC, AN e BC s˜ao paralelos,BN eAM s˜ao paralelos eM B ≡M C. Prove que AM BN ´e um losango.
A C
B
M
N
Fig. 110: Exerc´ıcio 7.
8. (UFMG-1990) Na figura 111, ABC ´e equil´atero com 8cm de lado e
M N ´e paralelo a BC.
A
C B
M N
Fig. 111: Exerc´ıcio 8.
A medida de M N para o qual o per´ımetro de M N CB ´e igual ao per´ımetro de AM N ´e:
a) 2cm
b) 3cm
c) 4cm
d) 5cm
e) 6cm
9. Prove que os ˆangulos opostos de um paralelogramo s˜ao congruentes.
10. Prove que as diagonais de um losango s˜ao perpendiculares.
11. Um trap´ezio ´e chamado is´osceles se os lados n˜ao paralelos s˜ao congru-entes. SeABCD´e um trap´ezio is´osceles em queAB´e uma base, prove que ˆA≡B e ˆC ≡Dˆ.
12. Prove que as diagonais de um paralelogramo se intersectam em um ponto que ´e ponto m´edio das duas diagonais.
13. As diagonais de um quadril´atero convexo s˜ao bissetrizes dos ˆangulos dos v´ertices. Prove que esse quadril´atero ´e um losango.
14. Prove que retas paralelas s˜ao equidistantes. Mais precisamente, se r e
s s˜ao retas paralelas, prove que a distˆancia deA as´e igual `a distˆancia de B a s, quaisquer que sejam A , B ∈r.
15. Prove que as diagonais de um trap´ezio is´osceles s˜ao congruentes.
16. Prove que a soma dos ˆangulos internos de um pol´ıgono convexo de n
lados ´e (n−2)180o. Sugest˜ao: Divida o pol´ıgono em n−2 triˆangulos usando as diagonais que partem de um ponto.
17. Prove que o n´umero de diagonais de um pol´ıgono de n lados ´e dado