Aula 10 – Semelhan¸
ca de triˆ
angulos
Objetivos
• Introduzir a no¸c˜ao de semelhan¸ca de triˆangulos
• Determinar as condi¸c˜oes m´ınimas que permitem dizer que dois triˆangulos
s˜ao semelhantes.
Introdu¸
c˜
ao
Vimos na aula 3 a no¸c˜ao de congruˆencia de triˆangulos. Intuitivamente falando, dois triˆangulos s˜ao congruentes quando apresentam o mesmo tama-nho e a mesma forma. Veremos, nesta aula, a no¸c˜ao de semelhan¸ca entre dois triˆangulos que, intuitivamente falando, significar´a que os mesmos tˆem a mesma forma.
Defini¸c˜ao 30
Dizemos que dois triˆangulos s˜aosemelhantes se existe uma correspondˆencia entre seus v´ertices de modo que ˆangulos correspondentes sejam congruentes e lados correspondentes sejam proporcionais.
O que a defini¸c˜ao anterior quer dizer ´e queABC eDEF s˜ao semelhan-tes (segundo a correspondˆenciaA↔D,B ↔E eC↔F) seBACb ≡EDFb , ABCb ≡DEFb ,BCAb ≡EF Db e
m(AB) m(DE) =
m(AC) m(DF) =
m(BC) m(EF).
Usaremos a nota¸c˜ao ABC ∼ DEF para indicar que ABC e DEF s˜ao semelhantes segundo a correspondˆencia A ↔ D, B ↔ E e C ↔ F. Como na congruˆencia de triˆangulos, a ordem em que as letras est˜ao escritas ´e importante (veja figura 185).
A
B C
D
E F
A raz˜ao comum entre os lados ´e chamadaraz˜ao de semelhan¸ca. ´E claro que dois triˆangulos congruentes s˜ao semelhantes, com raz˜ao de semelhan¸ca igual a 1. Mas existem triˆangulos semelhantes que n˜ao s˜ao congruentes: considere dois triˆangulos equil´ateros em que a medida do lado de um deles seja o dobro da medida do lado do outro. Como os trˆes ˆangulos dos dois triˆangulos medem 60o
, conclui-se que eles s˜ao semelhantes com raz˜ao de semelhan¸ca 1/2 (ou 2). Obviamente os dois triˆangulos n˜ao s˜ao congruentes. Veja figura 186.
A
B C
D
E F
Fig. 186: Triˆangulos equil´ateros semelhantes, mas n˜ao congruentes.
´
E claro que todo triˆangulo ´e semelhante a si mesmo (propriedade refle-xiva) e que se ABC ∼ DEF ent˜ao DEF ∼ ABC (propriedade sim´etrica). Al´em disso, se ABC ∼DEF e DEF ∼GHI ent˜ao ABC ∼ GHI (proprie-dade transitiva).
Analogamente `a congruˆencia de triˆangulos, em que determinamos condi¸c˜oes m´ınimas (casos de congruˆencia) para garantir a congruˆencia entre dois triˆangulos, existem tamb´em condi¸c˜oes m´ınimas que garantem que dois triˆangulos s˜ao se-melhantes. Essas condi¸c˜oes m´ınimas s˜ao oscasos de semelhan¸ca de triˆangulos.
Come¸caremos com a seguinte proposi¸c˜ao:
Proposi¸c˜ao 23
Se um triˆangulo tem dois de seus ˆangulos correspondentemente congruen-tes a dois ˆangulos de outro triˆangulo, ent˜ao os dois triˆangulos s˜ao semelhancongruen-tes.
A
B C
D
E F
Fig. 187: Proposi¸c˜ao 23.
Prova:
Sejam ABC e DEF triˆangulos tais queABCb ≡DEFb e BCAb ≡EF Db (figura 187). Queremos provar queBACb ≡EDFb e
m(AB) m(DE) =
m(AC) m(DF) =
Como a soma dos ˆangulos internos de qualquer triˆangulo ´e 180o
, segue da hip´otese que tamb´em se tem BACb ≡ EDFb . Se os segmentos BC e EF forem congruentes, segue queABC ≡DEF pelo caso de congruˆencia A.L.A.. Logo, ABC e DEF s˜ao semelhantes (com raz˜ao de semelhan¸ca igual a 1). Suponha agora que os segmentos BC e EF n˜ao sejam congruentes. Por exemplo, suponha queBC < EF. Marque um pontoGno segmento EF de modo que BC ≡ EG e por G trace uma reta paralela `a reta ←→DF. Seja H o ponto em que essa reta corta o segmento ED(Figura 188).
A
B
C E H
G D
F
Fig. 188: Proposi¸c˜ao 23.
Segue da proposi¸c˜ao 10, da aula 5 que HGEb ≡DF E. Mas os ˆangulosb ACBb e DF Eb s˜ao congruentes por hip´otese. Ent˜ao HGEb ≡ACBb e obtemos do caso de congruˆencia A.L.A. que ABC ≡ HEG. Conseq¨uentemente, os segmentosAB eHE s˜ao tamb´em congruentes. Usando o Teorema de Tales, conclui-se que m(H E)
m(DE) =
m(EG)
m(EF). Mas m(EG) = m(BC) e m(HE) = m(AB). Logo,
m(AB) m(DE) =
m(BC)
m(EF). (I)
Para completar a prova, considere um pontoI ∈EF tal queIF ≡BC
e, por I, trace uma reta paralela a DE. Seja J o ponto em que essa reta cortaDF (figura 189).
A
B
C E
D
F I
J
Fig. 189: Proposi¸c˜ao 23.
Raciocinando como antes, obt´em-se JIFb ≡ DEFb ≡ ABCb e ABC ≡ JIF. Segue que AC ≡JF e
m(AC) m(DF) =
m(J F) m(DF) =
m(I F) m(EF) =
m(BC)
Juntando (I) e (II) conclu´ımos finalmente que
m(AB) m(DE) =
m(BC) m(EF) =
m(AC) m(DF)
Portanto, ABC ∼DEF.
Q.E.D.
Vocˆe seria capaz de descobrir como Tales determinou a altura da pirˆamide? (Veja a primeira nota lateral da aula 9.)
A pr´oxima proposi¸c˜ao traz mais um caso de semelhan¸ca de triˆangulos.
Proposi¸c˜ao 24
Se dois triˆangulos ABC e DEF s˜ao tais que ABCb ≡ DEFb e
m(AB) m(DE) = m(BC)
m(EF), ent˜ao ABC eDEF s˜ao semelhantes. Prova:
Se AB e DE forem congruentes, ent˜ao m(AB) =m(DE) e m(BC) m(EF) = m(AB)
m(DE) = 1. Segue que BC e EF tamb´em s˜ao congruentes.
Como ABCb ≡ DEFb por hip´otese, conclui-se por L.A.L. que ABC
e DEF s˜ao triˆangulos congruentes. Assim, ABC e DEF s˜ao semelhantes (com raz˜ao de semelhan¸ca igual a 1). Suponha agora que AB e DE n˜ao sejam congruentes. Por exemplo, suponha queAB < DE. Nesse caso tem-se tamb´emBC < EF (pela nossa hip´otese). Marque um ponto Gno segmento DE de modo que AB ≡ GE. Pelo ponto G trace uma reta paralela `a reta
DF e sejaH o ponto em que essa reta corta o segmentoEF (figura 190).
A
B
C E
G
H D
F
Fig. 190: Proposi¸c˜ao 24.
Usando o Teorema de Tales obt´em-se que
m(GE) m(DE) =
m(EH) m(EF).
Masm(AB) =m(GE) por constru¸c˜ao do ponto G. Assim,
m(AB) m(DE) =
Como
m(AB) m(DE) =
m(BC) m(EF)
por hip´otese, segue que m(EH) = m(BC), ou seja, BC e EH s˜ao tamb´em congruentes. Como j´a temos que AB ≡ GE e ABCb ≡ DEFb , segue do caso L.A.L. de congruˆencia de triˆangulos que ABC e GEH s˜ao triˆangulos congruentes. Em particular tem-se GHEb ≡ ACB. Masb GHEb ≡ DF Eb pois GH//DF, donde se conclui queACBb ≡DF E. Ent˜ao os triˆangulosb ABC e DEF s˜ao tais que ABCb ≡ DEFb e ACBb ≡ DF E. A semelhan¸ca entre osb triˆangulosABC eDEF segue agora da proposi¸c˜ao 23.
Q.E.D.
A hip´otese da proposi¸c˜ao anterior significa que os lados AB e BC do triˆangulo ABC s˜ao proporcionais aos lados DE e EF do triˆangulo DEF. O que a proposi¸c˜ao 24 diz ent˜ao ´e que, se dois lados de um triˆangulo s˜ao proporcionais a dois lados de outro triˆangulo e os ˆangulos inclusos a esses lados s˜ao congruentes, ent˜ao esses triˆangulos s˜ao semelhantes.
Podemos relacionar semelhan¸ca com a redu¸c˜ao ou amplia¸c˜ao de fotos ou imagens.
Encerraremos os casos de semelhan¸ca com a seguinte proposi¸c˜ao:
Proposi¸c˜ao 25
Se dois triˆangulosABC eDEF s˜ao tais que
m(AB) m(DE) =
m(AC) m(DF) =
m(BC) m(EF),
ent˜ao ABC e DEF s˜ao semelhantes.
Prova:
A
B C
D
E F
H J
K I
G
Fig. 191: Proposi¸c˜ao 24.
Os triˆangulos ABC eKEF s˜ao semelhantes pela Proposi¸c˜ao 23. Tem-se portanto que
m(AB) m(KE) =
m(AC) m(KF) =
m(BC) m(EF). Mas
m(AB) m(DE) =
m(AC) m(DF) =
m(BC) m(EF)
por hip´otese. Portanto, m(KE) = m(DE) e m(KF) = m(DF), ou seja, KE ≡DE e KF ≡DF. Mas o exerc´ıcio 8 da aula 2 diz que essa situa¸c˜ao n˜ao pode ocorrer (compare com a prova do caso L.L.L. de congruˆencia de triˆangulos). Essa contradi¸c˜ao prova que devemos terBACb ≡EDFb ,ABCb ≡ DEFb ou ACBb ≡ DF E, o que implica, como vimos no in´ıcio desta prova,b queABC ´e semelhante a DEF.
Q.E.D.
O que a proposi¸c˜ao 25 diz ´e que, se os trˆes lados de um triˆangulo s˜ao proporcionais aos trˆes lados de outro triˆangulo, ent˜ao esses triˆangulos s˜ao semelhantes.
Resumo
Nesta aula vocˆe aprendeu...
• O que significa dizer que dois triˆangulos s˜ao semelhantes.
• Que, se dois ˆangulos de um triˆangulo s˜ao congruentes a dois ˆangulos
de outro triˆangulo, ent˜ao esses triˆangulos s˜ao semelhantes.
• Que, se dois lados de um triˆangulo s˜ao porporcionais a dois lados de
outro triˆangulo e os ˆangulos inclusos a esses lados s˜ao congruentes, ent˜ao esses triˆangulos s˜ao semelhantes.
• Que, se os trˆes lados de um triˆangulo s˜ao proporcionais aos trˆes lados
Exerc´ıcios
1. Determine os valores de x e de y na figura 192.
3
x 4
6 8
y
Fig. 192: Exerc´ıcio 1.
2. Determine o valor de x na figura 193.
4 6
3
8 12 x
Fig. 193: Exerc´ıcio 2.
3. Na figura 194, ABCD, EF GC e HIJG s˜ao quadrados. Determine o valor de x.
A B
C D
E F
G H
J x
9 6
I
Fig. 194: Exerc´ıcio 3.
4. Na figura 195, ABCD ´e um retˆangulo, m(BC) = 12 e M ´e o ponto m´edio de AB. Determine m(EF).
A B
C D
E
F M
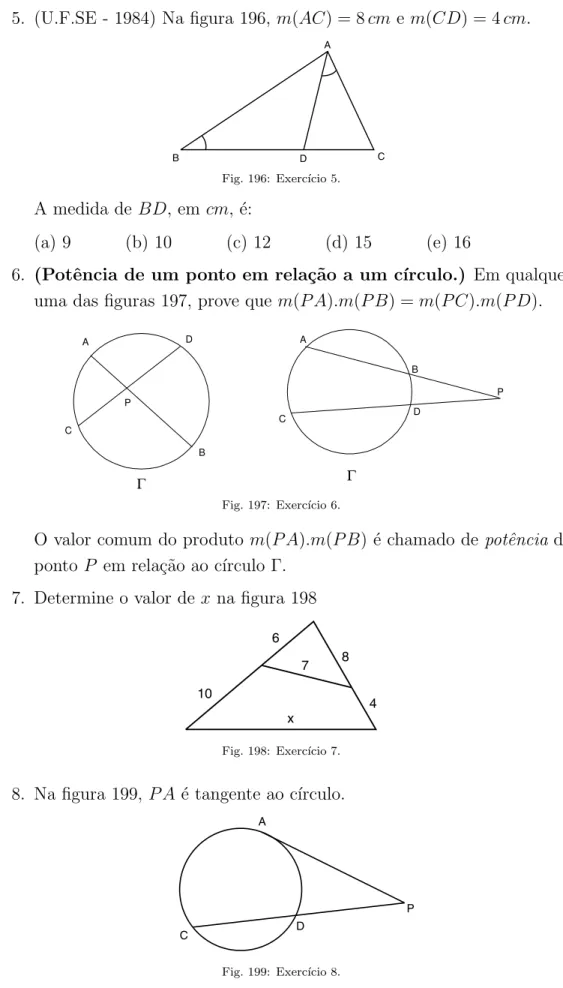
5. (U.F.SE - 1984) Na figura 196, m(AC) = 8cme m(CD) = 4cm.
A
B D C
Fig. 196: Exerc´ıcio 5.
A medida de BD, em cm, ´e:
(a) 9 (b) 10 (c) 12 (d) 15 (e) 16
6. (Potˆencia de um ponto em rela¸c˜ao a um c´ırculo.) Em qualquer uma das figuras 197, prove que m(P A).m(P B) = m(P C).m(P D).
A
B C
D
P
A
B
C D
P
Γ Γ
Fig. 197: Exerc´ıcio 6.
O valor comum do produtom(P A).m(P B) ´e chamado de potˆencia do pontoP em rela¸c˜ao ao c´ırculo Γ.
7. Determine o valor de xna figura 198
10
x
8
4 6
7
Fig. 198: Exerc´ıcio 7.
8. Na figura 199, P A´e tangente ao c´ırculo.
A
C D
P
Fig. 199: Exerc´ıcio 8.
9. Na figura 200, m(AB) = 4, m(BC) = 6, m(AC) = 8 e o per´ımetro de DEF vale 27.
A B
C D
E
F
Fig. 200: Exerc´ıcio 9.
Determine as medidas dos lados de DEF.
10. Calcule o raio do c´ırculo da figura 201, sabendo que BC ´e tangente ao c´ırculo.
A B
C
D
O 16
9
Fig. 201: Exerc´ıcio 10.
11. (FATEC-1978) Dado o triˆangulo ABC na figura 202, constru´ımos a poligonal L=BCB1C1B2C2B3C3. . ..
A B
C
p
n m
C3 C2
C1
B
3 B2 B1
60o 60o
60o
60o
Fig. 202: Exerc´ıcio 11.
O comprimento de L´e:
12. (UFF, 1994) O hex´agono regular da figura 203 possui lado medindo L.
M1
M2
M3
M4
M5
M6
M7
M8
M9
N1
N2
N3
N4
N5
N6
N7
N8
N9
Fig. 203: Exerc´ıcio 12.
Sabendo que os 9 segmentos M1N1, M2N2, . . . , M9N9 s˜ao todos
para-lelos e dividem o segmentoM1M9 em 8 partes iguais, pode-se afirmar
que a soma m(M1N1) +m(M2N2) +. . .+m(M9N9) ´e igual a:
(a) 11L (b) 12L (c) 13L (d) 14L (e) 15L
13. Determine o raio do c´ırculo circunscrito ao triˆangulo ABC da figura 204, sabendo quem(AB) = 4, m(AC) = 6 e m(AH) = 3.
A
B H C
Fig. 204: Exerc´ıcio 13.
14. (UFF, 1996) O quadril´ateroM N P Q, est´a inscrito no c´ırculo de centro O e raio 10cm, conforme a figura 205.
Q
M
N
P
O
Fig. 205: Exerc´ıcio 14.
Sabendo que a diagonalM P passa porO,QM = 8cmeM N = 12cm, pode-se afirmar que o valor do segmentoM H, em cm, ´e:
15. (FUVEST - 1979) Na figura 206, ABC ´e um triˆangulo retˆangulo em A,ADEF ´e um quadrado,m(AB) = 1 e m(AC) = 3.
B
D
E
A F C
Fig. 206: Exerc´ıcio 15.
Pode-se afirmar que o lado do quadrado mede:
(a) 0,70 (b) 0,75 (c) 0,80 (d) 0,85 (e) 0,90
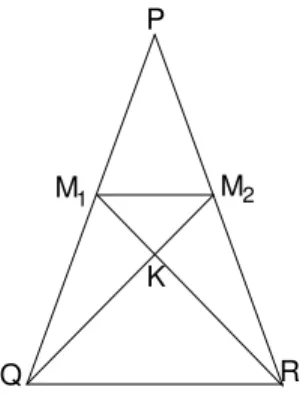
16. (UFF, 1993) Considere o triˆangulo is´osceles P QR da figura 207, de lados congruentes P Q e P R, cuja altura relativa ao lado QR ´eh.
M P
Q
K
R
1 2
M
Fig. 207: Exerc´ıcio 16.
Sabendo que M1 e M2 s˜ao, respectivamente, os pontos m´edios de P Q
e P R, a altura do triˆangulo KM1M2, relativa ao lado M1M2 ´e:
(a) 2h
3 (b)
h
6 (c)
h√3
2 (d)
h√3
3 (e)