Aula 3 – Triˆ
angulos: classifica¸
c˜
ao e
congruˆ
encia
Objetivos
• Introduzir o conceito de triˆangulo.
• Classificar os triˆangulos segundo lados e ˆangulos.
• Discutir o significado de congruˆencia de triˆangulos.
• Apresentar alguns casos de congruˆencia de triˆangulos.
Introdu¸
c˜
ao
Os triˆangulos, assim como as retas, os ˆangulos, os segmentos etc. s˜ao objetos ideais, nascidos da observa¸c˜ao de objetos materiais com forma tri-angular (como um guardanapo de papel dobrado, a vista de lado de um calend´ario de mesa, etc.). Identifique alguns triˆangulos na figura 31.
Fig. 31: Objetos com forma triangular.
Defini¸c˜ao 8 (Triˆangulo)
Umtriˆangulo´e a uni˜ao de trˆes segmentos de reta AB,AC eBC, em que A,
Os pontos A, B e C, referidos na defini¸c˜ao anterior, s˜ao chamados
v´ertices do triˆangulo, enquanto os segmentos AB, AC e BC s˜ao ditoslados
do triˆangulo, e os ˆangulosBACˆ ,ABCˆ eACBˆ (ou ˆA, ˆB e ˆC) s˜ao os ˆangulos internosdo triˆangulo. Veja figura 32.
A
B
C
Fig. 32: Triˆangulo.
O interior do triˆangulo ABC ´e a interse¸c˜ao dos interiores dos ˆangulos internos do triˆangulo ABC. Veja a figura 33.
A
B
C
Fig. 33: Interior do triˆanguloABC.
Classifica¸
c˜
ao dos triˆ
angulos
Existem triˆangulos com diversos formatos. Podemos classific´a-los de acordo com o tamanho de seus lados e de seus ˆangulos.
Quanto aos lados, podemos classificar os triˆangulos em equil´ateros, is´osceles e escalenos.
• Triˆangulo equil´atero - Os trˆes lados s˜ao congruentes.
• Triˆangulo is´osceles - Dois dos seus lados s˜ao congruentes. O
terceiro lado ´e chamadobase do triˆangulo.
• Triˆangulo escaleno - O triˆangulo n˜ao tem nenhum par de lados
congruentes.
(a) (b) (c)
Fig. 34: a) Triˆangulo equil´atero. b) Triˆangulo is´osceles. c) Triˆangulo escaleno.
Podemos, tamb´em, classificar os triˆangulos quanto aos ˆangulos.
• Triˆangulo retˆangulo - ´E aquele que possui um ˆangulo reto.
• Triˆangulo obtusˆangulo- ´E aquele que possui um ˆangulo obtuso.
• Triˆangulo acutˆangulo - ´E aquele em que os trˆes ˆangulos s˜ao
agudos.
(a) (b) (c)
Fig. 35: Triˆangulos segundo seus ˆangulos. a) acutˆangulo. b) obtusˆangulo. c) retˆangulo.
Atividade 1:
Responda falso ou verdadeiro `as afirma¸c˜oes abaixo e procure apresentar uma justificativa atrav´es de um desenho. Use compasso e transferidor se desejar.
a) ´E poss´ıvel desenhar um triˆangulo acutˆangulo escaleno.
b) N˜ao existe um triˆangulo obtusˆangulo is´osceles. Procure verificar quais as combina¸c˜oes poss´ıveis de acordo com seus desenhos.
Congruˆ
encia de triˆ
angulos
No in´ıcio da aula 2, vimos o que significa dizer intuitivamente que duas figuras planas s˜ao congruentes. Mas, aquela forma de apresentar o conceito de congruˆencia n˜ao nos oferece ferramentas para avan¸carmos no nosso estudo de Geometria. A defini¸c˜ao a seguir torna bastante preciso o significado da congruˆencia no caso de triˆangulos.
Defini¸c˜ao 9 (Triˆangulos congruentes)
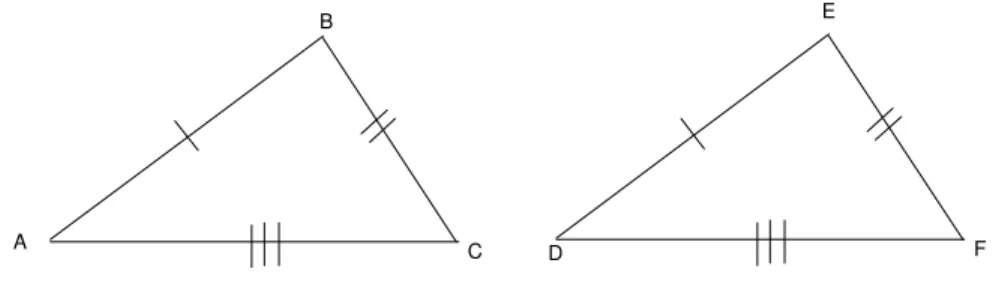
Dois triˆangulos,ABC eDEF, s˜ao congruentes se houver uma correspondˆen-cia entre seus v´ertices, de modo que os lados correspondentes e os ˆangulos correspondentes sejam congruentes.
Mais precisamente, os triˆangulosABC eDEF s˜ao congruentes segundo a correspondˆencia A ↔ D, B ↔ E e C ↔ F se as seis seguintes condi¸c˜oes
s˜ao satisfeitas: AB≡DE, AC ≡DF, BC ≡EF, ˆB ≡Eˆ, ˆC≡Fˆ, e ˆA≡Dˆ.
A
B C
D
E
F
Fig. 36: ABC≡DEF.
Observe na figura 36 que os ˆangulos congruentes est˜ao marcados com o mesmo n´umero de linhas indicativas. Utilizaremos essa marca¸c˜ao sempre que formos representar ˆangulos congruentes.
A congruˆencia de triˆangulos significa que eles tˆem o mesmo tamanho e forma ou, como dissemos na aula 2, que ´e poss´ıvel sobrepor um ao outro com exatid˜ao.
Usaremos a nota¸c˜aoABC ≡DEF para indicar que os triˆangulosABC
eDEF s˜ao congruentes e que a correspondˆencia ´e dada na ordem em que as letras est˜ao escritas (A corresponde a D,B a E e C a F).
Na verdade, n˜ao ´e preciso verificar as seis congruˆencias dadas na de-fini¸c˜ao para garantir que dois triˆangulos s˜ao congruentes. Existem condi¸c˜oes m´ınimas que, se verificadas, garantem essa congruˆencia. Essas condi¸c˜oes s˜ao chamadas casos de congruˆencia de triˆangulos.
Inicialmente, apresentaremos como axioma o caso de congruˆencia lado-ˆ
angulo-lado, ou simplesmente caso L.A.L.:
Caso L.A.L.
• Se dois triˆangulosABC eDEF s˜ao tais queAB ≡DE, ˆB ≡Eˆ
eBC ≡EF, ent˜ao ABC ≡DEF.
O que esse axioma diz ´e que, se dois lados de um triˆangulo e o ˆangulo entre eles (que se diz incluso aos dois lados) est˜ao fixados, s´o ´e poss´ıvel completar esse triˆangulo de uma ´unica maneira (e isso vocˆe pode constatar com exemplos). Ou seja, todos os triˆangulos que tˆem os mesmos dois lados e ˆangulo incluso s˜ao congruentes.
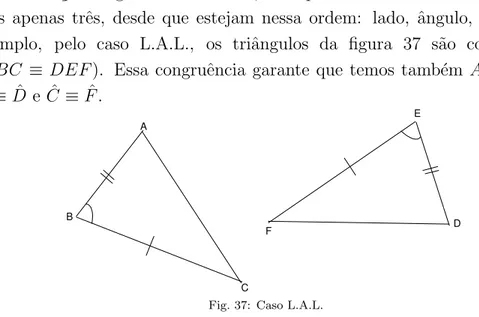
Aten¸c˜ao: segundo esse crit´erio, n˜ao ´e preciso verificar seis congruˆencias, mas apenas trˆes, desde que estejam nessa ordem: lado, ˆangulo, lado. Por exemplo, pelo caso L.A.L., os triˆangulos da figura 37 s˜ao congruentes (ABC ≡ DEF). Essa congruˆencia garante que temos tamb´em AC ≡ DF,
ˆ
A≡Dˆ e ˆC ≡Fˆ.
B
C A
E
F D
Fig. 37: Caso L.A.L.
Futuramente veremos outros casos de congruˆencia. Enquanto isso, vocˆe pode ir pensando em quais devem ser esses casos. Por exemplo, ser´a que A.L.A. (dois ˆangulos e o lado incluso congruentes) ou A.A.A. (trˆes ˆangulos congruentes) s˜ao casos de congruˆencia de triˆangulos? Ou pensando noutra dire¸c˜ao, ser´a que existem triˆangulos nessas condi¸c˜oes que n˜ao sejam congru-entes?
Proposi¸c˜ao 1
Se ABC ´e um triˆangulo is´osceles de base BC, ent˜ao ˆB ≡Cˆ.
Prova: Nossa estrat´egia para provar esse fato ´e considerar um triˆangulo is´oscelesABC e, usando o caso L.A.L., tentar mostrar que ele ´e congruente a ACB (lembrando que a ordem em que escrevemos os pontos no nome do triˆangulo ´e muito importante para o conceito de congruˆencia). Uma vez que isso fique provado, como conseq¨uˆencia conclu´ımos que os ˆangulos ˆB e ˆC s˜ao congruentes. Vamos provar ent˜ao que ABC ≡ACB.
Prova (ou demonstra¸c˜ao)
Uma proposi¸c˜ao em Matem´atica ´e umaverdade universal. Quando dizemos, por exemplo, que para
qualquertriˆangulo is´osceles os ˆangulos da base s˜ao congruentes, chegamos a essa conclus˜ao usando apenas o nosso racioc´ınio e as verdades universais j´a conhecidas (que podem ser axiomas ou outras proposi¸c˜oes j´a demonstradas). A esse tipo de argumenta¸c˜ao chamamos
provaoudemonstra¸c˜ao. N˜ao poder´ıamos ter chegado `a mesma conclus˜ao que chegamos realizando medi¸c˜oes em triˆangulos is´osceles, simplesmente porque existem infinitos deles, e n˜ao poder´ıamos medir todos eles.
Como terminar uma prova
Podemos terminar uma prova (ou demonstra¸c˜ao) com Q.E.D., que significa
Quod Erat Demonstrandum
(em latim) ou com C.Q.D., que significa Como Quer´ıamos Demonstrar (em portuguˆes). A B C A C B
Fig. 38: ABC≡ACB
Do fato que ABC ´e is´osceles com base BC, os lados AB e AC s˜ao congruentes. Ora, o ladoAB do primeiro triˆangulo ´e correspondente ao lado
ACdo segundo triˆangulo. Do mesmo modo, o ladoAC do primeiro triˆangulo ´e correspondente ao lado AB do segundo. O ˆangulo incluso a esses lados ´e o mesmo nos dois triˆangulos. Ent˜ao, pelo caso L.A.L., os triˆangulos ABC e
ACB s˜ao congruentes. Portanto, os ˆangulos ˆB e ˆC s˜ao congruentes.
Q.E.D.
Vocˆe pode estar se perguntando se n˜ao ´e ´obvio que o triˆangulo ABC
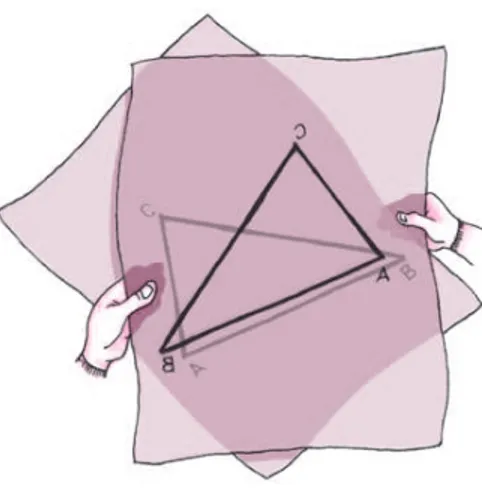
´e congruente a si mesmo. ´E verdade, de fato todo triˆangulo ´e congruente a si mesmo, mas o que acabamos de mostrar ´e que um triˆangulo is´osceles ´e congruente a si mesmo de duas maneiras diferentes. Se vocˆe recortar dois triˆangulos is´osceles iguais num papel, ser´a poss´ıvel sobrepor tanto o primeiro ao segundo, como tamb´em o verso do primeiro ao segundo. Note que isso n˜ao acontece com um triˆangulo que n˜ao seja is´osceles. Veja figura 39.
Fig. 39: Congruˆencia de triˆangulo is´osceles.
Atividade 2:
Recorte em papel cartolina 4 triˆangulos, sendo 2 deles is´osceles e iguais e 2 deles escalenos e iguais. Pinte as faces de cada um dos triˆangulos com as cores verde e amarela, respectivamente.
Observe que o par de triˆangulos is´osceles pode se sobrepor perfeita-mente tanto pela justa posi¸c˜ao de faces de mesma cor como de cores dife-rentes. Observe o que acontece com o par de triˆangulos escalenos! Qual ´e a explica¸c˜ao?
O pr´oximo caso de congruˆencia de triˆangulos ´e o caso ˆangulo-lado-ˆangulo (A.L.A.):
Caso A.L.A.
• Se um triˆangulo possui dois ˆangulos e o lado incluso
congruen-tes a dois ˆangulos e ao lado incluso de outro triˆangulo, ent˜ao, obrigatoriamente, esses triˆangulos s˜ao congruentes.
A veracidade desse caso de congruˆencia pode ser demonstrada usando o caso L.A.L..
Vocˆe sabia que...
A figura do cientista profissional surgiu na Gr´ecia. Alguns dos nomes mais representativos dessa classe, durante a civiliza¸c˜ao grega, viveram em Alexandria, onde Ptolomeu fez erigir um grande centro de pesquisas denominado Museo. Ali, a tradi¸c˜ao grega em Ciˆencia e Literatura foi preservada e desenvolvida.
Entre os primeiros pesquisadores associados com o Museo de Alexandria est´a Euclides, um dos matem´aticos mais influentes de todos os tempos. Prova:
Considere dois triˆangulos ABC e DEF tais que ˆB ≡ Eˆ, BC ≡ EF e
ˆ
C ≡ Fˆ. Queremos provar que ABC ≡ DEF. Nossa estrat´egia ser´a provar
queAB ≡DE (uma vez provado isso, seguir´a que o triˆanguloABC tem dois
lados e o ˆangulo incluso a esses lados, congruentes a dois lados e ao ˆangulo incluso de DEF. Do caso L.A.L. obteremos que ABC ≡DEF). Para isso,
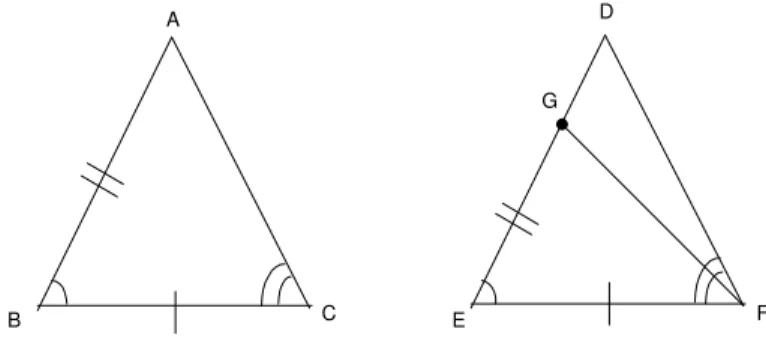
suponha que AB e DE n˜ao sejam congruentes. Ent˜ao um dos segmentos ´e menor que o outro. Suponha que o menor deles seja AB. Assim, existe um pontoG entreE e D tal que AB≡GE (veja a figura 40).
A B C D F E G
Comparando os triˆangulos ABC e GEF, tem-seAB ≡GE (por
cons-tru¸c˜ao do pontoG),ABCˆ ≡GEFˆ (por hip´otese) eBC ≡EF (por hip´otese).
A hip´otese ´e o conjunto das proposi¸c˜oes que se admitem verificadas, e a tese ´e o que se pretende concluir como conseq¨uˆencia da hip´otese. O conjunto de racioc´ınios feitos para concluir a tese constitui a demonstra¸c˜ao do teorema.
Com essas observa¸c˜oes constatamos que os triˆangulosABCeGEF tˆem dois lados e o ˆangulo incluso congruentes, sendo, de acordo com ocaso L.A.L., triˆangulos congruentes. Da´ı conclu´ımos que ACBˆ ≡ GF Eˆ (aqui damos os
“nomes completos”dos ˆangulos, para evitar confus˜ao). Como, por hip´otese,
ACBˆ ≡DF Eˆ , conclui-se que o ˆangulo GF Eˆ ´e congruente a DF Eˆ , o que ´e
um absurdo. Logo, devemos terAB≡DE (para que n˜ao seja poss´ıvel fazer
a constru¸c˜ao acima).
Comparamos agora os triˆangulos ABC e DEF temos que AB ≡ DE
(como acabamos de mostrar),ABCˆ ≡DEFˆ (por hip´otese) eBC ≡EF (por
hip´otese).
A partir do caso L.A.L., podemos concluir que ABC ≡DEF.
Q.E.D.
A demonstra¸c˜ao da proposi¸c˜ao anterior foi feita usando um argumento de contradi¸c˜ao: em linhas gerais, o que fizemos foi supor que a proposi¸c˜ao era falsa, e com isso chegamos a uma conclus˜ao absurda (ou contradit´oria). Com isso, conclu´ımos que a proposi¸c˜ao tem mesmo que ser verdadeira.
A pr´oxima proposi¸c˜ao ´e o caso de congruˆencia lado-lado-lado (L.L.L.).
Caso L.L.L.
• Se os trˆes lados de um triˆangulo s˜ao congruentes aos trˆes lados
de outro triˆangulo, ent˜ao esses triˆangulos s˜ao congruentes (ou seja, ter˜ao tamb´em ˆangulos congruentes).
O caso L.L.L. pode ser demonstrado usando os dois casos anteriores.
Prova:(do caso L.L.L.)
Considere dois triˆangulosABC eDEF tais que AB≡DE,BC ≡EF
eAC ≡DF. Queremos provar que ˆA≡Dˆ, ˆB ≡Eˆ e ˆC ≡Fˆ.
Nossa estrat´egia para essa prova ´e mostrar que um dos ˆangulos deABC
´e congruente ao ˆangulo correspondente de DEF. Como os lados correspon-dentes s˜ao congruentes, estaremos ent˜ao no caso L.A.L., e fica provada a congruˆencia dos triˆangulos.
A
B
C D
E
F
Fig. 41: Proposi¸c˜ao : caso L.L.L..
Vamos supor que nenhum par de ˆangulos correspondentes ´e congruente (ou seja, ˆA n˜ao ´e congruente a ˆD, ˆB n˜ao ´e congruente a ˆE e ˆC n˜ao ´e congru-ente a ˆF). Note que, nesse caso, um dos triˆangulos tem dois ˆangulos menores que os ˆangulos correspondentes do outro (por quˆe?). Vamos supor ent˜ao que
ˆ
A <Dˆ e ˆC <Fˆ.
A
B
C D
E
F H
I G
Fig. 42: ABC≡DGF.
Tome pontos I ∈ EF e H ∈ DE tais que IDFˆ ≡ Aˆ e HF Dˆ ≡ Cˆ e
sejaGo ponto de encontro entre os segmentos DI eF H (veja figura 42). De acordo com o caso A.L.A., os triˆangulosABC e DGF s˜ao congruentes.
A
B
C D
E
F G
Fig. 43: Observa¸c˜oes da proposi¸c˜ao .
Pelo que conhecemos sobre os triˆangulos, e usando a congruˆencia
ABC ≡DGF que acabamos de construir, podemos escrever que
m(DG) =m(AB) =m(ED) e
m(GF) =m(BC) =m(EF).
Ent˜ao no triˆangulo EDF vale
m(DG) +m(GF) =m(DE) +m(EF).
Intuitivamente creio que vocˆe concorda que a igualdade ´e absurda! E vocˆe est´a certo. Ela n˜ao pode acontecer. Em qualquer situa¸c˜ao sempre o lado esquerdo ´e inferior. Este resultado pedimos que vocˆe aceite como ver-dadeiro. Ele ser´a provado no exerc´ıcio 5 da Aula 4. Como a igualdade n˜ao pode acontecer ent˜ao nosso ponto de partida para conseguir esta igualdade era falso. Ou seja, pelo menos um par de ˆangulos correspondentes ´e congru-ente. Como observamos no in´ıcio desta demonstra¸c˜ao, isso basta para termos
ABC ≡DEF.
Q.E.D.
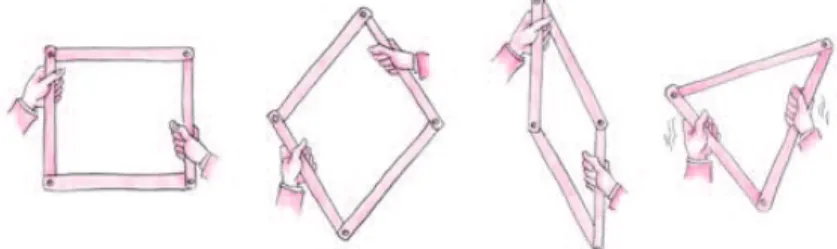
O caso de congruˆencia L.L.L. explica por que os triˆangulos s˜ao t˜ao utilizados em diversas aplica¸c˜oes: os triˆangulos s˜ao figuras r´ıgidas. Vamos explicar este conceito de rigidez com exemplos. Se vocˆe juntar quatro vare-tas, unindo cada duas com um alfinete ou parafuso atravessado, de forma a obter um quadril´atero, vocˆe vai notar que ´e poss´ıvel modificar a forma do quadril´atero de diversas maneiras (veja a figura 44).
Fig. 44: A forma do quadril´atero pode ser modificada, mas a do triˆangulo n˜ao.
Essa deforma¸c˜ao n˜ao ´e poss´ıvel quando se trata de triˆangulos, justa-mente porque n˜ao existem duas formas diferentes poss´ıveis para triˆangulos com lados de mesma medida. Vocˆe j´a deve ter notado que algumas estantes de livros tˆem no fundo uma ou duas barras atravessadas na diagonal. Essa ´e uma aplica¸c˜ao desse princ´ıpio: as barras s˜ao colocadas para evitar que a estante fique “balan¸cando”, ou seja, mude de formato. A barra diagonal tamb´em ´e usada em porteiras. A figura 45 a seguir ilustra essas situa¸c˜oes.
Fig. 45: Aplica¸c˜oes do caso L.L.L.
Outros casos de congruˆ
encia de triˆ
angulos
´
E poss´ıvel provar com os instrumentos que dispomos at´e agora, dois novos casos de congruˆencia de triˆangulos. Estes casos est˜ao descritos abaixo. No entanto, preferimos deixar a prova do primeiro destes casos para ser apresentado no final da Aula 5 e o segundo ap´os o estudo de semelhan¸cas, no momento em que estudarmos triˆangulos retˆangulos.
Caso de congruˆencia L.A.A
Se dois triˆangulos ABC e DEF s˜ao tais que BC ≡ EF, ˆB ≡ Eˆ e
ˆ
A≡Dˆ, ent˜ao ABC ≡DEF.
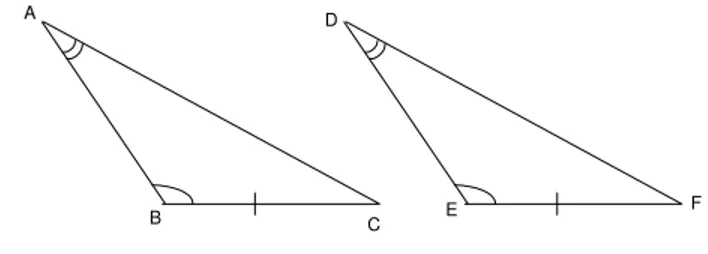
O caso de congruˆencia L.A.A. assegura que se dois triˆangulos ABC e
DEF s˜ao tais que BC ≡EF, ˆB ≡Eˆ e ˆA≡Dˆ, como indicado na figura 46,
ent˜ao ABC ≡ DEF. Ou seja, que tamb´em temos AB ≡ DE, AC ≡ DF e
ˆ
C≡Fˆ.
A
B C
D
E F
Fig. 46: Caso L.A.A.
Caso de congruˆencia de triˆangulos retˆangulos
Se um triˆangulo retˆangulo tem a hipotenusa e um cateto congruentes `a hipotenusa e a um cateto de outro triˆangulo retˆangulo, ent˜ao os triˆangulos s˜ao congruentes.
Este caso de congruˆencia assegura que se ABC e DEF s˜ao triˆangulos retˆangulos de hipotenusasAB e DE, respectivamente, tais que AB≡DE e AC ≡DF (veja figura 47), ent˜ao os dois triˆangulos s˜ao congruentes.
C A
B E D
F
Resumo
Nesta aula vocˆe aprendeu...
• O que significa a congruˆencia entre triˆangulos.
• Que os ˆangulos da base de um triˆangulo is´osceles s˜ao congruentes.
• Os casos de congruˆencia L.A.L., A.L.A. e L.L.L.
Exerc´ıcios
1. Considere a figura 48.
B
A
C
E
D
F 3
4
13
3
60o 4
60o
Fig. 48: Exerc´ıcio 1.
a) Pode-se dizer que ABC ≡DEF?
b) Pode-se dizer que ABC ≡EDF?
c) Determine o valor de m(EF).
2. Considere os triˆangulos ABC e DEF na figura 49. Determine m(BC) e m(DF). Enfatizamos que as indica¸c˜oes da figura 49 significam que
ˆ
A≡F , ACˆ ≡F E e ˆC ≡Eˆ).
A
B
C 6
D E
F 5
Fig. 49: Exerc´ıcio 2.
3. Na figura 50, os ˆangulos CABˆ e DBAˆ s˜ao retos. Como determinar o ponto E ∈AB em que AECˆ ≡BEDˆ ?
B A
C
D
E
Fig. 50: Exerc´ıcio 3.
4. Na figura 51, ABC ´e is´osceles de base BC e BD ≡ DC. Mostre que BADˆ ≡CADˆ e que os ˆangulos ADBˆ eADCˆ s˜ao retos.
B
A
C D
Fig. 51: Exerc´ıcio 4.
5. Na figura 52, ABC ´e is´osceles de base BC e BADˆ ≡ CADˆ . Mostre
que BD≡DC e que ADBˆ eADCˆ s˜ao retos.
B
A
C D
Fig. 52: Exerc´ıcio 5.
6. Na figura 53, BD≡DC e ADCˆ ´e reto.
B
A
C D
Fig. 53: Exerc´ıcio 6.
7. Na figura 54, BADˆ ≡CADˆ eADCˆ ´e reto.
B
A
C D
Fig. 54: Exerc´ıcio 7.
Prove que ABC ´e is´osceles de base BC.
8. Na figura 55, BADˆ ≡ CADˆ e BD≡ DC. Prove que ABC ´e is´osceles
de baseBC.
B
A
C D
Fig. 55: Exerc´ıcio 8.
9. Na figura 56, AD≡BC,ADCˆ e BCDˆ s˜ao ˆangulos retos e M eN s˜ao
os pontos m´edios de AB e DC, respectivamente.
N D
A M B
C
Fig. 56: Exerc´ıcio 9.
Prove que os ˆangulos AM Nˆ eDN Mˆ s˜ao retos.
Esse retˆangulo ´e conhecido comoretˆangulo de Saccheri.
Giovanni Saccheri
1667-1733 . It´alia.
Giovanni Saccheri entrou para a Ordem dos Jesu´ıtas em 1685. Cinco anos depois ele estudou Filosofia e Teologia em um col´egio jesu´ıta. Foi nesse per´ıodo que come¸cou a se dedicar `a Matem´atica. Saccheri fez importantes trabalhos em Geometria n˜ao-euclideana e em L´ogica Matem´atica. Consulte:
http://www-groups.dcs. st-nd.ac.uk/~history/ Mathematicians/Saccheri. html
Aula 4 – ˆ
Angulos externos de um triˆ
angulo
Objetivos
• Introduzir o teorema do ˆangulo externo.
• Apresentar algumas conseq¨uˆencias do teorema do ˆangulo externo.
Introdu¸
c˜
ao
Come¸caremos esta aula definindo o que chamamos ponto m´edio de um segmento.
Defini¸c˜ao 10 (Ponto m´edio)
Ponto m´edio de um segmento ´e um ponto que divide o segmento em duas partes congruentes. Nesse caso, a medida de cada parte ´e metade da medida total do segmento dividido.
A proposi¸c˜ao a seguir ´e bastante natural e admitiremos como verda-deira nesta aula. Convido vocˆe no entanto a, assim que tiver uma folguinha, consultar e aprender sua demonstra¸c˜ao que est´a no Apˆendice.
Proposi¸c˜ao 2
Todo segmento possui um ´unico ponto m´edio (Veja a figura 57).
A
B
M
Fig. 57: Ponto m´edio do segmentoAB.
Proposi¸c˜ao 3
Todo ˆangulo possui uma ´unica bissetriz.
Prova:
Seja o ˆangulo ˆA como mostrado na figura 58. Assinale pontos B e C
sobre lados distintos do ˆangulo, de modo queBA ≡CA. Em seguida, trace
o segmento BC. Seja D o ponto m´edio de BC e trace AD (veja figura 58).
A
B
C D
Fig. 58: Bissetriz de ˆangulo.
Como o segmento AD ´e comum aos triˆangulos ABD e ACD, segue por L.L.L. que ABD ≡ ACD. Conseq¨uentemente, BADˆ ≡ CADˆ , ou seja,
a semi-reta −AD−→ divide o ˆangulo BACˆ em dois ˆangulos congruentes. Est´a provada a existˆencia da bissetriz. ´E evidente que a semi-reta −AD−→ ´e a ´unica que tem a propriedade de dividir o ˆangulo em dois ˆangulos de mesma me-dida. Tente considerar uma outra possibilidade de bissetriz, e encontre que os ˆangulos obtidos n˜ao tem a mesma medida. Dessa forma, provamos a proposi¸c˜ao 3.
ˆ
Angulos externos de um triˆ
angulo
Definiremos, a seguir, um conceito muito importante associado aos triˆangulos.
Defini¸c˜ao 11
Chamamos deˆangulo externode um triˆanguloABC um ˆangulo formado por um lado deABC e pelo prolongamento de outro lado.
Note que cada triˆangulo possui seis ˆangulos externos, como vocˆe pode observar na figura 59. S˜ao eles: DACˆ , EABˆ , ABFˆ , GBCˆ , ACHˆ e BCIˆ . Marque esses ˆangulos na figura. Observe queFBGˆ n˜ao ´e um ˆangulo externo. Identifique outros ˆangulos na figura que n˜ao s˜ao ˆangulos externos do triˆangulo
ABC. A B C D E F G H I
Fig. 59: ˆAngulos externos deABC.
Os ˆangulosDACˆ eEABˆ s˜ao congruentes, pois ambos s˜ao suplementa-res adjacentes ao mesmo ˆangulo internoBACˆ . Assim tamb´emABFˆ ≡GBCˆ
eACHˆ ≡BCIˆ .
Nota: Angulos comoˆ DACˆ eEABˆ , da figura 59, s˜ao ditosopostos pelo v´ertice. Um ˆangulo ´e dito oposto a outro ˆangulo pelo v´ertice se as semi-retas que o formam s˜ao opostas `as semi-retas que formam o outro ˆangulo. ˆAngulos opostos pelo v´ertice s˜ao sempre congruentes.
Mas, voltemos aos ˆangulos externos. Cada ˆangulo externo possui dois ˆangulos internos quen˜aolhe s˜ao adjacentes. Por exemplo,BACˆ eBCAˆ s˜ao ˆangulos internos n˜ao adjacentes ao ˆangulo externoABFˆ (e tamb´em aGBCˆ ).
O pr´oximo resultado que veremos ´e conhecido como teorema do ˆangulo externo.
Lembre-se de que...
Dizemos que dois ˆangulos s˜aocomplementaresquando a soma de suas medidas ´e igual a 90o
. Dizemos que s˜ao
suplementaresquando a soma de suas medidas ´e igual a 180o
.
Aprendendo um pouco mais...
Teorema´e uma proposi¸c˜ao que se deduz de axiomas e de proposi¸c˜oes j´a conhecidas. O cojunto de racioc´ınios feitos para concluir o que o teorema diz constitui a demonstra¸c˜ao do teorema. Consulte:
http://www.terra.com.br /matematica/arq13-2.htm
Teorema do ˆAngulo Externo
Um ˆangulo externo de um triˆangulo ´e maior que qualquer ˆangulo interno que n˜ao lhe seja adjacente.
Prova:
Sejam ABC um triˆangulo eD um ponto tal que C esteja entreB eD. Provaremos que o ˆangulo externo ACDˆ ´e maior que cada um dos ˆangulos internos ˆA e ˆB. Para isso, tome M, o ponto m´edio de AC, e trace BM. Identifique o ponto E da semi-reta −BM−→ tal que BE ≡2BM. LigueC a E,
A
B
C D
E
M
Fig. 60: Teorema do ˆangulo externo.
Os triˆangulos AM B e CM E s˜ao congruentes por L.A.L. (observe que os ˆangulos opostos pelo v´ertice, AM Bˆ e CM Eˆ s˜ao congruentes). Como conseq¨uˆencia, ˆA≡ECMˆ . Como ACDˆ ´e maior que ECMˆ , segue queACDˆ
´e maior que ˆA.
Fazendo uma constru¸c˜ao como essa, usando o ponto m´edio de BC ao inv´es do ponto m´edio de AC, podemos tamb´em concluir que ACDˆ ´e maior que ˆB.
Q.E.D.
Conseq¨
uˆ
encias do teorema do ˆ
angulo externo
Dado um triˆanguloABC, dizemos que o ˆangulo ˆA´e oposto ao ladoBC(ou que
ˆ
Aop˜oe-se ao ladoBC). Analogamente dizemos que
ˆ
B´e oposto aACe ˆC´e oposto aAB.
Se vocˆe desenhar um triˆangulo ABC em que o ladoAC ´e maior que o ladoAB, vocˆe poder´a verificar, com a ajuda de um transferidor, que ˆB >Cˆ, ou seja, que o ˆangulo oposto a AC ´e maior que o ˆangulo oposto a AB. O resultado a seguir diz que isso sempre ocorre.
Proposi¸c˜ao 4
Dados dois lados de um triˆangulo, ao maior lado op˜oe-se o maior ˆangulo. Reciprocamente, dados dois ˆangulos de um triˆangulo, ao maior ˆangulo op˜oe-se o maior lado.
Prova:
SejaABC um triˆangulo tal que AB > AC, como na figura 61. O nosso objetivo ´e provar que ˆC > Bˆ. Para isso, marque um ponto D em AB tal que AD≡AC. Pelo fato de ADC ser um triˆangulo is´osceles com baseDC,
temos ADCˆ ≡ ACDˆ . Mas ADCˆ ´e um ˆangulo externo do triˆangulo CDB
n˜ao adjacente aABCˆ , e o Teorema do ˆangulo externo afirma queADC >ˆ Bˆ. Logo, podemos concluir que ACB > Aˆ CDˆ ≡ ADC >ˆ Bˆ. Provamos, ent˜ao
queAB > AC implica que ˆC >Bˆ, que ´e a primeira parte da proposi¸c˜ao.
A
D
C
B
Fig. 61: Maior ˆangulo oposto ao maior lado.
Vamos provar a segunda parte. Isto ´e, ACB > Aˆ BCˆ implica que
AB > AC. Portanto, suponha que ABC seja um triˆangulo em que ACB >ˆ ABCˆ . A partir do que foi dito antes, se tiv´essemosAC > AB, concluir´ıamos que ABC > Aˆ CBˆ , o que n˜ao acontece. Se tiv´essemos AC ≡ AB, ABC
seria is´osceles com base BC, e ter´ıamos ABCˆ ≡ ACBˆ , o que tamb´em n˜ao
acontece. Como AC n˜ao ´e maior nem congruente a AB, conclu´ımos que
AC < AB.
Q.E.D.
Com o intuito de simplificar a nota¸c˜ao, usaremos daqui em dianteBACˆ
para indicar tanto um ˆangulo quanto sua medida. Assim, para indicar que a medida deBACˆ ´e 30o
, escreveremos simplesmente BACˆ = 30o
.
Proposi¸c˜ao 5 (Desigualdade triangular)
Em qualquer triˆangulo, a medida de cada lado ´e sempre menor que a soma das medidas dos outros dois lados.
Prova:
Considere um triˆangulo ABC. Na semi-reta −→BA marque um ponto D
tal queAesteja entreB eD, eAD seja congruente aAC, como na figura 62. O triˆangulo ACD assim formado ´e is´osceles de base CD, e portanto temos
ADCˆ ≡ACDˆ .
A
B C
D
Como conseq¨uˆencia, no triˆangulo BDC o ˆangulo BCDˆ ´e maior que o ˆangulo BDCˆ , e, portanto, op˜oe-se a um lado maior. Da´ıBC < BD. Por constru¸c˜ao, temosm(BD) =m(BA) +m(AD) =m(BA) +m(AC). Assim, conclu´ımos que m(BC) < m(AB) +m(AC). Essa mesma constru¸c˜ao pode ser feita com base em qualquer lado.
Q.E.D.
Resumo
Nesta aula vocˆe aprendeu...
• Que todo segmento possui um ´unico ponto m´edio.
• Que todo ˆangulo possui uma ´unica bissetriz.
• Que um ˆangulo externo de um triˆangulo ´e maior que qualquer ˆangulo
interno a ele n˜ao adjacente.
• Que, num triˆangulo, ao maior lado op˜oe-se o maior ˆangulo e vice-versa.
• Que cada lado de um triˆangulo ´e menor que a soma dos outros dois
lados.
Exerc´ıcios
1. ´E poss´ıvel construir um triˆangulo cujas medidas sejam 3cm, 4cm e 8cm? Em caso afirmativo, diga como constru´ı-los.
2. ´E poss´ıvel construir um triˆangulo cujas medidas sejam 3cm, 4cm e 6cm? Em caso afirmativo, diga como constru´ı-los.
3. O semiper´ımetro de um triˆangulo ´e a metade da soma das medidas de seus lados. Por exemplo, se os lados de um triˆangulo medem 4cm, 6cm e 8cm, ent˜ao o semiper´ımetro desse triˆangulo vale 9cm. Prove que a medida de qualquer lado de um triˆangulo ´e menor que o semiper´ımetro.
Per´ımetro de um triˆangulo
O per´ımetro de um triˆangulo ´e a soma das medidas dos seus lados. Falaremos sobre per´ımetros de outras figuras na aula 7.
4. Seja ABC um triˆangulo qualquer e sejaD um ponto do segmentoBC.
Prove que m(AD)< m(AB) ou m(AD)< m(AC).
5. Na figura 63,P ´e um ponto interno qualquer do triˆanguloABC. Prove que m(P B) +m(P C)< m(AB) +m(AC).
A
B C
P
Fig. 63: Exerc´ıcio 5.
6. Na figura 64, m(AB) < m(AC) e AD ´e bissetriz de BAC.ˆ Prove que
m(BD)< m(DC).
A
B D C
Fig. 64: Exerc´ıcio 6.
7. Pode-se concluir que os triˆangulos ABC eDEF da figura 65 s˜ao con-gruentes? Justifique sua resposta.
A B
C
E
D F
8. Observe a figura 66.
F D
A E
B C
Fig. 66: Exerc´ıcio 8.
Determine:
a) Os ˆangulos menores do que o ˆangulo ABDˆ
b) Os ˆangulos maiores do que o ˆangulo CDBˆ
c) Os ˆangulos menores do que o ˆangulo BDFˆ
Vocˆe deve ser capaz de justificar suas respostas sem usar a figura.
Apˆ
endice: Para saber mais...
Neste apˆendice apresentamos uma prova da seguinte proposi¸c˜ao:
Proposi¸c˜ao 6
Todo segmento possui um ´unico ponto m´edio.
Prova:
Considere um segmento de reta AB. De acordo com os axiomas de medida de segmentos vistos na aula 2, existe um n´umero real positivo que representa a medida de AB. Chamemos esse n´umero de c. Ainda de acordo com aqueles axiomas, existe um segmento de reta, que chamaremosCD, cuja medida ´e exatamentec/2. TransportandoCD para a semi-reta−→AB, obtemos um ponto M entre A e B tal que AM tem medida c/2 (veja a figura 65). Da´ı,M B tamb´em tem medida c/2, ou seja,AM ≡M B, eM ´e ponto m´edio
do segmento AB.
A
B
M
Fig. 67: Ponto m´edio do segmentoAB.
Tomando um outro ponto N pertencente ao segmento AB, temos que
N est´a entre A e M ou entre M e B. Em ambos os casos a medida de
AN ´e diferente da medida de N B; isto ´e, N n˜ao ´e um ponto m´edio de AB. Provamos ent˜ao que o segmentoAB possui um ´unico ponto m´edio.