UNIVERSIDADE FEDERAL DE OURO PRETO
DÉBORA SILVA VELOSO
O DESENVOLVIMENTO DO PENSAMENTO E DA LINGUAGEM
ALGÉBRICOS NO ENSINO FUNDAMENTAL: ANÁLISE DE
TAREFAS DESENVOLVIDAS EM UMA CLASSE DO 6º ANO
Ouro Preto
DÉBORA SILVA VELOSO
O DESENVOLVIMENTO DO PENSAMENTO E DA LINGUAGEM
ALGÉBRICOS NO ENSINO FUNDAMENTAL: ANÁLISE DE
TAREFAS DESENVOLVIDAS EM UMA CLASSE DO 6º ANO
Dissertação apresentada ao Curso de Mestrado Profissional em Educação Matemática, oferecido pela Universidade Federal de Ouro Preto, como exigência parcial para obtenção do título de Mestre em Educação Matemática.
Orientadora: Ana Cristina Ferreira
Doutora em Educação Matemática
Ouro Preto
Catalogação: sisbin@sisbin.ufop.br V443d Veloso, Débora Silva.
O desenvolvimento do pensamento e da linguagem algébricos no ensino fundamental [manuscrito] : análise de tarefas desenvolvidas em uma classe do 6º ano / Débora Silva Veloso – 2012.
245 f.: il., color.; tabs.
Orientadora: Profª Dra. Ana Cristina Ferreira.
Dissertação (Mestrado) - Universidade Federal de Ouro Preto. Instituto de Ciências Exatas e Biológicas. Departamento de Matemática. Programa de
Mestrado Profissional em Educação Matemática. Área de concentração:Educação Matemática.
1. Matemática - Estudo e ensino - Teses. 2. Pensamento algébrico - Teses. 3. Álgebra - Estudo e ensino - Teses. 4. Ensino fundamental - Teses. I. Universidade Federal de Ouro Preto. II. Título.
AGRADECIMENTOS
É difícil encontrar palavras para expressar minha gratidão pelas pessoas que estiveram comigo nessa caminhada.
Primeiramente, agradeço a Deus que me iluminou e guiou os meus passos, não me deixando desistir em momentos de maior dificuldade.
À minha mãe, exemplo de dedicação, força e superação, que não mediu esforços para ver realizar os meus sonhos, sempre ao meu lado, orgulhosa e me dando forças.
Ao meu pai, preocupado e interessado, que, mesmo longe, fez questão de estar sempre presente, demonstrando carinho e apoio.
Aos meus irmãos, Breno, Romulo e Mônica, e à minha cunhada Paty, que alegraram os meus momentos de desespero! Amo vocês incondicionalmente! Sem vocês, não teria tanta graça!
À Kelly, amiga querida, principal incentivadora em meu ingresso em todo o processo. Você é muito especial!
A todos os colegas da turma 3, especialmente, ao Davidson, à Maíra e à Luciene que compartilharam, junto a mim, alguns momentos de desespero e angústia. Ao Célio e à Daila pelas divertidas noites de quinta-feira.
Às minhas queridas e tão fieis amigas de infância, Thaís, Maria Cristina, Daniela, Luciana e Raquel, pela força nos últimos meses.
A todos os professores do mestrado da UFOP que colaboraram, direta ou indiretamente, para minha formação.
À Márcia Cyrino, ao Plínio e à Vanessa, por aceitarem a tarefa de ler e apresentar contribuições valiosas para este trabalho.
À minha orientadora Ana Cristina, pelo apoio e orientações nos momentos de trabalho, e pela humanidade demonstrada em momentos delicados. Obrigada pelas palavras de apoio e carinho. Você é parte deste trabalho!
Aos alunos que aceitaram participar do projeto e à direção do colégio onde a proposta foi desenvolvida. Muito obrigada pela colaboração!
Ao Bruno, pela paciência, tranquilidade e apoio nos últimos meses! Você é iluminado e muito especial!
Enfim... muito obrigada a todos!
RESUMO
A Álgebra, apesar de seu valor inegável na formação matemática do cidadão, figura como uma das áreas que oferece grandes dificuldades para professores e alunos. Uma das explicações apresentadas pela literatura nacional e internacional é o fato de seu ensino ser predominantemente mecânico e desprovido de sentido para os alunos. Outra é a ênfase excessiva no simbolismo em detrimento do desenvolvimento do pensamento algébrico. Tais leituras e reflexões levaram-nos construir, desenvolver e analisar um conjunto de tarefas envolvendo padrões e sequências com o propósito de investigar como alunos iniciantes no estudo de Álgebra lidariam com as mesmas e responder a seguinte questão de investigação: Que contribuições uma proposta de ensino baseada na percepção e generalização de padrões e sequências pode trazer para o desenvolvimento do pensamento algébrico e da linguagem algébrica em alunos que se iniciam no estudo da Álgebra? A pesquisa aconteceu em uma classe do 6º ano do Ensino Fundamental de uma escola privada de Belo Horizonte (MG). Sete tarefas foram desenvolvidas nos horários regulares das aulas de Matemática. Esse estudo, de cunho qualitativo, fundamentou-se nos trabalhos de Radford (2009, 2010a, 2010b e 2011) acerca do pensamento algébrico e dos processos de objetificação e de generalização. Os dados foram coletados por meio de diário de campo, gravações em áudio e vídeo, bem como de registros produzidos pelos alunos. Os resultados evidenciam que a percepção de padrões e a construção e análise de sequencias não são triviais para os alunos, mas, quando estimulados, gradativamente, podem desenvolver as habilidades necessárias para trabalhar com esses temas. Os participantes do estudo, de modo geral, apresentaram considerável avanço na compreensão de padrões e percepção de regularidades. Nessa perspectiva, tivemos a oportunidade de perceber os processos de objetificação vivenciados pelos estudantes, no sentido de investigar as diversas estratégias utilizadas por eles durante a interação com as sequências, com os colegas e com a professora/pesquisadora. As tarefas abordadas e a forma como foram desenvolvidas em sala de aula propiciaram a domesticação do olhar de alguns alunos, os quais conseguiram desenvolveram formas de raciocínio organizadas e elaboradas, realizando generalizações algébricas –contextuais ou factuais -, características do pensamento algébrico. Observamos, também, uma evolução na forma de designar o objeto indeterminado e variável em cada uma das sequências trabalhadas e na escrita simbólica, em direção à construção da linguagem algébrica padrão. Tal como propõe a literatura, verificamos que é possível realizar tarefas que estimulem o desenvolvimento do pensamento algébrico em alunos iniciantes no estudo da Álgebra, antes mesmo que eles dominem a linguagem algébrica padrão. A pesquisa gerou ainda um livreto com uma síntese comentada das tarefas desenvolvidas, destinado a professores, futuros professores e formadores.
ABSTRACT
The Algebra, despite its undeniable value in the mathematical training of a citizen, shows as a difficult area for teachers and students. The national and international literature says that his teaching is predominantly mechanical and meaningless to students.The Algebra, despite its undeniable value in the mathematical training of a citizen, shows as a difficult area for teachers and students. One of the explanations given by the national and international literature is the fact that his teaching is predominantly mechanical and meaningless to students. Another explanation given is the excessive emphasis on symbolism rather than the development of algebraic thinking.These readings and reflections led us to build, develop and analyze a set of tasks that involves patterns and sequences in order to investigate how beginners in the study of algebra would deal with them. The research took place in a class of 6th graders at a private school in Belo Horizonte (MG). Seven tasks were developed in the regular schedule of mathematics classes. This qualitative study was based on Radford works (2009, 2010a, 2010b and 2011) about algebraic thinking and the processes of objectification and generalization. Data were collected through a field diary, audio, video and some records produced by the students. The results show that the perception of patterns and the construction and analysis of sequences are not trivial for students, but, when stimulated, may have a gradually development of the skills necessary to work with these issues. The participants generally displayed a considerable progress in understanding and perception of patterns. From this perspective, we had the opportunity to understand the processes of objectification experienced by the students, in an effort to investigate the various strategies used by them during the interaction with the sequences, with colleagues and with the teacher / researcher. The tasks and how they were developed in the classroom led to the domestication of the eyes of some students, which could have developed organized and elaborated thinking, performing algebraic generalizations - contextual or factual - , which is one of the characteristics of the algebraic thinking. We also observed an evolution in the way of designating the variable and undetermined object in each of the sequences and in symbolic writing in the way to the construction of the algebraic language standard. As literature proposes, we found that you can perform tasks that encourage the development of algebraic thinking in beginners, even before they dominate the algebraic language standard. The research also generated a booklet with a brief commentary of the tasks developed for teachers, future teachers and trainers.
LISTA DE FIGURAS
Figura 1: Sequência de figuras trabalhadas na pesquisa de Radford. Fonte: Radford (2010, p.
41). ... 40
Figura 2: Esquema representativo da regularidade percebida por Doug. Fonte: Radford (2010, p. 43). ... 40
Figura 3: Primeiros quatro termos de uma sequência trabalhada em uma turma do 2º ano. Fonte: Radford, 2010b, p. 3. ... 41
Figura 4: O momento em que um estudante (James) está desenhando o sexto termo; o quinto (linha de cima) e o sexto (linha de baixo) termos de James; oitavo termo de acordo com outra estudante (Sandra). Fonte: Radford, 2010b, p. 3. ... 41
Figure 5: Três cubos enfileirados no canto da sala. Fonte: Grecco (2008, p. 69). ... 79
Figure 6: Um cubo sobre a mesa. ... 80
Figura 7: Dois cubos enfileirados sobre a mesa. ... 82
Figura 8: Exemplo de 3 lembretes no painel. Fonte: Barbosa,Vale e Palhares (2008). ... 88
Figure 9: Exemplo de um lembrete afixado no painel. ... 89
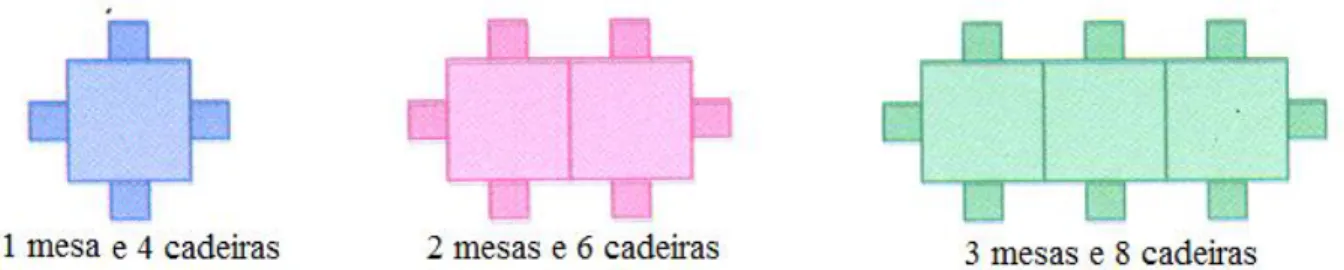
Figura 10: Sequência de mesas e cadeiras. Fonte: Matemática em Cena, 8º ano do Ensino Fundamental, página 57. ... 95
Figure 11: Primeiro slide apresentado à turma. ... 96
Figure 12: Segundo slide apresentado à turma. ... 97
Figure 13: Terceiro slide apresentado à turma. ... 97
Figure 14: Ordem de contagem das cadeiras. ... 98
Figure 15: Quarto slide apresentado à turma. ... 98
Figure 16: Quinto slide apresentado à turma ... 99
Figure 17: Sexto slide apresentado à turma. ... 100
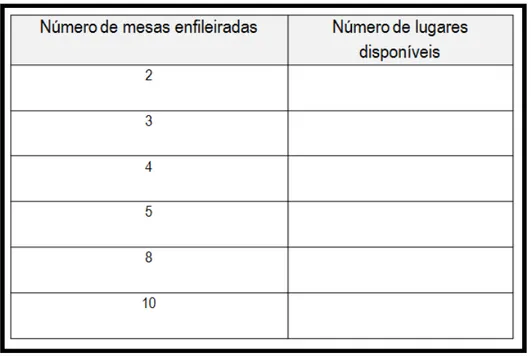
Figure 18: Tabela preenchida até o número de 5 mesas enfileiradas. ... 101
Figura 20: Esquema representativo da formação da sequência de 3 quadrados. ... 124
Figura 21: Termos utilizados para identificar cada face exposta do primeiro cubo. ... 145
Figura 22: Acrescentando o terceiro cubo. ... 148
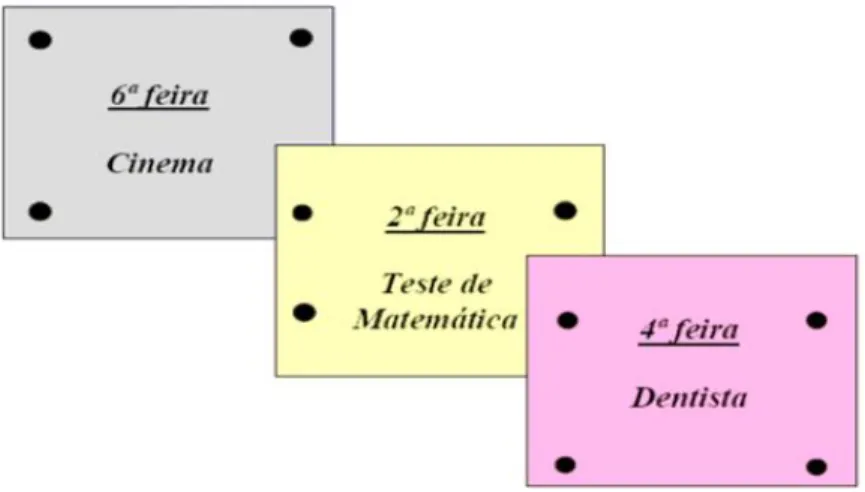
Figure 23: Exemplo de um lembrete afixado. ... 164
Figura 24: Ímãs comuns a mais de um lembrete. ... 165
Figure 25: Esquema representativo dos gestos durante contagem dos pontinhos de cola necessários para afixar 2 lembretes. ... 166
Figure 26: Disposição dos ímãs nos dois primeiros lembretes antes de adicionar o terceiro lembrete. ... 167
Figure 27: Relação entre as respostas da dupla 5 às questões 1 e 2 da tarefa IV. ... 171
Figura 28: Interpretação da reposta apresentada pela dupla 2 para a segunda questão da tarefa IV. ... 172
Figure 29: Possível regularidade percebida pelos alunos A6 e A12 na análise da sequência trabalhada na tarefa V. ... 177
Figure 30: Tabela apresentada no sexto slide e preenchida coletivamente pela turma. ... 179
Figure 31: Possível visualização da figura das mesas enfileiradas pelo aluno A10. ... 183
Figure 32: Registro da dupla 1 na segunda questão da tarefa V escrita. ... 184
Figure 33: Interpretação da resposta da dupla 1 para a quinta questão da tarefa V escrita. ... 189
LISTA DE IMAGENS
Imagem 1: Trecho transparência do trio 3. ... 70
Imagem 2: Registro em transparência trio 1. ... 73
Imagem 3: Modelo de canudo utilizado na confecção dos triângulos. ... 76
Imagem 4: Sugestão de encaixe dos canudos para montagem dos triângulos. ... 76
Imagem 5: Alunos encaixando canudos para confecção dos triângulos. ... 77
Imagem 6: Alunos mostrando um triângulo construído com 9 canudos. ... 77
Imagem 7: Tabela e registros da dupla 4 na atividade II. ... 87
Imagem 8: Sequência de lembretes do aluno A10. ... 92
Imagem 9: Sequência de lembretes da aluna A2. ... 93
Imagem 10: Registro dupla 1 na segunda questão da tarefa IV escrita. ... 104
Imagem 11: Esquema apresentado na transparência da dupla 4 para representar a gênese da sequência. ... 115
Imagem 12: Trecho da transparência produzida pelo trio 2. ... 122
Imagem 13: Trecho da transparência produzida pelo trio 2. ... 122
Imagem 14: Trecho da transparência produzida pela dupla 3. ... 125
Imagem 15: Resposta da dupla 6 à questão 4 da tarefa II escrita. ... 139
Imagem 16: Resposta da dupla 7 à questão 4 da tarefa II escrita. ... 139
Imagem 17: Resposta da dupla 4 à questão 4 da tarefa II escrita. ... 139
Imagem 18: Resposta da dupla 8 à questão 4 da tarefa II escrita. ... 140
Imagem 19: Resposta da dupla 1 à questão 4 da tarefa II escrita. ... 141
Imagem 20: Resposta da dupla 2 à questão 4 da tarefa II escrita. ... 141
Imagem 21: Registro da dupla 4 na segunda questão da atividade II. ... 157
Imagem 23: Imagem utilizada pela dupla 2 para representar o número de lembretes, na questão
2. ... 172
Imagem 24: Resposta da dupla 3 à questão 3 da tarefa V escrita. ... 186
Imagem 25: Resposta da dupla 1 à questão 3 da tarefa V escrita. ... 186
Imagem 26: Resposta da dupla 4 à questão 3 da tarefa V escrita. ... 186
Imagem 27: Resposta dupla 1 para a quinta questão da atividade IV. ... 188
Imagem 28: Resolução da dupla 4 para a quarta questão da atividade IV. ... 191
Imagem 29: Resolução da dupla 2 para a quarta questão da atividade IV. ... 193
Imagem 30: Resolução da dupla 5 para a quarta questão da atividade IV. ... 193
Imagem 31: Resolução aluna A6 na primeira questão da tarefa VI. ... 196
Imagem 32: Resolução aluno A10 na primeira questão da tarefa VI. ... 197
Imagem 33: Tabela e esquema da resolução da aluna A13 na atividade V. ... 197
LISTA DE TABELAS
Tabela 1: Respostas dos grupos à segunda questão da tarefa V escrita. ... 104
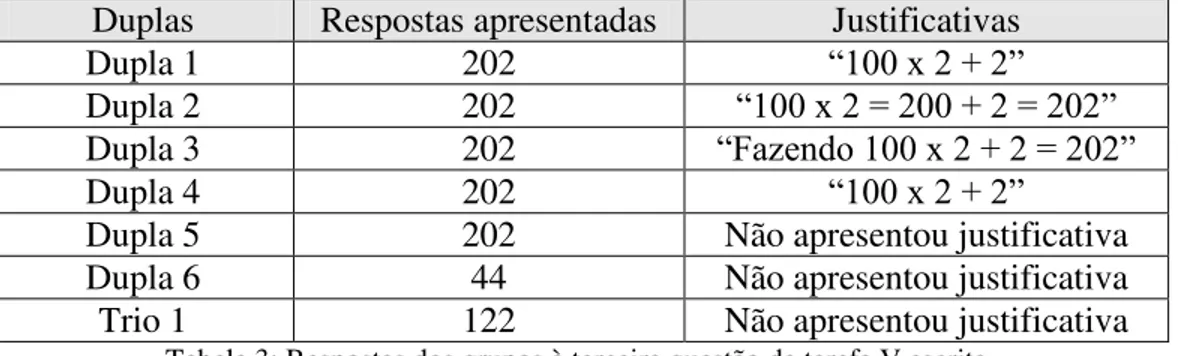
Tabela 2: Respostas dos grupos à terceira questão da tarefa V escrita. ... 105
Tabela 3: Questão da tarefa VI escrita. ... 107
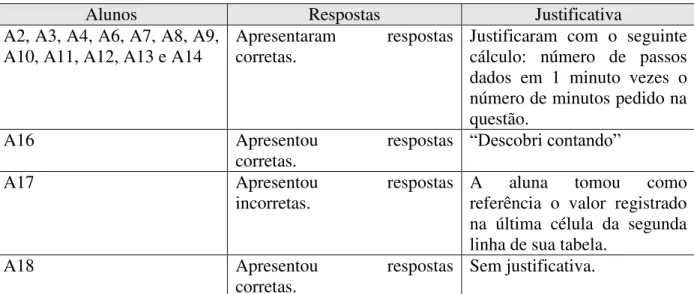
Tabela 4: Desempenho dos alunos para os itens “a”, “b” e “c” da tarefa VI. ... 108
Tabela 5: Respostas dos grupos para o item “b” da Tarefa 4. ... 113
Tabela 6: Respostas das duplas 1 e 3 e dos trios 2 e 3 para os itens “d” e “e” da Tarefa 4. ... 117
Tabela 7: Respostas da dupla 4 para os itens “d” e “e” da Tarefa 4. ... 118
Tabela 8: Respostas da dupla 2 e do trio 1 para os itens “d” e “e” da Tarefa 4. ... 119
Tabela 9: Respostas dos grupos para o item “f” da Tarefa 4. ... 120
Tabela 10: Respostas dos grupos para o item “g” da tarefa 4. ... 129
Tabela 11: Respostas e justificativas dos grupos para primeira e segunda questões da tarefa 2. ... 134
Tabela 12: Respostas das duplas 4, 5 e 8 para a questão 3 da segunda tarefa. ... 135
Tabela 13: Respostas das duplas 6 e 7 para a questão 3 da segunda tarefa. ... 136
Tabela 14: Respostas das duplas 1, 2 e 3 para a questão 3 da segunda tarefa. ... 137
Tabela 15: Respostas das duplas 2, 3, 6, 7 e 8 à primeira questão da tarefa III escrita. ... 157
Tabela 16: Respostas das duplas 1 e 5 à primeira questão da tarefa III escrita. ... 158
Tabela 17: Respostas das duplas 1, 2 e 5 à atividade escrita da tarefa IV. ... 169
Tabela 18: Respostas apresentadas pela dupla 3 às questões 1 e 2 da tarefa IV. ... 173
Tabela 19: Respostas da dupla 4 às questões 1 e 2 da tarefa IV. ... 174
Tabela 20: Respostas do trio 1 às questões 1 e 2 da tarefa IV. ... 175
Tabela 21: Respostas dos grupos à segunda questão da tarefa V escrita. ... 184
Tabela 23: Tabela da tarefa VI escrita. ... 196
SUMÁRIO
INTRODUÇÃO ... 18
CAPÍTULO 1: SITUANDO A PESQUISA NO CAMPO DA EDUCAÇÃO ALGÉBRICA ... 24
1.1. De onde vem essa forma de conceber o ensino da Álgebra? ... 24
1.2. Pensamento Algébrico versus Linguagem Algébrica ... 26
1.3. Dificuldades dos alunos que se iniciam em Álgebra ... 30
1.4. O uso e o significado das letras ... 34
CAPÍTULO 2: EM BUSCA DE UM OLHAR TEÓRICO SOBRE O PENSAMENTO ALGÉBRICO: A TEORIA DE RADFORD ... 37
2.1. Pensamento e Pensamento Algébrico ... 37
2.2. Objetificação do Conhecimento ... 39
2.3. Generalizações ... 44
2.4. Gênese da Formação: apreendendo e generalizando uma semelhança local ... 49
CAPÍTULO 3: METODOLOGIA ... 56
3.1. Contexto e participantes ... 58
3.2. Procedimentos ... 60
3.2.1. Dinâmica dos encontros ... 61
3.2.2. Coleta de dados ... 62
CAPÍTULO 4: O DESENVOLVIMENTO DA PROPOSTA DE ENSINO ... 64
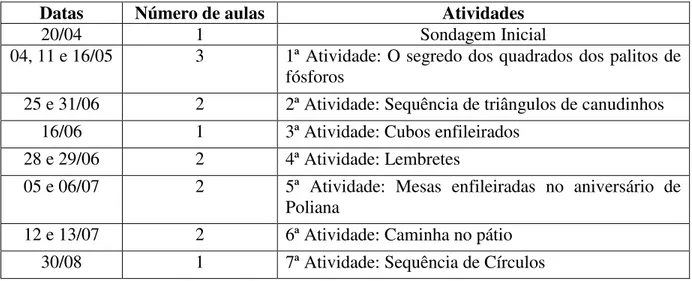
4.1. Sondagem inicial ... 64
4.2. Tarefa I: Descobrindo o segredo dos quadrados de palitos de fósforos! ... 67
4.2: Tarefa II: Triângulos com canudos ... 74
4.3. Tarefa III: Cubos enfileirados ... 79
4.4. Tarefa IV: Lembretes ... 88
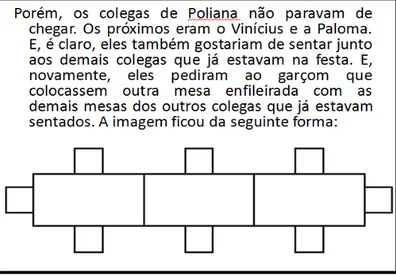
4.5. Tarefa V: Mesas enfileiradas no aniversário de Poliana ... 95
CAPÍTULO 5: ANÁLISE DE DADOS ... 112
5.1. Tarefa I: Descobrindo o segredo dos quadrados de ... 112
5.2. Tarefa II: Triângulos com Canudos ... 132
5.3. Tarefa III: Cubos enfileirados ... 142
5.4. Tarefa IV: Lembretes ... 163
5.5. Tarefa V: Mesas enfileiradas no aniversário de Poliana ... 176
5.6. Tarefa VI: Caminhada no pátio! ... 195
5.7. A título de síntese ... 200
CONSIDERAÇÕES FINAIS ... 202
REFERÊNCIAS BIBLIOGRÁFICAS ... 208
INTRODUÇÃO
Em nossa experiência docente, principalmente com alunos do 8º ano do Ensino Fundamental, pudemos verificar, mais de uma vez, o que já percebíamos desde o tempo de estudante: os alunos apresentam grande dificuldade no estudo da Álgebra e, em particular, na resolução de problemas que envolvem uma tradução da linguagem escrita corrente para a linguagem algébrica.
Trabalhando com Equações de 1º Grau ou Sistemas de Equações do 1º Grau em nossas classes, presenciamos comentários de alunos no sentido de que não conseguem ‘interpretar’ enunciados e resolver ‘problemas’. Porém, o que mais nos inquieta é o fato de que alguns desses alunos assumem enfaticamente que, por mais que se esforcem, não sabem e nunca vão aprender a resolver esse tipo de exercício.
Diante desse quadro, deparamo-nos também com nossa dificuldade como professoras: como ensinar Álgebra de modo que os alunos compreendam os conceitos envolvidos e construam sentido para os mesmos? Mais especificamente, como ensinar aos alunos a traduzir uma sentença escrita em linguagem natural para a linguagem algébrica?
Em busca de respostas para nossas indagações, recorremos à literatura e encontramos estudos, como por exemplo, Lochhead e Mestre (1995), André e Câmara dos Santos (2008), Almeida e Araújo (2010) e André (2011) que destacam a dificuldade dos alunos em resolver problemas que envolvem a “tradução” da linguagem natural para a linguagem algébrica. Em especial, Jacomelli (2006) chama a atenção para a importância de o aluno ser capaz de estabelecer relações entre diferentes tipos de representações do conhecimento matemático. Nas palavras da autora, ‘é dever do aluno, ao descrever, representar, apresentar e argumentar sobre os resultados obtidos, transitar em diferentes tipos de representação como, por exemplo, as representações em linguagem natural e em linguagem algébrica’ (JACOMELLI, 2006, p. 24).
o aluno consegue fazer tratamentos em diferentes registros de representação de um mesmo objeto matemático, entretanto não são capazes de realizar as conversões necessárias para apreensão deste mesmo objeto. Em outras palavras, essa constatação parece apontar que os alunos apresentam dificuldade em ler um problema posto em linguagem corrente e depois traduzir para a linguagem algébrica, através do uso de equações ou expressões algébricas, por exemplo (ANDRÉ E CÂMARA DOS SANTOS, 2008, p. 3). André e Câmara dos Santos (2008) e André (2011) destacam a dificuldade dos alunos em equacionar problemas ao fazer a transição da linguagem natural para a linguagem algébrica. Segundo tais autores, muitas vezes, os estudantes não resolvem um problema por não conseguirem relacionar os dados do enunciado de forma a encontrar uma equação algébrica para representar determinada situação.
Em vista disso, nosso interesse na presente pesquisa inicialmente esteve voltado para o ensino e a aprendizagem de problemas algébricos para alunos iniciantes no estudo da Álgebra. Desenvolver o pensamento algébrico e a linguagem algébrica desses estudantes passou a ser nossa meta. Assim, primeiramente, buscamos entender quais são os principais problemas encontrados no ensino e na aprendizagem da Álgebra.
A partir de nossas leituras, pudemos confirmar que, há décadas, o ensino da Álgebra ocupa um espaço importante nos currículos e textos escolares brasileiros e de inúmeros outros países. Segundo Ponte (2005, p. 36), “na maioria dos países, a Álgebra é um tema fundamental do currículo da Matemática escolar. Quem não tiver uma capacidade razoável de entender a sua linguagem abstrata e de a usar na resolução dos mais diferentes problemas e situações está seriamente limitado na sua competência matemática”.
De acordo com Fiorentini, Miorim e Miguel (1992), na década de 90 a Álgebra ocupava um lugar privilegiado nas escolas e nos livros didáticos. Porém, não raras vezes, os alunos apresentavam dificuldades para compreendê-la e aplicá-la em contextos que exigem habilidades além das manipulações de regras e algoritmos. Para esses autores, apesar da Álgebra ocupar lugar de destaque nos currículos, nas escolas e nos livros didáticos, parecia ainda não existir reflexões críticas dos educadores sobre seu ensino.
pesquisas recentes sobre ensino e aprendizagem da Álgebra e nos currículos escolares atuais. Ao analisar quantitativamente a produção brasileira de pesquisas relativas ao ensino e à aprendizagem das três áreas da Matemática (Aritmética, Álgebra e Geometria), Fiorentini, Miorim e Miguel (1992, p. 39) observaram que “dentre as mais de 150 teses e dissertações de mestrado ou doutorado produzidas no Brasil entre 1972 e 1990, tendo como objeto de pesquisa a educação matemática, 9 tem como preocupação básica o ensino da Aritmética, 8 o ensino de Geometria e nenhuma o ensino da Álgebra Elementar”.
É inegável que a Álgebra já tinha um lugar de destaque entre as áreas da Matemática. Contudo, poucas eram as reflexões críticas a respeito de seu ensino. Não se percebia a necessidade de renovações que pudesse dar ao ensino desse conteúdo novas direções e significações.
Hoje encontramos uma situação um pouco diferente. Ao realizar uma busca no Banco de Teses da CAPES (24/08/2010), utilizando os termos “ensino”, “aprendizagem” e “álgebra”, localizamos 151 trabalhos, entre dissertações de mestrados e teses de doutorado. Contudo, lendo os resumos, verificamos que apenas 40 desses 151 trabalhos tratam do ensino e/ou da aprendizagem da Álgebra abordada no Ensino Fundamental e Médio. As demais pesquisas tratam do ensino e/ou da aprendizagem da Álgebra ou Álgebra Linear em cursos de Engenharia ou afins.
Observamos que, apesar de termos encontrado uma grande quantidade de trabalhos voltados para o ensino-aprendizagem da Álgebra no Ensino Fundamental, nenhum deles tem como tema central de estudo problemas algébricos e a tradução da linguagem escrita corrente para a linguagem algébrica. A resolução de problemas, quando abordada em alguns trabalhos, foi utilizada como instrumento para a apropriação de conceitos algébricos, e, aparentemente, não houve, em nenhuma das pesquisas, uma preocupação específica e centralizada na mudança de representação da linguagem escrita corrente para a linguagem algébrica.
diversos campos da matemática.
Nesse sentido, Ayarza et al (2007, p. 82) criticam:
(...) os professores ensinam a álgebra inicial seguindo uma tradição centrada na manipulação mecânica com símbolos. Tipicamente os alunos aprendem a operar expressões algébricas e resolver equações de primeiro grau, sem que estas tarefas tenham significação para eles ou estejam vinculadas a problemas de contexto real, ou relacionadas com processos de modelação ou sirvam de aproximação a formas de pensamento matemático de tipo indutivo,
argumentativo, conjectural ou demonstrativo1 (tradução livre das autoras).
Nossa experiência como docente corrobora essas ideias. A ênfase na manipulação dos símbolos algébricos sem uma construção de sentido para os mesmos, não permite que a maioria dos alunos apreenda seu valor e cria obstáculos inclusive para a aprendizagem do tema.
Dessa forma, reflexões levaram-nos ao questionamento acerca de como é tratado o conhecimento algébrico em nossas classes e de como os estudantes estão concebendo esse conhecimento matemático.
Em vista disso, após nossas leituras e estudos, levantamos a hipótese de que uma das possíveis causas dos alunos apresentarem tantas dificuldades na mudança da representação de uma sentença escrita na linguagem corrente para a linguagem algébrica repousa no fato do ensino da Álgebra, principalmente nos anos iniciais, estar muito voltado para uma abordagem ligada à linguagem simbólica e sua manipulação, alheia à construção de sentido para tal linguagem e ao desenvolvimento do pensamento algébrico.
Portanto, decidimos, a partir de tal trabalho, construir e aplicar uma proposta de ensino, cujo foco fosse o desenvolvimento do pensamento algébrico em alunos iniciantes no estudo da Álgebra e a construção de uma linguagem simbólica específica para a manifestação de tal pensamento.
Elaboramos a proposta e a desenvolvemos em uma turma do 6º ano do Ensino Fundamental de uma escola da rede particular da cidade de Belo Horizonte (MG). A princípio, gostaríamos de investigar as contribuições que essa proposta traria para a habilidade dos alunos em ler e interpretar uma sentença escrita em linguagem corrente e transcrevê-la para
linguagem algébrica padrão. Porém, no decorrer da aplicação das tarefas, verificamos que esse processo se dava de modo muito mais lento do que esperávamos. Nesse sentido, concordamos que, em uma pesquisa de Mestrado, não dispúnhamos de tempo suficiente para que os alunos atingissem a familiaridade necessária com a linguagem algébrica a ponto de utilizá-la para descrever situações escritas na linguagem corrente.
Por conseguinte, decidimos voltar nosso olhar para o desenvolvimento do conhecimento algébrico em uma turma do 6º ano do Ensino Fundamental, buscando compreender as distintas estratégias construídas pelos alunos para expressar a indeterminação, a generalização e primeiras tentativas de utilizar uma linguagem simbólica.
Imersas no processo de desenvolvimento dos alunos, ansiamos responder à seguinte questão de investigação: que contribuições uma proposta de ensino baseada na percepção e generalização de padrões e sequências pode trazer para o desenvolvimento do pensamento algébrico e da linguagem algébrica em alunos que se iniciam no estudo da Álgebra?
O presente texto está organizado em cinco capítulos. Nos dois primeiros, apresentamos uma revisão da literatura e a fundamentação teórica. Tais ideias forneceram o embasamento necessário para a construção das tarefas desenvolvidas com os alunos e para a análise dos dados. O capítulo 3 contempla nossas opções metodológicas, bem como contexto no qual se dá o estudo e os participantes. Em seguida, no capítulo 4 descrevemos cuidadosamente o processo vivido, procurando evidenciar a dinâmica de realização das tarefas, as impressões e reações dos alunos durante o trabalho e os resultados apresentados. A análise dos dados é tratada no Capítulo 5. Ela se dá, principalmente, à luz da teoria de Radford (2009, 2010a, 2010b e 2011), especialmente no que diz respeito ao pensamento algébrico, processo de objetificação, perspectiva semiótica-cultural, processos de generalização de padrões e sequências e linguagem algébrica. Para finalizar, tecemos algumas considerações acerca de todo o trabalho desenvolvido. Referências e Anexos complementam nossa dissertação.
CAPÍTULO 1: SITUANDO A PESQUISA NO CAMPO DA EDUCAÇÃO ALGÉBRICA
Neste capítulo, contextualizamos nossa pesquisa no campo da Educação Algébrica. Para construir e implementar nossa proposta de ensino, buscamos entender, primeiramente, o motivo do caráter mecânico ao qual está vinculado o ensino da Álgebra hoje, a fim de encontrar alternativas para superar a abordagem simbolista. Apresentamos algumas reflexões em torno do desenvolvimento do pensamento algébrico vinculado à linguagem algébrica, de forma a evidenciar nosso ponto de vista acerca de tal assunto. Procuramos também, a partir da literatura, conhecer as principais dificuldades que os alunos iniciantes no estudo da Álgebra enfrentam e os diferentes papéis que a letra pode assumir nos diversos contextos algébricos em que ela está empregada, procurando definir nosso olhar teórico para uma posterior análise dos dados da pesquisa.
1.1. De onde vem essa forma de conceber o ensino da Álgebra?
Como já citado anteriormente, encontramos ainda hoje no cenário da Educação Algébrica, tanto nas pesquisas, quanto nos textos e currículos escolares, um ensino fortemente voltado para a manipulação simbólica em detrimento da construção de significado para tal manipulação e para a linguagem algébrica.
A questão do simbolismo em Álgebra atravessa séculos.
Dado o modo como foi ensinada durante séculos, a Álgebra é usualmente vista como tratando de regras de transformação de expressões (monômios, polinômios, frações algébricas, expressões com radicais) e processos de resolução de equações e sistemas de equações (PONTE, 2005, p. 2).
Segundo Gil (2008, p.2), “desde o início do estudo da Álgebra até o início da década de 60, quando se inicia o Movimento da Matemática Moderna, o seu ensino era predominantemente de caráter mecânico e reprodutivo, sem clareza alguma”. Dessa forma, os problemas atualmente enfrentados no ensino da Álgebra podem ser reflexos das etapas históricas de sua inserção nos currículos escolares. Faz-se necessário, então, um estudo, mesmo que breve, sobre a sua história no currículo brasileiro para que se compreenda melhor o que ocorre hoje.
pelo transformismo algébrico era o suficiente para que o aluno fosse capaz de resolver problemas. Os manuais didáticos de Álgebra da primeira metade do século XX, segundo Fiorentini, Miorim e Miguel (1993), conservavam a tradição de inúmeros textos franceses e ingleses do século XVIII, que davam ênfase ao uso de regras e algoritmos, devido, em boa parte, à incerteza que, na época, perdurava em relação aos seus fundamentos. Tais autores nomeiam essa concepção de linguístico-pragmática.
Com o Movimento da Matemática Moderna surge uma preocupação em superar esse ensino mecânico e a Álgebra passa a ter lugar de destaque, tornando-se o elemento unificador dos campos da Matemática.
Com esse movimento, veio também uma nova concepção para a educação algébrica, nomeada por Fiorentini, Miorim e Miguel (1993) de fundamentalista-estrutural, em que o papel da Álgebra é o de fundamentar os vários campos da Matemática escolar. Segundo Gil (2008, p. 3), “acreditava-se que a introdução de propriedades estruturais das operações que justificassem cada passagem presente nos transformismos algébricos capacitaria o aluno a aplicar essas estruturas nos mais diferentes contextos”.
Nesse sentido, a Álgebra envolve um conjunto de ações para as quais é possível produzir significados e estabelecer relações em termos de números e operações, de forma que os alunos, a partir de tarefas guiadas pelo professor, possam construir significado para o seu estudo e consigam aplicar o conhecimento adquirido em contextos diversos.
Com o declínio da Matemática Moderna, os educadores passaram a buscar a Geometria como elemento unificador, enquanto a Álgebra retorna ao papel que ela desempenhava no currículo tradicional, de um estudo introdutório, descontextualizado e estático. Essa concepção de ensino da Álgebra é chamada de fundamentalista-analógica e busca fazer uma síntese entre as duas concepções anteriores à medida que
tenta recuperar o valor instrumental da álgebra e preserva a preocupação fundamentalista, só que não com base nas propriedades estruturais, mas, sim, através do uso de modelos analógicos geométricos (blocos de madeira ou mesmo figuras geométricas) ou físicos (como a balança) que visualizam ou justificam as passagens do transformismo algébrico (FIORENTINI ET AL, 2005, p. 4).
Álgebra sob o aspecto lingüístico e transformista, dando destaque mais à sintaxe da linguagem algébrica do que ao desenvolvimento do pensamento algébrico e seu processo de significação.
Gil (2008), Ponte (2005), Fiorentini et al (2005), entre outros, concordam que esse excesso no estudo de regras algorítmicas trata-se, claramente, de uma visão redutora da Álgebra que desvaloriza muitos aspectos importantes desta área da Matemática.
Dessa forma, não cabe classificar a Álgebra como a área da Matemática que trata apenas de técnicas manipulatórias com símbolos. Usiskin (1995) afirma que a Álgebra é a “área-chave” de estudo da Matemática na escola secundária2, dado que ela fornece meios para a caracterização e a compreensão das estruturas matemáticas. Fiorentini et al (2005) destaca que a Álgebra é “uma forma específica de pensamento e de leitura do mundo”.
De fato, concordamos com todos os autores citados no sentido de que o ensino de uma linguagem algébrica já constituída, em detrimento da construção do pensamento juntamente com uma linguagem para expressão desse pensamento, deve ser repensado e reformulado. Nesse sentido, continuaremos no tópico a seguir abordando a relação entre pensamento e linguagem algébrica e sua importância para o desenvolvimento dos conceitos algébricos em alunos que se encontram na fase inicial desse estudo.
1.2. Pensamento Algébrico versus Linguagem Algébrica
De acordo com Fiorentini, Miorim e Miguel (1993), a Educação Algébrica pautava-se na ideia de que é a partir da manipulação simbólica que o pensamento algébrico se manifesta e desenvolve. Se pensarmos nessa vertente, concluímos que existe uma relação de subordinação do pensamento algébrico à linguagem, de forma a desconsiderar ‘o fato de que, tanto no plano histórico quanto no pedagógico, a linguagem é, pelo menos a princípio, a expressão de um pensamento’ (Fiorentini, Miorim e Miguel, 1993, p. 85).
De fato, acreditamos que o pensamento algébrico não depende de uma linguagem estritamente simbólico-formal para sua manifestação. Em uma análise histórica da evolução da linguagem algébrica, percebemos que não existe uma única forma de se expressar o pensamento algébrico.
Segundo Fiorentini, Miorim e Miguel (1993), na Álgebra dos egípcios, dos babilônicos e dos gregos pré-diofantinos, o pensamento era expresso a partir da linguagem
corrente. Não se fazia uso de símbolos nem de abreviações para demonstrar os passos relativos aos processos operatórios sobre números ou equações. Essa primeira fase histórica do desenvolvimento da linguagem algébrica foi chamada retórica ou verbal.
Já no século III, a fase sincopada da linguagem algébrica surgiu com Diofanto de Alexandria que utilizou uma forma mais concisa e abreviada para escrever suas equações e, pela primeira vez, utilizou uma letra (no caso, a letra “sigma” do alfabeto grego) para representar uma incógnita. Essa forma sincopada de expressar o pensamento algébrico foi, mais tarde, desenvolvida por vários povos, entre eles os hindus, árabes e italianos.
A fase simbólica, que é como encontramos a manifestação do pensamento algébrico avançado hoje, corresponde ao uso somente de símbolos, sem recorrer ao uso de palavras. Viète (1540-1603), embora utilizasse um estilo sincopado, foi o principal responsável pela introdução de vários símbolos na Álgebra. Porém, quem consolidou o uso da linguagem simbólica foi Descartes (1596-1650), utilizando as últimas letras do alfabeto (x, y, z...) como variáveis e as primeiras (a, b, c...) como quantidades fixas.
Dessa forma, observando a evolução histórica da linguagem algébrica, percebemos que não é só através da linguagem simbólica e específica para esse fim que é possível expressar o pensamento algébrico. ‘Ele pode expressar-se através da linguagem natural, através da linguagem aritmética, através da linguagem geométrica (...)’ (FIORENTINI, MIORIM E MIGUEL, p. 88, 1993).
E, assim como em Fiorentini, Miorim e Miguel (1993) e Fiorentini el al (2005), acreditamos que a compreensão da linguagem possa potencializar e promover o desenvolvimento do pensamento e vice-versa.
Percebemos, então, que um dos grandes objetivos ao ensinar Álgebra nas escolas é desenvolver nos alunos o pensamento algébrico que vai muito além da simples capacidade de manipular símbolos. O pensamento algébrico inclui a capacidade de lidar com o cálculo algébrico, com as estruturas matemáticas e saber aplicar tais conhecimentos na interpretação e resolução de problemas matemáticos ou de outros domínios.
Segundo Fiorentini, Miorim e Miguel (1993), alguns dos elementos que caracterizam o pensamento algébrico são a percepção de aspectos invariantes em contraste de outros que variam, as tentativas de expressar ou explicar a estrutura de uma situação problema e a presença do processo de generalização.
Ponte (2005, p. 37), apoiando-se no NCTM3 de 2000, afirma que o pensamento algébrico diz respeito aos quatro tópicos abaixo:
Compreender padrões, relações e funções (Estudo das estruturas);
Representar e analisar situações matemáticas e estruturas, usando símbolos algébricos (Simbolização);
Usar modelos matemáticos para representar e compreender relações quantitativas; Analisar mudança em diversas situações (Estudo da variação).
Entretanto, ao analisar o desenvolvimento de alunos imersos no trabalho com atividades que podem propiciar o desenvolvimento do pensamento algébrico, devemos estar atentos não apenas para o aparecimento dos itens caracterizadores do pensamento algébrico acima. Faz-se necessário também estudar os processos e os recursos aos quais os estudantes recorrem para atingir tais elementos, como, por exemplo, investigar de que forma o aluno compreende um padrão e o generaliza.
Nessa perspectiva, esperamos que o aluno que desenvolve o pensamento algébrico seja capaz de entender não só os algoritmos, mas, também, o sentido do símbolo, ou seja, desenvolva a capacidade de interpretar e usar esses símbolos nos diversos domínios da Matemática. Nesse tipo de pensamento, o estudante voltará sua atenção não só para as ‘letras’ empregadas nas expressões algébricas, mas também para as relações existentes entre elas, raciocinando e manipulando essas relações de modo geral e abstrato tanto quanto necessário.
Consideramos, assim, que as técnicas algorítmicas são parte do pensamento algébrico. No entanto, esse pensamento inclui igualmente a capacidade de lidar e aplicar as estruturas matemáticas de modo geral na interpretação e resolução de problemas e, até mesmo, em outros domínios.
Contudo, Ponte (2005) destaca que, apesar de na Educação Matemática não faltarem críticas ao simbolismo, não se pode negar que ele é parte essencial da Matemática. Em Álgebra, o uso dos símbolos tem o poder de aglutinar as ideia ideias concebidas
operacionalmente em agregados compactos, tornando a informação mais fácil de compreender e manipular.
Para Fiorentini et al (2005, p.6),
não podemos deixar de reconhecer que o pensamento algébrico se potencializa à medida que, gradativamente, o estudante desenvolve uma linguagem mais apropriada para ele. Assim, se de um lado, a introdução precoce e sem suporte empírico a uma linguagem simbólica e abstrata pode funcionar como obstáculo ao desenvolvimento do pensamento algébrico, de outro, o menosprezo ou recusa ao modo simbólico e formal de pensar algebricamente pode representar também um freio ao pleno desenvolvimento do pensamento algébrico.
Nesse sentido, se priorizamos a manipulação dos símbolos e perdemos de vista seu significado, corremos o risco de cair no formalismo sem sentido.
Diante desse impasse, encontramo-nos frente a um problema complicado, visto que o simbolismo acarreta um grande perigo para o processo de ensino-aprendizagem da Álgebra na escola básica. Segundo Araújo (2009), a questão da simbologia e de como ela é introduzida na sala de aula nos direciona ao papel do professor, pois, ao longo do processo de aprendizagem, o aluno poderá construir diferentes convicções sobre a Álgebra que poderão influenciar positiva ou negativamente seu sucesso.
Dessa forma, uma possibilidade seria ‘introduzir o estudo da Álgebra em contextos significativos, num quadro de trabalho que os convença de forma natural sobre a importância e o poder matemático da simbolização e da formalização’ (PONTE, 2005).
Essa capacidade de interpretar e usar de forma criativa os símbolos matemáticos pode ser desenvolvida a partir de tarefas que exijam do aluno competência para lidar com quantidades indeterminadas e variáveis em situações que envolvam processos de generalização – como no caso do trabalho com padrões e sequências. Nessa proposta, os estudantes têm liberdade de, inicialmente, recorrer a recursos que surgem naturalmente no contexto de cada tarefa (gestos, falas), para se comunicar e expressar uma indeterminação, uma incógnita, uma variável – o que, até então, não apresentava uma nomeação em seu ‘vocabulário’ matemático.
Dessa forma, a linguagem algébrica pode ser explorada a partir da necessidade dos alunos em expressar suas descobertas, diminuindo a ênfase dada ao simbolismo, ao menos inicialmente, a fim de nos preocupar em construir sentido para os símbolos.
Porém, para desenvolver nossa proposta de ensino baseada nas considerações acima, além da preocupação com o desenvolvimento do pensamento algébrico e com a construção de uma linguagem para expressar esse pensamento, buscamos estar cientes, a partir da literatura, de quais são os principais entraves e obstáculos enfrentados pelos alunos que são introduzidos no estudo da Álgebra.
1.3. Dificuldades dos alunos que se iniciam em Álgebra
De acordo com Socas et al (1996, p.91), “no ensino-aprendizagem da álgebra, como em toda a matemática, nos encontramos com uma grande variedade de dificuldades”. Entre elas, os autores comentam, primeiramente, as dificuldades relacionadas à natureza da Álgebra e aquelas que surgem dos processos de desenvolvimento cognitivo dos alunos e da estrutura e organização de suas experiências.
A segunda fonte de dificuldade apontada pelos autores diz respeito à natureza do currículo, à organização das aulas e aos métodos de ensino usados. Como já foi dito, o que muitas vezes ocorre é uma fixação exagerada nas manipulações mecânicas com símbolos, produzindo uma impressão muito forte de inutilidade de tal conteúdo.
Nesse sentido, consideramos que o sentido do símbolo e a capacidade de interpretá-los e usá-los de forma criativa na descrição de situação e resolução de problemas também constituem elementos fundamentais no desenvolvimento do conhecimento algébrico do aluno.
Por último, Socas et al (1996) citam as dificuldades devido a atitudes afetivas e não racionais dos alunos que, comumente, veem a Álgebra veem como uma matéria difícil.
1º) O foco da atividade algébrica e a natureza das “respostas”. A autora traz nesse tópico a diferença entre o foco de uma atividade aritmética e o foco de uma atividade algébrica.
Em aritmética, o foco da atividade é encontrar determinadas respostas numéricas particulares. Na álgebra, porém, é diferente. Na álgebra o foco é estabelecer procedimentos e relações e expressá-los numa forma simplificada geral. Uma razão para se estabelecerem essas afirmações gerais é usá-las como ‘regras de procedimento’ para a resolução de problemas adequados e, então, achar respostas numéricas, mas o foco imediato é o estabelecimento, a expressão e a manipulação da própria afirmação geral (BOOTH, 1995, p. 24). De acordo com nossa experiência docente, percebemos que, muitas vezes, os alunos não aceitam uma expressão algébrica simplificada como resposta final de um exercício. Para eles, apenas o estabelecimento de uma expressão e manipulação da afirmação geral não são suficientes e acreditam que devem apresentar uma resposta numérica.
2º) O uso da notação e da convenção em álgebra. De acordo com Booth (1995), em Aritmética, os símbolos da soma, subtração, multiplicação, divisão e igualdade são interpretados, geralmente, como ações a serem efetuadas, de maneira que: “+” significa efetivamente realizar uma soma e “=” encontrar um resultado. Já na Álgebra, a ideia de que o símbolo da adição pode ser tanto a indicação de uma soma como a ação, ou de que o símbolo de igualdade pode representar uma relação de equivalência e não uma resposta propriamente dita pode não ser percebida de imediato pelos alunos.
Tinoco et al (2008) comentam sobre a noção de equivalência representada pelo sinal de igualdade na Álgebra:
O aluno com experiência apenas em aritmética considera, muitas vezes, o sinal de igual como um símbolo unidirecional, que precede uma resposta numérica, um símbolo para ‘escreva a resposta’. [...] Embora seja essencial nas atividades algébricas, os alunos não se apropriam com facilidade da ideia do sinal de igualdade, visto como indicador de uma equivalência entre duas expressões, mesmo que numéricas (p. 4).
Ponte reforça a ideia da confusão que os alunos fazem ao trabalhar com os símbolos operatórios.
Outra dificuldade, ainda, é compreender as mudanças de significado, na Aritmética e na Álgebra, dos símbolos + e =, bem como das convenções adotadas; assim, em Aritmética, 23 tem um significado aditivo (20 + 3),
enquanto que em Álgebra 2x tem um significado multiplicativo (2 x x); em
Aritmética 3 + 5 significa uma “operação para fazer” (cujo resultado é 8),
mas em Álgebra x + 3 representa uma unidade irredutível (enquanto não se
Essas dificuldades dos alunos são compreensíveis devido à complexidade e à sutileza da linguagem algébrica. Segundo Booth (1995), a Álgebra exige uma precisão nos registro de suas afirmações que não é exigida em Aritmética.
Essa precisão, é claro, também é importante na aritmética, mas as consequências de impropriedades nesse aspecto podem ser menores se o aluno sabe o que se pretende e efetua a operação correta, independentemente do que está escrito. Em aritmética faz pouca diferença o aluno escrever 12 : 3 ou 3 : 12, desde que ele efetue corretamente o cálculo. Em álgebra, porém, é crucial a diferença entre p : q e q : p (BOOTH, 1995, p.29).
A esse respeito, vale ressaltar que a autora vê essa ‘falha’ no rigor da escrita durante os estudos da Aritmética como uma falta de atenção nas aulas de matemática por parte dos alunos no que se refere a afirmações verbais e sentenças corretas e precisas da linguagem Matemática.
Alguns alunos acham que a divisão, como a adição, é comutativa. Outros não veem a necessidade de distinguir as duas formas, acreditando que o maior número sempre deverá ser dividido pelo menor. Isso parece decorrer da recomendação bem-intencionada feita pelo professor de matemática, no início do aprendizado da divisão, e da própria experiência dos alunos, pois todos os problemas de divisão encontrados em aritmética elementar, de fato, exigem que o número maior seja dividido pelo menor (p. 29).
Dessa forma, percebemos que o aprendizado da Álgebra está fortemente vinculado ao conhecimento aritmético que o aluno possui e, como citado em Socas et al (1996), às estruturas e organização de suas experiências.
Portanto, um aluno que apresenta dificuldades em Aritmética poderá ter dificuldades para o aprendizado da Álgebra, principalmente no que tange à manipulação simbólica, que exige dos estudantes conhecimento e habilidade nas operações aritméticas.
3º) O significado das letras e das variáveis. A diferença mais flagrante entre a Aritmética e a Álgebra destacada por Booth (1995) está na utilização, nesta última, de letras para indicar valores. Quanto a tal diferença, a autora afirma:
Segundo Ponte (2005), os alunos apresentamdificuldades com o uso de letras para representar variáveis e incógnitas, não conseguindo ver uma letra como representando um número desconhecido e não percebendo o sentido de uma expressão algébrica.
Porém, Booth (1995) e Tinoco et al (2008) concordam que, mesmo quando os alunos interpretam as letras como representantes de números, há uma forte tendência a considerar as letras como valores específicos, únicos e possíveis de serem determinados, como em 3x - 1 = 5, e não como números genéricos ou variáveis, como em 3x + 5. Segundo Tinoco et al (2008), isso se deve ao fato de que, em muitos casos, a primeira e, às vezes, única experiência dos alunos com Álgebra é a partir do estudo das equações
Enfatizamos, então, a importância das diferentes concepções da Álgebra, de acordo com os papéis que a letra pode assumir nos mais variados contextos algébricos, os quais destacaremos adiante. É importante que o aluno perceba que a letra nem sempre tem um valor específico, único e possível de ser determinado. Dessa forma, conhecendo os vários significados que uma letra assume de acordo com o contexto em que está empregada, será mais fácil para o estudante aceitar uma expressão algébrica como resposta de algum exercício ou problema.
4º) Os tipos de relações e métodos usados em Aritmética. A Álgebra não está isolada da Aritmética e, em muitos casos, pode ser encarada como uma “aritmética generalizada”.
Nisso está a fonte das dificuldades. Para compreender a generalização das relações e procedimentos aritméticos é preciso primeiro que tais relações e procedimentos sejam apreendidos dentro do contexto aritmético. Se não forem reconhecidos, ou se os alunos tiverem concepções erradas a respeito deles, seu desempenho em álgebra poderá ser afetado (BOOTH, 1995, p. 33). Neste caso, as dificuldades dos alunos em Álgebra estariam relacionadas a deficiências em Aritmética que não foram corrigidas.
Outro ponto apontado por Booth (1995) é a utilização pelas crianças de métodos informais para resolver problemas em aritmética, o que pode ter implicações negativas na habilidade do aluno para estabelecer afirmações gerais em Álgebra. A autora exemplifica:
Assim, a autora destaca o papel do professor em mostrar ao aluno que o seu método informal de resolução pode ser eficaz em determinados tipos de problema, porém, em problemas que envolvem quantias maiores, o método falhará. Dessa forma, cabe ao docente reconhecer e revelar as limitações do método informal utilizado pelo aluno para que, assim, este possa reconhecer a necessidade de um procedimento mais geral, ou seja, formal.
A partir da análise das principais dificuldades dos alunos que se iniciam no estudo da Álgebra, percebemos a importância dos significados que as letras podem assumir nos diferentes contextos algébricos. Em vista disso, trataremos, em seguida, dos papéis das letras na iniciação em Álgebra e da importância de seu entendimento pelos alunos.
1.4. O uso e o significado das letras
Segundo Socas et al (1996), “o uso das letras como variáveis procede da geometria grega”. A comunicação escrita do conhecimento geométrico fez-se através de figuras que tinham seus pontos nomeados por letras do alfabeto. Porém, de acordo com os autores, o uso das letras dessa forma na geometria não propiciou o nascimento de uma linguagem algorítmica, nem gerou uma formalização das operações.
Como citado anteriormente, em Álgebra, o emprego das letras como variáveis e o passo decisivo para uma notação mais útil foi dado por Viète (1600), quando as letras foram, primeiramente, usadas para indicar números arbitrários e, mais tarde, também para funções arbitrárias. O uso das letras para indicação de magnitudes desconhecidas e variáveis em expressões algébricas, de acordo com Socas et al (1996), é o começo do desenvolvimento de uma linguagem algébrica própria.
Segundo os autores, “na álgebra, aparecem como variáveis expressões de qualquer classe de objetos, o que permite considerar diferentes tipos de álgebra: álgebra de conjuntos, aritmética, álgebra de funções, etc.”. E, como afirma Usiskin (1995), não é fácil definir a Álgebra.
Usiskin (1995) define a Álgebra da escola média como a área da Matemática que está relacionada com a compreensão do significado das letras, chamadas por ele de variáveis4, e com as operações que as envolvem .
4 Apesar de Usiskin (1995) utilizar o termo “variável” para tratar as letras usadas no estudo da Álgebra,
adotaremos o termo “letras” por considerarmos que a palavra “variável” é restrita a uma aplicação das letras em
Dessa forma, de acordo com o papel atribuído às letras, o autor apresenta quatro concepções básicas acerca da Álgebra que, para o presente estudo, consideramos fundamental, já que em cada uma delas “as letras” assumem umcaráter diferente:
1. A álgebra como aritmética generalizada: nessa concepção, as letras são ferramentas para generalização de modelos. Opera-se com letras que seriam números desconhecidos (incógnitas e variáveis).
2. A álgebra como ferramenta de resolução de problemas: nessa concepção, as letras são incógnitas. O procedimento algébrico permite ao indivíduo gerar uma equação, a partir do enunciado do problema.
3. A álgebra como a expressão de relações entre grandezas: neste caso, as letras são “variáveis que variam”. Como, por exemplo, no caso da fórmula da área de um retângulo A = b . h, expressando a relação entre as três grandezas, a área do retângulo, sua base e a altura.
4. A álgebra como estudo das estruturas: essa concepção envolve o estudo de estruturas como anéis, grupos, corpos, entre outros. Neste caso, as letras são símbolos arbitrários, e os alunos tendem a vê-las sem nenhuma referência numérica.
Para fins de nosso estudo, consideraremos as concepções apresentadas por Usiskin (1995), descritas acima, e daremos ênfase à concepção da Álgebra como Aritmética generalizada, visto que nosso trabalho desenvolveu-se com alunos inexperientes no estudo da Álgebra.
Porém, é importante ressaltar que, segundo Gil (2008), entre os estudiosos, não existe um consenso no que se refere à concepção de Álgebra. Existem dúvidas até mesmo em definir tópicos que fazem parte ou não do estudo da Álgebra.
De acordo com Radford (2009), isso não ocorre por acaso. O autor afirma que, dentre os ramos da matemática abordados na escola básica, nenhum é mais ‘assustador’ que a Álgebra. E, se ainda não temos uma resposta concisa e exata para os questionamentos acerca de tal temática, isso se deve à variedade de objetos e processos que estão atrelados a seu estudo.
Entretanto, quanto às discussões e pesquisas realizadas nas décadas de 80 e 90, existiu um consenso no que diz respeito a dois aspectos:
Álgebra lida com objetos de natureza indeterminada, como incógnitas, variáveis e parâmetros. Além disso, em Álgebra, tais objetos são tratados de
maneira analítica. Isso quer dizer que, em Álgebra, você calcula com quantidades desconhecidas (ou seja, você soma, subtrai, divide, etc. com incógnitas e parâmetros) como se você as conhecesse, como se elas fossem
quantidades específicas5 (RADFORD, 2009, p. 3, tradução livre das autoras).
Nesse sentido, percebemos que o pensamento algébrico, além da capacidade de manipulação simbólica, envolve também a capacidade dos estudantes em lidar com o objeto indeterminado, seja ele variável, incógnita ou parâmetro.
Portanto, para analisar a imersão dos alunos em situações que podem propiciar o desenvolvimento do pensamento algébrico e o estudo da Álgebra, precisamos ter claro em nossa mente o que consideramos ser o pensamento algébrico, no sentido de analisar a forma como os alunos envolvem-se nas tarefas, a fim de verificar se eles estão ou não no campo de estudo da Álgebra.
Para tal, utilizamos algumas ideias do pesquisador Luis Radford, principalmente no que diz respeito aos processos que alunos iniciantes no estudo da Álgebra desenvolvem, quando envolvidos em atividade de padrões e sequências. Em vista disso, reservamos o capítulo II para expor, resumidamente, a teoria desse autor.
CAPÍTULO 2: EM BUSCA DE UM OLHAR TEÓRICO SOBRE O PENSAMENTO ALGÉBRICO: A TEORIA DE RADFORD
No presente capítulo, apresentamos resumidamente as principais ideias de Radford (2009, 2010a, 2010b, 2011), referentes a pensamento – mais especificamente pensamento algébrico –, processo de objetificação, perspectiva semiótica-cultural e processos de generalização de padrões e sequências, na busca de uma teoria que nos ampare, posteriormente, na análise dos dados coletados em nossa pesquisa de campo.
2.1. Pensamento e Pensamento Algébrico
Assim como destacamos, Radford também enfatiza em suas pesquisas que a manipulação simbólica é apenas uma parte do vasto campo de estudo da Álgebra e que o pensamento algébrico e o estudo da Álgebra não podem ser reduzidos ao uso das letras.
Nesse sentido, o que o autor defende e mostramos neste trabalho é que existe uma pluralidade de formas semióticas para expressar a ideia algébrica referente a incógnitas, variáveis e parâmetros. De fato,
incógnitas, variáveis e outros objetos algébricos podem ser representados indiretamente, com auxílio de signos. Esses signos podem ser, mas não serão, necessariamente, as letras. Usar letras não equivale a ‘fazer’ álgebra. A história da matemática mostrou claramente que a álgebra também pode ser praticada recorrendo a outros sistemas semióticos’6 (RADFORD, 2010a, p.
39, tradução livre das autoras).
Dessa forma, o autor retira do simbolismo o ‘direito exclusivo’ de designar e expressar uma indeterminação algébrica e afirma que existe uma pluralidade de formas semióticas para esse fim.
Essa diversidade de formas semióticas baseia-se numa perspectiva de pensamento que, segundo o Radford (2009), está diretamente em conflito com a concepção de pensamento que foi defendido na maioria das pesquisas dos anos 90 em Educação Matemática. Nas palavras do autor,
dentro dessa concepção de pensamento, os signos eram muitas vezes
6
(...) unknowns, variables and other algebraic objects can only be represented indirectly, through means of constructions based on signs (see Kant, 1929, p. 579). These signs may be letters, but not necessarily. Using letters does not amount to doing algebra. The history of mathematics clearly shows that algebra can also be
considerados ‘sintomas’ da atividade mental – portanto a distinção entre representações internas e externas. Dentro da psicologia de Vygotsky, a partir da perspectiva semiótica-cultural defendida aqui, a questão da relação entre signos e pensamento é tematizada de um modo diferente. Primeiro, signos são considerados em um sentido amplo, como algo que engloba escrita, bem como termos linguísticos orais, símbolos matemáticos, gestos, etc. Segundo, signos não são considerados como simples indicadores de atividade mental. Pelo contrário, signos são partes constitutivas do pensamento. Mais precisamente, dentro dessa perspectiva semiótica-cultural, o pensamento é
considerado uma atividade reflexiva sensorial mediada por signos e baseada
na corporalidade de ações, gestos e artefatos7 (RADFORD, 2009, p. 4, tradução livre das autoras).
Nesse sentido, para o autor, o pensamento engloba muito mais do que apenas essa natureza “sensorial” da cognição matemática. O pensamento é algo ligado ao contexto e à cultura dentro dos quais ele ocorre. É uma atividade que se desenvolve em um conjunto cultural de práticas visando à construção de significados, bem como a formação de conceitos de natureza ética, política, científica e estética constituídos historicamente.
Em vista disso, o pensamento de uma forma geral, assim como o pensamento matemático em particular, é uma práxis cognitiva histórica mediada por ferramentas, pelos signos e até mesmo pelo nosso corpo. Logo, a partir de uma perspectiva educacional, a densidade histórica de tais práticas que, através dos séculos, vem refinando as formas de ação, reflexão e raciocínio matemático, mostra-se complexa para os estudantes. Tornar-se familiarizado com as práticas sedimentadas em formulações altamente sistematizadas, abstratas e compactas não é uma tarefa trivial para os nossos alunos.
Quando tratamos do desenvolvimento do pensamento e do simbolismo algébrico a situação é ainda pior, pois, segundo Radford (2011, p. 308 e 309, tradução livre das autoras), ‘o pensamento algébrico não surge na ontogenia ao acaso, nem como uma consequência necessária da maturação cognitiva. Para fazer com que o pensamento algébrico apareça e seja
7Within this mental conception of thinking signs were often considered ―symptoms‖ of mental activity —hence
acessível aos estudantes, algumas condições pedagógicas precisam ser criadas’8. Em outras palavras, o estudo da álgebra é algo especificamente escolar, que depende fortemente da intervenção do professor.
Portanto, ao enfatizar a questão da simbologia algébrica, desprovida de um embasamento e de um real entendimento de seu significado pelos estudantes, estamos desconsiderando o fato de que, de acordo com Rardford (2010a), a formação de significados e o uso dos signos, assim como a evolução de algumas notações algébricas, têm suas raízes em um sistema que dependia muito da fala, além de outros recursos semióticos. Em vista disso, nós, professores, temos fortes razões para não ignorar ou menosprezar os momentos que antecedem ou que fazem parte de todo processo de formação e apropriação dos conceitos algébricos pelos nossos alunos, bem como da linguagem que lhes é própria.
2.2. Objetificação do Conhecimento
Ao nascermos, o mundo com o qual nos deparamos constitui-se como um mundo histórico, repleto de objetos concretos e conceituais, os quais vêm sendo desenvolvidos e lapidados através de séculos de atividades cognitivas. Nesse sentido, as formas culturais de raciocínio desenvolvidas e refinadas ao longo de milhares de anos estão longe de serem triviais para os estudantes.
Portanto, para alunos ‘inexperientes’– que nunca trabalharam ou trabalharam pouco com tarefas que envolvam generalizações –, perceber um traço comum (ou uma regularidade) entre os elementos de uma sequência não é algo simples, que acontece de repente ou ao acaso, mas sim, de acordo com Radford (2011), um processo gradual, sustentado por uma observação buscando semelhanças e diferenças entre os termos da sequência a ser trabalhada. Mesmo em atividades simples, existem várias características nas figuras dadas que podem ser consideradas semelhantes, assim como existem outras que podem ser consideradas diferentes.
Como exemplificado por Radford (2010a), em uma atividade aplicada para uma turma de alunos com idade igual a 13 ou 14 anos9, envolvendo a sequência de figuras abaixo,
8 Algebraic thinking does not appear in ontogeny by chance, nor does it appear as the necessary consequence of cognitive maturation. To make algebraic thinking appear, and to make it accessible to the students, some pedagogical conditions need to be created (RADFORD, 2011, p. 308 e 309).
Mel – uma das alunas da turma – percebeu uma regularidade diferente daquela percebida por Doug – outro aluno da mesma turma.
Figura 1: Sequência de figuras trabalhadas na pesquisa de Radford. Fonte: Radford (2010, p. 41).
De acordo com o exposto por Radford (2010), Mel percebeu a figura como dividida em duas linhas e, dessa forma, foi capaz de observar que o número de círculos da linha de cima é sempre o número da figura mais um, enquanto o número de círculos na linha de baixo é sempre o número da figura mais dois.
Já Doug percebeu e mostrou, através de gestos rítmicos, que, apesar de todas as figuras terem a mesma forma, elas são diferentes. E o que as fazem diferentes são os dois círculos a mais que cada figura tem em relação àquela imediatamente anterior e que estão dispostas na diagonal e no final de cada uma delas, como demonstrado abaixo:
Figura 2: Esquema representativo da regularidade percebida por Doug. Fonte: Radford (2010, p. 43).
Dessa forma, Doug e Mel perceberam regularidades diferentes em uma mesma sequência de figuras, visto que os traços comuns destacados pelos estudantes nem sempre são os mesmos.
Isso se deve ao fato de que a imagem de um objeto em nossa mente não é simplesmente um mapeamento de seus atributos físicos e/ou uma apreensão de todas as suas possíveis características observáveis aos nossos olhos e à nossa percepção intelectual.
de um modo intencional, indo além de suas características especificamente físicas e/ou numéricas.
A atividade a seguir (RADFORD, 2010b) ilustra tais ideias. Em uma classe composta por estudantes de 7 ou 8 anos10
é apresentada a sequência de termos ilustrada na seguinte figura:
Figura 3: Primeiros quatro termos de uma sequência trabalhada em uma turma do 2º ano. Fonte: Radford, 2010b, p. 3.
Os alunos foram apresentados aos quatro primeiros termos da sequência, conforme ilustrado, e convidados a continuá-la até o seu sexto termo. Alguns estudantes, focados apenas na relação numérica entre termos consecutivos, perceberam que em determinada posição havia dois quadrados a mais do que o termo da posição imediatamente anterior e apresentaram a seguinte resolução:
Figura 4: O momento em que um estudante (James) está desenhando o sexto termo; o quinto (linha de cima) e o sexto (linha de baixo) termos de James; oitavo termo de acordo com outra estudante (Sandra). Fonte: Radford, 2010b, p. 3.
Conforme apresentado na parte central da figura 4, os termos referentes à quinta e à sexta posições da sequência foram desenhados pelo estudante como se tivessem uma única linha. Percebemos, assim, que a característica espacial, ou seja, a forma como os quadrados estavam dispostos em cada uma das figuras da primeira até a quarta posição não foi levada em consideração no momento da resolução.
Nesse caso, os alunos focaram sua percepção apenas na quantidade de