Parâmetro de regularização em problemas inversos: estudo numérico com a transformada de Radon

(1)

Universidade Federal do Rio Grande do Norte

Centro de Ciˆencias Exata e da Terra

Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica

Ivanildo Freire Pereira

Parˆ

ametro de Regulariza¸

c˜

ao em Problemas Inversos:

Estudo num´erico com a transformada de Radon

(2)

Ivanildo Freire Pereira

Parˆ

ametro de Regulariza¸

c˜

ao em Problemas Inversos:

Estudo num´erico com a transformada de Radon

Trabalho apresentado ao Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica da Universidade Federal do Rio Grande do Norte, em cumprimento com as exigências legais para obten¸cão do t´ıtulo de Mestre.

´

Area de Concentra¸c˜ao: Modelagem Mate-m´atica

Orientador:

Prof. Dr. Roberto Hugo Bielschowsky

(3)

Cataloga¸c˜ao da Publica¸c˜ao na Fonte. UFRN / SISBI / Biblioteca Setorial

Centro de Ciˆencias Exatas e da Terra – CCET.

Pereira, Ivanildo Freire.

Parâmetro de regulariza¸cão em problemas inversos: estudo numérico com a transformada de Radon / Ivanildo Freire Pereira. - Natal, 2013

171 f. il.

Orientador: Prof. Dr. Roberto Hugo Bielschowsky.

Disserta¸cão (Mestrado) – Universidade Federal do Rio Grande do Norte. Centro de Ciên-cias Exatas e da Terra. Programa de Pós-Gradua¸cão em Matemática Aplicada e Estat´ıstica.

1. Matemática - Disserta¸cão. 2. Modelagem matemática - Disserta¸cão. 3. Problemas inver-sos - Disserta¸cão. 4. Regulariza¸cão - Disserta¸cão. 5. Discrepância - Disserta¸cão. 6. Parâmetro ´

otico - Disserta¸c˜ao. I. Bielschowsky, Roberto Hugo. II. T´ıtulo.

RN/UF/BSE-CCET CDU: 51

(4)

Dedicat´

oria

(5)

Agradecimentos

Grato a Deus por ter me guiado e me ajudado nos momentos dif´ıceis. Aos meus pais, Arnor Pereira e Maria de Lourdes, que me auxiliaram a superar os obst´aculos, desde os meus primeiros passos e mais fortemente na vida acadˆemica.

A todos os meus familiares, em especial Raimundo e Maria Dulce, pois sem os seus préstimos e cuidados a caminhada teria sido mais árdua. A seus filhos e respectivos cônjuges, João Maria e Maria das Vitórias, Gilvaneide e Sérgio Mur´ılo, bem como Gilvan e Neide, pela companhia, risadas e momentos de descontra¸cão, mesmo que em muitas vezes não conseguir comparecer, pois estava estudando. Aos meus irmãos, principalmente Ivo Pereira e Anderson Freire, pelas colabora¸cões no decorrer desta caminhada. Ao meu orientador, o Professor Roberto Hugo Bielschowsky, que, com muita paciência e aten¸cão, dedicou o seu valioso tempo para me orientar em cada passo deste trabalho.

A minha namorada e amiga, Tatiana Maria, pela paciência e por ceder seu tempo para ser meu porto seguro nos momentos de afli¸cões, angústias e dúvidas.

A todos os professores do Programa de Pós-Gradua¸cão de Matemática e Estat´ıstica, por toda dedica¸cão destinada ao ensino e aprendizagem nas disciplinas ministradas; em especial, o professor Bernardo pela paciência e aux´ılios nos métodos computacionais.

Aos professores do C&T, Leo Gouvêia, Leo Mafra e André, pela aten¸cão e compre-ensão enquanto estava no programa de bolsa REUNI.

Aos meus amigos de turma Márico (Marcinho), Aldemir (o Will), Jucimeire (a Ju), Alex (Arhex), Fábio (Fabão), Josemir (Jorheu) e Elisângela.

Aos meus amigos que encontrei no percurso, Hérica, Elvis, Antônio, Rafaella. Em especial a Cátia, pelas dicas e aux´ılio nas implementa¸cões.

Aos Professores Dr. Nir Cohen, Dr. Walter Eugˆenio de Medeiros, Dr. Edgar Silva Pereira e Dr. Reginaldo de Jesus Santos por aceitarem o convite para participar da minha banca de defesa.

A CAPES pelo apoio financeiro.

(6)

Resumo

Em linhas bem gerais, um problema inverso corresponde a encontrar um valor para um elementoxem algum espa¸co vetorial adequado, dado um vetor de medidas y. Quando discretizamos o problema, usualmente se recai num sistema de equa¸c˜oes f(x) = y, onde f : U _⊂ Rm _→_Rn _{representa a fun¸c˜ao de medidas em algum dom´ınio}_U _do _Rm

adequado. Via de regra, chega-se a um problema mal-posto. A resolu¸cão de problemas inversos tem sido amplamente pesquisada ao longo das últimas décadas, pois muitos problemas nas ciências puras e indústria consistem na determina¸cão de grandezas que buscamos conhecer através de efeitos observados.

Nosso tema geral desta disserta¸cão é a escolha do parâmetro de regulariza¸cão de Tykhonov de um problema linear mal condicionado, conforme discutiremos no cap´ıtulo 1 da disserta¸cão, com foco nos três métodos mais “populares” hoje na literatura da área. Nosso foco mais espec´ıfico nesta disserta¸cão consiste nas simula¸cões realizadas no cap´ıtulo 2, visando comparar a performance dos três métodos na recupera¸cão de imagens medidas com a transformada de Radón e acrescidas de ru´ıdos gaussianos iid. Como regularizador usamos um operador de diferen¸cas.

A contribui¸cão que tentamos dar, nesta disserta¸cão, consiste na discussão das simu-la¸cões numéricas que realizamos, conforme exporemos no cap´ıtulo 2. Entendemos que o sentido desta disserta¸cão está muito mais nas questões que levanta do que no fato de poder dizer algo definitivo sobre o tema em tela. Em parte, por se tratar de experimen-tos numéricos sem resultados matemáticos novos que os acompanhem. Em parte, por se tratar de experimentos numéricos realizados com um único operador. Em compen-sa¸cão, chegamos a algumas observa¸cões que nos parecem interessantes, nas simula¸cões realizadas, considerada a literatura da área. Em especial destacamos observa¸cões que fizemos sobre as diferentes voca¸cões dos métodos GCV e L-curve e, em particular, so-bre a tendência dos parâmetros obtidos com o método L-curve de se agruparem num pequeno intervalo fortemente correlacionado com o comportamento da curva de va-lores singulares generalizados dos operadores envolvidos, sob condi¸cões razoavelmente abrangentes de regularidade nas imagens a serem recuperadas.

Palavras-chave: Problemas Inversos, Regulariza¸cão, Tykhonov, GCV, L-curve, Discrepância, Radón, GSVD, Parâmetro Ótimo

(7)

Abstract

In general, an inverse problem corresponds to find a value of an elementxin a suitable vector space, given a vector y measuring it, in some sense. When we discretize the problem, it usually boils down to solve an equation system f(x) = y, where f : U _⊂ Rm _→ _Rn _{represents the step function in any domain} _U _{of the appropriate} _Rm_{. As a}

general rule, we arrive to an ill-posed problem. The resolution of inverse problems has been widely researched along the last decades, because many problems in science and industry consist in determining unknowns that we try to know, by observing its effects under certain indirect measures.

Our general subject of this dissertation is the choice of Tykhonov’s regulaziration parameter of a poorly conditioned linear problem, as we are going to discuss on chapter 1 of this dissertation, focusing on the three most popular methods in nowadays litera-ture of the area. Our more specific focus in this dissertation consists in the simulations reported on chapter 2, aiming to compare the performance of the three methods in the recuperation of images measured with the Radon transform, perturbed by the addition of gaussian i.i.d. noise. We choosed a difference operator as regularizer of the problem. The contribution we try to make, in this dissertation, mainly consists on the discus-sion of numerical simulations we execute, as is exposed in Chapter 2. We understand that the meaning of this dissertation lays much more on the questions which it rai-ses than on saying something definitive about the subject. Partly, for beeing based on numerical experiments with no new mathematical results associated to it, partly for being about numerical experiments made with a single operator. On the other hand, we got some observations which seemed to us interesting on the simulations performed, considered the literature of the area. In special, we highlight observations we resume, at the conclusion of this work, about the different vocations of methods like GCV and L-curve and, also, about the optimal parameters tendency observed in the L-curve method of grouping themselves in a small gap, strongly correlated with the behavior of the generalized singular value decomposition curve of the involved operators, under reasonably broad regularity conditions in the images to be recovered.

Keywords: Inverse Problems, Regularization, Tykhonov, GCV, L-curve, Discrepancy, Rad´on, GSVD, Optimal Parameter

(8)

Sum´

ario

1 Escolha do parˆametro na regulariza¸c˜ao de Tykhonov 1

1.1 Problemas Inversos e Regulariza¸c˜ao . . . 3

1.2 SVD e GSVD . . . 6

1.3 L-Curve . . . 13

1.3.1 L-curve contra Mudan¸cas de escala no regularizadorL . . . 18

1.4 GCV . . . 22

1.5 Discrepˆancia ou Crit´erio de Morozov . . . 25

1.6 Compara¸c˜oes na Literatura: L-Curve versus GCV . . . 26

2 Simula¸cões para obten¸cão de parâmetros ótimos de regulariza¸cão 28 2.1 Imagens para teste . . . 28

2.2 Simula¸c˜ao com GSVD . . . 30

2.2.1 Experimentos num´ericos realizados . . . 30

2.2.2 Ambiguidades no m´etodo L-curve . . . 34

2.2.3 Resultados colhidos . . . 39

2.3 Discuss˜ao dos resultados obtidos . . . 42

2.3.1 Com rela¸c˜ao aos ¯λ ´otimos . . . 42

2.3.2 Erros relativos nas recupera¸c˜oes . . . 47

2.3.3 P´os-processamento . . . 49

3 Considera¸c˜oes Finais 52 3.1 Conclus˜oes . . . 53

3.2 Trabalhos futuros . . . 55

(9)

C.2 Ordena¸cão das imagens relativamente à fatora¸cão GSVD do par (A, L) . 68

D Pontos de m´aximo da curvatura da L-curve 73

D.1 Gr´aficos das curvaturas da L-Curve na escala loglog . . . 76 D.2 Imagens correspondentes aos m´aximos locais na curvatura . . . 82

E Tabelas dos desvios padr˜oes 91

F Tabelas dos λ ´otimos 94

G Figuras das Recupera¸c˜oes 97

(10)

Lista de Figuras

1.1 Gr´afico t´ıpico do m´etodo L-curve . . . 15

1.2 Gráfico t´ıpico do método L-curve dividida em 3 partes . . . 15 1.3 As seis figuras acima correspondem a recupera¸cões feitas com parâmetro

de regulariza¸c˜ao calculado pelo m´etodo L-curve linlin e dado por 1.44-1.45, para os problemas 1.37, com 6 valores diferentes para C =Cd. λC

representa o parˆametro ´otimo, correspondente a cada C e λβ = λCC

é o parâmetro da solu¸cão ótima ¯xλC = xλβ correspondente. No

qua-dro abaixo, mais à esquerda, estão as L-curves correspondentes a cada uma das 6 escalas para a regulariza¸cão. Nos dois quadros derradeiros estão gráficos da curvatura nas variáveis tratadas. O da direita, usa uma variávelλcomum a todas as curvas e às solu¸cões ótimas como reparame-triza¸cões da curva originalxλ. Ao meio, cada curvatura está representada

em sua escala espec´ıfica ¯λ=λ/Cd. . . 21

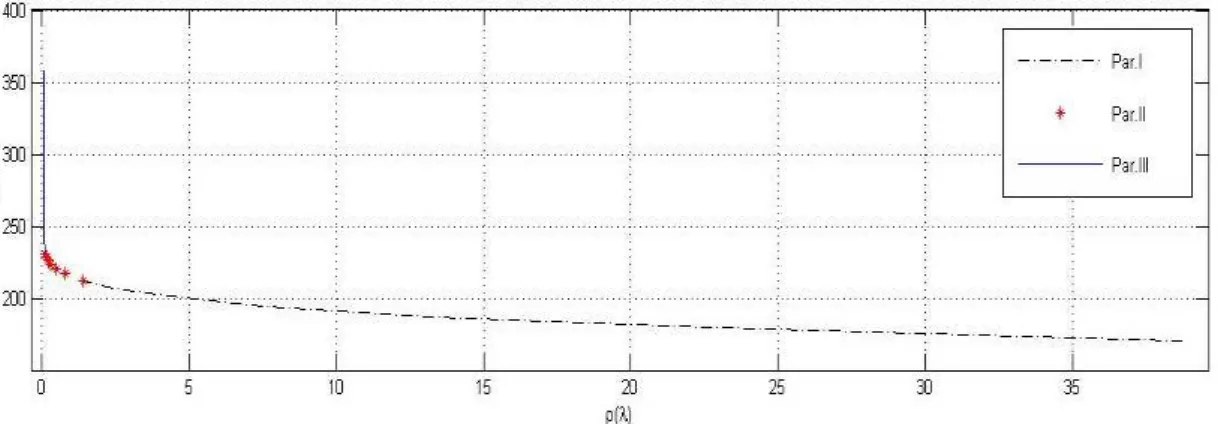
2.1 12 imagens para testes em ordem aproximadamente decrescente de con-centra¸cão, tanto na base dos vetores singulares à direita da decomposi¸cão GSVD, como na transformada discreta de cossenos em torno da origem. 29 2.2 Em cada quadro, situamos os pontos de máximo da curvatura da L-curve

na escala loglog em cima do gr´afico dos valores singulares generalizados do par (A, L), para um dos valores de ǫ indicados e para cada uma das imagens S1,S2, · · ·, S12. A regra para situar cada ponto no gr´afico

´e de forma que a cada ponto de m´aximo local ¯λLC da curvatura, lhe

corresponda um valor de i entre 1 e N, tal que λLC =Cdλ¯LC =γi, para

algum i entre 1 eN. . . 37

(11)

2.4 Cada quadro representa um n´ıvel de ruido e cada curva os valores es-timados de cada parâmetro ótimo, ou seja, cada curva representa os parâmetros ¯λ ótimos obtidos por um dos 3 métodos (L-curve, GCV e Discrepância) ou para o parâmetro ¯λEmin, para cada uma das 12

ima-gens. Note que, os dois primeiros gráficos estão com escalas diferentes dos três derradeiros e que os parâmetros ótimos estão todos na escala de ¯

λ=λ/Cd. . . 40

2.5 Cada quadro representa um dos parâmetros ¯λ ótimos considerados e cada curva seus valores para cada uma das imagens, em um dos n´ıveis de ruido. Note que para a L-curve a escala é diferente da que empregamos nos demais e que os parâmetros ótimos estão todos na escala de ¯λ=λ/Cd. 41

2.6 As curvas mostram os erros relativos correspondentes às solu¸cões obtidas a partir de cada ¯λ ótimo, para os 5 n´ıveis de ruidos e 12 imagens. Vale verificar que as escalas dos dois primeiros quadros são diferentes dos demais. . . 48

2.7 Nas duas imagens do meio da figura, estão as recupera¸cões da imagem S5, obtidas com os parâmetros ¯λ ótimos dos métodos L−curveeGCV.

Nas duas da direita, estas mesmas imagens filtradas via convolu¸c˜ao com um filtro 3x3 . . . 50

A.1 Transformada Radon. Reproduzido de [21]. . . 57

A.2 Discretiza¸c˜ao da Transformada Radon . . . 58

C.1 Distribui¸c˜ao de Picard vT

i sj, em valor absoluto, para cada uma das 12

imagensSj, vetorizadas e normalizadas, ou seja, com norma de Frobenius

unit´aria. As curvas em preto representam os ajustes a Ckα_{, dos dados}

dos coeficientes de Picard de Vt_∗_s

j entre k0 = 10 e k =N, para cada

uma das 12 imagens. No gr´afico abaixo e `a esquerda, resgistramos os expoentes α obtidos para cada uma das 12 imagens. . . 65

(12)

C.2 Compara¸c˜ao do ajuste `a _kP rojKk via GSVD das duas maneiras

indi-cadas logo acima. Cada um dos 12 quadros iniciais corresponde a uma das Sj da figura 2.1. Nas linhas cheias azuis est˜ao os gr´aficos de cada

kP rojKk, correspondentes a cada Sj. Nas linhas curva tracejada preta

temos os correspondentes ajustes a _kP rojKk, obtidos a partir do ajuste

de pick via C.1 e usando a f´ormula C.3. Na linha pontilhada vermelha

temos o ajuste feito diretamente aF(K,Γ, α) via C.4. Na curva de baixo temos um gr´afico com os coeficientesα que medem a “ regularidade `a la

Picard” via SVD, obtidas com os dois ajustes. . . 67

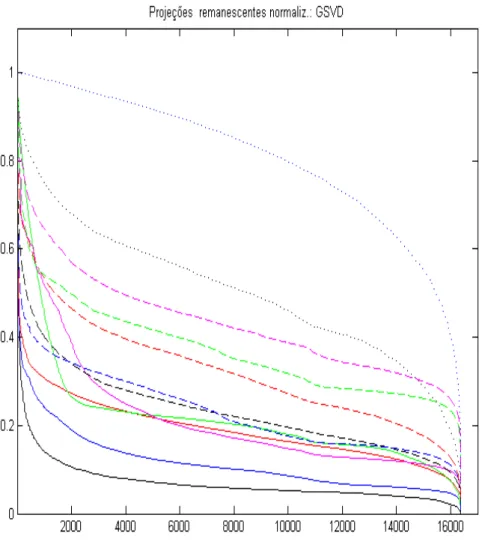
C.3 Cada curva representa _kP rojKk, via GSVD e de forma correspondente a cada uma das doze imagens, ordenadas da forma que indicamos na figura 2.1 da se¸c˜ao 2.1. . . 69

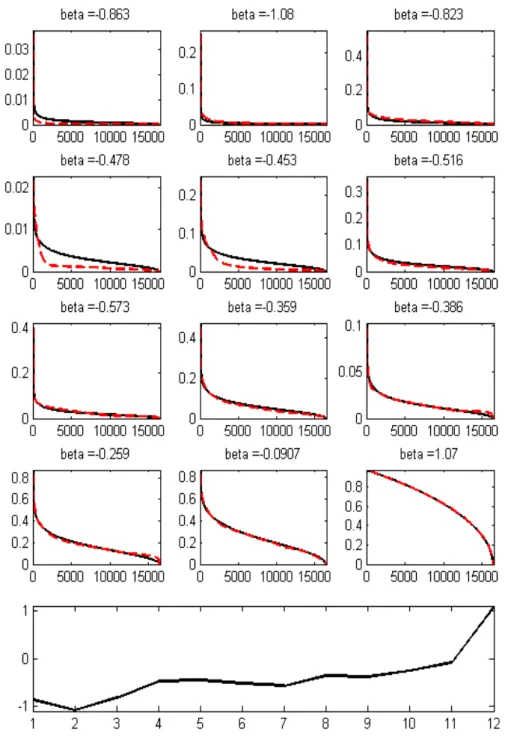
C.4 Nos doze quadros iniciais estão os ajustes de_kP rojKk=k P k=1 N−K (ϕkx∗)wkk a F(K,Γ, α) = Γ q 1₋(K/N)β, via quadrados m´ınimos, onde x∗ ₌ ΣN_k₌₁−Kϕkwk. No último quadro tra¸camos um gráfico do expoente β, em fun¸cão das 12 imagens encontradas. . . 70

C.5 Gráficos de _kP rojKk, para cada uma das imagens, relativamente a pro-je¸cões segundo tres bases diferentes, conforme discutidas no último pa-rágrafo deste apêndice. Na de cima, a norma da proje¸cão ortogonal no SEV dos vetores singulares à esquerda associado aos K menores valores singulares de SVD. Na do meio, a norma da proje¸cão definida por C.5 e na de baixo, a norma da proje¸cão no subespa¸co associado às frequências fora do quadradoK_×K. Devidamente normalizadas a partir da segunda componente. . . 72

D.1 Gráficos de ¯λLC2, que estamos definindo como pontos de ótimo no mé-todo L-curve, das 12 imagens consideradas, para 5 n´ıveis de ru´ıdo, com ǫ=.001, .004, .01, .04, .1 . . . 74

D.2 Gráficos com a curvaturaKlog(¯λ) delog(L(¯λ) = [log( ¯rho(¯λ)), log(¯η(¯λ))]contra ¯ λ, para um ru´ıdo gaussiano i.i.d. com norma ǫ_kb ₋ mean(b)_k, onde ǫ = .001 e de forma a explicitar seus pontos de máximo. Observe nos t´ıtulos de cada quadro os valores correspondentes destes máximos para ¯ λ no vetor ¯λ0(KM) = [LC1, LC2, LC3], sendo que LCi = − − −,caso não haja o correspondente valor de máximo. . . 77

D.3 O mesmo que na figura anterior, s´o que para ǫ= 0.004 . . . 78

(13)

D.6 O mesmo que na figura anterior, só que para ǫ= 0.1 . . . 81 D.7 Recupera¸cões das imagens nos pontosx_λ¯_LCi, onde ¯λLCi é um dos pontos

de m´aximo da curvatura da L-Curve na escala loglog, correspondentes a S1 e a um n´ıvel de ru´ıdo = 0.004 . . . 82

D.8 Recupera¸c˜oes das imagens nos pontosx_λ¯_LCi, onde ¯λLCi ´e um dos pontos

(14)

de m´aximo da curvatura da L-Curve na escala loglog, correspondentes a

S7 e a um n´ıvel de ru´ıdo = 0.04 . . . 88

D.19 Recupera¸cões das imagens nos pontosx_λ¯_LCi, onde ¯λLCi é um dos pontos de máximo da curvatura da L-Curve na escala loglog, correspondentes a S8 e a um n´ıvel de ru´ıdo = 0.04 . . . 88

G.1 Imagem originalS1. . . 98

G.2 N´ıvel de ru´ıdo ǫ = 0.001 . . . 99

G.3 N´ıvel de ru´ıdo ǫ = 0.01 . . . 100

G.4 N´ıvel de ru´ıdo ǫ = 0.1 . . . 101

G.6 N´ıvel de ru´ıdo ǫ = 0.001 . . . 103

G.7 N´ıvel de ru´ıdo ǫ = 0.01 . . . 104

G.8 N´ıvel de ru´ıdo ǫ = 0.1 . . . 105

G.10 N´ıvel de ru´ıdo ǫ = 0.001 . . . 107

G.11 N´ıvel de ru´ıdo ǫ = 0.01 . . . 108

G.12 N´ıvel de ru´ıdo ǫ = 0.1 . . . 109

G.14 N´ıvel de ru´ıdo ǫ = 0.001 . . . 111

G.15 N´ıvel de ru´ıdo ǫ = 0.01 . . . 112

G.16 N´ıvel de ru´ıdo ǫ = 0.1 . . . 113

G.18 N´ıvel de ru´ıdo ǫ = 0.001 . . . 115

G.19 N´ıvel de ru´ıdo ǫ = 0.01 . . . 116

G.20 N´ıvel de ru´ıdo ǫ = 0.1 . . . 117

(15)

G.22 N´ıvel de ru´ıdo ǫ = 0.001 . . . 119

G.23 N´ıvel de ru´ıdo ǫ = 0.01 . . . 120

G.24 N´ıvel de ru´ıdo ǫ = 0.1 . . . 121

G.26 N´ıvel de ru´ıdo ǫ = 0.001 . . . 123

G.27 N´ıvel de ru´ıdo ǫ = 0.01 . . . 124

G.28 N´ıvel de ru´ıdo ǫ = 0.1 . . . 125

G.30 N´ıvel de ru´ıdo ǫ = 0.001 . . . 127

G.31 N´ıvel de ru´ıdo ǫ = 0.01 . . . 128

G.32 N´ıvel de ru´ıdo ǫ = 0.1 . . . 129

G.34 N´ıvel de ru´ıdo ǫ = 0.001 . . . 131

G.35 N´ıvel de ru´ıdo ǫ = 0.01 . . . 132

G.36 N´ıvel de ru´ıdo ǫ = 0.1 . . . 133

G.38 N´ıvel de ru´ıdo ǫ = 0.001 . . . 135

G.39 N´ıvel de ru´ıdo ǫ = 0.01 . . . 136

G.40 N´ıvel de ru´ıdo ǫ = 0.1 . . . 137

G.42 N´ıvel de ru´ıdo ǫ = 0.001 . . . 139

G.43 N´ıvel de ru´ıdo ǫ = 0.01 . . . 140

G.44 N´ıvel de ru´ıdo ǫ = 0.1 . . . 141

G.46 N´ıvel de ru´ıdo ǫ = 0.001 . . . 143

G.47 N´ıvel de ru´ıdo ǫ = 0.01 . . . 144

G.48 N´ıvel de ru´ıdo ǫ = 0.1 . . . 145

(16)

Lista de Tabelas

2.1 A coluna 1 representa cada imagem rodada e as outras colunas a raz˜ao E(_kAx¯_λGCV¯ −bk)/E(Ax¯_λ¯

Emin −b

) para cada n´ıvel de ruido . . . 44 2.2 A coluna 1 representa cada imagem rodada e as outras colunas a raz˜ao

2.6 para cada n´ıvel de ruido . . . 45 2.3 A coluna 1 representa cada imagem rodada e as outras colunas a raz˜ao

kx¯¯

λGCV−x¯¯

λEmink

kx∗₋_x∗_m_k para cada n´ıvel de ruido . . . 45

D.1 Cada coluna representa o valor de ¯λLC2, que estamos definindo como o

ponto de ´otimo no m´etodo L-curve. Cada coluna corresponde a um n´ıvel de erro associado a um dado valor de ǫ . . . 74

E.1 A primeira coluna representa as imagens testadas. As outrasdesvio padrão_média dos parâmetros ótimos testados e indicados na primeira linda da tabela, para ǫ= 0.0001 . . . 91 E.2 A primeira coluna representa as imagens testadas. As outrasdesvio padrão_média

dos parâmetros ótimos testados e indicados na primeira linda da tabela, para ǫ= 0.001 . . . 92 E.3 A primeira coluna representa as imagens testadas. As outrasdesvio padrão_média

dos parˆametros ´otimos testados e indicados na primeira linda da tabela, para ǫ= 0.1 . . . 93

F.1 Os parâmetros ótimos para os método L-curve, GCV e o Discrepância, junto com o m´ınimo de _kx∗0₋_x_¯

¯

(17)

¯

λk, respectivamente, para o ǫ= 0.001 . 95

¯

λk, respectivamente, para o ǫ= 0.01 . . 95

¯

(18)

Lista de Siglas

GCV Generalized Cross Validation

i.i.d. Independente identicamente distribu´ıda.

SVD Singular Value Decomposition.

GSVD Generalized Singular Value Decomposition.

RAM Random Access Memory.

GHz Gigahertz (unidada de frequˆencia).

OCV Ordinary Cross Validation.

DCT2 Transformada Discreta de Cossenos Bidimensional.

fminbnd Fun¸cão do software matlab que calcula o m´ınino local de uma fun¸cão de uma variável num intervalo.

fzero Fun¸cão do software matlab que encontra as ra´ızes de fun¸cões de uma variável.

(19)

Lista de S´ımbolos

x Imagem vetorizada a ser recuperada.

A Transformada de R´adon.

N N´umero de vari´aveis da matriz de medidas.

M N´umero de linhas de A.

L Matriz de regulariza¸c˜ao.

p N´umero de linhas de L.

q ´Indice da norma (ou semi-norma) do termo de regulariza¸c˜ao.

λ Parˆametro de regulariza¸c˜ao.

x0 Aproxima¸c˜ao inicial para a solu¸c˜ao desejada.

xλ Solu¸c˜ao da regulariza¸c˜ao de Tykhonov.

I Matriz identidade.

b∗ _{Medidas sem ru´ıdos.}

x∗ _{Imagem original.}

b Medidas com a presen¸ca de ru´ıdo b=b∗_{+ ru´ıdo.}

bm M´edia dosbi.

r Ru´ıdo gaussiano de m´edia zero, i.i.d. nas M medidas realizadas.

(20)

U, V e WT _U _{Matriz dos vetores singulares a esquerda de} _A_{, associada a SVD,}

bem como a matriz dos vetores singulares a esquerda deAno GSVD. Já V é a matriz dos vetores singulares a direita de A na decompo-si¸cão SVD e a matriz dos vetores singulares a esquerda de L para a decomposi¸cão GSVD. WT _{é uma matriz não-singular associada ao}

lado direito das matrizes A e L na decomposi¸cão GSVD para o par matricial (A, L). Vale dizer que as matrizes U, V e Σ da GSVD são diferentes, para L ₆= I, das geradas pela decomposi¸cão SVD de A. Mantemos a mesma nomenclatura para não carregar as nota¸cões.

ΣN Matriz diagonal N ×N, com os valores singulares da matriz A na

diagonal, de 1 aN.

Σ Matriz com dois blocos, onde acima fica ΣN e abaixo um bloco de

zeros.

ui,vi ewTi ui i-´esimo vetor singular a esquerda deA, , ou i-´esimo vetor singular

a esquerda de A, na i-ésima coluna da matriz U da decomposi¸cão GSVD. A i-ésima coluna de V é denotada por vi nas duas

decom-posi¸c˜oes, SVD e GSVD, sendo V dado como prescrito acima. E wT i

é a i-ésima coluna da matriz não-singular WT_{, na decomposi¸cão do}

par matricial (A, L). Lembramos queui evi na decomposi¸c˜ao GSVD,

para L₆=I, s˜ao diferentes dos ui evi da decomposi¸c˜ao SVD.

σi i-´esimo valor singular da matriz A = UΣVT, na diagonal de Σ, na

decomposi¸cão SVD e, correspondentemente, também na fatora¸cão A=UΣWT _{que se obtem via GSVD.}

C Matriz diagonal associada os valores singulares deLna decomposi¸c˜ao GSVD.

µi i-´esimo valor singular da matriz L, conforme aparece na diagonal de

M, na fatora¸c˜ao A=V_CW−1_{, obtida via decomposi¸c˜ao GSVD.}

γi i-´esimo valor singular generalizado do par matricial (A, L),γi = σ_µi_i.

L2 _{Espa¸co dos operadores na norma 2.}

xLS Solu¸c˜ao usando quadrados m´ınimos.

Sj Imagens artificias utilizadas nos experimentos, onde j = 1, ...,12.

(21)

s Imagem vetorizada.

n n_×n a dimens˜ao de Sj, ou seja, o n´umero de pixels da imagem.

F(λ)i O i-ésimo filtro do método de regulariza¸cão de Tykhonov. F(λ)i = σ2

i

σ2

i+λ

2, associado a SVD. F(λ)i = γi

γ2

i+λ

2, na base GSVD.

AT _{Matriz transposta da matriz} _A_.

LT _{Matriz transposta da matriz} _L_.

k._k₂ Norma euclidiana, bem como _k ._k.

LC(λ) Curva do m´etodo L-curve, parametrizada por λ, LC(λ) = (ρλ, ηλ).

ρλ Norma do ajuste aos dados.

ηλ Norma (semi-norma) da solu¸c˜ao.

ρ0 Medida de inconsistˆencia.

k Fun¸c˜ao da curvatura do m´etodo L-curve.

λLC Parâmetro ótimo gerado pelo método L-curve.

k._k_F Norma de Frobenius.

Cd Constante associada `a mudan¸ca de escalano regularizador de L ←

CdL. Vari´avel no cap´ıtulo 1 e assumido como Cd = k_kA_Lk_kF

F

∼

= 5.495, para n= 128, no cap´ıtulo 2.

¯

xλ Solu¸c˜ao na regulariza¸c˜ao Tykhonov quando mudamos a escala do

regularizador L_←CdL. Vale dizer,

xλ = ¯xλCd = min

λ

kAx₋b_k2+λ2_kCdLxk2 .

¯

λ O parˆametro λ em uma nova escala, ¯λ= _Cλ

d.

¯

ρλ O ajuste aos dados, dado por ¯ρλ =kAx¯λCd −bk. (d´uvida)

¯

ηλ A semi-norma da solu¸c˜ao, dada por ¯ηλ =kCdLxk.

¯

LC(λ) A curva do m´etodo L-curve com (¯ρλ,η¯λ).

(22)

βCd(λ) A curva do m´etodo L-curve parametrizada com o λ em uma nova

escala. (duvida) ¯

λLC O parâmetro ótimo, do método L-curve, para a curva βCd(λ).

¯

xLC Solu¸cão da regulariza¸cão de Tykhonov, gerada a partir do parâmetro

´otimo do m´etodo L-curve, com a curva βCd(λ).

KCd Curvatura da L-curve βCd(λ).

λad Parˆametro com escala alterada, λad = _Cλ_d, onde Cd = k_kA_Lk_kF

F.

δ Desvio padr˜ao.

E Operador esperan¸ca.

T r Operados tra¸co.

G(λ) Fun¸c˜ao do m´etodo GCV.

λGCV Parâmetro ótimo fornecido pelo método GCV.

ˆ

λmin Parˆametro que minimiza a distˆancia kAx−bk.

λEmin Parˆametro que minimiza kxλ−x∗k.

¯

G(λ) Fun¸c˜ao GCV obtida com a mudan¸ca de escala do regularizador,L_← CdL.

pick A proje¸cão dex∗ na k-ésima dire¸cão do vetor singularvk na fatora¸cão

SVD deA, em valor absoluto.

D Matriz diferen¸ca que calcula as diferen¸cas entre os pixels. Utilizada como matriz regularizadora.

λDisc Parâmetro ótimo fornecido pelo método Discrepância.

x∗

m M´edia da imagem original.

λLC1 Parâmetro referente ao máximo local menor que o máximo fornecido peloλLC, caso não exista, λLC1 = 0.001.

λLC1∗ _{Parˆametro limite, caso o} _λLC_{1 n˜ao exista, ou seja,}_λLC₁∗ _{= 0}_._001.

(23)

LC3 Parâmetro correspondente ao ponto de máximo local da curvatura, que seja maior que o máximo fornecido por LC, da curva do método L-curve.

λsuav Limite superior para os parˆametros. J´a que com λ = 15 temos

pa-rˆametros da ordem dos 200 maiores valores singulares genelarizados. Assim, λsuav = 15.

SrLC Imagens correspondentes às recupera¸cões com os valores ótimos do

m´etodo L-curve.

SrGCV Imagens correspondetes às recupera¸cões com os valores ótimos do

m´etodo GCV.

SrLCF Imagens relativas as imagens SrLC com aplica¸c˜ao de um filtro

passa-baixa.

SrGCV F Imagens relativas as imagensSrGCV com plica¸c˜ao de um filtro

passa-baixa.

P rojK Proje¸c˜oes dex∗ nos subespa¸cos soma dos vetores singulares `a direita

deK a N, P rojK =PNk=K = vTkx∗

vk.

(24)

Cap´ıtulo 1

Escolha do parˆ

ametro na regulariza¸

c˜

ao de

Tykhonov

Em linhas bem gerais, um problema inverso corresponde a encontrar um valor para um elemento x em algum espa¸co vetorial adequado, dado um vetor de medidas b. Quando discretizamos o problema, usualmente se recai num sistema de equa¸c˜oesf(x) = b, ondef :U _⊂Rm _→_Rn _{representa a fun¸c˜ao de medidas em algum dom´ınio}_U _do_Rm

adequado [27; 23]. O que vem se tornando uma marca comum aos problemas inversos consiste no fato de recairmos em problemas frequentemente mal postos, no sentido que discutiremos na se¸cão 1.1 e/ou de porte computacional considerável. A resolu¸cão de problemas inversos tem sido amplamente pesquisada ao longo das últimas décadas, pois muitos problemas nas ciências, nas engenharias, na medicina e na indústria consistem na determina¸cão de grandezas que buscamos conhecer através de efeitos observados. Entre as áreas do conhecimento que se deparam frequentemente com problemas inversos mal-postos estão: medicina (tomografia e ressonância magnética), observa¸cão espacial (inversões Helios´ısmicas), engenharia (problemas de vibra¸cões, inversão de combustão, determina¸cão de for¸ca inversa), geof´ısica (determina¸cão de parâmetros no subsolo), entre outras.

Nosso tema geral desta disserta¸cão é a regulariza¸cão de Tykhonov de um problema linear mal condicionado, conforme discutiremos na se¸cão 1.1 e nosso objetivo mais geral neste primeiro cap´ıtulo é discutir alguns dos principais métodos na literatura para a escolha do parâmetro de regulariza¸cão. Em especial, os métodos GCV, L-curve e discrepância. Nosso foco mais espec´ıfico nesta disserta¸cão consiste nas simula¸cões realizadas no cap´ıtulo 2 com a matriz da transformada de Radón que introduzimos na próxima se¸cão (vide ainda [30],[21] e [20]) e descrevemos com mais detalhes no apêndice A.

(25)

2

ótimos designados como L-curve [19], GCV [14] e Discrepância [28], respectivamente. Dedicamos a se¸cão 1.6 a discutir algumas das compara¸cões entre os métodos L-curve e GCV na literatura.

Com rela¸cão às simula¸cões numéricas, não tivemos nenhuma preocupa¸cão com im-plementa¸cões eficientes para a transformada de Radón, mas apenas em utilizá-la para estudar o comportamento de diferentes métodos de obten¸cão do parâmetro de regula-riza¸cão no método de Tykhonov dispon´ıveis, num problema linear importante e mal condicionado. Basicamente, testamos a recupera¸cão com imagens discretizadas e medi-das com a transformada de Radón, às quais adicionamos ruido branco em diversos n´ıveis de intensidade e numa dimensão compat´ıvel com a obten¸cão de solu¸cões via GSVD. Utilizamos um regularizador de diferen¸cas, conforme explicamos na se¸cão seguinte e uma bateria com 12 imagens de diferentes n´ıveis de “regularidade”, num certo sentido. Entendemos que o sentido desta disserta¸cão está muito mais nas questões que levanta do que no fato de poder dizer algo definitivo. Em parte por se tratar de experimentos numéricos praticamente sem resultados matemáticos novos, de algum significado. Em parte por se tratar de experimentos numéricos realizados com um único operador.

Em compensa¸cão chegamos a algumas observa¸cões que nos parecem interessantes sobre diferen¸cas essenciais na natureza dos métodos L-curve e GCV, que se confirmam numericamente e que lhes conferem voca¸cões diferentes e complementares. Essencial-mente, em nossos testes numéricos, o método GCV nos parece confirmar sua voca¸cão de origem para procurar imagens próximas da imagem a ser recuperada na norma_k._k2,

dentro da fam´ılia de solu¸cões regularizadas, porém a custa de suaviza¸cões excessivas em casos de medidas significativamente contaminadas por ruidos. Já o método L-curve tem por voca¸cão ser mais barato computacionalmente e procurar parâmetros que regulari-zem o problema mal posto com baixa perda de informa¸cões sobre o problema original, porém devolvendo solu¸cões por vezes excessivamente contaminadas por ruidos e exi-gindo algum tipo de pós-processamento para filtrá-los. Em particular tornando, pelo menos neste caso da transformada de Radón, um pouco sem sentido realizar compa-ra¸cões relativamente à qualidade na recupera¸cão das imagens pelos dois métodos, sem levar em conta algum tipo de pós-processamento, como tem sido comum na literatura recente da área.

(26)

1.1 Problemas Inversos e Regulariza¸c˜ao 3

e de forma muito correlacionada com uma pequena janela de varia¸c˜ao relativamente r´apida dos valores singulares generalizados do par (A, L), entre dois patamares nos quais os valores singulares generalizados variam mais lentamente.

Um terceiro ponto que destacamos corresponde a uma certa ambiguidade que encon-tramos na defini¸cão do ponto de máximo no método da L-curve e que nos conduziu a optar por um formato para resolver que nos pareceu adequadamente justificado.

Demos ainda um argumento que nos parece definitivo contra o uso do método L-curve na escala linear, que passa por mostrar a dependência da solu¸cão ótima obtida com rela¸cão a mudan¸cas de escala no regularizador.

Discutimos com algum detalhe, no apêndice C, formas de classificar as imagens a serem tratadas em mais ou menos regulares, em fun¸cão do decaimento de suas compo-nentes na base de vetores singulares generalizados à esquerda, de modo a ordená-las e testar o comportamento dos parâmetros de regulariza¸cão, em fun¸cão desta ordena¸cão. Os testes realizados confirmam parcialmente o que se esperaria com a ordena¸cão, mas não de forma integral.

1.1 Problemas Inversos e Regulariza¸

c˜

ao

Neste trabalho estamos interessados nas solu¸cões de um problema do tipo resolver f(x) = b, onde f : U _⊂ Rn _→ _Rm _{é a fun¸cão de medidas e} _b _∈ _Rm _{é o vetor de}

observa¸c˜oes (usualmente acrescido de algum ruido). De acordo com Hadamard, um problema ´e bem posto quando,

• Existe solu¸c˜ao.

• A solu¸cão é única.

• Est´avel a perturba¸c˜oes nos dados do problema.

e mal posto quando uma das condi¸cões acima não é satisfeita. Problemas Inversos são tip´ıcamente mal postos e frequentemente sequer têm solu¸cão, principalmente quando levamos em conta ruidos na medida deb. O fato de poder nem ter solu¸cão nos conduz a buscar solu¸cões aproximadas de b = f(x), reescrevendo-os como um problema de minimiza¸cão ,

x=min_kb₋f(x)_k_p (1.1)

(27)

de solu¸cões para (1.1). Este fato deu origem a diferentes métodos para regularizar o problema. Os três mais usuais são:

• M´etodo da itera¸c˜ao truncada

Corresponde a aplicar algum método iterativo para resolverf(x) = be usar algum critério de parada antes que apare¸cam instabilidades. Como ressalta Santos em [33], “em alguns casos funciona e em outros simplesmente não funciona”. Contudo, é muito empregado em algumas situa¸cões espec´ıficas, especialmente se o problema é de grande porte, como costuma ser o caso na tomografia médica. Além disto há também uma farta literatura a respeito, inclusive teórica. Vide [33] e [15] para acessá-la.

• Métodos que explicitamente alternam passos em dire¸cão a solu¸cão com filtros

Artigos como [3] e [4] trabalham com m´etodos iterativos da forma xn+1 =SQxn,

ondeQxé, tipicamente, alguma combina¸cão convexa de proje¸cões ortogonais, por exemplo ART, e S é uma matriz de suaviza¸cão, que pode ser pensada como um filtro aplicado após Qxn, visando regularizar o problema.

O método mais tradicional para recuperar uma imagemx, a partir de uma medida com a transformada de Radón (vide apêndice A) é o da retroproje¸cão filtrada (vide [20] e [21]). A idéia da retroproje¸cão filtrada pode ser vista sob diferentes ângulos. O mais usual talvez seja olhando pelo teorema das fatias de Fourier, conforme expõe Kak no cap´ıtulo 3 de seu livro [21]. A idéia de se estar alternando entre métodos que dão passos em dire¸cão à solu¸cão do problema inverso com passos visando regularizar o problema de maneira expl´ıcita fica mais clara no sentido que lhe dá Gabor, no cap´ıtulo 8.1 de [20], sem fazer referência ao teorema das fatias de Fourier, e corresponde a aplicar um filtro unidimensional numa dada etapa da opera¸cão com cada uma das vistas da transformada de Radon, antes de fazer a retroproje¸cão, com o objetivo de regularizar a inversão. Isto é equivalente a alternar, num mesmo algoritmo, passos para resolver o problema com passos para suavizá-lo.

• M´etodo de regulariza¸c˜ao de Tykhonov

(28)

de penalizar o problema original (1.1), com um termo regularizador do problema considerado, substituindo-o por:

xλ =minkb−f(x)kmp +λ2kL(x−x0)knq (1.2)

onde a segunda parte refere-se ao termo de regulariza¸cão, ou ainda, dito como de penaliza¸cão. Os casos mais usuais correspondem a n =q = 1 ou n =q = 2 e a definir L como a matriz identidade, ou então a discretiza¸cão de um operador de derivadas. x0 6= 0 corresponderia a indicar uma aproxima¸cão conhecida da

solu¸cão e λ > 0 é um parâmetro de regulariza¸cão que controla a quantidade de regulariza¸cão imposta na solu¸cão. O parâmetro de regulariza¸cão pondera o termo de penaliza¸cão, isto é, se λ for alto, suaviza muito o problema perdendo-se importantes informa¸cões, caso contrário, os componentes do erro dominam, tendo como resultado uma solu¸cão inútil. Desta forma, o termo de regulariza¸cão introduz um viés na solu¸cão a ser encontrada e um dos desafios nas aplica¸cões é buscar formas de regularizar o problema que introduzam implicitamente, através da escolha do regularizadorLe das normaspeq, informa¸cão adicional compat´ıvel com o problema. Uma boa escolha representa uma solu¸cão de compromisso entre regularizar o problema e garantir fidelidade aos dados medidos. .

O caso padrão na escolha do regularizador é fazer L=I, sendo I a identidade. Com x0 = 0, L = I significa que se penaliza solu¸cões de norma grande. Quando L é uma

matriz de diferen¸cas, que discretiza a derivada de primeira ordem, a idéia associada é a de se penalizar “saltos” no problema inicial, suavizando assim os contrastes no vetor x a ser recuperado e o λ pondera esta suaviza¸cão. Por outro lado, Phillips e Scott em [31], realizaram uma bateria de testes com seis regularizadores diferentes para recuperar problemas 2D com varia¸cões bruscas na imagem e concluiram que a matriz de diferen¸cas teve a melhor performance entre os seis regularizadores testados. De qualquer modo, conforme se pode ver em [16] e teremos a oportunidade de discutir rapidamente na próxima se¸cão, de um modo geral, a regulariza¸cão com q = 2 pode ser vista sob a ótica de eliminar as instabilidades devidas a ruidos de alta freqûencia nas medidas e fatalmente tende a suavizar contornos, independentemente até doLutilizado. A escolha de p tem a ver com a distribui¸cão do ruido presente na medida b =Ax∗ ₊_r_{, de uma}

imagem x∗ _{a ser recuperada. No caso do ruido} _r _{ter distribui¸c˜ao gaussiana i.i.d., de}

m´edia zero, um estimador de m´axima verossimilhan¸ca para x∗ _{seria (1.3) com} _p _{= 2,}

(29)

1.2 SVD e GSVD 6

Nesta disserta¸cão visamos discutir a escolha do parâmetro de regulariza¸cão λ, no método de regulariza¸cão de Tykhonov, para fun¸cões lineares em dimensão finita, no caso p=q = 2 e n=m= 2. Vamos adotar ainda como regularizador uma discretiza¸cão da derivada de primeira ordem, sem dispor de uma aproxima¸cãox0previamente assumida.

Na pr´atica, com x0 = 0. De forma que, para n´os, o problema 1.2 se especializa para:

xλ =argminx∈Rnkb−Axk2

2+λ 2

kLx_k2₂ (1.3)

Mais precisamente ainda, as simula¸cões com as quais trabalharemos nesta disserta¸cão correspondem à reconstru¸cão de imagens medidas pela Transformada de Radon [30; 21; 20]. No apêndice A descrevemos a transformada de Radón com as caracter´ısticas que nos interessam explorar nesta disserta¸cão. Em especial, no que se refere a discretiza¸cão utilizada. A publica¸cão original de Radón é de 1917 [32], mas sua importância cresceu enormemente na segunda metade do século XX, com o advento dos computadores. Sua aplica¸cão maior está na tomografia, que corresponde a reconstruir um objeto por meio de medidas associadas a variáveis que desejamos medir indiretamente, por não termos o acesso direto ao objeto estudado, e associadas a raios que percorrem o objeto a ser medido. No caso da tomografia médica, o exemplo mais t´ıpico corresponde a desferir feixes de raio X sobre algum peda¸co do corpo de um paciente e medir o decaimento na energia destes raios, em algum receptor, após atravessar o tecido de interesse. No caso da geof´ısica, um exemplo t´ıpico é medir o tempo que explosões realizadas em determinados pontos levam para atingir receptores previamente determinados, muito embora neste caso o problema seja não linear, por natureza, e só pode ser modelado pela transformada de Radón numa primeira aproxima¸cão. Este tipo de reconstru¸cão de imagens é bastante utilizada na medicina, em deteçcão de tumores e na ruptura da estrutura óssea entre outros. Na geof´ısica, em prospeçcão de petróleo, deteçcão de depósitos de res´ıduos e etc. Trata-se de um problema inverso tipicamente mal condicionado, igualmente designado como mal posto.

1.2 SVD e GSVD

Uma ferramenta matemática bastante útil para analisar problemas inversos mal pos-tos é a fatora¸cão SVD [13]. Só para simplificar a reda¸cão, discutiremos a fatora¸cão SVD de matrizes com mais linhas que colunas. Em especial, este é o caso tratado nas nossas simula¸cões.

(30)

1.2 SVD e GSVD 7

U _∈RM×M _e _V _∈_RN×N_{, tais que}

A=UΣVT =

N

X

i=1

σiuiviT

sendo U = (u1...uM) e V = (v1...vN). As colunas de U e de V s˜ao denominadas de

vetores singulares `a esquerda e `a direita de A, respectivamente. A matriz Σ _∈ RM×N

se divide naturalmente em dois blocos, Acima, um bloco diagonalΣN ∈RN×N. Abaixo,

um bloco de zeros. Na diagonal de ΣN est˜ao os valores singulares σi de A, que s˜ao

positivos e est˜ao dispostos em ordem n˜ao-crescente, ou seja,

σ1 ≥...≥σN ≥0

Como estamos interessados em discutir a escolha de parâmetros de regulariza¸cão para a tranformada de Radón, vamos supor que todos os σi são não nulos, pois isto

é o que acontece com discretiza¸cões da transformada de Radón, muito embora tenha-mos σN cada vez menor, relativamente a σ1, à medida que tomamos malhas cada vez

mais refinadas. Por exemplo, no nosso caso trabalharemos com recupera¸c˜ao de imagens quadradas com 128_×128 pixels. No caso N = 1282 _{= 16384, por exemplo, obt´em-se}

σ1 = 125.64 e σN = 0.0302, resultando num n´umero de condi¸c˜aoK2 =σ1/σN = 4160.

Segundo Natterer em [30], a transformada de Rad´on ´e suavemente mal condicionada, no sentido que, sem discretizar, ou seja, operando emL2_{, apesar de se tratar de um}

ope-rador linear descont´ınuo, seus valores singulares caem para zero segundoσi =O(i−1/2).

Em especial, K2 → ∞, comN → ∞.

Podemos representar a solu¸cão para o problema de quadrados m´ınimos (1.1) utili-zando a decomposi¸cão SVD na solu¸cãoxLS. Segue que:

xLS =

h

UΣVTT

UΣVTi−1 UΣVTT b

xLS = VΣTUTUΣVT

−1

VΣUTb

ComoU e V s˜ao matrizes ortogonais resultaU−1 ₌_UT _e _V−1 ₌_VT_{. Portanto,}

xLS = VΣ2VT

−1

VΣUTb

xLS = Σ−1V−1VΣ2VT

−1

UTb= ΣVT−1 UTb

(31)

1.2 SVD e GSVD 8

xLS = N X i=1 uT i b σi

vi, (1.4)

E ainda, lembrando que b = b∗ ₊_r_{, onde} _x∗ _{´e a solu¸c˜ao para o problema sem ruido}

Ax∗ ₌_b∗ _{em (1.1), temos}

xLS = N

X

i=1

uT

i b∗

σi vi + N X i=1 uT i r σi vi (1.5)

Vamos nos deter um pouco na equa¸cão (1.5), pois ela nos indica dois pontos relevan-tes, quando se trata de recuperar sinais medidos por operadores mal condicionados. O primeiro deles é a condi¸cão de Picard. Veja que um sinalx∗_{, com significado f´ısico}

x∗ =

N

X

i=1

(vT_i x∗)vi = r

X

i=1

uT

i b∗

σi

vi

(1.6)

medido por Ax∗ ₌ _b∗_{, usualmente deveria ter um tamanho compat´ıvel com a escala}

do problema onde está formulado e não deveria depender excessivamente de ruidos, no caso de medidas com ruido significativo. Este é o significado da condi¸cão de Picard, que pode se formular como:

Defini¸c˜ao 1.2.1. Condi¸c˜ao de Picard Os coeficientes de b∗ ₌_Ax∗ _{na base de vetores}

singulares `a esquerda, ou seja, _|uT

i b∗|, devem decair mais rapidamente que σi. Em

termos assint´oticos com i, isto significa que:

u_iTb∗

=o(σ_i) (1.7)

Na figura 2.1 da se¸c˜ao 2.1 apresentamos 12 imagens Sj, com n ×n pixels, onde

n = 128, escolhidas para servirem de teste na recupera¸cão com a transformada de Radón, variando desde imagens muito bem comportadas até imagens formadas por pixels aleatoriamente escolhidos. Seb∗ ₌_As

j, 1.6 nos diz que:

vT_i sj =uTi b∗/σi (1.8)

Veja que 1.7 ´e equivalente a se pedir vT

i sj → 0 e que (1.7)-(1.8) s´o fazem

verdadeira-mente sentido numa representa¸c˜ao cont´ınua das imagenssj. No apˆendice C discutimos

(32)

1.2 SVD e GSVD 9

particular, na figura C.1 do apˆendice C representamos os gr´aficos dos coeficientes desj

na base dos vetores singulares `a direitavi.

O segundo ponto relevante a se destacar da equa¸cão (1.5) é que um ruido brancornão satisfará à condi¸cão de Picard, uma vez que, pelo fato de U ser uma matriz ortogonal, UT_r _{igualmente será uma distribui¸cão iid, com média zero e mesma variância que} _r_.

Para fixar id´eias, pensemos no seguinte exemplo:

Exemplo 1.2.1. Recupera¸c˜ao de sinal medido com Radon versus amplifica¸c˜ao de ruido branco

Considere um ruido branco r, de norma ǫ_kb₋bmk, onde bm ´e a m´edia dos bi e uma

matrizA=UΣVT _{com as caracter´ısticas da matriz de Rad´on que vamos trabalhar em}

nossas simula¸c˜oes. Vale dizer, com valores singulares variando numa faixa entre 0.03 e 125 e N = 1282 _{= 16384. Como ˆ}_r ₌ _UT_r _{tem exatamente a mesma variˆancia que} _r_,

quase com toda a certeza teremos componentes ˆrgug, do ruido na base definida pelos

vetores singulares `a esquerda, comg grande, bem pr´oximo de N e_|rˆg| ≈ √ǫ_Nkb−bmk.

A recupera¸c˜ao de ˆrgug seria amplificada por 1/σg ≈1/0.03. Resulta algo da ordem

ǫ_{∗ k}b₋bmk

√ N σg

≈ ǫ₁₂₈∗ kb−bmk

∗0.03 ≈0.26ǫ∗ kb−bmk .

Se uiTb∗ ≈ kb−bmk/10, isto indica que ¯x∗i =uiTb∗/σi tende a ser uma componente

importante na imagemPN

1 x¯∗ivi medida porb∗ =Ax∗. Principalmente no caso de

ima-gens satisfazendo fortemente à condi¸cão de Picard, no sentido de ter sua representa¸cão na base dos vetores singulares _{vi} fortemente concentrada nas componentes iniciais.

Se i for pequeno, podemos esperarσi ≈100, ou seja, da mesma ordem de grandeza de

σ1. Em ordem de grandeza, isto nos daria:

|x¯∗_i_| = _|ui

T_b∗

σi | ≈ k

b₋bmk/1000 , seguindo-se (1.9)

ˆ rg ˆ x∗ i ≈

0.26ǫ_kb₋bm_k kb₋bmk/1000 ≈

260ǫ (1.10)

Vale dizer, com um ǫ na faixa de 0.01, teremos ruido sendo recuperado pela solu¸c˜ao de quadrados m´ınimos com tamanho suficiente para competir com o sinal original x∗

a ser recuperado. Ou seja, podemos esperar que uma perturba¸c˜ao r com estas carac-ter´ısticas, quase com toda a certeza, ter´a coeficientes uT

(33)

1.2 SVD e GSVD 10

valores singulares pequenos e de modo a fazer com que, mesmo com ruidos de intensi-dade relativamente modestas, tais componentes possam vir a ser dominantes, tornando assim, a solu¸c˜ao de quadrados m´ıninos (1.1) in´util.

A solu¸cão para o problema (1.3) regularizado com L=I pode ser descrita usando a decomposi¸cão SVD de A aplicada ao problema de quadrados m´ınimos, de maneira inteiramente análoga ao que fizemos para obter (1.5) e nos daria:

xλ = N X i=1 σ2 i σ2

i +λ2

uT i b

σi

vi (1.11)

xλ = N X i=1 σ2 i σ2

i +λ2

uT i b∗

σi

vi+ N X i=1 σ2 i σ2

i +λ2

uT i r

σi

vi (1.12)

Como bem aponta Hansen em [16], podemos entender a regulariza¸c˜ao de Tykhonov como um filtro de passa baixaF(λ), com

Fi(λ) =

σ2

i

σ2

i +λ2

(1.13)

Se λ << σi, Fi(λ) ≈ 1. Neste caso, a correspondente componente da solu¸c˜ao (1.11)

na dire¸cão de vi é aproximadamente a mesma prescrita em (1.5). Já no caso em que

λ >> σi,Fi(λ)≈0 e a correspondente componente da solu¸c˜ao (1.11) na dire¸c˜ao de vi

´e filtrada.

Conforme Hansen destaca em ([16]), a medida que consideramos vetores singularesvi

associados a valores singulares cada vez menores, êles estarão crescentemente concen-trados nas altas frequências , em sua representa¸cão em Fourier. Neste sentido, o trade off propiciado pela regulariza¸cão de Tykhonov, entre fidelidade no ajuste aos dados versus regulariza¸cão, pode ser pensado como um filtro para as componentes de alta frequência no ruido da solu¸cão obtida, que são exatamente aquelas amplificadas pelos valores singulares baixos. Na contrapartida, uma criteriosa escolha do parâmetroλ te-ria o papel de evitar maiores preju´ızos às informa¸cões relevantes do sinal, usualmente associadas aos vetores singulares com menores ´ındices, sobretudo na recupera¸cão de sinais sob condi¸cões de Picard favoráveis. Em especial, este nos parece um bom ponto de vista para se analisar os diferentes métodos que visam otimizar a escolha do pa-râmetro de regulariza¸cão, conforme teremos a oportunidade de praticar ao analisar as simula¸cões apresentadas no próximo cap´ıtulo.

(34)

1.2 SVD e GSVD 11

identidade, ou sejaL₆=I, consideramos importante a introdu¸c˜ao da Decomposi¸c˜ao em Valores Singulares Generalizados (GSVD). Vide [13; 16].

Teorema 1.2.2. (GSVD) Seja o par matricial (A, L) com A _∈ RM×N _e _L _∈ _Rp×N_,

com M +p_≥N. Podemos decompor A e L como

A = UΣW−1 (1.14)

L = V_CW−1 (1.15)

Em que, U _∈ RM×M _e _V _∈ _Rp×p _{s˜ao matrizes ortogonais tais que} _UT_U ₌ _I M e

VT_V ₌_I

p e W ∈RN×N, ´e uma matriz n˜ao-singular. A cada uma das matrizes Σ e C

est˜ao associados N n´umeros ordenados, respectivamente, da seguinte forma:

0 _≤ σ1 ≤...≤σN ≤1, (1.16)

1 _≥ µ1 ≥...≥µN ≥0 e de tal forma que (1.17)

1 = σ_i2+µ2_i , para i= 1_{· · ·}N (1.18)

As matrizes Σ e _C tˆem estes n´umeros, ordenados desta forma, numa de suas diago-nais, da seguinte maneira:

• Se M _≥N, Σ = ΣN 0

!

e ΣN ´e uma matriz diagonal

• Se M _≤ N, σ1 = ...=σN−M = 0, Σ =

0 ΣM

e ΣM =diag(σN−M+, ....σN)

´e uma matriz diagonal

• Se p_≥N, _C = CN 0

!

e _CN ´e uma matriz diagonal

• Se p_≤N, mp+ 1 =mp+ 2 =· · ·=mN, C =

Cp 0

e _Cp =diag(m1, ..., mp)

´e uma matriz diagonal

Os valores singulares generalizados γi de (A, L) s˜ao definidos, para cada i= 1, ..., N

como

γi ≡

σi

µi

. (1.19)

Observe que podemos entender a fatora¸c˜ao SVD como um caso particular da GSVD, se L = In. Neste caso, levando W−1 = C−1VT em A = U(ΣC−1)VT e fazendo β =

(35)

1.2 SVD e GSVD 12

matrizW−1_{deixar de ser ortogonal. Ainda assim, espera-se que seja aceitavelmente bem}

condicionada. Hansen aponta em [16] que os valores singulares deW s˜ao os mesmos que os da matriz A

L !

No caso com o qual trabalharemos nas simula¸c˜oes, comN = 1282_,

obtemos W com um n´umero de condi¸c˜ao de aprox. K2 = 82.

Analogamente ao que fizemos com a SVD, podemos utilizar GSVD para solucionar o problema (1.3). Teremos,

xλ =

h

W−1T

ΣTUTUΣW−1+λ2 W−1T

CTVTV_CW−1i−1 W−1T

ΣTUTb (1.20)

xλ =W Σ2+λ2C2

−1 ΣUTb

xλ = p X i=1 σ2 i σ2

i +λ2µ2i

uT i b

σi

wi (1.21)

= p X i=1 γ2 i γ2

i +λ2

uT i b

σi

wi (1.22)

Igualmente a antes, podemos pensar na regulariza¸c˜ao de Tykhonov neste caso, como correspondente a aplicar filtrosFi(λ) aos coeficientes de Picard u

T ib

σi .Fi(λ) continua com

a mesma f´ormula (1.13) de antes, apenas substituindo-se os valores singulares usuais σi pelos valores singulares generalizados como definidos em (1.19).

Igualmente ao que acontecia com L = I, seu efeito ´e amortizar as contribui¸c˜oes a xλ correspondentes a valores singulares generalizados γi << λ. Em especial, como

já ocorria no caso SVD, filtrando ruidos de alta frequência e tornando a solu¸cão bem menos sens´ıvel a perturba¸cões do que a solu¸cão de quadrados m´ınimos, conforme analisa Hansen em [16]. Do ponto de vista computacional, uma vez obtida a fatora¸cão GSVD, o cálculo da solu¸cão (1.19) é muito barato, pois corresponde essencialmente a uma multiplica¸cão matriz-vetor. Para que se tenha uma idéia de tempos, num computador com HD de 1 Terabyte , 24.0 Gb de memória RAM, 2 processadores Xeon Intel de 3.20 GHz, como o que usamos, dispondo da fatora¸cão GSVD, se pode calcular as solu¸cões para 400 valores de λ em cerca de 1 minuto, no caso N = 1282 _{= 18384, com o}

matlab. Já para obter a fatora¸cão GSVD do par (A, L) com o qual trabalhamos no caso N = 1282_{, foram necessárias mais de 48 horas, no mesmo computador. Além}

(36)

1.3 L-Curve 13

próximo cap´ıtulo. Contudo, para problemas de porte maior, a fatora¸cão GSVD tende a tornar-se computacionalmente inviável e temos de recorrer a métodos iterativos se queremos resolver (1.3). No caso da máquina que citamos, a fatora¸cão GSVD para N = 256_×256 já se tornava completamente inviável.

1.3 L-Curve

Como vimos nas se¸cões anteriores, tipicamente os métodos de regulariza¸cão de Tykho-nov, para propiciarem uma solu¸cão estável apropriada, envolvem um “trade-off” entre o “tamanho” da solu¸cão regularizada, medido por _kLxλk e a qualidade do ajuste aos

dados, medida pelo res´ıduo_kAxλ−bk2. Em especial, vimos que a solu¸c˜ao “ingˆenua” de

quadrados m´ıninos (1.1) tende a ficar completamente dominada por ruidos, em pro-blemas mal condicionados, tornando, assim, essa solu¸cão inútil. Se λ for relativamente grande, a solu¸cão sai muito “suave” e o ajuste aos dados _kAxλ−bk₂ ficará

prejudi-cado. Caso contrário, se λ for excessivamente pequeno obtemos um “bom” res´ıduo, mas a solu¸cão será tomada pelo ruido fazendo com que a penaliza¸cão_kLxλk₂ aumente

consideravelmente.

Hansen, a partir de seus artigos seminais do in´ıcio da década de 90, [19] e [15], é o principal nome associado ao método designado por L-curve para encontrar um parâme-tro ótimo para a regulariza¸cão de Tykhonov. Este método se tornou, a partir da década de 90 um dos mais populares para definir um bom parâmetro para a regulariza¸cão de Tykhonov. Hansen cita ainda o livro de Lawson e Hanson de 1974, [24], como precursor na utiliza¸cão do método. O método L-curve baseia-se na curva

LC(λ) = [ρλ, ηλ] , onde (1.23)

ρλ =kAxλ−bk₂ (1.24)

ηλ =kLxλk2 (1.25)

Conforme veremos a seguir, a forma da L-curve sugere naturalmente uma região na qual a L-curve varia rapidamente sua dire¸cão como a mais natural para se procurar um parâmetro λ que estabele¸ca um adequado equil´ıbrio entre a regulariza¸cão e o ajuste aos dados.

(37)

1.3 L-Curve 14

nesta disserta¸c˜ao, mais adiante:

ρ(λ) = _kAxλ−bk2 = N

X

i=1

((1₋Fi)uTi b)2+ρ20 (1.26)

η(λ) = _kLxλk2 = N

X

i=1

µiFi

uT i b σi 2 = N X i=1 Fi uT i b γi 2 (1.27) (1.28) onde,

ρ0 = b−

N

X

i=1

(uT_i b)ui (1.29)

Fi(λ) =

γ2

i

γ2

i +λ2

(1.30)

e γi representa os valores singulares generalizados do par matricial (A, L). (1.26-1.27)

indicam queρ(λ) é crescente, enquanto queη(λ) é decrescente e ambas são curvasC∞_.

Em especial, podemos pensar emρ(λ) como uma fun¸cão monotonamente crescente de η(λ). A curva [ρ(λ), η(λ)], será então uma curva C∞_{, tipicamente com a forma de um}

L (ver figura 1.1).

Um resultado bem básico sobre a L-curve pode ser encontrado em [17] e essencial-mente se segue das observa¸cões acima e da aplica¸cão do método dos multiplicadores de Lagrange aos problemas (1.31-1.32) abaixo:

Teorema 1.3.1. Seja xλ a solu¸cão para (1.2). Então kLxλk é uma fun¸cão monótona

decrescente de _kAxλ−bk e qualquer ponto (ρ, η) na curva (kAxλ −bk,kLxλk) ´e uma

solu¸c˜ao para:

ρ=min_kAx₋b_k sujeito a _kLx_{k ≤}η, 0_≤η _{≤ k}Lx0k (1.31)

η =min_kLx_k sujeito a _kAx₋b_{k ≤}ρ, ρ0 ≤ρ≤ρ∞ (1.32)

onde, ρ_∞ =ρ0+

U UTb

.

Basicamente esse teorema nos diz que é imposs´ıvel construir qualquer solu¸cão para o problema (1.3) que esteja abaixo da L-curve. Como destaca Hansen, a solu¸cão de Tykhonov xλ é ótima no sentido que, dado η não existe solu¸cão de (1.3) com res´ıduo

(38)

1.3 L-Curve 15

Figura 1.1 Gr´afico t´ıpico do m´etodo L-curve

que_kLxλk. Em especial, ainda de acordo com Hansen, isto nos daria parˆametros para

caracterizar a qualidade de solu¸cões obtidas por outros métodos de regulariza¸cão. Ainda segundo Hansen, tipicamente, a L-curve tem três partes bem distintas, cons-tituindo uma curva em forma de L, conforme se ilustra na figura (1.2). Da´ı seu nome ser L-curve:

Figura 1.2 Gr´afico t´ıpico do m´etodo L-curve dividida em 3 partes

• I - Parte “horizontal”, paraλrelativamente grande, onde os erros de regulariza¸c˜ao dominam.

• II - Regi˜ao de transi¸c˜ao relativamente abrupta, ou seja, com curvatura elevada. • III - Parte “´ıngreme”, para λ relativamente pequeno, na qual o ajuste ao erro

(39)

1.3 L-Curve 16

Em [19], entre outras coisas, Hansen demonstra esta caracteriza¸c˜ao para a L-curve, no caso L = I, supondo

i a condi¸c˜ao de Picard para a medida b∗ ₌_Ax∗ _{de um sinal,}

ii adiciona um ruido r que seja iid, de m´edia zero na medida b iii e tal que _kr_k<_kb∗_k

Em [17] êle estende esta caracteriza¸cão para o caso onde Ltenha seu posto igual ao número de linhas, porém sem dar uma demonstra¸cão deste fato.

Em [19], Hansen explora esta propriedade da L-curve para definir métodos de encon-trar o parâmetro de regulariza¸cão ótimo, em algum sentido. Oλ ótimo se encontraria em algum lugar do canto da curva, onde há uma rela¸cão mais equilibrada entre regu-lariza¸cão e ajuste de dados. Segundo Hansen [19], há pelo menos duas maneiras de se pensar noλ ótimo:

1 Encontrando o λ que fornece a menor distância entre a curva e a origem. Segundo Hansen, a maneira de medir a distância entre a L-curve e a origem deveria levar em conta o método de regulariza¸cão utilizado e que a medida de distância mais natural neste caso seriaρ+λ2_η_{. Contudo, em nossos experimentos}

esse medida não funciona, pois é sempre crescente, com o λ. Utilizando a distân-cia Euclidiana usual para encontrar o ponto da L-curve mais próximo da origem, fomos surpreendidos pelo fato que ele parecia produzir um λ constante, indepen-dentemente do ruido e das imagens empregadas. Na verdade, fazendo as contas, vimos que se trata de um resultado que, à falta de outro nome, denominaremos de Lema do λ ótimo a priori. Aparentemente trata-se de um resultado surpreen-dente, embora simples de estabelecer. ’‘Enganoso”, contudo, conforme teremos a oportunidade de mostrar na subse¸cão que se segue.

Lema 1.3.1. λ ´otimo a priori

λ = 1´e o ponto da L-curve mais pr´oximo da origem, na medida euclidiana usual do R2

Demonstra¸c˜ao 1.3.1. De 1.26 e 1.27, temos

ρ(λ)2+η(λ)2 =

N

X

i=1

((1₋Fi)uTi b)2+ρ02+

N X i=1 Fi uT i b γi 2 (1.33) = N X i=1

((1₋Fi)uTi bui)2+

(40)

1.3 L-Curve 17

Derivando, em λ, para encontrar o ponto cr´ıtico e lembrando que Fi = γ 2

i

γ2

i+λ

2

(ρ(λ)2+η(λ)2)′ =

N

X

i=1

4λ3_α2

i (γi2+λ2)

2

−2 (γ2

i +λ2) 2λ(λ4+γi2α2i)

(γ2

i +λ2)

4

=

N

X

i=1

α2i (γi2+λ2) (4λ5+ 4λ3γi2−4λ5−4λγi2)

(γ2

i +λ2)

4 = N X i=1 α2

i (γi2+λ2) (λ3−λ) 4γi2

(γ2

i +λ2)

4

= λ3₋_λ

N

X

i=1

4γ2

iα2i

(γ2

i +λ2)

3

Resulta um ´unico ponto cr´ıtico paraρ(λ)2₊_η₍_λ₎2_{, como solu¸c˜ao de} ₍_λ3₋_λ_{) = 0}_. Ou seja, λ= 1.

2 Calculando o λ que corresponde a curvatura m´axima da L-curve.

J´a que a L-curveLC(λ) ´eC∞_{, sua curvatura, como se pode ver em [37], pode ser}

expressa por:

k(λ) = ρ′η′′−ρ′′η′

((ρ′₎2_{+ (}_η′₎2₎3/2 (1.35)

onde ′ _{são as diferencia¸cões em rela¸cão ao} _λ_.

Na parteIda curva, pequenas mudan¸cas noλresultam em grandes varia¸cões no res´ıduo e na parte III observa-se grandes varia¸cões no valor _kLxλk₂ para pequenas varia¸cões

de λ. Entre outros argumentos heur´ısticos, para amenizar essas varia¸cões bruscas e destacar melhor a região de transi¸cão, Hansen sugere o uso da escala log-log para a L-curve. Ou seja, que se busque os pontos de máxima curvatura para a L-curve no plano log-log, definida por:

LC(λ) = [log(ρλ), log(ηλ)] = [log(kAxλ−bk2), log(kLxλk2)] (1.36)