Dans notre recherche, nous mettrons à jour cet outil pour analyser la dynamique des processus de recherche dans le contexte de l'étude de la conjecture d'Erdös-Straus. Le premier axe du travail didactique consiste en l'élaboration de l'environnement expérimental a priori pour construire une situation de recherche autour de la conjecture d'Erdös-Straus. Deuxièmement, nous développons une grille d'analyse, élaborée à partir de nos analyses mathématiques et épistémologiques, pour étudier les processus de recherche mis en œuvre dans l'étude de la recherche de la conjecture d'Erdös-Straus.
Origine du projet de recherche
Nous supposons qu’un problème ouvert au sens de la recherche mathématique (c’est-à-dire non résolu) peut répondre à ces différents critères. Charles Pisot, cité par Nimier (1989), évoque la place particulière de la théorie des nombres au sein des mathématiques. Nous pensons donc que l'arithmétique constitue un terrain favorable à la mise en œuvre d'une méthode expérimentale dans le cadre de la résolution de problèmes de recherche.
Problématique et questions de recherche
L'intérêt du mathématicien et ses recherches efficaces sur la conjecture montrent alors la pertinence du problème pour questionner épistémologiquement et mathématiquement la démarche de recherche d'un chercheur. Le problème choisi est pertinent pour étudier et comparer les processus de recherche de différents groupes cibles. Une étude comparative des processus de recherche de différents groupes cibles est pertinente pour analyser puis développer l'activité de recherche des étudiants.
Caractérisation de notre méthodologie
L’environnement épistémologique et mathématique (au sens de Bloch) s’est donc construit dans une oscillation constante entre l’analyse mathématique de divers travaux sur les hypothèses et l’analyse épistémologique de l’activité de recherche mathématique. Deuxièmement, afin d’améliorer notre analyse a priori de la situation résultante, nous avons mené des pré-expérimentations. Nous avons donc analysé plus en détail le rôle de certains exemples dans les recherches sur la résolution de la conjecture et surtout dans les recherches en cours du mathématicien que nous avons suivies.
Schéma de la méthodologie générale de la recherche
Thèse
Milieu expérimental a priori Milieu théorique mathématique
Confrontation à la contingence
Points de vue épistémologique et didactique sur l’ac- tivité mathématique
- La place des problèmes dans l’activité mathématique
- Le caractère expérimental de l’activité mathématique
- Spécificités du raisonnement en arithmétique
Thèse de Giroud (2011) intitulée : Enquête sur l'approche expérimentale dans des situations de recherche en classe. La première raison est liée à l'attitude de l'auteur face au rôle des objets mathématiques dans l'apprentissage de la démarche expérimentale. Cet outil épistémologique sera également utilisé pour analyser le processus de recherche des étudiants confrontés à la solution de la conjecture d'Erdös-Straus (Chapitre 7).
Les aspects dialectiques dans la théorie des situations
- Phases d’action - formulation - validation
- Élaboration de preuves
- Dialectique syntaxe-sémantique
Cela implique de fournir les garanties nécessaires pour s’engager à agir ; ici l'acte d'établir la vérité d'une déclaration. On assiste ici à une prise en compte de la dimension expérimentale des mathématiques dans le processus de preuve et de développement des preuves dans son articulation entre preuves pragmatiques et preuves intellectuelles. Barrier ajoute que l'approche sémantique est également riche pour les processus de validation de type décisionnel (c'est-à-dire se convaincre de la véracité d'un énoncé).

Le milieu
- Milieu antagoniste de type expérimental
- Les différents modèles de milieux selon Bloch
Cet environnement didactique doit permettre « le fonctionnement des connaissances comme production libre de l'élève » (Brousseau, 1998, p. 302). Notre recherche n'est pas liée à des situations fondamentales au sens de la théorie des situations, nous avons adapté ce cadre analytique à la recherche de situations de résolution de problèmes. Ce deuxième modèle environnemental développé par Bloch soutient l'organisation efficace de l'enseignement d'une situation selon les scénarios considérés.
Le courant Problem-Solving
Le deuxième concept (qui peut être associé à la résolution de problèmes en tant que compétence) est l’accès à la culture mathématique de la résolution de problèmes. La référence pour résoudre les problèmes est celle de l’expert, du chercheur mathématique. Le troisième concept (qui peut être associé à la résolution de problèmes en tant qu'art) décrit par Castela est la résolution de problèmes en tant qu'activité qui nécessite un ensemble de connaissances très étendu.
Quelques dispositifs français
- La pratique des problèmes ouverts
- Les situations de recherche pour la classe de Maths à modeler
- Les situations de recherche du groupe DREAM
En ce sens, la conjecture d’Erdös-Straus peut être considérée comme une situation de recherche pour la classe. La relation dialectique entre les connaissances théoriques et le développement de l'heuristique est prise en compte lors de l'apprentissage des mathématiques dans le cadre de la résolution de problèmes de recherche. Nous partageons notamment les hypothèses suivantes sur la motivation des situations de recherche pour l’apprentissage des mathématiques.
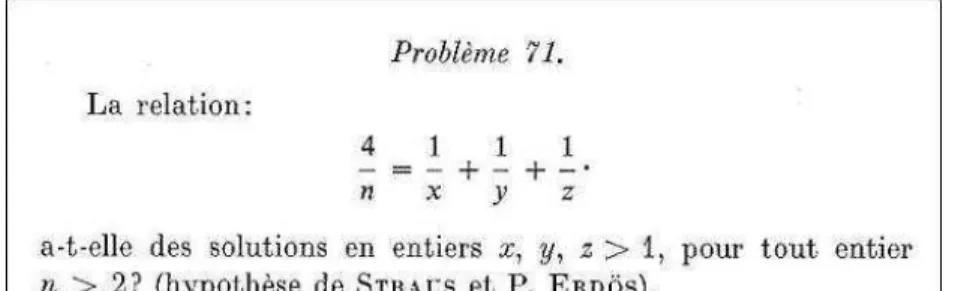
La conjecture d’Erdös-Straus
Pour tout n au moins égal à 2, on peut trouver des entiers (pas forcément différents) tels que. Ainsi, le premier ouvrage publié sur la recherche d'une solution à la conjecture d'Erdös-Straus serait celui d'Oblàth (1950). Il a trouvé des solutions à l'équation pour tout nombre naturel n ≤ 106128 et décrit la méthode par laquelle il est arrivé à ce résultat.
En 1954, Rosati s'appuie sur les travaux d'Oblàth et améliore son résultat en trouvant des solutions à l'équation pour tout nombre naturel n < 141649. Il fait également progresser le résultat général en définissant une condition nécessaire et suffisante pour trouver des solutions à l'équation ( Rosati, 1954) . Il trouve des solutions à l'équation pour tout nombre naturel n < 8000 et exprime également une condition nécessaire et suffisante pour l'existence de solutions, proche de celle de Rosat (Bernstein, 1962).
A priori il ne connaît pas les ouvrages antérieurs, puisqu'il ne cite ni Oblàth ni Rosati. Il cite seulement Bernstein ; on pourrait penser qu'il ignorait l'œuvre d'Oblàth et de Rosati. En 1999, Swett a publié une page Internet vérifiant l'existence de solutions pour tout nombre naturel n < 1014 (Swett, 1999).
Les articles traitent de la solution de la conjecture d'Erdös et Straus ou donnent des résultats quantitatifs, par extensions, sur les numéros des solutions.
État de l’art
- Démonstrations de résultats théoriques
On peut donc supposer, sans perte de généralité (en divisant si nécessaire par δ), que l'on a l'équation suivante : pa+b+c= 4abck, avec k entier naturel non nul et pgcd(a, b) = 1. Première étape : Montrons que si p est un nombre premier supérieur ou égal à 3, alors x, y, z ne peuvent pas tous être des multiples de p. Donc soit un seul est un multiple de p, disons x, soit deux sont des multiples de p. p, par exemple y et z, ou tous les trois sont des multiples de p.
Il existe donc un multiple de dep, par exemple x, ou il existe deux multiples de dep, par exemple y et z. Or, s'il existe un diviseur commun aux encouragements, on a pgcd(4ab, s)6= 1, ce qui contredit les hypothèses. Pour démontrer ce théorème, nous utilisons le symbole de Legendre et ses généralisations, les symboles de Jacobi et de Kronecker.
C'est ce que nous appelons le symbole de Jacobi : pour a, b ∈ Z, avec factorisation b impaire sous la forme b = pe11..perr, nous définissons le symbole de Jacobi ab. Soit a, b∈ Z, avec b factorisé en facteurs premiers de la forme b=upe11..perr où u=±1, le symbole de Kronecker ab. Les symboles de Jacobi et Kronecker peuvent ensuite être étendus aux rationnels n = ab avec pgcd(p, ab) =gcd(a, b) = 1 at.
Si b est un résidu quadratique modulo a, alors il n'existe pas de polynômes F1, F2, F3 dans Z[X] à coefficients positifs tels que.
- Résultats algorithmiques
- Recherches récentes
- Recherche de Thépault
- Recherche de Mizony
- Articulation des différents résultats
- Sur la conjecture forte
- Sur la conjecture faible
- Sur la programmation
- Conclusion
Sur sa page internet (Swett, 1999), Allan Swett explique comment il a vérifié l'existence de solutions à l'équation d'Erdös-Straus pour n < 1014. Cependant, le programme montre qu’il ne reste que 7 132 des 1 014 cas. L'équation de Straus n'a pas de solution. L'approche pour rechercher une solution à la conjecture d'Erdös-Straus de Thépault était la suivante.
Les conditions b divise a2 et 4a−1 divise a+bn sont des conditions suffisantes pour l'existence de solutions de l'équation d'Erdös-Straus. Ainsi, si n est suivi d'un multiple d'un nombre de la forme 4k−1, alors n est une solution de l'équation d'Erdös-Straus. Le deuxième résultat établi par Thépault lors de ses récentes recherches est la vérification de l'existence de solutions à l'équation d'Erdös-Straus pour n < 10000 à l'aide d'un tableur.
Le premier intérêt de l’identité (4.26) est de reformuler la conjecture d’Erdös-Straus sous la forme Un intérêt majeur de ce nouveau point de vue est la reformulation de la conjecture d’Erdös-Straus. Pour tout entier premier p de la forme 4k+ 1, k entier, il existe une décomposition de 4p en somme de trois fractions unitaires, donnée par l'égalité ci-dessus.
Les différentes méthodes pour vérifier l'existence de solutions de l'équation d'Erdös-Straus reposent sur le même schéma : construire des filtres pour limiter les nombres.
Conjecture d’ Erdös-Straus
Première approche de la conjecture
Deuxième approche de la conjecture Conjecture forte
- Une analyse d’épistémologie historique et contempo- raine
- Sur le processus de découverte ou d’invention mathématique
- Sur l’heuristique de la découverte
- Conclusion
- Sur l’émergence de gestes
- La notion de « geste » en philosophie des mathématiques
- La notion de « geste » en didactique des mathématiques
- La notion de « geste » pour analyser les processus de recherche
- Conclusion
- Une analyse d’épistémologie contemporaine sur la conjec- ture d’Erdös-Straus
- Sur la démarche de recherche de Thépault
- Sur la démarche de recherche de Mizony
- Analyse des processus de recherche des chercheurs dans leur étude de la conjecture d’Erdös-Straus
- Conclusion
- Remarques sur la genèse d’un résultat mathématique : entre preuves et algorithmes
- Conclusion
Nous avons rassemblé et suivi les recherches en cours menées par des chercheurs engagés dans l'étude de la résolution de la conjecture d'Erdös-Straus. Le deuxième marqueur des progrès de la recherche est la production de résultats partiels sur la conjecture d'Erdös-Straus. Dans la troisième section (5.3.3), nous analysons spécifiquement les processus de recherche mis en œuvre dans leur étude de la conjecture d'Erdös-Straus.
Dans la suite de notre entretien, il évoque les prochaines étapes de ses recherches sur la conjecture d'Erdös-Straus. Dans un deuxième paragraphe, nous présentons l'heuristique de découverte d'un résultat majeur dans ses recherches sur la conjecture d'Erdös-Straus. Il a donc recherché la conjecture d'Erdös-Straus sans lire la littérature existante sur le sujet.
Une dernière conséquence de cette voie de recherche est le fait qu'il a acquis une vision large et multiple de la présomption. Rappelons que Mizony a pris conscience de l'existence de la conjecture d'Erdös-Straus lors d'un séminaire où nous présentions nos travaux. La suite de l'étude de la conjecture d'Erdös-Straus s'appuiera ensuite sur la méthode utilisée pour décomposer 4n en somme de deux fractions égyptiennes.
Ce geste est important car il réduit le champ de recherche des soupçons. Ce geste permet à Mizony de limiter le champ de recherche de la conjecture d'Erdös-Straus aux nombres premiers. Cela conduit à une nouvelle formulation de la conjecture d'Erdös-Straus (pour tout nombre premier n > 3 et pour x=kn (k entier naturel), il existe un entier naturel etz tel que n4 = 1x+y1+1z) et ' n nouveau recherche de trace (recherche de décompositions avec cette propriété sur x).