PONTIFÍCIA UNIVERSIDADE CATÓLICA DE
SÃO PAULO PUC/SP
Cleusiane Vieira Silva
A prática docente e sua influência na construção de
conceitos geométricos: um estudo sobre o ensino e a
aprendizagem da Simetria Ortogonal
DOUTORADO EM EDUCAÇÃO MATEMÁTICA
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE
SÃO PAULO PUC/SP
CLEUSIANE VIEIRA SILVA
A prática docente e sua influência na construção de
conceitos geométricos: um estudo sobre o ensino e a
aprendizagem da Simetria Ortogonal
Tese apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para a obtenção do título de Doutora em Educação Matemática sob a orientação
do Professor Doutor Saddo Ag
Almouloud.
Autorizo, exclusivamente para fins acadêmicos e científico s, a reprodução total ou parcial dessa T ese por processos de fotocopiadoras ou eletrônicos.
DEDICATÓRIA
AGRADECIMENTOS
Primeiramente, a Deus, que me permitiu ter saúde para concluir mais essa etapa da minha vida, que em todos os momentos me ofereceu Sua mão protetora.
Ao professor doutor Saddo Ag Almouloud, pelo trabalho de orientação competente e cuidadoso, pela amizade e carinho que me proporcionou ao longo da confecção desta tese.
Aos professores doutores, Gerson Pastre de Oliveira, Bárbara Lutaif Bianchini, Gilson Bispo de Jesus e André Ricardo Magalhães, que fizeram parte da banca de qualificação, cujas sugestões e reflexões foram valiosas para a finalização deste trabalho.
À minha amiga de todas as horas, Ana Paula Perovano dos Santos Silva pelo apoio e amizade nos momentos de dificuldades, pelas leituras e contribuições realizadas durante a confecção deste trabalho.
Aos professores da escola-alvo da pesquisa que, gentilmente, participaram deste trabalho doando seu precioso tempo, refletindo e compartilhando experiências conosco.
À minha amiga Diana Maia pela amizade e pela forma como me acolheu no programa de Estudos Pós-Graduados em Educação Matemática.
Às minhas irmãs Cleuzilene Vieira da Silva e Cleuzilaine Vieira da Silva que me escutaram nos momentos de angústia e me apoiaram.
Ao meu marido João Arlindo Batista Pereira pela participação direta neste trabalho, pelas leituras e preciosa ajuda na formatação.
Obrigada à Eliana Gomes de Oliveira por ter dividido comigo momentos especiais durante o tempo em que permanecemos juntas em São Paulo.
Ao grupo de pesquisa PEA-Mat, cujas discussões e contribuições nas reuniões me ajudaram no estudo de teorias da Educação Matemática e me auxiliaram por meio da troca de experiências.
Agradeço a CAPES, pelo apoio com a bolsa de estudo do tipo taxa.
A todos que, direta ou indiretamente, contribuíram para a realização deste trabalho,
Epígrafe
SILVA, Cleusiane Vieira. A prática docente e sua influência na construção de conceitos geométricos: um estudo sobre o ensino e a aprendizagem da simetria ortogonal. 301 p. 2015. Tese (doutorado em Educação Matemática) – Pontifícia Universidade Católica de São Paulo - São Paulo, 2015.
RESUMO
Esta tese teve por objetivo investigar como um ambiente de ação e reflexão, que envolve a pré-análise, reflexões sobre a pré-análise, experimentação com alunos do Ensino Fundamental II, pós-análise e reflexões sobre a pós-análise relacionadas a uma sequência didática sobre a simetria ortogonal, interfere nos saberes docentes de professores de Matemática desse mesmo nível de ensino. Portanto, foi pretensão desta pesquisa responder à seguinte questão: como um ambiente de ação e reflexão constituído nos horários destinados às Atividades Complementares (A.C.) pode influenciar os saberes docentes de professores de Matemática do Ensino Fundamental II, sobre a simetria ortogonal? A metodologia utilizada para este estudo apoiou-se nos pressupostos da Engenharia Didática, segundo Artigue (1995) e nas contribuições de Schön (1995; 2000). O referencial teórico baseou-se na Teoria das Situações Didáticas de Brousseau (1997), para fazer um estudo sobre a influência das variáveis didáticas escolhidas nos procedimentos e respostas de professores de Matemática do Ensino Fundamental II e de seus alunos, e Margolinas (2002; 2004), para realizar a análise da atividade do professor no sentido de compreender como esse profissional desenvolve sua prática docente e como esta influência na aprendizagem dos alunos. O referencial teórico baseou-se ainda no quadro dos Paradigmas Geométricos de Parzysz (2001; 2006) na análise da natureza do trabalho geométrico desenvolvido por professores nos momentos de resolução e análise das situações-problema e por alunos nos momentos de interação com essas mesmas situações-problema. Foram utilizados, como trabalho de referência, os estudos de Grenier (1988) para observar as concepções de alunos do Ensino Fundamental II quanto à simetria ortogonal. A análise nos registros fornecidos pelos alunos propiciou a identificação de concepções relativas à simetria ortogonal, algumas corroboram os resultados obtidos nos estudos realizados por Grenier (1988), outras parecem específicas do grupo de alunos investigado. A análise nos registros de professores de Matemática também expôs algumas concepções acerca da simetria ortogonal, cujas concepções parecem estar relacionadas à forma como esse conceito é apresentado nos livros didáticos. Durante a investigação, os professores avaliaram a própria prática e ponderaram sobre os métodos de ensino adotados por eles, no sentido de observar se tais métodos estão ou não surtindo efeito na aprendizagem de seus alunos. Constatou-se que um ambiente de ação e reflexão, constituído na escola, influencia nos saberes docentes de professores de Matemática, embora sua influência seja limitada.
SILVA, Cleusiane Vieira. The teaching practice and its influence in the building of geometric concepts: a study on the teaching and learning of orthogonal symmetric. 301 p. 2015. Thesis (Doctorate in Mathematical Education) – Pontifícia Universidade Católica de São Paulo - São Paulo, 2015.
ABSTRACT
This thesis aimed to investigate how an environment of action and reflection that involves the pre-analysis , reflections on the pre-analysis , experimentation with students from Elementary School II , post-analysis and reflections on the post-analysis that is related to a didactic sequence on orthogonal symmetric , interferes in the Mathematics teachers’ knowledge , in the mentioned level. Nevertheless, this research aimed to answer the following question: how can an environment of action and reflection that is constituted in the times for the
Complementary Activities, influence the Mathematics teachers’ (from
Elementary School II) knowledge on orthogonal symmetric? The methodology that was used in this study was based on the presupposition of Didactical Engineering according to Artigue (1995) and on the contributions by Schön (1995; 2000). The theoretical referential had its basis on the Theory of Didactical Situations - Brousseau (1997) - to do a study on the influence of the didactical variables that were chosen in the Math teachers’ (Elementary School II) procedures and answers, as well as their students’, and Margolinas (2002; 2004) to hold an analysis on the teacher’s activity, in view of understanding how he/she develops the teaching practice and how it can influence students’ learning. Yet, the theoretical referential was based in Parzysz Picture of Geometric Paradigms (2001; 2006), in the analysis of the nature of the geometric work that is developed by teachers in the moments of construction and analysis of problem – situations, and by students in the moments of interaction with these problems. The studies by Grenier (1988) were used as a reference in order to observe the students’ conceptions of Elementary School II according to orthogonal symmetric. The analysis of the registers that had been provided by the students made it possible the identification of conceptions that are related to the orthogonal symmetric – some of them corroborate with the results from studies done by Grenier (1988); other ones seem to be specific in the group of investigated students. The analysis of registers of Math teachers also showed some concepts about orthogonal symmetric, and these conceptions seem to be related to the way this concept is presented in the course books. During the investigation, teachers had the opportunity to evaluate their own practice and reflected on the teaching methods they were using, to really know if they were working or not with their students. It was noted that an environment of action and reflection that is constituted at school, have influence on Math teachers’ knowledge, but this influence is limited.
LISTA DE FIGURAS
Figura 1. Questão 5 do teste 1 aplicado aos alunos na pesquisa “Análise dos erros cometidos por discentes de cursos de Licenciatura em Matemática das
universidades estaduais baianas” ... 34
Figura 2. Representação do Teorema de Desargues ... 42
Figura 3. Representação do Teorema de Menelau ... 43
Figura 4. Representações do Teorema de Menelau para os triângulos OQR, ORP e OPQ, respectivamente. ... 43
Figura 5. Involução de Desargues ... 44
Figura 6. Exemplo ilustrativo para métodos de transformação de figuras ... 45
Figura 7.Ponto P’ simétrico do ponto P em relação à reta r. ... 51
Figura 8. Transformações Geométricas no plano ... 52
Figura 9. Reflexão do ponto P com relação à reta t e do ponto P’ com relação à reta r ... 53
Figura 10. Reflexão do ponto P com relação às retas r e s respectivamente .. 54
Figura 11. A simetria ortogonal em torno do eixo OX transforma P=(x, y) em P’=(x, -y). ... 55
Figura 12. A simetria com relação à r leva OX em OX1 e OY em OY1 ... 56
Figura 13. A simetria com relação à reta
y
ax
b
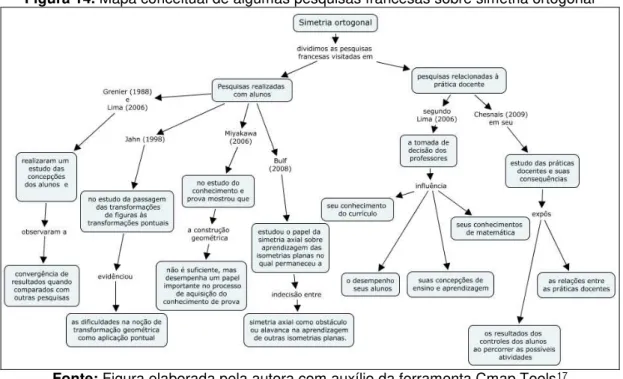
leva P em P1, com etapas intermediárias de P’ a P’’. ... 57Figura 14. Mapa conceitual de algumas pesquisas francesas sobre simetria ortogonal ... 67
Figura 15. A importância do papel do professor... 68
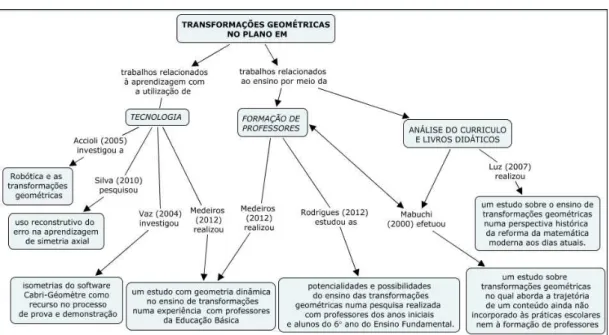
Figura 16. Algumas pesquisas brasileiras sobre transformações geométricas no plano ... 74
Figura 17. Situações propostas por Grenier ... 79
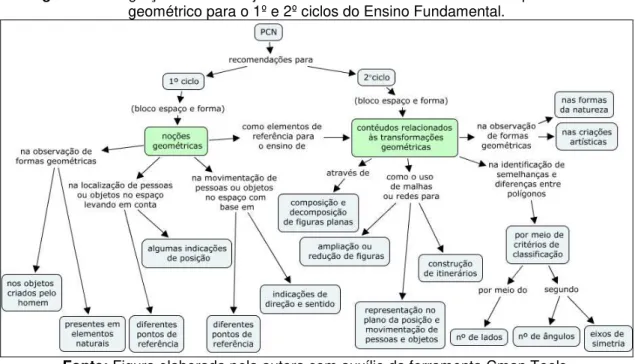
Figura 18. Integração entre os objetos envolvidos no desenvolvimento do pensamento geométrico para o 1º e 2º ciclos do Ensino Fundamental. ... 89
Figura 19. Mapa conceitual sobre a relação entre os conteúdos que envolvem a simetria ortogonal no 3º ciclo do Ensino Fundamental. ... 90
Figura 22. Atividade lúdica sobre simetria ortogonal ... 100
Figura 23. Os eixos de simetria do triângulo equilátero ... 101
Figura 24. Os eixos de simetria do losango e do quadrado ... 101
Figura 25. Exemplos de revestimentos utilizando mosaicos ... 102
Figura 26. Figura referente à situação 1, na análise de livros didáticos ... 104
Figura 27. Figura referente à situação 2, na análise de livros didáticos ... 106
Figura 28. Figura referente à situação 3, na análise de livros didáticos ... 107
Figura 29. Figura referente à situação 4, na análise de livros didáticos ... 109
Figura 30. Figura referente à situação 5, na análise de livros didáticos ... 110
Figura 31. Exemplo ilustrativo da estruturação do milieu, segundo Margolinas (2004). ... 124
Figura 32. Construção intuitiva do segmento simétrico ... 125
Figura 33. Desenho de pontos simétricos a A e B ... 125
Figura 34. Construção do segmento A'B' ... 126
Figura 35. Articulação entre os quadros teóricos ... 138
Figura 36. Fluxograma de processos 1ª parte ... 153
Figura 37. Fluxograma de processos 2ª parte ... 154
Figura 38. Fluxograma de processos 3ª parte ... 155
Figura 39. Continuação da 3ª parte do fluxograma de processos... 157
Figura 40. Fluxograma de processos 4ª parte ... 158
Figura 41. Questão 2 referente à concepção de aprendizagem do professor ... 160
Figura 42. Ponto de partida para a construção dos mapas conceituais ... 165
Figura 43. Rascunho de mapa conceitual confeccionado pelos professores no ambiente papel e lápis. ... 166
Figura 44. Mapa conceitual construído pelos professores ... 168
Figura 45. Situação-problema 1 do instrumento aplicado aos professores.... 172
Figura 46. Situação-problema 2 do instrumento aplicado aos professores.... 178
Figura 47. Situação-problema 3 do instrumento aplicado aos professores.... 183
Figura 48. Questão discursiva 1 para análise do professor sobre as situações-problema ... 191
Figura 49. Questão discursiva 2 do instrumento aplicado aos professores .. 191
Figura 51. Questão discursiva 4 do instrumento aplicado aos professores ... 192
Figura 52. Resposta do professor Narciso à questão discursiva 3 do
instrumento aplicado aos professores ... 205
Figura 53. Observação dos professores quanto à posição da figura
simétrica em relação à posição do eixo de simetria, item (i). ... 213
Figura 54. Observação dos professores quanto à posição da figura
simétrica em relação à posição do eixo de simetria no item (d)... 215
Figura 55. Item sugerido pelos professores para ser adicionado à
sequência didática aplicada aos alunos. ... 217
Figura 56. Exemplos de eixos de simetria desenhados na figura
correspondente ao item (a) da situação-problema 1 pelas duplas B, E e M respectivamente. ... 223
Figura 57. Exemplos de eixos de simetria desenhados na figura
correspondente ao item (b) da situação-problema 1 pelas duplas B, L e M respectivamente. ... 224
Figura 58. Exemplos de eixos de simetria desenhados na figura
correspondente ao item (c) da situação-problema 1 pelas duplas K e Q
respectivamente. ... 225
Figura 59. Exemplos de falsos eixos de simetria desenhados na figura correspondente ao item (d) da situação-problema 1 pelas duplas E, D e K respectivamente. ... 226
Figura 60. Exemplos de eixos de simetria desenhados na figura
correspondente ao item (e) da situação-problema 1, pelas duplas C, E, I e L, respectivamente. ... 227
Figura 61. Desenhos das duplas B e N respectivamente ... 231
Figura 62. Desenhos das duplas A e D respectivamente. ... 231
Figura 63. Item (b) não respondido pela dupla H e item (n) respondido
erroneamente pela dupla H. ... 255
Figura 64. Resposta da dupla H para os itens (c) e (f) da
situação-problema 3. ... 256
Figura 65. Resposta das duplas D e E para os itens (c) e (f),
respectivamente, da situação-problema 3. ... 257
Figura 67. Atividade preparatória, em vista da Avaliação Complementar,
proposta pela professora Margarida ... 272
Figura 68. Questão 26 proposto na Avaliação Complementar da
Secretaria de Educação do Estado da Bahia para alunos do 7º ano... 273
Figura 69. Questão 31 proposta na Avaliação Complementar da
LISTA DE QUADROS
Quadro 1. Variáveis didáticas e concepções detectadas por Grenier (1988) .. 80
Quadro 2. Síntese dos resultados de uma investigação preliminar ... 81
Quadro 3. Conteúdos de geometria listados por série (1ª a 4ª série) ... 93
Quadro 4. Conteúdos de geometria listados por série (5ª a 8ª série) ... 94
Quadro 5. Importância dada à simetria nos livros didáticos aprovados no PNLD 2014 ... 97
Quadro 6. Variáveis didáticas e valores levados em conta na elaboração e escolha das tarefas ... 120
Quadro 7. Estruturação do milieu ... 123
Quadro 8. Estruturação do milieu ascendente para o exemplo ilustrativo ... 127
Quadro 9. Diferentes aspectos dos Paradigmas Geométricos ... 131
Quadro 10. Síntese da classificação dos paradigmas apresentados por Parzysz ... 132
Quadro 11. Aplicação do quadro dos Paradigmas Geométricos ao exemplo 1. ... 133
Quadro 12. Articulação entre os estudos desenvolvidos por Parzysz, Van Hiele, Houdement e Kuzniak... 136
Quadro 13. Quatro primeiras questões do questionário 1 aplicado aos professores ... 148
Quadro 14. Formação dos docentes sujeitos da pesquisa. ... 148
Quadro 15. Respostas dos professores sobre cursos realizados ... 150
Quadro 16. Respostas dos professores à questão: o que você entende por geometria? ... 151
Quadro 17. Questões 3 a 6 referentes ao ensino de Geometria ... 161
Quadro 18. Respostas dos professores referentes à questão 3. ... 162
Quadro 19. Questões 7, 8,9 ,10 e 11 ... 163
Quadro 20. Variáveis didáticas e valores identificados na situação-problema 1 ... 173
Quadro 22. Variáveis didáticas e valores identificadas para a
situação-problema 2 ... 178
Quadro 23. Análise da segunda situação-problema, de acordo com os Paradigmas Geométricos (PARZYSZ, 2001; 2006) ... 179
Quadro 24. Estruturação do milieu das situações-problema sobre reconhecimento de figuras simétricas e construção de eixos de simetria ... 181
Quadro 25. Variáveis didáticas e valores levados em conta na elaboração e escolha do conjunto de atividades ... 185
Quadro 26. Análise da terceira situação-problema, de acordo com os Paradigmas Geométricos (PARZYSZ, 2001; 2006) ... 185
Quadro 27. Estruturação do milieu da situação-problema 3 ... 189
Quadro 28. Indicação dos eixos de simetria para cada figura dos itens propostos na situação-problema 1. ... 193
Quadro 29. Justificativa dada pelos professores às respostas fornecidas por eles na situação-problema 1 ... 194
Quadro 30. Estratégias dos professores, de acordo com as variáveis didáticas e seus valores para a situação-problema 1. ... 195
Quadro 31. Respostas dos professores à situação-problema 2 ... 197
Quadro 32. Identificação de estratégias escolhidas pelos professores para a situação problema 2, de acordo com as variáveis didáticas e seus valores outrora fixados. ... 198
Quadro 33. Repostas dos professores aos itens (a) e (m) ... 199
Quadro 34. Respostas dos professores aos itens (b), (h), (i) e (l) ... 200
Quadro 35. Respostas dos professores aos itens (c), (e) e (f) ... 201
Quadro 36. Respostas dos professores aos itens (d), (g) e (j) ... 202
Quadro 37. Identificação de estratégias escolhidas pelos professores para a situação-problema 3 de acordo com as variáveis didáticas e seus valores outrora fixados. ... 203
Quadro 38. Respostas dos professores, com relação à questão discursiva 2 ... 206
Quadro 39. Respostas dos professores com relação à questão discursiva 4 ... 207
Quadro 41. Procedimentos de resolução, identificados nos registros das duplas de alunos para a situação problema 1. ... 228
Quadro 42. Procedimentos de resolução, identificados nos registros das
duplas de alunos para a situação-problema 1. ... 232
Quadro 43.Exemplos de desenhos de figura “simétrica” para os itens (a) e (m) fornecidos por algumas duplas de alunos. ... 234
Quadro 44.Exemplos de desenhos de figura “simétrica” para os itens (b), (h), (i) e (l) apresentados por algumas duplas de alunos. ... 236
Quadro 45. Exemplos de desenhos de figura “simétrica” para os itens (c), (e) e (f) nos registros de algumas duplas de alunos. ... 237
Quadro 46. Exemplos de desenhos de figura “simétrica” para os itens (d), (g), (j) e (n), apresentados por algumas duplas de alunos. ... 239
Quadro 47. Procedimentos de resolução identificados nos registros das
duplas de alunos para a situação problema 1. ... 242
Quadro 48. Respostas fornecidas pelos docentes ao analisarem os
registros de algumas duplas de alunos ... 247
Quadro 49. Comparativo entre o que foi previsto pelos docentes e a pós- análise nos registros das duplas de alunos B, D, E e H, quanto às
dificuldades que os alunos poderiam encontrar no item (a). ... 249
Quadro 50. Comparativo entre o que foi previsto pelos docentes e a pós-análise nos registros das duplas de alunos B, D, E e H, quanto às
dificuldades que os alunos poderiam encontrar no item (b). ... 250
Quadro 51. Comparativo entre o que foi previsto pelos docentes e a pós-análise nos registros das duplas de alunos B, D, E e H, quanto às
dificuldades que os alunos poderiam encontrar no item (c). ... 251
Quadro 52. Comparativo entre o que foi previsto pelos docentes e a pós-análise nos registros das duplas de alunos B, D, E e H, quanto às
dificuldades que os alunos poderiam encontrar no item (d). ... 252
Quadro 53. Comparativo entre o que foi previsto pelos docentes e a pós-análise nos registros das duplas de alunos B, D, E e H, quanto às
dificuldades que os alunos poderiam encontrar no item (e). ... 253
Quadro 54. Respostas dos professores ao analisarem os registros das
Quadro 55. Respostas dos professores ao analisarem os registros dos
alunos com relação à construção de figura simétrica ... 256
Quadro 56. Respostas dos professores ao analisarem os registros dos
alunos sobre a influência das variáveis didáticas. ... 258
Quadro 57. Pós-análise nos registros das duplas de alunos B, D, E e H
quanto à influência das variáveis didáticas. ... 258
Quadro 58. Respostas dos professores ao analisarem os registros dos
alunos sobre a utilização dos instrumentos de desenho geométrico ... 259
LISTA DE TABELAS
Tabela 1. Quantidade de tarefas propostas nos livros didáticos analisados sobre simetria ortogonal ... 113
Tabela 2. Frequência da utilização de alguns materiais para planejamento das aulas de matemática ... 159
Tabela 3. Frequência das respostas dos alunos para o item (a) da
situação-problema 1 ... 222
Tabela 4. Frequência das respostas dos alunos para o item (b) da
situação-problema 1 ... 223
Tabela 5. Frequência das respostas dos alunos para o item (c) da
situação-problema 1 ... 225
Tabela 6. Respostas das duplas de alunos para o item (d) da
situação-problema 1 ... 226
Tabela 7. Respostas das duplas de alunos para o item (e) da
situação-problema 1 ... 227
Tabela 8.Frequência do número de respostas e justificativas das duplas de alunos para a situação-problema 2 ... 230
Tabela 9. Frequência das respostas das duplas de alunos para a
SUMÁRIO
INTRODUÇÃO ... 33
CAPÍTULO 1... 39
UM ESTUDO SOBRE O OBJETO MATEMÁTICO TRANSFORMAÇÕES GEOMÉTRICAS NO PLANO ... 39
1.1 Um breve histórico sobre as transformações geométricas ... 39
1.1.1 A Geometria projetiva e seus precursores ... 41
1.1.2 A gênese das primeiras transformações... 45
1.1.3 A importância da geometria de Descartes para a evolução das transformações geométricas ... 46
1.1.4 Os trabalhos de Felix Klein e de Sophus Lie ... 47
1.2 O grupo das Transformações Geométricas ... 48
1.3 A escolha da Simetria Ortogonal como objeto matemático a ser estudado ... 51
CAPÍTULO 2... 61
A PROBLEMÁTICA ... 61
2.1 Algumas pesquisas relacionadas ao ensino e à aprendizagem de transformações geométricas no plano ... 61
2.1.1 Pesquisas francesas relacionadas ao ensino e à aprendizagem de simetria ortogonal ... 62
2.1.2 As pesquisas brasileiras relacionadas ao ensino e à aprendizagem de transformações geométricas ... 69
2.2 Caracterização do termo concepção ... 75
2.3 Especificidade de nosso estudo ... 78
2.4 Justificativa e relevância de nosso estudo ... 79
CAPÍTULO 3... 83
UM ESTUDO SOBRE A SIMETRIA ORTOGONAL À LUZ DA ECOLOGIA DO DIDÁTICO ... 83
3.1 A simetria ortogonal numa problemática ecológica ... 83
3.3 Os documentos curriculares oficiais e o ensino da simetria
ortogonal no ensino fundamental ... 87
3.3.1 As transformações geométricas segundo os Parâmetros Curriculares Nacionais ... 87
3.3.2 A simetria ortogonal segundo as Diretrizes Curriculares de Matemática para o Ensino Fundamental do Estado da Bahia ... 92
3.4 A Simetria Ortogonal e as condições de sua existência ... 95
3.4.1 A simetria ortogonal em alguns livros didáticos de matemática para Ensino Fundamental II ... 97
3.4.2 Análise das quatro coleções de livros didáticos de Matemática ... 99
3.4.2.1 A organização praxeológica ... 102
3.5 Algumas reflexões ... 116
CAPÍTULO 4 ... 119
FUNDAMENTAÇÃO TEÓRICA ... 119
4.1 A Teoria das Situações Didáticas ... 119
4.2 O quadro dos Paradigmas Geométricos ... 128
4.2.1 O modelo do desenvolvimento do pensamento geométrico de Van Hiele ... 128
4.2.2 O quadro dos Paradigmas Geométricos apresentados por Houdement e Kuzniak... 130
4.2.3 O quadro teórico dos Paradigmas Geométricos apresentado por Parzysz ... 131
4.2.4 Uma articulação entre o quadro dos Paradigmas Geométricos proposto por Parzysz e a Teoria das Situações Didáticas de Brousseau ... 137
CAPÍTULO 5 ... 141
METODOLOGIA E PROCEDIMENTOS METODOLÓGICOS ... 141
5.1 A engenharia didática e a formação de professores ... 141
5.2 A produção e coleta de dados ... 145
5.3 O campo e os sujeitos da pesquisa ... 146
5.3.1 A escola ... 146
5.3.2 Caracterização dos sujeitos ... 147
CAPÍTULO 6 ... 159
6.2 Mapas Conceituais ... 164 6.2.1. Análise dos mapas conceituais concebidos pelos professores ... 165
CAPÍTULO 7... 171
O ESTUDO EXPERIMENTAL SOBRE AS CONCEPÇÕES DE
PROFESSORES E ALUNOS SOBRE A SIMETRIA ORTOGONAL ... 171
7.1 Análise, a priori, das situações-problema apresentadas para a pré-análise dos professores ... 171 7.1.1 Problemas de reconhecimento de figuras simétricas e construção de eixos de simetria ... 172 7.1.2 Problemas de construção de figura simétrica ... 183 7.1.3 Análise das questões discursivas propostas aos professores ... 190 7.2 Experimentação 1: aplicação das situações-problema e do
questionário sobre estas situações aos professores sujeitos da pesquisa ... 192 7.2.1 Etapa 1 da experimentação 1: análise, aposteriori, das respostas apresentadas pelos professores às situações-problema ... 193 7.2.1.1 Análise, a posteriori, das respostas apresentadas pelos
professores à situação--problema 1 ... 193 7.2.1.2 Análise, a posteriori, das respostas apresentadas pelos
professores a situação--problema 2 ... 196 7.2.1.3 Análise, a posteriori, das respostas dos pelos professores a
situação-problema 3 ... 199 7.2.2 Etapa 2 da experimentação 1: as respostas dos professores ao
questionário discursivo e as discussões nas reuniões sobre a pré-análise das situações-problema ... 204 7.2.2.1 Análise dos dados provenientes das discussões no debate coletivo sobre a pré-análise realizada pelos docentes sobre a situação-problema 1 .. 208 7.2.2.2 Análise dos dados oriundos das discussões no debate coletivo sobre a pré-análise realizada pelos professores para a
situação-problema 2 ... 211 7.2.2.3 Análise dos dados provenientes das discussões no debate
coletivo sobre a pré-análise realizada pelos professores, para a
7.2.2.4 Uma síntese de nossa análise sobre as respostas de professores ao questionário discursivo e as discussões nas reuniões sobre a pré-análise desses docentes às situações--problema ... 216 7.3 Experimentação 2: aplicação das situações-problema analisadas pelos professores, sujeitos da pesquisa, a alunos do 8º ano do Ensino
Fundamental ... 220 7.3.1 Análise, aposteriori, dos procedimentos e respostas
apresentadas pelas duplas de alunos à sequência didática ... 222 7.3.1.1 Análise, a posteriori, das respostas de alunos do 8º ano do
Ensino Fundamental a situação-problema 1 ... 222 7.3.1.2 Uma síntese de nossa análise sobre as respostas de alunos do 8º ano do Ensino Fundamental a situação-problema 1 ... 228 7.3.1.3 Análise a posteriori das respostas de alunos do 8º ano do Ensino Fundamental a situação-problema 2 ... 229 7.3.1.4 Uma síntese de nossa análise sobre as respostas de alunos do 8º ano do Ensino Fundamental à situação-problema 2 ... 232 7.3.1.5 Análise, a posteriori, das respostas de alunos do 8º ano do Ensino Fundamental ao conjunto de atividades que compõem a
situação-problema 3 ... 233 7.3.1.6 Uma síntese de nossa análise sobre as respostas de alunos do 8º ano do Ensino Fundamental à situação-problema 3 ... 241 7.3.1.7 Algumas considerações sobre a experimentação 2 e a análise dos registros das duplas de alunos, sujeitos da pesquisa ... 244 7.4 Experimentação 3: as respostas de algumas duplas de alunos do 8º ano à sequência didática sob o olhar de docentes, sujeitos da
pesquisa ... 246
CONSIDERAÇÕES E PERSPECTIVAS ... 279
REFERÊNCIAS ... 291
APÊNDICE 1 ... 299
APÊNDICE 2 ... 301
APÊNDICE 3 ... 302
APÊNDICE 4 ... 303
APÊNDICE 7 ... 312
ANEXO 1 ... 315
ANEXO 2 ... 316
ANEXO 3 ... 317
ANEXO 4 ... 318
ANEXO 5 ... 319
INTRODUÇÃO
A trajetória para a construção de nosso objeto de estudo iniciou-se em 2007, quando nós, professores do curso de Licenciatura em Matemática com Enfoque em Informática da Universidade Estadual do Sudoeste da Bahia (UESB), Campus Jequié, inquietados com as altas taxas de reprovação e evasão das disciplinas desse curso, propusemos à Fundação de Amparo à Pesquisa do Estado da Bahia (FAPESB) o projeto de pesquisa intitulado “Análise dos erros cometidos pelos discentes de cursos de Licenciatura em Matemática das universidades estaduais baianas” (BORTOLOTI, et al. 2007) que foi aprovado com recurso financeiro.
Como a equipe de investigadores tinha a pretensão de obter um panorama das dificuldades em Matemática (referentes aos conteúdos da Educação Básica) que incidiam sobre os alunos no Estado da Bahia, delimitamos como campo de pesquisa as quatro Universidades Estaduais baianas, das quais, duas são multicampi. Foram abrangidos dez campi que possuem cursos de licenciatura em Matemática.
Os sujeitos investigados foram alunos ingressantes (1º semestre) e alunos veteranos (6º semestre) dos cursos de licenciatura em Matemática das Universidades Estaduais baianas. Ao aplicar o teste 1 a alunos ingressantes, o objetivo da pesquisa era investigar como esses alunos estavam chegando à universidade, isto é, qual o background deles em relação a conteúdos básicos de Matemática. Quanto aos alunos do 6º semestre, tínhamos como meta verificar se, após a metade do curso, eles haviam adquirido habilidades para resolver questões matemáticas referentes a conteúdos da Educação Básica.
geometria plana, pelo fato de nosso interesse de investigação estar voltado para esse eixo.
Para concretização da pesquisa, utilizamos como instrumentos de coleta de dados dois testes diagnósticos e um questionário socioeconômico. O teste 1, constava de seis questões de conteúdos de matemática da Educação Básica. Dessas, duas contemplavam o conteúdo de geometria plana. A primeira questão tratava de um problema quotidiano e vem enunciado a seguir:
Um fazendeiro comprou um terreno de forma retangular com 30m de perímetro, notando que o triplo da medida do menor lado é igual ao dobro da medida do lado maior. Resolveu plantar grama em todo o terreno, exceto em uma semicircunferência, cujo diâmetro coincide com lado menor. Considerando--se que o valor aproximado de π=3,14 e que o m2 da grama custa R$40,00, determine quanto o fazendeiro gastou.
A análise quantitativa dos dados evidenciou que, com relação à resolução dessa questão, apenas 8,02% dos alunos do 1° semestre e 30,07% dos alunos do 6° semestre a acertaram. Observamos, ainda, que 30,67% dos sujeitos de 1º semestre e 20,98% dos sujeitos dos 6º semestre não responderam a questão.
A segunda questão tinha como foco a semelhança de triângulos, e era enunciada da seguinte forma. Na figura, AB= 8 u.c., BC= 1 u.c., e os triângulos sombreados são equiláteros. Sobre os triângulos sombreados, calcule o quociente entre o valor da área do triângulo maior e a área do triângulo menor.
Figura 1.Questão 5 do teste 1 aplicado aos alunos na pesquisa “Análise dos erros cometidos por discentes de cursos de Licenciatura em Matemática das universidades estaduais baianas”
Fonte: Adaptada do Vestibular UESC, 2008
Esses dados nos fizeram refletir sobre algumas questões ligadas ao ensino de geometria na Educação Básica e no Ensino Superior. No que diz respeito à Educação Básica, algumas dúvidas nos inquietaram. Entre elas, as dificuldades relacionadas com o conteúdo de geometria plana parecem ligadas às práticas de ensino, adotadas por professores dos níveis Fundamental e Médio. Segundo as observações de Almouloud et al. (2004, p. 99), “[...] a maioria dos professores do Ensino Fundamental e do Ensino Médio não está preparada para trabalhar segundo as recomendações e orientações didáticas dos PCN1”.
Com relação ao Ensino Superior, apesar de o desempenho dos alunos do 6º semestre ser melhor do que o desempenho dos alunos ingressantes, essa diferença deveria ser maior, em função do avançado processo de formação que apresentavam os alunos veteranos. Isso nos estimulou a refletir sobre a formação de professores que ensinam Matemática, no que se refere ao ensino e à aprendizagem da geometria. Essa inquietação é reforçada por Almouloud et al. (2004), quando afirmam que a formação de professores:
[...] é muito precária quando se trata de geometria, pois os cursos de formação inicial não contribuem para que façam uma reflexão mais profunda a respeito do ensino e da aprendizagem dessa área da matemática. Por sua vez a formação continuada não atende ainda aos objetivos esperados em relação à geometria. (p. 99)
A análise das respostas dos estudantes assinalou que as dificuldades apresentadas são relacionadas, principalmente, à interpretação de significados e conceitos geométricos.
interfere nos saberes docentes de professores de Matemática do Ensino Fundamental II.
Assim, abordaremos nesta pesquisa, a seguinte questão: como um ambiente de ação e reflexão constituído nos horários destinados às Atividades Complementares (A.C.) pode influenciar os saberes docentes de professores de Matemática do Ensino Fundamental II sobre a simetria ortogonal? Para isso, construímos uma sequência didática sobre a simetria ortogonal, com a intenção de que, por meio da ação, esta pudesse provocar a reflexão de professores de Matemática sobre o ensino e a aprendizagem deste objeto matemático com a finalidade de ponderar como esse movimento pode interferir nos saberes docentes.
Para o presente trabalho, escolhemos como metodologia de pesquisa a Engenharia Didática de Artigue (1995) por acreditar que essa metodologia seja adequada para um estudo que envolve os processos de ensino e de aprendizagem, uma vez que ela permite, a partir do confronto das análises a
priori e a posteriori, confirmar ou refutar hipóteses. A escolha foi fortalecida pelos argumentos de Chesnais (2009) sobre a necessidade de seus estudos serem confrontados com outros contextos. Apoiamo-nos, ainda, em Schön (1995; 2000) com o objetivo de criar um ambiente de ação e reflexão em que os professores sejam capazes de refletir sobre sua própria prática. Durante a experimentação, trabalhamos com professores de Matemática do Ensino Fundamental II e seus alunos, em uma escola da rede estadual de ensino do Estado da Bahia. Utilizamos como instrumentos de coleta de dados: questionários, entrevistas, fichas de observação e gravações de áudio.
Para este estudo, utilizamos como referencial teórico o quadro dos Paradigmas Geométricos no modelo apresentado por Parzysz (2001; 2006) associado à Teoria das Situações Didáticas. Escolhemos o quadro dos Paradigmas Geométricos por acreditar que ele permite um estudo sobre o desenvolvimento do raciocínio geométrico dos sujeitos, para os docentes nos momentos de análise da sequência didática e registros dos alunos, e para os alunos nos momentos de interação com o conjunto de atividades que compõem a referida sequência.
didáticas escolhidas nos procedimentos e respostas de professores de Matemática do Ensino Fundamental II e de seus alunos. Apoiamo-nos em Margolinas (2002; 2004), seguindo o modelo de níveis de atividade do professor, para compreender as várias fases do trabalho docente. Esse modelo deve permitir fazer um estudo da atividade do professor nas diferentes dialéticas que ele deve vivenciar no processo de aprendizagem, isto é, as dialéticas de ação, formulação, validação e institucionalização.
A seguir, apresentamos a estrutura do trabalho, composto de sete capítulos.
No primeiro capítulo, apresentamos um estudo sobre as transformações geométricas no plano, o qual é iniciado com um breve histórico sobre esses objetos geométricos, seguido por uma apresentação sobre o grupo das transformações geométricas e os motivos que nos levaram a escolher a simetria ortogonal como objeto matemático a ser estudado.
No segundo capítulo, tratamos da problemática que envolveu nossa investigação, a partir do estudo de algumas pesquisas relacionadas ao ensino e à aprendizagem das transformações geométricas no plano, em especial, a simetria ortogonal. Apresentamos, ainda, a questão de pesquisa, os objetivos, a especificidade do estudo e, por fim, sua justificativa e relevância.
No terceiro capítulo, realizamos um estudo ecológico sobre a simetria ortogonal, cujo objetivo principal foi o estudo das condições de existência desse objeto matemático em um sistema de ensino público. Para isso, realizamos estudos nos documentos curriculares oficiais, tanto no contexto nacional quanto no contexto estadual e análise de livros didáticos.
No quarto capítulo, apresentamos o quadro teórico utilizado na pesquisa, em que optamos por utilizar a Teoria das Situações Didáticas no sentido de Brousseau (1997) e de Margolinas (2002; 2004) associada ao quadro dos Paradigmas Geométricos propostos por Parzysz (2001; 2006).
No sexto capítulo, trataremos dos procedimentos iniciais de experimentação, cujo foco é a prática docente relacionada ao ensino de geometria, por meio da análise de um questionário aplicado aos professores e da análise dos mapas conceituais sobre simetria por eles construídos e discutidos durante encontros na escola.
No último capítulo, apresentamos o estudo experimental, que está dividido nas seguintes subseções: análise a priori do conjunto de atividades que compõem a sequência didática; experimentação 1; experimentação 2; experimentação 3; a visão dos professores, sujeitos da pesquisa, durante e após a investigação sobre o ensino e a aprendizagem da simetria ortogonal.
Na experimentação 1, apresentamos a aplicação da sequência didática aos professores, a análise a posteriori e a análise do questionário discursivo respondidos por esses docentes sobre as atividades que compõem a sequência didática. Na experimentação 2, descrevemos a aplicação da sequência didática, analisada e modificada pelos professores, a alunos do 8º ano do Ensino Fundamental e a análise a posteriori dos registros fornecidos pelos discentes. Na experimentação 3, fazemos uma análise do olhar dos docentes sobre as respostas de algumas duplas de alunos do 8º ano à sequência didática. Por fim, apresentamos as considerações e perspectivas futuras para o estudo.
CAPÍTULO 1
UM ESTUDO SOBRE O OBJETO MATEMÁTICO
TRANSFORMAÇÕES GEOMÉTRICAS NO PLANO
Nosso objetivo, neste capítulo, é fazer um estudo sobre o objeto matemático transformações geométricas no plano, mais especificamente sobre simetria ortogonal. Inicialmente, apresentamos alguns elementos do desenvolvimento histórico e epistemológico das transformações geométricas, seguido pela importância do grupo das transformações geométricas na classificação das geometrias e, por fim, os motivos que nos levaram a escolher a simetria ortogonal como objeto matemático para pesquisa.
1.1 Um breve histórico sobre as transformações geométricas
O desenvolvimento da geometria tem como um dos fundamentos a necessidade de entender o mundo que nos cerca. Entre outras hipóteses, Boyer (1996, p. 05) declara que, “o desenvolvimento da geometria pode também ter sido estimulado por necessidades práticas de construção e demarcação de terras, ou por sentimentos estéticos em relação à configuração e ordem”. Esse autor, ainda exemplifica essa preocupação estética ao citar a presença de padrões geométricos em potes, cestas e tecidos que expressavam exemplos de congruência e simetria.
Ainda sobre esta busca de padrões Fedorov2, um cristalógrafo que
estudou grupos espaciais cristalográficos, afirma, segundo Galiulin (2003), que o cérebro humano sempre busca por regularidade em tudo e que isso é
2 Evgraf Stepanovich Fedorov foi um russo matemático, cristalógrafo e mineralogista. Ele
compreensível, porque um homem pode ser orientado em sua busca para um trabalho adequado, considerando apenas materiais agrupados regularmente. Contudo, a falta de documentos faz com que não seja possível, segundo Boyer (1996), acompanhar a evolução da matemática desde um desenho até um teorema que nos seja conhecido.
De acordo com esse mesmo autor, “os elementos de Euclides, não só constituem a mais antiga obra matemática a chegar até nós, mas o texto mais importante e influente de todos os tempos” (BOYER, 1996, p. 82). Segundo Jahn (1998), a geometria euclidiana fez uma amálgama entre uma descrição teórica da realidade e o desenvolvimento do raciocínio puramente dedutivo; ela ainda afirma que isto vai dominar durante todo o período compreendido entre a antiguidade e a aparição dos métodos axiomáticos modernos. A autora refere-se, especificamente, à geometria de Hilbert no final do século XIX. Justificando essa extensa espera, Boyer (1996, p.74) afirma que “durante esse longo intervalo a maioria dos matemáticos considerou a exposição de Euclides como logicamente satisfatória e pedagogicamente aceitável”.
Ao fazer uma descrição de como são tratados os objetos geométricos nos Elementos de Euclides, Jahn (1998) declara que as primeiras definições fornecidas por Euclides têm como referência uma percepção dos objetos da realidade, e que, portanto, seu papel é fazer um suporte concreto, uma referência ao senso comum para expor os fundamentos da geometria. A autora ainda afirma que Euclides não investigou como conferir a essas definições um status operatório no sentido de explicar sua axiomática.
Sobre a noção de figura, Vitrac3 citado por Jahn (1998) enfatiza que as
declarações de Euclides sugerem que uma figura é determinada sob três critérios: sua posição, sua forma e sua grandeza. Segundo ela, esse autor acrescenta que a figura não se reduz à sua fronteira (à superfície que a contém e de que faz parte), mas que isto significa que uma figura é um objeto constituído do espaço incluído entre as figuras. A autora afirma que “os objetos da geometria de Euclides são as figuras, tratadas de maneira estática e consideradas em sua globalidade como formas. Elas são constituídas de
elementos particulares tais como pontos e linhas.” (JAHN, 1998, p.27-28, tradução nossa)
A visão das figuras geométricas, levando em conta seus elementos particulares e a possibilidade de essas serem transformadas por meio da manipulação de suas propriedades, foi estudada na geometria projetiva. Na próxima seção apresentamos a motivação para tais estudos.
1.1.1 A Geometria projetiva e seus precursores
Sobre o aparecimento e a evolução da noção de transformações geométricas propriamente ditas, Jahn (1998, p.32, tradução nossa) pontua que “os problemas de representação dos objetos no espaço e os problemas de sombra foram preocupações dos pintores e artistas do Quattrocento4 que os
conduziu ao método das transformações e à geometria projetiva”. Segundo Eves (2002), famílias aristocráticas italianas patrocinavam artistas e poetas que estudavam trabalhos dos mestres gregos e italianos antigos. Dentre os artistas do renascimento podemos citar Leonardo da Vinci (1452-1519), Michelangelo (1475-1564), Benvenuto Cellini (1500-1571), Filippo Brunelleschi (1377-1446), Dürer (1471-1528) e Sandro Botticelli (1445-1510). As obras do Renascimento têm, como características principais, a simetria, a preocupação com a harmonia e com o equilíbrio, seja ela uma pintura ou uma escultura. Procurando dar mais realismo e naturalidade para suas obras, os artistas introduziram conceitos como ponto de fuga5 e perspectiva.
Em sua obra “Aperçu historique sur l’origine et le développement des méthodes en géométrie”, Chasles (1793-1880) cita como os trabalhos de Desargues (1591-1661), principalmente sua obra sobre seções cônicas, influenciou com aspectos da geometria projetiva alguns artistas do Renascimento. Este autor afirma que,
Desargues se ocupou das aplicações da Geometria para as artes, e tratou este assunto em relação ao homem superior, trazendo, com uma exatidão frequentemente desconhecida dos artistas, os princípios da universalidade que fazem reconhecer nele [em seu
4 Foram eventos culturais e artísticos do século XV na Itália que marcaram o início do
renascimento.
5 O ponto de fuga é a convergência de todas as linhas que representam planos perpendiculares
trabalho] pesquisas de pura geometria (CHASLES, 1875, p.84, tradução nossa).
Um dos trabalhos mais conhecidos de Desargues, e que deu início aos estudos que levaram à geometria projetiva é o teorema que traz o seu nome, apresentado juntamente com sua demonstração por Coxeter e Greitzer (1967) da seguinte forma:
Teorema de Desargues: Se dois triângulos estão em perspectiva6 em
relação a um ponto e se as retas suportes de seus pares de lados correspondentes se cortam, então os três pontos de concorrência são colineares.
Figura 2. Representação do Teorema de Desargues
Fonte: Figura elaborada pela autora, baseada em Coxeter eGreitzer (1967)
Demonstração: Dados dois triângulos PQR e P’Q’R’ em perspectiva em relação a um ponto O, tal que as retas suportes de seus pares de lados correspondentes se encontram nos pontos D, E, F (Figura 2), queremos mostrar que esses pontos são colineares. A demonstração aqui apresentada depende do Teorema de Menelau7 enunciado como “os pontos E, F, D
6 Segundo Coxeter e Greitzer (1967) duas figuras de um mesmo tipo estão em perspectiva por
um ponto se essas figuras compostas por pontos e linhas puderem ser colocadas em correspondência de tal forma que pares de pontos correspondentes são unidos por retas concorrentes.
pertencentes às retas suportes dos lados YZ, XZ e XY, do triângulo XYZ, são
colineares, se somente se, 1 YD XD XF ZF ZE YE ”.
Figura 3. Representação do Teorema de Menelau
Fonte: Figura elaborada pela autora, de acordo com Coxeter e Greitzer (1967)
Vamos aplicar o Teorema de Menelau, para as três tríades de pontos colineares DR’Q’, EP’R’ e FQ’P’ nos lados dos triângulos OQR, ORP e OPQ respectivamente.
Fazendo separadamente as representações do Teorema de Menelau para os triângulos citados temos:
Figura 4. Representações do Teorema de Menelau para os triângulos OQR, ORP e OPQ, respectivamente.
Fonte: figura elaborada pela autora
Para cada uma das representações da figura 4, obtemos referentes aos triângulos OQR, ORP e OPQ as relações apresentadas a seguir:
I) 1
' ' ' ' QQ OQ OR RR RQ QD
II) 1 ' ' ' ' RR OR OP PP PE RE
III) 1
Após multiplicar as três equações consecutivamente e efetuarmos um número modesto de cancelamentos obtemos:
1
QF PF PE RE RD QD
, portanto, D, E, e F são colineares como queríamos.
Outro teorema, que Chasles classifica como famoso é o teorema da involução de Desargues, enunciado por Ayres (1967) como:
Teorema: Se um quadrângulo simples é inscrito numa cônica C e se uma linha k, que não passa por nenhum dos seus vértices, é tal que intersecta
C em dois pontos, estes pontos são um par recíproco na involução8 sobre k
determinada pelo par de lados opostos do quadrângulo.
Figura 5. Involução de Desargues
Fonte: Elaboração da autora, segundo Ayres (1967)
A importância desses teoremas deve-se ao fato de servirem de fundamentos da teoria das cônicas de Desargues e de serem a origem de numerosas propriedades sobre as cônicas. Essas propriedades surgiram, muitas vezes, por meio de transformações geométricas. Segundo Jahn (1998), essas transformações eram utilizadas como ferramentas de demonstração, na medida em que elas permitiram transferir as propriedades sobre os objetos geométricos mais complexos que aqueles aos quais eram iguais. Ela ainda afirma que o estudo das transformações pretendia fazer aparecerem as propriedades geométricas invariantes no momento das transformações. Porém, como vimos na apresentação do teorema de Desargues, as transformações
utilizadas foram somente as projeções e elas permaneceram no contexto das cônicas.
Jahn (1998) ainda declara que as transformações geométricas como um objeto podem ser entendidas em vários níveis. De acordo com a autora, esse objeto pode ser considerado como as relações entre duas configurações geométricas ou entre duas partes de uma mesma configuração, o que pode ser observado quando analisamos figuras decorrentes da simetria ortogonal. Os conceitos aparecem, assim, ligados ao contexto das figuras e se trata em determinado momento de uma transformação de figuras.
A seguir, discorreremos sobre alguns métodos de transformações de figuras.
1.1.2 A gênese das primeiras transformações
Sobre a evolução dos métodos para a transformação de figuras, Chasles (1875) cita, como ponto de partida, as numerosas maneiras de originar cônicas sobre o plano, uma pela outra, além de dois processos que, segundo ele, se tornaram muito frequentes nas artes. Esse autor argumenta que o primeiro processo empregado por Stévin (1548-1667) e Mydorge (1585-1647) consistia em fazer crescer, a uma proporção constante, a ordenada de uma curva, e o segundo, em fazer girar essas ordenadas em torno de seus pés, a uma mesma grandeza angular, de forma que permaneçam paralelas entre si.
A seguir, construímos um exemplo que ilustra o primeiro método, e outro para ilustrar o segundo método de transformações de figuras descrito acima.
Figura 6. Exemplo ilustrativo para métodos de transformação de figuras
Chasles (1875) ainda declara que esses processos foram utilizados separadamente ou combinados de diversas maneiras, por Gregoire de St Vicent (1584 -1667) para transformar o círculo em elipse.
Ainda sobre os métodos para transformações de figuras, de acordo com Chasles (1875), o caso mais simples de um método de deformação de figuras tomou extensão entre as mãos de La Hire (1640-1718) e Newton (1643-1727). Esse autor ainda declara que Poncelet (1788-1867), no seu “tratado das propriedades projetivas”, alargou as figuras para três dimensões, apresentando na segunda parte daquela obra, um dos métodos mais poderosos da geometria moderna intitulada “Deformação Homográfica”.
1.1.3 A importância da geometria de Descartes para a evolução das transformações geométricas
No que tange à geometria de Descartes (1596 - 1650), ao falar sobre os métodos criados por Cavalieri (1598 – 1647), Fermat (1601 - 1665), Roberval (1602 – 1675) e Gregoire de St Vincent, Chasles (1875, p. 95, tradução nossa) pondera que “a concepção de Descartes, somente procurou os meios de aplicar estes métodos de uma maneira uniforme e geral, ela foi a introdução necessária aos novos cálculos de Leibniz (1646 - 1716) e de Newton”.
Ainda sobre as contribuições da geometria analítica com seus processos algébricos às transformações geométricas, Chasles (1875, p.196, tradução nossa) questiona: “não seria natural, introduzir, paralelamente, na geometria pura transformações análogas que atingissem diretamente as figuras propostas e as suas propriedades?” O autor ainda observa que
Nesse sentido, a geometria de Descartes fornece uma nova visão aos métodos de transformações de figuras desenvolvidos até então.
Piaget e Garcia (1987, p.108) argumentam que “o intervalo de tempo desde Desargues e Pascal até Poncelet e Chasles é o período durante o qual se consolida a geometria analítica, tendo como ponto de apoio as transformações algébricas. As transformações realizam-se através de equações”.
Segundo as observações acima, podemos notar que a geometria analítica exerceu um importante papel na evolução dos conceitos relativos às transformações geométricas. Foi com o trabalho de Felix Klein e Sophus Lie que esses conceitos foram formalizados com o rigor matemático.
1.1.4 Os trabalhos de Felix Klein e de Sophus Lie
Apesar de os estudos sobre como tornar as propriedades das figuras invariantes por métodos de transformações terem sido alvo de árduo trabalho por mais de dois séculos, foi nas mãos de Felix Klein (1849-1925) e Sophus Lie (1842-1899) que conceitos complexos como a aplicação da teoria de grupos à geometria se desenvolveram. O resultado dos esforços desses dois pesquisadores culminou com a proposição da teoria de grupos de transformações, resultando na classificação das geometrias.
Felix Klein tornou-se conhecido por meio do Programa Erlanger, considerado como um marco importante na Matemática do século XIX. Birkhoff e Bennett (1988) avaliam que a estreita amizade entre Felix Klein e Sophus Lie, no momento do Programa Erlanger, desempenhou um importante papel na vida acadêmica de ambos. De acordo com Birkhoff e Bennett (1988), os trabalhos de Klein e Lie eram complementares; exemplificam esse fato, dizendo que “Klein chamou a atenção para aspectos globais básicos da geometria, ao passo que os teoremas de Lie eram puramente locais.” (p. 146, tradução nossa).
podia ser aplicado, como um meio conveniente para caracterizar as várias geometrias que tinham aparecido durante o século”.
Na visão de Coxeter e Greitzer (1967), Felix Klein propôs a classificação das geometrias, de acordo com os grupos de transformações, isto sem alterar conceitos, axiomas e teoremas da geometria euclidiana, considerada, nesse caso, como uma das muitas geometrias.
Como este trabalho tem como foco principal a formação continuada de professores, acreditamos ser de grande importância o conhecimento desses sobre o contexto matemático em que a simetria ortogonal está inserida. Faremos na próxima seção um breve estudo sobre o grupo das transformações9.
1.2 O grupo das Transformações Geométricas
Inicialmente, definiremos transformação geométrica. Começando pela palavra transformação, segundo o dicionário Aurélio, da Língua Portuguesa, do ponto de vista matemático transformação é “qualquer operação em que se modifica um ente matemático ou que se mapeia uma configuração em outra” (FERREIRA, 2010, p. 2069). Já na Matemática definimos: uma transformação T no plano é uma aplicação T:, isto é, uma correspondência que
associa, a cada ponto P do plano, outro ponto P1 T
P do plano, denotado sua imagem por T. Seja um conjunto de transformações sobre o plano .Uma transformação T: diz-se injetiva, quando pontos P e Q
distintos em têm sempre imagens distintas, isto é, T
P T Q . Ou, ainda, Té injetiva, quando T
P T Q implicar em P=Q.Uma transformação T diz-se sobrejetora quando todo ponto
P
1 em
éimagem de pelo menos um ponto P, ou seja, para todo
P
1 em
existe P em
, tal que T
P P1. Sendo assim, uma transformação T que é, simultaneamente, injetiva e sobrejetiva é dita bijetiva.
9 Utilizamos como referências para este estudo as obras “isometrias” de Lima (1996) e “Um
Uma transformação bijetiva T: possui uma inversa T1:,
isto é, para todo ponto
P
1 em
, sua imagem 1
1P
T pela imagem inversa
1
T
é o único ponto P de
, tal que T
P P1. Se T1, dizemos que
possui inversa.Finalmente, definiremos uma transformação geométrica como uma aplicação bijetiva do plano nele mesmo. Sendo assim, se F é uma figura (um conjunto de pontos do plano) definiremos FT(F) como conjunto das
imagens dos pontos de F. Observemos que dessa última e das definições anteriores deriva que toda transformação geométrica possui inversa.
A transformação geométrica I:, definida por I(P) = P para todo
ponto P, é chamada transformação identidade. Se
I
, dizemos que
possui identidade.
Dadas duas transformações geométricas T1,T2 :, a composta
:
1 2 T
T é a aplicação que associa a cada ponto P do plano o ponto
T P
T2 1 . Portanto, por definição,
T2T1
P T2
T1
P
, ou seja,
T2T1
consiste em aplicar primeiro
T
1 e em seguidaT
2.Proposição: A composição de duas transformações geométricas é também uma transformação geométrica.
De fato, vamos mostrar inicialmente que a composição de duas
transformações geométricas é sobrejetora. Sejam
T
1 eT
2 duastransformações geométricas sobrejetoras em
. Temos que mostrar que dado
P
,
T2T1
P P. Observando queT
2 é sobrejetora, dado Pexiste P tal que T2
P P. Notando queT
1 também é sobrejetora, temos que dado P existe P tal que T1
P P. Logo.
T2T1
P PPortanto,
T2T1
é sobrejetora.Mostremos agora que
T2 T1
é injetora. Suponhamos
T2T1
P T2T1
Q ,então, por definição T2
T1
P
T2
T1
Q
, comoT
2 éinjetora, temos que T1
P T1
Q . Da mesma forma, comoT
1 é injetora P=Q.Como a composição
T2 T1
está em
, ou seja,
T2T1
é uma transformação geométrica quandoT
1 eT
2 também o são, dizemos que é umconjunto fechado com relação à composição.
Dizemos que o conjunto das transformações geométricas
possui apropriedade associativa se, para quaisquer elementos
T
1,T
2 eT
2 em
,satisfaz a lei associativa T1
T2 T3
T1T2
T3. Com efeito, para todo
P temos
T1
T2T3
P T1
T2T3
P
T1T2
T3
P
T1T2 T3
P .
Observamos que os conjuntos importantes de transformações geométricas são aqueles que apresentam identidade, inversa e satisfazem, simultaneamente, as propriedades de fechamento e associatividade. Tais conjuntos são chamados de grupos de transformações geométricas.
A importância de tais conjuntos, segundo Eves (2002), deve-se ao fato de Felix Klein definir geometria como “o estudo das propriedades de um conjunto S que permanecem invariantes quando se submetem os elementos de S às transformações de algum grupo de transformações ” (p. 606).
Segundo Coxeter e Greitzer (1967, p. 80, tradução nossa), “a geometria euclidiana é caracterizada particularmente pelo grupo das transformações semelhantes. Um caso particular importante das transformações semelhantes são as transformações isométricas”. Esse autor, ainda declara que as isometrias10 nos fornecem a ideia familiar de congruência, já que duas figuras
são congruentes se, e somente se, uma pode ser transformada em outra por meio de uma isometria.
O breve estudo histórico realizado ajudou-nos a compreender que a simetria ortogonal, apresentada como uma transformação geométrica no plano, que está inserida em um conjunto com propriedades específicas (o grupo das transformações) reveste o professor de uma série de conhecimentos necessários à sua formação profissional. Esses conhecimentos possibilitam ao professor utilizar a simetria ortogonal como ferramenta para estabelecer relações entre vários conceitos geométricos, além de auxiliá-lo na busca de
estratégias de ensino, cujo objetivo seja tornar a aprendizagem, de fato, efetiva e significativa para o aluno.
Além disso, o estudo sobre o surgimento e desenvolvimento das transformações geométricas mostrou a necessidade de investigar a importância das criações humanas (artísticas), principalmente, no ensino da simetria ortogonal. O estudo expôs, ainda, a importância de se observar o enfoque dado nos livros didáticos e as relações matemáticas propostas, quando se leva em conta o ensino de transformações geométricas no plano, de forma específica, sobre o ensino da simetria ortogonal. Expôs, também, a relevância de se estudar, por meio de um ambiente de ação e reflexão, a maneira como o professor faz tais relações.
1.3 A escolha da Simetria Ortogonal como objeto matemático a ser estudado
Nesta seção, apresentamos nossa motivação para a escolha da simetria ortogonal11 como objeto matemático para compor nossa pesquisa. Do ponto de
vista geométrico, definimos a simetria ortogonal (também designada como simetria axial ou reflexão) da seguinte forma: Seja P um ponto do plano que não pertence à reta r, a imagem de P por esta transformação é um ponto P’ tal que r seja a mediatriz do segmento PP’. Por outro lado, se P pertence à reta r, a imagem de P, P’ é o próprio ponto P.
Figura 7.Ponto P’ simétrico do ponto P em relação à reta r.
Fonte: Figura elaborada pela autora
11 Utilizamos como referência as obras “Um estudo geométrico das transformações
Em resumo, a simetria ortogonal tem como característica as seguintes propriedades:
Conservação do alinhamento (a imagem de uma reta é uma reta);
Conservação do paralelismo (quando duas retas r e t são paralelas, suas imagens r’ e t’ também são paralelas);
Conservação de distâncias (A imagem de um segmento s é um segmento s’ de mesmo comprimento);
Conservação da área (se uma figura F tem área de medida
a
suaimagem F’ também tem área de medida
a
); Conservação da medida dos ângulos e, portanto, da ortogonalidade.
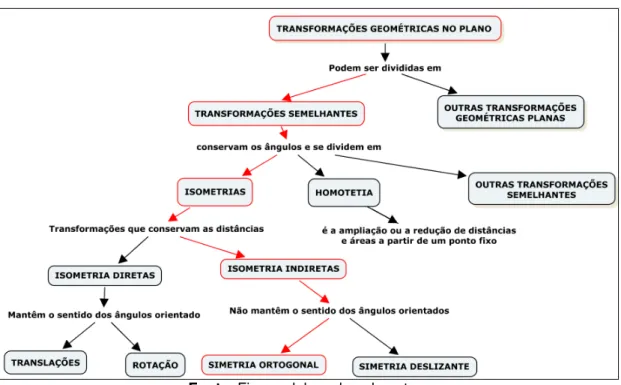
Com o objetivo de situar a simetria ortogonal nas transformações geométricas planas, construímos a Figura 8, um esquema que leva em consideração algumas das suas propriedades.
Figura 8. Transformações Geométricas no plano
Fonte: Figura elaborada pela autora