The Two-Dimensional Quantum Heisenberg
Antiferromagnet with Ising-Like Anisotropy
AlessandroCuoli,Valerio Tognetti,TommasoRosilde, PaolaVerruhi,
DipartimentodiFisiadell'Universitadi Firenze
andIstituto NazionalediFisiadellaMateria(INFM),
LargoE.Fermi2,I-50125Firenze,Italy
and RuggeroVaia
Istituto diElettroniaQuantistiadelConsiglioNazionaledelleRierhe,
viaPaniatihi 56/30,I-50127Firenze,Italy,
andIstituto NazionalediFisiadellaMateria(INFM)
Reeivedon5August,2000
WestudythetwodimensionalquantumHeisenbergantiferromagnetonthesquarelattiewith
easy-axisexhangeanisotropybythesemilassialmethodalledpure-quantumself-onsistentharmoni
approximation. Inpartiular, we fous on the problem of the existene of a nite-temperature
transitioninsuhamodel,andstudytheorrespondingritialtemperatureasthespinvalueand
the anisotropy vary. Wendthat anIsing-like transition haraterizes the modelevenwhenthe
anisotropyisoftheorderof10 2
J(Jbeingtheintra-layerexhangeintegral). Thegoodagreement
found between our theoretial results and the experimental data for the ompounds Rb
2 MnF
4 ,
K2MnF4,andK2NiF4showsthattheinsertionoftheeasy-axisexhangeanisotropy,withquantum
eetsproperlytakenintoaount,providesaquantitativedesriptionandexplanationofthereal
system'sritialbehaviour.
Theeasy-axisquantumHeisenbergantiferromagnet
onthesquarelattie(EA-QHAF)isdened bythe
fol-lowingHamiltonian:
^
H= J
2 X
i;d h
^
S x
i ^
S x
i+d +
^
S y
i ^
S y
i+d
+ ^
S z
i ^
S z
i+d i
(1)
where i = (i
1 ;i
2
) runs over the sites of a square
lat-tie, d onnets eah site to its four nearest
neigh-bours, J > 0 is the antiferromagneti exhange
in-tegral and the anisotropy parameter takes values
2[0;1) foreasy-axismodels. Thespinoperators ^
S
i
( = x;y;z) are suh that j ^
Sj 2
= S(S+1) and obey
[ ^
S
i ;
^
S
j ℄=i"
Æ
ij ^
S
i .
Theanisotropyparametermeasuresthe strength
of theeasy-axisharaterofthemodel: For =0the
Ising-limit (equivalenttotheIsingmodelifS=1=2)is
reovered;in theoppositelimit,Eq.(1)with=1
de-sribesthefullyisotropiQHAF.Atalassiallevelthe
EA-HAF isknownto share itsritial behaviour with
the Ising model [1℄, with a nite-temperature
seond-order phase transition orresponding to the onset of
Neelantiferromagnetiorder. Theritialtemperature
T l
isadereasingfuntionof,andvanishes
logarith-miallyintheisotropilimit[2℄.
Whenquantum eets are onsidered,one expets
the ritial behaviour of the model to remain the
same, as the universality lass of the system annot
be hanged by short-rangedquantum utuations [3℄;
however,these may be responsiblefor anevident
low-eringoftheritial temperature, asquantum disorder
opposestheonsetofNeelorder. Inpriniple,thiseet
ouldbestrongenoughtopushtheritialtemperature
downtoT
=0,thusdestroyingthetransitionitself;the
parameterregionwhere suh asenarioouldpossibly
ouristhat of low ritialtemperatures('1) and
strongquantumeets (S=1=2)[4℄.
Toaddresstheproblem of theexistene ofa nite
temperaturetransitionintheEA-QHAF,oneneedsto
analyse the -dependene of the ritial temperature
for dierent spins; results relativeto preise spin and
anisotropyvalues,typialoutputofquantumnumerial
simulations, are heneinsuÆient, albeit useful. The
maingoalofthispaperisinfattodeterminethe
riti-altemperatureoftheEA-QHAFasafuntionofboth
andS, andompare ourtheoretial resultswiththe
There exist several real ompounds whose
mag-neti behaviour [5℄ is well desribed by the
Hamilto-nianEq.(1);mostofthem,despitebeingharaterized
by a veryweak easy-axisanisotropy ( ' 1), show a
nite-temperaturephase-transition. Whetherthe
tran-sition is due to the anisotropy-driven onset of
two-dimensional Neel order or to some other eet (suh
as the inter-layer exhange interation), is not
eas-ilydetetableexperimentally,but strongindiationsin
favouroftherstpossibilityderivefromtheanalysisof
severalthermodynamiquantities. Thisworkonrms
suhapiture, astheritial temperaturesrelativeto
the ompounds Rb
2 MnF
4
[6℄ (S = 5=2, = 0:994),
K
2 MnF
4
[7℄ (S = 5=2, = 0:995) and K
2 NiF
4 [8℄
(S = 1, = 0:996) agree niely with the theoretial
resultsforthetwo-dimensionalEA-QHAF.
In order to study the thermodynami and ritial
behaviour of the model desribed by Eq. (1), we use
thepure-quantumself-onsistentharmoni
approxima-tion (PQSCHA)[9℄: this approximation allowsoneto
take into aount exatly the full lassial, and the
linear quantum ontributions to the thermodynamis
ofthesystem,thusapproximating(one-looplevel)the
non-linearpure-quantumontributiononly. Asthe
lat-ter plays a seondary role in determining the ritial
properties of models with a not-too-strong quantum
harater, the PQSCHA is an ideal tool to study the
thermodynami and ritial behaviour of many
quan-tum systems, as shown by its many suessful
appli-ations[10℄, inpartiularto low-dimensionalmagneti
systems[11,12℄.
The method, based on the path-integral
formula-tion of quantum statistial mehanis, allows one to
write statistial averages of quantum operators in the
form of lassial-like expressions: These may then be
evaluated by lassial(possiblynumerial)tehniques,
like the transfer-matrix method in one dimension, or
lassialMonteCarlosimulationintwodimensions. In
greaterdetail,thePQSCHAexpressionforthe
statisti-alaverageofaofquantumoperator ^
O,foramagneti
systemN spins,reads
h ^ Oi= 1 Z e Z d N sO e e H e (2)
where =T 1 , Z e = R d N se H e
, s=(s x ;s y ;s z )
isalassialunit vetor,and R d N s= N i=1 R ds i .
Quantum eets ome into play via the spin and
temperaturedependene of H
e andO
e
: this
depen-denerelatestheoriginalquantumsystemtoaninnite
lassof lassialeasy-axismodels, eah denedby
dif-ferent parameters. This means that the PQSCHA
re-duesthestudy ofquantum statistialaveragesto the
evaluationoflassial-likeeetiveaveragesdened by
Eq. (2), forto eetivemodels whih are dierentfor
dierenttemperaturesandspinvalues.
The spei PQSCHA expression for the eetive
HamiltonianoftheEA-QHAFisfoundtobe
H e = 1 2 J e S 2 X i;d h 4 ? s x i s x i+d +s y i s y i+d + 2 k 2 ? s z i s z i+d i + G(t; e
S); (3)
d
where, e
S = S +1=2, and t = T=J e
S 2
is the redued
temperatureusedhereafter.
Therenormalizationparametersare
2 k =1 D k 2 ; 2 ? =1 D ? 2 ; (4)
wheretheoeÆients
D k = 1 N e S X k a k b k 1 k L k ; D ? = 1 N e S X k a k b k 1 k L k (5)
areself-onsistentlydeterminedbysolvingEqs.(4)and
(5),with a 2 =4 2 k + 2 ? k ; b 2 =4 2 k 2 ? k ; (6) and k = 1 4 X d e ikd ; L k
=othf
k 1 f k ; f k = a k b k 2 e St ;
kbeingthewavevetorintherstBrillouinzone.
Thetemperatureandspindependentuniformterm
G(t; e
S)=2J e S 2 (1 2 k 2 ? )+J
e S 2 t X k ln sinhf k 2 ? f k ;
does not enter the expressions for the statistial
av-erages, but ontributes to the free energy and to the
relatedthermodynamiquantities.
Ifonedenestheeetiveexhangeintegraland
ef-fetiveanisotropy,
Eq. (3)anbewritten intheform
H
e =
1
2 J
e e
S 2
X
i;d h
e
s x
i s
x
i+d +s
y
i s
y
i+d
+s z
i s
z
i+d i
+ G(t; e
S); (7)
d
showingthatthethermodynamibehaviourofthe
EA-QHAF is that of a lassial EA-HAF with exhange
integralJ
e
(t;S) and anisotropy parameter
e (t;S).
As J
e
<J and
e
>weseethat quantum
utua-tionsindueasofteningofboththeenergysaleandthe
anisotropy,thusinduingahigherdegreeofdisorderin
thesystem.
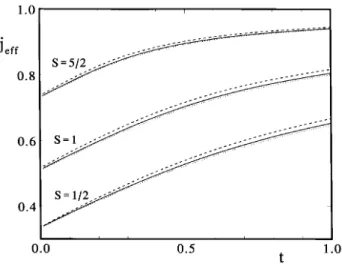
In Fig.1 we show j
e =J
e
=J as afuntion of t,
for dierentspin and anisotropyvalues: Quantum
ef-fetsaremarkedlystrongerforlowerspins,whilethe
-dependene oftheenergysalerenormalizationisseen
to beextremelyweak.
Figure 1. Renormalizedexhangeintegral je =Je=J vs.
tforS=1=2,1,and5=2;dierentvaluesoftheanisotropy
parameter=0:9,0:5,and0arealsoshownbythedashed,
full anddottedurves,respetively.
In Fig.2, the ratio (
e
)= is plotted against
fordierentspinandtemperaturevalues: the
quan-tumrenormalizationishereseentomorestronglyaet
themostanisotropimodels,duetothefatthat,when
foredtoalignalongtheeasyaxis,eahspinreatswith
larger quantum utuations perpendiular to theaxis
itself.
Figure2. Ratio(e )=vs.for S=1=2,1,and5=2;
dierenttemperaturevaluest=0:001and0:1areshownby
thefullanddashedurves,respetively.
FromEq. (7)wesee that thesymmetryproperties
ofthe originalquantum Hamiltonianare preservedby
therenormalization proedure leading to the eetive
Hamiltonian: thismeansthattheritialbehaviourof
theEA-QHAFanbediretlyrelatedtothat ofits
ef-fetive lassialounterpart. In partiular, if t l
() is
thereduedritialtemperatureofalassialEA-HAF
with anisotropy parameter , then, for the quantum
system,itis
t
(S;)= t
l
e (t
)
j
e (t
)
: (8)
For xed S and , the t dependene of j
e and
e
make Eq. (8) rather ompliated. Its solution,
how-ever,anbeobtainediteratively,onet l
()isavailable
asan analytialfuntion of . Toobtainsuh a
fun-tionweusedthelassialMonteCarlodatareportedin
Refs.[13℄ and[14℄: thesedataarewelldistributedover
the interval 0 < 1 and an aurate interpolating
funtion mayhenebedetermined. Inpartiular we
haveused
l
()=a=
1+b 2
+ 4
d ln (1 2
)
; (9)
witha=0:917,b=0:068,=0:097,and d=0:0636.
Thelogarithmidependene upon (1 2
)isrequired
in order to properly desribe the logarithmi drop of
t l
for ! 1; l
to ensure the ferro- and antiferromagneti models to
be equivalent, as required for the stati behaviour of
lassialmagnetisystems.
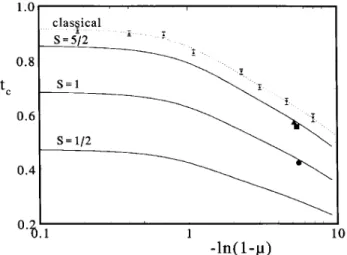
Figure 3. Critial temperature t(S;) of the EA-QHAF
vs. ln(1 ) for S = 1=2, 1, 5=2, and 1
(lassi-al model). Large symbols indiate the experimentally
determined ritial temperatures for Rb2MnF4 (triangle),
K2MnF4 (square), andK2NiF4 (irle). Smallsymbolsare
lassialMonteCarlodatafromRefs.[13 ℄and[14 ℄,upwards
anddownwardstriangles,respetively. Thedottedurveis
theinterpolatingfuntion l
()(seetext).
InFig.3theresultingsolutionofEq.(8)isplotted
against ln(1 )to expandthe'1region,where
data for real ompounds are available; the agreement
betweenoururvesandtheexperimentallydetermined
ritial temperaturesis verygoodfor bothS =1and
S=5=2,givenalsothefatthatnobest-tproedureis
involvedintheomparison. Ontheotherhand,the
ex-atlyknown[15℄ritialtemperatureoftheIsingmodel
t
(1=2;0)=0:567,notrepresentedinFigure,isnotwell
reproduedin viewofthelargevaluesofthe
renormal-izationoeÆientsEq.(5),andweexpetourresultsto
beonlyqualitativelysigniantintheextremeS=1=2
quantum ase. This respet, we annotgiveadenite
answerto theproblem, reentlyaddressed in Ref. [4℄,
oftheexisteneofanite-interval,neartheisotropi
limit = 1, where t (1=2;)=0, i.e. where the
EA-QHAFshowsnonite-temperaturetransition.
In onlusion, we have studied the EA-QHAF in
terms of the eetive Hamiltonian determined by the
PQSCHA method; by analyzing the ritial
tempera-ture dependene on the anisotropy parameter , the
Ising-likephase-transitionharaterizingthemodelhas
beenfoundto ourat nite temperature8 <1and
8S1;aqualitativeindiationinfavourofthevalidity
ofthisresultforS=1=2hasalsobeenobtained.
Referenes
[1℄ M. BanderandD. L. Mills, Phys.Rev.B 38,12015
(1988).
[2℄ L.P.Kadanoetal.,Rev.Mod.Phys.39,395(1967).
[3℄ J.A.Hertz,Phys.Rev.B14,1165(1976).
[4℄ N.S.BranoandJ.RiardodeSousa,preprint,
ond-mat/0006345(June2000).
[5℄ J. Kanamori, in Magnetism vol.1, ed. G.T.Rado e
H.Suhl,AademiPress,New York(1963).
[6℄ R. A. Cowley, G. Shirane, R. J. Birgeneau, H. J.
Guggenheim,Phys.Rev.B15,4292(1977).
[7℄ R.J.Birgeneau,H.J.Guggenheim,G.Shirane,Phys.
Rev.B8,304(1973).
[8℄ H.W.deWijn,L. R.Walker,R.E.Walstedt,Phys.
Rev.B8,285(1973).
[9℄ A. Cuoli, V. Tognetti, P. Verruhi and R. Vaia,
Phys.Rev.A45,8418 (1992).
[10℄ A.Cuoli,R.Giahetti,V.Tognetti,R.Vaia,andP.
Verruhi,J.Phys.,Condens.Matter7,7891(1995).
[11℄ A. Cuoli, V. Tognetti, R. Vaia, and P. Verruhi
Phys.Rev.B46,11601(1992).
[12℄ A. Cuoli, V. Tognetti, R. Vaia, and P. Verruhi
Phys.Rev.Lett. 77, 3439 (1996), Phys.Rev.B 56,
14456(1997).
[13℄ P.A.Serena,N.GaraandA.Levanyuk,Phys.Rev.
B47,5027(1993).
[14℄ M.E.Gouv^eaelal.,Phys.Rev.B59,6229 (1999).