Efeitos de campos aleatórios no modelo Blume-Capel de alcance infinito

Priscila Valdênia dos Santos

Efeitos de Campos Aleatórios no Modelo

Blume-Capel de Alcance Infinito

Priscila Valdênia dos Santos

Efeitos de Campos Aleatórios no Modelo Blume-Capel de

Alcance Infinito

Tese apresentada à Coordenação do Programa de Pós-Graduação Stricto Sensu em Física da Universidade Federal do Rio Grande do Norte, em complementação aos requisitos para obten-ção do Título de Doutor em Física na Área de Concentração Física da Matéria Condensada.

Universidade Federal do Rio Grande do Norte

Centro de Ciências Exatas e da Terra

Programa de Pós-Graduação Stricto Sensu em Física

Orientador: Prof. Dr. Francisco Alexandre da Costa

Coorientador: Prof. Dr. João Medeiros de Araújo

Agradecimentos

• A Deus por tudo o que tem feito na minha vida.

• Aos meus orientadores, prof. Dr. Francisco Alexandre da Costa e prof. Dr. João Medeiros de Araújo, pela orientação, apoio e incentivo.

• À minha família, especialmente à minha mãe, por todo apoio e compreensão que tem dado durante a minha jornada acadêmica.

• Aos professores do Departamento de Física Teórica e Experimental da UFRN pela preciosa contribuição para a minha formação acadêmica.

• Aos meus colegas de Pós-Graduação em Física da UFRN, em particular aos meus colegas de sala.

• Aos colegas de docência assistida na Escola de Ciências e Tecnologia: Micejane, Maria Romênia, Maytê, Reben, Gladstone, Alessandro e Leonardo por todos os momentos compartilhados durante os quatro anos de estágio e pela amizade que levarei para a vida.

• Aos professores de Física da Escola de Ciências e Tecnologia, pelo incentivo e contribuições à minha carreira docente, especialmente aos professores doutores Ronai Lisboa, André Bessa, José Henrique Fernandez, Neemias Alves e Lúcio Marassi.

• Aos meus alunos da Escola de Ciências e Tecnologia, por me fazerem querer melhorar a cada dia como docente e como pessoa.

• A Horácio, por ter me ajudado a não desistir e pelo apoio e incentivo, sempre. Em especial, pelo último ano, no qual temos dividido nossos dias.

• Aos funcionários do Programa de Pós-Graduação em Física da UFRN.

• Aos membros da banca examinadora pela disponibilidade e contribuições a este trabalho.

Resumo

Neste trabalho investigamos o modelo Blume-Capel (BC) ferromagnético, com spin 1 e interações de longo alcance, sob o efeito de desordem temperada (quenched) em sítios. O modelo é exatamente solúvel no ensemble canônico, e sua densidade de energia livre nos leva a resultados correspondentes a uma teoria de campo médio. Inicialmente estudamos o modelo BC sob a influência de um campo de anisotropia cristalina diluído e na ausência de campo magnético. Em seguida revi-sitamos o modelo BC sob o efeito de um campo magnético aleatório com distribuição bimodal e campo cristalino uniforme, introduzido por Kaufman e Kanner, dando atenção especial para os diagramas de fases em termos de anisotropia versus tempe-ratura, onde surgem efeitos de reentrância. Finalmente, iniciamos um estudo com um modelo geral, em que ambos os campos - magnético e de anisotropia cristalina -, são diluídos, e seguindo distribuições discretas de probabilidade. Os diagramas de fases obtidos exibem uma rica variedade de comportamentos multicríticos, apresentando linhas de transições contínuas e de primeira ordem. Em alguns casos verificamos a ocorrência de fenômenos de reentrância, que tem sido uma característica em modelos de Blume-Capel sob efeito de desordem.

Palavras-chaves: Sistemas Desordenados; Modelos Solúveis; Teoria de

Abstract

In the presente work we investigate the ferromagnetic Blume-Capel (BC) model, for spin 1 and infinite-ranged interactions, under the influence of local quenched disorder. The model is exactly solved within the canonical ensemble. The obtained free energy density lead us to mean-field results. In the first part we study the BC model under the influence of a random crystal-field anisotropy, but otherwise without a magnetic field. In the second part we consider the BC model under a bimodal random magnetic field and a uniform crystal-field anisotropy term. This model was previously studied by Kaufman and Kanner. We give special attention to anisotropy versus temperature phase diagrams which may present reentrant phenomena. Finally, in the third part we consider a generalized version where both local fields - magnetic and crystal-field anisotropy - are diluted and, in the present case, modeled by discrete probability distribution. The phase diagram obtained and presented in this work exhibit a rich variety of multicritical behavior, presenting both continuous and first-order transition lines. Also, for some specific cases there is room for the existence of reentrant effects. This seems to be a characteristic of the Blume-Capel model under the presence of randomness.

Key-words: Disordered Systems; Soluble Models; Mean Field Theory; Multicritical

Lista de ilustrações

Figura 1 – Comportamento de um parâmetro de ordem típico φ em função da

temperatura: (a) em uma transição contínua ou de segunda ordem; (b) em uma transição descontínua ou de primeira ordem. . . 26 Figura 2 – Diagrama de fases do modelo descrito pela equação (2.33) mostrando

(a) um ponto bicrítico (BP); (b) um ponto tetracrítico (TP). . . 27 Figura 3 – A densidade de energia livre, f = 1₂A2m2 +A4m4, como função da

magnetização, para diferentes temperaturas. . . 31 Figura 4 – Diagrama de fases T versus H para o composto Dy3Al5O12. A curva

contínua representa a linha crítica e a pontilhada uma linha de primeira ordem. O círculo cheio representa o ponto tricrítico. . . 33 Figura 5 – Diagrama de fases esquemático para um metamagneto no espaço de

temperatura T, campo magnético uniforme H e campo magnético

staggered H† _{. . . 34}

Figura 6 – A densidade de energia livre f, em função de m, até a sexta ordem em m, Eq. (2.43), quando A4 <0. Existe uma transição de primeira ordem

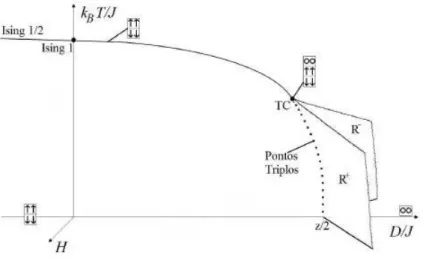
para T =Tc. T⋆⋆ _eT⋆ _{são os limites de metaestabilidade (coexistência} de fases) das fases ordenada e desordenada, respectivamente. . . 35 Figura 7 – Diagrama de fases esquemático tridimensional do modelo Blume-Capel

para spin-1. As duas "asas"R+ e R− são superfícies de transições de primeira ordem. . . 41 Figura 8 – Diagrama de fases qualitativo do modelo Blume-Capel no plano D₋H

destacando as transições de fases de primeira ordem. . . 43

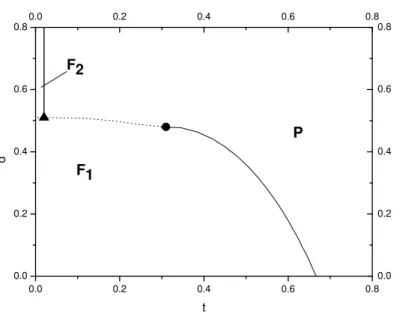
Figura 9 – Diagrama de fases no plano d₋ t para p = 0.5, correspondendo à

Topologia I . . . 50 Figura 10 – Diagrama de fases no planod₋tparap= 0.75, que também corresponde

à Topologia I. . . 51 Figura 11 – Diagrama de fases no plano d₋ t para p = 0.9, correspondendo à

Topologia II . . . 51 Figura 12 – Diagrama de fases no plano d ₋t para p = 0.95, correspondendo à

Topologia II, exibindo o mesmo comportamento do diagrama parap= 0.9 52

Figura 13 – Diagrama de fases no plano d ₋t para p = 0.98, correspondendo à

Topologia III. . . 52 Figura 14 – Diagramas de fases do modelo Blume-Capel cujo campo cristalino

II é caracterizada por uma linha contínua no plano d₋t, uma linha de

transição de primeira ordem e um ponto crítico ordenado. . . 54

Figura 16 – Diagrama de fases no planod₋tdo modelo Blume-Capel bidimensional

com campo cristalino aleatório ep= 0.97. As linhas sólidas e pontilhadas

representam as transições contínuas e de primeira ordem. O círculo preto indica o ponto tricrítico . . . 54

Figura 17 – Diagrama de fases no plano d₋t do modelo Blume-Capel

bidimensi-onal com campo cristalino aleatório e p = 0.8. O círculo branco e os

asteriscos são o ponto crítico terminal e os pontos multicríticos isolados, respectivamente. O1 e O2 indicam duas fases ordenadas. . . 55

Figura 18 – Diagrama de fases no plano D₋ H para temperatura nula. As

fa-ses ferromagnética (F), não-magnética (NM), paramagnética (P) e ferromagnética-não-magnética (F-NM) são separadas por linhas de transição de primeira ordem. . . 58

Figura 19 – Diagrama de fases no planoh₋t parad=₋0.5 com um ponto tricrítico.

A linha pontilhada representa a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 61

Figura 20 – Diagrama de fases no planoh₋tpara d= 0.4 com um ponto tricrítico e um ponto crítico ordenado. As linhas pontilhadas representam a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 61

Figura 21 – Diagrama de fases no planoh₋tparad= 0.47 com dois pontos tricríticos e um ponto crítico ordenado. As linhas pontilhadas representam a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 62

Figura 22 – Diagrama de fases no planoh₋t para d= 0.492 com dois pontos

tricrí-ticos e um ponto crítico ordenado. As linhas pontilhadas representam a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 62

Figura 23 – Diagrama de fases no plano h₋t para d = 0.493 com dois pontos

Figura 24 – Diagrama de fases no plano h₋ t para d = 0.75 com dois pontos

tricríticos. As linhas pontilhadas representam a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 63 Figura 25 – Diagrama de fases no planod₋tpara h= 0.25 com um ponto tricrítico.

A linha pontilhada representa a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 64 Figura 26 – Diagrama de fases no plano d₋t parah= 0.4 com um ponto tricrítico

e um ponto crítico ordenado. A linha pontilhada representa a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. É possível notar ainda uma reentrância bastante pronunciada em baixas temperaturas. . . 65 Figura 27 – Diagrama de fases no planod₋tparah= 0.5 com dois pontos tricríticos

e um ponto triplo. As linhas pontilhadas representam a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 65 Figura 28 – Diagrama de fases no plano d₋ t para h = 0.75 com dois pontos

tricríticos. As linhas pontilhadas representam a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 66 Figura 29 – Diagrama de fases no plano h₋t para q = 0.25 e d = 0.25 com um

ponto tricrítico. A linha pontilhada representa a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 70 Figura 30 – Diagrama de fases no planoh₋tpara q= 0.25 ed= 0.75 com um ponto

tricrítico e um ponto crítico ordenado. A linha pontilhada representa a linha de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 70 Figura 31 – Diagrama de fases no plano h₋t paraq = 0.5 ed= 0.25 com um ponto

tricrítico. As linhas pontilhadas representam as linhas de transição de primeira ordem e a linha contínua, a transição de segunda ordem ou contínua. . . 71 Figura 32 – Diagrama de fases no planoh₋tparaq = 0.5 ed= 0.75 com três pontos

tricríticos. As linhas pontilhadas representam as linhas de transição de primeira ordem e as linhas contínuas, a transição de segunda ordem ou contínua. . . 71 Figura 33 – Diagrama de fases no plano h₋t para q = 0.75 e d = 0.25 exibindo

Lista de tabelas

Tabela 1 – Expoentes críticos para T < Tc, onde C, M, χ eξ representam o calor

específico, a magnetização total, a suscetibilidade e o comprimento de correlação, respectivamente. . . 28 Tabela 2 – Expoentes críticos para T > Tc, ondeC,χeξ representam o calor

espe-cífico, a suscetibilidade e o comprimento de correlação, respectivamente. 29 Tabela 3 – Expoentes críticos em T =Tc;m,h,G(r) edrepresentam a

magnetiza-ção por partícula, o campo magnético externo, a funmagnetiza-ção de correlamagnetiza-ção entre dois spins separados por uma distânciar e a dimensão do sistema,

Lista de ilustrações . . . . 7

Lista de tabelas . . . 11

1 Introdução . . . 14

2 Fundamentos Teóricos . . . 17

2.1 Introdução . . . 17

2.2 Modelagem teórica do magnetismo . . . 18

2.3 Aproximação de campo médio . . . 21

2.3.1 Modelo de Curie-Weiss . . . 22

2.4 Transições de Fases e Fenômenos Críticos . . . 24

2.5 Expoentes críticos . . . 27

2.6 Teoria de Landau . . . 29

2.6.1 Teoria de Landau para pontos tricríticos . . . 32

2.7 Sistemas magnéticos desordenados . . . 35

2.8 Diluição, interação e campo aleatórios . . . 37

2.9 O modelo Blume-Capel . . . 40

3 O Modelo Blume-Capel com campo cristalino aleatório . . . 44

3.1 Introdução . . . 44

3.2 O modelo . . . 45

3.3 Diagramas de Fases . . . 49

4 O Modelo Blume-Capel com campos cristalino e magnético aleatórios . . . 56

4.1 Introdução . . . 56

4.2 Modelo Blume-Capel com campo magnético aleatório: a versão Kaufman-Kanner revisitada . . . 57

4.2.1 O modelo . . . 57

4.2.2 Diagramas de Fases . . . 60

4.3 Modelo Blume-Capel com campos cristalino e magnético aleatórios . . . . 66

4.3.1 O modelo . . . 66

4.3.2 Diagramas de Fases . . . 69

5 Conclusões e perspectivas . . . 73

Apêndices

86

19

1 Introdução

Um dos temas de maior interesse na Física desde a primeira metade do século XIX tem sido o estudo e a compreensão dos chamados estados condensados da matéria. Este interesse surgiu juntamente com as primeiras análises dos sistemas simples, como por exemplo, a descrição de Van der Waals para a transição líquido-gás e a aproximação de campo médio para explicar o ferromagnetismo. Os fenômenos críticos nestes sistemas ocorrem de maneira que acontecem mudanças estruturais e/ou no tipo de ordenamento em uma determinada pressão (Pc) ou temperatura (Tc) [1, 2]. Um dos principais conceitos da teoria dos fenômenos críticos é o de universalidade, o qual prediz que os valores de algumas quantidades, como os expoentes críticos, independem dos detalhes microscópicos do sistema, dependendo somente de alguns poucos parâmetros, tais como a dimensionalidade e a simetria do parâmetro de ordem. Conforme a teoria dos fenômenos críticos foi se desenvolvendo, sistemas mais complexos foram também sendo investigados gradualmente, através da introdução de aleatoriedades (desordens) nas interações e nos campos do sistema, e desta forma os conceitos de universalidade foram ficando menos precisos [3, 4, 5]. Um exemplo disso é que, de acordo com a hipótese de universalidade, o alcance das interações torna-se irrelevante se estas forem finitas, o que implica que ao adicionar acoplamentos entre segundos vizinhos a um sistema de spins cujas interações são originalmente entre primeiros vizinhos, sem introduzir competição entre estas interações, o comportamento crítico não deveria mudar qualitativamente. Por outro lado, quando as interações entre segundos vizinhos e aquelas entre spins primeiros vizinhos competem entre si, pode haver uma mudança no comportamento crítico do sistema. Da mesma forma, para sistemas magnéticos desordenados cujas interações obedecem a uma determinada distribuição de probabilidades, uma questão que ainda não se encontra completamente esclarecida é a de uma possível quebra de universalidade associada à diferentes distribuições de probabilidades para estas interações.

magnéticos, puros ou diluídos, sabe-se que eles apresentam muitos fenômenos interessantes e seu estudo ainda é de grande interesse para teóricos e experimentais atualmente [11, 12]. Em particular, um interesse significativo tem sido devotado às impurezas, não apenas pela dificuldade de se encontrar na natureza sistemas completamente puros, mas também pela dificuldade de se obter amostras puras em laboratório. Materiais magnéticos, por exemplo, podem conter imperfeições nas redes cristalinas ou mesmo outros elementos não magnéticos, e essas impurezas, de forma geral, alteram o diagrama de fases e podem modificar o comportamento crítico dos sistemas.

Paralelamente aos estudos experimentais, vários modelos teóricos foram propostos na tentativa de descrever as propriedades termodinâmicas apresentadas por esses sistemas, dos quais o mais importante talvez seja o modelo de Ising [12, 13]. Nesta linha, vários outros modelos foram sugeridos, tais como os modelos de Heisenberg, Blume-Capel e Baxter-Wu, dentre outros. No entanto, do ponto de vista teórico, poucos modelos propostos possuem soluções analíticas exatas e, por este motivo, foram desenvolvidas várias técnicas aproximadas para tentar estudá-los. Tais técnicas vão desde aproximações do tipo campo médio, expansões em séries, grupo de renormalização, até simulações de Monte Carlo [11, 14]. Como se pode notar, estes métodos podem ser completamente analíticos, quando possível, ou estritamente numéricos.

Introduzir uma determinada desordem em um modelo apresenta além de dificuldades em suas abordagens analíticas, alguns desafios na obtenção dos resultados por meio da implementação de algoritmos computacionais. Um exemplo dessas dificuldades ocorre no estudo do magnetismo através do modelo de Ising com acoplamentos ferromagnéticos entre spins primeiros vizinhos. Tal problema já encontra-se solucionado exatamente para uma e duas dimensões [13, 15], mas permanece sem solução em três dimensões [1, 16, 17]. Neste último caso, no entanto, os métodos de aproximações, como por exemplo, as simulações de Monte Carlo [18, 19] tem fornecido resultados satisfatórios [20]. Por outro lado, ao incorporarmos campos magnéticos aleatórios no modelo de Ising ferromagnético, apesar de já haver solução deste modelo para interações de alcance infinito, ou seja, na aproximação de campo médio [21], quando consideramos interações de curto alcance seus resultados são polêmicos [22]. Novos algoritmos tem sido desenvolvidos para o modelo de Ising puro, na tentativa de reduzir o custo computacional, mas tais algoritmos ainda apresentam limitações quando são aplicados a sistemas com desordem. Dessa maneira, métodos analíticos que incluem as interações de curto alcance, tais como o grupo de renormalização, consistem em recursos bastante utilizados para investigar o comportamento real do sistema [23].

21

distribuição dos campos e dos acoplamentos. Além disso, considerar os efeitos de possíveis campos de anisotropia pode enriquecer a criticalidade do sistema, uma vez que a introdução destes campos pode dar origem a pontos multicríticos no diagrama de fases original.

23

2 Fundamentos Teóricos

2.1 Introdução

A história do magnetismo remonta à Grécia Antiga, onde, na região da Magnésia foi primeiro observado que uma determinada rocha (magnetita) tinha o poder de atrair o ferro.

No entanto, poucos avanços no tocante ao entendimento dos fenômenos magnéticos foram feitos durante um longo período, com exceção dos trabalhos de Gilbert, nos anos de 1600, que descobriu que a Terra funciona como um ímã esférico gigante, tendo pólos magnéticos quase coincidentes com os pólos geográficos. Muito tempo depois, vieram os trabalhos de Oersted, que em 1820 fez a descoberta da ação magnética da corrente elétrica, e os resultados de Ampère, também em 1820 , sobre a eletrostática e eletrodinâmica, quando ele mostrou, por exemplo, a existência de interação entre fios condutores e o comportamento de uma bobina circular de fio metálico como se fosse um ímã, quando por ela circula uma corrente elétrica. Ainda no século XIX, Faraday mostrou que, para que um ímã produzisse uma corrente elétrica, era necessário que o mesmo se movimentasse onde o fio condutor se encontrava. Faraday também introduziu o conceito do que conhecemos hoje como linhas de força do campo magnético [25]. Mais tarde, estudando os trabalhos de Faraday, o físico inglês James Clark Maxwell forneceu o tratamento matemático necessário à definição de linhas de força e, posteriormente, unificou a eletricidade e o magnetismo através daquelas que depois ficaram conhecidas como Equações de Maxwell do Eletromagnetismo [26].

Em 1907, Pierre Weiss apresentou uma teoria fenomenológica capaz de explicar qualitativamente os fenômenos ferromagnéticos [26]. Em 1905, Pierre Curie havia mostrado que algumas substâncias sofriam transições de fase, em certas temperaturas, as quais ficaram conhecidas como temperaturas de Curie. Weiss explicou, em seus estudos sobre ferromagnetismo, que estes materiais tem magnetização espontânea (sem a aplicação de campo magnético externo ao sistema) para valores de temperatura abaixo de uma temperatura crítica Tc (temperatura de Curie), tornando-se paramagnéticos paraT > Tc (magnetização nula).

A teoria de Weiss (ou teoria do campo molecular) representa o ponto de partida para estudos de sistemas magnéticos interagentes. Tal teoria baseia-se no fato de que um único momento magnético, associado a um determinado íon do material, interage com o restante do cristal por meio de um campo, ao qual ele nomeou campo molecular, que é

alinhava com o campo magnético externo e com o campo magnético médio produzido pelas demais moléculas da amostra. Portanto, quando o campo magnético externo fosse removido, as moléculas magnéticas permaneciam alinhadas com o campo magnético interno, e assim a amostra permanecia magnetizada. Apesar de a teoria do campo molecular ser uma teoria fenomenológica, pois não explica a origem microscópica do campo molecular, até por volta do final da década de vinte, esta era a teoria do magnetismo mais bem sucedida.

Seguindo a ideia do campo molecular, no começo da década de vinte, Lenz sugeriu um modelo no qual cada partícula (dipolos magnéticos) interagia com seus vizinhos mais próximos. Esse modelo ficou conhecido como modelo de Ising, por ter sido resolvido por Ising como sua tese de doutorado, em uma dimensão [13]. A solução exata mostrou que tal modelo em uma dimensão não conseguia explicar o ferromagnetismo, pois quando o campo magnético externo aplicado fosse zero, a magnetização se anulava, isto é, nessa dimensão não havia transição de fase. Esse resultado se mostrou correto posteriormente e podia ser explicado com argumentos bastante simples. Já no final da década de vinte, como um problema de Mecânica Quântica, Heisenberg e Dirac mostraram que a origem do campo molecular, agora acoplamento de troca, era devida à repulsão coulombiana entre elétrons associada com o princípio de exclusão de Pauli. Trataremos disso na próxima seção.

2.2 Modelagem teórica do magnetismo

Como foi visto na seção anterior, em 1920 W. Lenz introduziu o modelo de dipolos magnéticos que resultou no que ficou mais tarde conhecido como modelo de Ising. No entanto, as interações correspondentes a dipolos magnéticos elementares associados aos spins dos elétrons tem magnitude muito pequena para explicar o ferromagnetismo. Desta forma, para explicar o forte magnetismo do ponto de vista microscópico, Heisenberg propôs que o forte alinhamento dos spins em um sistema ferromagnético se devia aos seus vizinhos mais próximos. Essa energia de troca corresponde fisicamente à diferença de energia entre as configurações de spins paralelos (_↑↑) e antiparalelos (_↑↓). Assim, o modelo de Heinsenberg consiste em expressar a dependência do Hamiltoniano de um dado sistema de dois elétrons com o spin.

2.2. Modelagem teórica do magnetismo 25

Do princípio da exclusão de Pauli, as auto-funções de onda dos férmions devem ser, necessariamente, anti-simétricas. Fisicamente, o estado singleto corresponde ao estado de spins antiparalelos (_↑↓), com função de onda anti-simétrica (A),

ψ1 =φS(r~1, ~r2)χA(σ1, σ2), (2.1)

e o estado tripleto, ao estado de spins paralelos (_↑↑), função de onda de spin simétrica (S)

ψ2 =φA(r~1, ~r2)χS(σ1, σ2), (2.2)

Se levarmos em consideração apenas a forma das funções de onda dependentes da posição, ficamos com:

φS,A= 1

√₂[φ1(r~1)φ2(r~2)±φ2(r~1)φ1(r~2)], (2.3)

onde o sinal +(₋) corresponde à função simétrica (anti-simétrica). Desenvolvendo a teoria de perturbação em primeira ordem para a energia, temos que as contribuições perturbativas são dadas por:

* ψ1 −e 2 r12 ! ψ1 +

=A+B, (2.4)

* ψ2 −e 2 r12 ! ψ2 +

=A₋B, (2.5)

com A e B dados por

A=

*

φ1(r~1)φ2(r~2)

−e 2 r12 !

φ1(r~1)φ2(r~2)

+

, (2.6)

e

B =

*

φ1(r~1)φ2(r~2)

− e2 r12 !

φ2(r~1)φ1(r~2)

+ , (2.7) respectivamente. Então * ψ1 −e 2 r12 ! ψ1 + − * ψ2 −e 2 r12 ! ψ2 +

= 2B. (2.8)

menor energia é o tripleto, prevalecendo a orientação de spins paralelos (ferromagnetismo) e para J <0, o estado de menor energia é o singleto, de modo que prevalece a orientação

antiparalela (antiferromagnetismo). Para altas temperaturas, os spins flutuam no tempo, de maneira que a magnetização total,M =P

iSi é zero, caracterizando a fase paramagnética. Uma característica importante da energia de troca é que ela decresce rapidamente, de maneira exponencial, com a distância entre os íons, diferentemente da interação coulombiana, que decresce mais lentamente (1/r). Isso ocorre porque J contém o produto

de funções de onda de elétrons ligados em diferentes núcleos, dependendo assim do envolvimento (overlap) das funções de onda, e esteoverlap decresce exponencialmente com

a distância. Portanto, a interação de troca corresponde a uma interação de curto alcance.

Seguindo Salmon [28], podemos demonstrar que um Hamiltoniano efetivo de spin da forma

H=C ~S1. ~S2 +D, (2.9)

onde C e D são constantes, pode representar a interação dos elétrons em dois níveis de energia. A função de onda anti-simétrica, associada aos spins dos elétrons,

χA= 1

√

2(αβ−βα), (2.10)

é um singleto com spin total nulo eα e β são estados de spin para cima _|↑i e para baixo

|↓i, respectivamente. Por outro lado, a função de onda simétrica é dada por um tripleto

com spin total igual a 1:

χS =

         αα ββ 1 √

2(αβ+βα)

(2.11)

Podemos escrever o Hamiltoniano na forma

H=C

1

2

~ S1+S~2

2

− 1₂S~1 2

−1₂S~2 2

+D, (2.12)

Lembrando que

~ S1+S~2

2

χA= 0,

~ S1+S~2

2

χS = 0,

~ S1,2

2

χA= 3 4χA,

~ S1,2

2

2.3. Aproximação de campo médio 27

e temos que

hχS|H|χSi= 1

4C+D, (2.13)

hχA|H|χAi=− 3

4C+D. (2.14)

Assim, segue das eqs. (2.13)- (2.14) que:

hχS|H|χSi − hχA|H|χAi=C, (2.15) relaciona o coeficiente C no Hamiltoniano (2.9) (mais comumente denotado por J) do produto escalar entre dois spins, com o termo de troca de natureza coulombiana da equação (2.8).

Tomando agora o Hamiltoniano de Heisenberg

H=−J X

<i,j>

~

Si. ~Sj, (2.16)

em que P

<i,j> indica uma soma entre pares distintos de spins vizinhos mais próximos, pois como foi dito anteriormente, a constante de trocaJ envolve a superposição de funções

de onda, cujas contribuições significativas são somente para pares de sítios vizinhos.

A interação de Heisenberg é um efeito eletrostático de origem quântica, de maneira que não possui qualquer análogo clássico. Contudo, é importante mencionar o papel da interação eletrostática coulombiana usual sobre os elétrons dos íons de uma rede. A rede cria sobre os íons um campo eletrostático que é denominado de campo cristalino, o qual apresenta importantes consequências para as propriedades magnéticas dos materiais. Os efeitos do campo cristalino sobre os estados eletrônicos dos íons estão relacionados às simetrias da rede.

2.3 Aproximação de campo médio

forma, a TCM torna-se uma aproximação exata apenas quando o alcance das interações é infinito. Assim, esta teoria permite a descrição qualitativa do comportamento do sistema de maneira bastante simplificada, mas faz algumas predições corretas sobre alguns aspectos das transições de fases, por exemplo, os expoentes críticos. Em geral, o Hamiltoniano pode ser expandido em termos da magnitude das flutuações em torno do campo médio. A dimensionalidade desempenha um papel essencial para determinar se a TCM é apropriada a um problema particular, pois uma vez que as interações são substituídas por uma única interação efetiva, a precisão é maior quanto maior o número de interações que atuam sobre um corpo. Isto acontece em altas dimensões ou para interações de longo alcance. Seguindo [29], vamos analisar o Hamiltoniano de um spin Si no modelo de Ising:

Hi =−JSi





z

X

j=1

Sj(i)



, (2.17)

onde z é o número de vizinhos mais próximos que rodeiam o spin i e Sj(i) simboliza o vizinho j do spin i. Desta maneira, a TCM substitui cada spin Sj(i) pelo valor médiohSii. O Hamiltoniano é então aproximado para

Hi ≈ −hef fSi, (2.18)

em quehef f =zJhSii é o campo efetivo. Para o Hamiltoniano acima, a função de partição associada ao spin do sítioi, no ensemble canônico é dada por:

Zi =

X

Si=±1

e−βHi = 2 cosh (_zJβhS

ii), (2.19)

ondeβ = 1/kBT. O valor médio da magnetização pode ser calculada a partir da função de partição anterior e é proporcional a _hSii,

hSii= tgh (zJβhSii). (2.20)

Faremos a seguinte mudança de variáveis na equação anterior: x=_hSii, e então notamos que existe uma temperatura a partir da qual as curvasy=xe y= tgh(zJβx) se cruzam,

o que acontece quando suas derivadas são iguais, ou seja,zJβ = 1. Logo, a temperatura crítica é dada por:

Tc =zJ/kB. (2.21)

Esta aproximação prediz a existência de uma transição em temperatura finita em qualquer dimensão, o que funciona qualitativamente para d _≥ 2, ou seja, em sistemas com alta

dimensionalidade a TCM reproduz satisfatoriamente bem os resultados experimentais.

2.3.1

Modelo de Curie-Weiss

2.3. Aproximação de campo médio 29

de Curie-Weiss é representado pelo Hamiltoniano:

H =−₂J_N

N

X

<i,j>

SiSj−H N

X

i

Si. (2.22)

Nesse Hamiltoniano cada spin interage com todos os outros através de uma interação J

fraca, mas de longo alcance e igual para qualquer par de spins. A soma é realizada sobre todos os pares de spins, e a divisão por N garante a existência do limite termodinâmico. Devido à interação ser de longo alcance, o Hamiltoniano pode ser reescrito como:

H=−₂J_N

N X i Si !2 −H N X i

Si, (2.23)

desprezando um termo subextensivo que não contribui no limite termodinâmico. Essa última forma do Hamiltoniano possibilita o cálculo exato da função de partição, que é dada por:

Z =T r

  exp        βJ 2N !1 2 N X i Si !  2 +βH N X i Si       

. (2.24)

Usando a identidade gaussiana dada por:

exp

a2= √1

π

Z ∞

−∞exp

−x2+ 2axdx, (2.25)

e fazendo a correspondência

a= βJ

2N

!1/2

X

Si, (2.26)

podemos escrever exp   βJ 2N

!1/2

X

Si





2

= √1

π

Z ∞

−∞exp



−x2+ 2

βJ

2N

!1/2

X

Six



dx. (2.27)

Conforme será visto mais adiante, nesta altura torna-se interessante realizar uma mudança de variáveis por meio de:

x=qN βJm_→dx=qN βJdm. (2.28)

Usando a nova variável m e efetuando o traço sobre os spins livres, a função de partição passa a ser dada por:

Z =

s

βJN

2π

Z ∞

−∞dm exp

(

−βJN m

2

2 +Nln [2 cosh (βJm+H)]

)

. (2.29)

Portanto, na aproximação de Curie-Weiss, a função de partição é representada da seguinte maneira: Z = s βJN 2π Z ∞

sendo

φ(T, D, H;m) = Jm2

2 −

1

β ln [2 cosh (β(Jm+H))], (2.31)

No limite N _{→ ∞}, segue que a energia livre de Gibbs por spin é dada por g(T, D, H) =minmφ(T, D, H;m). A energia livre contém todas as informações termodi-nâmicas do sistema e, portanto, todas as equações de estado podem ser derivadas dela. Minimizando o funcional φ da densidade de energia livre em relação à magnetização, ou

seja, impondo que∂g/∂m= 0, obtemos a equação de estado que determina a magnetização

por spin do sistema

m= tghβ(Jm+H). (2.32)

Fazendo a identificação _hSiie zJ na equação (2.20), com m e J, respectivamente, na equação anterior, notamos que elas tornam-se idênticas. O Hamiltoniano descrito pela equação (2.22), representa um sistema com interações uniformes de longo alcance que, através do uso da identidade gaussiana, pode ser resolvido exatamente. Por esta razão, modelos deste tipo são considerados generalizações do modelo Curie-Weiss dado pelo Hamiltoniano correspondente à equação (2.23).

2.4 Transições de Fases e Fenômenos Críticos

A teoria moderna das transições de fases e dos fenômenos críticos originou-se na década de 60, quando os conceitos básicos de classe de universalidade e escala das funções termodinâmicas foram introduzidos, bem como os princípios associados ao grupo de renormalização. Uma transição de fases [1, 2, 29] envolve quase sempre uma mudança de simetria ao passar de uma fase para outra. Por exemplo, quando um fluido se transforma em um sólido cristalino, ocorre uma quebra de simetria translacional contínua, pois em um fluido homogêneo cada ponto é similar a outro. No entanto, em um sólido regular, com invariância translacional, nem todos os pontos são similares, a menos que o mesmo seja deslocado por uma distância determinada pela regularidade da rede. Então, é conveniente introduzir uma variável que descreva o grau do ordenamento do sistema, levando em consideração sua simetria, o parâmetro de ordem,φ. No exemplo anterior, esse parâmetro é a magnetização por sítio, que assume o valor 1 quando a ordem no sistema é máxima, e zero quando a ordem desaparece. Para descrever adequadamente as fases do sistema, às vezes necessita-se de um parâmetro de ordem mais completo, que deve ser definido de acordo com as características da transição [1].

2.4. Transições de Fases e Fenômenos Críticos 31

uma variável termodinâmica, a partir da qual existe a descontinuidade. A transição de fase de um sistema caracteriza-se por singularidades nas funções termodinâmicas e, no caso dos sistemas magnéticos, a energia livre e suas derivadas, associadas à magnetização e susceptibilidade. Por exemplo, uma transição de primeira ordem caracteriza-se pela descontinuidade da magnetização e, em uma transição de segunda ordem, a magnetização vai a zero continuamente quando T _→T−

c , onde estamos considerando o sistema a campo nulo. Para uma transição de primeira ordem, há coexistência de duas fases distintas no ponto em que o sistema sofre transição. Assim, os dois tipos de transições mais comuns são: a transição contínua e a descontínua (ou de primeira ordem). Na transição contínua não existe calor latente associado, nem coexistência de fases, mas o parâmetro de ordem muda continuamente; a transição ferromagnética e a superfluida são deste tipo. No segundo caso, o parâmetro de ordem varia de maneira descontínua, caracterizando-se pela existência de um calor latente, o qual não altera a temperatura, num intervalo de tempo onde existe coexistência de fases, e após isto, uma das fases desaparece. Como um exemplo podemos considerar a água, que não passa imediatamente para o estado gasoso, mas forma uma mistura turbulenta de líquido e gás. Como não leva em consideração os casos comuns em que as derivadas da energia livre divergem, a classificação de Ehrenfest não é completa.

Os parâmetros externos relevantes para as transições de fases dos sistemas magnéti-cos são a temperaturaT e o campo magnético uniformeH. Desta forma, para temperaturas

abaixo de uma temperatura crítica (Tc) o sistema está ordenado, próximo de Tc ele começa a se desordenar e logo acima de Tc o sistema encontra-se desordenado (simétrico). Em geral, nos sistemas magnéticos, a magnetização é o parâmetro de ordem. Se o parâmetro de ordem cresce continuamente a partir de zero, temos uma transição contínua. Se φ pula

descontinuamente de zero para um valor não-nulo abaixo de Tc, a transição é de primeira

ordem. A entropia também é contínua se a transição for contínua e descontínua numa transição de primeira ordem, onde ocorre absorção de calor do sistema quando este vai da baixa para a alta temperatura. Esse é o calor latente QL= Tc∆S, em que ∆S é a variação da entropia e Tc é a temperatura de transição [30].

Na Figura (1) estão representados estes tipos de transição, segundo o comporta-mento de um dado parâmetro de ordem φ em função da temperatura.

Podemos estudar o comportamento das transições de fase de um dado sistema através de um diagrama de fases, o qual delimita a região de existência de cada fase, por meio de uma função de estado ou em função da variação dos parâmetros externos. A função de estado deve refletir a variação de um parâmetro externo. Se essa função assume diferentes valores nas diferentes fases e se anula na fase mais desordenada, então ela é denominada parâmetro de ordem.

Figura 1 – Comportamento de um parâmetro de ordem típicoφ em função da temperatura: (a) em

uma transição contínua ou de segunda ordem; (b) em uma transição descontínua ou de primeira ordem. Adaptada de [28].

vários graus de liberdade do sistema. Quando a temperatura varia, passa a existir uma competição entre a agitação térmica (que resulta em desordem no sistema) e o acoplamento dos momentos magnéticos (responsável por manter o sistema ordenado). Sendo assim, as transições de fases ocorrem em resposta à variação na temperatura do sistema, de modo que o diagrama de fases para este sistema pode ser construído, e tal diagrama apresenta um ponto crítico separando a fase ordenada (a baixas temperaturas) da fase desordenada (a altas temperaturas). Em sistemas em que há mais de um campo desordenado (por exemplo, temperatura e pressão), os diagramas de fases tornam-se multidimensionais e podem ocorrer os chamadospontos multicríticos. A seguir, relacionamos alguns pontos

multicríticos, de acordo com [30]:

• Ponto tricrítico: é o ponto que separa, no diagrama de fases, uma linha de transição de primeira ordem de uma linha contínua. Tal ponto tem sido detectado experimental-mente em misturas de He3_−He4_{, materiais metamagnetos (F eCl}

2 eN iN O3.2H2O),

caracterizados por alta anisotropia, além de modelos teóricos como o de Ising com campo aleatório [31, 32, 33, 34] e Blume-Capel [35, 36, 37, 38, 39, 40]. Tais pontos serão melhor discutidos na seção 2.6.

• Ponto bicrítico: Consideremos um sistema com dois parâmetros de ordemφ1 eφ2 e

com a energia livre de Landau dada por:

f = 1

2r(φ21+φ22)−

1

2g(φ21−φ22) +u1φ41+u2φ42+ 2u12φ21φ22. (2.33)

Quando g ₆= 0 temos quebra de simetria. Nesse caso, se g > 0, φ1 vai ordenar o

sistema antes de φ2, ocorrendo o inverso se g < 0. A forma do diagrama de fase

depende dos termos de quarta ordem: Se u1u2 < u212 (u12 =u1 =u2 quando g = 0),

temos uma linha de transição de primeira ordem ao longo de g = 0, com r < 0, separando a fase com φ1 6= 0, φ2 = 0 da fase com φ1 = 0 e φ2 6= 0, como mostra a

2.5. Expoentes críticos 33

pontor = 0,g = 0, que é chamado de ponto bicrítico. Este tipo de ponto é detectado

no diagrama de fases no plano T ₋H em cristais antiferromagnéticos com baixa

anisotropia.

• Ponto tetracrítico: Quando u1u2 > u212 existe uma fase intermediária com ambos φ1

e φ2 não-nulos, separada por uma linha de transição contínua das fases com φ2 = 0

e φ1 = 0, como mostrado na Figura (2). Neste caso, quatro linhas de transição

contínua se encontram no ponto r = 0, g = 0, que agora é um ponto tetracrítico. Este tipo de ponto é detectado quando se inclui anisotropia cúbica no Hamiltoniano de Heisenberg e também pode ser encontrado experimentalmente no composto

CoBr2.6H2O parcialmente deuterado.

• Ponto crítico terminal: Além dos pontos mencionados acima, um diagrama de fases pode apresentar também um ponto crítico terminal, que corresponde à interseção de uma linha contínua que separa a fase paramagnética de uma das fases ferromagnéticas com uma linha de primeira ordem separando a fase paramagnética da outra fase ferromagnética [37, 41].

Figura 2 – Diagrama de fases do modelo descrito pela equação (2.33) mostrando (a) um ponto bicrítico (BP); (b) um ponto tetracrítico (TP). Adaptada de [30].

2.5 Expoentes críticos

O comportamento singular ou divergente de certas funções termodinâmicas numa transição de fase de segunda ordem é descrito em termos de expoentes críticos. No ponto crítico (T =Tc), o comprimento de correlação do materialξ1diverge, ou seja, as flutuações ocorrem em todas as escalas de comprimento e as correlações entre dois spins separados por uma distância r, G(r), decaem como uma lei de potência. Em consequência, o comportamento das quantidades termodinâmicas do sistema, nas vizinhanças do ponto crítico, pode ser 1

ξ mede a distância espacial sobre a qual as flutuações dos graus de liberdade microscópicos estão

descrito por uma lei de potência [1, 2, 29]. Historicamente, esta descrição originou-se da mecânica dos fluidos, a partir de análises dimensionais que são conhecidas como leis de escala. É confirmado experimentalmente que diferentes sistemas podem apresentar um comportamento universal, ou seja, em transições contínuas, as leis de potência apresentam os mesmos expoentes próximos do ponto crítico. Se um conjunto de sistemas apresenta os mesmos expoentes críticos, dizemos que eles pertencem à mesma classe de universalidade. Acredita-se, embora não esteja ainda provado, que os expoentes críticos não dependem dos detalhes microscópicos dos sistemas físicos, mas apenas dos parâmetros globais, como a dimensão do sistema, o alcance das interações e a dimensão do parâmetro de ordem.

Para descrevermos o comportamento de uma dada quantidade físicaf em torno da

temperatura críticaTc, devemos definir a grandeza adimensional t=|T ₋Tc|/Tc , a qual chamamos de temperatura reduzida. Logo, definimos o expoente críticok como

k = lim

t→0

ln f(t)

ln t , (2.34)

que resulta na lei de potência

f(t) ≈ tk_{, t∼0. (2.35)}

A relação acima representa o comportamento assintótico da função f(t) quando t _→ 0. Geralmente

f(t) =Atλ(1 +btλ1 +_{. . .})_. (2.36) Para temperaturas diferentes da temperatura crítica, acima ou abaixo dela, o sistema se encontra em duas fases distintas caracterizadas por um parâmetro de ordem φ, que tende

para zero quando a temperatura vai para Tc. Por exemplo, para um ferromagneto simples

onde o parâmetro de ordem é a magnetização M do sistema, os expoentes críticos na fase

ordenada (T < Tc) são definidos de maneira convencional na Tabela 1.

Expoente Comportamento

α C_∼t−α β M _∼tβ

γ χ_∼t−γ

ν ξ_∼t−ν

Tabela 1 – Expoentes críticos paraT < Tc, ondeC,M,χeξrepresentam o calor específico, a magnetização

total, a suscetibilidade e o comprimento de correlação, respectivamente.

Na Tabela 2 a seguir, temos os expoentes críticos da fase desordenada (T > Tc),

2.6. Teoria de Landau 35

Expoente Comportamento

α′ _{C ∼t}−α′

γ′ _χ∼t−γ′

ν′ _ξ∼t−ν′

Tabela 2 – Expoentes críticos paraT > Tc, ondeC,χeξ representam o calor específico, a suscetibilidade

e o comprimento de correlação, respectivamente.

E na Tabela 3 são apresentados os expoentes críticos para o ponto crítico (T = Tc).

Expoente Comportamento

δ h_∼mδ

η G(r) =_hS(0)S(r)_{i ∼}r−d+2−η

Tabela 3 – Expoentes críticos emT =Tc;m,h,G(r) edrepresentam a magnetização por partícula, o

campo magnético externo, a função de correlação entre dois spins separados por uma distância r e a

dimensão do sistema, respectivamente.

Baseados em argumentos de estabilidade dos potenciais termodinâmicos, na década de sessenta vários autores obtiveram relações de desigualdade entre os expoentes críticos [1]:               

α+ 2β+γ _≥2 (desigualdade de Rushbrooke, 1963)

α+β(1 +δ)≥2 (desigualdade de Griffiths, 1965)

νd_≥2₋α (desigualdade de Josephson, 1967)

(2₋η)ν_≥γ (desigualdade de Fisher, 1969).

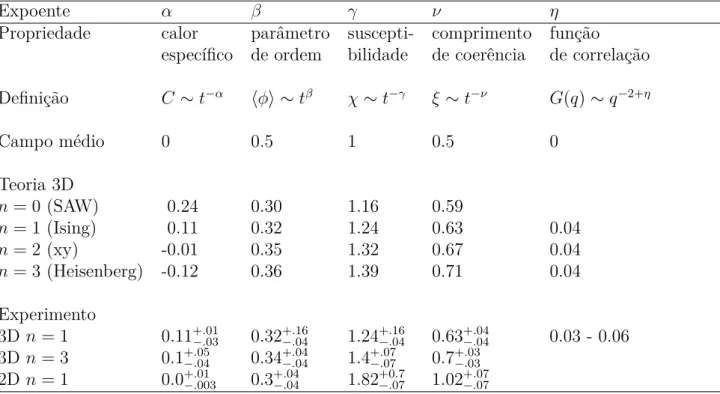
O modelo de Ising numa rede anisotrópica, onde J e J′ _{são as interações entre} primeiros vizinhos na direção horizontal e vertical, respectivamente, foi discutido por Onsager [15], e também por Chang [42], mostrando que os expoentes críticos deste modelo independem da razão J/J′ _{> 0 , indicando uma certa universalidade nos valores dos} expoentes críticos. Na Tabela a seguir são mostrados alguns valores dos expoentes críticos obtidos teoricamente por meio de diversos métodos de aproximação e ainda de resultados experimentais.

2.6 Teoria de Landau

Expoente α β γ ν η

Propriedade calor parâmetro suscepti- comprimento função específico de ordem bilidade de coerência de correlação

Definição C _∼t−α _{hφi ∼t}β _χ∼t−γ _ξ∼t−ν _G(q)∼q−2+η

Campo médio 0 0.5 1 0.5 0

Teoria 3D

n= 0 (SAW) 0.24 0.30 1.16 0.59

n= 1 (Ising) 0.11 0.32 1.24 0.63 0.04

n= 2 (xy) -0.01 0.35 1.32 0.67 0.04

n= 3 (Heisenberg) -0.12 0.36 1.39 0.71 0.04

Experimento

3D n= 1 0.11₋+..0103 0.32+−..0416 1.24+−..1604 0.63+−..0404 0.03 - 0.06

3D n= 3 0.1+₋..0405 0.34−+..0404 1.4−+..0707 0.7+−..0303

2D n= 1 0.0+.01

−.003 0.3+−..0404 1.82−+0.07.7 1.02+−..0707

Experimentos em 3Dn= 1 compilados para transições líquido-gás, fluido binário, ferromagnéticas e antiferromagnéticas.

Experimentos em 3Dn= 3 compilados para transições ferromagnéticas e antiferromagnéticas.

Experimentos em 2Dn= 1 compilados para transições antiferromagnéticas.

Tabela 4 – Alguns expoentes críticos obtidos da teoria e de experimentos.

que apenas os termos de ordens mais baixas são necessários para manter a simetria. A maior utilidade desta teoria reside no fato que muitas de suas predições podem ser determinadas resolvendo-se equações bastante simples. A teoria de Landau nos permite determinar qualitativamente os diagramas de fases nas vizinhanças dos pontos críticos e multicríticos. Trata-se na realidade da transição entre fases que possuem simetrias distintas. Sua aplicabilidade é mais adequada na vizinhança das transições de fases contínuas, onde o parâmetro de ordem é pequeno.

De acordo com Landau [17, 43], o potencial termodinâmico apropriado, f, pode

ser expandido em torno da temperatura crítica (T =Tc) e em termos do parâmetro de

ordem (m= 0), neste caso a magnetização, que por razões de simetria fica:

f(T, m) = A0+A2m2+A4m4+A6m6+· · · . (2.37)

A título de ilustração, vamos considerar o ferromagneto de Ising. Para este caso, é suficiente escrever a densidade de energia livre até a quarta potência da magnetização. Assim, vamos considerar:

2.6. Teoria de Landau 37

Para altas temperaturas, m é zero quando o campo magnético h se anula, portantof tem

que apresentar um mínimo em m= 0, para este caso. Por outro lado, espera-se um estado

ferromagnético, a baixas temperaturas, e pelo menos um mínimo de f com m₆= 0. Isto

ocorre se A2 muda de sinal quando T ultrapassa uma temperatura Tc,

A2 =a(T −Tc), (a >0). (2.39) Na Figura (3), temos a funçãof representada para três valores deT, com a condição

que A4 seja independente da temperatura. Observa-se que paraT > Tc temos um único mínimo emm = 0. Por outro lado, paraT < Tc, existem dois mínimos simétricos em torno

de m= 0.

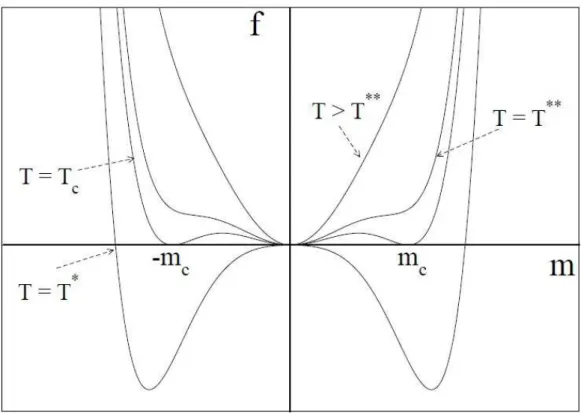
Figura 3 – A densidade de energia livre, f = 1 2A2m

2 ₊

A4m4, como função da magnetização, para

diferentes temperaturas. Adaptado de [28].

A equação de estado para o casoh = 0 é dada por

A2m+ 4A4m3 = 0, (2.40)

cujas soluções são dadas por:

m =







0, T > Tc

±(−A2/4A4)1/2, T < Tc.

(2.41)

Portanto, existe uma transição contínua predita pela teoria de Landau, em que:

comβ sendo o expoente crítico associado à magnetização, o qual controla a dependência do

parâmetro de ordem na vizinhança da temperatura crítica. Se as flutuações são relevantes, ou seja, nas proximidades da criticalidade, β é geralmente menor que 1/2, como por

exemplo, para três dimensões, em queβ _≈1/3 (veja a Tabela (4)). As soluções da equação

de estado, dadas acima, mostram que tem-se dois valores possíveis param quando T < Tc eh= 0, os quais correspondem aos dois sentidos diferentes da magnetização.

Podemos usar a teoria de Landau para compreender como surgem os pontos tricríticos. Para tanto, a expansão deve levar em conta o termo A6m6, com A6 > 0 e

permitir queA4 possa mudar de sinal.

2.6.1

Teoria de Landau para pontos tricríticos

De acordo com [44], define-se um ponto crítico em um diagrama de fases como o ponto que marca o final de uma linha de coexistência, onde duas fases distintas e coexistentes se tornam idênticas. Em analogia, um ponto tricrítico deve ser definido como o ponto final de uma linha de coexistência de três fases, ou seja, de uma linha tripla, na qual três fases coexistentes tornam-se idênticas simultaneamente.

Em um determinado diagrama de fases pode haver pontos nos quais várias fases coexistem, são os denominados pontos multicríticos. Nesta tese, daremos atenção especial aos chamados pontos tricríticos que, como mencionado anteriormente, correspondem ao ponto onde três fases se tornam idênticas ou três linhas críticas se interceptam, conforme mostrado na Fig. 4 a seguir. Esta Figura mostra um diagrama de fases para um sistema do tipo antiferromagneto com anisotropia uniaxial. Como podemos observar, a campo nulo ocorre uma transição de fases contínua à temperatura de Néel, TN, abaixo da qual o sistema encontra-se antiferromagneticamente ordenado. Se o sistema é colocado na presença de um campo magnético pequeno, a temperatura de transição diminui, mas a transição permanece sendo contínua e temos uma linha de pontos críticos (linha cheia). Por outro lado, a aplicação de um campo suficientemente forte, a baixas temperaturas, leva a uma transição de primeira ordem da fase antiferromagnética para a fase paramagnética. A temperatura para a qual isso ocorre irá depender do valor do campo H, de maneira que

temos uma linha de coexistência (linha pontilhada). As linhas cheia e pontilhada da Fig. 4 separam fases simetricamente distintas e, como foi notado por Landau [43], elas devem se encontrar em um ponto P, que é o ponto crítico. Do ponto de vista teórico, podemos simular um ponto tricrítico, do tipo descrito no diagrama de fase da Fig. (4), introduzindo no Hamiltoniano o campostaggered H† _{que se acopla ao parâmetro de ordemm}† _{[44]. Tal}

campo não pode ser produzido diretamente em laboratório, mas pode ser induzido [45, 46].

2.6. Teoria de Landau 39

Figura 4 – Diagrama de fasesT versusH para o compostoDy3Al5O12. A curva contínua representa a

linha crítica e a pontilhada uma linha de primeira ordem. O círculo cheio representa o ponto tricrítico. Dados experimentais de [47].

de transição de primeira ordem, isto é, a coexistência das fases AF e P. Por sua vez, a linha contínua (Lλ) representa, no mesmo plano, a transição de fase de segunda ordem, ou a transição contínua. Considerando H†

6

= 0, é possível obter duas superfíciesS₋ eS+

de transição de fase, conforme H†_{<0 e H}† _{>0, respectivamente. Assim, a interseção de}

S₋ com o plano H†_{= 0 será a linha L}

−, do mesmo modo que S+ intercepta no mesmo

plano seguindo a mesma linha L+. O ponto (Tt, Ht,0) foi denominado por Griffiths [48] de ponto tricrítico.

Voltando à teoria de Landau para pontos tricríticos, consideremos agora a seguinte densidade de energia livre de Landau:

f = 1

2A2m2+A4m4+A6m6, (2.43)

onde A2 =a(T −T⋆).

SeA4for positivo, então o termo de sexta ordem não exerce influência na vizinhança

da transição contínua. Mas, se A4 for negativo, o termo de sexta ordem é importante

para manter a estabilidade. Neste caso, irá surgir um segundo mínimo da energia livre, simétrico em torno de m = 0, quando T diminui, como pode ser observado na Fig. (6).

Uma vez que a energia livre do segundo mínimo (com m₆= 0) é zero, haverá uma transição de primeira ordem. A temperatura T⋆ _{é o limite da metaestabilidade da fase isotrópica} (paramagnética), pois temos que para T⋆ _{< T < T}

Figura 5 – Diagrama de fases esquemático para um metamagneto no espaço de temperaturaT, campo

magnético uniformeH e campo magnéticostaggered H†_{. Adaptado de [48].}

na temperatura T⋆⋆_{, na qual não há mais o segundo mínimo. Desta forma, seA}

4 >0 a

transição acontece para A2 = A2c = 0 e Tc = T⋆. Para A4 <0 a transição de primeira

ordem é determinada pela condição de igualdade das energias,f(A2c, m) = 0, e da condição de equilíbrio,∂f(A2c, m)/∂m= 0. Assim:

A2c =a(Tc −T⋆) =







0, A4 >0 1

2|A4|2/A6, A4 <0,

(2.44)

e

mc =±(A4/2A6)1/2. (2.45)

Como vimos, a TCM troca a configuração real das variáveis locais (por exemplo, spins) por seu valor médio, desprezando os efeitos das flutuações, que podem ou não ser importantes. Por exemplo, vamos considerar um spin teste S. Quanto mais spins

interagem comS mais o spin teste sente os efeitos de uma média efetiva ou campo médio.

SeS interage apenas com dois vizinhos, a média é pequena e as flutuações são grandes e

2.7. Sistemas magnéticos desordenados 41

Figura 6 – A densidade de energia livref, em função dem, até a sexta ordem emm, Eq. (2.43), quando A4<0. Existe uma transição de primeira ordem paraT =Tc.T

⋆⋆ e

T⋆são os limites de metaestabilidade

(coexistência de fases) das fases ordenada e desordenada, respectivamente.

dimensão crítica, dc, as flutuações não mais são importantes, de maneira que a TCM

fornece uma descrição analiticamente correta das transições de fases contínuas. À medida que a dimensão decresce, as flutuações se tornam mais importantes e até 3 dimensões a TCM ainda produz uma boa descrição qualitativa. Abaixo disso, as flutuações podem destruir o estado ordenado e as transições de fases a temperaturas finitas. Concluímos então que existe uma dimensão crítica superior, (tipicamente dc = 4), abaixo da qual as flutuações são importantes e tornam a TCM inválida para temperaturas próximas de Tc.

Este fato motivou uma generalização da teoria de Landau através de uma teoria de campo que enfatiza o papel das flutuações no parâmetro de ordem. Para mais detalhes veja, por exemplo, [30].

2.7 Sistemas magnéticos desordenados

diferentes configurações no comportamento crítico de um sistema puro.

Um dos efeitos que tais desordens podem produzir é a redução da temperatura crítica com respeito ao sistema homogêneo. Os sistemas que apresentam transição de fase contínua podem sofrer mudanças na sua classe de universalidade. Se o sistema uniforme exibe transição de fase de primeira ordem, as descontinuidades das funções termodinânicas na fronteira de fase podem ser suavizadas, podendo levar o sistema a exibir uma transição de fases contínua [49]. Em condições mais extremas, a desordem pode eliminar completamente a transição de fase.

Existem dois tipos de classificação para a desordem: temperada (quenched), que

ocorre nos sistemas sólidos, em que as partículas estão fixas na amostra, ou recozida (annealed), que ocorre nos sistemas fluidos, nos quais as partículas estão livres para

se movimentarem na amostra. A desordem temperada pode ser realizada através do resfriamento rápido de uma amostra, partindo de altas temperaturas, imediatamente após a difusão das impurezas. Por sua vez, a desordem recozida corresponde a um resfriamento lento, de modo que as impurezas tenham tempo suficiente para se deslocar no interior da amostra, minimizando assim a energia livre. Existe um grande interesse no estudo dos materiais magnéticos reais sob efeito de desordem do tipoquenched (vidros de spins ou modelos com campos aleatórios), pois nesses casos as moléculas (ou spins) não apresentam grande mobilidade na rede cristalina. A desordem quenched ocorre quando a variável

aleatória está associada à escalas de tempo muito longas em relação às demais variáveis do sistema. Nesse caso, a dita variável lenta pode demorar um tempo muito longo para entrar em equilíbrio térmico com as demais variáveis e deve receber um tratamento diferenciado. Muito esforço foi dedicado a compreender de que maneira os cálculos estatísticos deveriam ser feitos de modo a contemplar essa diferença. Por fim, chegou-se à conclusão que, para sistemas com desordemquenched deve-se considerar uma certa configuração dessas variáveis, calcular a função de partição, obtendo a energia livre e em seguida tomar a média da energia livre com respeito à distribuição de probabilidades associada à variável aleatóriaquenched [50]. Tomar a média da energia livre com respeito à distribuição de

probabilidades da variável lenta requer que seja realizada a média do logaritmo de uma função de partição, o que implica em um trabalho árduo. Dessa maneira, foi desenvolvido um método especial para lidar com esse problema: o chamado método das réplicas [51].

O método das réplicas consiste em considerar a seguinte identidade logarítmica da função de partição, associada a n cópias (réplicas) do sistema original:

hlnZi= lim n→0

hZn_i

n , (2.46)

em seguida calcular_hZn_{iparaninteiro e obter a energia livre por meio de uma continuação} analítica emn. Veja o apêndice A para mais detalhes a respeito deste método.

2.8. Diluição, interação e campo aleatórios 43

nos modelos puros, temos a diluição aleatória de sítio, a ligação aleatória e ainda o campo aleatório. Neste trabalho estudaremos apenas sistemas desordenados tipo quenched, onde

a desordem ocorre em campos aleatórios, excluindo o caso mais complexo dos chamados vidros de spins.

2.8 Diluição, interação e campo aleatórios

Um dos exemplos mais simples de sistemas desordenados é o problema da diluição aleatória [11], isto é o que ocorre, por exemplo, com o composto Rb2CopM g1−pF4 [52, 53] emd= 2.

No caso deste composto, os átomos de M g substituem os átomos magnéticos de Co

em sítios aleatórios na rede. O modelo de Ising com diluição aleatória é descrito pelo Hamiltoniano:

H(S, ǫ) = ₋J X

<ij>

ǫiSiǫjSj −h

X

i

ǫiSi. (2.47)

No qual a primeira soma é sobre todos os pares de primeiros vizinhos < i, j >de uma rede d-dimensional e a segunda sobre todos os sítios i, Si denotam os spins de Ising e ǫi são números de ocupação, que em uma dada configuração de desordem ǫ descreve a ocupação

de um sítio i por um spin ǫi = 1 com probabilidade p, ou a não ocupação ǫi = 0, com probabilidade 1₋p. As variáveis ǫi são aleatórias quenched.

Um outro caso de grande interesse considera a desordem nas interações de troca. Dessa forma, o Hamiltoniano do modelo de Ising com ligação aleatória é dado por

H(S, Jij) =−

X

<i,j>

JijSiSj −h

X

i

Si, (2.48)

em que as variáveis aleatórias Jij obedecem a uma distribuição de probabilidades binária, como, por exemplo

P(Ji,j) =pδ(Jij −J1) + (1−p)δ(Jij −J2). (2.49)

No caso especial em que J2 = 0, teremos a diluição aleatória de ligações. No caso em

que J1 e J2 são ambos positivos, o sistema é ferromagnético e o estado fundamental é