Geometria Basica Aula 13 Volume1

Aula 13 – Pol´ıgonos regulares

Objetivos

• Determinar a ´area de pol´ıgonos regulares.

Introdu¸

c˜

ao

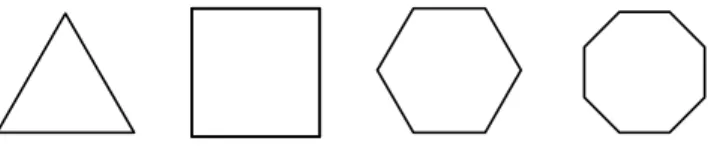
Um pol´ıgono ´e chamadoequil´atero se todos os seus lados s˜ao congruen-tes. ´E chamado equiˆangulose todos os seus ˆangulos internos s˜ao congruentes. Um pol´ıgono que ´e ao mesmo tempo equil´atero e equiˆangulo ´e chamado re-gular. Veja na figura 253 alguns exemplos de pol´ıgonos regulares.

Fig. 253: Pol´ıgonos regulares.

Vocˆe pode estar se perguntando se as duas defini¸c˜oes n˜ao significam a mesma coisa. Na verdade, se estivermos falando de triˆangulos, as duas pro-priedades s˜ao equivalentes. Isso acontece por causa da propriedade que tˆem os triˆangulos de o maior ˆangulo se opor ao maior lado, e vice-versa. Assim, se um triˆangulo ´e equil´atero, ent˜ao, como conseq¨uˆencia, todos os seus ˆangulos s˜ao iguais e ele ´e equiˆangulo. Da mesma forma, se um triˆangulo tem todos os ˆangulos congruentes, prova-se que seus lados tamb´em s˜ao congruentes. Por-tanto, para mostrar que um dado triˆangulo ´e regular, basta mostrar que ele ´e equil´atero ou que ele ´e equiˆangulo, n˜ao sendo necess´ario verificar as duas coisas.

No caso de pol´ıgonos com mais de trˆes lados isso n˜ao ´e verdade, nem mesmo para quadril´ateros. Um retˆangulo com base e altura n˜ao congruentes ´e equiˆangulo, pois todos os seus ˆangulos s˜ao retos, mas n˜ao ´e equil´atero. Um losango que n˜ao seja quadrado ´e equil´atero, mas n˜ao ´e equiˆangulo (figura 254).

(a)

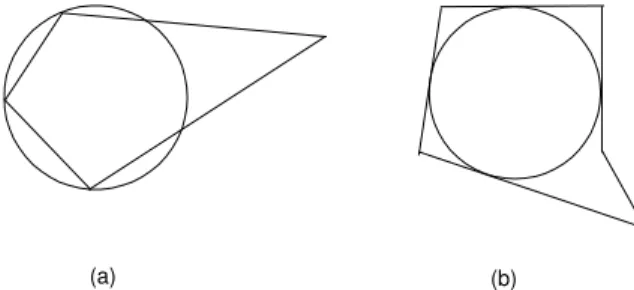
Quando acontece de existir um c´ırculo contendo todos os v´ertices de um pol´ıgono, dizemos que esse pol´ıgono est´a inscrito em tal c´ırculo, ou que ele ´einscrit´ıvel. Quando ocorre de existir um c´ırculo que ´e tangente a todos os lados de um pol´ıgono, dizemos que esse pol´ıgono est´a circunscrito a tal c´ırculo, ou que ele ´ecircunscrit´ıvel. Veja a figura 255.

(a) (b) (c)

Fig. 255: a) Pol´ıgono inscrito (o pol´ıgono n˜ao ´e regular)). b) Pol´ıgono circunscrito (o pol´ıgono n˜ao ´e regular). c) Pol´ıgono regular inscrito.

Vamos provar que todo pol´ıgono regular ´e inscrit´ıvel e circunscrit´ıvel. Para isso considere um pol´ıgono regularP =A₁A₂. . . Anqualquer. Tracemos

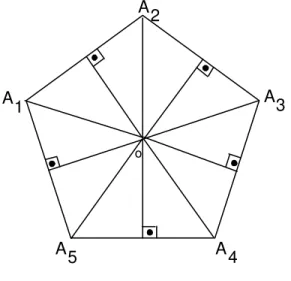
as mediatrizes dos lados A₁A₂ e A₂A3, as quais encontram-se num ponto O. A figura 256 mostra um caso particular em que P ´e um pent´agono.

o

A 1

A 2

A₃

A₄ A₅

Fig. 256: Pent´agono regularA1A2A3A4A5.

Como O est´a na mediatriz do lado A1A2, ent˜ao a distˆancia de O aos v´ertices A1 e A2 ´e a mesma, que chamaremos r. Pelo mesmo motivo, a distˆancia de O a A3 ´e a mesma distˆanciar deO aA2. Os triˆangulosOA1A2 eOA2A3 s˜ao, assim, is´osceles. Al´em disso,OA1A2 ≡OA2A3, por L.L.L.. Se-gue que os ˆangulosOAˆ1A2, OAˆ2A1, OAˆ2A3 e OAˆ3A2 s˜ao todos congruentes.

ComoA1Aˆ2A3 ≡A2Aˆ3A4(pois o pol´ıgono ´e equiˆangulo), conclui-se que

OAˆ3A4 ≡OAˆ3A2. Por L.A.L., os triˆangulos OA3A4 e OA3A2 s˜ao congruen-tes, donde se conclui que OA4 ≡ OA2. Assim, tem-se que a distˆancia entre

O e A4 ´e tamb´em r. Da mesma forma se prova que a distˆancia do ponto O aos outros v´ertices do pol´ıgono P ´e tamb´emr. Conseq¨uentemente, o c´ırculo de centroO e raio r passa por todos os v´ertices do pol´ıgonoP.

Al´em disso, os triˆangulos OA₁A2, OA₂A3, . . ., OAnA₁ s˜ao todos

con-gruentes. Segue que os segmentos unindo o ponto O aos pontos m´edios de cada lado s˜ao todos congruentes. Chamemos de a a medida desses seg-mentos. Como esses segmentos s˜ao perpendiculares aos lados do pol´ıgono

P, conclu´ımos que o c´ırculo de centro O e raio a ´e tangente a todos os lados de P.

Provamos, assim, que:

Todo pol´ıgono regular ´e inscrit´ıvel e circunscrit´ıvel

O ponto O considerado na demonstra¸c˜ao anterior ´e chamado centro do pol´ıgono regular, e o n´umero a ´e chamado ap´otema. Tamb´em chamaremos de ap´otema a todo segmento ligandoO ao ponto m´edio de um dos lados.

Veja na figura 257 um hex´agono regular e os c´ırculos em que est´a ins-crito e circunsins-crito.

Fig. 257: C´ırculos inscrito e circunscrito a um hex´agono regular.

Um pol´ıgono, contudo, pode ser inscrit´ıvel ou circunscrit´ıvel sem ser regular, como mostra a figura 255. Por outro lado, existem pol´ıgonos que n˜ao s˜ao inscrit´ıveis, ou circunscrit´ıveis. Veja a figura 258.

(a) (b)

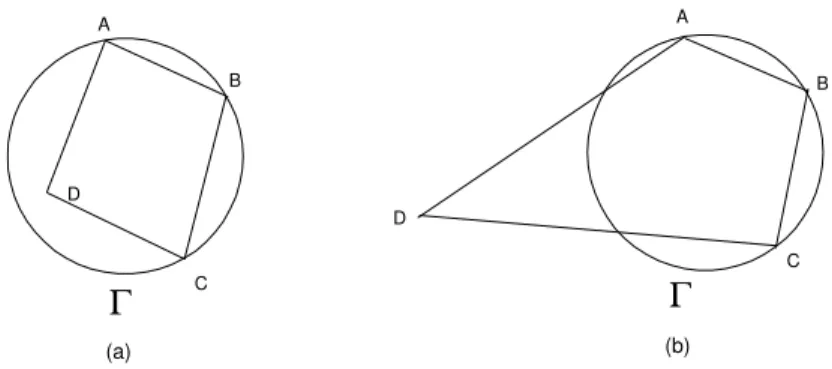
Veremos a seguir um crit´erio que permite decidir se um quadril´atero qualquer ´e inscrit´ıvel ou n˜ao. Primeiro consideremos um quadril´ateroABCD

inscrito no c´ırculo Γ, como na figura 259.

A

B

C D

G

Fig. 259: ˆAQuadril´atero inscrito.

Os ˆangulos BADˆ e BCDˆ s˜ao ˆangulos inscritos em Γ, e os arcos de-terminados por esses ˆangulos comp˜oem o c´ırculo completo, intersectando-se apenas nos extremos. Da´ı, conclui-se que 2 ˆBAD+ 2 ˆBCD = 360o

, ou seja, ˆ

BAD+BCDˆ = 180o

e esses ˆangulos s˜ao suplementares. Do mesmo modo, s˜ao suplementares os ˆangulos ADCˆ e ABCˆ .

Reciprocamente, suponhamos queABCD seja um quadril´atero tal que os ˆangulos opostos s˜ao suplementares. Tracemos o c´ırculo Γ que cont´em os pontosA,B e C. Vamos mostrar que o ponto Dtamb´em est´a em Γ.

Suponhamos que o ponto D n˜ao esteja no c´ırculo Γ. Nesse caso, h´a duas possibilidades: D est´a no interior de Γ ouDest´a no exterior de Γ (veja as duas possibilidades na figura 260).

A

B

C D

(a) (b)

A

B

C

Γ Γ

D

Fig. 260: (a)D_{no interior de Γ. (b)}D_{no exterior de Γ.}

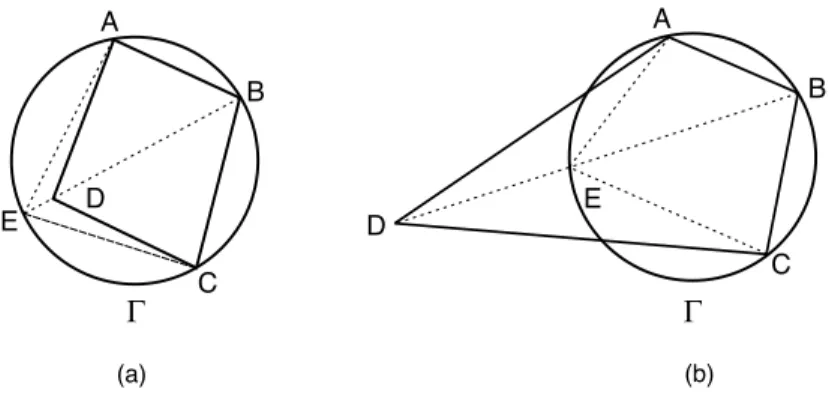
Em qualquer das possibilidades, sejaE o ponto em que a semi-reta−−→BD

intersecta Γ, como na figura 261.

A

B

C D

E

(a)

A

B

C D

E

(b)

G G

Fig. 261: (a)Dno interior de Γ. (b)Dno exterior de Γ.

Se D est´a no interior de Γ, temos ADB >ˆ AEBˆ e CDB >ˆ CEBˆ , donde se conclui que ADC >ˆ AECˆ . Mas ADCˆ e ABCˆ s˜ao suplementares, por hip´otese, eAECˆ e ABCˆ s˜ao suplementares porqueABCE est´a inscrito em Γ. Logo ADCˆ _≡ AECˆ . Mas j´a t´ınhamos conclu´ıdo que ADC >ˆ AECˆ . Essa contradi¸c˜ao mostra que D n˜ao pode estar no interior de Γ. Deixamos como exerc´ıcio a prova de queD n˜ao pode estar no exterior de Γ.

Com isso mostramos a seguinte proposi¸c˜ao:

Proposi¸c˜ao 31

Um quadril´atero ´e inscrit´ıvel num c´ırculo se e somente se seus ˆangulos inter-nos opostos s˜ao suplementares.

Veja na proposi¸c˜ao seguinte como fica a ´area de um pol´ıgono regular.

Proposi¸c˜ao 32

A ´area de um pol´ıgono regular ´e a metade do produto do per´ımetro pelo ap´otema.

Prova:

Se A1A2. . . An ´e um pol´ıgono regular de n lados, ligando cada um

de seus v´ertices ao centro O do pol´ıgono, ficam determinados n triˆangulos is´osceles congruentes de base igual a m(A1A2) e altura igual ao ap´otema do pol´ıgono, que denotaremos por a. A ´area de cada um desses triˆangulos ´e

m(A1A2)a

2 . Pelas propriedades de ´area, conclu´ımos que

AA1A2...An =n

m(A1A2)a

2

= nm(A1A2)a

2

Como nm(A1A2) ´e justamente o per´ımetro do pol´ıgono, j´a que seus n lados s˜ao todos congruentes a A1A2, fica demonstrada a proposi¸c˜ao.

Sejam Γ e Γ′ _{c´ırculos com o mesmo centro O (dizemos nesse caso que}

s˜ao concˆentricos) e seja P =A1A2. . . An um pol´ıgono regular inscrito em Γ.

Definamos um pol´ıgono P′ _{inscrito em Γ}′ _{da seguinte forma: B}

1 =−−→OA1∩Γ′,

B2 =−−→OA2∩Γ′ etc. O pol´ıgono assim definido ´e chamado proje¸c˜ao radial de

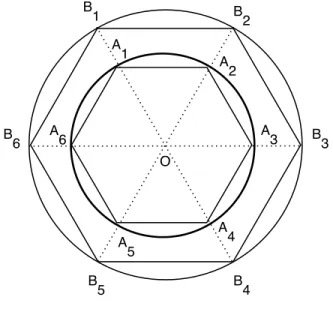
P sobre Γ′_{. Veja na figura 262 o caso particular em que P ´e um hex´agono.}

Nota: na figura 262, Γ′_{´e o}

c´ırculo externo e Γ ´e o c´ırculo interno. Os ap´otemasa_ea′_s˜ao,

respectivamente, a distˆancia do centroO_{at´e os lados dos}

pol´ıgonosP _eP′_.

B

1 B₂

B

6 B3

B

5 B4

A 1

A 2

A

6 A3

A 4 A

5 O

Fig. 262: Proje¸c˜ao radial do hex´agono.

Deixaremos como exerc´ıcio a prova de que P′ _{tamb´em ´e regular.}

De-terminaremos agora a rela¸c˜ao entre as ´areas deP eP′_{. Para isso, chamemos}

de r e r′ _{os raios de Γ e Γ}′_{, a e a}′ _{os ap´otemas, A e A}′ _{as ´areas e p e}

p′ _{os per´ımetros de P e P}′_{, respectivamente. J´a sabemos que A =} 1 2ap e

A′ ₌ 1 2a

′_p′_{. Considere os triˆangulos A}

1OA2 e B1OB2. Como ambos s˜ao is´osceles e tˆem o ˆangulo central A₁OAˆ ₂ em comum, podemos concluir que s˜ao semelhantes. Como conseq¨uˆencia dessa semelhan¸ca, decorre que

r r′ =

m(A1A2)

m(B1B2) =

a

a′ (6)

onde a ´ultima igualdade vem do fato de a e a′ _{serem as alturas de A}

1OA2 e B₁OB₂ com respeito `as bases A₁A₂ e B₁B2. Como P e P′ _{s˜ao regulares,}

temos p=nm(A₁A2), e p′ _=nm(B

1B2), o que nos d´a

p p′ =

m(A1A2)

m(B1B2)

.

Substituindo na equa¸c˜ao (6), obtemos

r r′ =

p p′ =

a a′.

Da´ı conclu´ımos que

A A′ =

ap a′_p′ =

r

r′ 2

.

Um racioc´ınio an´alogo pode ser feito para os pol´ıgonos circunscritos. A f´ormula acima ser´a muito ´util na pr´oxima aula, quando faremos o c´alculo da ´area do c´ırculo.

Resumo

Nesta aula vocˆe aprendeu...

• O que s˜ao pol´ıgonos regulares.

• Que todo pol´ıgono regular ´e inscrit´ıvel e circunscrit´ıvel.

• Que um pol´ıgono pode ser inscrit´ıvel ou circunscrit´ıvel sem ser regular.

• Que existem pol´ıgonos que n˜ao s˜ao inscrit´ıveis ou circunscrit´ıveis.

• Um crit´erio para verificar se um quadril´atero ´e inscrit´ıvel ou n˜ao.

• A f´ormula para calcular a ´area de um pol´ıgono regular.

Exerc´ıcios

1. Prove que todo triˆangulo equiˆangulo ´e tamb´em equil´atero.

2. Prove que um pol´ıgono regular circunscrito a um c´ırculo tangencia o mesmo no ponto m´edio de cada lado.

3. Prove que a soma dos ˆangulos externos de um pol´ıgono convexo ´e 360o

.

4. Na figura 263,ABP ´e um triˆangulo equil´atero eABCDE´e um pent´agono regular.

A B

C D

E

P

5. Determine os pol´ıgonos regulares para os quais os ˆangulos internos e externos s˜ao iguais.

6. Determine o n´umero de lados de um pol´ıgono regular, sabendo que seus ˆangulos internos medem 144o

.

7. Determine os raios dos c´ırculos inscrito e circunscrito em um hex´agono regular de 6cm de lado.

8. Determine a medida do lado e o ap´otema de um hex´agono regular inscrito em um c´ırculo de raio 2√3cm.

9. Prove que a ´area de um triˆangulo ´e dada pelo produto do semi-per´ımetro pelo raio da circunferˆencia inscrita.

10. Prove que a soma das distˆancias de um ponto interno de um triˆangulo equil´atero aos lados n˜ao depende do ponto interno considerado.

11. Determine a maior ´area que um triˆangulo pode ter se ele est´a inscrito em um c´ırculo de raioR.

12. Na figura 264, ABCDEF ´e um hex´agono regular. Sobre seus lados foram constru´ıdos quadrados.

A B

D C

E F

G H

I

J

K

L

M N

O P Q

R

Fig. 264: Exerc´ıcio 12.

Prove que o pol´ıgono GHIJ KLM N OP QR´e um dodec´agono regular.

13. (EPUSP-1966) As bases de um trap´ezio is´osceles circunscrito a um c´ırculo medem 9cme 6cm. Cada um dos outros dois lados do trap´ezio mede:

(a) 4,5cm (b) 6cm (c) 7,5cm (d) 8cm (e) N.R.A.

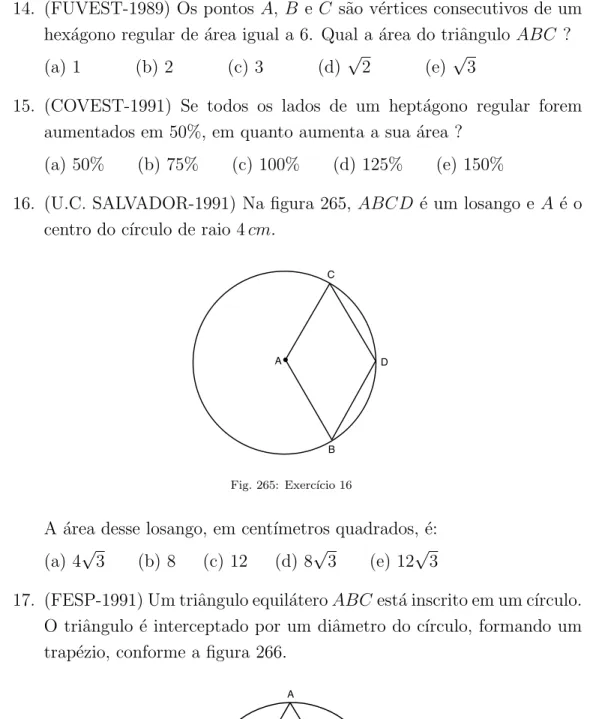
14. (FUVEST-1989) Os pontos A, B e C s˜ao v´ertices consecutivos de um hex´agono regular de ´area igual a 6. Qual a ´area do triˆangulo ABC ?

(a) 1 (b) 2 (c) 3 (d) √2 (e) √3

15. (COVEST-1991) Se todos os lados de um hept´agono regular forem aumentados em 50%, em quanto aumenta a sua ´area ?

(a) 50% (b) 75% (c) 100% (d) 125% (e) 150%

16. (U.C. SALVADOR-1991) Na figura 265, ABCD ´e um losango e A ´e o centro do c´ırculo de raio 4cm.

A

B C

D

Fig. 265: Exerc´ıcio 16

A ´area desse losango, em cent´ımetros quadrados, ´e:

(a) 4√3 (b) 8 (c) 12 (d) 8√3 (e) 12√3

17. (FESP-1991) Um triˆangulo equil´ateroABC est´a inscrito em um c´ırculo. O triˆangulo ´e interceptado por um diˆametro do c´ırculo, formando um trap´ezio, conforme a figura 266.

A

B C

M N

O

P Q

Fig. 266: Exerc´ıcio

A raz˜ao entre a ´area do triˆangulo ABC e a do trap´ezio ´e igual a:

a) 5

4 (b)

9

5 (c)

9

8 (d)

9 4 (e)

18. Prove que o pol´ıgono P′ _{da f´ıgura 262 ´e regular.}

19. Seja Q=A1A2. . . An um pol´ıgono regular circunscrito a um c´ırculo Γ

e sejamT1, T2, . . . , Tn os pontos em queA1A2, A2A3, . . . , AnA1 tangen-ciam Γ. Considere um c´ırculo Γ′ _{concˆentrico a Γ e sejamT}′

1 =←−−OT1∩Γ′, etc. Por T′

1, T2′, . . . , Tn′ trace tangentes a Γ′, obtendo um pol´ıgono

Q′ _=B

1B2. . . Bn (veja figura 267).

A B A B A B 1 1 ₂ 2 3 n A_n

B O 1 T' 2 T 2 T ' 1 T 3 n T n T'

Fig. 267: Exerc´ıcio

Prove que Q′ _{´e tamb´em regular. Se r e r}′ _{s˜ao os raios de Γ e Γ}′_,

respectivamente, prove que a raz˜ao entre a ´area Ade Qe a ´area de Q′

´e dada por A

A′ = r

r′ 2

.

Sugest˜ao: Prove que OT₁A_{2 ≡} OT₂A₂ e OT′

1B2 ≡ OT2′B2 e conclua que O, A₂, e B₂ s˜ao colineares. Da mesma forma s˜ao colineares os termosO, A₃, B₃, . . . , O, A₁, B₁. Use o exerc´ıcio 1 desta aula e a seme-lhan¸ca entre os triˆangulosOA₁A₂ eOB₁B₂, . . . , OAnA₁ eOBnB₁ para

provar que OT′

1B2 ≡ OT1′B1, OT2′B3 ≡ OT2′B2, . . . , OTn′B1 ≡ OTn′Bn.

Lembrando que j´a sabemos que OT′

nB1 ≡ OT1′B1, OT2′B2 ≡ OT1′B2, etc, prove queQ′ _{´e regular. Para provar que} A

A′ = r

r′ 2

, observe que

OA₁A₂´e semelhante aOB₁B2,OA₂A₃´e semelhante aOB₂B3, etc, com raz˜ao de semelhan¸ca igual a r

r′.