World Reords in the Size of Simulated Ising Models
DietrihStauer
InstituteforTheoretialPhysis,
CologneUniversity,D-50923 Koln,Euroland
e-mail: stauerthp.uni-koeln.de
Reeivedon15July,2000
Monte Carlo simulations with up to 176 5
spins onrm the Chen-Dohm theory for the
ve-dimensional Ising model. Also world reordsizes 1000192 2 ; 9984 3 ;880 4 ;48 6 and 21 7 spins were
simulatedintheliterature,andwedesribetheneededmulti-spinodingalgorithm.
Brazil does good Ising researh, but Ising was not
bornthere. Thusinontrastthispaperreportsonsome
work done in the town where Ernst Ising wasborn a
entury ago: Monte Carlo simulations of large Ising
models in d dimensions: nearest-neighbour spin 1/2
modelwithoutanyfurtherquantumeets,periodior
helialboundariesonhyperubiallattiesofL d
spins.
It is a waste of memory to store every spin of an
Ising model in a full omputer word of, say, 32 bits.
FriedbergandCameron[1℄seemtohavestartedputting
spinsintosinglebits,ClaudioRebbi[2℄madethe
teh-niquepopularasmulti-spinoding,butinbiologysuh
bitstringswereknownfrom Eigen'squasispeiesmodel
[3℄, alsoof1972. Sinein three dimensionswehaveto
sumupoversixneighbours,givingzerotosix
antipar-allelspins,theenergyrequiresthreebits. Inmorethan
three dimensions, more bits are needed. Here we use
four bits perspin,allowingsimulationsin upto seven
dimensions and tting niely into modern 32- or
64-bit words. (Rebbi used 3 bits on 60-bit words.) I do
not dealherewiththe moreeÆientbut less versatile
method of using one bit per spin and doing the sum
overthenearestneighboursthroughpurelylogial
op-erations. Instead, the program allowsfor varying the
dimensionality d by just hangingone parameter. Its
priniples werealreadyexplainedlongago[4,5℄.
Let us assume we already have a working
three-dimensionalIsingprogramwithmulti-spinodingusing
4bitsperspin,onasuperomputerliketheCray-T3E
with64bitsperwordandthus16spinsperword. The
spin words are alled IS(ii;i) with ii going from 1to
LL = L=16 and i = 1:::L d 1
in d dimensions. To
add a fourth or fth dimension we just have to add
two or four neighbours. If we do this with an
inner-most loop over the 6 (or 2d) neighbours then vetor
omputing issloweddown. If wedealwith traditional
if-ommandsthenbothvetorandsalaromputersare
sloweddown. Thetrikistouseif-ommands
depend-ning through a Fortran PARAMETER statement (or
analogousonstrutsinlesserlanguages). Thena
state-mentlike if(idim:eq:3) goto 8is evaluated already at
ompiletime,theompilermightevengiveyoua
warn-ing that the following line is neverreahed, and after
ompilation the exeutation is no longer sloweddown
bythenumerousif-statements.
Ofourse,itisstillawasteofmemorytohavefour
bitsperspinwhenonesuÆes. Awayoutis
ompres-sion: only the urrenthyperplane and the two
neigh-bouring hyperplanes are stored as IS with four bits
perspin,whileforallotherplanesfourwordsare
om-pressedinto oneafter shiftingthem by zero, one,two
orthree bitpositions. Theyanbere-readfrom there
bylogial-ANDstatementswithsomeMASK of0001
sequenes, alled MK(0);:::MK(3) here. Normally
this would redue the main spin array ISM(ii;i) to
ii=1:::L=64; i=1:::L d 1
.
However,inthisasetheminimumlineardimension
would beL=128sineatleast twowordsareneeded
for eah lattie line in multi-spin oding. This would
retrit the appliations of the program very muh.
Therefore,this4:1ompression wasinsteadperformed
fortheseondindexi,thusrequiringamainspinarray
ISM(ii;i) with ii=1:::L=16; i=1:::L d 1
=4.
Un-fortunately, this makesprogramming ompliated,
in-volving the variables I0;IM;IP;INDEX;INDX
af-ter the loop DO 4 in my program. And I annot
useitfortwodimensionsanymore,where ompression
wasmadein theii-diretioninstead. (In aseof need,
askstauerthp.uni-koeln.deforasimplerprogram
is-pardd9.fin twoto sevendimensionswithout
ompres-sion; the ompliated one is ispardd0.f.) More than
twentyspinswereupdatedeverymiroseondonevery
proessorof afastCray-T3Ein Julih, forve
dimen-sions.)
[Tehnial remarks: This program waswritten for
di-ness L=NPR OC 2. The message-passing
om-mand shmemget(a;b;;d) gets words from
proes-sor d, starting with word b there, and stores them
into the memory of the urrent proessor NODE =
shmemmy pebeginningatworda. ThelineINFO=
BAR R IER () synhronizes the proessors:
omputa-tion proeeds after all nodes have reahed this line.
POPCNT ounts the number of set bits in a word,
IR TCthenumberofmahineyles,andthenalloop
doiadd=1;npro 1givesaprimitiveglobal
summa-tionoverthemagnetizationineverynode. Weusethe
HeatBathalgorithm.℄
PARAMETER(TTC = 0.7, NPROC=88, LL=11, IDIM=5, max= 5,
1 L=LL*16,L2=L*L,L3=L2*L,L4=L3*L,L5=L4*L,N=L**(IDIM-1)/4,
2 NPLANE=N/L, LLP=LL-1, N8=N/NPROC, IMAX=N8+2*NPLANE,
3 NPLAN4=NPLANE*4, ID2=2*IDIM, LENGTH=N/16)
DIMENSION IS(LL,3),ISM(LL,IMAX),IEX(0:ID2),MK(0:3)
COMMON /T3E/ ISM,M,MSUM
INTEGER SHMEM_N_PES, SHMEM_MY_PE
ISII(K)=ISHFT(IAND(MASK,ISM(II,1+K/4)),-INDEX)
DATA ISEED/ 2/,MSK/X'1000000000000000'/,
1 MK/X'1111111111111111',X'2222222222222222',
2 X'4444444444444444',X'8888888888888888'/
NODE=SHMEM_MY_PE()
NUMBER=SHMEM_N_PES()
IF(IDIM.EQ.3) T=0.2216544
IF(IDIM.EQ.4) T=0.149695
IF(IDIM.EQ.5) T=0.113915
IF(IDIM.EQ.6) T=0.092295
IF(IDIM.EQ.7) T=0.077706
T=T/TTC
IF(NODE.EQ.0) PRINT 11, TTC,IDIM,L,MAX,ISEED,NUMBER,
1 (LL*IMAX)/131072
LNPROC=L/NPROC
11 FORMAT(1X,F9.6,6I5)
NODEU=NODE-1
NODED=NODE+1
IF(NODE.EQ.0) NODEU=NUMBER-1
IF(NODE.EQ.NUMBER-1) NODED=0
IBM=2*ISEED-1
MULT=16807
DO ITER=0,NODE
IBM=IBM*65539
END DO
DO 2 I=0,ID2
EX=EXP((4*I-2*ID2)*T)
2 IEX(I)=2147483648.0*(4.0*EX/(1.0+EX)-2.0)*2147483648.0
DO 1 I =1,IMAX
DO 1 II=1,LL
1 ISM(II,I)=0
TIME=IRTC()*3.33E-9
DO 6 ITIME=1,MAX
INFO = BARRIER()
CALL SHMEM_GET(ISM(1,1),ISM(1,1+N8),LENGTH,NODEU)
INFO = BARRIER()
DO 7 II=1,LL
IS(II,2)=ISHFT(IAND(MK(3),ISM(II,NPLANE)),-3)
7 IS(II,3)= IAND(MK(0),ISM(II,NPLANE+1))
DO 49 IPLANE=1,LNPROC
INFO = BARRIER()
CALL SHMEM_GET(ISM(1,1+NPLANE+N8),ISM(1,NPLANE+1)
1 ,LENGTH,NODED)
INFO = BARRIER()
9 CONTINUE
DO 4 I=1,NPLAN4
I0=I+LPLANE
IM=1 + I0 /4
IP=1+(I0+1)/4
INDEX=MOD(I-1,4)
INDX =MOD(I ,4)
MASK=MK(INDEX)
NOTMSK=NOT(MASK)
DO 10 II=1,LL
IS(II,1)=IS(II,2)
IS(II,2)=IS(II,3)
10 IS(II,3)=ISHFT(IAND(MK(INDX),ISM(II,IP)),-INDX)
DO 4 II=1,LL
IF(II.EQ. 1) GOTO 40
IF(II.EQ.LL) GOTO 41
IEN=IS(II-1,2)+IS(II+1,2)
GOTO 42
40 IEN=IS(2,2)+IOR(ISHFT(IS(LL,2),-4),ISHFT(IS(LL,2),60))
GOTO 42
41 IEN=IS(LLP,2)+IOR(ISHFT(IS(1,2),4),ISHFT(IS(1,2),-60))
42 IEN=IEN+IS(II,1)+IS(II,3)+ISII(I0-L)+ISII(I0+L)
IF(IDIM.EQ.3) GOTO 8
IEN=IEN+ISII(I0-L2)+ISII(I0+L2)
IF(IDIM.EQ.4) GOTO 8
IEN=IEN+ISII(I0-L3)+ISII(I0+L3)
IF(IDIM.EQ.5) GOTO 8
IEN=IEN+ISII(I0-L4)+ISII(I0+L4)
IF(IDIM.EQ.6) GOTO 8
IEN=IEN+ISII(I0-L5)+ISII(I0+L5)
8 ICI=0
DO 3 IB=1,16
IBM=IBM*MULT
ICI=ISHFT(ICI,-4)
IF(IBM.LT.IEX(IAND(15,IEN))) ICI=IOR(ICI,MSK)
3 IEN=ISHFT(IEN,-4)
IS(II,2)=ICI
4 ISM(II,IM)=IOR(IAND(NOTMSK,ISM(II,IM)),ISHFT(ICI,INDEX))
49 CONTINUE
IF(ITIME.NE.(ITIME/10)*10) GOTO 6
M=0
DO 5 I =NPLANE+1,NPLANE+N8
DO 5 II=1,LL
5 M = M + POPCNT(ISM(II,I))
INFO = BARRIER()
IF (NODE .EQ. 0 .AND. NPROC .GT. 1) THEN
DO IADD = 1,NPROC-1
CALL SHMEM_GET (MSUM, M, 1, IADD)
M = M + MSUM
ENDDO
ENDIF
6 CONTINUE
TIME = IRTC() * 3.33E-9 -TIME
IF(NODE.EQ.0)PRINT *,4*TIME,NUMBER,
1 (MAX*L**IDIM/NPROC)/(4000000.0*TIME)
100 FORMAT(1x,I4,I20,F12.9)
END
What an we do with this program? As the
ti-tle promises it allows to simulate world reord sizes,
with L = 10 6
in two dimensions, mathing Linke et
al. [6℄, L =10 4
in three dimensionsequalizing
pero-lation [7℄, and 880 4
; 176 5
and 48 6
spins in higher
di-mensions. These worldreordswereestablishedatthe
same time as the predition of Ceperley [8℄ was
pub-lished, that 10 12
sites ould be simulated. (Sine we
need at least two hyperplanes per proessor, the 512
nodes of the Cray-T3Eannot all be used for higher
dimensions. Fortunately, inphysisthere islittleneed
formorethanvedimensions.) Someof theresultsin
lowerdimensionsweregivenbefore[9℄andare
ompat-ible with those from smallersystems [10℄. Now ome
somenewve-dimensionalsimulations.
AordingtoChenandDohm[11℄, thebehaviorin
vedimensions, abovethe upperritial dimensionof
four, is farfrom trivial: Some nite-sizeeld theories
are invalid, and nite-size saling is not of the usual
one-parameter type. This work was ritiized [12℄ as
beinginontraditiontoMonteCarlosimulations,and
thatritiisminturnwasreentlyrefuted[13℄. A
om-parisonof eld theory, 4
lattietheory, and the true
Isingmodelrequirestotseveralparameterssinee.g.
the ritial temperature is not the same. Ref.[12℄ set
one of these parameters to unity, while Ref. [13℄
al-lowed it to be dierent from one. This latter hoie
removed[13℄somedisrepanybetweenthetheoretial
predition [11℄ and Monte Carlo simulation [12℄. As
a result, several bulk amplitudes dier depending on
whetherweusethetofMainz[12℄orAahen[13℄,and
we nowperform newsimulations to nd out whih of
thesetwopreditions,[12℄or[13℄,tsournewdata
bet-ter. (Theparametersappearinginthetheoryof[11,13℄
havebeen identied as bulkparameters relatedto the
amplitudesofthebulkorrelationlength,thebulk
sus-eptibilityandthebulkmagnetization. Thusthevalues
oftheirparametersanbetestedbybulksimulations.)
First, we determined the orrelation length ,
de-nedthroughthe exponentialdeayof theorrelation
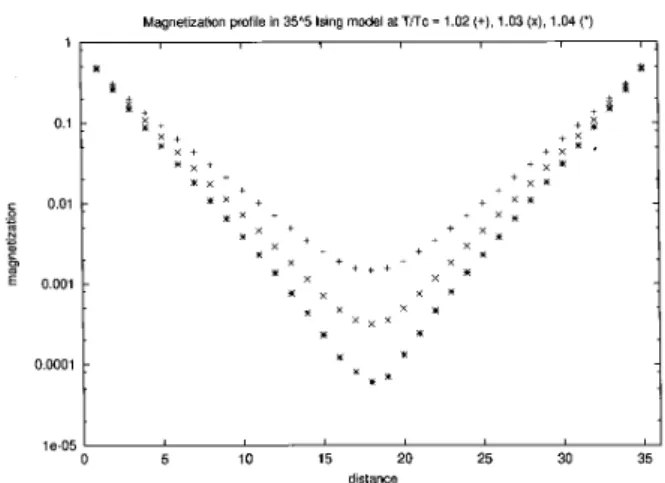
funtion, by observing the magnetization prole
be-tween two hyperplanes of up spins, tting an
expo-nentialon an intermediate spae region somewhat
re-moved from the surfae but where the magnetization
used one-word-per spin oding for typially 35 5
spins
above T
in zero magneti eld and multi-spin
od-ing (4 bits perspin) for 48 5
; 80 5
; 112 5
at T = T
in
a magneti eld h = B=k
B
T, where is the
mag-neti dipole moment. Typially, 2000 Monte Carlo
steps per spinwere simulated. Fig. 2shows thedata
for T > T
in zero eld, Fig.3 the ase T = T
in a
positive eld. In spite of the larger latties, the
re-sults in a magneti eld are less aurate sine then,
asopposedto paramagnets,thebulk magnetizationis
nonzeroandhastobesubtratedfromthe
magnetiza-tionprole. Wethus estimateh 1=3
=0:270:03and
[(T T )=T ℄ 1=2
= 0:360:02, in better agreement
withtheAahenpreditions(0.273and0.396)thanthe
Mainz estimates(0.390and0.549).
ThemagnetizationManbedeterminedmore
au-ratelysinenot toanexponentialproleisinvolved.
Fig. 4 shows at T = T
the amplitude M=h 1=3
and
Fig.5 shows M=(1 T=T
)
1=2
below T
in zero eld.
Again the lower horizontal line is the Aahen
predi-tion,whihagreesbetterwiththedatathantheupper
horizontal line from Mainz. Moroever,Fig.5 using up
to 176 5
spins shows, as predited by analyti theory
[13℄,asalingorretion2:25 1:1(1 T=T
)
1=2
whih
tsbetterthantheorretionlinearinT T
suggested
byCheonetal[11℄.
Figure 1. Examplesof themagnetization prole. Straight
lines in this semilogarithmi plot determine 1=. Two
Figure 2. Correlation length amplitudes above T inzero
eld.
Figure 3. Correlation length amplitudes at T inpositive
eld.
Figure4. MagnetizationamplitudesatTinpositiveeld.
Figure5. Magnetizationamplitudes below T inzero eld
with t = T=T 1; the straight line with negative slope
suggestssalingorretions/ p
t.
Figure 6. Six-dimensional dynamis. The orret ritial
temperaturerequires z =2asymptotially. Ourslight
de-viationT=T
=0:99980:0001 may omefrom the nite
L=48.
Thus in all ases the Aahen predition ts
bet-terthantheMainzalternative,andonlyFig.2suggests
thatAahenisonlyapproximate.
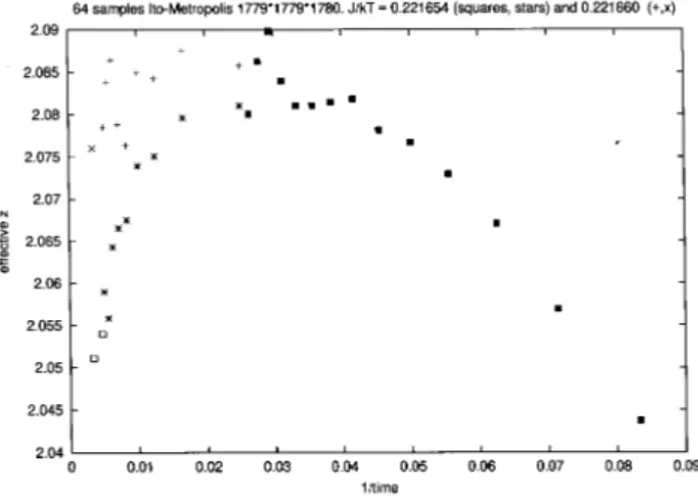
[Twosideremarks: (i)Insixandsevendimensions,
Figs. 6 and 7 onrm the series estimate J=k
B T
=
0:092295(3) and 0.077706(2) less aurately [16℄: For
theorrettemperaturetheintereptofthe
extrapola-tiongivestheasymptotikinetiexponentz=2. The
21 7
spins were simulated without multi-spin oding.
ForSwendsen-Wanglusterips,Fig.8showsnielythe
exponentialdeayofthemagnetizationwithtimeintwo
dimensions:z=0. Three-dimensionalQ2Rellular
au-tomatastill have anunexplained dynamis, z =3:37,
Fig.9. Fig.10showsresultsforMetropoliskinetiswith
Ito'sone-bit-per-spinandparallelizationinstripesand
10 10
updates per seond. These system sizes an be
ofL=4million,10000,611,127,49,and26fortwoto
sevendimensions.
Figure7. Seven-dimensionaldynamisanalogousto Fig.6,
with21 7
spins.
Figure 8. Two-dimensional Swendsen-Wang dynamis[18,
19 ℄forLupto14001.
Figure 9. Three-dimensional Q2R ellular automatawith
12
Figure 10. Three-dimensional Ito-Metropolis algorithm,
suggesting z ' 2:06 depending on the hoie [10 ℄ of T
.
Thespeedwas11Gigaupdatesperseond,andweassume
==0:515.
(ii)AtthelastonfereneinBeloHorizonteinwhih
I took part,theBrazilianomputationalphysis
meet-ing, Ilearned[14℄ thatsimulationsofdipole fores are
easy. Asaresult,thestabilityofarraysofparallelstrips
of Ising spins interating also with long-range dipole
fores, asforironmonolayersonstepped surfaes[15℄,
wasinvestigatedbyMihelsen[17℄. HefoundtheCurie
point to be stable for large systems, and not just a
gradualfreezing-inasin aglass.℄
I thank X.S. Chen and V. Dohm for
stimulat-ing disussions and for sending the various 5D
am-plitude preditions, N. Ito for heking a parallel
al-gorithm, P.M.C. de Oliveira for a ritial reading of
the manusript, SFB 341for partial support, and the
GermanSuperomputerCenterJulihfortimeontheir
Cray-T3E.
Referenes
[1℄ R. Friedberg and J.E. Cameron, J. Chem. Phys. 52,
6049(1972)
[2℄ M. Creutz, L. Jaobs andC. Rebbi, Phys.Rev.Lett.
42,1390(1979)
[3℄ M. Eigen, J. MCaskilland P. Shuster,Adv. Chem.
Phys.75,149(1990).SeealsoH.J.Muller,Mutat.Res.
1,2(1964).
[4℄ D. Stauer, F.W. Hehl, N. Ito, V. Winkelmann and
J.G. Zabolitzky, Computer Simulation and Computer
Algebra,Springer,Heidelberg-Berlin1993
[5℄ D. Stauer, page 5 in: Computer simulation studies
inondensedmatterphysisVI,D. P.Landau, K.K.
Mon,H.B.Shuttler,eds.,Springer,Heidelberg1993
[6℄ A. Linke, D.W. Heermann, P. Altevogt, M. Siegert,
PhysiaA222,205(1995)
[8℄ L. Ceperley,Rev.Mod.Phys.71,S438(1999)
[9℄ D. Stauer, PhysiaA 244, 344(1997), Int. J.Mod.
Phys.C10,807,809,931(1999)
[10℄ N.Ito,K.Hukushima,K.OgawaandY.Ozeki,J.Phys.
So.Jpn.69,1931(2000)
[11℄ X.S.ChenandV.Dohm,Int.J.Mod.Phys.C9,1007
and 1073 (1998);seealsoM. Cheon,I. ChangandD.
Stauer,Int.J.Mod.Phys.C10,131(1999)andPhys.
Rev.E,inpress(Jan.2001).
[12℄ E. Luijten, K.BinderandH.W. J.Blote, Eur.Phys.
J. B9, 289 (1999); K.Binderet al., PhysiaA 281,
112(2000).
[13℄ X. S.Chen and V. Dohm, e-print ond-mat 0005022
andpriv.omm.
[14℄ T.G.Rappoport,T.S.deMenezes,L.C.Sampaio,M.P.
AlbuquerqueandF.Mello,Int.J.Mod.Phys.C9,821
(1998)
[15℄ P.Sen,D.StauerandU.Gradmann,PhysiaA245,
361(1997)
[16℄ M.Gofman,J.Adler,A.Aharony,A.B.HarrisandD.
Stauer,J.Stat.Phys.71,1221(1993)
[17℄ A.Mihelsen,Masters Thesis,Hamburgand Cologne,
Feb.2000
[18℄ J.S. Wang and R.H. Swendsen, Physia A 167, 565
(1990)
[19℄ R.Hakl,H.G.Matuttis,J.M.Singer,T.Husslein,and