PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PUC/SP
GILSON BISPO DE JESUS
CONSTRUÇÕES GEOMÉTRICAS: UMA ALTERNATIVA
PARA DESENVOLVER CONHECIMENTOS ACERCA DA
DEMONSTRAÇÃO EM UMA FORMAÇÃO CONTINUADA
MESTRADO EM EDUCAÇÃO MATEMÁTICA
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE SÃO PAULO
PUC/SP
GILSON BISPO DE JESUS
CONSTRUÇÕES GEOMÉTRICAS: UMA ALTERNATIVA
PARA DESENVOLVER CONHECIMENTOS ACERCA DA
DEMONSTRAÇÃO EM UMA FORMAÇÃO CONTINUADA
Dissertação apresentada à Banca Examinadora da Pontifícia Universidade Católica de São Paulo, como exigência parcial para obtenção do título de MESTRE EM EDUCAÇÃO MATEMÁTICA, sob a orientação do(a) Prof. Dr. Saddo Ag Almouloud.
Banca Examinadora
________________________________________
________________________________________
Autorizo, exclusivamente para fins acadêmicos e científicos, a reprodução total ou parcial desta Dissertação por processos de fotocopiadoras ou eletrônicos.
“A Bahia já me deu
régua e compasso.
Quem sabe de mim sou eu
Aquele abraço!”
AGRADECIMENTOS
A DEUS, por me oportunizar realizar este sonho.
Ao Professor Doutor Saddo Ag Almouloud, pela sua orientação, por confiar em mim, por respeitar o meu tempo e por ter me dado autonomia para a realização desta pesquisa.
Aos membros da banca, Professoras Doutoras Elenice de Souza Lodron Zuin e Maria José Ferreira da Silva, pelas valiosas contribuições e sugestões para essa pesquisa.
A todos os professores, que voluntariamente se disponibilizaram a ser sujeitos deste trabalho.
Aos colegas Messildo, Ana Maria, Milton, Ricardo, Victoria, Sérgio e Eliana, pelas observações realizadas durante a coleta dos dados, especialmente a Vânia pelo companheirismo, presente como observadora em todos os encontros.
A todos os colegas de grupo e as professoras Cileda, Renata e Ana Maria pelas discussões e contribuições para esse trabalho.
As professoras Maria José e Maria Inez, por terem aceitado o desafio de serem formadoras nesse estudo.
A todos os funcionários do Centro de Ciências Exatas, da PUC-SP, pelo convívio durante esse tempo, especialmente ao Francisco pela valiosa companhia em muitos momentos.
A todos os colegas com os quais tive a oportunidade de conviver durante o curso, em especial aqueles que se tornaram meus amigos: Patrícia, Eurivalda, Victoria, Gabriela, Irene, Aida, Jacinta, Liu, Ana Maria, Milton, Denise, André, Dani, Guilherme, Cássia, Alexis, Franciana e Ivete.
Ao corpo docente do Programa de Estudo Pós-Graduados em Educação Matemática da PUC-SP, com o qual tive o privilégio de conviver, sobretudo aqueles com os quais tive a oportunidade de ser aluno: Saddo Almouloud, Wagner Valente, Lulu Healy, Sandra Magina, Ana Paula Jahn, Sílvia Machado, Benedito Silva, Sonia Igliori, Cristina Maranhão e Antonio Carlos Brolezzi.
Aos professores e colegas baianos, Adelaide, Elda, Antônio e Auxiliadora, que em minha trajetória sempre pontuaram a Educação Matemática.
Ao meu amigo Celso, pelo grande apoio dado nessa cidade imensa.
A todos os amigos e colegas do grupo EMFOCO, pela presença constante em minha vida desde o final da especialização.
Aos meus pais, Laurinda e José Miguel, por terem sempre me proporcionado condições para estudar. Amo vocês!
A minha Cláudia, que sempre compreendeu a minha ausência-presente com o seu amor e companheirismo. Eu te amo!
Aos meus irmãos: Carlinhos, Zete, Gersinho, Rosana e Lene; meus cunhados: Mello, Cláudio, Helton, Luciana, Terezinha e Fátima; minha sogra Vilma e meus sobrinhos: Tati, Bia, Lai, Jajá, Jeferson, Nari, Ingrid, Ruan e Artur. E a todos os meus familiares, por acreditarem em mim, mesmo quando não sabiam onde eu desejava chegar e por estarem ao meu lado sempre.
A Secretaria de Educação do Estado da Bahia, pelo investimento em minha formação, concedendo-me o afastamento.
Ao CNPq, pela concessão da bolsa, me permitindo dedicação exclusiva aos estudos.
RESUMO
O presente trabalho tem como objetivo analisar uma sequência de atividades
desenvolvidas em uma formação continuada para professores. Esta seqüência
visava que os participantes construíssem a definição de mediatriz de um segmento
e, a partir desta, demonstrassem propriedades inerentes a esse objeto matemático.
Além disso, objetivava que os professores justificassem matematicamente, com
base na Geometria plana, algumas construções geométricas em que esse objeto era
a principal ferramenta para a resolução do problema. A questão pesquisada foi: uma
seqüência de ensino com enfoque em construções geométricas pode contribuir para o desenvolvimento de conhecimentos acerca da demonstração em Geometria em uma formação continuada de professores? Assim, aplicamos junto a um grupo de
professores de Matemática (Ensino Fundamental e Médio) em formação continuada,
a seqüência de atividades. Para tal, nos baseamos nos estudos de Duval (2003) e
Brousseau (1986), sobre os registros de representação semiótica e a Teoria das
Situações Didáticas respectivamente. Trabalhamos também com Duval e Egret
(1989) e De Villiers (2001; 2002), no que diz respeito às demonstrações e com
autores especializados em formação de professores, para a fundamentação teórica
dessa pesquisa. A escolha metodológica pela pesquisa-ação e pelos pressupostos
da Engenharia Didática contribuíram para o alcance dos objetivos desse estudo. A
análise das discussões e comportamentos dos professores durante a formação
revelou-nos que as atividades provocaram reflexões sobre definições, propriedades,
teoremas recíprocos, justificativas matemáticas, demonstrações, além de oportunizar
a descoberta e construção de alguns conceitos da Geometria plana ao realizarem
construções geométricas. Nesse sentido, pudemos destacar o registro material de
representação, identificado por nós, e inferir que essa formação contribuiu para a
autonomia dos professores.
Palavras-chave: Construções Geométricas. Demonstração em Geometria.
ABSTRACT
The purpose of this study is to analyze a sequence of activities carried out with in
service teachers, aiming the construction of the definition of line bisector of a
segment and, from this definition, to allow them to demonstrate inherent properties of
this mathematical object. Moreover, the study also aimed that the teachers were able
to justify it mathematically, based on plane Geometry, some geometric constructions
in which this object was the main tool to solve the problem. Our research question
was: Can a teaching sequence, carried out with in service teachers, and focus on
geometric constructions, contribute for the development of knowledge about demonstration in Geometry? In order to answer this question, we developed a
sequence with a group of in-service teachers of Mathematics for Elementary and
secondary school. To reach such aim, we base our study on the theoretical approach
of Duval (2003) and Brousseau (1986), about Semiotics Representation Registers,
and the Didactic Situation Theory respectively. We also used the Duval and Egret
(1989) and De Villiers (2001; 2002) ideas about demonstrations. Finally, we still used
some authors’ ideas about teacher’s formation. The methodological choice was
research-action and Didactic Engineering, which had contributed to achieve the
objective of this study. The analysis of the discussions and the behaviors of the
teachers during the formation reveled that the activities had caused reciprocal
reflections about definitions, properties, theorems, mathematical justifications,
demonstrations. Moreover, the sequence allowed these teachers to discover and to
construct some plane Geometry concepts, whilst they made geometric constructions.
In this sense, we do highlight to the importance of material representation register.
We conclude that this formation contributed for the autonomy of these teachers.
Keywords: Geometric Constructions. Demonstration in Geometry. Teachers
SUMÁRIO
INTRODUÇÃO ... 14
CAPÍTULO 1: PROBLEMÁTICA ... 16
1.1OINTERESSEPELOTEMA ... 16
1.2OPROBLEMADEPESQUISA... 19
1.3ASPECTOSMETODOLÓGICOS... 24
1.4CONSTRUINDOAFUNDAMENTAÇÃOTEÓRICA... 28
1.4.1 REGISTROS DE REPRESENTAÇÃO SEMIÓTICA... 28
1.4.2 QUADRO, REGISTRO E PONTO DE VISTA ... 34
1.4.3 TEORIA DAS SITUAÇÕES DIDÁTICAS ... 35
1.4.4 DEMONSTRAÇÕES ... 40
1.4.5 FORMAÇÃO DE PROFESSORES ... 44
CAPÍTULO 2: BREVE ESTUDO HISTÓRICO-EPISTEMOLÓGICO ... 50
2.1AMEDIATRIZNOCONTEXTODAGEOMETRIA ... 50
2.2ADEMONSTRAÇÃO ... 54
2.3ASCONSTRUÇÕESGEOMÉTRICAS ... 59
CAPÍTULO 3: CONSIDERAÇÕES SOBRE O ENSINO E APRENDIZAGEM... 62
3.1GEOMETRIA... 62
3.2DEFINIÇÃO... 67
3.3DEMONSTRAÇÃO... 69
3.4CONSTRUÇÕESGEOMÉTRICAS... 74
3.5PARÂMETROSCURRICULARESNACIONAIS ... 78
CAPÍTULO 4: AS ATIVIDADES E SUAS ANÁLISES ... 82
4.1PROCEDIMENTOSMETODOLÓGICOS ... 82
4.2OSPROFESSORES... 84
4.3DESCRIÇÃODAAPLICAÇÃODASEQÜÊNCIA... 89
4.4ASATIVIDADESESUASANÁLISESPRÉVIASEAPOSTERIORI... 89
CONSIDERAÇÕES FINAIS ... 196
REFERÊNCIAS ... 202
APÊNDICE A – QUESTIONÁRIO PERFIL... 207
LISTA DE FIGURAS
FIGURA 1:TRIÂNGULO OBTUSÂNGULO... 32
FIGURA 2:TRIÂNGULO ACUTÂNGULO... 33
FIGURA 3:MEDIATRIZ DO SEGMENTO AB ... 52
FIGURA 4:MEDIATRIZ DE UM SEGMENTO... 95
FIGURA 5:SOLUÇÃO DA ATIVIDADE 02 ... 98
FIGURA 6:SOLUÇÃO DA PROFESSORA EVA... 99
FIGURA 7:REPRESENTAÇÃO DA CONJECTURA... 100
FIGURA 8:REPRESENTAÇÃO DO PAR SIMÉTRICO... 100
FIGURA 9:LINGUAGEM FIGURAL - ATIVIDADE 3... 102
FIGURA 10:REPRESENTAÇÃO DA PROFESSORA RUTE... 106
FIGURA 11:LINGUAGEM FIGURAL - ATIVIDADE 4... 109
FIGURA 12:MUDANDO DE PONTO DE VISTA... 113
FIGURA 13:PONTOS EQÜIDISTANTES PERTENCEM À MEDIATRIZ... 114
FIGURA 14:DEMONSTRAÇÃO VIA TRIÂNGULO ISÓSCELES... 115
FIGURA 15:DEMONSTRAÇÃO SEM USO DO TRIÂNGULO ISÓSCELES... 115
FIGURA 16:UMA OUTRA DEMONSTRAÇÃO... 118
FIGURA 17:ÂNGULOS CONGRUENTES QUE NÃO SÃO O.P.V... 120
FIGURA 18:CONSTRUÇÃO DA MEDIATRIZ... 127
FIGURA 19:CONSTRUÇÃO DA MEDIATRIZ - PROFESSORES MIRTES E JOSÉ... 129
FIGURA 20:CONSTRUÇÃO DA MEDIATRIZ - PROFESSORA JOANA... 130
FIGURA 21:CONSTRUÇÃO DA MEDIATRIZ – MÉTODO DO LOSANGO... 131
FIGURA 22:CONSTRUÇÃO - PROBLEMA I... 133
FIGURA 23:CONSTRUÇÃO - PROBLEMA II... 137
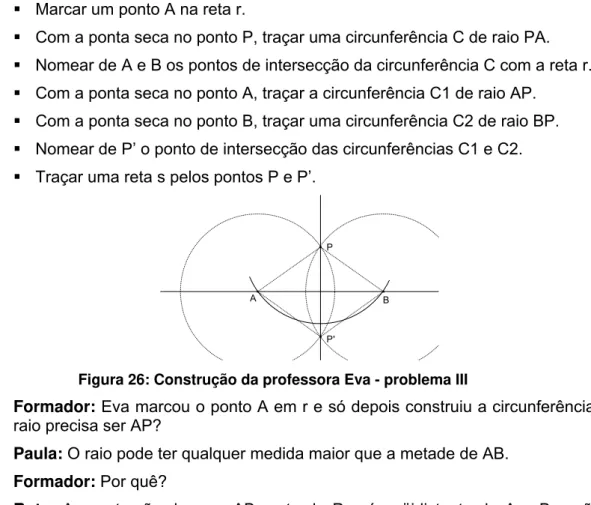
FIGURA 24:CONSTRUÇÃO - PROBLEMA III... 141
FIGURA 25:CONSTRUÇÃO DA PROFESSORA MIRTES - PROBLEMA III... 143
FIGURA 26:CONSTRUÇÃO DA PROFESSORA EVA - PROBLEMA III ... 144
FIGURA 27:CONSTRUÇÃO - PROBLEMA IV ... 145
FIGURA 28:CONSTRUÇÃO DA PROFESSORA MIRTES - PROBLEMA IV ... 146
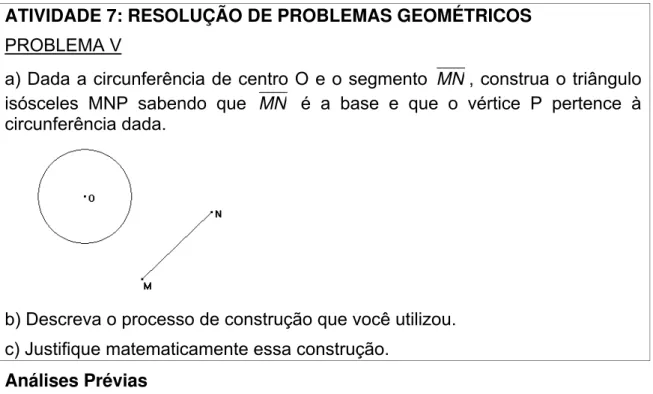
FIGURA 29:CONSTRUÇÃO - PROBLEMA V ... 148
FIGURA 30:CONSTRUÇÃO DO FORMADOR - PROBLEMA V... 150
FIGURA 31:CONSTRUÇÃO - PROBLEMA VI ... 152
FIGURA 32:CONSTRUÇÃO DO PROFESSOR RENATO - PROBLEMA VI... 154
FIGURA 33:CONSTRUÇÃO DA PROFESSORA RUTE - PROBLEMA VI ... 154
FIGURA 34:CONSTRUÇÃO - PROBLEMA VII ... 155
FIGURA 35:CONSTRUÇÃO DO PROFESSOR JOSÉ - PROBLEMA VII ... 157
FIGURA 36:CONSTRUÇÃO DOS PROFESSORES JOSÉ E MIRTES - PROBLEMA VII... 157
FIGURA 37:LEI DO PONTO MÉDIO... 160
FIGURA 38:CONSTRUÇÃO 1 DA PROFESSORA EVA - ATIVIDADE 8 ... 161
FIGURA 39:CONSTRUÇÃO 2 DA PROFESSORA EVA - ATIVIDADE 8 ... 162
FIGURA 40:CONSTRUÇÃO DA PROFESSORA RUTE - ATIVIDADE 8... 162
FIGURA 41:CONSTRUÇÃO DA PROFESSORA MIRTES - ATIVIDADE 8 ... 162
FIGURA 42:CONSTRUÇÃO DO PROFESSOR CARLOS - ATIVIDADE 8 ... 163
FIGURA 43:CONSTRUÇÃO DA PROFESSORA JOANA - ATIVIDADE 8 ... 164
FIGURA 44:UMA NOVA PROPRIEDADE... 169
FIGURA 45:ESPAÇO AÉREO... 169
FIGURA 46:REGIÃO EM UMA FAZENDA... 169
FIGURA 47:ESPAÇO AÉREO - CONSTRUÇÃO DA PROFESSORA MIRTES... 172
FIGURA 48:INSTITUCIONALIZAÇÃO DA NOVA PROPRIEDADE... 174
FIGURA 49:CONSTRUÇÃO - QUESTÃO 01... 176
FIGURA 50:CONSTRUÇÃO DA PROFESSORA MIRTES - QUESTÃO 01... 179
FIGURA 51:REPRESENTAÇÃO DO RAIO. ... 179
FIGURA 52:CONSTRUÇÃO - QUESTÃO 02... 181
FIGURA 53:CONSTRUÇÃO DA PROFESSORA MIRTES - QUESTÃO 02... 182
FIGURA 54:CONSTRUÇÃO DA PROFESSORA JOANA - QUESTÃO 02. ... 183
FIGURA 55:CONSTRUÇÃO - QUESTÃO 03... 184
FIGURA 56:CONSTRUÇÕES DO PROFESSOR CARLOS - QUESTÃO 03 ... 186
FIGURA 58:CONSTRUÇÃO A2- ATIVIDADE 12... 188
FIGURA 59:CONSTRUÇÃO DA PROFESSORA RUTE - ATIVIDADE 12 ... 191
FIGURA 60:CONSTRUÇÃO DAS PROFESSORAS ANGÉLICA E PAULA - ATIVIDADE 12... 192
FIGURA 61:CONSTRUÇÃO DA PROFESSORA MIRTES - ATIVIDADE 12... 192
FIGURA 62:CONSTRUÇÃO 01 DA PROFESSORA JOANA - ATIVIDADE 12. ... 193
FIGURA 63:CONSTRUÇÃO 02 DA PROFESSORA JOANA - ATIVIDADE 12 ... 193
FIGURA 64:CONSTRUÇÃO 03 DA PROFESSORA JOANA - ATIVIDADE 12 ... 193
FIGURA 65:CONSTRUÇÃO 04 DA PROFESSORA JOANA - ATIVIDADE 12 ... 194
FIGURA 66:ÂNGULO DE 60º E TRIÂNGULO EQÜILÁTERO... 194
LISTA DE QUADROS QUADRO 1:DIFERENTES REGISTROS DE REPRESENTAÇÃO... 33
QUADRO 2:DIFERENÇAS ENTRE PEDAGOGIA E ANDRAGOGIA... 47
QUADRO 3:CARACTERÍSTICAS DO CONTÍNUO PEDAGÓGICO-ANDRAGÓGICO... 48
INTRODUÇÃO
Esse trabalho se iniciou a partir de uma percepção, advinda da nossa
experiência em sala de aula, enquanto professor de Matemática e Desenho
Geométrico1. A oportunidade de lecionar essa segunda disciplina nos fez vislumbrar
que um trabalho focado nas construções geométricas2 poderia minimizar algumas
dificuldades no desenvolvimento de conceitos geométricos.
O ingresso no Programa de Estudos Pós-Graduados em Educação Matemática
na Pontifícia Universidade Católica de São Paulo – PUC/SP, mais especificamente no
grupo de pesquisa (CoFE – Conceitos: Formação e Evolução) ao qual pertencemos,
nos levou a ter contato com o tema demonstrações em um curso de formação
continuada de professores. Sendo assim, resolvemos elaborar a nossa dissertação
sobre a temática: demonstrações, construções geométricas e formação continuada de
professores. Faltava, então, escolher o objeto de estudo, optamos pela mediatriz de
um segmento.
Inicialmente, fizemos uma revisão dos trabalhos que focavam esse tema, com
o intuito de verificar a relevância do mesmo e quais alternativas eram apontadas, para
que pudéssemos efetuar as escolhas adequadas para a nossa pesquisa. Em primeiro
lugar fizemos leituras de trabalhos cujo tema era a Geometria e alguns deles já
apontavam para um trabalho com foco nas demonstrações geométricas, sobretudo
em formações continuadas de professores. No entanto, os trabalhos com construções
geométricas eram poucos, encontramos apenas duas indicações. Entendemos, então,
que a nossa temática tinha relevância e passamos a construir os passos desse
trabalho.
Resolvido que o trabalho seria com professores, partimos para o segundo
passo, ou seja, nos colocamos a fazer um estudo sobre o ensino e a aprendizagem
dos temas abordados e fizemos a opção metodológica que levava em consideração
________________ 1
No Ensino Fundamental as disciplinas Matemática e Desenho Geométrico eram ministradas separadas, no qual a segunda compunha a parte diversificada do currículo.
2
os pressupostos da Engenharia Didática e da pesquisa-ação. Fizemos, também, um
estudo histórico-epistemológico da temática dessa pesquisa.
O nosso terceiro passo foi escolher a fundamentação teórica do trabalho.
Encontramos nos estudos de Duval (2003), sobre os registros de representação
semiótica, de Brousseau (1986), sobre a Teoria das Situações Didáticas, nos
trabalhos de Duval e Egret (1989) e De Villiers (2001; 2002), sobre demonstrações e
em alguns autores de formação de professores, o apoio necessário.
Com essa bagagem, partimos para a elaboração da seqüência de atividades
que seria desenvolvida com os professores em formação continuada. Durante essa
elaboração, mudanças e ajustes foram realizados a fim de que ela pudesse nos
fornecer dados que dessem subsídios a responder a questão de pesquisa. Partimos,
então, para a aplicação da seqüência, que propiciou a coleta e análise dos dados.
Fizemos, em seguida, algumas considerações a respeito do trabalho realizado.
Apresentamos agora a estrutura do trabalho. A dissertação está configurada
em quatro capítulos, além das considerações finais. No capítulo 1 apresentamos a
problemática, na qual destacamos o interesse pelo tema, o problema de pesquisa, os
aspectos metodológicos e a construção da fundamentação teórica. O capítulo 2 traz
um breve estudo histórico-epistemológico, no qual destacamos a mediatriz de um
segmento no contexto da Geometria, a demonstração e as construções geométricas.
O capítulo 3 tece considerações sobre o ensino e a aprendizagem da
Geometria, da definição em matemática, da demonstração e das construções
geométricas. Destacaremos, ainda, às recomendações dos Parâmetros Curriculares
Nacionais de Matemática para o 3º e 4º ciclos do Ensino Fundamental – PCN. No
capítulo 4, apresentamos os procedimentos metodológicos, os sujeitos da pesquisa,
uma descrição da aplicação da seqüência e as atividades em conjunto com as
análises prévias e posteriores.
Finalizando, apresentamos algumas considerações finais, apontando possíveis
conclusões oriundas da análise dos dados que coletamos para essa pesquisa.
Deixamos, ainda, algumas sugestões para trabalhos futuros a partir das questões que
não objetivamos responder, bem como pistas para estudos que possam resultar do
CAPÍTULO 1
PROBLEMÁTICA
Neste capítulo inicial da nossa dissertação apresentamos a justificativa do
nosso trabalho, a qual reflete parte da trajetória profissional do autor, uma vez que,
essa trajetória contribuiu, em grande medida, para a temática do presente trabalho.
Apresentamos também o problema de pesquisa, seguido dos aspectos metodológicos
que delinearam esse estudo e, por fim, a fundamentação teórica.
1.1 O INTERESSE PELO TEMA
Sou professor de Matemática há 14 anos e, durante seis anos (1993 – 1998),
tive a oportunidade de lecionar não apenas a disciplina de Matemática, mas também
Desenho Geométrico para turmas de 5ª a 8ª séries do Ensino Fundamental, o que me
propiciou um maior envolvimento com as construções geométricas, além de
desenvolver um novo olhar para questões de ensino e aprendizagem desse campo da
matemática.
No retorno às atividades de Matemática, comecei a perceber algumas
dificuldades dos alunos em relação ao desenvolvimento de conceitos geométricos,
dificuldades essas não identificadas no tempo em que lecionava concomitantemente
Matemática e Desenho Geométrico. Por esse motivo, comecei a buscar novas
abordagens que pudessem minimizar tais dificuldades.
Com essa inquietação, ingressei no Programa de Especialização em Educação
Matemática, proposto pela Universidade Católica do Salvador (UCSAL), em 2002. Os
estudos teóricos nesse programa foram motivadores da busca de mais
conhecimentos acerca de tais reflexões e indicaram que os problemas de ensino e
Educação Matemática. Com essa perspectiva, desenvolvi a monografia de final de
curso sobre essa temática3.
Os estudos desenvolvidos na especialização me instigaram a buscar novas
teorias relacionadas à Educação Matemática. Com o final do curso, mas não de
minha vontade em aperfeiçoar e ampliar os conhecimentos até então adquiridos,
fundei juntamente com alguns colegas da especialização o grupo de estudos EMFoco
– Educação Matemática em Foco – do qual faço parte até os dias de hoje. Os estudos
nesse grupo, a motivação intrínseca a ele e a busca por mais conhecimentos me
levaram a fazer a seleção no Programa de Estudos Pós-Graduado em Educação
Matemática para cursar o mestrado acadêmico em Educação Matemática oferecido
pela Pontifícia Universidade Católica de São Paulo (PUC–SP).
Neste programa participei do projeto intitulado: O raciocínio dedutivo no
processo de ensino-aprendizagem da matemática nas séries finais do Ensino Fundamental – financiado pelo CNPq (Conselho Nacional de Pesquisa) –, o que me
levou a refletir sobre o tema demonstrações, tanto no decorrer da minha formação
inicial – Licenciatura em Matemática, pela Universidade Federal da Bahia (UFBA) –,
como no contexto da formação continuada de professores de Matemática.
Na graduação, o meu contato com as demonstrações foi muito grande, porém
com o viés formalista da matemática, ou seja, a demonstração tinha como único
intuito, verificar a validade de um teorema, e nós, os alunos, com a postura apenas de
aprendizes, isto é, “aprendíamos” a demonstrar pelo processo de imitação de nossos
professores. As aulas eram ministradas sob o esquema: definições, axiomas,
teoremas e demonstrações, como se esse fosse um processo linear, infalível e sem
interrupções. Poucas foram as discussões em que os professores se preocupavam
com a gênese do objeto matemático, ou seja, demonstrações construídas em um
processo de ir e vir, fazer e refazer, buscar refutações e contra-exemplos, que
evidenciassem a demonstração como um processo de construção humana e histórica.
Todavia, sempre me preocupei em compreender as entrelinhas do que se expunha
nas demonstrações, preocupando-me em entender e “destrinchar” os aspectos
implícitos presentes, em grande medida, nas demonstrações feitas pelos professores
e apresentadas nos livros didáticos.
________________ 3
Nesse período, na UFBA, participei como aluno de iniciação científica do
Programa Especial de Treinamento (PET), no qual tive bolsa da CAPES por três anos
e aprofundei estudos na área de Álgebra e Geometria Diferencial, entrando em
contato, cada vez mais, com as demonstrações no campo da matemática pura. Nessa
época, conduzia os meus estudos ao bacharelado em matemática e assim o fiz até o
sétimo semestre. Por questões diversas, no oitavo semestre matriculei-me nas
disciplinas da licenciatura e dei seqüência a concluir primeiro esta modalidade,
percebendo que as disciplinas pedagógicas e as de fundamentos da matemática não
se relacionaram com as disciplinas de matemática pura e/ou apresentavam a
demonstração com a mesma estrutura, ou seja, não traziam nenhuma novidade para
o trabalho desse tópico em sala de aula.
Meu primeiro contato com a Educação Matemática ocorreu no primeiro ano de
graduação ao participar, por motivações próprias, do III ENEM (III Encontro Nacional
de Educação Matemática – 1990) e, em seguida, do IV EBEM (IV Encontro Baiano de
Educação Matemática – 1991). Sempre fui preocupado e inserido em questões
ligadas ao ensino e aprendizagem da matemática (fui monitor de Matemática durante
dois anos, ainda aluno do 2º grau, na Escola Técnica Federal da Bahia). Nas
disciplinas Didática da Matemática e Metodologia e Prática de Ensino da Matemática
tive a oportunidade de ter aulas com professores engajados no movimento da
Educação Matemática, porém, o contato com questões inerentes à demonstração
permanecia o mesmo, isto é, era sempre via verificação de uma verdade matemática.
Conforme relatei anteriormente, fui professor de Desenho Geométrico durante
alguns anos e as atividades desenvolvidas tinham como foco realizar construções
geométricas com as respectivas justificativas matemáticas. Recordo-me da fala de um
aluno, quando comuniquei que não iria demonstrar o teorema de Tales: “Tomara que
não seja difícil de acreditar”. Outro episódio instigante ocorreu quando propus aos alunos o problema da construção da bissetriz de um ângulo, quando não se tem
acesso ao vértice. Para essa questão, só busquei uma justificativa matemática ao
ministrar este curso e os alunos trouxeram três formas diferentes e justificadas. Minha
surpresa foi grande, pois esperava uma única resposta: aquela sugerida, de maneira
sutil, por um problema de construção, que eles já haviam resolvido (foi o que tinha me
Ao retornar a ministrar apenas aulas da disciplina Matemática e perceber as
dificuldades em Geometria apresentadas pelos alunos, comecei a acreditar que as
atividades, nas aulas de Desenho Geométrico, poderiam contribuir para a superação
das dificuldades de aprendizagem em Geometria.
Essa inquietação me levou a elaborar o anteprojeto de pesquisa, durante o
curso de Metodologia da Pesquisa, oferecido pelo programa de Educação
Matemática, com a temática: “Geometria, construções geométricas e demonstração”.
Assim sendo, me debrucei a ler outros trabalhos cuja temática era próxima, para
perceber sua relevância e se ainda existiam questões por responder. Encontrei alguns
trabalhos e percebi que parte deles apontava para a formação de professores, no que
diz respeito aos conhecimentos geométricos, mais especificamente, às
demonstrações nesse campo, o que influenciou, em grande medida, a realização
desta pesquisa em um grupo de formação continuada com professores da disciplina
Matemática do Ensino Fundamental.
Deste modo, meu orientador e eu, decidimos realizar esse estudo, do qual
apresentamos a seguir, a questão de pesquisa.
1.2 O PROBLEMA DE PESQUISA
De acordo com Almouloud e Mello (2000), um dos problemas enfrentados pelo
sistema de ensino brasileiro refere-se ao baixo desempenho dos alunos do Ensino
Fundamental em Matemática. As recentes avaliações feitas pelo SAEB/MEC (Sistema
de Avaliação da Educação Básica – Ministério da Educação e Cultura), pela
Secretaria de Educação de São Paulo evidenciam que esse desempenho torna-se
ainda mais baixo quando o tema abordado é a Geometria. Embora os currículos mais
recentes destaquem a importância de se resgatar o trabalho com Geometria no
Ensino Fundamental, o professor não sabe claramente o que fazer. A Secretaria de
Ensino Fundamental do MEC colocou em discussão nacional os Parâmetros
Curriculares e apontou a necessidade de formar professores para a efetiva
implantação de novas alternativas.
Para Fainguelernt (1999):
preocupação do compromisso de se apoiar no processo exaustivo de formalização (FAINGUELERNT, 1999, p. 20).
Maioli (2002) ao propor a questão: “como trabalhar com formação de
professores de forma a contribuir com saberes referentes à Geometria e, ao mesmo
tempo, proporcionar aprimoramento em conhecimentos didáticos inerentes a este
conteúdo?”, alcançou seus objetivos. Porém, relata na conclusão:
Com relação à demonstração, constatamos que a oficina contribuiu no sentido de chamar a atenção para sua necessidade, os professores avançaram, visto que na primeira atividade com demonstrações, não conseguiam utilizar a ferramenta sugerida (paralelas cortadas por uma transversal) e nas últimas, já conseguiam explicitar o caminho da demonstração. No entanto, a oficina não deu conta de desenvolver conhecimentos a ponto do professor escrever sozinho uma demonstração completa. Se faz necessário um estudo mais profundo sobre demonstrações (MAIOLI, 2002, p. 144).
A formação sólida em Geometria, por parte dos professores de todos os níveis,
se faz necessária para que qualquer proposta de ensino seja implantada, afirmam
Almouloud e Manrique (2001) e, ainda relatam, que uma das dificuldades que
apareceu na resolução de um problema proposto a um grupo de professores foi a
falta de competência em relação à demonstração.
A necessidade de uma formação adequada do professor para trabalhar a
demonstração em Geometria, a fim de que os alunos possam se apropriar dos
conceitos e habilidades geométricas, no âmbito do Ensino Fundamental, é uma das
vertentes defendidas por Almouloud e Mello (2000).
A proposta de trabalhar a demonstração em Geometria via construções
geométricas, nos leva a corroborar com as hipóteses de José Carlos Putnoki, quando
diz:
Já faz um bom tempo que o Desenho Geométrico foi banido das nossas escolas de 1º e 2º graus. “Coincidentemente”, de lá para cá, a Geometria, cada vez mais, vem se tornando o grande terror da Matemática, tanto para alunos quanto para professores. Com certeza, não se trata apenas de uma coincidência, mas sim, em parte, de uma conseqüência (PUTNOKI, 1988, p. 13).
Tendo em vista essa temática, Zuin (2001) aponta para a falta de trabalhos que
construções geométricas como um saber escolar no Brasil”, sugerindo questões para
pesquisas futuras, dentre as quais destacamos:
Qual o papel das construções geométricas na elaboração do conhecimento da Geometria?
Qual a importância das construções geométricas na construção do raciocínio lógico-dedutivo? (ZUIN, 2001, p. 192).
Entretanto, Maioli (2002) relata que os professores, com os quais trabalhou em
sua investigação, estavam abertos para conhecer e discutir pesquisas realizadas na
área de Educação Matemática, deixando a seguinte pergunta como sugestão: “que
outras formas de trabalho podem contribuir para estabelecer um elo entre a pesquisa
e o professor de Matemática do ensino fundamental e médio que estão trabalhando
em sala de aula?” (Ibid, p. 105).
Este relato nos levou a refletir sobre a formação continuada do professor de
Matemática e a pensarmos em contemplar aspectos didáticos – pesquisas na área de
Educação Matemática – que pudessem ser discutidos com os professores em
formação continuada no trabalho que pretendíamos desenvolver.
Já Gouvêa (1998), propunha, como um dos objetivos de sua pesquisa, uma
reflexão por parte dos professores sobre o ensino de Geometria com demonstrações,
detectando que esses professores subestimavam a capacidade de seus alunos,
constatando que eles não trabalhavam com a Geometria dedutiva, pois possuíam
pouca habilidade em lidar com o tema, além de não encontrarem subsídios para tal
trabalho em livros didáticos. Percebemos, no trabalho de Gouvêa, uma sugestão de
se trabalhar com as demonstrações geométricas na formação continuada de
professores.
No programa de Educação Matemática da PUC–SP, tivemos a oportunidade de
discutir sobre prova e demonstração, no contexto da Educação Matemática, ou seja,
relacionados ao ensino e aprendizagem. Tal contato nos levou a refletir sobre o nosso
interesse em Geometria, mais especificamente sobre as construções geométricas e
como o tema demonstração poderia estar inserido nesse processo. O contato com
outras pesquisas veio reforçar o tema escolhido e me permitiu vislumbrar um trabalho
centrado na formação continuada de professores de Matemática. A participação no
projeto de pesquisa, citado anteriormente, nos permitiu fazer reflexões sobre a nossa
desenvolver no projeto. Sendo assim, resolvemos desenvolver esta pesquisa com o
tema: Geometria, construções geométricas e demonstrações em uma formação
continuada de professores de Matemática.
Escolhido os temas Geometria, demonstração, construções geométricas e
formação continuada de professores, passamos à busca do objeto matemático que
daria subsídios ao desenvolvimento dessa pesquisa.
Ao buscarmos o objeto geométrico que serviria de referência para conceber a
seqüência de atividades a serem desenvolvidas nas oficinas, com os professores em
formação continuada, fizemos escolha pelo objeto: mediatriz de um segmento.
Realizamos um estudo epistemológico acerca desse objeto, pesquisando em
livros didáticos franceses4 e em livros didáticos de Desenho Geométrico5, podendo
assim constatar a riqueza desse objeto para resolução de problemas de construções
geométricas. Destacamos que a possibilidade de os professores participantes dessa
pesquisa construírem a definição de mediatriz, enunciarem e demonstrarem a
propriedade referente a esse objeto, sob “pontos de vista” diferentes, contribuiu de
forma singular para essa escolha.
Além disso, corroboraram com a nossa escolha, a diversidade de problemas e
situações-problema, ligados a esse objeto, em que se podem exigir justificativas
matemáticas da construção geométrica realizada, a possibilidade de formular
conjecturas e fazer demonstrações, trabalhar em vários registros de representação
semiótica, com teoremas recíprocos, propriedades diversas e ainda poder explorar as
várias funções da demonstração sugeridas por De Villiers (2001; 2002).
Na verdade, a riqueza matemática e a possibilidade de sua exploração didática
em atividades a serem desenvolvidas, tomando por base a Teoria das Situações
Didáticas, com os professores em formação continuada foram os pilares de motivação
que nos levou a escolher o objeto geométrico mediatriz de um segmento como
referência para desenvolver as oficinas de formação.
________________ 4
Os livros didáticos consultados foram: MATHS 4E de Raymond Barra, Georges Borion, Marie Lampin e Joel Malaval, 1988 e MATHÉMATIQUES PYTHAGORE 4E de Gerard Bonnefond, Daniel Daviaud e Bernard Revranche, 1992.
5
Diante do exposto, esperávamos contribuir para reflexões, estudos e para o
debate em Educação Matemática sobre o ensino de Geometria, em particular, a
demonstração, com o viés das construções geométricas, em uma formação
continuada de professores de Matemática, ao respondermos à questão:
Uma seqüência de ensino com enfoque em construções geométricas pode contribuir para o desenvolvimento de conhecimentos acerca da demonstração em Geometria e, ao mesmo tempo, proporcionar o aprimoramento em conhecimentos didáticos em uma formação continuada de professores?
No entanto, devido às dificuldades encontradas durante a formação como, por
exemplo, a quantidade de encontros possíveis, visto que estávamos finalizando o ano
letivo, resolvemos redimensionar nossa questão de pesquisa e optarmos por
responder a seguinte questão:
Uma seqüência de ensino com enfoque em construções geométricas pode contribuir para o desenvolvimento de conhecimentos acerca da demonstração em Geometria em uma formação continuada de professores?
Na tentativa de responder a essa questão de pesquisa objetivamos
desenvolver, com os professores em formação continuada, uma seqüência de
atividades que pudesse permitir aos participantes construir a definição de mediatriz de
um segmento, e, a partir desta, justificar de maneira formal, ou seja, fazer a
demonstração de propriedades inerentes a esse objeto matemático, bem como
justificar matematicamente, com base na Geometria plana, algumas construções
geométricas em que esse objeto é a principal ferramenta para a resolução do
problema.
Ao buscarmos subsídios para resolver essa questão, nos apoiamos nos
pressupostos da Engenharia Didática para conceber a seqüência de atividades da
oficina e também para validar as nossas hipóteses. A literatura sobre formação de
analisar os dados coletados. Os trabalhos sobre o ensino e a aprendizagem de
Geometria e demonstração, bem como aqueles que apontam a construção de
definições em matemática como contribuição para a ampliação de conceitos, foram
todos de grande valia para o desenho dessa pesquisa. Além disso, fizemos a escolha
da fundamentação teórica desse estudo.
A seguir, passaremos a destacar os aspectos metodológicos desse trabalho.
1.3 ASPECTOS METODOLÓGICOS
Essa pesquisa se insere no projeto: O raciocínio dedutivo no processo de
ensino-aprendizagem da matemática nas séries finais do Ensino Fundamental, o qual
já estava em andamento, e tornou-se mais um trabalho a ser desenvolvido com um
grupo de professores em formação continuada e, por isso, deveria se adequar aos
aspectos metodológicos adotados nesse projeto.
A metodologia utilizada para a formação dos professores, nesse projeto, é a
pesquisa-ação, que destacamos enquanto linha de pesquisa associada a diversas
formas de ação coletiva orientada em função da resolução de problemas ou de
objetivos de transformação. Para Thiollent (2003, p. 14):
A pesquisa-ação é um tipo de pesquisa social com base empírica, que é concebida e realizada em estreita associação com uma ação ou com a resolução de um problema coletivo e no qual os pesquisadores e participantes representativos da situação e do problema estão envolvidos de modo cooperativo ou participativo.
Segundo esse autor, uma pesquisa pode ser qualificada de pesquisa-ação
quando houver realmente uma ação por parte das pessoas ou grupos implicados no
problema sob observação. Além disso, é preciso que a ação seja uma ação
não-trivial, o que quer dizer uma ação problemática merecendo investigação para ser
elaborada e conduzida. Com relação ao pesquisador ele destaca: ‘‘com a
pesquisa-ação os pesquisadores pretendem desempenhar um papel ativo na própria realidade
dos fatos observados” (THIOLLENT, 2003, p. 16).
Thiollent (2003) diz, ainda, que a pesquisa-ação não é constituída apenas pela
ação ou pela participação, mas pela necessidade de produzir conhecimento, adquirir
questões abordadas. A seu ver, parte da informação gerada deve ser divulgada, sob
formas e meios apropriados, no seio da comunidade.
Para o nosso projeto, uma das qualidades fundamentais da pesquisa-ação,
consiste no fato de que as populações não são consideradas como ignorantes e
desinteressadas. Levando a sério o saber espontâneo e cotejando-o com as
explicações dos pesquisadores, um conhecimento descritivo e crítico é gerado acerca
da situação, com todas as sutilezas que escapam aos procedimentos padronizados.
Para a construção e análise da seqüência de atividades tratada nesse trabalho
nos baseamos nos pressupostos da Engenharia Didática, que garantiu aos
professores em formação continuada construir conhecimentos acerca da
demonstração em Geometria apoiada na mediatriz de um segmento e nas
construções geométricas. Essa escolha deu oportunidade ao pesquisador de avaliar
as atividades propostas fundamentado na teoria e utilizar a linha metodológica da
pesquisa-ação.
A Engenharia Didática visa entender “as relações entre a investigação e a ação
do sistema de ensino” (ARTIGUE, 1996, p. 193). De acordo com a autora, esse
método caracteriza-se por ser um processo empírico que objetiva conceber, realizar,
observar e analisar situações didáticas em sala de aula. Apesar de não tratarmos os
professores em formação continuada como alunos, acreditamos que as atividades
desenvolvidas nas oficinas de formação tiveram momentos similares à sala de aula.
Nesse sentido, Artigue (1996) distingue quatro fases para uma Engenharia
Didática:
Análises prévias ou preliminares;
Concepção e análise a priori das situações didáticas da engenharia;
Experimentação;
Análise a posteriori – validação.
Na primeira fase da pesquisa, das análises preliminares, conforme Artigue
(1996), foram feitas ponderações envolvendo o quadro teórico da Teoria das
Situações Didáticas, de Brousseau (1986), e dos Registros de Representação
Semiótica, de Duval (2003); além de aspectos de conhecimentos ligados a:
Geometria, demonstrações e construções geométricas, e destacamos o objeto
aspectos históricos e epistemológicos, ao processo de ensino e aprendizagem e a
presença de possíveis obstáculos, de modo que pudessem respaldar ou possibilitar
previsões ao elaborarmos as atividades. Além disso, fizemos um estudo teórico sobre
formação de professores.
Na segunda fase, intitulada concepção e análise a priori das atividades,
conforme Artigue (1996), delimitamos as variáveis didáticas a serem consideradas e
que foram abordadas nas sessões de formação desenvolvidas em forma de oficinas.
Para Brousseau (1986), é fundamental na investigação em didática fazer a análise a
priori da situação, pois a previsão dos efeitos da situação que o pesquisador elaborou
antes de colocá-la em experimentação é fundamental para, posteriormente, poder
comparar com os comportamentos observados nos dados coletados. Nas atividades
dessa seqüência foram considerados os seguintes aspectos e/ou objetivos:
Orientar os professores em formação na resolução das
situações-problema propostas;
Desenvolver situações controladas que promovam o desequilíbrio e a
adaptação dos sujeitos ao “milieu”6;
Propiciar o desenvolvimento de fases adidáticas, propostas na teoria das
situações didáticas de Brousseau (1986), como ação, formulação e
validação;
Propiciar os momentos de institucionalização – fase didática – que serão
coordenados pelo formador;
Criar condições para que os professores em formação continuada criem
conjecturas, realizem construções geométricas, justifiquem
matematicamente tais construções e possam em vários momentos
realizar demonstrações;
Que as atividades contemplem as funções da demonstração propostas
por De Villiers (2001; 2002): explicação, descoberta e sistematização,
bem como os professores em formação continuada utilizem vários
registros de representação semiótica efetuando conversões.
Na terceira fase, de experimentação, propusemos aos professores trabalharem
com a seqüência didática que concebemos. Durante os encontros de formação não
________________ 6
deixamos de considerar os aspectos do contrato didático7, ou seja, cabia aos
professores em formação continuada, a responsabilidade de administrar sua relação
com o conhecimento na fase adidática (ação, formulação e validação) e ao formador,
a responsabilidade de coordenar as atividades fazendo devoluções na fase adidática
e institucionalizar o conhecimento na fase didática.
Na análise a posteriori e validação, quarta fase da Engenharia Didática,
analisamos a produção dos professores a partir dos dados coletados, ou seja,
comparamos os dados coletados com as análises a priori.
Os dados desta pesquisa foram coletados mediante observações dos
encontros durante a oficina. Essas observações foram realizadas por mestrandos e
mestres que participavam do projeto. Nesse sentido, nos apoiamos em Vianna (2003)
quando afirma que os estudos observacionais podem ser realizados em diferentes
lugares, destacando em particular o processo de formação de professores.
Esclarecemos que, neste trabalho, os participantes já estavam familiarizados
com o processo de observação. E, com relação aos aspectos positivos do trabalho
com observadores, concordamos com Vianna (2003, p. 32) quando diz: “a observação
demanda um período mais longo de contato entre o observador, gerando, um
relacionamento emocional (amizade, simpatia, etc. e mesmo emoções negativas) que
pode facilitar, ou dificultar, uma melhor compreensão do observado”.
Com relação aos observadores, os mesmos já estavam participando da coleta
de dados com os professores em formação continuada antes do início dessa
pesquisa, o que corrobora com as idéias de Vianna (2003, p. 10) quando diz:
Um artifício para minimizar a influência do efeito do observador seria a presença do mesmo em sala várias vezes, mas sem coletar dados, a fim de que o professor e alunos, a serem observados, se acostumem com a sua presença e possam agir com maior naturalidade durante o processo efetivo de realização da observação.
________________ 7
A fim de suprir possíveis dúvidas das observações efetuadas na coleta de
dados, recorremos às gravações em áudio, realizadas durante todas as oficinas de
formação.
Definido nosso problema de pesquisa e os aspectos metodológicos adotados,
apresentamos, em seguida, a fundamentação teórica que norteou este trabalho.
1.4 CONSTRUINDO A FUNDAMENTAÇÃO TEÓRICA
Nesta parte do trabalho, destacaremos as teorias de Raymond Duval sobre os
Registros de Representação Semiótica e de Guy Brousseau sobre a Teoria das
Situações Didáticas, destacando as idéias de Marc Rogalski sobre “ponto de vista” e
autores que darão suporte ao desenvolvimento do trabalho em relação a
demonstração e a formação de professores.
1.4.1 REGISTROS DE REPRESENTAÇÃO SEMIÓTICA
Os objetos de estudo em matemática: conceito, propriedades, relações e
estruturas não são diretamente perceptíveis aos sentidos humanos. Recorremos,
então, a notações simbólicas, códigos, tabelas, gráficos, esquemas, escritas, como
representantes para estes objetos. Partindo dessa premissa, Raymond Duval
desenvolveu a Teoria dos Registros de Representação Semiótica.
Sabendo que uma expressão, uma noção, um símbolo representam objetos
matemáticos como: um número, uma função, um ponto, um círculo, percebemos uma
distinção entre o objeto matemático e sua representação e, por isso, não devem ser
confundidos. Segundo Duval (2003), toda confusão implicará numa perda da
compreensão e, conseqüentemente, os conhecimentos adquiridos não estarão
disponíveis no contexto da aprendizagem. Para este pesquisador, a distinção entre
um objeto matemático e a sua representação é um ponto estratégico na compreensão
da matemática e, apesar de se buscar uma apreensão conceitual dos objetos
matemáticos, é só por meio de uma representação semiótica que uma atividade é
possível sobre eles. A confusão entre objeto e representação é quase inevitável, pois,
a apreensão dos objetos matemáticos é conceitual, mas, é somente por meio de
Duval (1995) usa as terminologias sémiosis e noésis para esclarecer esse ponto ao
afirmar que:
O funcionamento cognitivo do pensamento humano se revela inseparável de existência dos diversos registros de representação semiótica. Chamarei de sémiosis a apreensão ou a produção de uma
representação semiótica e de noésis a apreensão conceitual do
objeto, é necessário afirmar que a noésis é inseparável da sémiosis (ibid, p. 39-40).
Podemos, então, dizer que para ocorrer a apreensão do objeto matemático, é
necessário que a noésis ocorra por meio de várias e significativas sémiosis. Dessa
forma, temos que o paradoxo cognitivo do pensamento matemático e a dificuldade
que resulta na aprendizagem é que não se tem noésis sem sémiosis (DUVAL, 1993).
Mas o que é um registro de representação semiótica? Uma figura geométrica,
um enunciado em língua materna, uma fórmula algébrica ou uma representação
gráfica, por exemplo, são representações semióticas em registros semióticos
diferentes. Duval (1995, p. 20) explica a noção de registro de representação semiótica
da seguinte forma:
Em primeiro lugar, constituir um traço ou um conjunto de vestígios perceptíveis, que sejam identificáveis como uma representação de
algo num sistema determinado. Em seguida transformar as
representações pelas únicas regras próprias ao sistema, de maneira a obter outras representações que podem constituir uma correspondência de conhecimentos em relação às representações iniciais. Por último, converter as representações produzidas num sistema de representações para outro sistema, de tal maneira que este último permita esclarecer outros significados relativos ao que é representado. Não são todos os sistemas semióticos que permitem estas três atividades cognitivas fundamentais [...] Mas as línguas naturais, as línguas simbólicas, as representações gráficas, as figuras geométricas, etc., permitem-no. Falamos então de registro de representação semiótica.
Para melhor entendermos como se dá a aprendizagem segundo essa teoria,
diferenciar tratamento de conversão é fundamental. Para Damm (2002):
O tratamento de uma representação é a transformação dessa representação no próprio registro onde ela foi formada. O tratamento é uma transformação interna a um registro. Por exemplo, às estruturas simbólicas (cálculo numérico, cálculo algébrico,...)
confundida com o tratamento. O tratamento se estabelece “dentro” do registro, já a conversão se dá entre registros diferentes (DAMM, 2002, p. 145-146).
A esse respeito Henriques, Attie e Farias (2007, p. 19) relatam:
A conversão tem uma importância particular. No entanto, é geralmente negligenciada no ensino da matemática, enquanto que, como sublinha Duval, uma das condições essenciais para a apreensão conceitual dos objetos matemáticos é dispor, para um mesmo objeto, de várias representações semióticas.
A escolha de um registro de representação adequado pode favorecer o tratamento (transformações das representações ao interior de um mesmo registro). No entanto, dispor de vários registros de representação não é suficiente para garantir a compreensão. Uma
segunda condição é necessária: a coordenação dos registros de
representações. Ela se manifesta pela capacidade de reconhecer, em duas representações diferentes, representações de um mesmo objeto. Ela aparece como a condição fundamental para todo tipo de aprendizagem.
Sendo assim, “é necessário que o professor tenha claro o objeto matemático a
ser ensinado, isto lhe possibilitará definir quais os registros de representação
semiótica que possibilitarão a construção do mesmo” (DAMM, 2002, p. 142), bem
como, a garantia de poder mudar de registro de representação semiótica. Isso
significa fazer conversões, pois ao fazermos conversões estamos mudando a forma
pela qual o conhecimento é representado.
Diante do que foi relatado, percebemos que a conversão é uma atividade
cognitiva diferente e independente do tratamento. Por exemplo, pode-se trabalhar
com números racionais na forma decimal ou na forma fracionária, sem, no entanto,
pensar em converter de uma forma a outra, ou seja, trabalhando-se no mesmo
registro de representação semiótica (efetuando-se tratamentos). Podemos destacar
que um elemento facilitador, ao se usar várias representações, é a possibilidade de
poder efetuar alguns tratamentos que não são possíveis em outros registros de
representação semiótica.
Na verdade, a originalidade da atividade matemática (com compreensão) está
na mobilização simultânea de, ao menos, dois registros ao mesmo tempo, ou na
possibilidade de trocar a todo momento de registro de representação (Duval, 2003).
Logo, o que garante a apreensão do objeto matemático é a coordenação entre vários
pode-se privilegiar explicitamente um determinado registro, porém deve existir a
possibilidade de passar de um registro a outro, pois, ao efetuarmos conversões entre
registros de representação semiótica, estamos possibilitando o acesso a propriedades
e/ou aspectos diferentes de um mesmo objeto matemático que não são perceptíveis
nem acessíveis em alguns registros. O autor destaca, ainda, que o ponto decisivo
está no fato de que o conteúdo de uma representação depende mais do registro da
representação do que do objeto representado e justifica essa afirmação com o
seguinte argumento: “porque passar de um registro de representação a outro não é
somente mudar o modo de tratamento, é também explicar as propriedades ou os
aspectos diferentes de um mesmo objeto” (DUVAL, 2003, p. 22).
Segundo Duval (2003, p. 21), “o sucesso, para grande parte dos alunos em
Matemática, ocorre no caso dos monoregistros. Existe como que um
‘enclausuramento’ de registros que impede o aluno de reconhecer o mesmo objeto
matemático em duas de suas representações bem diferentes”. Sendo assim, a
compreensão matemática está ligada ao fato de podermos efetuar conversões, pois
essa é a única possibilidade de que se dispõe para não fazer confusão entre o objeto
matemático e a sua representação.
Como vimos, ao mudar de registro podemos ter acesso a propriedades
diferentes do mesmo objeto (não observadas no outro registro), isto é, dois registros
de representação não trazem o mesmo conteúdo. De acordo com Duval (1993, p. 49):
Esta situação se faz em função das possibilidades e das dificuldades semióticas de cada registro. Uma linguagem não oferece as mesmas possibilidades de representação de uma figura ou diagrama. Isso quer dizer que toda representação é cognitivamente parcial em relação ao que ela representa.
O autor afirma que a evolução dos conhecimentos matemáticos conduziu ao
desenvolvimento e a criação de vários registros de representação para o mesmo
objeto. No entanto, o estudo dos isomorfismos em matemática teve uma contribuição
no que diz respeito a não se valorizar as mudanças de registros de representação, já
que, se existe isomorfismo, tanto faz trabalhar com as propriedades em um registro
ou em outro. Não queremos aqui negar a importância dos isomorfismos para o
desenvolvimento de muitos aspectos da matemática, mas que este não sirva de
justificativa para não se privilegiar os vários registros de representação de um mesmo
simultaneamente. Na verdade, quando mudamos de registro de representação não
estamos mudando apenas de tratamento, estamos abrindo horizontes para explicar
propriedades e/ou perceber aspectos diferentes de um mesmo objeto.
Com relação à heterogeneidade dos dois sentidos de conversão, Duval (2003)
afirma que nem sempre a conversão se efetua quando se invertem os registros de
partida e chegada. Este autor relata que, em geral, no ensino se privilegia um sentido
de conversão, acreditando que a conversão no outro sentido estaria automaticamente
proposta. A identificação dos objetos por suas diferentes representações é uma
atividade fundamental defendida por esse pesquisador, pois garante que tarefas de
estrito reconhecimento são tão importantes para a aprendizagem, quanto à de
resolução de problemas, uma vez que os conhecimentos disponíveis e mobilizáveis
por um indivíduo são aqueles que permitem reconhecimentos relativamente rápidos.
No ensino de Geometria, geralmente, se privilegiam questões no registro
figural, que exigem apenas um reconhecimento dos dados em língua natural, seguido
de algum tratamento, em detrimento de se propor questões no registro da língua
natural, para posterior conversão para o registro figural e, por último, o tratamento.
Isto pode ser verificado em situações do tipo:
Calcule o valor do ângulo Cna figura
(Figura 1), sabendo que 50º e que o
ângulo 60º.
ˆ
=
C Aˆ B
=
S Aˆ H
Figura 1: Triângulo obtusângulo
Nesta situação o aluno apenas reconheceria os segmentos AS e AH como
bissetriz interna do ângulo  e altura relativa ao lado BC respectivamente. A seguir
determinaria os dados numéricos e efetuaria alguns tratamentos, concluindo no final
que a medida do ângulo Cˆ é 5º.
Essa mesma situação poderia ser apresentada de forma a possibilitar a
construção da figura, isto é, a mudança do registro em língua natural para o figural:
25°
60°
Neste caso o aluno teria que conhecer as definições de altura e bissetriz
interna, e perceber que a altura pode ser externa ao triângulo – informação dada na
proposta anterior – pois, em geral, os problemas que envolvem ângulo formado pela
altura e pela bissetriz interna são dados com esses segmentos internos ao triângulo.
O aluno poderia fazer um registro figural da situação, como apresentado na figura 2 e
se perguntar: como será que 60º poderá caber em 50º? E depois avançaria
percebendo que a figura correta é a apresentada na situação anterior.
25°
60°
Figura 2: Triângulo acutângulo
Como salientamos, anteriormente, na maioria das salas de aula de Matemática,
o sucesso do aluno ocorre nos monoregistros, isto é, quando lhe é solicitado resolver
um problema que exija a mudança de registros ou mesmo a articulação simultânea de
dois registros diferentes, o sucesso nem sempre é alcançado.
Desta forma, em nosso trabalho caracterizaremos os objetos matemáticos no
quadro geométrico, mais especificamente no campo da Geometria plana, usando três
tipos de registro de representação semiótica: o registro em língua natural, o registro
simbólico e o registro figural, que podem ser exemplificados com o caso da
representação de retas perpendiculares mostrados no quadro 1.
Linguagem natural Linguagem simbólica Linguagem figural
A reta r é perpendicular
à reta s. r ⊥ s
Por tudo que foi dito, as idéias de Duval corroboraram com a nossa pesquisa,
pois, acreditamos que o ponto de partida para se realizar uma demonstração com
êxito é compreender o que se deseja demonstrar. Neste sentido, ao se pedir para
enunciar as propriedades geométricas, sempre o fizemos exigindo, no mínimo, dois
registros de representação e, em alguns casos, três, buscando assim garantir que a
propriedade que se desejava demonstrar e/ou justificar fosse explicitada e entendida.
Acreditamos também que a conversão de registros ocorreu de maneira natural, pois
esperávamos que os professores participantes testassem uma representação,
tomando outra como base, e percebessem que um registro pode apresentar algumas
vantagens em relação ao outro. Assim, percebendo que a mudança de um registro
para outro, possibilita a percepção de diferentes facetas do mesmo objeto
matemático, além de permitir a realização de tratamentos mais simples.
No entanto, se faz necessário esclarecer diferenças entre registros de
representação semiótica, “ponto de vista” e quadro, pois é comum esses termos
serem confundidos. Uma vez que trataremos na nossa seqüência dos dois primeiros.
1.4.2 QUADRO, REGISTRO E PONTO DE VISTA
Para Almouloud (2007), ao trabalhar, ensinar e aprender matemática, é
necessário entender que uma noção matemática funciona em vários registros de
representação semiótica, além de ser necessário mudar de quadros, de “ponto de
vista” e/ou de registro de representação semiótica. Uma vez que, para compreender
um conceito, demonstrar teoremas, resolver problemas, é necessário saber em quais
domínios ele funciona e bem escolher os registros de representação semiótica e/ou
compreender os vários “pontos de vista” ligados a esse saber.
Douady (1993) caracteriza o quadro como sendo:
constituído de ferramentas de uma parte da matemática, de relações entre os objetos, de formulações eventualmente diferentes e de imagens mentais associadas a essas ferramentas e relações. Dois quadros podem ter os mesmos objetos e serem diferentes por causa das imagens mentais e da problemática desenvolvida (Ibid apud ALMOULOUD, 2007, p. 64).
Podemos citar, como exemplo, o quadro algébrico, o quadro geométrico, o
quadro numérico, entre outros. Para essa pesquisadora, uma mudança de quadro é
diferentes de um mesmo problema. Tal mudança, muitas vezes, é necessária para
resolver um problema de matemática ou para facilitar sua resolução.
Quanto a “ponto de vista”, Rogalski (1995 apud ALMOULOUD, 2007) usa esse
termo para designar uma maneira de entrar em um problema matemático, de olhar
(interpretar), de fazê-lo funcionar ou, eventualmente, definir um objeto matemático.
Para a resolução de um determinado problema, um “ponto de vista” pode apresentar
vantagens em relação a outro. Ao olharmos um objeto nos diferentes quadros e/ou
registros, temos vários “pontos de vista”, porém podemos ter vários “pontos de vista”
no mesmo quadro e/ou registro.
Neste sentido, muitas vezes, não é necessário mudar de quadro e/ou registro,
pois para facilitar a resolução de um problema, basta mudar de “ponto de vista”.
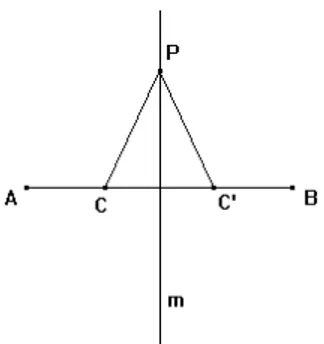
Pode-se olhar, por exemplo, a mediatriz de um segmento sob dois “pontos de vista”
diferentes no quadro da Geometria e no registro da língua natural:
• A mediatriz de um segmento é a reta que passa pelo ponto médio desse segmento e é perpendicular a ele;
• A mediatriz de um segmento é o conjunto de todos os pontos que eqüidistam das extremidades desse segmento.
Nesta pesquisa, solicitamos aos professores em formação continuada a
construção da definição de mediatriz de um segmento sob diferentes “pontos de
vista”, de maneira que, ao resolverem problemas de construções geométricas, tais
“pontos de vista” facilitem a abordagem do problema e a construção solicitada. Neste
sentido, esperamos que objetos geométricos, em geral, vistos sob um único “ponto de
vista”, possam ser olhados e/ou definidos sob diferentes “pontos de vista”.
Apesar de não focarmos nas atividades que desenvolvemos, a mudança de
quadro, foi oportuno o esclarecimento acerca dessa questão, pois, desta forma
evitamos possíveis confusões e/ou distorções quanto a essa terminologia.
1.4.3 TEORIA DAS SITUAÇÕES DIDÁTICAS
Encontramos na Teoria das Situações Didáticas (TSD), proposta por Guy
Brousseau, um embasamento teórico que deve ser considerado ao se preparar e
apresentar atividades de matemática, visando realizar uma Educação Matemática
Segundo Brousseau (1986), o objetivo da TSD é caracterizar o processo de
aprendizagem por uma série de situações reprodutíveis, que conduzem a uma
modificação de um conjunto de comportamentos dos alunos. Esta modificação é que
gera o conhecimento, isto é, a aprendizagem com significado. Na verdade, o objeto
central de estudo dessa teoria não é o sujeito e sim a situação didática que irá gerar
interações na tríade professor–aluno–saber e as modificações descritas
anteriormente.
Brousseau (1996a) descreve o trabalho do matemático (cientista) colocando o
“status” da obtenção deste conhecimento no mesmo pelo qual deveria passar o aluno,
com um detalhe: no caso do aluno, haveria uma simulação da situação. Destacando
também que o ensino axiomático é não verdadeiro em termos de conhecimento, ou
seja, sendo o aluno responsável pela construção do seu conhecimento a sua
compreensão deve ser garantida. A esse respeito, Freitas (2002, p. 67) afirma:
É evidente que não se trata de simplesmente tentar reproduzir o ambiente científico em que o saber foi originalmente estabelecido e nem tampouco teatralizar uma redução do trabalho do matemático. A idéia pedagógica de trabalhar com as aparentes facilidades de uma redescoberta do conhecimento não é tão fácil de ser colocada em prática e somente faz sentido num quadro muito bem refletido.
E o que é uma situação didática? Brousseau (1986) define situação didática
como:
O conjunto de relações estabelecidas explicitamente e/ou implicitamente entre um aluno ou um grupo de alunos, um certo “milieu”8 (contendo eventualmente instrumentos ou objetos) e um sistema educativo (o professor) para que estes alunos adquiram um saber constituído ou em constituição (BROUSSEAU, 1986 apud ALMOULOUD, 2007, p. 33).
No entanto, a compreensão efetiva das possibilidades do milieu é necessária.
Segundo Almouloud (2007), a TSD se baseia em três vertentes:
– O aluno aprende adaptando-se a um “milieu” que é fator de
dificuldades, de contradições, de desequilíbrio, um pouco como acontece na sociedade humana. Esse saber, fruto da adaptação do aluno, manifesta-se pelas respostas novas, que são a prova da
________________ 8
aprendizagem. Esta hipótese é uma referência à epistemologia construtivista de Piaget, segundo a qual, a aprendizagem decorre de processos de adaptação, no sentido biológico do termo, desenvolvidos pelo sujeito frente a situações problemáticas.
– O “milieu” não munido de intenções didáticas é insuficiente para permitir a aquisição de conhecimentos matemáticos pelo aprendiz. Para que haja essa intencionalidade didática, o professor deve organizar um “milieu” no qual serão desenvolvidas as situações suscetíveis de provocar essas aprendizagens.
– A terceira hipótese postula que esse “milieu” e essas situações devem engajar fortemente os saberes matemáticos envolvidos no processo de ensino e aprendizagem. (ALMOULOUD, 2007, p. 32) Nesse contexto, o trabalho pedagógico inicia-se com a escolha das
situações-problema (atividades) a serem trabalhadas com os alunos. Esta é uma etapa
fundamental e deve ser realizada com bastante cuidado pelo professor, já que ele é
quem conhece a realidade da turma e deverá fazer as escolhas das variáveis
didáticas9 adequadas e compatíveis para os alunos.
Porém, para analisar o processo de aprendizagem, a TSD observa e
decompõe esse processo em quatro fases diferentes: ação, formulação, validação e
institucionalização, sendo que as três primeiras caracterizam a fase adidática, ou seja,
situação na qual a intenção de ensinar não é revelada ao aprendiz, porém foi
planejada pelo professor para proporcionar condições do educando de se apropriar do
novo saber que o professor deseja ensinar. Essa situação é caracterizada por uma
ATIVIDADE ou conjunto de ATIVIDADES que faça o aluno agir, falar, refletir, ... de
forma a adquirir novos conhecimentos por meio dessa situação, isto é, sem apelo a
razões didáticas impostas pelo professor. Vale ressaltar que a situação adidática é
diferente de uma situação não didática, pois, na primeira, existe uma intenção do
professor de ensinar algo novo, o que não ocorre na segunda. A esse respeito,
Freitas (2002, p. 70) relata que:
As situações adidáticas representam os momentos mais importantes da aprendizagem, pois o sucesso do aluno nas mesmas significa que ele, por seu próprio mérito, conseguiu sintetizar um conhecimento. Neste sentido não podem ser confundidas com as situações não didáticas, que são aquelas que não foram planejadas visando uma aprendizagem.
Vejamos os aspectos fundamentais das fases de ação, formulação, validação e
institucionalização.
________________ 9