Lat. Am. j. solids struct. vol.11 número7

(1)

Abs tract

The aim of the present paper is to study the propagation of Lamb waves in micropolar generalized thermoelastic solids with two

temperatures bordered with layers or half-spaces of inviscid liquid

subjected to stress-free boundary conditions in the context of Green and Lindsay (G-L) theory. The secular equations for go

v-erning the symmetric and skew-symmetric leaky and nonleaky Lamb wave modes of propagation are derived. The computer simulated results with respect to phase velocity, attenuation coe f-ficient, amplitudes of dilatation, microrotation vector and heat

flux in case of symmetric and skew-symmetric modes have been depicted graphically. Moreover, some particular cases of interest have also been discussed.

Key words

Micropolar thermoelastic solid, Two temperatures, Leaky and nonleaky Lamb waves, Phase velocity, Symmetric and Skew-symmetric amplitudes.

Propagation of waves in micropolar generalized

thermoelastic

materials

with

two

temperatures

bordered with layers or half-spaces of inviscid liquid

1 IN T R O D U C T IO N

Eringen (1966) developed the theory of micropolar elasticity which has aroused much interest in recent years because of its possible usefulness in investigating the deformation properties of solids for which the classical theory is inadequate. There are at least two different generalizations relat-ed to the classical theory of thermoelasticity. The first one given by Lord and Shulman (1967) admits only one relaxation time and the second one given by Green and Lindsay (1972) involves two relaxation times.

The linear theory of micropolar thermoelasticity has been developed by extending the theory of micropolar continua. Eringen (1970, 1999) and Nowacki (1986) have given detailed reviews on the subject. Boschi and Iesan (1973) extended the generalized theory of micropolar thermoelastic-ity which allows the transmission of heat as thermal waves of finite speed. The generalized

ther-Raj n ee s h Kum ara, Ma nd e ep Kau r*, b, S. C . Raj van s hic

a_{Department of Mathematics, Kurukshetra}

University, Kurukshetra 136119, India

b_{Department of Applied Sciences, Guru Nanak}

Dev Engineering College, Ludhiana, Punjab 141008, India.

c_{Department of Applied Sciences, Gurukul}

Vidyapeeth Institute of Engineering and Tech-nology, Sector-7, Banur, District Patiala, Punjab 140601, India

Received in 12 Feb 2013 In revised form 02 Aug 2013

(2)

Latin American Journal of Solids and Structures 11 (2014) 1091-1113

moelasticity was presented by Dost and Taborrok (1978) by using Green and Lindsay theory. Chandrasekharaiah (1986) developed a heat flux dependent micropolar thermoelasticity.

Thermoelasticity with two temperatures is one of the non-classical theories of thermoelasticity. The thermal dependence is the main difference of this theory with respect to the classical one. A theory of heat conduction in deformable bodies depends on two distinct temperatures, the

con-ductive temperature � and thermodynamic temperature

_T

. The thermodynamic temperature

_T

�

has been introduced by Chen et al. (1968, 1969). The difference between these two temperatures is proportional to the heat supply for time independent situations. For time dependent and for wave propagation problems, the two temperatures are in general different, regardless of the pres-ence of heat supply. Warren and Chen (1973) investigated the wave propagation in the two tem-peratures theory of thermoelasticity.

The study related to the interaction of elastic waves with fluid loaded solids has been recog-nized as a viable means for deriving the non-destructive evaluation of solid structures. The re-flected acoustic field from a fluid-solid interface provides details of many characteristics of solids.

These phenomena have been investigated for the simple isotropic semi-space as well as the complicated systems of multilayered anisotropic media. A detailed review in this respect is given by Nayfeh (1995). Qi (1994) investigated the influence of viscous fluid loading on the propagation of leaky Rayleigh waves in the presence of heat conduction effects. Wu and Zhu (1995) suggested an alternative approach to the treatment of Qi (1994). They presented solutions for the dispersion relations of leaky Rayleigh waves in the absence of heat conduction effects. Zhu and Wu (1995) used this technique to study Lamb waves in submerged and fluid coated plates. Nayfeh and Nagy (1997) formulated the exact characteristic equations for leaky waves propagating along the inter-faces of systems which involve isotropic elastic solids loaded with viscous fluids, including half-spaces and finite thickness fluid layers.

Youssef (2006) presented a new theory of generalized thermoelasticity by considering the in-teraction of heat conduction in deformable bodies. A uniqueness theorem for generalized linear thermoelasticity involving a homogeneous and isotropic body was also recorded in this study. Various authors, e.g. (Puri and Jordan (2007), Youssef and Lehaibi (2007), Youssef and Al-Harby (2007), Magana and Quintanilla (2009), Mukhopadhyay and Kumar (2009), Kumar and Mukhopadhyay (2010), Kaushal et al. (2010, 2011) studied the problems of thermoelastic media with two temperatures.

Various investigators have studied the wave propagation problems in micropolar media e.g. Boschi (1973), Maugin (1974), Yerofeyev and Soldatov (1999), Erofeev (2003), Altenbach et al.

(2010), Eremeyev et al. (2007), Eremeyev (2005).

The problems of wave propagation in micropolar thermoelastic plates have been investigated by Nowacki and Nowacki (1969), Kumar and Gogna (1988), Tomar (2002, 2005), Kumar and Pratap (2006, 2007a,2007b, 2008, 2009, 2010), Sharma et al. (2008), Sharma and Kumar (2009).

Qingyong Sun et al. (2011) studied propagation characteristics of longitudinal displacement wave in micropolar fluid with micropolar elastic plate, Singh (2010) discussed propagation of thermoelastic waves in micropolar mixture of porous media.

(3)

liquid have been investigated. The secular equations have been derived. The phase velocity, at-tenuation coefficient, amplitudes of dilatation, microrotation vector and heat flux for the symmet-ric and skew-symmetsymmet-ric wave modes are computed numesymmet-rically and presented graphically for G-L theory.

2 V IB R A T IO N O F P LA T E O N FO U N D A T IO N A N D IN T EG R A L T R A N SFO R M

The field equations following Eringen (1966), Ezzat and Awad (2010) and Green and Lindsay (1967) in a homogeneous, isotropic, micropolar elastic medium in the context of generalized theo-ry of thermoelasticity with two temperatures, without body forces, body couples and heat sources, are as follows

(

λ

+

µ

)

u

j,ij

+

(

µ +

K

)

u

i,jj

+

Kε

ijk

ϕ

k,j

−

ν

[(

Φ −

aΦ

,jj

)

,i

+

τ

1

(

Φ

.

−

a

Φ

.

,jj

)

_,_i

] =

ρ

u

_i

..

,

(1)

(

)

2 =

,

..

, .

,ij ijj imn nm i i

j

γφ

K

ε

u

K

φ

ρ

j

φ

β

α

+

−

(2)

,

)]

(

)

[(

=

,

.

0 ,

..

0 , . ..

0 . * ,

*

j j jj

jj

rr

c

a

T

u

K

Φ

ρ

Φ

+

τ

Φ

−

Φ

+

τ

Φ

+

ν

(3)

and the constitutive relations are

(

)

(

)

,

=

.

1 ,

, ,

,r ij i j ji ji ijr r ij

r

ij

u

K

u

T

t

λ

δ

µ

ε

φ

ν

τ

_⎟

δ

⎠

⎞

⎜

⎝

⎛

₊

−

+

(4)

3 2,

1,

=

,

=

_, _, _,

i

j

r

m

_ij

αφ

_r_r

δ

_ij

+

βφ

_i_j

+

γφ

_j_i (5)

λ

_and

_µ

_{are Lame's constants.}

_K

_,

α

_,

_β

_and

_γ

_{are micropolar constants.}

_t

ij and

m

ij are the components of stress tensor and couple stress tensor respectively.

u

i and

ϕi

are the

dis-placement and microrotation vectors,

ρ

is the density ,

j

is the microinertia,

K

* is the thermal conductivity,

c

*_{is the specific heat at constant strain,}

_T

_{is the thermodynamic temperature,}

_Φ

is the conductive temperature,

T

0 is the reference temperature,

ν

= 3

(

λ

+

2µ +

K

)

α

_T

,

where

α

T is the coefficient of linear thermal expansion,

τ

0 and

τ

₁ are the thermal relaxation time

δ

ij is the Kronecker delta,

ε

ijr is the alternating tensor. The relation connecting

T

and

Φ

is given

by

T

₌

(1

−

a

∇

2

)

Φ

_{, where}

a

_{is a two temperature parameter.}

(4)

p

_L

₌

−

ρ

L

ϕ

L

.

,

(6)

(ϕL

,ii

−

1 c

L 2

ϕL

..

)

=

0,

u

L

=

∇ϕ

L

,

(7)

where

c

_L2

₌

λL

ρL

is the velocity of acoustic fluid,

λ

L is the bulk modulus,

ρ

L is the density of the

fluid,

p

L is the acoustic pressure in the fluid,

ϕ

L is the velocity potential of the fluid,

u

L is the

velocity vector,

∇

_{is gradient operator,}

∇

2_{is the Laplacian operator.}

3 N U M ER IC A L R ESU LT S

An infinite homogeneous isotropic, thermally conducting micropolar thermoelastic plate of thickness

₂

d

_{initially undisturbed and at uniform temperature}

_T

₀ _{is considered. We consider}

that two infinitely large homogeneous inviscid liquid half-spaces or layers of thickness

h

_bordered

the plate on both sides as shown in figures 1(a) and 1(b) respectively. The origin of the coordinate system

(

x

₁

,

x

₂

,

x

3

)

is taken on the middle of the plate and the axis normal to the solid

plate along the thickness is taken as

x

3-axis. We consider the propagation of plane waves in the

−

3 1

x

_{plane with a wavefront parallel to the}

2

x

_{-axis so that field components are independent of}

2

x

_{-coordinates.}

The displacement and microrotation vectors for two dimensional problem are taken as

u

₌

u

1

(

x

1

,

x

3

)

, 0,

u

3

(

x

1

,

x

3

)

(

)

,

ϕ

= 0 ,

(

ϕ

2

(

x

1

,

x

3

)

, 0

)

(8)

For inviscid fluid, we take

(

)

(

)

(

1

,

3

,

0,

1

,

3

)

=

u

L

x

w

L

x

L

u

(5)

,

=

,

=

,

=

,

=

₃ 0 1 * ' 3 1 0 1 * ' 1 1 3 * ' 3 1 1 * ' 1

u

T

c

u

T

c

u

c

x

c

x

ν

ρω

ν

ρω

ω

,

=

,

=

,

=

,

=

0 ' 0 ' 1 * ' 1 * ' 2 0 2 1 ' 2

T

t

T

c

_Φ

=

Φ

τ

ω

τ

ω

φ

ν

ρ

φ

,

=

,

1 =

0 1 * ' 0 ' ij ij ij ij

m

T

c

m

t

T

t

ν

ω

ν

0

* ' 0

=

ω

τ

, ₂

,

1 2 * '

a

c

a

₌

ω

,

1 ,

,

=

,

=

,

=

0 ' 2 0 * ' 0 1 ' 0 1 ' L L L L L L L L L L L

p

T

p

c

T

w

T

c

w

u

T

c

u

ν

ρ

λ

φ

ν

ρω

φ

ν

ρ

ν

ρ

=

1 * ' * 1 '

,

c

d

h

c

h

ω

=

(9) where

ρ

µ

λ

ρ

ω

c

K

c

₊

₂

₊

=

,

=

* 12

2 1 * *

such that

_ω

*

is the characteristic frequency of the medium.

The displacement components u

!,u! and

u

3_{are related to the potential functions}ϕ,ψ and

ψ

in dimensionless form as

,

=

,

=

1 3 3 3 1 1

x

u

x

u

∂

+

∂

−

∂

φ

ψ

φ

ψ

(10)

In the liquid layers, we have

,

=

,

=

3 1

x

w

x

u

i L Li

i L L i

∂

φ

(11)

where

i

L

φ

are the scalar velocity potential components for the top liquid layer (

i

₌

₁

_{) and for the}

bottom liquid layer (

i

₌

₂

).

u

_iL_and L i

w

₍

i

₌

₁

_,

₂

) are the 1

x

and

3

x components of the particle

velocity for the top liquid layer and the bottom liquid layer respectively.

(6)

0,

=

)

1 (

1

₂ 2 2 1 2

t

a

t

∂

−

Φ

∇

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

−

∇

φ

τ

φ

(12)

,

0 =

2 2 2 2 1 2

t

a

∂

−

+

∇

ψ

φ

ψ

(13)

,

0 =

2 2 2 5 2 4 2 3 2 2

t

a

∂

−

∇

−

∇

φ

ψ

φ

(14)

,

)

1 (

1 =

₆ ₀ 2 ₇ 2

2

_τ

_∇

_φ

∂

+

Φ

∇

−

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

Φ

∇

t

a

t

a

₍₁₅₎

2 ,

1 ,

0

1

2 2 2 2

=

∂

−

∇

i

t

i i L L L

φ

δ

φ

(16) where

a

1

=

K

µ

+

K

,

a

2

=

ρ

c

1

2

µ

+

K

,

a

3

=

Kc

1

2

γω

*2

,

a

4

= 2

a

3

,

a

5

=

ρ

jc

1

2

γ

,

a

6

=

ρ

c

*

c

1 2

K

*

_ω

*

,

a

7

=

ν

2

T

0

ρK

*

ω

*

,

∇

2

=

∂

2

∂

x

1 2

+

∂

2

∂

x

3 2

,

δ

L

2

=

c

L

2

c

1

2

The solutions of eqs. (12)-(16) are assumed as

(ϕ,

ψ

,ϕ

2

,

Φ

,ϕ

L1

,ϕ

L2

)

=

⎡⎣

f

1

( )

x

3

,

f

2

( )

x

3

,

f

3

( )

x

3

,

f

4

( )

x

3

,

f

5

(

x

3

),

f

6

(

x

3

)

⎤⎦

e

ιξ(x1−ct)

_,

₍₁₇₎

such that

ξ

ω

=

c

_{is the phase velocity,}

ω

_{is the frequency and}

ξ

is the wave number.

Making use of eq. (17) in eqs. (12)-(16) and subsequent elimination of

f

4

( )

x

3 and

f

3

( )

x

3 from the resulting equations, yields the equations

,

0 )

(

)

(

∇

*4

₊

_A

∇

*2

₊

_B

_f

₁

_x

₃

₌

₍₁₈₎

,

0 )

(

)

(

∇

*4

₊

_C

∇

*2

+

_D

_f

₂

_x

₃

=

₍₁₉₎

such that 2 2

3 2 2 *

/

₋

_ξ

=

(7)

The roots of eqs. (18) and (19) are given as

n

[

A

₄

B

]

2

1

2

2 2 ,

1

=

−

±

−

and

[

C

D

]

n

₄

2

1

2

2 4 ,

3

=

−

±

−

The appropriate potentials

ϕ

,

Φ

,

ψ

,

ϕ

2

,

ϕ

L1 and

ϕ

L2 are taken as

ϕ

=

(

A

1

cos

n

1

x

3

+

A

2

cos

n

2

x

3

+

B

1

sin

n

1

x

3

+

B

2

sin

n

2

x

3

)

e

ιξ(x₁−ct)

,

(20)

,

)

sin

cos

(

_h

₁

_A

₁

_n

₁

_x

₃

_h

₂

_A

₂

_n

₂

_x

₃

_h

₁

_B

₁

_n

₁

_x

₃

_h

₂

_B

₂

_n

₂

_x

₃

_e

(x1−ct)

+

=

Φ

ιξ (21)

,

)

sin

cos

(

_A

₃

_n

₃

_x

₃

_A

₄

_n

₄

_x

₃

_B

₃

_n

₃

_x

₃

_B

₄

_n

₄

_x

₃

_e

(x1−ct)

+

=

ιξ

ψ

(22)

,

)

sin

cos

(

₃ ₃ ₃ ₃ ₄ ₄ ₄ ₃ ₃ ₃ ₃ ₃ ₄ ₄ ₄ ₃ ( )

2

1 ct

x

e

x

n

B

h

x

n

B

h

x

n

A

h

x

n

A

h

₊

−

=

ιξ

φ

(23)

,

)

(

₅ 3 ₅ 3 ( 1 )

1

ct x x x

L

E

e

F

e

L

L − −

+

=

γ γ ιξ

φ

(24)

,

)

(

₆ 3 ₆ 3 (1 ) 2

ct x x x

L

E

e

F

e

L

L − −

+

=

γ γ ιξ

φ

(25)

where the expressions for h_i,h_j;i₌1,2, j ₌3,4 are given in Appendix.

4 B O U N D A R Y C O N D IT IO N S

We consider the following boundary conditions at the solid-liquid interfaces

x

₌

_±

d

3 :

(i) Continuity of the normal stress component of solid and liquid.

L s

p

t

)

₌

₋

(

₃₃ (26)

(ii) Vanishing of the tangential stress component.

0 )

(

t

₃₁ s

₌

(27)

(iii) Vanishing of the tangential couple stress component.

0 )

(

m

₃₂ s

₌

(28)

(8)

(

u

3 .

)

s

=

(

w

L

)

(29)

(v) The thermal boundary condition is given by

,

0

3

=

+

∂

HT

x

T

(30)

where

_H

is the surface heat transfer coefficient. Here

_H

→0 and

_H

→_∞ corresponds to

thermally insulated and isothermal boundaries, respectively.

4.1 Leaky Lam b W aves

The solutions for solid media of finite thickness

₂

d

_{sandwiched between two liquid half-spaces is} given by eqs. (20)-(23) together with

d

x

e

E

x d x ct

L

−

<

∞

−

=

+ − 3

) ( ) (

5

,

1 3

1

ιξ γ

φ

(31)

∞

<

=

− − − 3

) ( ) (

6 1

,

3 2

x

d

e

F

x d x ct

L

L ιξ

γ

φ

(32)

4.2 Nonleaky Lam b W aves

The corresponding solutions for a solid media of finite thickness

₂

d

_{sandwiched between two finite} liquid layers of thickness

h

_{are given by eqs. (20)-(23) and}

d

x

h

d

e

h

d

x

E

_L x ct

L

=

+

−

+

<

−

3 )

( 3

5

sinh

[

(

)]

1

,

(

)

1

ιξ

γ

φ

(33)

)

(

,

)]

(

[

sinh

₃ ( ) ₃

6

1 2

h

d

x

d

e

h

d

x

F

x ct

L

=

−

+

<

+

−

ιξ

γ

φ

(34)

Nonleaky and leaky Lamb waves are distinguished by selecting the functions

1 L

φ

and

2 L

φ

in

such a way that the acoustical pressure is zero at

x

₃

₌

_∓

(

d

₊

h

)

_{. This shows that} 1

L

φ

and

2 L

φ

are solutions of standing wave and travelling wave for nonleaky Lamb waves and leaky Lamb waves respectively.

5 D ISP E R SIO N E Q U A T IO N S

(9)

5.1 Leaky Lam b W aves

We consider an isotropic thermoelastic micropolar plate with two temperatures completely im-mersed in a inviscid liquid as shown in fig. 1(a).

Figure 1(a) Geometry of leaky Lamb waves

The thickness of the plate is

₂

d

_{and thus the lower and upper portions of the fluid extend} from

d

_to

_∞

_and

₋

d

_to

₋

_∞

_{respectively. In this case, the partial waves exist in the plate as}

well as the fluid. The appropriate formal solutions for the plate and fluids are those given by eqs. (20)-(23), (31) and (32). By applying the boundary conditions (26)-(30) at

x

₌

_±

d

3 and

subse-quently selecting nontrivial values of the partial wave amplitudes

E

_k_and

F

_k

₍

k

₌

₁

_,

₂

_,

₃

_,

₄

₎

_;

5

E

,

6

F

and

γ

_L

≠

0 ,

we arrive at the characteristic dispersion equations as

T₁ T₃ ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1

− T2 T₃ ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1

P₁− T₁ T₄ ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1

P₂+ T₂ T₃ ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1

P₁P₂+ P₃S

n₄G

P₄n₃h₃

h₄n_{2 [}T_{4 ]}± − P5

[T_{3 ]}± ⎡

⎣

⎢ ⎤

⎦ ⎥=

−P₃Qm₃n_{3 (}h₄ −h_{3 )}

h₄

(35)

for stress-free thermally insulated boundaries (

_H

→

0

_{) of the plate} where

)

(

),

(

,

)

(

,

₄ 2 ₃ ₆ ₅ 2 ₃ ₅

2 5 1 1 2 1 3 5 4 4 6 3 3 2 1 2 2 2 1 1

1

P

cm

Rm

P

cm

Rm

h

m

n

h

P

m

h

n

m

h

n

P

m

h

n

m

h

n

P

₌

−

₌

_ξ

₊

₌

_ξ

₊

and T₁ T3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1 − T2

T3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1

P₆+ T₄ T3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1 P₇h₃m₆

n4Q + 1−

P₄n₃h₃

P5n4h4 T₄ T3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟P₈

T₁ T3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1 − T2

T3 ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1 P₆ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ =

P₇h₄m₅

n3

(10)

for stress-free isothermal boundaries (

_H

→

∞

_{) of the plate.}

where

)

(

,

)

(

)

(

,

4 3 3 3 4 5 8 3 4 3 2 1 1 2 2 1 7 2 1 1 2 6

h

QG

m

n

S

h

P

h

m

h

n

h

m

h

m

P

h

n

h

n

P

−

=

−

=

5.2 N onleaky Lam b W aves

We consider an isotropic thermoelastic micropolar plate with two temperatures bordered with layers of inviscid liquid on both sides as shown in Fig. 1(b).

Figure 1(b) Geometry of nonleaky Lamb waves

The appropriate formal solutions for the plate and fluids are given by eqs. (20)-(23), (33) and

(34). By applying the boundary conditions (26)-(30) at

x

₌

_±

d

3 and subsequently selecting

non-trivial values of the partial wave amplitudes

E

_kand

F

k

(

k

=

1 ,

2 ,

3 ,

4 )

;

E

5,

F

6and

γ

_L

≠

0 ,

we

arrive at the characteristic dispersion equations as

T₁ T₃ ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1 − T2

T₃ ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1

P₁− T₁ T₄ ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1

P₂+ T₂ T₃ ⎡ ⎣ ⎢ ⎤ ⎦ ⎥ ±1

P₂n₁h₁m₆

n₂h₂m₂ +

P₃S

n₄G T₅

P₄n₃h₃

h₄n_{2 [}T_{4 ]}± − P5

[T_{3 ]}± ⎡

⎣

⎢ ⎤

⎦ ⎥=−

P₃Qm₃n_{3 (}h₄−h_{3 )}

h₄

(37)

for stress-free thermally insulated boundaries (

_H

→

0

_{) of the plate.}

T1 T₃ ⎡ ⎣ ⎢ ⎤_⎦⎥ ±1 − T2

T₃ ⎡ ⎣ ⎢ ⎤_⎦⎥

±1

P6+ T4 T₃ ⎡ ⎣ ⎢ ⎤_⎦⎥ ±1 P7h3m6

n₄Q + 1−

P4n3h3

P₅n₄h₄ T4 T₃ ⎡ ⎣ ⎢ ⎤_⎦⎥ ±1 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟P8T3T5

T1 T₃ ⎡ ⎣ ⎢ ⎤_⎦⎥ ±1 − T2

T₃ ⎡ ⎣ ⎢ ⎤_⎦⎥ ±1 P6 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ =

P7h4m5

(11)

for stress-free isothermal boundaries (

_H

→

∞

_{) of the plate.}

Here the superscript +1 refers to skew-symmetric and -1 refers to symmetric modes. All the coefficients and other quantities are recorded in Appendix.

Eqs. (35) and (38) are the general dispersion relations involving wave number and phase velo-city of various modes of propagation in a micropolar thermoelastic plate bordered with layers of inviscid liquid or half-spaces on both sides.

5.3 Special cases

The removal of the liquid layers or half-spaces on the both sides, provide the wave propagation in

micropolar thermoelastic solid with two temperatures. Analytically, if we take

₌

0

L

ρ

in eqs. (35)

and (37) then the secular equations for stress-free thermally insulated boundaries (

_H

→

0

_{) for}

the said case reduce to

(

T

1

T

3

)

±

_N

1

+

(

T

1

T

4

)

±

_N

2

+

(

T

2

T

3

)

±

_N

3

+

(

T

2

T

4

)

±

_N

4

+

(

T

3

T

4

)

±

_N

5

=

0

(39)

where

)

)(

(

,

1 2 3 4 3 4 3 2 1 5 5 2 4 1 4 1 4 6 2 3 1 3 1 3 5 1 4 2 4 2 2 6 1 3 2 3 2 1

h

QG

m

n

N

G

m

n

h

N

G

m

n

h

N

G

m

n

h

N

G

m

n

h

N

−

=

−

=

−

=

If we take

a

₌

0

_{in eq. (30), then we obtain the secular equations in micropolar generalized}

thermoelastic plate.

6 A M P LIT U D E S O F D ILA T A T IO N , M IC R O R O T A T IO N A N D H E A T FLU X

The amplitudes of dilatation, microrotation and heat flux for symmetric and skew-symmetric modes have been computed for micropolar thermoelastic plate. By using eq. (17) in (12)-(16) and then using eqs. (20)-(25), we obtain

(

e

)

_sy

₌

[

−

M

₁

cos

n

₁

x

₃

+

M

2

h

1

n

1

S

1

h

2

n

2

S

2

cos

n

₂

x

₃

]

A

₁

e

ιξ(x1−ct)

_,

(40)

(

e

)

_asy

₌

[

−M

1

sin

n

1

x

3

+

M

₂

h

₁

n

₁

C

₁

h

₂

n

₂

C

₂

sin

n

2

x

3

]

B

1

e

ιξ(x1−ct)

,

₍₄₁₎

,

]

sin

[

)

(

₄ ₃ ₃ ( )

4 4 3 3 3 1 3 3 2 1 ct x

sy

n

x

B

e

C

n

C

n

h

x

n

h

−

=

ιξ

(12)

,

]

cos

[

)

(

₄ ₃ ₃ ( )

4 4 3 3 3 3 3 3 2 1 ct x

asy

n

x

A

e

S

n

S

n

h

x

n

h

−

=

ιξ

φ

₍₄₃₎

,

]

sin

[

)

(

2 3 1 ( )

* 1 2 2 1 1 1 3 1 * 1 1 1 ct x

sy

n

K

n

x

A

e

S

n

S

n

h

x

n

K

h

n

q

₌

−

ιξ − ₍₄₄₎

.

]

cos

[

)

(

*' ₂ ₃ ₁ ( )

2 1 1 1 3 1 * 1 1 1 ct x

asy

K

n

x

B

e

C

n

h

x

n

K

h

n

q

₌

−

₊

ιξ − ₍₄₅₎

7 N U M E R IC A L R E SU LT S A N D D ISC U SSIO N

For numerical computation we select Magnesium crystal (micropolar thermoelastic solid). The physical data for this medium is given below:

(i) The values of micropolar constants are taken from Eringen (1984):

;

10

0 .

2 ,

10

74 .

1 ,

10

0 .

1 ,

10

779 .

0 ,

10

0 .

4 =

,

10

4 .

9 =

2 20 3 3 2 10 9 2 10 2 10

m

j

kgm

Nm

K

N

Nm

− − − − − −

×

=

×

=

×

=

×

=

×

ρ

γ

µ

λ

(ii) and thermal parameters are taken from Dhaliwal and Singh (1980):

,

10

1.04 =

,

10

0.268 =

7 −2 −1 * 3 2 −2 −1

×

Nm

K

c

m

sec

K

ν

,

5 .

0 ,

10

1.7 =

,

0.298 =

* 2 1 1

0

×

=

−

_K

_a

Nsec

K

T

m

d

sec

_,

₌

_0.813

₁₀

_,

₌

₁

_,

₁

_.

₀

10

0.613 =

12 ₁ 12

0

×

=

− −

ω

τ

For numerical calculations, water is taken as liquid and the speed of sound in water is given by

sec

/

10

5 .

1 =

3

m

c

_L

_×

In general, wave number and phase velocity of the waves are complex quantities, therefore, the waves are attenuated in space. If we write

,

1 1 1

Q

V

C

−

=

−

+

ιω

− ₍₄₅₎

then

ξ

=

R

₊

ι

Q

,

where

R

₌

ω

V

and

Q

are real numbers. This shows that

V

is the

(13)

In figures 2 to 9, GLS and GNLS refer to leaky and nonleaky symmetric waves in micropolar thermoelastic solid with two temperatures, GLSK and GNLSK refer to leaky and nonleaky skew-symmetric waves in micropolar thermoelastic solid with two temperatures, GALS and GANLS refer to leaky and nonleaky symmetric waves in micropolar thermoelastic solid, GALSK and GANLSK refer to leaky and nonleaky skew-symmetric waves in micropolar thermoelastic solid. In figures 10 to 15, GT represents the amplitude for micropolar thermoelastic solid with two tem-peratures and TS represents the amplitude for micropolar thermoelastic solid.

7.1 Phase velocity

Leaky Lam b W aves

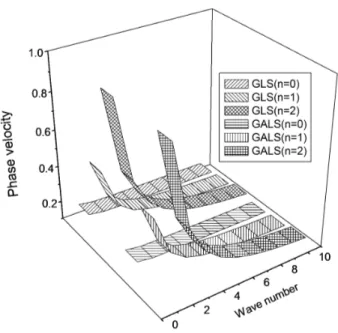
Figure 2 Variations of phase velocity for symmetric leaky Lamb waves

It is depicted from fig. 2 that the phase velocity for lowest symmetric mode of propagation for GLS and GALS coincide. The magnitude of phase velocity for GALS is greater than GLS for (n=1) symmetric mode of propagation for

ξ

d

₌

₁

_,

3 _≤

_ξ

d

_≤

6

_{and in the remaining range the}

(14)

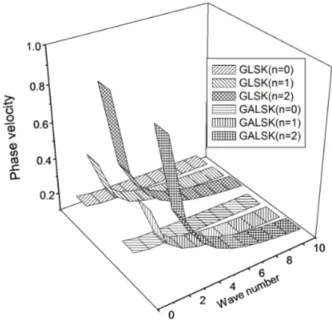
Figure 3 Variations of phase velocity for skew-symmetric leaky Lamb waves

It is noticed from figs. 3 that the phase velocities for (n = 0) and (n = 1) skew-symmetric leaky Lamb wave mode of propagation for GLSK and GALSK coincide. The velocities for

GALSK are greater than the velocities for GLSK for wave number

ξ

d

₌

₂

_{and in the remaining}

region, the velocities coincide.

Leaky Lam b W aves

(15)

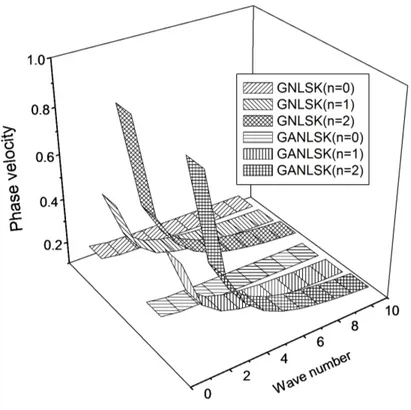
Fig. 4 shows that for (n=0) symmetric mode of propagation, the velocities for GANLS are greater than GNLS for

ξ

d

₌

2, 4

≤

ξ

d

_≤

6, 8

≤

ξ

d

_≤

10

and in the remaining region, the behavior is op-posite. It is also noted that for (n=1) mode, the phase velocities for GANLS are greater than the phase velocities for GNLS in the whole region. The values for GANLS are greater than the values for GNLS in the whole region, except for

ξ

d

₌

1.

Figure 5 Variations of phase velocity for skew-symmetric nonleaky Lamb waves

(16)

7.2 Attenuation Coefficients

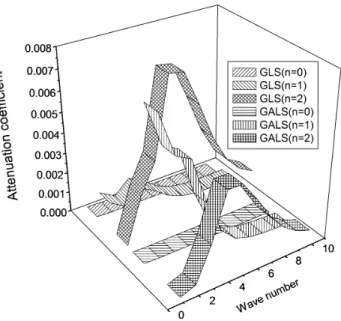
Figure 6 Variations of attenuation coefficient for symmetric leaky Lamb waves

Fig. 6 depicts that for symmetric leaky Lamb wave mode (n=0), the attenuation coefficient for

GLS remain more than the attenuation coefficient for GALS when

ξ

d

₌

₁

_and

3 _≤

_ξ

d

_≤

6

_{, while}

in the remaining region, the behavior is reversed. For (n=1), the values for GLS oscillate and attain maximum value at

ξ

d

₌

10

_{. It is noticed that for (n=2), the attenuation coefficient for}

GALS remain more than the values for GLS in the whole region, except in the region

7 _≤

_ξ

d

_≤

10

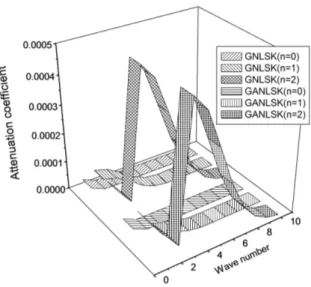
_{, where the behavior is reversed.}

(17)

Fig. 7 shows that for (n=0) mode, the magnitude of attenuation for GLSK and GALSK attain

maximum value at

ξ

d

₌

₁

_{. For (n=1) skew-symmetric mode, the values for GLSK decrease with}

increase in wave number. It is noticed that for (n=2) mode, the magnitude of attenuation coeffi-cient for GALSK remain more than in case of GLSK in the whole region, except for

ξ

d

₌

₁

_,

where the values coincide.

Figure 8 Variations of attenuation coefficient for symmetric nonleaky Lamb waves

It is evident from fig. 8 that for symmetric nonleaky Lamb wave mode (n=0), the attenuation

coefficient for GNLS and GANLS attain maximum value at

ξ

d

₌

₁

_{. It is noticed that the}

mag-nitude of attenuation coefficient for GNLS and GANLS attain maximum value 0.01212 and 0.00756 at

ξ

d

₌

3

_{respectively for (n=1) mode. For (n=2) mode, the values for GNLS and}

GANLS attain maximum value at

ξ

d

₌

5.

(18)

Fig. 9 depicts that for (n=0) skew-symmetric nonleaky Lamb wave mode of propagation, the magnitude of attenuation coefficient for GNLSK and GANLSK decrease with increase in wave number. It is depicted that for (n=1) mode, the magnitude for GNLSK and GANLSK attain

maximum value at

ξ

d

₌

₁

_{. For (n=2) mode, the values for GANLSK are greater than GNLSK in}

the whole region except for

ξ

d

₌

2,10.

7.3 Am plitudes

In figures 10 to 15, GT represents the amplitude for micropolar thermoelastic solid with two tem-peratures and TS represents the amplitude for micropolar thermoelastic solid.

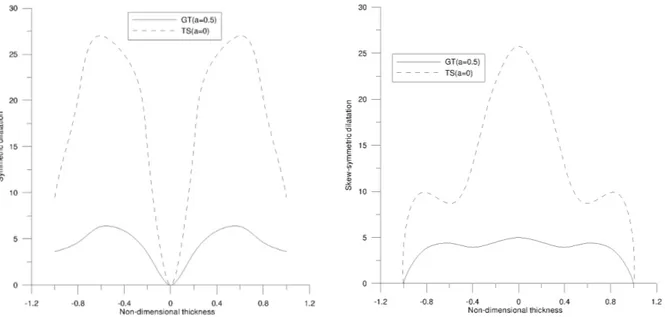
Figure 10 Amplitude of symmetric dilatation Figure 11 Amplitude of skew-symmetric dilatation

(19)

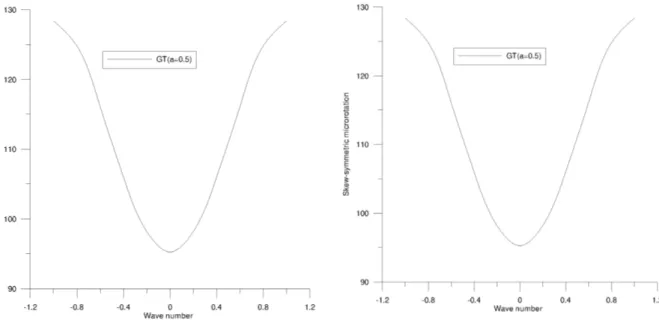
Latin American Journal of Solids and Structures 11 (2014) 1091-1113 Figure 12 Amplitude of symmetric microrotation Figure 13 Amplitude of skew-symmetric microrotation

It is evident from figs. 12 and 13 that the amplitude of symmetric and skew-symmetric micro-rotation is minimum at the centre and obtain maximum value at the surfaces.

The amplitude of symmetric and skew-symmetric heat flux is oscillatory. For symmetric mode and skew-symmetric mode, the amplitude of heat flux attain maximum value at the sufaces and minimum value at the centre, as shown in figures 14 and 15.

(20)

8 C O N C LU SIO N

It is observed that the variation of phase velocities of lowest symmetric and skew-symmetric mode for leaky and nonleaky Lamb waves almost coincide with increase in wave number. The phase velocities for higher symmetric and skew-symmetric mode attain maximum value at vanish-ing wave number and as wave number increase the phase velocities get decreased sharply. For (n=2) symmetric mode, the attenuation coefficient for GLS is greater than the values for GALS in the whole region . It is noticed that the values of attenuation coefficient for lowest symmetric and skew-symmetric mode for leaky and nonleaky Lamb waves are very small as compared to the values for highest mode. The values of symmetric and skew-symmetric dilatation for TS are high-er in comparison to GT that reveals the effect of two temphigh-eratures.

References

Achenbach J.D., 1976. Wave propagation in elastic solids, North-Holand, Amsterdam.

Altenbach H., Eremeyev V.A., Lebedev L.P., Rend’on L.A., 2010. Acceleration waves and ellipticity in ther-moelastic micropolar media. Archive of Applied Mechanics, 80_:217-227.

Bochi E., 1973. Lamb and Love wave-propagation in an infinite micropolar elastic plate. Ann. Geofisica,

26_:341-355.

Boschi E. and Iesan D., 1973. A generalized theory of linear micropolar thermoelasticity. Meccanica, 7

:154-157.

Chandrasekharaiah D.S., 1986. Heat flux dependent micropolar thermoelasticity. International Journal of En-gineering Science, 24_:1389-1395.

Chen P.J., Gurtin M.E. and Williams W.O., 1968. A note on non simple heat conduction. Zeitschrift für An-gewandte Mathematik und Physik, 19:_960-970.

Chen P.J., Gurtin M.E. and Williams W.O., 1969. On the thermoelastic material with two temperatures. Zeitschrift für angewandte Mathematik und Physik, 20_:107-112.

Dhaliwal R.S. and Singh A., 1980. Dynamic coupled thermoelasticity, Hindustan Publication Corporation, New Delhi, India.

Dost S. and Taborrok B., 1978. Generalized micropolar thermoelasticity. International Journal of Engineering Science, 16_:173-178.

Eringen A.C. 1966. Linear Theory of micropolar elasticity. Journal of Applied Mathematics and Mechanics,

15_:909-923.

Eringen A.C., 1970. Foundations of micropolar thermoelasticity. International Centre for Mechanical Science, Udine Course and Lectures 23, Springer-Verlag, Berlin.

Eringen A.C., 1999. Microcontinuum Field theories I: Foundations and Solids; Springer-Verlag, Berlin.

Eringen A.C., 1984. Plane waves in non local micropolar elasticity. International Journal of Engineering Sci-ence, 22_{, 1113-1121.}

Eremeyev V.A., 2005. Acceleration waves in micropolar elastic media. Doklady Physics, 50_:204-206.

(21)

Ezzat M.A. and Awad E.S., 2010. Constitutive relations, Uniqueness of solution and thermal shock application in the linear theory of micropolar generalized thermoelasticity involving two temperatures. Journal of Thermal Stresses, 33_:226-250.

Green A.E. and Lindsay K.A., 1972. Thermoelasticity. Journal of Elasticity, 2_:1-7.

Kaushal S., Sharma N. and Kumar R., 2010. Propagation of waves in generalized thermoelastic continua with two temperature. International Journal of Applied Mechanics and Engineering, 15_:1111-1127.

Kaushal S., Kumar R. and Miglani A., 2011. Wave propagation in temperature rate dependent thermoelastici-ty with two temperatures. Mathematical Sciences, 5_:125-146.

Kumar R. and Gogna M. L., 1988. Propagation of waves in micropolar elastic layer with stretch immersed in an infinite liquid. International Journal of Engineering Science, 27_:89-99.

Kumar R. and Mukhopahyay S., 2010. Effect of thermal relaxation time on plane wave propagation under two temperature thermoelasticity. International Journal of Engineering Science, 48_:128-139.

Kumar R. and Partap G., 2006. Rayleigh Lamb waves in micropolar isotropic elastic plate. Applied Mathe-matics and Mechanics, 27_:1049-105.

Kumar R. and Partap G., 2007a. Propagation of micropolar thermoeastic waves in plate. International Journal of Applied Mechanics and Engineering, 12_:655-675.

Kumar R. and Partap G., 2007b. Wave propagation in a circular crested micropolar generalized thermoelastic plate. Buletinul Institutului Polithehnic din Iasi, 3-4_:53-72.

Kumar R. and Partap G., 2008. Propagation of waves in thermoelastic micropolar cubic crystals bordered with layers or half spaces of inviscid fluid. International Journal of Applied Mathematics and Mechanics, 4_:19-38.

Kumar R. and Partap G., 2009. Free vibrations in micropolar thermoelastic plate loaded with viscous fluid with two relaxation times. International Journal of Applied Mathematics and Mechanics, 5_:39-58.

Kumar R. and Partap G., 2010. Propagation of waves in micropolar thermoelastic cubic crystals. Applied Mathematics and Information Sciences, 4_:107-123.

Lord H.W. and Shulman Y., 1967. A generalized dynamical theory of thermoelasticity. Journal of the Mechan-ics and PhysMechan-ics of Solids, 15_:299-309.

Magana A. and Quintanilla R., 2009. Uniqueness and growth of solution in two temperature generalized ther-moelastic theories. Mathematics and Mechanics of Solids, 14_:622-634.

Maugin G.A., 1974. Acceleration waves in simple and linear viscoelastic micropolar materials. International Journal of Engineering Science, 12:_143-157.

Mukhopadhyay S. and Kumar R., 2009. Thermoelastic interaction on two temperature generalized thermoelas-ticity in an infinite medium with a cylindrical cavity. Journal of Thermal Stresses, 32_:341-360.

Nayfeh A.H., 1995. Wave propagation in layered anisotropic media, North-Holland, Amsterdam.

Nayfeh A.H. and Nagy P.B., 1997. Excess attenuation of leaky Lamb waves due to viscous fluid loading. Jour-nal of Acoustical Society of America, 101_:2649-2658.

Nowacki W., 1986. Theory of Asymmetric Elasticity, Oxford: Pergamon.

Nowacki W. and Nowacki W.K., 1969. Propagation of monochromatic waves in an infinite micropolar elastic plate. Buletin de Academie Polonaise des Sciences, Sere des Sciences Techniques, 17_:45-53.

Puri P. and Jordan P., 2006. On the propagation of harmonic plane waves under the two temperature theory. International Journal of Engineering Science, 44_:1113-1126.

(22)

Sharma J.N. and Kumar S., 2009. Lamb waves in micropolar thermoelastic solid plates immersed in liquid with varying temperature. Meccanica, 44_:305-319.

Sharma J.N., Kumar S. and Sharma Y.D., 2008. Propagation of Rayleigh waves in microstretch thermoelastic continua under inviscid fluid loadings. Journal of Thermal Stresses, 31_:18-39.

Singh B., 2010. Propagation of Thermoelastic Waves in Micropolar Mixture of Porous Media, International Journal of Thermophysics, 31_{, 637–647.}

Sun Qingyong, Xu Hongyu, Liang Bin, 2011. Propagation characteristics of longitudinal displacement wave in micropolar fluid with micropolar elastic plate, Materials Science Forum, 694_{: 923-927.}

Tomar S.K., 2002. Wave propagation in a micropolar elastic layer, Proceedings of National Academy of Sci-ences, India, 72_{(A), IV: 339-350.}

Tomar S.K., 2005. Wave propagation in a micropolar plate with voids, Journal of Vibration and Control,

11_:849-863.

Warren W.E. and Chen P.J., 1973. Wave propagation in the two temperature theory of thermoelasticity. Acta Mechanica, 16_:21-23.

Wu J. and Zhu Z., 1995. An alternative approach for solving attenuated Rayleigh waves. Journal of Acoustical Society of America, 97_:3191-3193.

Yerofeyev V.I. and Soldatov I.N., 1999. A shear surface wave at the interface of an elastic body and a mi-cropolar liquid. Journal of applied Mathematics and Mechanics, 63_:277-281.

Youssef H.M., 2006. Theory of two temperature generalized thermoelasticity. IMA Journal of Applied Mathe-matics, 71_:383-390.

Youssef H.M. and Al-Lehaibi E.A., 2007. A state approach of two temperature generalized thermoelasticity of one dimensional problem. International Journal of Solids and Structures, 44_:1550-1562.

Youssef H.M. and Al-Harby H.A., 2007. State space approach of two temperature generalized thermoelasticity of infinite body with a spherical cavity subjected to different types of thermal loading. Archive of Applied Me-chanics, 77_:675-687.

Zhu Z. and Wu J., 1995. The propagation of Lamb waves in a plate bordered with a viscous fluid, An alterna-tive approach for solving attenuated Rayleigh waves. Journal of Acoustical Society of America, 98_:1059-1064.