Broad Histogram: Tests for a Simple and
EÆient Miroanonial Simulator
Paulo Murilo Castro de Oliveira
Instituto deFsia,UniversidadeFederalFluminense
av. Litor^anea s/n,BoaViagem,NiteroiRJ,Brazil24210-340
e-mail PMCOIF.UFF.BR
Reeivedon5August,2000
TheBroadHistogramMethod(BHM)allowsonetodeterminetheenergydegenerayg(E),i.e. the
energyspetrumofagivensystem,fromtheknowledgeofthemiroanonialaverages<N up
(E)>
and < N dn
(E) > of twomarosopi quantities N up
and N dn
dened within the method. The
fundamentalBHMequationrelatingg(E)tothequoted averagesis exatand ompletelygeneral
foranyoneivablesystem. Thus,theonlypossiblesoureofnumerialinauraiesresidesonthe
measurementoftheaveragesthemselves. Inthistext,weintrodueaMonteCarloreipetomeasure
miroanonialaverages. Inordertotestitsperformane,weappliedittotheIsingferromagneton
a3232squarelattie. Theexatvaluesofg(E)areknownuptothislattiesize,thusitisagood
standardtoompareournumerial resultswith. Measuring thedeviations relativeto theexatly
knownvalues,we veriedadeayproportionalto 1= p
ounts , by inreasingtheounter(ounts)
ofaveragedsamplesoveratleast6deades. Thatiswhywebelievethismiroanonialsimulator
presentsnobiasbesidesthenormalstatistialutuations.Forounts10 10
,wemeasuredrelative
deviationsnear10 5
for bothg(E)andthespeiheatpeak,obtainedthroughBHMrelation.
Monte Carlo methods are applied to statistial
physisinordertomeasure thethermalaverage
<Q>
T =
P
S Q
S
exp( E
S =T)
P
S
exp( E
S =T)
(1)
of some marosopi quantity Q (magnetisation,
den-sity, et). The temperature T is xed, and the
Boltz-mannonstantisset to unity. Bothsumsrun overall
possible mirostates S available for the system. The
energy(quantity Q)orrespondingto S isdenoted by
E
S (Q
S
). Withintraditionalomputersimulations,
in-steadoftakingallpossiblestates,onetakesonlyanite
setof them,i.e. aMarkovianhain ofstatesrandomly
tossedaordingtoprobabilitiesditatedbythe
Boltz-mann exponential fators exp( E
S
=T), the so-alled
importane sampling. Thus, one needsto xa
parti-ular value for the temperature T, before running the
omputer job. In order to determine the full
depen-dene of < Q >
T
upon T, one needs to run the job
againandagain,fordierentvaluesofT.
Analternativeistore-writethesameaverageas
<Q>
T =
P
E
<Q(E)>g(E)exp( E=T)
P
E
g(E)exp( E=T)
; (2)
with energy E, and both sums run over all possible
energies. Themiroanonialaverage
<Q(E)>= P
S[E℄ Q
S
g(E)
(3)
of thesamequantity Qorrespondsto axed energy,
i.e. the sumin (3) runs onlyoverthe statesS[E℄
be-longing to energy level E. This miroanonial
aver-age(3)issimplerthantheanonialounterpart(1)or
(2), presribingexatlythe sameweightto all
averag-ingstates,i.e. itisauniformaveragingproesswithin
eahenergylevelseparately.
Only the Boltzmann fator exp( E=T) appearing
in equation (2) depends on the temperatute,
arry-ingallthermodynami informationaboutthe
environ-ment whih ontinuously exhanges energy with the
system under study. Contrary to this, bothg(E)and
<Q(E) >are independent ofthe partiular waythis
energy exhange ours, independent of the
environ-ment: theyaremorefundamentalpropertiesofthe
sys-tem alone, dened onlybyits energyspetrum. They
arenotthermodynami quantities,and donotdepend
upon thermodynamionerns liketemperature,
equi-librium, et. In pratial terms, equation (2) allows
oneto determine<Q>
T
The Broad Histogram Method (BHM) [1℄ relates
g(E) with the miroanonial averages of two
maro-sopi quantities N up
and N dn
, measured at the
ur-rent state S. First, one needs to adopt some
proto-ol of allowed movements whih ould be performed
on S, leading to another possible state S 0
. One an
adopt any suh a protool, the only restrition being
its reversibility(if S ! S 0
is allowed, sois S 0
! S).
Considering the Ising model, for instane, the
proto-ol ould be hosen to be thewhole set of single-spin
ips (among many other alternative hoies). Given
suhaprotool,N up
(S)ountsthenumberof allowed
movementswhih ouldbeperformedonS,leadingto
a xed energy inrement E (whih must be hosen
a priori, although the method is also independent of
this hoie). Analogously, N dn
(S) ountsthe number
of allowed movements dereasing the energy of S by
the same xed amount E. The fundamental BHM
relation[1℄is
g(E)<N up
(E)>= g(E+E)<N dn
(E+E)> ;
(4)
wherethemiroanonialaveragesofN up
andN dn
are
denedbyequation(3). Byknowingtheseenergy
fun-tions,equation(4)allowsoneto determineg(E)along
alltheenergyaxis,instepsofE |aonstant,
unim-portant pre-fator is anelled out by performing the
average in equation (2). Relation (4) is shown to be
valid for any energy spetrum, under ompletely
gen-eral grounds [2℄. Also, the same reasoning ould be
applied foranotherbasiquantityq, insteadofthe
en-ergy, by onsidering the degeneraies g(q) instead of
g(E). Forsimpliity, we will restrit ourselvesto the
aseoftheenergy.
Thus, theBroadHistogramMethod onsistsin: i)
to hoosesomeprotoolofallowedmovements,aswell
asanenergyjumpE;ii)tomeasure,byanymeans,
themiroanonialaverage<Q(E)>asafuntionof
the energy, as well as < N up
(E) >and <N dn
(E) >
whihdetermineg(E)throughequation(4);iii)to
ob-tainthedesiredthermalaveragethroughequation(2).
Thereisnoapproximationatall,andthenal
numeri-alauraydependsexlusivelyuponthe
miroanon-ialmeasuringstrategyadoptedinstepii. Themethod
is reviewedin [3℄. Somerefereneswhereitisused are
[4-16℄.
Let's briey analyse hereafter some possible
om-puterstrategiesoneanadoptinorderto measurethe
miroanonialaverages<Q(E)>, <N up
(E)>and
< N dn
(E) >, as funtions of the energy. A
Marko-vianhainofstatesisobtainedbyperformingrandom
These movements are tossed among some previously
denedset of possibilities, anotherprotool whih has
nothingtodowiththeBHMprotoolofvirtual
move-ments. Both protools ouldeven behosentobethe
same,but notneessarily.
Therstdiret strategyistokeepalwaysthesame
xedvalueE: bystartingfromsomestate
orrespond-ingtothedesiredenergy,onesimplyrejetsanytossed
movementwhihhangestheurrentenergy. Afterone
hasalreadyalargeenoughnumberofvisitedstates
in-sidethispartiularenergylevel,thesameproessis
re-peatedforotherlevels. Dependingontheadopted
pro-tool of (real) movements, this strategy ould lead to
ergodiityproblems: duetoitshigh rejetionrate,one
risksto sampleonly abiasedsub-setof states
belong-ing to energy level E, violating the required uniform
visitation. Moreover,it is also an ineÆient strategy,
in what onerns the omputertime, againdue to its
highrejetionrate.
Theopposedalternativeistoaeptalsomovements
leadingtoenergyjumps,storingseparatedaveragesfor
eah energy level, in parallel. Obviously, this option
is muh moreeÆient in what onerns theomputer
time. However, one annot simply aept any tossed
movement: energyinrements wouldourmoreoften
than derements, beause g(E) is normally a fast
in-reasing funtion of the energy. As a result, at the
end, only states orresponding to the region near the
maximum of g(E) would be sampled. Thus, some
movement-rejetionpresriptionmustbeadopted,and
weget bakto theuniformityviolation problem. One
an adopt some already well established
movement-rejetion presriptionbased on detailed balane
argu-ments. Forinstane, anonial,xed-temperature
dy-namis ould be adopted [4,6℄, sampling statesinside
thenarrow energy windoworrespondingto the xed
valueofT. Inordertogetresultsonabroaderenergy
window, one an simply superimpose the histograms
obtainedfordierentomputer runs orresponding to
dierentvaluesofT.
Another possibility is to adopt one of the many
multianonialdynamis[7,9,11,13,14℄. Withinthis
ap-proah, onetunestheE-dependent rejetionrate
dur-ing the omputer run, in order to obtain the same
visit probability for all energy levels, i.e. a at
dis-tribution along the energy axis, at the end. In this
ase,thevisitation probabilitytoeahpartiularstate
wouldbeproportionalto1=g(E). Theso-alled
multi-anonialmethods[17-19℄arebasedjustonthisfeature:
by reording the aeptane probability for
energy-inreasing movements E ! E 0
, aumulated during
therun andwhihmustbeequaltog(E)=g(E 0
tantglobalfatorwhihanelsinequation(2). BHM
is ompletely distint from multianonial approahes
in many features. In partiular, the infomations
ex-trated from eah E-state S belonging to the
averag-ing Markovian hain are the marosopi values of
N up
(S) and N dn
(S), not themere one-more-visit
up-grade V(E) ! V(E)+1. That is why BHM gives
moreaurateresultsthanmultianonialapproahes,
even taking into aount the same Markovian hain
of averagingstates, asshown in [15℄ where the
multi-anonialdynamis[18℄isadoptedinordertomeasure
< N up
(E) > and < N dn
(E) >. At the end, g(E) is
determined twie, byfollowingthemultianonial
tra-ditionalwayor,alternatively,bytheBHMequation(4),
bothusing data takenfrom thesameset of averaging
states. AlearaurayadvantageforBHMisreported
[15℄. Moreover,duetothemarosopiharaterofthe
BHM quantities N up
and N dn
this advantagestill
in-reasesforlargerandlargersystems.
Another ruial dierene relative to
multianoni-al approahes is that BHM requires only the
unifor-mity of visits among the states inside eah energy
level, separately, in order to get the orret
miro-anonial averages. BHM doesnot need any detailed
balanebetweenvisitstodierentlevelsEandE 0
,nor
the multianonial at distribution along the energy
axis. Any dynami strategy whih is good for
multi-anonialmethodswillbealsogood forBHM(besides
theaurayadvantagequotedin thelast paragraph),
but the reverseis nottrue. Thus, within BHM,other
not-so-restriteddynami strategiesouldbeused.
Protingfromthisfeature,wedeidedtotestavery
simpledynamistrategyinspiredbyreferene[20℄
(al-thoughwithinadierentmethod,thedynamirule
in-trodued in [20℄ is essentially the same as presented
hereafter). The idea is to avoid movement rejetions
at all,within theenergylevelurrentlybeingsampled
foraveragingpurposes. Rejetionswillberestritedto
otherenergies,whosestatesareneverinludedintothe
averagingstatistis. Let's onsiderthat themaximum
energyjump allowedby theadoptedprotoolof (real)
movementsorrespondston levelsaboveorbelowthe
urrent energy E. Then, let'stakean energy window
of 2n+1adjaentlevels, startingfrom somestate
in-sideit. Anymovementwhihkeepsthesystemstill
in-sidethiswindowwillbeaepted. Thisisthedynami
strategyweproposehere. Averages aretakenonlyfor
the entral level E inside the hosen energy window:
the systemisallowedto visit theother nlevelsabove
it, as well asthe n levels below it, nevertheless
with-outmeasuringanythingduring these side visits. Note
that no tossed movement will be rejeted, if the
ur-ompletely rejetion-free,avoidinganysystematibias
duetoartiialrejetionsrules. Thesamestrategyan
beeasilyappliedalsoforontinuousenergyspetra,by
takingaveragesonlywithinanarrow,rejetion-free
en-ergywindowenteredinsideanotherbroader,free-visit
window: anymovementtooutsidethislatterwouldbe
rejeted.
Inwhat follows,weonsideraLLsquare lattie
Ising ferromagnet, with L = 32 for whih the exat
funtion g(E)isknown[21℄. Theenergyoftheurrent
stateS isountedasthetotalnumberofitsunsatised
bonds, i.e. the total numberof neighbouringpairs of
spinspointingoneupandtheotherdown. Theenergy
spetrum orresponds to all even numbers between 0
and2;048,i.e. E=0,2,4,6,8:::2,048,whihanalso
berepresented byenergy densitiese =E=(2L 2
). The
degeneraies are g(E) = 2, 0, 2,048, 4,096, 1,057,792
:::2,respetively. Thisspetrumissymmetriin
rela-tionto itsenterat E
max
=1;024(ore=0:5),where
g(E
max
)6:310 306
. Weneedonlyitsrsthalf,
orre-spondingtopositivetemperatures. Theritialenergy
(atthethermodynamilimit)orrespondstoe
0:147
(E
300,forL=32).
We will adopt single-spin ips as the protool of
movements(bothfortherealmovementstossedduring
theomputerrun,aswellasforthevirtualoneswe
on-siderinordertoountN up
andN dn
). Startingfromthe
urrentstateSwithenergyE,1;024movementswould
beavailable,bytossingone randomspintoip. They
anbelassiedaordingtothepossibleenergyjumps,
E!EE,where E ouldbe0;2or 4. Thus, our
energy window will have5adjaent levels, theentral
one, E, where the averages will be measured, whih
isrejetion-free, plustwoneighbouringlevelsaboveit,
andtwoothersbelowit. Duringtherandomwalk
per-formed inside this window, we measure the values of
N up
and N dn
for the urrentstate, everytime its
en-ergyisE,andaumulatethemintotwoE-histograms
H up
(E)and H dn
(E). AlsoavisitounterV(E)is
up-gradedtoV(E)+1. Iftheenergyoftheurrentstateis
notE,nothingismeasuredoraumulated. Attheend,
wetaketheaverages<N up
(E)>=H up
(E)=V(E)and
< N dn
(E) >= H dn
(E)=V(E). Note that this is the
onlyroleplayedbythenalV(E): noomparisonwith
theneighbouringvaluesV(EE)isneeded,no
fur-therinformation is extrated from thesevalues. They
must onlybe largeenoughin order to provide agood
statistis. ForeahnewE, anew5-levelsenergy
win-dowenteredonitissampled,andthewholeproessis
repeated.
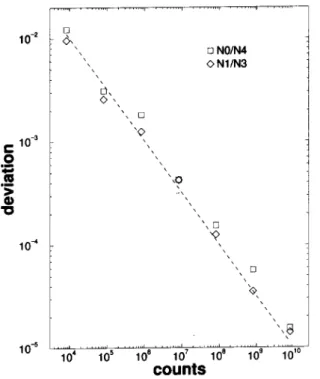
E)=g(E)℄for15adjaentlevelsE=300,302:::328,
at the ritial region. The deviations from the exat
valueswereaveraged(rootmeansquare)overthese 15
levels,andareshownasafuntionofthenumberof
av-eragingstatessampledinsideeahenergylevel(ounts),
in Fig. 1. Thesquares orresponds to E =4, while
the diamonds representE =2. Thedashedstraight
line (1= p
ounts) indiates that no systemati errors
besidesthenormalstatistialutuationsour,giving
redit to oursimpledynami rule. Aording tothese
results, to improvethe numerialaurayis asimple
matteroftakingmoreandmoreaveragingstatesinside
eahenergylevel,uptotheomputertimeavailable.
Figure1.Deviationsbetweenmeasuredg(E)andtheexat
values,asafuntionofthenumber(ounts)ofsampled
av-eragingstates. Thedashedlineorrespondsto1= p
ounts .
Datafor3232Isingferromagnet.
Inorder toperformthermalaverages,onedoesnot
need the same auray along the whole energy axis.
The funtion [g(E)exp( E=T)℄ 2
is displayed by the
dotted linein Fig. 2,whereT
=2:293930istheexat
loationofthe spei heat peak. This urvedisplays
the (squared) relative ontribution of eah energy to
thepartitionfuntion. Asthenumberofsampled
aver-aging statesinside eahenergylevelisproportionalto
the squarednumerialauray, thedottedline in
g-ure2showstheidealproleofvisitsoneneedsinorder
tohaveequallyaurateontributionsfromeahenergy
level. Itisasharppeakedurve,aordingtowhihthe
omputationaleortanbeonentratedonlyinsidea
narrowenergywindow. Protingfrom thisfeature, we
line,ingure2. Thepossibilityofdesigningthisprole
ofvisits,samplingdierentnumbersofaveragingstates
for dierentenergies, aordingto the relative
ontri-butionofeahenergyregion,isafurtherbigadvantage
of BHM overmultianonial methods. Almost all the
omputationaleortisonentratednear thepeak.
Figure2. Proleofvisitsalongtheenergyaxis,whihould
beshapedaordingtotheimportaneofeahenergy
on-tributiontothepartitionfuntion(dottedline).
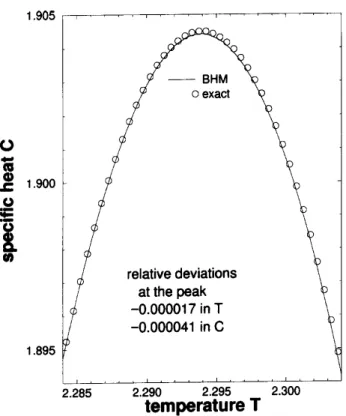
Fig. 3showsadetailed omparisonof our
simula-tional results with the exat spei heat urve, near
its peak. Being a derivative, whih orresponds to a
mathematialproedureinwhihnumerialaurayis
stronglyompromised,thisquantityisagoodstandard
for worst-ase omparisons, moreover near its peak.
Nevertheless, the relative deviations we obtained are
ompatiblewiththenumber(ounts=810 9
)of
av-eragedstatesperenergylevel,at thepeak. Moreover,
betteryet auraieswere obtainedalong allthe
tem-peraturerangefrom0to1,alwaysbyusingthesame
simulationaldata,i.e. thesameaveragedvaluesforthe
BHMquantitiesN up
andN dn
sin-Figure3. Detailofthespeiheatpeak,aworst-ase
omparison.
Inshort, we havetested asimple dynamis whih
is veryeÆientin measuringmiroanonialaverages.
It is essentially the same dynamis as introdued in
[20℄, for other purposes. Here, the aim is to measure
themiroanonialaveragesof somepartiular
maro-sopi quantities dened within the broad histogram
method [1-3℄. One one knows these averaged
quan-tities asfuntions of the energy, the method provides
theenergydegenerayfuntiong(E)throughanexat
relation. During the same omputer run, the
miro-anonialaverage<Q(E)>ofthequantityQof
inter-est is alsomeasured. Then, one oneknowsg(E)and
<Q(E)>,theanonialthermalaverage<Q>
T an
bedeterminedbyequation(2),forany,ontinuously
varyingtemperatureT,withoutresortingagainto
further omputer simulations. Aording to our
tests,theurrentdynamiruledoesnotintrodueany
systematiaveragingbias,besidesthenormalstatistial
utuationswhihdeayproportionallyto1= p
ounts.
Thus, by applying this dynami rule to BHM, to
im-provemoreand morethenumerialaurayisa
sim-ple matter of inreasing the omputer time. Among
the further advantages of the miroanonial
dynam-is tested here, we an quote: i) its implementation
simpliity, withoutdetailed balane andother
ompli-ations; ii) no movement-rejetions at all, within the
averagingenergylevel;iii)thepossibilitytoshapethe
desired auray; iv) no randomness at all is used in
order to deideto perform ornot theurrentlytossed
movement[22℄;v)short andnon-periodiwaitingtime
betweenonseutiveaveragingstates[24℄.
I am indebted to Kim Doohul who warned me
about referene [20℄, reading whih I have had the
ideatoapplyitsdynamirulestothebroadhistogram
method. D. Stauer was kind enough to perform a
ritial reading of the manusript. This work is
par-tially supported by Brazilianagenies CAPES,CNPq
andFAPERJ.
Referenes
[1℄ P.M.C. deOliveira,T.J.P.PennaandH.J. Herrmann,
Braz. J. Phys. 26, 677 (1996) (also in Cond-Mat
9610041).
[2℄ P.M.C.deOliveira,Eur.Phys.J.B6,111(1998)(also
inCond-Mat9807354).
[3℄ P.M.C.deOliveira,Braz.J.Phys.30,195(2000)(also
inCond-Mat0003300).
[4℄ P.M.C. deOliveira,T.J.P.PennaandH.J. Herrmann,
Eur. Phys. J. B1, 205 (1998); P.M.C. de Oliveira,
inComputerSimulationStudiesinCondensed Matter
PhysisXI,169,eds.D.P.LandauandH.-B.Shuttler,
Springer,Heidelberg/Berlin(1998).
[5℄ P.M.C.deOliveira,Int.J.Mod.Phys.C9,497(1998).
[6℄ J.-S.Wang, T.K.Tay andR.H.Swendsen,Phys.Rev.
Lett.82,476(1999).
[7℄ J.-S.Wang,Eur.Phys.J.B8,287(1999)(alsoin
Cond-Mat9810017).
[8℄ J.D. Mu~noz and H.J. Herrmann, Int. J. Mod. Phys.
C10, 95 (1999); Comput. Phys. Comm. 121-122, 13
(1999).
[9℄ R.H.Swendsen,B.Diggs,J.-S.Wang,S.-T.Li,C.
Gen-oveseandJ.B. Kadane,Int.J.Mod. Phys.C10,1563
(1999)(alsoinCond-Mat9908461).
[10℄ P.M.C. de Oliveira, Comput. Phys. Comm.121-122,
16 (1999), presented at the APS/EPS Conferene on
ComputationalPhysis,Granada,Spain(1998).
[11℄ J.-S. Wang, Comput. Phys. Comm. 121-122, 22
(1999).
[12℄ A.R. de Lima, P.M.C. de Oliveira and T.J.P. Penna,
SolidStateComm.114,447(2000)(alsoinCond-Mat
9912152).
[13℄ J.-S.WangandL.W.Lee,Comput.Phys.Comm.127,
131(2000)(alsoinCond-Mat9903224).
[14℄ J.-S.Wang,Prog.Theor.Phys.Supp.138,454(2000)
(alsoinCond-Mat9909177).
[15℄ A.R.deLima,P.M.C.deOliveiraandT.J.P.Penna,J.
Stat.Phys.99,691(2000)(alsoinCond-Mat0002176).
[17℄ B.A. Berg and T. Neuhaus, Phys. Lett. B267, 249
(1991); A.P. Lyubartsev, A.A. Martsinovski, S.V.
ShevkunovandP.N.Vorontsov-Velyaminov,J.Chem.
Phys.96,1776(1992);E.Marinari andG.Parisi,
Eu-rophys. Lett.19, 451(1992); B.A. Berg, Int.J. Mod.
Phys.C4,249(1993).
[18℄ J.Lee,Phys.Rev.Lett.71,211(1993).
[19℄ B. Hesselbo and R.B. Stinhombe, Phys. Rev. Lett.
74,2151(1995).
[20℄ K.-C.Lee,J.Phys.A23,2087(1990).
[21℄ P.D.Beale,Phys.Rev.Lett.76,78(1996).
[22℄ Withinsingle-spinips,forinstane,randomnumbers
are used only to toss whih spin would be ipped, a
oarse grained deision onerning onlyinteger
num-bers. One doesnot need to ompare them with
pre-iselydenedaeptaneratios,adeliateomparison
betweenrealnumberswhihouldintrodueundesired
biasesasin
[23℄ A.M.Ferrenberg, D.P.LandauandY.J. Wong, Phys.
Rev.Lett.69,3382(1992).
[24℄ Inthepresentaseofa3232lattie,anewstatewas
sampledafterevery40spinips,inaverage,instead
ofL 2