Nonequilibrium Kineti Ising Models:
Phase Transitions and Universality
Classes in One Dimension
Nora Menyhard
and Geza
Odor
ResearhInstitute forSolidState PhysisandOptis,
H-1525Budapest,P.O.Box49,Hungary
Researh InstituteforTehnialPhysisandMaterialsSiene,
H-1525 Budapest,P.O.Box49, Hungary
Reeived1Deember1999
NonequilibriumkinetiIsingmodelsevolving undertheompetingeetofspinipsatzero
tem-peratureandKawasaki-typespin-exhangekinetisatinnitetemperatureT areinvestigatedhere
inonedimensionfromthepointofviewofphasetransitionandritialbehaviour. Branhing
anni-hilatingrandomwalkswithanevennumberofospring(onthepart oftheferromagneti domain
boundaries),isadeisiveproessinformingthesteadystateofthesystemforarangeofparameters,
inthefamilyofmodelsonsidered. Awidevarietyofquantitiesharaterizetheritialbehaviour
ofthesystem.Resultsofomputersimulationsandofageneralizedmeaneldtheoryarepresented
anddisussed.
I Introdution
The Ising model is a well known stati, equilibrium
model. Its dynamial generalizations, the kineti
Ising models, were originally intended to study
relax-ationalproessesnearequilibriumstates[1,2℄. Glauber
introdued the single spin-ip kineti Ising model,
while Kawasaki onstruted a spin-exhange version
for studying the ase of onserved magnetization. To
hek ideas of dynami ritial phenomena [3℄ kineti
Ising models were simple enough for produing
ana-lytial and numerial results,espeially in one
dimen-sion,wherealsoexatsolutionsouldbeobtained,and
thushaveproventobeausefulgroundfortestingideas
and theories [4℄. On the other hand, when attention
turnedtonon-equilibriumproesses,steadystates,and
phasetransitions,kinetiIsingmodelswereagainnear
athand. NonequilibriumkinetiIsingmodels,inwhih
the steady state is produed by kineti proesses in
onnetion with heat baths at dierent temperatures,
have been widely investigated [5-8℄, and results have
shown that various phasetransitions are possible
un-der nonequilibrium onditions, even in one dimension
(1d) (forareviewseetheartilebyRazinRef. [9℄.
Alsointheeldoforderingkinetis,universalityis
strongly inuenedbythe onservedornon-onserved
harater of the order parameter. The saling
be-areofentral importane. Kineti Isingmodelsoera
usefullaboratoryagain toexplore thedierentfators
whihinuene theseproperties[10℄.
Mostofthesestudies,however,havebeenonerned
with the eets the nonequilibrium nature of the
dy-namismightexertonphasetransitionsdrivenby
tem-perature. In some examples nonloal dynamis an
generatelong-rangeeetiveinterationswhihleadto
mean-eld(MF)-type phasetransitions(see, e.g.,Ref.
[9℄).
A dierent line of investigating nonequilibrium
phasetransitions has been via branhing annihilating
randomwalk(BARW) proesses. Here partiles
ho-sen at random arry out random walks (with
proba-bility p) and annihilate pairwise on enounter. The
inrease of partiles is ensured throughprodution of
n ospring, with probability 1 p. Numerial
stud-ieshaveledto theonlusionthat ageneralfeature of
BARW is a transition as a funtion of p between an
ative stationary state with non-zero partile density
and an absorbing, inative one in whih all partiles
areextint. Theparityonservation ofpartilesis
de-isiveindeterminingtheuniversalitylassofthephase
transition. In the odd-n ase the universalitylass is
thatofdiretedperolation(DP)[11℄,whiletheritial
numer-andTretyakov[13℄. Thisnewuniversalitylassisoften
alled parity onserving(PC)(however,other authors
allittheDI[14℄orBAWelass[15℄);wewillalsorefer
to itbythisname. A oherentpitureofthis senario
isprovidedfromarenormalizationpointofviewin[16℄.
TherstexampleofthePCtransitionwasreported
byGrassbergeret al.[17,18℄,whostudied probabilisti
ellular automata. These 1d models involve the
pro-esses k ! 3k and 2k ! 0 (k stands for kink), very
similar to BARW with n = 2. The two-omponent
interating monomer-dimer model introdued by Kim
andPark[14℄representsamoreomplexsystemwitha
PCtypetransition. Otherrepresentativesof thislass
arethethree-speiesmonomer-monomermodelsof[15℄,
andageneralizedDomany-KinzelSCA[19℄,whih has
twoabsorbingphasesandanativeone.
AlassofgeneralnonequilibriumkinetiIsing
mod-els(NEKIM)withombinedspinipdynamisatT =
0andKawasakispinexhangedynamisatT =1has
beenproposedbyoneoftheauthors[20℄inwhih,fora
rangeofparametersofthemodel,aPC-typetransition
takesplae. Thismodelhasturnedouttobeveryrih
inseveralrespets. AsomparedtotheGrassbergerCA
models, in NEKIM the rates of random walk,
annihi-lation and kink-produtionanbeontrolled
indepen-dently. Italsooersthesimplestpossibilityofstudying
the eet of a transition whih ours on the level of
kinks upon the behaviour of the underlying spin
sys-tem. Thepresentreviewisintendedtogiveasummary
oftheresultsobtainedviaomputersimulationsofthe
ritialpropertiesof NEKIM [21-25℄. Dynamial
sal-ingandageneralizedmeaneldapproximationsheme
havebeenappliedintheinterpretation. Somenew
vari-ants ofNEKIM arealso presentedhere, togetherwith
new high-preisiondata for some of the ritial
expo-nents.
II Non- equilibrium kineti
Ising model (NEKIM)
A. 1d Ising model
BeforegoingintothedetailsofNEKIM,letusreall
somewellknownfatsabouttheone-dimensionalIsing
model. Itisdened onahainoflengthL;the
Hamil-tonianinthepreseneofamagnetieldH isgivenby
H=3D J P
i s
i s
i+1 H
P
i s
i ,(s
i
=1). Themodel
doesnothaveaphasetransitionintheusualsense,but
whenthetemperatureT approaheszeroaritial
be-haviour is shown. Speially, p
T = e
4J
k T
plays the
roleof T T
T
in1d,andintheviinityofT =0ritial
exponentsanbe dened aspowersofp
T
. Thus, e.g.,
theritialexponent oftheoherenelengthisgiven
through /p
T
. Conerning statis,from exat
so-lutions,keepingtheleading-ordertermsforT !0,the
ritialexponentsof(k
B
T times)thesuseptibility,the
oherene length and the magnetisationare known to
be
s
= = 1=2, and
s
= 0, respetively. We an
say thatthe transitionis of rstorder. Fisher's stati
salinglaw
s
=d 2
s
isvalid.
The Ising model possesses no intrinsi dynamis;
with the simplest versionof Glauberkinetis (see
be-low)itis exatlysolvableandthedynami ritial
ex-ponentZ denedviatherelaxationtimeofthe
magne-tizationas =
0
Z
hasthevalueZ=2. (Here
0 isa
harateristitimeoforderunity.)
Turningbaktostatis,ifthemagnetielddiers
from zero themagnetization is alsoknownexatly; at
T =0thesolutiongives:
m(T =0;H)=sgn(H): (1)
Moreover,for 1andH=kT 1theexatsolution
reduesto
m2h; h=H=k
B
T: (2)
Insalingformonewrites:
m
s
g(h
) (3)
whereisthestatimagnetiritialexponent.
Com-parisonofeqs. (2)and(3)resultsin
s
=0and=.
ItislearthatthetransitionisdisontinuousatH =0
aswell[i.e.,uponhangingthesignofH inEq. (1)℄. In
the following theorder of limits will always bemeant
as: (1)H !0,andthen(2)T !0.
B. Denition of the model
A general form of the Glauber spin-ip transition
ratein one-dimension forspin s
i
sittingat sitei is [1℄
(s
i =1):
W
i =
2 (1+Æs
i 1 s
i+1 )
1
2 s
i (s
i 1 +s
i+1 )
(4)
where =tanh2J=kT , withJ denotingthe oupling
onstantintheferromagnetiIsingHamiltonian, and
Æarefurtherparameterswhihan,ingeneral,also
de-pend on temperature. (Usually the Glauber model is
understood asthespeialaseÆ=0, =1,while the
Metropolismodel[26℄isobtainedbyhoosing =3=2,
Æ= 1=3). Therearethreeindependentrates:
w
same =
2
(1+Æ)(1 ) (5)
w
oppo =
2
(1+Æ)(1+) (6)
w
indif
wherethesubsriptssame,et.,indiatethethree
pos-sible neighborhoods ofagivenspin(""";#"#and ""#,
respetively). InthefollowingT =0willbetaken,thus
=1,w
same
=0and ,Æareparameterstobevaried.
The Kawasaki spin-exhange transition rate of
neighbouringspinsis:
w
i;i+1 (s
i ;s
i+1 )=
p
ex
2 (1 s
i s
i+1 )[1
2 (s
i 1 s
i +s
i+1 s
i+2
)℄: (8)
d
AtT =1(=0)theaboveexhangeissimplyan
unonditionalnearestneighborexhange:
w
i;i+1 =
1
2 p
ex [1 s
i s
i+1
℄ (9)
where p
ex
istheprobabilityofspinexhange.
The transition probabilities in Eqs. (4) and (9)
are responsible for the basi elementary proesses of
kinks. Kinksseparatingtwoferromagnetially ordered
domainsanarryoutrandomwalkswithprobability
p
rw /2w
indif
= (1 Æ) (10)
while twokinks at neighbouringpositions will
annihi-latewith probability
p
an /w
oppo
= (1+Æ) (11)
(w
same
isresponsibleforreationofkinkpairsinsideof
ordereddomainsat T 6=0).
In aseof thespin exhanges, whih also at only
at domainboundaries,theproessofmainimportane
here is that a kink an produe two ospring at the
nexttimestepwithprobability
p
k !3k /p
ex
: (12)
The above-mentionedthree proesses ompete, and it
depends onthe valuesof the parameters , Æ and p
ex
whattheresultofthisompetitionwillbe. Itis
impor-tanttorealizethattheproessk!3kandevelopinto
propagatingospringprodutiononlyifp
rw >p
an ,i.e.,
the new kinks are able to travelon the average some
lattie points away from their plae of birth, and an
thus avoidimmediate annihilation. Itisseenfrom the
abovedenitionsthatÆ<0isneessaryforthisto
hap-pen. Intheoppositeasetheonlyeet ofthek!3k
proessontheusual Isingkinetisis tosoftendomain
walls. This heuristi argumentis supported by
simu-lations aswellastheoretialonsiderations, aswill be
C. Phase boundary of the PC transition
in NEKIM
Inallofourinvestigationswehaveonsidereda
sim-pliedversionoftheabovemodel,keepingonlytwo
pa-rametersinsteadofthreebyimposingthenormalization
onditionp
rw +p
an +p
k !3k
=1,i.e.,
2 +p
ex
=1: (13)
Intheplaneofparametersp
ex
and Æ=
pr w=pan 1
p
r w =p
an +1
the
phasediagram,obtainedbyomputersimulation,isas
shownin Fig. 1. There isalineofseond-orderphase
transitions, the order parameter being the density of
kinks. The phaseboundary was obtainedby
measur-ing(t), the density of kinks, startingfrom arandom
initial distribution, and loating the phase transition
pointsvia (t)/t
with =:28:01. The lattie
was typially L = 2000 sites; we generally averaged
over 2000 independent runs. The dotted vertialline
in Fig. 1 indiates the ritial point that we
investi-gated in greater detail; further ritial harateristis
weredeterminedalongthisline.
Figure1. Phase diagramofthetwo-parametermodel. The
ative phase lies above the boundary. The dotted
verti-alline indiatesthe ritial point that we investigatedin
greaterdetail.
Theline ofphasetransitionsseparatestwokindsof
steadystates reahable bythe systemfor large times:
in one of thepossibleferromagnetistatesof all spins
up or all spins down, while the ative phase is
disor-dered, from thepointof viewof theunderlying spins,
duetothesteadilygrowingnumberofkinks.
For determining the phase boundary, as well as
other exponents disussed below, we used the
sal-ingonsiderationsof Grassberger[17,18℄. The density
(x;t;)ofkinkswasassumedtofollowthesalingform
(x;t;)/t
(x 1=?
;t 1=
k
) (14)
Here measuresthe deviationfrom theritial
proba-bilityatwhihthebranhingtransitionours,
? and
k
areexponentsofoherenelengthsinspaeandtime
diretions,respetively. Bydenition,
k =
?
Z,where
Z is thedynami ritialexponent. (a;b) isanalyti
neara=0andb=0. UsingEq. (14)thefollowing
re-lationsanbededued. Whenstartingfromarandom
initialstatetheexponent haraterizesthegrowthof
theaveragekink densityintheativephase:
()= lim
t!1
(x;t;)/
(15)
while the derease of density at the ritial point is
givenby
(t)/t
: (16)
Theexponentsareonnetedbythesalinglaw:
=
k
=
?
Z (17)
The phase boundary shown in Fig. 1 was
identi-edusing Eq. (16)[20℄. Theinitialstatewasrandom,
withzeroaveragemagnetization. At theritialpoint
marked on the phase boundary we reently obtained
thevalue =:280(5). This point washosen in a
re-gionoftheparameters(p
ex
;Æ),wheretheeetof
tran-sientsin time-dependent simulationsis small. Critial
exponentswere measuredaroundthepoint: =0:35,
Æ
= 0:395:001and p
ex
=0:3. Thedeviation from
the ritial point was taken in the Æ-diretion. It
is worth noting that in all of our simulations of the
NEKIM rule, spin-ips and spin-exhanges alternated
at eah time step. Spin-ips were implemented
us-ingtwo-sublattieupdating,whileLexhangeattempts
were ountedas one time-stepfor exhangeupdating.
The numerial value of the phase transition point is
sensitive to the manner of updating (thus, e.g., with
random-sequential updating in both proesses, j Æ
j
dereasesbymorethantenperentatthesamevalues
of andp
ex ).
Conerning, wearriedoutquitereentlya
high-preision numerial measurement; the result is shown
determinedtheeetiveexponent
eff
(),whihis
de-nedastheloalslopeof()inalog-logrepresentation
betweenthedatapoints(i 1;i)
eff (
i )=
ln(
i
) ln(
i 1 )
ln
i ln
i 1
; (18)
where
i =Æ
Æ
i
,providinganestimate
=lim
!0
eff
(): (19)
As shown in Fig. 2, the eetive exponent inreases
slowly and tends towards the expeted PC value as
! 0. A simple linear extrapolation yields the
esti-mate =0:95(2).
Figure 2. Eetive exponent
eff
near the ritial point.
Simulations were performed on a 1d NEKIM ring of size
L=24000. Averagingwasdoneafterthe steadystatewas
reahedforonethousanddatapointsand10 4
independent
samples.
Thetransientsmentionedabovein onnetionwith
thetime-dependentsimulationsshowupforsmalltimes
and arepartiularly disernibleat thetwoendsof the
phaseboundary,wherethespin-ip andspin-exhange
proesseshaveverydierenttimesales. For this
rea-son, near p
ex
= 1:0, where we get loseto Æ =0 (the
Glauberase),itisverydiÆulttogetreliable
numer-ialestimates,evenfor;theexponenthasbeenfound
to grow slowly with time, from a value near zero at
smalltimes. Itisimportanttonotiethataordingto
Eq. (13),p
ex
=1is approahedtogether with !0;
thus pex
!1,asotherwiseÆ
=0annotbereahed.
Severalrunswithdierentparametervalues[inluding
aseswithouttherestrition,Eq. (13)℄,havebeen
per-formed in this Glauber limit; all show that the Æ =0
aseremains Ising-likeforallvaluesof andp
ex : the
exponent tends to 0:5 for late times. Wetherefore
onjetured[20℄thattheasymptoteofthephase
bound-aryisÆ=0forp
ex
=1:0,andthusthatp
rw >p
In a reent paper, using exat methods,
Mussaw-isade,SantosandShutz[27℄onrmedtheabove
on-jeture. Theseauthorsstudyaone-dimensionalBARW
model with an even number of nearest-neighbour
o-spring. Theystartwith spinkinetis;intheirnotation
D, and are the rates of spin diusion,
annihila-tion andspin-exhange, respetively, andtransformto
a orresponding partile (kink) kinetis to arrive at a
BARW model. (In theirnotation D = p
RW
, =p
an
and=2p
ex .)
Usingstandardeld-theoretitehniques,
Mussaw-isadeetal. deriveddualityrelations
~
=; (20)
~
D=+; (21)
~
=D (22)
whihmapthephasediagramontoitselfinanontrivial
way and divide the parameter spae into two distint
regionsseparatedbytheself-dualline :
D=+: (23)
Theregionsmappedontoeahotherhave,ofourse,the
samephysial properties. Inpartiular,theline =0
mapsontothelineD=andthefast-diusionlimitto
thelimit!1. Inthefastdiusionlimittheauthors
ndthatthesystemundergoesamean-eldtransition,
butwithpartile-numberutuationsthatdeviatefrom
those givenby the MF approximation. Sothe nature
ofthephasetransitioninthislimitisnotPCbutMF.
The observation that for largeD, any small brings
the system into the ativephase, together with
dual-ity, preditsaphase transition at D =, in the limit
!1. The exatresultof [27℄ onrms the
onje-ture-stemmingfromoursimulations-ontheloation
of the phasetransition point in thephase diagram of
NEKIMin thelimitp
ex
!1,whihisindeed atÆ=0.
TheduallimitD!1overstheneighbourhoodofthe
pointÆ= 1,p
ex
=0. Thisresultpreditsaninnite
slopeof thephaseboundary in this representation,at
this point,asisalsoapparentin Fig.1. Itisimportant
tonotiethatthedualitytransformationdoesnot
pre-serve the normalization ondition of NEKIM, eq(13),
used in allofournumerialstudies. Theself-dualline
of[27℄D=+,whihintermsofourparametrization
reads
Æ= 2p
ex
1 p
ex
(24)
doesnot onserve the above-mentioned normalization
ondition either. In the phase diagram of Fig. 1 it
orrespondstoalinewhihstartsat(0;0)andendsat
(1=3; 1)in the(p ;Æ)plane.
Finally, in ref. [27℄ a proportionality relation
be-tween the (time-dependent) kink density for a
half-lledrandominitialstate,andthesurvivalprobability
of twosingle partiles in an initially otherwise empty
systemhasalso beenderived. Conerning the
respe-tiveritialexponentsandÆ(thelatterbeingdened
through the ritial behaviour of the survival
proba-bility P(t) / t Æ
), they havebeen shown to oinide
withintheerrorofnumerialsimulationsin[24℄,as
re-quiredbysaling.
D. Long-range initial onditions
Thesymmetrybetweenthetwoextremeinitalases
in time dependent simulations (single seed versus
ho-mogeneousrandomstate) onerning thekink density
deay inspiredusto investigateinitial onditionswith
long-rangetwo-pointorrelationsintheNEKIMmodel.
Thisproedurewasshowntoauseontinuously
hang-ingdensity deayexponentsin aseof DP transitions
[28℄. In this way it has been possible to interpolate
ontinuouslybetweenthetwoextremeinitialases.
In the present ase we have started from initial
states ontaining an even number of kinks to ensure
kinknumberonservation mod 2and possessing
kink-kink orrelations of the form < k
i k
i+x
> / x (1 )
with lying in the interval (0;1). Here k
i
denotes a
kink at site i. These states have been generated by
thesameserialalgorithmasdesribedandnumerially
testedinref. [28℄.
Thekinkdensityinsurvivingsampleswasmeasured
in systemsofL=12000sites, forupto t
max
=80000
time steps; we observe good quality of saling overa
timeintervalof three deades (80;80000)(see Fig. 3)
[32℄.
Asone ansee, thekinkdensityinreaseswith
ex-ponent0:28for =0,where inprinipleonlyone
pairof kinksisplaedonthelattieowingto thevery
shortrangeorrelations. Withouttherestritionto
sur-vivingsampleswewouldhaveexpetedaonstant,the
above exponent orresponds to dividingthe kink
den-sity by the survival probability, P(t) / t Æ
and the
abovevalueisinagreementwithourformersimulation
resultsforÆ[24℄.
In theother extreme ase for =1 thekink
den-sitydeayswithwithanexponent 0:28,againin
agreement with our expetations in ase of a random
initial state [20℄. In between the exponent hanges
linearly as a funtion of and hanges its sign at
= 0:5. This means that the state generated with
= 1=2 is very near to the situation whih an be
Figure3.log(
k ink
(t))versuslog(t)inNEKIMsimulations
for initialonditions with=0;0:1;0:2:::;1(from bottom
totop).
Wementionedattheendofthelastsetionthatthe
dualitytransformation of ref.[27℄preditstheequality
oftheabovetwoextremalexponents(thoughitalso
fol-lowsfromsaling). Oneanmaketheonjeturethatin
greatergeneralitythe duality transformation may
on-net also ases with initial two-point orrelation
expo-nents: $(1 ).
E. Variants of the NEKIM model
1. Varying exhange-range model
NowwegeneralizetheoriginalNEKIMmodelby
al-lowingtherangeofthespin-exhangetovary. Namely,
Eq. (9)isreplaedby
w
i;i+k =
1
2 p
ex [1 s
i s
i+k
℄; (25)
where i isarandomly hosensiteand s
i
isallowedto
exhangewiths
i+k
withprobabilityp
ex
. Sitekisagain
randomly hosenin theinterval1R , R beingthus
therangeofexhange. Thespin-ippartofthemodel
willbeunhanged.Wehavearriedoutnumerial
stud-ies with this generalizedmodel [21℄ in order to loate
the lines of Ising-to-ative PC-type phase transitions.
The method of updating was as before. It is worth
mentioning, that besidesk !3k, the proessk !5k
an also our forR 3, and the newkink pairsare
notneessarily neighbors. The harater of the phase
transition line at R >1 is similar to that for R = 1,
exept that the ative phase extends, asymptotially,
downto Æ =0.
Figure 4. Phase diagram of NEKIM for Æ
(R ;p
ex ) and
a) R = 1, and b) R = 3, as a funtion of p
ex (with
2 =1 p
ex
),andfor) =0:35(p
ex
=0:3)asafuntion
of(R =1+R) 4
(fullline).
This isillustrated in Fig. 4, where besides R =1,
the ase R = 3is also depited: the ritial value of
Æ
is shown as a funtion of p
ex
[urves a) and b)℄.
Moreover, Æ
asafuntionofR isalsoshownat
on-stant =:35 . Theabsissahasbeensuitablyhosen
to squeeze the whole (innite) range of R between 0
and 1 and for getting phase lines of omparable size
(hene the power4 of R =(1+R ) in aseof urve)).
Thephaseboundarieswereobtainedbymeasuring(t),
thedensityofkinks,startingfromarandominitial
dis-tribution and loating the phase transition points by
(t) / t
with =0:27:04. Wetypially used a
system ofL =2000 sites and averagedover500
inde-pendentruns.
Besides the ritial exponents we have also
deter-minedthehangeof Æ
with1=Rnumeriallyatxed
=:35;p
ex
= :3. Overthe deadeof R = 4 40 we
havefound
Æ
2:0(1=R ) 2
; (26)
whih is reminisent of a rossovertype behaviour of
equilibrium and non-equilibrium phasetransitions [4℄,
herewith rossoverexponent1=2. It should be noted
here,thattogetlosertotheexpetedÆ
MF
=0,longer
hains (weused lvaluesupto 20000)and longerruns
(here up to t = 510 4
) would have been neessary.
The former to ensure l R [29℄ and the latter to
overome the long transients present in the rst few
deades of time steps. Inwhat follows wewill always
refertotheMF limitin onnetionwithp
ex
!1(i.e.,
p
ex
= !1), forthesakeofonreteness, butkeepin
2. Cellular automatonversionof NEKIM
Another generalization is the probabilisti
ellu-lar automaton version of NEKIM, whih onsists in
keepingtheratesgivenin eqs.(7)and presribing
syn-hronousupdating. Vihnia[30℄investigatedthe
ques-tion how well ellular automata simulate the Ising
model with the onlusion that the unwanted
feed-bak eets present at nite temperatures are absent
atT =0andthegrowthofdomainsisenhaned;
equi-librium isreahedquikly. Inthelanguageof Glauber
kinetis,thisreferstotheÆ0ase.
With synhronous updating, it turns out that the
T =0Glauberspin-ip partofNEKIM itselfleadsto
proesses of the type k ! 3k, and for ertain values
of parameter-pairs( ;Æ) with Æ < 0,a PC-type
tran-sition takesplae. For =:5the ritialvalueof Æis
Æ
= :425(5), while e.g., for =:35;Æ
= :535(5).
For j Æj >j Æ
j the phase is the ative one,while in
the opposite aseit is absorbing. All the
harateris-tiexponentsanbehekedwithamuhhigherspeed
than for theoriginal NEKIM. The phaseboundaryof
theNEKIM-CA in the( ; Æ)plane issimilar tothat
in Fig. 1exeptfor thehighestvalueof =1,Æ
=0
annot be reahed; the limiting value is Æ
= :065.
For the limit Æ = 0 Vihnia's onsiderations apply,
i.e., itisanIsingphase. Thelimitingase !0with
Æ
! 1is veryhard from the pointof viewof
simu-lations, moreoverthe ase = 0 is pathologial: the
initial spin-distribution freezes in. Theorresponding
phasediagramisshownin Fig. 5.
Figure5. PhasediagramoftheCAversionofNEKIM.The
phase transition pointshave been determinedinthesame
wayasfor Fig. 1.
3. NEKIM in a magneti eld
It has been shown earlier, in the framework of
a model dierent from NEKIM exhibiting a PC-type
phase transition[31℄, that upon breaking theZ
2
sym-ered. Inaseof theGlaubermodel asimilarsituation
ariseswiththeintrodutionofamagnetield. Inthe
preseneofamagnetieldtheGlaubertransitionrates
giveninSe. 2aremodiedso:
w h
indif
= w
indif (1 hs
i
); (27)
w h
oppo
= w
oppo (1 hs
i
); (28)
h = tanh( H
k
B T
) : (29)
Fig. 6showsthephase diagram of NEKIM in the
(h;Æ)plane[22℄,startingatthereferenePCpointfor
h=0usedinthispaper(Æ
= :395).
We haveapplied only random initial state
simula-tionsto ndthepointsof thelineof phasetransitions
(ritialexponents:=:17(2), =:26(2),
orrespond-ingtotheDPuniversalitylass,asexpeted.) Itisseen,
thatwith inreasing eld strengththe ritialpoint is
shiftedtomoreandmorenegativevaluesofÆ.
Finally, it is worth mentioning a further possible
varint of NEKIM - again without a magneti eld
-in whih the Kawasaki rate Eq. (8) is onsidered at
somenitetemperature,insteadofT =1,butkeeping
T =0in theGlauberdynamis. Asloweringthe
tem-peratureofthespin-exhangeproessatsagainstkink
prodution,theresultisthattheativephaseshrinks.
Forfurther detailsseeRef. [32℄.
Figure6. Phase diagram ofNEKIM inthe (h;Æ) planein
the preseneof anexternal magnetield. Parameters of
the transition probabilities: = :35;p
ex
=:3. Naturally,
thephasediagramanbedrawnsymmetriallyfornegative
III Generalized mean- eld
the-ory and Coherent anomaly
extrapolation
UsingtheCAversionofNEKIMdesribedinthe
previ-oussetionweperformedn-sitelustermean-eld
al-ulations(GMF)upto n=6,andaoherentanomaly
extrapolation(CAM), resultingin numerialestimates
for ritial exponents in fairly good agreement with
those of other methods. With this method we ould
also handle a symmetry-breakingeld that favors the
spin-ips inonediretion. ForthisSCAmodelwe
ap-plied the generalized mean-eld tehnique introdued
byGutowitz[33℄ andDikman[34℄ fornonequilibrium
statistial systems. Thisisbasedonthealulationof
transitionsofn-siteluster probabilitiesP
n (fs i g) as P t+1 n (s 1 ;:::;s
n
)=F(fP t
m (s
1 ;:::;s
m )g)=P
t n (s 1 ;:::s n ) (30)
where F is a funtion depending on the update rules
andthelastequationreferstooursolutioninthesteady
statelimit. Atthek-pointlevelofapproximation,
or-relationsarenegletedforn>k,that is,P
n (s
1 ;:::;s
n )
is expressed by using the Bayesian extension proess
[33,35℄.
P
n (s
1 ;:::;s
n )= Q j=n k j=0 P k (s 1+j ;:::;s
k +j ) Q j=n k j=1 P k 1 (s 1+j ;:::;s
k 1+j )
: (31)
Thenumberofindependentvariablesgrowsmoreslowly
than 2 n
1, owingto internal symmetries(reetion,
translation)oftheupdateruleandthe`blok
probabil-ityonsisteny'relations:
P
n (s
1 ;:::;s
n ) = X sn+1 P n+1 (s 1 ;:::;s
n ;s n+1 ); P n (s 1 ;:::;s
n ) = X s0 P n+1 (s 0 ;s 1 ;:::;s
n ):
The series of GMF approximations an now
pro-videabasisforanextrapolationtehnique. Onesuha
methodistheoherentanomalymethod(CAM)
intro-dued by Suzuki [36℄. Aording to the CAM (based
onsaling)theGMFsolutionforaphysialvariableA
(example the kink density)at agiven level (n)of
ap-proximation{in theviinity oftheritialpoint, Æ
{
anbeexpressedastheprodutofthemean-eld
sal-inglawmultipliedbytheanomalyfatora
n : A n =a n (Æ=Æ n 1) MF ; (32)
andthen-thapproximationofritialexponentsofthe
true singular behavior (
n
) an be obtained via the
salingbehaviorofanomaly fators:
a n n MF n (33)
wherewehaveusedthe
n =(Æ =Æ n Æ n =Æ )invariant
variable insteadof , thatwasintrodued tomakethe
CAMresults independent ofusing Æ
or1=Æ
oupling
([37℄). HereÆ
istheritialpointestimatedby
extrap-olationfromthesequeneapproximationsÆ n
. Sinewe
ansolvetheGMFequationsforn6,wehavetaken
intoaountorretionstosaling,anddeterminedthe
trueexponentswiththenonlinearttingform :
a n =b n MF n +
n MF+1
n
(34)
whereb andareoeÆientstobevaried.
Asdisussedin aprevioussetion,byduality
sym-metry thep
ex
=0axisis mapped into theÆ =0axis
andtheneighborhoodofthe(p
ex
=1;Æ=0)triritial
pointwhihanbewelldesribedbythemean-eld
ap-proximationstothe(p
ex
=0;Æ= 1)point. Therefore
this pointis also atriritial pointand themean-eld
resultsareappliablein theneighborhood.
A. Z
2
symmetriase
FirstweshowtheresultsoftheGMF+CAM
alu-lations withoutexternal eld. Forn=1,we havethe
traditionalmean-eldequationforthemagnetization:
dm=dt= Æ m(m 2
1) (35)
andforthekinkdensity:
d=dt=2Æ (1 3+2 2
) (36)
The stable, analyti solution of the kink density
ex-hibitsajump atÆ=0.
1 (1)=
1=2 : Æ<0
0 : Æ0
Then=2approximationgivesforthedensityofkinks,
(1), thefollowingexpression:
forÆ<0. ForÆ>0(1)=0,i.e., GMFstill preditsarst-ordertransition forÆ=0;thejump sizein (1) at
Æ=0,however,dereasesmonotoniallywithdereasing ,aordingto eq. (37).
Figure7. (1)asafuntionofÆasobtainedfromGMF forn=3;::;6inaseofa: =:35,b: =:05
The GMF equations an only be solved
numeri-ally for n > 2. We determined the solutions of the
n=3;4;5;6approximationsforthekinkdensityati).
=0:35(Fig. 7a)andofthen=3;4;5approximations
at ii). =0:05(Fig. 7b).
Asweansee,thetransitionurvesbeome
ontinu-ous,withnegativevaluesforÆ n
(Æ
n
denotesthevalueof
Æ inthen-th approximationfor whihthe
orrespond-ing (1) beomes zero). Moreover, j Æ n
j inreases
with growing n values. As inreasing n orresponds
todereasingmixing,i.e.,dereasingp
ex
,thetendeny
shownbytheaboveresultsisorret.
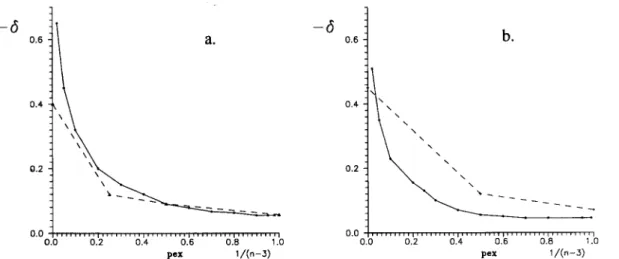
Figs. 8a) and 8b) show a quantitative - though
onlytentative-omparisonbetweentheresultsofGMF
and the simulated NEKIM phase diagrams. The
ob-tainedGMFdataforÆ n
,orrespondington=3;4;:::;6
( = 0:35) are depited in Fig. 8a) as a funtion of
1=(n 3), together with results of simulations. The
orrespondene between n and p
ex
washosen as the
simplestoneivableone. (NotethatÆ
6=0isobtained
rstforn=4.) Thesimulatedphasediagramwas
ob-tained without requiring the normalization ondition,
Eq. (13), at xed =0:35. In this ase, the Æ
=0
limit, of ourse, is not reahed and a purely
seond-order phase transition line an be ompared with the
GMFresults(fornvalueswherethelatteralsopredits
aseond-ordertransition).
Figure 8. Comparison between simulation results and GMF preditions. GMF results for Æ
are plotted as afuntion of
1=(n 3),whilesimulationresultsfor Æ
aredepitedasafuntionof p
ex
atonstant ,withR=3, =0:35inase(a),
Simulationsfor R = 3were found to lead to j Æ
j
valueslowenoughtotGMF data. The(polynomial)
extrapolation of GMFdata to n! 1(orresponding
to p
ex
=0, i.e.,plain spin-ip), alsoshownin Fig. 8,
ould be expeted to approah Æ = 1. That this is
not ase may be due to the irumstanes that upon
inreasingni) GMFstartsherefrom arst-orderMF
phase transition,whih ii) beomesseond-order, and
iii) GMFshould endupat thedualpointdisussed in
Se. II.C, while this symmetry is not inluded in the
appliedapproximationproedure. Fig. 8(b)showsthe
n = 3;4;5 results for = 0:05, whih are ompared
nowwiththeR=1simulationdata.
TheresultsofourGMFapproximationusefulfora
CAManalysisarethen=4;5;6data,whilethen=3
result an be taken to represent the lowest-order MF
approximation(withÆ
MF
=0)foraontinuous
tran-sition (no jump in
3
). For Æ
we use a polynomial
extrapolation.
In the n = 3 approximation the exponent =
1:0064,thus
MF
1. Consequently, asthetable
be-low shows, the anomaly fator doesnot depend on n.
This means,aordingto Eq. (33), that theexponent
isestimatedtobeequaltotheMFvalue '
MF =1.
TableI.CAMalulationresults
n
n
n
4 2:49043 0:01083
5 1:81022 0:01074
6 1:45766 0:01079
B. Broken Z
2
symmetryase
ThetransitionprobabilitiesofNEKIM,inthe
pres-eneofenexternalmagnetieldHhavebeengivenin
eqs.(27)-(29), in the previoussetion. Now we extend
the method for the determination of the exponent of
theorder-parameterutuationaswell:
()=L(< 2
> <> 2
) n
: (38)
The traditional mean-eld solution (n = 1) results in
stable solutionsforthemagnetization :
m
1 =
h
Æ
; if Æ<0 and h 2
=Æ 2
<1 (39)
m
1
= sgn(h); otherwise: (40)
andforthekink-onentration:
1 (1)=
1
2 (1 (
h
Æ )
2
); if Æ<0andh 2
=Æ 2
<1 (41)
1
(1)=0; otherwise: (42)
Forn>1thesolutionsanagainonlybefound
nu-merially. Inreasing the order of approximation, the
ritialpointestimatesÆ n
shifttomorenegativevalues
similarly totheH =0ase. Thelim
n!1 Æ
n
(h) values
havebeendeterminedwithquadratiextrapolationfor
h =0:01;0:05;0:08,and 0.1. The resulting urvesfor
n
(Æ) and
n
(Æ)are shown in Figs. 9(a) and (b),
re-spetively,for theaseofh=0:1 in dierentordersn
oftheGMFapproximation.
Naturally, these urves exhibit a mean-eld type
singularityattheritialpoint:
n
n (Æ=Æ
n
1)
MF
(43)
n
n (Æ=Æ
n
1)
MF
; (44)
with
MF
= 1 and
MF
= 1. The results of the
CAM extrapolation for various h-values are shown in
thetablebelow:
As to the aseh =0, weould not determine the
exponent
n
beause the low level GMF alulations
resulted in disontinuous phase transition solutions {
whih weannot usein theCAMextrapolation{and
sowehadtoofewdatapointstoahieveastable
non-lineartting. Higher-orderGMFsolutionswouldhelp,
butthatrequiresthesolutionofasetofnonlinear
equa-tions with morethan 72 independent variables. This
problemdoesnotourforh6=0;theaboveresults-
be-ingbasedonthefullsetofapproximations(n=1;:::;6)
-arefairlystable.
Table2. CAMalulationresults
h 0.0 0.01 0.05 0.08 0.1 DP PC
1.0 0.281 0.270 0.258 0.285 0.2767(4) 0.94(1)
Figure9. Thekinkdensity(a)and(b)theseondmomentofthekinkdensityintheneighbourhoodoftheritialpointÆ
(h)
forh=0:1. Theurvesfromrighttoleftorrespondton=1;:::;6(levelofGMFalulation). Thepointsweredetermined
witharesolutionof10 5
inÆ,inordertobeable toextratCAManomalyoeÆients.
IV Domain growth versus
luster growth properties;
Hypersaling
Intheeld ofdomain-growthkinetisithaslongbeen
aeptedthatthesalingexponentofL(t),the
hara-teristidomainsize,isequalto1=2iftheorder
parame-terisnotonserved. Intheaseofa1dIsingspinhain
of lengthL, the struture fator at the ferromagneti
Bragg peak is dened as: S(0;t) = L[< m 2
> <
m > 2
℄; m = 1
L P
i s
i , (s
i
=1). If the onditionsof
validityofsalingarefullled [38℄then
S(0;t))/[L(t)℄ d
; L(t)/t x
(45)
where now d = 1 and x = 1=2. Another quantity
usually onsidered [38℄ is the exess energy E(t) =
E(t) E
T (E
T
istheinternalenergyofamonodomain
sampleatthetemperatureofquenh),whihinourase
isproportionalto thekink density
(t)= 1
L <
X
i 1
2 (1 s
i s
i+1 )>;
whihfollows
(t)/ 1
L(t) /t
y
(46)
with y=1=2intheGlauber-Isingase, expressingthe
well known time dependene of annihilating random
walks (y = in the notation of setion 2.). Wealso
measured S(t) at the PC point and found power-law
behaviourwithanexponentx=0:575(5)[22℄.
Theseond harateristigrowthlengthatthe PC
pointisthelustersize,denedthroughthesquare-root
of <R 2
(t) >/ t z
. The latteris obtainedby starting
e.g.[12℄), or from a single kink [18,20℄. Both
length-exponentsare,howeveronnetedwithZ,thedynami
ritial exponent, sine at the PC transition the only
dominant length is the (time-dependent) orrelation
length. Itwasshownin[18℄and[39℄that z
2 =
1
Z
follows
fromsalingforone-kinkandtwo-kinkinitialstates,
re-spetively. In our simulationswealso found [22℄ that
x=1=Z,within numerialerror,atthePCpoint,and
thus
x=z=2 (47)
follows. Exponentsof lustergrowthareonnetedby
ahypersalingrelationrstestablishedbyGrassberger
anddelaTorre[40℄forthediretedperolation
transi-tion. ItdoesnotapplytothePCtransitioninthesame
form [12℄, where the dependene on the initial state
(oneortwokinks)manifestsitselfintwoluster-growth
quantities: thekink-numberN(t;)/t
f(t 1
? Z
) and
the survival probability P(t;) / t Æ
g(t 1
? Z
) (This
Æ has, of ourse, nothing to do with the parameterÆ
of NEKIM). In systems with innitely many
absorb-ing states, where Æ and depend on the density of
partilesintheinitialonguration,ageneralised
sal-ingrelationwasfoundto replaetheoriginal relation,
2Æ+ =z=2,namely[41℄:
2( 0
+) 1
? Z
+2 0
=z 0
(48)
whih is also appliable to the present situation. In
eq(48) 0
is dened through lim
t!1
P(t;) /
0
and
thesalingrelation 0
=Æ 0
?
Z holds. A prime onan
exponent indiates that it may depend on the initial
state. ForthePCtransitiontheexponentzhasproven
(withinerror)tobeindependentoftheinitial
Inaseofasinglekinkinitialstateallsamples
sur-vivethusÆ 0
=0,andviatheabovesalingrelationalso
0
= 0. Eq(48) then beomes: 2
?Z +2
0
= z. For
t ! 1, however, lim
t!1
N(t;) /
has to hold (
the steady statereahed annot depend onthe initial
stateprovidedsamplessurvive). Thususingtheabove
saling form forN(t;), =
? Z
follows,and the
hy-persalinglawanbeastintotheform:
4
? Z
=z: (49)
Startingwithatwo-kinkinitialstate,however, 0
=
and 0
= 0 holds [12℄. With these valuesEq. (48)
leadsagaintoEq. (49). Asz=2=Z,Eq. (49)involves
onlysuhquantities,whiharedenedalsowhen
start-ing with a random initial state. Using Eq. (17), Eq.
(49)beomes
2y=1=Z =x (50)
Inthiswaythefatoroftwobetweenxandyappearing
atthePCpointbetweentheexponentsofaspin-bound
andakink-boundquantity(andwhihhasbeenfound
also for avarietyof ritial exponents, see [22℄) ould
beexplainedasfollowingfrom(hyper)saling.
V Eet of thePC transition on
theproperties of the
underly-ing spin system
Time-dependentsimulations,nite-sizesalingandthe
dynamiearly-timeMCmethod[43℄havebeenapplied
to investigate thebehaviourof the1dspinsystem
un-dertheeetofthePCtransition. Wefound[22℄that
withinerrorofthenumerialstudies,thedynami
rit-ialexponent of thekinks Z and that of the spinsZ
agree, and have the value: Z = Z
= 1:75. Thus in
omparison with the Glauber-Ising value Z = 2:0, Z
dereases, as do and : = = :444 (instead of
1/2). The PC point is the endpointof aline of
rst-orderphasetransitions(bykeepingp
ex
and xedand
hangingÆthroughnegativevaluestoÆ
),where=0
stillholds,asdoesFisher'ssalinglaw: =d 2. To
obtainthesevaluesthePCpointhasbeenapproahed
fromthediretionofnitetemperaturesofthespin-ip
proess,byvaryingp
T =e
4J=k T
.
Thedynamialpersistenyexponentandthe
ex-ponent [44℄ haraterisingthe two-time
autoorrela-tionfuntionofthetotalmagnetizationunder
nonequi-librium onditions havealso been investigated
numer-ially at the PC point. It has been found that the
PCtransitionhasastrongeet: theproessbeomes
non-Markovianand theaboveexponentsexhibit
dras-tihangesasomparedtotheGlauber-Isingase[23℄.
Theseresultstogetherwithritialexponentsobtained
earlierin[22℄ aresummarizedinTableIII.
s
Z
Glauber-Ising 0 1=2 1=2 2 1=4 1
PC :00(1) .444(2) :444(2) 1.75(1) :67(1) 1.50(2)
TableIII.SimulationdataforstatianddynamiritialexponentsforNEKIM
Wehavealsoinvestigatedtheeet ofritial
u-tuations at the PC point on the spreading of spins,
and found the analogue of ompat direted
perola-tion (CDP) [46℄ to exist. Compat direted
perola-tion is known to appear at the endpoint of the
di-reted perolation ritial line of the Domany-Kinzel
ellular automaton in 1+1 dimensions [46℄.
Equiva-lently, suhatransition ours at zerotemperature in
amagnetield h,uponhangingthesignofh,inthe
one-dimensionalGlauber-Isingmodel,withwellknown
exponentsharaterisingspin-lustergrowth[42℄.
in the sea of downward spins (s(j) = 1 for j 6= i),
the exponentsÆ
s ,
s and z
s
aredened at the
transi-tion point bythe power-laws governingthe densityof
1'sn
s /t
s
, thesurvivalprobabilityP
s (t)/t
Æ
s
,and
themean-squaredistaneofspreading<R 2
s
(t)>t zs
.
Weobtained=0,Æ=1=2andz=1,in aordwith
the hypersalingrelation [42℄ in the form appropriate
forompatlusters:
s +Æ
s =z
s
=2 (51)
ouldbeexpeted. Butbasisimilaritiesremain. Thus
thetransitionwhihtakesplaeuponhangingthesign
of themagnetield isofrst-orderanditsexponents
satisfy Eq. (51). Aordingly it an be termed as
'ompat',andweallittheompatparity-onserving
transition (CPC).Forthephasediagram,seeFig. 10.
On the basis of Eq. (3), the t-dependene of the
magnetization insalingformmaybewrittenas
m(t;h)t
s
Z
~ g(ht
Z
) (52)
Wehaveinvestigated theevolutionofthe
nonequi-libriumsystemfromanalmostperfetlymagnetized
ini-tialstate(or ratheran ensemble ofsuh states). This
state is prepared in suh a way that asingle up-spin
is plaed in the sea of down-spins at L=2. Using the
languageofkinks this orrespondsto the usualinitial
stateof twonearestneighbourkinksplaedatthe
ori-gin. At theritial point thedensity of spinsis given
as
n
s
(t;h)t
s
g
1 (ht
Z
) (53)
for the deviation of the spin density from its initial
value, n
s
= m(t;h) m(0). The results are
summa-rizedin TableIV.
s
s 0
s
Æ
s
z
s
NGI-CDP 0 :99(2) 1=2 :0006(4) :500(5) 1(=2=Z)
CPC :00(2) :45(1) :49(1) .288(4) :287(3) 1:14(=2=Z)
TableIV.Spin-lusterritialexponentsforNEKIMin amagnetieldTheNGI-CDPdataareresultsof
simulationsatthepointÆ=0,p
ex =0:3
Figure10. Phase diagramofNEKIM inthe(h; ~
Æ) plane.
ThehosenPC-pointisat ~
Æ= 0:395. Forsmallervaluesof
~
Æ,intheGlauber-Isingregime,thevertiallineonneting
thePCandthenonequilibriumGlauberIsing(NGI)points
(ath=0)onsistsofallCDPpoints,withitsharateristi
ritial exponents. The simulations around the PC
tran-sition weredone for the interval0 h 0:1. The other
NEKIMparameters,inthewhole plane,are: =0:35and
p
ex =0:3.
Conerningstatiexponents,onlythemagneti
ex-ponent remains unhanged under the eet of the
ritialutuations. Thisisnotanobviousresult(see,
e.g., theoherene-length exponentabove).
s 0
,
har-aterizingthelevel-ovaluesofthesurvivalprobability
of thespinlustersisdened through
lim
t!1 P
s
(t;h)/h s
0
; (54)
thisisanewstatiexponentonnetedwithothersvia
thesalinglaw
s 0
= Æ
s Z
(55)
whih is satised by the exponents obtained
numeri-ally,withinerror.
VI Damage-spreading in
vesti-gations
Whiledamagespreading(DS) wasintrodued in
biol-ogy [47℄ it has beome an interesting topi in physis
as well [48-50℄. Themain questionis ifdamage
intro-dued in a dynamial system survives or disappears.
Toinvestigatethistheusualtehniqueistoonstruta
pairofinitialongurationsthatdieratasinglesite,
and let them evolvewith the samedynamis and
ex-ternal noise. This method has been foundveryuseful
foraurate measurementsof dynamialexponents of
equilibriumsystems[51℄.
In[25℄weinvestigatedtheDSpropertiesof several
1dmodelsexhibitingaPC-lassphasetransition. The
orderparameterthatwemeasuredinsimulationsisthe
Hammingdistanebetweenthereplias:
D(t)= *
1
L L
X
i=1 js
i s
;
i j
+
(56)
wheres
i
andthereplias ;
i
maydenotenowspinorkink
variables.
If there is aphase transition point, the Hamming
distanebehavesin apowerlawmanneratthatpoint.
Inaseofinitialreplias dieringat asinglesite(seed
simulations)thislookslike:
D(t)/t
Similarly the survival probability of damage variables
behavesas:
P
s (t)/t
Æ
(58)
and the average mean square distane of damage
spreadingfrom theentersalesas:
R 2
(t)/t z
: (59)
Inaseof theNEKIM model wehave investigated
theDSonboththespinandkinklevels. Wefoundthat
the damage-spreading point oinides with the
riti-al point, and that the kink-DS transition belongs to
thePC lass. The spindamage exhibits a
disontinu-ousphasetransition,withompatlustersandPC-like
spreadingexponents. Thestatiexponentsdetermined
bynite-sizesaling areonsistentwith thoseof spins
of the NEKIM model at the PC transition point and
thegeneralisedhypersalinglawissatised.
Byinspetingourlargedataset forvariousmodels
exhibitingmultipleabsorbingstates,weareledtoa
-nal onjeture: BAWe dynamis and Z
2
symmetry of
the absorbingstates together formthe neessary
ondi-tiontohaveaPC-lasstransition.
VII Summary
Thepresentpaperhasbeendevotedtoreviewingmost
of the authors' investigations of a nonequilibrium
ki-netiIsingmodel(NEKIM).
NEKIM has proven to be a good testing ground
forideas,espeially onnetedwithdynamialsaling,
in the eld of nonequilibrium phase transitions. The
eldoveredherebelongstothelassofabsorbing-state
phasetransitionswhihareusuallytreatedonthelevel
ofpartiles, thebest known examplesbeingbranhing
annihilatingrandomwalkmodels. Thephasetransition
on the level of kinks in the Ising system belongs the
the so-alledparity-onserving universalitylass. The
NEKIM model oers the possibility of revealing and
larifying features and properties whih takeplae on
the level of the underlying spin system as well. The
introdution of a magneti eld in the Ising problem
has also led to understand dierent features, e.g.,the
hange of theuniversalitylassfrom PC toDPin the
ritial behaviorat (and in the viinity of) the phase
transitionofkinks.
Investigations of various ritial properties have
beenarriedoutmainlywiththehelpofnumerial
sim-ulations(time-dependentsimulations,nite-sizesaling
and dynami early-time MC methods have been
ap-plied). In addition, a generalized mean-eld
approxi-a limiting situation of the phase diagram of NEKIM,
where the usually seond-order phase transition line
ends at aMF-typerst-order point. Someof the
rit-ialexponents,espeially that oftheorder parameter,
ouldbepreditedtohighaurayin thisway.
Whilefromthesideofnumerisalotofinformation
hasaumulatedoverthelastveyearsonerningthe
PCuniversalitylass,furtherinvestigationsareneeded
at themirosopilevel.
Aknowledgements
Theauthors would liketothanktheHungarian
re-searhfund OTKA (Nos. T-23791,T-025286 and
T-023552)forsupportduringthisstudy. Oneofus(N.M.)
would like to aknowledge support by SFB341 of the
Deutshe Forshungsgemeinshaft, during her stay in
Koln, where this work wasompleted. G.
O
aknowl-edges support from Hungarian researh fund Bolyai
(No. BO/00142/99)aswell. Thesimulationswere
per-formed partially on the FUJITSU AP-1000 and
AP-3000 superomputers and Aspex's System-V parallel
proessingsystem(www.aspex.o.uk).
Referenes
[1℄ R.J.Glauber, J.Math.Phys.4,191(1963).
[2℄ See,e.g.,K.KawasakiinPhaseTransitionsand
Crit-ialPhenomena,editedbyC.DombandM.S.Green
(AademiPress,NewYork,1972),vol.2.
[3℄ R.A.Ferrell,N.Menyhard,H.Shmidt,F.Shwabl,
andP.Szepfalusy,Phys.Rev.Lett.18,891(1967); B.
I.HalperinandP.C.HohenbergPhys.Rev.177,952
(1969).
[4℄ Z.RazandR.K.PZia,Phys.Rev.E49,139(1994),
andreferenestherein.
[5℄ A. DeMasi, P.A. Ferrari,and J.L. Lebowitz, Phys.
Rev. Lett. 55 1947 (1985); J. Stat. Phys. 44, 589
(1986).
[6℄ J.M.Gonzalez-Miranda,P.L.Garrido,J.Marro,and
J.L.Lebowitz,Phys.Rev.Lett.59,1934(1987).
[7℄ J.S.WangandJ.L.Lebowitz,J.Stat.Phys.51,893
(1988).
[8℄ M. Droz,Z. Razand J.Shmidt,Phys.Rev.A 39,
2141(1989).
[9℄ Z. Raz, \Kineti Ising models with ompeting
dy-namis: mappings, steady states and phase
transi-tions,"inNonequilibriumStatistialMehanisinone
Univer-[10℄ S. J. Cornell, \One-dimensional kineti Ising
mod-els at low temperatures - ritial dynamis, domain
growth and freezing," in Nonequilibrium Statistial
Physis in one Dimension, edited by V. Privman
(CambridgeUniversityPress, Cambridge,1996).
[11℄ Variouspapersondiretedperolationaretobefound
inPerolationStruturesandProesses,editedbyG.
Deutsher,R.ZallenandJ.Adler,AnnalsoftheIsrael
PhysialSoiety,Vol.5(Hilger,Bristol,1983).
[12℄ I.Jensen,Phys.Rev.E50,3623(1994).
[13℄ H.TakayasuandA. Yu.Tretyakov,Phys.Rev.Lett.
68,3060(1992).
[14℄ M. H. Kimand H. Park, Phys.Rev.Lett. 73, 2579
(1994);H.ParkandS.Kwon,thisvolume.
[15℄ K.E.BasslerandD.A.Browne,Phys.Rev.Lett.77,
4094 (1996); K.E.Basslerand D.A.Browne,Phys.
Rev.E55,2552(1997).
[16℄ J. Cardy and U.Tauber, Phys.Rev.Lett. 77, 4780
(1996).
[17℄ P. Grassberger, F.Krause, and T. vonder Twer, J.
Phys.A:Math.Gen. 17,L105(1984).
[18℄ P. Grassberger, J. Phys. A:Math.Gen. 22, L1103
(1989).
[19℄ H.Hinrihsen,Phys.Rev.E55,219(1997).
[20℄ N.Menyhard,J.Phys.A:Math.Gen.27,6139(1994).
[21℄ N. Menyhard and G.
Odor, J. Phys. A 28, 4505
(1995).
[22℄ N. Menyhard and G.
Odor, J.Phys.A: Math. Gen.
29,7739(1996).
[23℄ N. Menyhard and G.
Odor, J.Phys.A: Math. Gen.
30,8515(1997).
[24℄ N. Menyhard and G.
Odor, J.Phys.A: Math. Gen.
31,6771(1998).
[25℄ G.
Odor and N. Menyhard, Phys. Rev. E 57, 5168
(1998).
[26℄ N.Metropolis,A.W.Rosenbluth,M.N.Rosenbluth,
A.H. Teller,andE.Teller, J.Chem.Phys.21,1087
(1953).
[27℄ K.Mussawisade,J. E.Santos, and G.M. Shutz, J.
Phys.A31,4381 (1998).
[28℄ H. Hinrihsen and G.
Odor, Phys. Rev. E 58, 311
(1998).
[29℄ K. K. Mon and K. Binder, Phys. Rev. E 48, 2498
(1993).
[30℄ G.Y.Vihnia,PhysiaD10,96(1984).
[31℄ H.ParkandH.Park,PhysiaA221,97(1995).
[32℄ G.
Odor, A. Krikelis, G. Vesztergombi and F.
Rohrbah, Proeedings of the 7-th Euromiro
work-shop on parallel and distributed proessing,
Fun-hal (Portugal), edited by B. Werner, (IEEE
Com-puter soiety press, Los Alamos, 1999); e-print:
physis/9909054
[33℄ H.A.Gutowitz,J.D.Vitor,andB.W.Knight
Phys-iaD28,18(1987).
[34℄ R.Dikman,Phys.Rev.A38,2588 (1988).
[35℄ G. Szabo, A. Szolnoki, and L. Bodos, Phys. Rev.
A44,6375 (1991);G.
Odor,Phys.Rev.E 51,6261
(1995);G.SzaboandG.
OdorPhys.Rev.E59,2764
(1994),andreferenestherein.
[36℄ M.Suzuki,J.Phys.So.Jpn.55,4205(1986).
[37℄ M.KolesikandM.Suzuki,PhysiaA215,138(1995).
[38℄ A. Sadiq and K. Binder, Phys. Rev. Lett. 51, 674
(1983).
[39℄ P.Grassberger,J.Phys.A22,3673(1989).
[40℄ P.GrassbergerandA.delaTorre,Ann.Phys.(NY)
122,373(1979).
[41℄ J.F.F.Mendes,R.Dikman,M.Henkel,and M.C.
Marques,J.Phys.A27,3019 (1994).
[42℄ R.DikmanandA.Yu.Tretyakov,Phys.Rev.E52,
3218(1995).
[43℄ R.E.Blundell,K.Hamayun,andA.J.Bray,J.Phys.
A25,L733(1992);Z.B.Li,L.Shulke,andB.Zheng,
Phys.Rev.Lett.74,3396 (1995); L. Shulke andB.
Zheng,Phys.Lett.A204,295(1995).
[44℄ S.N.Majumdar,A.J.Bray,S.J.Cornell,andC.Sire,
Phys.Rev.Lett.77,3704(1996).
[45℄ H. K. Janssen, B. Shaub, and B. Shmittman, Z.
Phys.43,539(1989).
[46℄ E.DomanyandW.Kinzel,Phys.Rev.Lett.53,311
(1984).
[47℄ S.A.Kauman,J.Theor.Biol.22,437(1969).
[48℄ M.Creutz,Ann.Phys.167,62(1986).
[49℄ H.Stanley,D.Stauer,J.KerteszandH.Herrmann,
Phys.Rev.Lett.59,2326(1986).
[50℄ B.Derridaand G.Weisbuh,Europhys.Lett.4,657
(1987).