Ergodi Magneti Limiter for the TCABR
Elton C. daSilva, Iber^eL. Caldas,
Instituto deFsia,UniversidadedeS~aoPaulo
C.P.66318, 05315-970,S~aoPaulo,SP,Brazil.
and Riardo L. Viana
Departamento deFsia,Universidade FederaldoParana
C.P.19081, 81531-990,Curitiba,PR,Brazil.
Reeivedon3July,2001
Inthisworkitisonsideredtheeetofanergodimagnetilimiterontheplasmaonnedinthe
TCABRtokamak.Thepoloidaldistributionofthelimiterurrentsisdeterminedtakingintoaount
the toroidalgeometry of this tokamak. Theplasma equilibrium eld is analytially obtained by
solvingtheGrad-Shluter-Shafranovequationinpolartoroidaloordinates. Theperturbinglimiter
eldisobtainedasavauumeldbysolvingtheLaplaeequation.Supposingthelimiterationasa
sequeneofdelta-funtionpulses,asympletimapisderivedbyusingaHamiltonianformulation
for the perturbedeld line. Examples are givento illustrate the inuene of this design onthe
topologyoftheperturbedeldlinestruture.
I Introdution
Theplasmaonnementin tokamaks anbeimproved
by reatinga haoti eld line region whih dereases
theplasma-wallinteration[1,2℄. Thishaotiregionis
reated bysuitably designed resonantmagneti
wind-ings whih produe the overlapping of two or more
hainsofmagnetiislandsand,onsequently,the
mag-netisurfaesdestrution.
However,thosewindingshavetobeinstalledonthe
outsideofthevauumvessel,whihisoupiedby
sev-eraldiagnostis. ThisdiÆultyanbeoveromeby
us-ingasetofErgodiMagnetiLimiters(EML)that are
narrowsliesofhelialwindingsintheform ofurrent
rings,whiharemountedalongthetoroidaldiretion.
The rst oneptual and physial test of an EML
sheme was arried out on the Texas Experimental
Tokamak (TEXT)[3,4℄. Sine then EMLs havebeen
used inotherstokamaks [5,6℄asawayofpartileand
heat ontrolattheplasmaedge[7℄.
Furthermore,ithasreentlybeenreported[8,9℄that
runawayeletronavalanhesanbesuppressed by the
presene of radialdiusion. As the eletronswith
en-ergies higher thanthe thermal energyare more
sensi-tivetomagnetiutuationsitouldbehelpfulto use
EMLs inorder toimprovetheradialdiusionofthose
eletronsbyproduingaregionofhaotieldlines.
A suitable design of an EML ring depends on the
detailed knowledge of the toroidal geometry inuene
ontheequilibriumeld lineonguration.
In this work, we present a sympleti map that
desribes the ation of a set of EMLs for the
toka-makTCABR.
This map allows us to generate Poinare
ross-setions faster in omparison with those obtained
throughnumerialintegrationofeldlineequations.
Inaddition,the mapweobtainanberegardedas
aanonial transformation between angle-ation
vari-ables derived from a Hamiltonian formulation. It is
worth noting that this sympleti map embodies two
importantfeatures: (i)itomesstraightlyfromthe
ex-pressionsfor the magneti elds, and (ii) it preserves
themaintoroidalharateristisduetotheonnement
vesselgeometry.
This map has reently been used to investigate
anomalouseld line diusion and lossdue to ollision
withthetokamakwall[10℄;aswellastheonsetofhaos
andbifurationsofmagnetiaxes[11℄.
Ourpaperisorganizedasfollows. InsetionII,we
outlinetheequilibriumand perturbingmagneti elds
thatareusedinthiswork. InsetionIII,the
symple-timapforthesetofEMLsispresented. InsetionIV,
theinueneoftheEMLsonthemagnetisurfaesfor
theTCABRtokamakparametersisdisussed. Finally,
insetionV,ouronlusionsaresummarized.
II Magneti eld ongurations
The equilibrium magneti eld B
0
is alulated from
equi-libriumgivenbythefollowingsetofequations:
JB
0
=rp; (1)
rB
0 =
0
J; (2)
rB
0
=0; (3)
wherepandJaretheequilibriumpressureandurrent
density, respetively.
For an axisymmetri onguration, the above set
ofequationsisreduedtotheGrad-Shluter-Shafranov
equation, whih desribesthebehaviorof thepoloidal
magnetiux .
Toobtain ,in termsofthe polar toroidal
oordi-natesystem[12℄(r
t ;
t ;'
t
),weassume[13℄thefollowing
peakedurrentprole,ommonlyobservedintokamak
disharges: J 3 (r t )= I p R 0 0 a 2
(+1) 1 r 2 t a 2 ; (4)
inthisexpression,I
p
andaaretheplasmaurrentand
radius,respetively. Theradialpositionofthemagneti
axisintheylindrialoordinatesystemisR 0
0
andis
aonstant.
As a funtion of , the ontravariant omponents
oftheequilibriummagnetieldB
0 are: B 1 0 = 1 R 0 0 r t t ; (5) B 2 0 = + 1 R 0 0 r t r t ; (6) B 3 0 = 0 I e 2R 2 ; (7) where I e
is the external urrent that generates the
toroidalmagneti eld omponentand R isthe radial
oordinatein theylindrialsystem.
At lowest order in rt
R 0
0
, we obtain (r
t ) and
the followingequilibrium magneti eld ontravariant
omponents:
B 1
0
= 0; (8)
B 2 0 = B 2 a a 2 r 2 t " 1 1 r 2 t a 2 +1 # ; (9) B 3 0 = B 3 T 1 1 2 rt R 0 0 os( t ) : (10)
Fig. 1 shows the ontravariant omponents of the
equilibrium magneti eld. Wenormalize the
ompo-nent B 2
0
to its valueat r
t
= a, B 2 a = 0Ip 2a 2
, (Fig. 1a)
andB 3
0
toits valueat themagneti axis,B 3 T = 0 I e 2R 0 0 2 , (Fig.1b).
Theorrespondingsafetyfatorqis:
q = 1 2 Z 2 0 B 3 0 (r t ; t ) B 2 0 (r t ; t ) d t = q (r t ) q 1 4 r 2 t R 0 0 2 ; (11) with q (r t )= I e I p r t R 0 0 2 1 1 1 r 2 t a 2 +1 : (12)
−1.0
−0.5
0.0
0.5
1.0
(R−R
0
)/b
0.0
1.0
2.0
3.0
4.0
Contravariant components of
B
0
(a)
(b)
Figure 1. Contravariant omponents of the equilibrium
magneti eld B
0
. In (a), we show B 2
0
normalized to B 2
a
andin(b)weshowB 3
0
normalizedtoB 3
T .
This safety fator shows a paraboli prole with
q 1:0 at the magneti axis and q 5:0 at plasma
edge(Fig. 2).
0.0
0.2
0.4
0.6
0.8
1.0
r
t
/a
0.0
1.0
2.0
3.0
4.0
5.0
q
Figure 2. Radial prole of the safety fator. The radial
oordinater
t
wasnormalizedtotheplasmaradiusa.
The perturbing magneti eld we onsider in this
paperisproduedbyapairofhelialwindingsinstalled
on theexternalvauum vessel surfae. These
ondu-tors drive urrentsI
h
in opposite diretions. To
pro-due an eÆient resonant eet they must have the
same pith as the eld lines in the rational magneti
surfae with q = m0 n (m 0 and n 0
to disturb. The toroidalgeometrymakesthe eldline
pithnonuniform. Inordertotthisnonuniformitywe
hoose the followingwinding law for the urrent
on-dutors:
u
t =m
0 [
t
+sin(
t )℄ n
0 '
t
=onstant: (13)
Theparameterisobtainedbyttingthiswinding
lawtotheequilibriumeldlinepathintherational
sur-fae withq= m
0
n
0
. For(m
0 ;n
0
)=(5;1)thisparameter
takesthevalue=0:59[13℄.
Therefore,weadoptthefollowingexpressionforthe
helialurrentdensity:
J
h =
I
h
R 0
0 r
t Æ(r
t b
t )[Æ(u
t ) Æ(u
t )℄e
ut
; (14)
that desribes two urrent ondutors loated at the
toroidal surfaer
t =b
t
, oneofthem driving aurrent
I
h
alongthehelixu
t
=0andtheotherdrivingaurrent
I
h
alongthehelixu
t =.
Basially,therearethreedierentapproahesto
al-ulate the perturbing magneti eld. The rst one is
the diret determination of the magneti eld using
the Biot-Savart law. The seond one is to alulate
straightly the vetor potential for the magneti eld.
Thethirdone,whihistheapproahwehoose,
orre-sponds to the appliation of boundaryonditions,
de-rived from the helial urrent density, on a magneti
salar potential
M
. The boundary onditions to be
appliedatthewallr
t =b
t
omefrom:
B ext
1 B
int
1
=
0 Z
ext
int dr
n J
h
; (15)
wheredr
n
isthedierentialvetorperpendiulartothe
surfaer
t =b
t
. Heretheperturbingmagnetield isa
vauum eld: B
1
=r
M
, where the magnetisalar
potential
M
satisestheLaplaeequationr 2
M =0.
Inpolartoroidaloordinatesystem,theLaplae
equa-tionreads[13℄:
1
r
t
r
t
r
t
M
r
t
+ 1
r 2
t
2
M
2
t r
t
R 0
0
os(
t )
2
2
M
r 2
t +
+ 3
r
t
M
r
t
sin(
t )
1
r 2
t
M
t +
2
r
t
2
M
t r
t
+
+ 1
R 2
2
M
' 2
t
=0: (16)
d
Figure3. ShematidiagramofanErgodiMagneti
Limiter.
Aswehavestatedintheintrodution,Ergodi
Mag-netiLimiters may beregardedasnarrowsliesof
he-lialwindings with lengthsl<<2R
0
(seeFig.3), so
it is enough to take the lowest order solution of the
Eq.(16)to modeltheEMLperturbingmagnetield.
This lowest order solutionof the Laplae equation
isobtainedbytakingtherealpartofthefollowing
ex-pression:
M =
0 I
h
i m
0
X
k = m
0 J
k (m
0 )
r
t
b
t
m
0 +k
e
i[(m
0 +k )
t n
0 '
t ℄
: (17)
Notethat,duetothetoroidalgeometryeet,other
modesbesidesthe(m
0 ;n
0
)=(5;1) areexited, whose
amplitudesdeayproportionallyto Besselfuntions of
orderk.
Therefore,fromtheabovemagnetisalarpotential
M
, and keeping in mind that only the lowest order
solutionisenoughto modeltheEML ation, the
on-travariantomponentsoftheperturbingmagnetield
B
1 are:
B 1
1 =
M
r
B 2
1 =
1
r 2
t
M
t
; (19)
B 3
1
= 0: (20)
0
π
/2
π
3
π
/2
2
π
θ
t
−10.0
−5.0
0.0
5.0
10.0
B
1
1
/B
T
x10
3
Figure4.ContravariantomponentB 1
1
poloidalprole
al-ulatedat rt
a
=1andnormalizedtoB
T
. EMLparameters:
(m
0 ;n
0
) =(5;1),I
h
=3:2 kA,=0:59 andN
r
=4rings
symmetriallydistributedalongthetoroidaldiretion.
Fig.4 showsthe poloidal prole of the perturbing
magneti eld ontravariantomponentB 1
1
alulated
atplasmaedgeandnormalizedtoB
T
. Fig.5showsthe
radial prole of hjB 1
1 (r
t ;
t ;'
t )ji
t
normalized also to
B
T
. Thesymbolh i
t
meansan averagetakenalong
thepoloidal diretion,
t
,keepingr
t and '
t
onstant.
Thisperturbingontravariantomponentishosen
beauseitismostrelevanttotopologialmodiations
ofmagnetisurfaesthantheontravariantomponent
B 2
1 .
ToalulatetheseprolesweusethefollowingEML
parameters: I
h
=3:2kA,(m
0 ;n
0
)=(5;1),N
r
=4and
=0:59.
From Fig.5, wean see that the perturbing
mag-netield strength deaysrapidly withthe radial
dis-tanefrom theplasma edge. Thus, theEML
perturb-ing eet is important only lose to the plasma edge,
aetinglesstheplasmaentral region.
0.0
0.2
0.4
0.6
0.8
1.0
r
t
/a
0.0
1.0
2.0
3.0
4.0
5.0
<B
1
1
/B
T
> x10
3
Figure5. RadialproleofhjB 1
1 ji
t
normalizedtoBT. EML
parametersarethesameasinFig.4.
Exluding marginal stability states, for whih the
plasmaresponsewouldhaveto betakeninto aount,
thetotalmagnetieldisthesuperpositionofthe
equi-librium andperturbingelds:
B=B
0 +B
1
: (21)
III The sympleti map for the
ergodi magneti limiter
The perturbing magnetield B
1
weobtainedanbe
desribed in terms of a vetor potential A as B
1 =
rA. This vetor potential is related to the salar
potential
M
through the following expression: A =
iR 0
0
M e
3
.
Thetrajetoryof amagnetield line isdesribed
bytheequation:
Bdl=0; (22)
wheredlisanunitarydisplaementalongtheeldline.
Intermsofthepolartoroidaloordinates,thiseld
line equation redues to a set of ordinary dierential
equations:
dr
t
d'
t =
1
rtBT h
1 2 rt
R 0
0 os(
t )
i
t
( +A
3 ); (23)
d
t
d'
t =+
1
r
t B
T h
1 2 r
t
R 0
0 os(
t )
i
r
t
( +A
3 ):(24)
After transformingfrom the polar toroidal
oordi-nate system (r
t ;
t ;'
t
) to a more suitable system of
anonialoordinates(J;#;t), theaboveset of
dier-entialequationsbeomesthewellknownpairof
Hamil-tonequations:
dJ
dt =
H
#
; (25)
d#
dt =
H
J
: (26)
Thesenewangle-ationvariablesarerelatedto the
polartoroidaloordinatesinthefollowingway[14℄:
J =
1
4 1
s
1 4 r
2
t
R 0
0 2
!
; (27)
# = 2artan
1
(r
t )
sin(
t )
1+os(
t )
; (28)
t = '
t
; (29)
where
(r
t )=
q
1 2 rt
R 0
0
q
1+2 rt
R 0
in suh awaythat wehave:
H(J;#;t) = H
0
(J)+H
1
(J;#;t)
= 1
B
T R
0
0 2
(J)+ 1
B
T R
0
0 2
A
3
(J;#;t);
(31)
astheHamiltonianfuntion.
Finally,iftheringlengthlissmallenough,wean
modeltheEMLationas asequene ofimpulsive
per-turbationsentered at eah ringposition. This model
allowsustoadopt theEML Hamiltoniangivenbelow:
H
L =H
0 (J)+
l
R 0
0 H
1
(J;#;t) 1
X
k = 1 Æ
t k 2
N
r
;
(32)
for N
r
rings symmetrially distributed along the
toroidaldiretion.
TotheEMLHamiltonian(32)weanassoiatethe
followingarea-preservingmapping:
J
n+1
= J
n +f(J
n+1 ;#
n ;t
n
); (33)
#
n+1
= #
n +
2
N
r q(J
n+1 )
+g(J
n+1 ;#
n ;t
n );(34)
t
n+1 = t
n +
2
N
r
; (35)
with
f = H
1
#
; g= H
1
J
; (36)
= 2
l
R 0
0 I
h
I
e
: (37)
Whenthe perturbingurrentis turned o ( =0)
this map beomes a typial radial twist map,
hara-teristiofintegrableHamiltoniansystems.
IV Poinare ross-setion for the
tabr tokamak
This setion is dediated to present some results for
the TCABR tokamak. Below, it is shown its typial
parameters[15℄:
TABLE1. TCABRParameters.
Parameter Symbol Value
Majorradius R
0
0:61m
Minorradius a
b 0:22m
Plasmaradius a 0:18m
Toroidalmagnetield B
T
1:2T
Plasmaurrent Ip 70kA
Safetyfatorattheedge q 5
Eletronthermalenergyattheedge kTe 20eV
Durationoftheplasmadisharge 120ms
Eetiveatominumber Zeff 4
Plasmaurrentexponent 3
a
TheTCABRhasretangularross-setion,sobisthe
in-sribedirumfereneradiusinthisross-setion.
−1.00
−0.50
0.00
0.50
1.00
(R−R
0
)/b
−1.25
−0.75
−0.25
0.25
0.75
1.25
Z/b
−I
h
+I
h
suface r
t
=b
t
Figure6.TCABRross-setionwhereitisshownsome
equi-libriummagnetisurfaesandthesymbolsandÆindiate
theurrentondutorloations.
In Fig. 6, we see a TCABR vessel ross-setion
('
t
=0)andsomeequilibriummagnetisurfaes
repre-sentedin termsof ylindrialoordinatesystem. Also
itis possibleto observe thesurfaer
t =b
t
where the
nonuniformly distributed urrentsegmentsare. These
equilibriumsurfaeshavealmostirularross-setions
andtheShafranovshift,due tothe toroidalgeometry,
islearlyseenfromtheinnerones.
Fig.7showsthesameequilibriummagnetisurfaes
ofFig.6representedintermsofanonialoordinates.
0
π
/2
π
3
π
/2
2
π
ϑ
0.00
0.01
0.02
0.03
0.04
0.05
J
−Ih
+Ih
Figure7. Equilibriummagnetisurfaes depitedinterms
ofanonialoordinates.
Although wehavebeen doingmost of our
alula-tionsintermsofbothpolartoroidaloordinatesystem
(r
t ;
t ;'
t
)andanonialoordinatesystem(J;#;t),it
ommonlyused loalpolaroordinate system(r;;').
The relationship between this oordinate system and
theylindrialoordinatesystemisasfollows:
R = R
0
ros(); (38)
= '; (39)
Z = rsin(): (40)
Fig. 8 shows the same surfaes that are shown in
Fig.7,butnowintermsoftheloalpolaroordinates.
Fromnowon,wewillusetheloalpolaroordinate
systemtopresentthePoinareross-setionweobtain
fortheTCABRtokamak.
When the perturbation is turned on, the
mag-netisurfaetopologyhangesnotablyandmanyisland
hains appeardue totheresonantinterationbetween
the equilibrium and the perturbing magneti elds.
There is amain hain of vemagneti islandsaround
the equilibrium surfae with q = m0
n
0 =
5
1
and many
otherssatelliteislandhainsas well.
0
π
/2
π
3
π
/2
2
π
θ
0.00
0.04
0.08
0.12
0.16
0.20
r(m)
+Ih
−I
h
Figure8. SurfaesshowninFig.7nowdepitedintermsof
theloalpolaroordinates ('=onstant).
Inreasing the perturbing urrent, these island
hains overlapand generateasizablehaotield line
region. If the perturbing urrent is not large enough,
this haoti region does not reah the tokamak
ves-selwallbeause therestill are somemagneti surfaes
that are not destruted between the vessel wall and
thehaotiregion. An exampleof thisproess anbe
seen in Fig. 9 where a Poinare ross-setion for the
TCABR is shown orresponding to the following
per-turbing strength D
B 1
(a)
B
T E
=2:310 3
(I
h
=1:5 kA,
(m ;n )=(5;1)and=0:59).
0
π
/2
π
3
π
/2
2
π
θ
0.00
0.04
0.08
0.12
0.16
0.20
r(m)
+I
h
−I
h
Figure9. Poinare ross-setion forthe TCABRtokamak.
TheEMLparameters are: Ih =1:5 kA,(m0;n0) =(5;1),
Nr=4and=0:59.
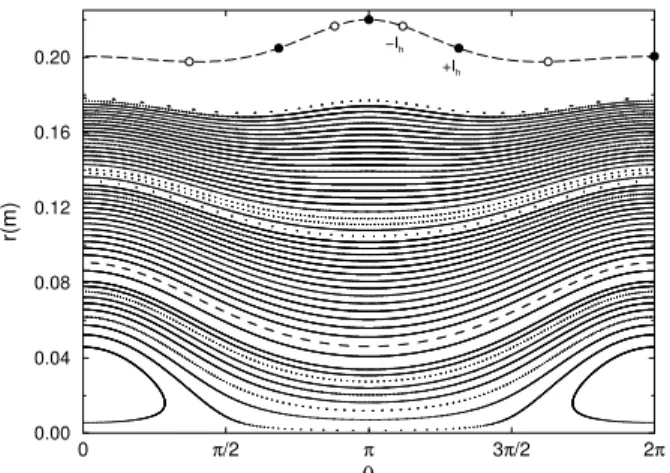
Inreasing further the perturbing urrent, the last
unperturbed surfae whih is loated between the
haoti region and thevessel wall isdestruted.
Con-sequently,ahaotieldline mayreahthevesselwall
after anite numberof turns aroundthe onnement
hamber. AnexampleofthisisshowninFig.10where
a urrent I
h
= 3:2 kA produes the EML perturbing
ationwith strength D
B 1
(a)
BT E
=5:010 3
. Theother
parametersarethesameasinFig.9.
0
π
/2
π
3
π
/2
2
π
θ
0.00
0.04
0.08
0.12
0.16
0.20
r (m)
−Ih
+Ih
Figure10. Poinareross-setionfortheTCABRtokamak.
TheEMLparameters are: I
h
=3:2 kA,(m
0 ;n
0
) =(5;1),
N
r
=4and=0:59.
AsanEMLeetivenessestimationwealulatethe
averagenumberofturns,hn
i,ittakesforahaotield
line to hit thevessel wall. Westart withan ensemble
ofN =2000uniformlydistributed initialpointsin the
haotiregionandwealulatehn
ias follows:
hn
i=
1
N N
X
i=1 n
i
; (41)
where n
i
is the number of turns it takesfor the i-th
haoti eld line starting at the i-th initial point to
With hn
iweestimateanesapetimerequired for
an ionized impurity partile to hit the vessel wall.
This esape time is given by
=
2R0hni
v
T
where
v
T =
q
2k
B T
mp
is the partile thermal veloity, k
B T is
the thermal energy and m
p
is the partile mass. We
hoosetheBerylliummass(m
p
=1:5010 26
kg)
be-ause itsatomi numberZ =4is almost equalto the
TCABR plasmaeetiveatominumberZ
eff .
TakingintoaounttheperturbingurrentI
h =3:2
kA, the esape time is
28 ms. This esape time
is almost onefourth of thetypialdisharge duration
=120ms. Therefore,theEMLanbeativated
dur-ingtheplasmadisharge. Asweuseathermalveloity,
this estimationmayunderevaluatepossibleeetsdue
to theollisionsbetweenveryfastpartiles(inthetail
of theveloitydistribution) andthetokamakwall.
V Conlusions
A oneptual design for a set of EML rings was
pro-posed, whih took into aount toroidal geometry
ef-fets. The magneti eld of suh a set of EML rings
wasalulatedbyusingthesameoordinatesystemas
fortheequilibriumeld.
ConsideringtheEML ringsationas asequeneof
impulsive perturbations and looking at the eld line
dynamifromaHamiltonianpointofviewweobtained
a sympleti map, in terms of angle-ation variables,
whihembodiesthefollowingimportantharateristis:
(i)itresultsdiretlyfrom theperturbing magneti
eld expressions;
(ii)ithasaontrolparameterintroduedtomath
theatualequilibriumeld linepathand
(iii)itpresentsmagnetiislandswithdierentsizes
and nonuniform poloidal distribution when they are
representedintermsofloalpolaroordinates.
We applied this sympleti map for the TCABR
tokamak onditions to estimate an impurity esape
time. The esape time we estimated was almost one
fourth of the disharge duration, so the EML rings
ould be used eetively to improve the plasma
on-nement.
Referenes
[1℄ F.Karger andK.Lakner, Phys.LettersA61 (6), 385
(1977).
[2℄ W. Feneberg and G. H. Wolf, Nul. Fusion 21, 669
(1981).
[3℄ N.Ohyabu,J.S.DeGrassie,etal.,J.Nul.Mater.121,
363(1984).
[4℄ S.C. MCool, A. J. Wootton, et al., Nul.Fusion 29
(4),547(1989).
[5℄ Y. Shen, M. Miyake, et al., J. Nul. Mater. 168, 295
(1989).
[6℄ A.Vannui,I.C.NasimentoandI.L.Caldas,Plasma
Phys.andControlledFusion31,147(1989).
[7℄ N.Ohyabu,Nul.Fusion21,519(1981).
[8℄ R.Yoshino,T.Kondoh,etal.,Plas.Phys.Contr.Fusion
39,313(1997).
[9℄ P. Helander, L. G. Eriksson and F. Andersson, Phys.
Plas.7(10),4106(2000).
[10℄ E. C. da Silva, I. L. Caldas and R. L. Viana, Phys.
Plasmas8(6),2855 (2001).
[11℄ E.C. daSilva, I.L. Caldasand R.L. Viana,
\Bifur-ations and Onset of Chaos on the Ergodi Magneti
LimiterMapping",tobepublishedinChaos,Solitons&
Fratals(2001).
[12℄ M.Y.Kuinski,I.L. Caldas,etal.,J.Plas.Phys.44,
303(1990).
[13℄ E. C. da Silva, I. L. Caldas and R. L. Viana, IEEE
Trans.onPlasmaSiene29(4),617(2001).
[14℄ A. H. Boozer and A. B.Rehester, Phys.Fluids 21,
682(1978).
[15℄ I. C. Nasimento et al., \ The TCABR Tokamak:
Overview, Operational Regimes and Limits", in these