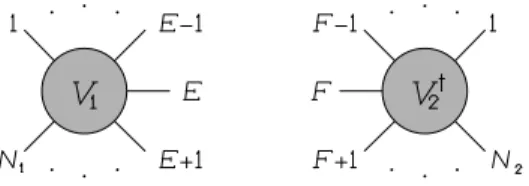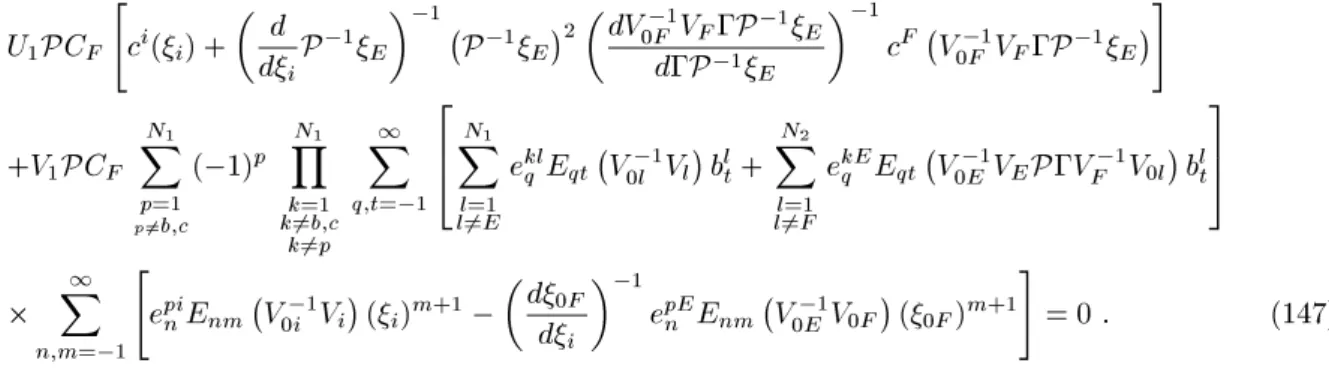Sewing String Tree Verties with Ghosts
LeonidasSandoval Junior
Department ofMathematis
CentrodeCi^eniasTenologias
UDESC,UniversidadedoEstadodeSantaCatarina,Brazil
Reeivedon13November,2001
Itisshownhowtosewstringvertieswithghostsattreelevelinordertoproduenewtreeverties
usingthe GroupTheoreti approahtoStringTheory. It isthenveriedtheBRSTinvarianeof
thesewnvertexandshownthatithastheorretghostnumber.
I Introdution
Inthe early daysof String Theory, oneway to obtain
amplitudesforthesatteringofanarbitrarynumberof
strings was by using the fatorization property, what
meansthat thesatteringamplitudeofN stringsmay
beinterpretedasthesatteringamplitudesofasmaller
numberofstringssewntogether. Thismadeitpossible
tobuildtheN stringsatteringamplitudebyknowing
the expression for three string sattering amplitudes.
Even thoughthey were veryingenious and suessful,
those alulations didn't take into aount the ghost
strutureoftheverties,andthatiswhatisdonehere.
In[1℄,itwasshownhowtosewtreevertieswithout
ghosts using the Group Theoreti approah to String
Theory[2℄in ordertoobtainanew,ompositevertex.
Following the same proedure, we shall alulate the
sattering amplitude of N strings taking aount the
ghoststruture.
Weshallstartwithashortreviewofhowtosewtree
vertieswithoutghosts. Whatwemust dois sew two
legsoftwoverties,onelegfromeahvertex. Whatwe
havein thebeginningare twovertiesV
1 andV
2 with
N
1 andN
2
legs, respetively(Fig. 1).
Figure1. Individualverties.
Wenow sew leg E from V
1
withthe adjointof leg
F from V
2
. What we have now is the substitution of
thetwosewnlegsbyapropagator(Fig. 2). Whenthis
propagatoris writteninparametriform,itisan
inte-grationof oneof the variables (in order to anel one
spurious degreeof freedom) and aonformalfator P
whihontainstermsofL
n
'satingonlegE only.
Figure2. Sewnverties.
SotheresultingvertexV
(alledtheomposite
ver-tex)hasthegeneriform
V
=V
1 PV
y
2
; (1)
wherethehermitianonjugateofV
2
isforthesewnleg
F onlyand
P = Z
dxP (2)
wherexisasuitablevariable. Inwhatfollows,weshall
oftenwrite P insteadofP,alling attentiontothe
in-tegrationwhenneessary.
Whenthetwovertiesare sewntogether, we
iden-tify legs E and F. We also identify theKoba-Nielsen
variable z
E
with oneof the Koba-Nielsen variables of
vertexV y
2
, and theKoba-Nielsen variable z
F
we
iden-tify with one of the Koba-Nielsen variables of vertex
V
1
. In[1℄, this identiation is made in the following
way: z
E
maybeidentied withz
F 1 orz
F+1 , and z
F
maybeidentiedwithz
E 1 orz
E+1
. Sotherearefour
possibleombinations: a) z
E =z
F 1 ; z
F =z
E 1 ; b)
z
E =z
F+1 ; z
F =z
E+1 ;)z
E =z
F 1 ; z
F =z
E+1 ;d)
II Osillator ase
Thetwooriginalvertiessatisfysomeoverlapidentities
and so shall do the omposite vertex. One partiular
overlap identity is given by onsidering the operator
Q i
withonformalweightd=0dened by[2℄
Q i
(
i )=
1
X
n= 1
n6=0 1
p
n
i
n (
i )
n
+ i
0 ln
i +
i
0 :
(3)
where i
n
arebosoniosillatorswithommutation
re-lations
[ i
n ;a
j
m ℄=
Æ ij
Æ
n; m
; n;m6=0; (4)
[ i
0 ;a
j
n
℄=0; 8n : (5)
Theoverlapidentityisgivenby
V
Q i
(
i ) Q
j
(
j )
: (6)
Beause we areonsidering the adjointof leg F in
vertexV
2
,wemustseewhattheadjointoftheseoverlap
identities are. First,by thedenition of Q i
,wehave
that
Q iy
(
i )= Q
i
(
i ) =Q
i
(
i
): (7)
So,theadjointoftheoverlapequationsisgivenby
Q i
(
i ) Q
j
(
j )
V y
=0: (8)
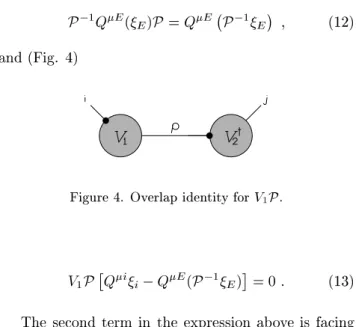
We now take the overlap identity onsidering the
eets of the operator Q i
(
i
) on the vertex V
1 on a
generilegiandonleg E 1
(Fig. 3):
Figure3. OverlapidentityforV
1 .
V
1
Q i
(
i ) Q
E
(
E )
=0: (9)
We may then insert the unit operator 1 = PP 1
andmultiplybyP withoutalteringtheresult:
V
1 PP
1
Q i
(
i ) Q
E
(E)
P : (10)
SinetheonformaloperatorP atsonlyonleg E,
it will haveno eet onQ i
(
i
). Inorder to ompute
the eet of P on Q E
(
E
), we must know that, for
a onformal transformation V ating on a onformal
operatorR (z)ofweightd,
VR (z)V 1
=
dVz
dz
d
R (z): (11)
SineQ E
(
E
)hasonformalweightd=0,wehave
P 1
Q E
(
E
)P =Q E
P 1
E
; (12)
and(Fig. 4)
Figure4. OverlapidentityforV1P.
V
1 P
Q i
i Q
E
(P 1
E )
=0: (13)
The seond term in theexpression aboveis faing
now leg F of vertex V y
2
, orbest, its Hermitian
onju-gate. ConsideringthattheHermitianonjugateofQ i
(givenby(7)),wethenhavethefollowingoverlap
iden-titybetweenlegsiandF:
V
1 P
Q i
(
i ) Q
F
( P 1
F )
=0: (14)
Weanthenmakeaylingtransformationinorderto
obtaintheorretfatorforanarbitraryleg j(j 6=F)
ofvertexV y
2
. Theonlytermthatwillbeaetedisthe
termdependingonlegF:
V 1
j V
F Q
F
P 1
E
V 1
F V
j =
Q j
V 1
j V
F P
1
E
: (15)
Doingthis, theoverlapidentity fortheomposite
ver-texV
(Fig. 5)anbewrittenas
Figure5.OverlapidentityforV
.
V
Q i
(
i ) Q
j
(V 1
j V
F P
1
E )
=0; (16)
whih is the overlap equation between two arbitrary
legsiandj oftheompositevertexV
.
1
But the overlap identity for the omposite vertex,
sinenoneoflegs i orj involvesthepropagator,must
begivenby
V
Q i
(
i ) Q
j
(
j )
=0 (17)
and soin order for theequation wehaveobtainedfor
the overlapof the omposite vertex V
to be true we
musthave
V
F P
1
V 1
E
=1)P 1
= 1
V 1
F V
E
(18)
whihimpliesthat thepropagatorisgivenby
P =V 1
E V
F
: (19)
Inordertogiveanexpliitexpressionforthe
prop-agator,wewillnowhoose
i
tobeoftheform
i =V
1
i
z=z z
i
: (20)
This hoie is alled the\simple yling" [1℄ and it is
the one that simplies our alulations the most. In
thishoie, thepropagatorisgivenby
Pz= 1
z +z
F z
E
; (21)
orin termsoftheL E
n
operators 2
,
P=e (z
F z
E 1)L
E
1
( 1) L
E
0
e L
E
1
e L
E
1
: (22)
This form works for all hoies for the omposite
vertexdisussedbefore 3
. Thetruepropagatorisgiven
by expression (22)integrated overasuitable variable.
Choosingthisvariabletobes=z
F z
E
,wethenhave
P = Z
0
1
dsP = 1
L E
1 ( 1)
L E
0
e L
E
1
e L
E
1
; s=z
F z
E :
(23)
Before going any further,wemust disuss another
aspetofthetheorythatdependsonthepartiularway
in whih thelegs areidentied during thesewing
pro-edure. Let us onsider the more general ase of an
arbitraryyling V
i
. Thiskindof ylingmaydepend
onotheroordinatesthatarenotz
i
. Asanexample,let
ussupposethatweareidentifyingoordinatez
E ofleg
E with oordinate z
F 1
of vertex V y
2
and oordinate
z
F
of leg F with oordinate z
F 1
of vertex V
1 . The
overlapidentitybetweenlegsiandE 1onvertexV
1
is
V
1 h
Q i
V 1
0i z
Q (E 1)
V 1
0(E 1) z
i
(24)
where we are alling V 1
0j
the yling transformation
onlegj (j =1;:::;N). Theseylingtransformations
maydependontheotherlegs. Asanexamplewhenthis
happens, wetake another hoie of the yling
trans-formations
i
that isnot astrivialas(20)but givesa
simplerformulaforthepropagator. Thishoieisgiven
by[1℄[3℄
i =V
1
0i z=
(z
i+1 z
i 1 )
(z
i+1 z
i )
(z z
i )
(z z
i 1 )
(25)
whihisthetransformationthattakesz
i 1 ,z
i andz
i+1
to1,0and1,respetively. Itsinverseisgivenby
V
0i z=
z
i 1 (z
i z
i+1 )z+z
i (z
i+1 z
i 1 )
(z
i z
i+1 )z+(z
i+1 z
i 1 )
: (26)
Intheaseoftheylinggivenby(25),theyling
forlegE 1willdependonlegE,whihisnotpresent
in the omposite vertex. On this vertex, the overlap
betweenlegE 1andanarbitrarylegj reads
V
h
Q (E 1)
V 1
0(E 1) z
Q j
V 1
0j z
i
: (27)
This overlap equation involves terms that depend on
legE,whihisnon-existentintheompositevertexV
.
Theorretoverlapsshouldbegivenby
V
h
Q (E 1)
V 1
E 1 z
Q j
V 1
j z
i
; (28)
where the yling transformations V 1
E 1 and V
1
j do
notdepend onlegsE orF. So,in ordertorestore the
orret yling transformation for the omposite
ver-tex, a onformaltransformationmust be madeon the
yling transformationson vertexV
1
. These aregiven
by
V 1
0j
!C
1 V
1
0j
; j6=E ; (29)
where
C
1 =
N1
Y
i=1 V
1
i V
0i
: (30)
In this denition,weonsider impliitthat the
trans-formationV 1
E V
0E
=1sinetheonformal
transforma-tionsonlegE willnotbepartoftheompositevertex
andsoneednotbemodied.
Consideringthegeneralase,wehavethatthe
over-lap equation forV
1
(Fig. 6) that will lead to the
or-retompositevertexisnowobtainedfromtheoriginal
overlap
2
Otherformsforthispropagatoraregivenby[1℄:
P = e L
E
1 =s
( 1) L
E
0
s 2L
E
0
e L
E
1 =s
P = ( 1) L
E
0 L
E
1 =s
s 2(L
E
0 L
E
1 =s)
e (L
E
1 L
E
1 )=s
:
3
Figure6. OverlapidentityforV
1 .
V
1
Q i
(
0i ) Q
E
(
0E )
=0; (31)
where
0i =V
1
0i
z and
0E =V
1
0E
z. Byinserting
on-formaltransformation(30),weobtain(Fig. 7)
Figure7. Overlapidentityfor V1C 1
1 .
V
1 C
1
1
Q i
(
i ) Q
E
(
E )
=0: (32)
Insertingnowthepropagator,weobtain(Fig. 8)
Figure8. OverlapidentityforV
1 C
1
1 P.
V
1 C
1
1 P
Q i
(
i ) Q
E
(P 1
E )
=0 (33)
and we expet the omposite vertex to have a
dier-entform(givenshortly)thanin(1)inordertoamount
fortheontributionsoftheonformaltransformations.
The seond termofthe overlapis nowfaingleg F of
vertexV y
2
sothatwehavethefollowingoverlapbetween
legs iandF:
V
1 C
1
1 P
Q i
(
i ) Q
F
( P 1
E )
=0: (34)
We arenowfaingtheonformaltransformationC
F 4
,
dened by
C
F =V
1
F V
0F
(35)
whihisneessaryinordertohange
0F !
F .
Intro-duingthistransformationweobtain(Fig. 9)
Figure9. OverlapidentityforV1C 1
1 PCF.
V
1 C
1
1 PC
F
Q i
(
i ) Q
F
(V 1
0F V
F P
1
E )
=0:
(36)
Making aylingtransformation from legF toleg
j,wethenobtain(Fig. 10)
Figure10. OverlapidentityforV1C 1
1 PCFV
y
2 .
V
1 C
1
1 PC
F V
y
2
Q i
(
i ) Q
j
(V 1
0j V
F P
1
E )
=0:
(37)
One again, a onformal transformation must be
in-trodued beause of theyling transformationsV 1
0j .
Thisisdenedby
C
2 =
N
2
Y
i=1
i6=F V
1
i V
0i
: (38)
sothatwenowhave(Fig. 11)
Figure11. OverlapidentityforV1C 1
1 PCFV
y
2 C
1
2 .
4
V
1 C
1
1 PC
F V
y
2 C
1
2
Q i
(
i ) Q
j
(V 1
j V
F P
1
E )
=0: (39)
Theompositevertexmustbedened intermsofthenewylingtransformationsand soitmustnowinlude
theonformaltransformationsthatperformthishange. So,itwillnowbedenedby
V
=V
1 C
1
1 PC
F V
y
2 C
1
2
: (40)
Consideringthis, theoverlapidentityfortheompositevertexV
anbewrittenas
V
Q i
(
i ) Q
j
(V 1
j V
F P
1
E )
=0: (41)
Sinetheorretoverlapidentityfortheompositevertexisgivenby
V
Q i
(
i ) Q
j
(
j )
=0 (42)
wemusthave
V
F P
1
V 1
E
=1 (43)
whihimpliesoneagainthat
P =V 1
E V
F
: (44)
Fortheylingtransformation(25),itisonlyneessarytodoonformaltransformationsonlegsE 1,E,E+1,
F 1,F and F +1,depending onthepartiular waythevariables assoiated withthese legs are identiedwith
thevariables assoiated tolegs E andF. Inthis partiularexample(whih isasea seenbefore), theonformal
transformationsaregivenby
V 1
0(E 1) !C
1 V
1
0(E 1)
; C
1 =r
L E 1
0
; (45)
V 1
0(F 1) !C
2 V
1
0(F 1)
; C
2 =t
L F 1
0
(46)
where
r= (z
F 1 z
E 2 )
(z
F 1 z
E 1 )
(z
E 1 z
E )
(z
E 2 z
E )
; t= (z
E 1 z
F 2 )
(z
E 1 z
F 1 )
(z
F 1 z
F )
(z
F 2 z
F )
: (47)
Fortheyling(25),thepropagatorsobtainedforthefourpossibleombinationsdisussedbeforearegivenby
a) P
a =a
L E
0
; b) P
b =e
L E
1
a L
E
0
e L
E
1
; ) P
=e
L E
1
b L
E
0
; d) P
d =b
L E
0
e L
E
1
; (48)
where 5
a= (z
E+1 z
E 1 )(z
F+1 z
F 1 )
(z
E+1 z
F 1 )(z
F+1 z
E 1 )
; b= (z
E+1 z
E 1 )(z
F+1 z
F 1 )
(z
E+1 z
F+1 )(z
F 1 z
E 1 )
: (49)
Thetruepropagatorsareobtainedwhenweintegratetheexpressionsabovemultipliedbyasuitableonstant. The
resultsare:
a) P
a =
Z
1
0 daa
L E
0 1
= 1
L E
0
; b) P
b =
Z
1
0 dae
L E
1
a L
E
0 1
e L
E
1
=e L
E
1 1
L E
0 e
L E
1
; (50)
) P
=
Z
1
0 dbe
L E
1
b L
E
0 1
=e L
E
1 1
L E
0
; d) P
d =
Z
1
0 dbb
L E
0 1
e L
E
1
= 1
L E
0 e
L E
1
: (51)
Itisnowneessarytoverifytheeet ofthegaugetransformationsC
1 andC
2
ontheompositevertexasgiven
byformula(40). Weshall doit byverifyingtheeetof C
1
onvertexV
1
. Inorderto dothis weneedtheexpliit
expressionforthebosoniosillatorvertexV
1
,givenby[1℄[4℄
V
1 =
N
Y
i=1 i
h0j !
exp 2
6
6
4 1
2 N
1
X
i;j=1
i6=j 1
X
n;m=0
i
n D
nm V
1
0i V
0j
j
m 3
7
7
5
(52)
5
TheoeÆientaanbeonnetedwiththeoeÆientinreferene[1℄bya=
whereV 1
0i
andV
0j
areylingtransformationsinvolvinglegE andtheosillators i
n
haveommutationrelations
givenby(4, 5). MatriesD
nm
()aredenedin thefollowingway[3℄:
D
n0 () =
1
p
n [(0)℄
n
; (53)
D
nm () =
r
m
n 1
m!
m
z m
[(z)℄ n
z=0
; (54)
D
00 () =
1
2 ln
d
dz (z)
z=0
(55)
andhavethefollowingmultipliationproperty:
D
nm (
1
2 )=
1
X
p=1 D
np (
1 )D
pm (
2 )+D
n0 (
1 )Æ
0m +Æ
0n D
0m (
2
): (56)
InordertoalulatetheeetsoftheonformaltransformationC
1
ontheseosillatorswemustmakeuseofthe
followingonformaloperator[2℄
P i
(
0i )=
1
X
n= 1
n6=0 p
jnj i
n (
0i )
n 1
+ i
0 (
0i )
1
(57)
whihhasonformalweightone,whatmeansittransformslike
P i
(
0i )=
d
0j
d
0i P
j
(
0j
): (58)
Anosillator i
n
(n1)anbeexpressedintermsofthisonformaloperatorinthefollowingway:
i
n =
1
p
n I
0i =0
d
0i (
0i )
n
P i
(
0i
): (59)
AtingonitwiththeonformaltransformationC
1
,wehave
C
1
i
n C
1
1 =
1
p
n I
0i=0 d
0i (
0i )
n
d
d
0i V
1
i V
0i
0i
P i
(V 1
i V
0i
0i
): (60)
Makingnowahangeofvariables
0i !
i
, wehave
C
1
i
n C
1
1 =
1
p
n I
i=0 d
i (V
1
0i V
i
i )
n
P i
(
i
): (61)
Expanding(V 1
0i V
i
i )
n
intermsofD
nm
()matriesandP i
(i)intermsoftheosillators,weobtain
C
1
i
n C
1
1 =
1
X
p= 1
p6=0 r
p
n I
i =0
d
i "
p
nD
n0 V
1
0i V
i
(
i )
p 1
+ 1
X
m=1 r
n
m D
nm V
1
0i V
i
(
i )
m p 1 #
i
p
+ 1
p
n I
i=0 d
i "
p
nD
n0 V
1
0i V
i
(
i )
1
+ 1
X
m=1 r
n
m D
nm V
1
0i V
i
(
i )
m 1 #
i
0
: (62)
Performingtheintegrationswethenobtain
C
1
i
n C
1
1 =
1
X
m=0 D
nm V
1
0i V
i
i
m
: (63)
Usingthesameproessfor i
0
, weobtain
C
1
i
C 1
= i
Using these transformation properties, the multipliation rules of matries D
nm
() (equation (56)) and the
property[3℄
D
nm
()=D
mn (
1
); (65)
weanshowthat theeetoftheonformaltransformationC
1
onvertexV
1
isgivenby
V
1 C
1
1 =
N
Y
i=1 i
h0j !
exp 2
6
6
4 1
2 N1
X
i;j=1
i6=j 1
X
n;m=0
i
n D
nm V
1
i V
j
j
m 3
7
7
5
; (66)
d
i.e. theeet ofC
1
on vertex V
1
is to hange V 1
0i !
V 1
i
andV
0j !V
j
thus eliminatingthedependene of
theylingtransformationsofeverylegexeptlegEon
thelatter. Thesame anbe doneto obtainthe eet
ofonformaltransformationC
2
onvertexV y
2
,withthe
same results. So, the eet of these transformations
isto eliminatefromthe ylingtransformationsofthe
ompositevertexalldependeneonthesewnlegsEand
F.
III Introdution of ghosts
Wenowintrodueghostsinthevertexsothatwhatwe
must sew now are two verties with someghost
vari-ablesattahedto them,i.e. wewillbeonsideringthe
physialverties[4℄whihhavetheorretghost
num-ber. In this ase, in addition to satisfying the
over-lapidentitieswiththeonformaloperatorQ i
,thetwo
physial verties and the omposite vertex must also
satisfy someoverlapidentities with the onformal
op-eratorsb i
and i
,givenby[4℄
b i
(
i ) =
1
X
n= 1 b
i
n (
i )
n 2
; (67)
i
(
i ) =
1
X
n= 1
i
n (
i )
n+1
(68)
where i
n and b
i
n
are ghost antiommuting osillators
withantiommutationrelations
f i
n ;b
j
m g=Æ
n; m
: (69)
These operators have, respetively, onformal weights
2and 1,whatmeansthattheytransformlike
b i
(
i ) =
d
j
d
2
b j
(
j
); (70)
i
(
i ) =
d
j
d
i
1
j
(
j
): (71)
TheoverlapidentitiesforavertexV withthese
op-eratorsaregivenby
V "
b i
(
i )
d
j
d
i
2
b j
(
j )
#
=0; (72)
V "
i
(
i )
d
j
d
i
1
j
(
j )
#
=0: (73)
Weshallbeworkingherewithoverlapidentitiesfor
the physial vertex U [4℄, whih hasthe orretghost
number,insteadof theoverlapidentities for vertexV.
Thephysialvertexisgivenby[4℄
U =V N
Y
i=1
i6=a;b; N
X
j=1 1
X
n= 1 e
ij
n b
j
n
(74)
where a;b; are any three legs of the vertex and the
matrixe ij
n
isgivenby
1
X
n= 1 e
ij
n L
j
n =V
1
j
zi V
j
(75)
where the yling transformations are now dened on
the omplete generators L i
n
of the onformal algebra
of the bosoni osillators and of the ghost osillators.
These vetorse ij
n
havethefollowingproperty:
V
z
i =V
N
X
j=1 1
X
n= 1 e
ij
n L
j
n
: (76)
Inordertoderivetheoverlapidentityforthe
physi-alvertexU,wemustmultiplytheoverlapidentityfor
V "
b i
(
i )
d
j
d
i
2
b j
(
j )
# 0
B
N
Y
k =1
k 6=a;b; N
X
l=1 1
X
n= 1 e
k l
n b
l
n 1
C
A
=0; (77)
V "
i
(
i )
d
j
d
i
1
j
(
j )
# 0
B
N
Y
k =1
k 6=a;b; N
X
l=1 1
X
n= 1 e
k l
n b
l
n 1
C
A
=0 (78)
andpassitthroughtheoverlapidentities,obtaining
U "
b i
(
i )
d
j
d
i
2
b j
(
j )
#
=0; (79)
U "
i
(
i )
d
j
d
i
1
j
(
j )
#
+V N
X
p=1
p6=a;b; ( 1)
p N
Y
k =1
k 6=a;b;
k 6=p N
X
l=1 1
X
q= 1 e
k l
q b
l
q 1
X
n= 1 "
e pi
n (
i )
n+1
d
j
d
i
1
e pj
n (
j )
n+1 #
=0: (80)
d
From(80)weanseethat therewill bean
anoma-lous term in the i
overlap of the physial vertex U
unless both legs i and j are preisely those legs (a, b
or ) that do not have any ghosts attahed to them.
These ghosts whih are attahed to all the other legs
areresponsiblefortheanomalousterms.
III.1 Analysis of the ghost number
Before going any further, it is neessary to make
some onsiderationson theghost numberof the
om-positevertex. Asweshallseeshortly,intheasewhere
weperformthesewingwith ghostsinluded,usingthe
physialverties,theresultingompositephysial
ver-tex will nothave the orret ghost number unless we
insertsomeextraghostsinvertexU
1
beforethesewing
takesplae. Consideringthis,weshalldenethe
om-positevertexto begivenby
U
=U
1 GPU
y
2
(81)
where Garesomeextraghoststhatwill beintrodued
inordertomakevertexU
havetheorretghost
num-berandP isthepropagator(initsintegratedform).
Wemustnowanalyzetheghostnumberofthe
om-posite vertexand of itsparts in orderto alulate the
ghost number that theextra ghosts G must have. In
order todothis, weshallusetheghostnumber
opera-tor N
gh
. Fora vertex with N legs, theghost number
operatorisdenedby
N gh
= N
X
i=1 1
X
n= 1
i
n b
i
n 1
X
n=2 b
i
n
i
n !
: (82)
The reason why the ghost number operator is a sum
fromi=1toi=N isbeausethere areN vauathat
willannihilatetheoperatorsorrespondingtoeahone
ofthem. Whenatingonthephysialvertex,this
oper-atorgivesaghostnumberN,whatistheorretghost
numberforatreevertexwithN legs.
Intheaseoftheompositevertex,ithasN
1 + N
2 2
legs(beauseitdoesnothavelegsEandF,whihhave
beensewntogether)andsoitmusthaveghostnumber
(N
1 +N
2
2). Forthisvertex,theghostnumber
oper-atorN gh
anbedividedintotwoparts:
N gh
=N
gh
1 +N
gh
2
(83)
where
N gh
1 =
N1
X
i=1
i6=E 1
X
n= 1
i
n b
i
n 1
X
n=2 b
i
n
i
n !
; (84)
N gh
2 =
N
2
X
i=1
i6=F 1
X
n= 1
i
n b
i
n 1
X
n=2 b
i
n
i
n !
: (85)
Thisghostnumberoperator willhavethefollowing
ef-fetontheompositevertex:
U
N
gh
=U
N gh
1 +N
gh
2
=(N
1 +N
2 2)U
: (86)
Given formula (81)for the omposite vertex, we then
have
U
N
gh
= U
1 N
gh
1 GPU
y
2 +U
1 h
G;N gh
1 i
PU y
2
+ U
1 GPU
y
N gh
Inordertoalulatethis, wemustpaysome
atten-tion to terms one and three of the righthand side of
theexpressionabove. Weknowthat
U
1
N gh
1 +N
gh
E
=N
1 U
1
; (88)
U
2
N gh
2 +N
gh
F
=N
2 U
2
(89)
where
N gh
E =
1
X
n= 1
E
n b
E
n 1
X
n=2 b
E
n
E
n
; (90)
N gh
F =
1
X
n= 1
F
n b
F
n 1
X
n=2 b
F
n
F
n
: (91)
Taking theHermitian onjugate ofequation (89) only
onlegF,weobtain
U y
2 N
gh
2 +N
gh
F y
U y
2 =N
2 U
y
2
: (92)
SineforN gh
F y
(andforanyarbitraryghostnumber
operator)
N gh
F y
= N
gh
F
+3 (93)
we then obtain, substituting (88), (92) and (93) into
equation(87),
U
N
gh
=(N
1 +N
2 3)U
1 GPU
y
2 +U
1 h
G;N gh
1 i
PU y
2 U
1 N
gh
E GPU
y
2 +U
1 GPN
gh
F U
y
2
: (94)
PassingN gh
E
throughtheextraghostsG,wethenobtain
U
N
gh
= (N
1 +N
2 3)U
1 GPU
y
2 +U
1 h
G;N gh
1 i
PU y
2
U
1 h
N gh
E ;G
i
PU y
2 U
1 GPN
gh
E U
y
2 +U
1 GPN
gh
F U
y
2
: (95)
Wemustnowrememberthat, inthe ompositevertex, weidentify everyoperator onleg E with operators on
legF sothat N gh
E =N
gh
F
. Doingthis,thelasttwotermsin (95)anelandweobtainthefollowingresult:
U
N
gh
=(N
1 +N
2 3)U
1 GPU
y
2 +U
1 h
G;N gh
1 +N
gh
E i
PU y
2
: (96)
d
ThefatthatU
hasghostnumberN
1 +N
2
2then
impliesthat
h
G;N gh
1 +N
gh
E i
=G; (97)
i.e. theextraghoststhatmustbeintroduedinvertex
U
1
musthaveghostnumber1. 6
There is an innite number of ombinations of
ghosts that haveghost number1. Weould haveany
linear ombination of ghosts of the type b, bb, bbb,
et. butitwillprovetobesimplertohooseGtobea
ombinationofb 0
sonlysothatwemayrepresentitas
G= N1
X
i=1 1
X
n= 1
i
n b
i
n
(98)
where i
n
aretheoeÆientsofthelinearombination.
Inordertodeterminetheorretlinearombination,we
mustuse someotheronditions,likeBRST invariane
ofthesatteringamplitude. Thisweshallseenext.
III.2 BRST invariane
Wemustnowimposethatthesatteringamplitude
obtainedfromtheompositevertexisBRSTinvariant
and hek whether this ondition is strong enough to
determineG. Thesatteringamplitude[1℄isobtained
byatingwiththeompositevertex
U
=U
1 GPU
y
2
(99)
on a ertain number of physial states
(j
1 ij
2 i:::j
N
i)andthenbyintegratingoverall
vari-ablesz
i
(i=1;:::;N
1 +N
2
;i6=E;F):
W = Z
N
1 +N
2
Y
i=1
i6=E;F dz
i U
1 GPU
y
2 j
1 ij
2 i:::j
N
i: (100)
6
P is the propagatorin its integrated form and G are
theextraghoststobeinsertedinU
1 .
TheationoftheBRSThargeQonthissattering
amplitudeisgivenby
WQ= Z
N
1 +N
2
Y
i=1
i6=E;F dz
i [U
1
;Q℄GPU y
2 j
1 ij
2 i:::j
N i
+ Z
N1+N2
Y
i=1
i6=E;F dz
i U
1
[G;Q℄PU y
2 j
1 ij
2 i:::j
N i+
Z
N1+N2
Y
i=1
i6=E;F dz
i U
1
G[P;Q℄U y
2 j
1 ij
2 i:::j
N i
+ Z
N1+N2
Y
i=1
i6=E;F dz
i U
1 GP
h
U y
2 ;Q
i
j
1 ij
2 i:::j
N
i: (101)
d
Therstandthirdtermswillresultintotalderivatives
that givezerowhen oneintegratesoversomevariables
[1℄ and so what remain are just the seond and third
terms.
The ommutator P is given by a pure onformal
transformation, and it is a funtion of the generators
L E
n
(n= 1;:::)only. AstheBRSThargeommutes
withallL E
n 's,i.e.
L E
n ;Q
=0 (102)
wehave
[P;Q℄=0: (103)
Consideringnowthat
b i
n ;Q
=L i
n
; (104)
wethenhave,forGgivenby(98),
U
1
[G;Q℄=U
1 N1
X
i=1 1
X
n= 1
i
n L
i
n
: (105)
InorderforthesatteringamplitudeW tobeBRST
invariant, expression (105) must be zero or a total
derivative(thatanbeintegratedouttobeomeanull
surfaeterm). At thesametime, wewantthese extra
ghoststo plae(talkingintermsofthesimpleyling)
aghoston oneof the legsin U
1
that donot haveany
ghostsattahedtothem. Ifwenowrememberproperty
(76),wesee that we ansatisfythese onstraintsin a
niewaybyhoosingGtobegivenby
G=( 1) N1+a
N1
X
j=1 1
X
n= 1 e
aj
n b
j
n
(106)
wherea(a6=E)isoneofthelegsofvertexU
1
thatdoes
nothaveghosts attahed to it. Inserting these ghosts
invertexU
1
,wehave
U
1 G=V
1 N
1
Y
i=1
i6=a;b; N
1
X
k =1 1
X
m= 1 e
ik
n b
k
m ( 1)
N1+a N
1
X
j=1 1
X
n= 1 e
aj
n b
j
n =V
1 N
1
Y
i=1
i6=b; N
1
X
j=1 1
X
n= 1 e
ij
n b
j
n
: (107)
Usingformula(106)fortheextraghostsG,wethenhave
U
1
[G;Q℄ = U
1 ( 1)
N1+a N
1
X
j=1 1
X
n= 1 e
aj
n
b j
n ;Q
=( 1) N1+a
U
1 N
1
X
j=1 1
X
n= 1 e
aj
n L
j
n
= ( 1) N1+a
V
1
z
a N1
Y
i=1
i6=a;b; N1
X
j=1 1
X
n= 1 e
ij
n b
j
n
(108)
d
Inreferenes[5℄and[6℄,theextraghostshavebeen
plaedin the propagator. Although this anbedone,
thereisnowayoneanderiveaformulafortheghosts
in the propagatorfor a generalyling. In that ase,
theextraghostsmustbederivedandBRSTinvariane
hastobehekedforeahpartiularyling. Also,the
resultingompositevertexobtainedinthat aseis not
similarinitsghoststruturetoanordinarytreevertex,
althoughithastheorretghostnumber.
III.3 Overlap identities
Wemustnowusetheoverlapidentitiestodetermine
thepropagatorthatsatises them. Inorder todothis
weshallstartwithvertexU 0
1
,whihisthevertexwith
ylingtransformationsV 1
i
whihinvolvelegE.
Con-sideringequations(79)and(80),theoverlapidentities
forvertexU 0
1
betweenanarbitraryleg iandlegE are
givenby(Fig. 12)
Figure12. OverlapidentityforU 0
1 .
U 0
1 "
b i
(
0i )
d
0E
d
0i
2
b E
(
0E )
#
=0; (109)
U 0
1 "
i
(
0i )
d
0E
d
0i
1
E
(
0E )
#
+V 0
1 N
1
X
p=1
p6=a;b; ( 1)
p N
1
Y
k =1
k 6=a;b;
k 6=p N
1
X
l=1 1
X
q= 1 e
k l
q b
l
q 1
X
n= 1 "
e pi
n (
0i )
n+1
d
0E
d
0i
1
e pE
n (
0E )
n+1 #
=0: (110)
Theextraghostsmust then be insertedin vertex U 0
1
so that theomposite vertex will havetheorretghost
number. Multiplyingexpressions(109)and(110)bytheextraghostsG(givenby(106))andpassingthemthrough
theoverlapsweobtain(Fig. 13)
Figure13. OverlapidentityforU 0
1 G.
U 0
1 G
"
b i
(
0i )
d
0E
d
0i
2
b E
(
0E )
#
=0; (111)
U 0
1 G
"
i
(
0i )
d
0E
d
0i
1
E
(
0E )
#
+U 0
1 ( 1)
N1+a 1
X
n= 1 "
e ai
n (
0i )
n+1
d
0E
d
0i
1
e aE
n (
0E )
n+1 #
+V 0
1 N1
X
p=1
p6=a;b; ( 1)
p N1
Y
k =1
k 6=a;b;
k 6=p N1
X
l=1 1
X
q= 1 e
k l
q b
l
q !
0
N1
X
j=1 1
X
n= 1 e
aj
n b
j
n 1
A
1
X "
e pi
n (
0i )
n+1
d
0E
d
0i
1
e pE
n (
0E )
n+1 #
Theseondandthird termsof equation(112)anbeombinedsothat itbeomes
U 0
1 G
"
i
(
0i )
d
0E
d
0i
1
E
(
0E )
#
+V 0
1 N
1
X
p=1
p6=b; ( 1)
p N
1
Y
k =1
k 6=b;
k 6=p N
1
X
l=1 1
X
q= 1 e
k l
q b
l
q !
1
X
n= 1 "
e pi
n (
0i )
n+1
d
0E
d
0i
1
e pE
n (
0E )
n+1 #
=0: (113)
Atthispoint,wemustintrodueonformaltransformationsofthetypeofC
1
,givenby(30)inordertohaveat
the endtheorret ylingtransformations fortheomposite vertex. Inorder todo thisweneedto usematries
E
nm
(),dened by[5℄
E
nm ()=
1
(m+1)!
m+1
z m+1
"
(z) n+1
z z
1 #
z=0
(114)
whihhavethefollowingproperties:
1
X
t= 1 E
rt (
1 )E
ts (
2 )=E
rs (
1
2
) ; r;s;t= 1;0;1; (115)
E
rn
()=0 ; r= 1;0;1 ; n2; (116)
1
X
p= 1 E
np (
1 )E
pm (
2 )=E
nm (
1
2
) ; n;m 1; (117)
1
X
p=2 E
np (
1 )E
pm (
2 )=E
nm (
1
2 )
1
X
r;s= 1 E
nr (
1 )E
rs (
2 )Æ
sm
; n;m2: (118)
TheationoftheoperatorC
1
ontheghostsb i
n
anthenbealulatedinthefollowingway: rstwewriteb i
n in
termsofanintegralovertheonformaloperatorb i
n (
i )
b i
n =
I
0i =0
d
0i (
0i )
n+1
b i
(
0i
): (119)
ThenweinserttheoperatorC
1 :
C
1 b
i
n C
1
1 =
I
0i=0 d
0i (
0i )
n+1
d
d
0i V
1
i V
0i
0i
2
b i
V 1
i V
0i
0i
: (120)
Afterahangeofvariables
i =V
1
i V
0i
0i
wehave 7
C
1 b
i
n C
1
1 =
I
i=0 d
i V
1
0i V
i
i
n+1
d
d
i V
1
0i V
i
i
1
b i
(
i
): (121)
UsingmatriesE
nm
(),wethenmayexpand
0i
in termsof
i
. Ifwealsoexpandb i
(
i
),wethenobtain
C
1 b
i
n C
1
1 =
1
X
m= 1 1
X
p= 1 I
i =0
d
i E
nm (V
1
0i V
i )(
i )
m+1
b i
p (
i )
p 2
: (122)
Performingtheintegrationwethenhave
C
1 b
i
n C
1
1 =
1
X
m= 1 E
nm (V
1
0i V
i )b
i
m
: (123)
Using(123)inequations(111)and(113)andmultiplying(111)by(d
i =d
0i )
2
and(113)byd
i =d
0i
,wethen
have(Fig. 14)
7
Figure14. OverlapidentityforU 0
1 GC
1
1 .
U 0
1 GC
1
1 "
b i
(
i )
d
E
d
i
2
b E
(
E )
#
=0; (124)
U 0
1 GC
1
1 "
i
(
i )
d
E
d
i
1
E
(
E )
#
+V 0
1 C
1
1 N
1
X
p=1
p6=b; ( 1)
p N
1
Y
k =1
k 6=b;
k 6=p "
N
1
X
l=1 1
X
q;t= 1 e
k l
q E
qt V
1
0l V
l
b l
t #
1
X
n;m= 1 "
e pi
n E
nm V
1
0i V
i
(
i )
m+1
d
E
d
i
1
e pE
n E
nm V
1
0E V
E
(
E )
m+1 #
=0: (125)
Beforegoingfurther,somewordsmustbesaidabouttheeetsof C 1
1
onvertexU 0
1
withtheextraghostsG.
Thisisgivenexpliitlyby[4℄[5℄
U 0
1
G =
N1
Y
i=1 i
h0j !
exp 2
6
6
4 N1
X
i;j=1
i6=j 1
X
n=2 1
X
m= 1
i
n E
nm V
1
0i V
0j
b j
m 3
7
7
5
1
Y
r= 1 N
1
X
i=1 1
X
s= 1 E
rs (V
0i )b
i
s
N
1
Y
i=1
i6=b; N
X
j=1 1
X
n= 1 e
ij
n b
j
n
: (126)
MakinguseofmatriesF
nm
(),denedby[5℄
F
nm ()=
1
(m 2)!
m 2
z m 2
(
[(z)℄ n 2
z (z)
1 )
z=0
(127)
wemayalulate inasimilarwayaswedidfortheb i
n
ghoststheeetofC
1
onthe i
n
ghosts,obtaining
C
1
i
n C
1
1 =
1
X
m=2 F
nm (V
1
0i V
i )
i
m
: (128)
Usingthistogetherwiththeproperty
F
nm
()=E
mn (
1
) (129)
andequation(123),wemaythenshowthattheresultofatingwithC 1
1 onU
0
1 Gis
U 0
1 GC
1
1 =
N1
Y
i=1 i
h0j !
exp 2
6
6
4 N1
X
i;j=1
i6=j 1
X
n=2 1
X
m= 1
i
n E
nm V
1
i V
j
b j
m 3
7
7
5
1
Y
r= 1 N1
X
i=1 1
X
s= 1 E
rs (V
i )b
i
s
N1
Y
i=1 N
X
j=1 1
X
n;m= 1 e
ij
n E
nm (V
0j V
j )b
j
m
Soweansee that inthis asetheationofC 1
1 onU
0
1
Gisnotjust to hange V
0i !V
i
. Beauseof thepeuliar
nature ofe ij
n
,ittransformsas
e ij
n !
1
X
m= 1 e
ij
n E
nm (V
0j V
j )b
j
m
: (131)
Onlyinonepartiulargroupofylingtransformations(asweshallseelater)willthisbejustequivalenttohanging
V
0i !V
i
. WeshallallfromnowonU 0
1 GC
1
1 U
1 andV
0
1 C
1
1 V
1
. ThealulationforvertexC
F U
y
2 C
1
2
willbe
similar totheonewehavejust madeforU 0
1 GC
1
1 .
Havingdonethis,wemustinsertthepropagatorP intotheoverlapidentities(124)and (125)inthesameway
asintheasewithnoghosts. Butnowwemusttakeextraaresinetherearetermsdependingonb E
q
intheseond
termofequation(125). Usingequation(123)asaguideline,wehave
P 1
b E
q P =
1
X
t= 1 E
qt (P)b
E
t
(132)
sothattheresultof insertingP intooverlaps(124)and(125)is(Fig. 15)
Figure15. OverlapidentityforU
1 P.
U
1 P
"
b i
(
i )
d
d
i P
1
E
2
b E
P 1
E
#
=0; (133)
U
1 P
"
i
(
i )
d
d
i P
1
E
1
E
P 1
E
#
+V
1 P
N1
X
p=1
p6=b; ( 1)
p N1
Y
k =1
k 6=b;
k 6=p 1
X
q;t= 1 2
6
4 N1
X
l=1
l6=E e
k l
q E
qt (V
1
0l V
l )b
l
t +e
k E
q E
qt (V
1
0E V
E P)b
E
t 3
7
5
1
X
n;m= 1 "
e pi
n E
nm (V
1
0i V
i )(
i )
m+1
d
E
d
i
1
e pE
n E
nm (V
1
0E V
E )(
E )
m+1 #
=0: (134)
TheoperatorsoftheoverlapequationsarenowfainglegF ofvertexU y
2
. Inordertoobtaintheoverlapidentities
forthisleg,wemustnowidentifytheoperatorsoflegE withtheonesof legF, whihareadjointoperators:
b E
t !b
F
t y
; b E
!b F
y
; E
! F
y
: (135)
First,asb F
and F
areonformaloperatorswithweights2and 1,respetively,wehave
b F
y
(
F
) = b
F
(
F ) =
d
d
F
F
2
b F
(
F )=(
F )
4
b F
(
F
); (136)
F
y
(
F
) =
F
(
F ) =
d
d
F
F
1
F
(
F ) (
F )
2
F
(
F
): (137)
Then, forb F
n and
F
n
,weobtain
F
n y
=
F
n
=
F
n
; (138)
b F
y
= b
F
b F
Then,wemustalsomakethehange
d
E
d
i
1
e pE
n (
E )
n+1
=
d
F
d
i
1
d
E
d
F
1
e pE
n (
E )
n+1
=
d
F
d
i
1 1
X
m= 1 e
pE
n E
nm V
1
E V
F
(
F )
m+1
: (140)
So,theoverlapequationsbeome
U
1 P
"
b i
(
i )
d
d
i P
1
E
2
P 1
E
4
b F
P 1
E
#
=0; (141)
U
1 P
"
i
(
i )+
d
d
i P
1
E
1
P 1
E
2
F
P 1
E
#
+V
1 P
N1
X
p=1
p6=b; ( 1)
p N1
Y
k =1
k 6=b;
k 6=p 1
X
q;t= 1 2
6
4 N1
X
l=1
l6=E e
k l
q E
qt V
1
0l V
l
b l
t +e
k E
q E
qt V
1
0E V
E P
b F
t 3
7
5
1
X
n;m= 1 "
e pi
n E
nm V
1
0i V
i
(
i )
m+1
d
F
d
i
1
e pE
n E
nm V
1
0E V
F
(
F )
m+1 #
=0: (142)
Wearethen faingtheonformaltransformationC
F
that takes
F into
0F
. Insertingthis transformationwe
obtain(Fig. 16):
Figure16. OverlapidentityforU
1 PC
F .
U
1 PC
F "
b i
(
i )
d
d
i P
1
E
2
P 1
E
4
dV 1
0F V
F P
1
E
d P 1
E 2
b F
V 1
0F V
F P
1
E
#
=0; (143)
U
1 PC
F "
i
(
i )+
d
d
i P
1
E
1
P 1
E
2
dV 1
0F V
F P
1
E
d P 1
E
1
F
V 1
0F V
F P
1
E
#
+V
1 PC
F N1
X
p=1
p6=b; ( 1)
p N1
Y
k =1
k 6=b;
k 6=p 1
X
q;t= 1 2
6
4 N1
X
l=1
l6=E e
k l
q E
qt V
1
0l V
l
b l
t e
k E
q E
qt V
1
0E V
E P V
1
F V
0F
b F
t 3
7
5
1
X
n;m= 1 "
e pi
n E
nm V
1
0i V
i
(
i )
m+1
d
0F
d
i
1
e pE
n E
nm V
1
0E V
0F
(
0F )
m+1 #
=0: (144)
WearefaingnowvertexV 0y
2
. Thisvertexsatisesthefollowingoverlapidentity[4℄:
1
X
s= 1 E
rs (V
0F )b
F
s V
0y
2
= V 0y
2 N2
X
i=1 1
X
s= 1 E
rs (V
0i )b
i
s
Usingequation(117),wehave
E
qt (V
1
0E V
E P V
1
F V
0F )b
F
t =
1
X
u= 1 E
qu (V
1
0E V
E P V
1
F )E
ut (V
0F )b
F
t
: (146)
All terms on b F
t
with t 2 get annihilated by the onjugate vauum j0i
F
, while we may use identity (145) to
substitutethetermsinb F
r
, r= 1;0;1. Doingthis,equation(144)beomes
U
1 PC
F "
i
(
i )+
d
d
i P
1
E
1
P 1
E
2
dV 1
0F V
F P
1
E
d P 1
E
1
F
V 1
0F V
F P
1
E
#
+V
1 PC
F N
1
X
p=1
p6=b; ( 1)
p N
1
Y
k =1
k 6=b;
k 6=p 1
X
q;t= 1 2
6
4 N
1
X
l=1
l6=E e
k l
q E
qt V
1
0l V
l
b l
t +
N
2
X
l=1
l6=F e
k E
q E
qt V
1
0E V
E P V
1
F V
0l
b l
t 3
7
5
1
X
n;m= 1 "
e pi
n E
nm V
1
0i V
i
(
i )
m+1
d
0F
d
i
1
e pE
n E
nm V
1
0E V
0F
(
0F )
m+1 #
=0: (147)
Equations(143)and(147)aretheoverlapidentities betweenlegsiandF.
In orderto obtainthe overlapsbetweenleg i of vertex U
1
and anarbitrary leg j of vertexU y
2
, we must now
performaylingtransformationthatwilltaketheoperatorsfromlegF tolegj. Theeetofthistransformation
on F
P 1
V 1
E V
i
i
is
V 1
j V
F
F
V 1
0F V
F P
1
E
V 1
F V
j =
dV 1
0j V
F P
1
E
dV 1
0F V
F P
1
E !
1
j
V 1
j V
F P
1
E
: (148)
Then, wemustalsowrite
d
0F
d
i
1 1
X
m= 1 e
pE
n E
nm V
1
0E V
0F
(
0F )
m+1
=
d
0j
d
i
1 1
X
m= 1 e
pE
n E
nm V
1
0E V
0j
(
0j )
m+1
: (149)
Doingthis,overlapequations(143,147)beome(Fig. 17)
Figure17. OverlapidentityforU1PCFV 0y
2 .
U
1 PC
F V
0y
2 "
b i
(
i )
d
d
i P
1
E
2
P 1
E
4
dV
1
0j V
F P
1
E
d P 1
E !
2
b F
V 1
0j V
F P
1
E
3
5
=0; (150)
U
1 PC
F V
0y
2 2
4
i
(
i )+
d
d
i P
1
E
1
P 1
E
2 dV
1
0j V
F P
1
E
d P 1
E !
1
F
V 1
0j V
F P
1
E
3
+V
1 PC
F V
0y
2 N1
X
p=1
p6=b; ( 1)
p N1
Y
k =1
k 6=b;
k 6=p 1
X
q;t= 1 2
6
4 N1
X
l=1
l6=E e
k l
q E
qt V
1
0l V
l
b l
t +
N2
X
l=1
l6=F e
k E
q E
qt V
1
0E V
E P V
1
F V
0l
b l
t 3
7
5
1
X
n;m= 1 "
e pi
n E
nm V
1
0i V
i
(
i )
m+1
d
0j
d
i
1
e pE
n E
nm V
1
0E V
0j
(
0j )
m+1 #
=0: (151)
TheoperatorsarenowfaingtheghoststhatsurroundvertexU 0y
2
(likeinequation(74)):
N
2
Y
k =1
k 6=d;g;h 0
B
N
2
X
l=1
l6=F 1
X
q= 1 e
k l
q b
l
q +
1
X
q= 1 e
k F
q b
F
q 1
C
A
: (152)
sothat we mustinsertthese ghosts intothe expressionsfor theoverlaps. Before doingthat, wemustnotie that
theextraghostsatingonvertexV 0y
2
haveat theirleftboththeonformaltransformationC
F
andthepropagator
P sothatwemustrstpassthemthroughin ordertoreahvertexU
1 :
PC
F N2
Y
k =1
k 6=d;g;h 0
B
N2
X
l=1
l6=F 1
X
q= 1 e
k l
q b
l
q +
1
X
q= 1 e
k F
q b
F
q 1
C
A
= N
2
Y
k =1
k 6=d;g;h 0
B
N
2
X
l=1
l6=F 1
X
q= 1 e
k l
q b
l
q 1
X
q;t= 1 e
k F
q E
qt (V
1
0F V
F P
1
)b F
t 1
C
A PC
F
: (153)
Then,identifying legsEand F,wehavethefollowingexpressionfortheghosts:
N2
Y
k =1
k 6=d;g;h 2
6
4 N2
X
l=1
l6=F 1
X
q= 1 e
k l
q b
l
q 1
X
q;t= 1 e
k F
q E
qt V
1
0F V
F P
1
b E
t 3
7
5
P : (154)
WemaynowpassitthroughtheonformaltransformationC
1
,obtaining
N2
Y
k =1
k 6=d;g;h 2
6
4 N2
X
l=1
l6=F 1
X
q= 1 e
k l
q b
l
q 1
X
q;t= 1 e
k F
q E
qt V
1
0F V
F P
1
V 1
E V
0E
b E
t 3
7
5
P : (155)
This isnowfaingvertexV 0
1
,whihsatisesthefollowingoverlapidentity[4℄:
V 0
1 1
X
s= 1 E
rs (V
0E )b
E
s = V
0
1 N1
X
i=1
i6=E 1
X
s= 1 E
rs (V
0i )b
i
s
; r= 1;0;1: (156)
Usingthisidentity,wemaythenwritetheextraghostsas
N
2
Y
k =1
k 6=d;g;h 2
6
4 N
2
X
l=1
l6=F 1
X
q= 1 e
k l
q b
l
q +
N
1
X
l=1
l6=E 1
X
q;t= 1 e
k F
q E
qt V
1
0F V
F P
1
V 1
E V
0l
b l
t 3
7
5
: (157)
PassingitbakthroughC
1
wethenhave
N
2
Y
k =1 2
6
4 N
2
X
l=1 1
X
q= 1 e
k l
q b
l
q +
N
1
X
l=1 1
X
q;t= 1 e
k F
q E
qt V
1
0F V
F P
1
V 1
E V
l
b l
t 3
7
5
Wenowinserttheseghostsintoexpressions(150)and(151). Wedosobymultiplyingthemby(158)andpassing
itthroughthersttermoftheoverlaps. Whatweobtainis(Fig. 18)
Figure18. OverlapidentityforU1PCFU 0y
2 .
U
1 PC
F U
0y
2 "
b i
(
i )
d
d
i P
1
E
2
P 1
E
4
dV
1
0j V
F P
1
E
d P 1
E !
2
b F
V 1
0j V
F P
1
E
3
5
=0; (159)
U
1 PC
F U
0y
2 2
4
i
(
i )+
d
d
i P
1
E
1
P 1
E
2 dV
1
0j V
F P
1
E
d P 1
E !
1
F
V 1
0j V
F P
1
E
3
5
+U
1 PC
F V
0y
2 N
2
X
p=1 ( 1)
p N
2
Y
k =1
k 6=d;g;h
k 6=p 2
6
4 N
2
X
l=1
l6=F 1
X
q= 1 e
k l
q b
l
q +
N
1
X
l=1
l6=E 1
X
q;t= 1 e
k F
q E
qt V
1
0F V
F P
1
V 1
E V
l
b l
t 3
7
5
1
X
n= 1 "
1
X
m= 1 e
pF
n E
nm V
1
0F V
F P
1
V 1
E V
i
(
i )
m+1
+
d
d
i P
1
E
1
P 1
E
2 dV
1
0j V
F P
1
E
d P 1
E !
2
e pj
n V
1
0j V
F P
1
E
n+1 3
5
+V
1 PC
F V
0y
2 N
1
X
p=1
p6=b; ( 1)
p N
1
Y
k =1
k 6=b;
k 6=p 1
X
q;t= 1 2
6
4 N
1
X
l=1
l6=E e
k l
q E
qt (V
1
0l V
l )b
l
t +
N
2
X
l=1
l6=F e
k E
q E
qt V
1
0E V
E P V
1
F V
0l
b l
t 3
7
5
1
X
n;m= 1 "
e pi
n E
nm (V
1
0i V
i )(
i )
m+1
d
0j
d
i
1
e pE
n E
nm (V
1
0E V
E )(
0j )
m+1 #
N2
Y
k =1
k 6=d;g;h 2
6
4 N2
X
l=1
l6=F 1
X
q= 1 e
k l
q b
l
q +
N1
X
l=1
l6=E 1
X
q;t= 1 e
k F
q E
qt V
1
0F V
F P
1
V 1
E V
l
b l
t 3
7
5
=0: (160)
We are then faing the last term of this omposite vertex: the onformal transformation C
2
on vertex V 0y
2 .
Insertingitintoequations(159)and(160), weobtain(Fig. 19)
Figure19. OverlapidentityforU1PU y
U 1 PU y 2 " b i ( i ) d d i P 1 E 2 P 1 E 4 dV 1 j V F P 1 E d P 1 E ! 2 b F V 1 j V F P 1 E 3 5
=0; (161)
U 1 PU y 2 2 4 i ( i )+ d d i P 1 E 1 P 1 E 2 dV 1 j V F P 1 E d P 1 E ! 1 F V 1 j V F P 1 E 3 5 +U 1 PV y 2 N2 X p=1 ( 1) p N2 Y k =1 k 6=d;g;h k 6=p 1 X q;t= 1 2 6 4 N2 X l=1 l6=F e k l q E qt (V 1 0l V l )b l t + N1 X l=1 l6=E e k F q E qt V 1 0F V F P 1 V 1 E V l b l t 3 7 5 1 X n= 1 " 1 X m= 1 e pF n E nm V 1 0F V F P 1 V 1 E V i ( i ) m+1 + d d i P 1 E 1 P 1 E 2 dV 1 j V F P 1 E d P 1 E ! 2 e pj n V 1 j V F P 1 E n+1 3 5 +V 1 PV y 2 N1 X p=1 p6=b; ( 1) p N1 Y k =1 k 6=b; k 6=p 1 X q;t= 1 2 6 4 N1 X l=1 l6=E e k l q E qt (V 1 0l V l )b l t + N2 X l=1 l6=F e k E q E qt V 1 0E V E P V 1 F V l b l t 3 7 5 1 X n;m= 1 " e pi n E nm (V 1 0i V i )( i ) m+1 d j d i 1 e pE n E nm (V 1 0E V E )( j ) m+1 # N2 Y k =1 k 6=d;g;h 1 X q;t= 1 2 6 4 N2 X l=1 l6=F e k l q E qt (V 1 0l V l )b l t + N1 X l=1 l6=E e k F q E qt V 1 0F V F P 1 V 1 E V l b l t 3 7 5
=0 (162)
wherewehavealledC
F U 0y 2 C 1 2 U y 2 andC F V 0y 2 C 1 2 V y 2 .
WemustnowextrattheghostsfromvertexU
1
in theseondtermofequation(162):
U
1
P = V
1 N1 Y k =1 k 6=b; 1 X q;t= 1 2 6 4 N1 X l=1 l6=E e k l q E qt (V 1 0l V l )b l t +e k E q E qt (V 1 0E V E )b E t 3 7 5 P = V 1 P N 1 Y k =1 k 6=b; 1 X q;t= 1 2 6 4 N 1 X l=1 l6=E e k l q E qt (V 1 0l V l )b l t +e k E q E qt (V 1 0E V E P)b E t 3 7 5 : (163) Identifying b E t withb F t
andpassingnowtheseghoststhroughtheonformaltransformationC
F
,weobtain
U 1 PC F =V 1 PC F N1 Y k =1 k 6=b; 1 X q;t= 1 2 6 4 N1 X l=1 l6=E e k l q E qt (V 1 0l V l )b l t e k E q E qt (V 1 0E V E P V 1 F V 0F )b F t 3 7 5 : (164)
Usingnowoverlapidentities (145)forvertexV y
2
andinsertingtheonformaltransformationC
2
,wethenobtain
Substituting (165)intoequation(162)wethenobtaintheoverlapidentitiesbetweenlegsiandj: U " b i ( i ) d d i P 1 V 1 E V i i 2 P 1 V 1 E V i i 4 d d i P 1 V 1 E V i i 2 b j V 1 j V F P 1 V 1 E V i i #
=0; (166)
U " i ( i )+ d d i P 1 V 1 E V i i 1 P 1 V 1 E V i i 2 d d i P 1 V 1 E V i i 1 j V 1 j V F P 1 V 1 E V i i # +V N 1 Y k =1 k 6=b; k 6=p 1 X q;t= 1 2 6 4 N 1 X l=1 l6=E e k l q E qt (V 1 0l V l )b l t + N 2 X l=1 l6=F e k E q E qt V 1 0E V E P V 1 F V l b l t 3 7 5 N 2 X p=1 p6=d;g;h 1 p N 2 Y k =1 k 6=d;g;h k 6=p 1 X q;t= 1 2 6 4 N 1 X l=1 l6=E e k F q E qt V 1 0F V F P 1 V 1 E V l b l t + N 2 X l=1 l6=F e k l q E qt (V 1 0l V l )b l t 3 7 5 1 X n;m= 1 " e pF q E nm V 1 0F V F P 1 V 1 E V i ( i ) m+1 + d d i P 1 V 1 E V i i 1 P 1 V 1 E V i i 2 dV 1 j V F P 1 E d P 1 E ! 2 e pj n E nm (V 1 0j V j ) V 1 j V F P 1 V 1 E V i i m+1 3 5 +V N1 X p=1 p6=b; ( 1) p N1 Y k =1 k 6=b; k 6=p 1 X q;t= 1 2 6 4 N1 X l=1 l6=E e k l q E qt (V 1 0l V l )b l t + N2 X l=1 l6=F e k E q E qt V 1 0E V E P V 1 F V l b l t 3 7 5 1 X n;m= 1 " e pi n E nm (V 1 0i V i )( i ) m+1 d j d i 1 e pE n E nm V 1 0E V j ( j ) n+1 # N2 Y k =1 k 6=d;g;h k 6=p 1 X q;t= 1 2 6 4 N1 X l=1 l6=E e k F q E qt V 1 0F V F P 1 V 1 E V l b l t + N2 X l=1 l6=F e k l q E qt (V 1 0l V l )b l t 3 7 5
=0: (167)
Ifwenowimposethat thesearetheorretoverlapequationsbetweenlegs iandj oftheompositevertexwe
thenmusthave:
V 1 j V F P 1 E = j (168)
what xesthepropagatoras
P =V 1
E V
F
(169)
whihis thesameform ofthepropagatorforthebosonipart,butnowwiththeylingsdened ontheomplete
generatorsL i
n
. Theoverlapequationsnowread
U " b i ( i ) d j d i 2 b j ( j ) #
=0; (170)